Controllable Manipulation of Wi-Fi Signals Using Tunable Metasurface
DOI: 10.12000/JR21012 cstr: 32380.14.JR21012
-
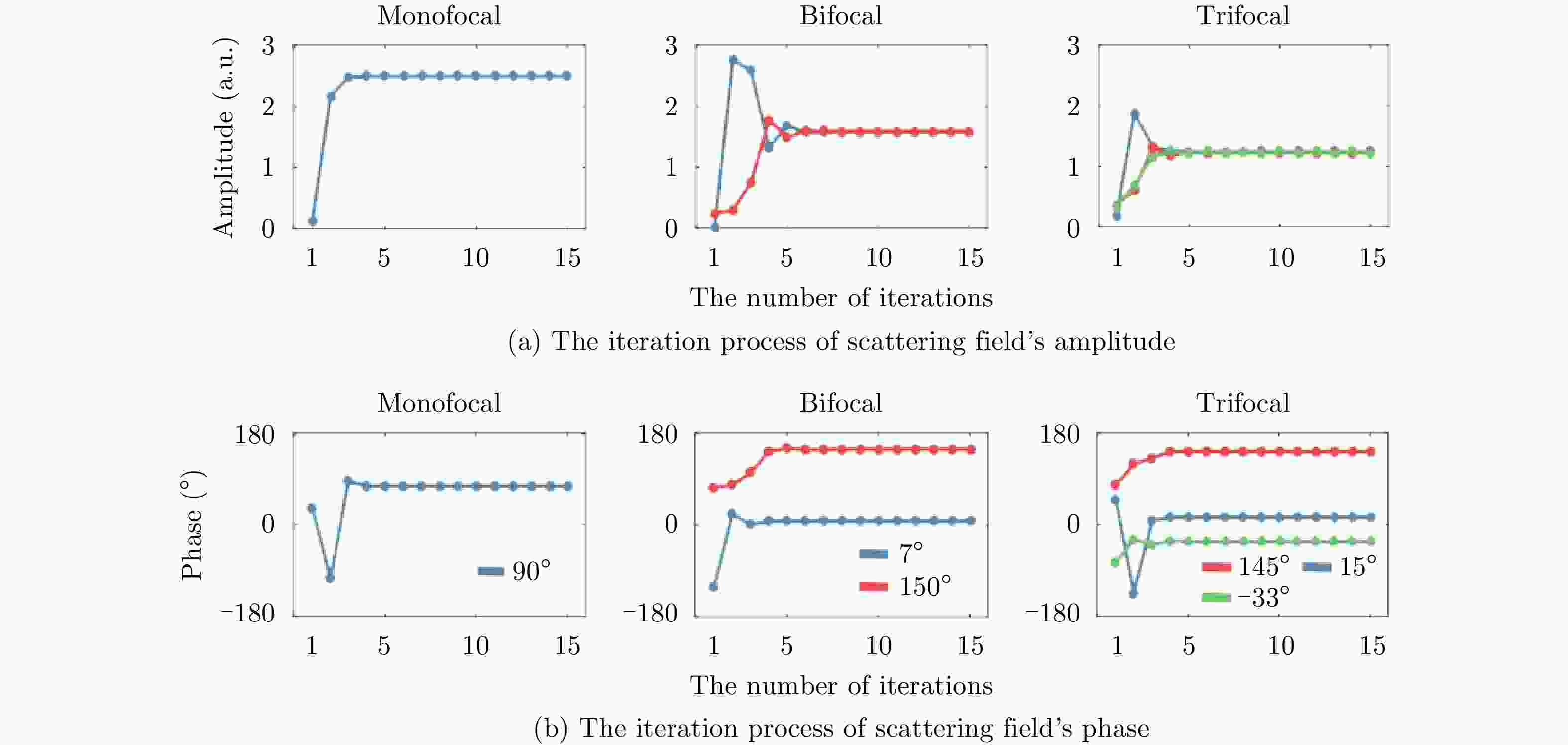
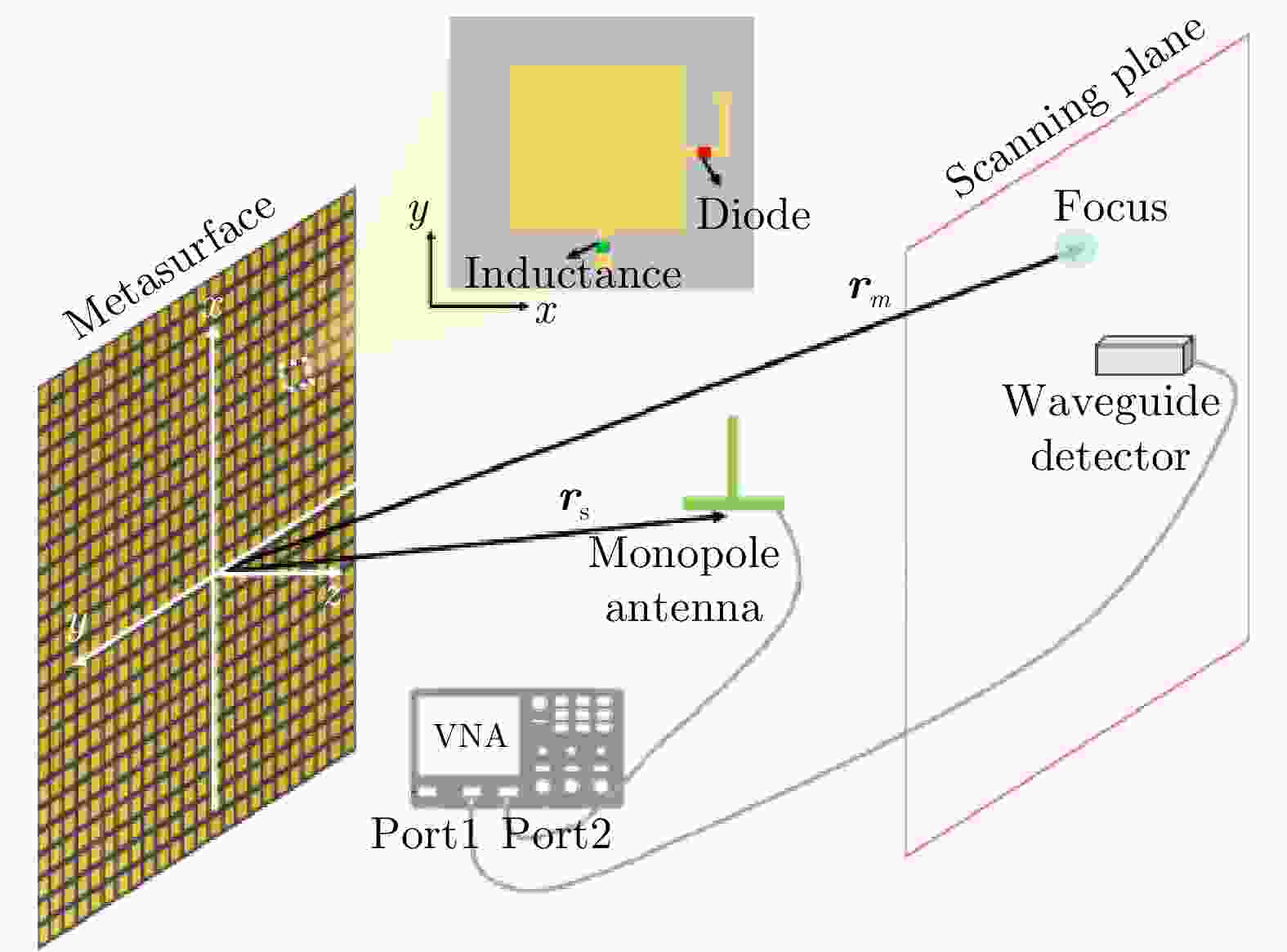
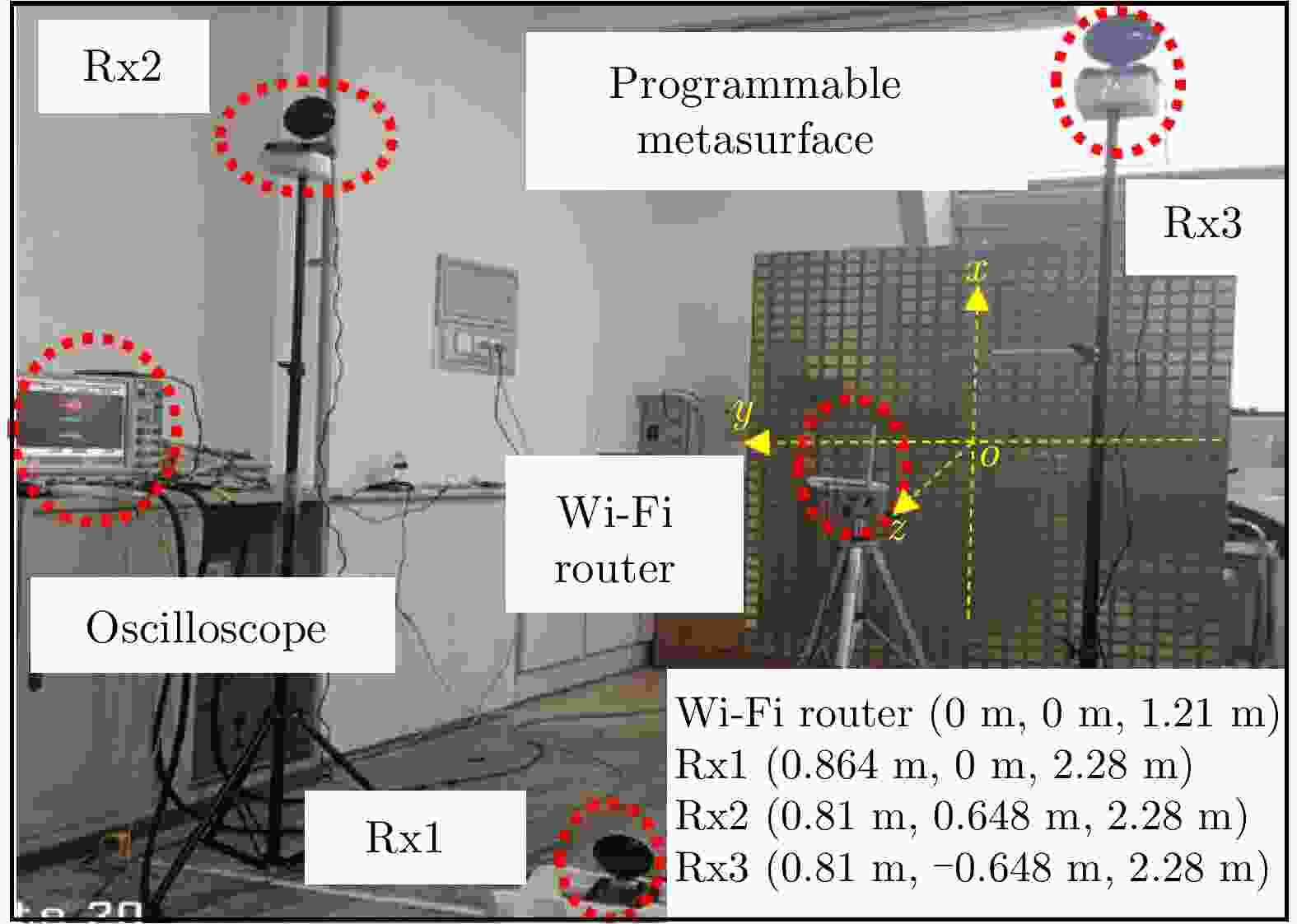
摘要: 可编程超表面是由可调谐的单元在二维平面上组成的平面阵列,具有任意、动态操控电磁波波前的能力,是微波领域前沿研究方向之一。尽管目前基于可编程超表面的电磁调控研究已取得丰硕进展,但是现有技术都需要采用专用发射源主动馈电超表面,这不仅增加了实际系统的复杂性和成本,而且在一定程度上限制了这些技术在现实环境中的应用。因此,该文提出了一种利用可编程超表面灵活调控周围Wi-Fi信号的方法,并通过理论和实验证明了其对Wi-Fi信号的优越调控性能。首先,该文首次提出一种基于可编程超表面散射模型的高效优化算法CWGS,该算法可以重新设计可编程超表面散射场的复振幅分布,从而实现指定位置处的Wi-Fi信号显著增强。其次,该文制作了一款工作频率为2.4 GHz的大规模可编程超表面,并基于该超表面实验验证了优化算法应用于Wi-Fi信号增强调控的可行性和有效性。理论和实验结果均证明,可编程超表面可以在多个位置处实现Wi-Fi信号的动态增强。实验结果表明,经可编程超表面调控后的Wi-Fi信号强度提高了23.5 dB。该文提出的方法提高了可编程超表面在实际应用中的可用性和实用性,有望为无线通信、未来智能家居等领域开辟新的道路。
-
关键词:
- 商用Wi-Fi 信号 /
- 可编码超表面 /
- 空间能量分配
Abstract: In this paper, we propose the utilization of a programmable metasurface for flexibly manipulating ambient Wi-Fi signals. First, we propose a new and efficient optimization algorithm CWGS (Complex Weighted Gerchberg-Saxton), which is based on an electromagnetic scattering model of the metasurface. The proposed algorithm quickly redesigns the complex amplitude distribution of the Wi-Fi field bounced off the programmable metasurface to enhance the Wi-Fi signals at desired locations significantly. Second, we fabricated a large-scale programmable metasurface that operates at the 2.4 GHz frequency band. We conducted several experiments using the fabricated metasurface to verify the proposed optimization algorithm’s feasibility and effectiveness. Both the theoretical and experimental results show that the programmable metasurface can dynamically boost Wi-Fi signals at multiple locations. Besides, we experimentally verified that using the developed strategy could improve the Wi-Fi signals by 23.5 dB. The results of our work improve the usability and practicality of the programmable metasurface in real-world applications and pave the way for wireless communications, future smart homes, and other applications. -
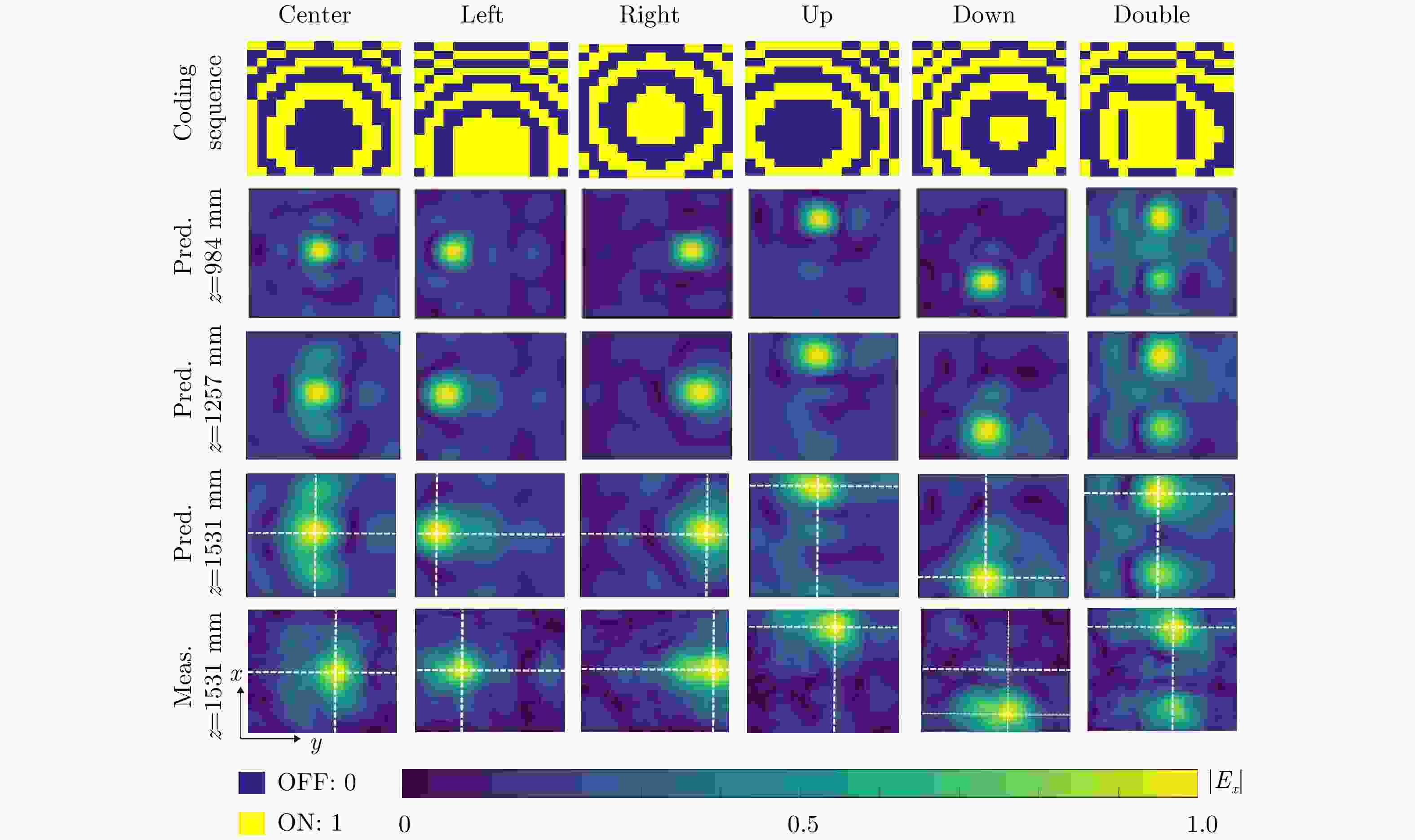
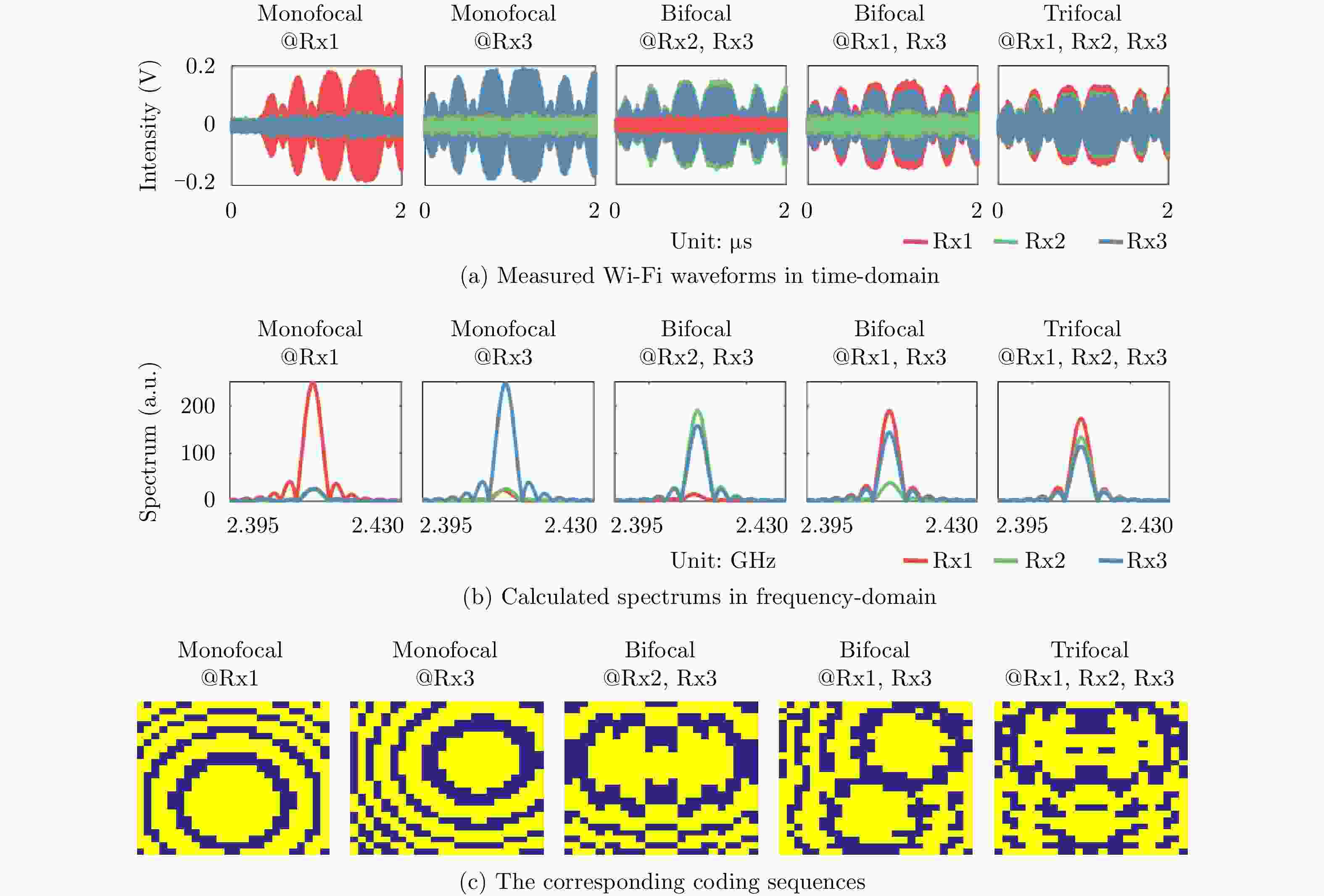
Figure 4. Results comparison between prediction and measurement
The first row are the coding sequences. The second to fourth rows are the normalized spatial intensity distributions predicted respectively at z=0.984 m, z=1.257 m, and z=1.531 m using the proposed method. The fifth row are the measured normalized spatial intensity distributions at z=1.531 m using the near-field scanning technology
Table 1. The focus efficiency for six different cases
Cases
(dB)Center
(%)Left
(%)Right
(%)Up
(%)Down
(%)Double
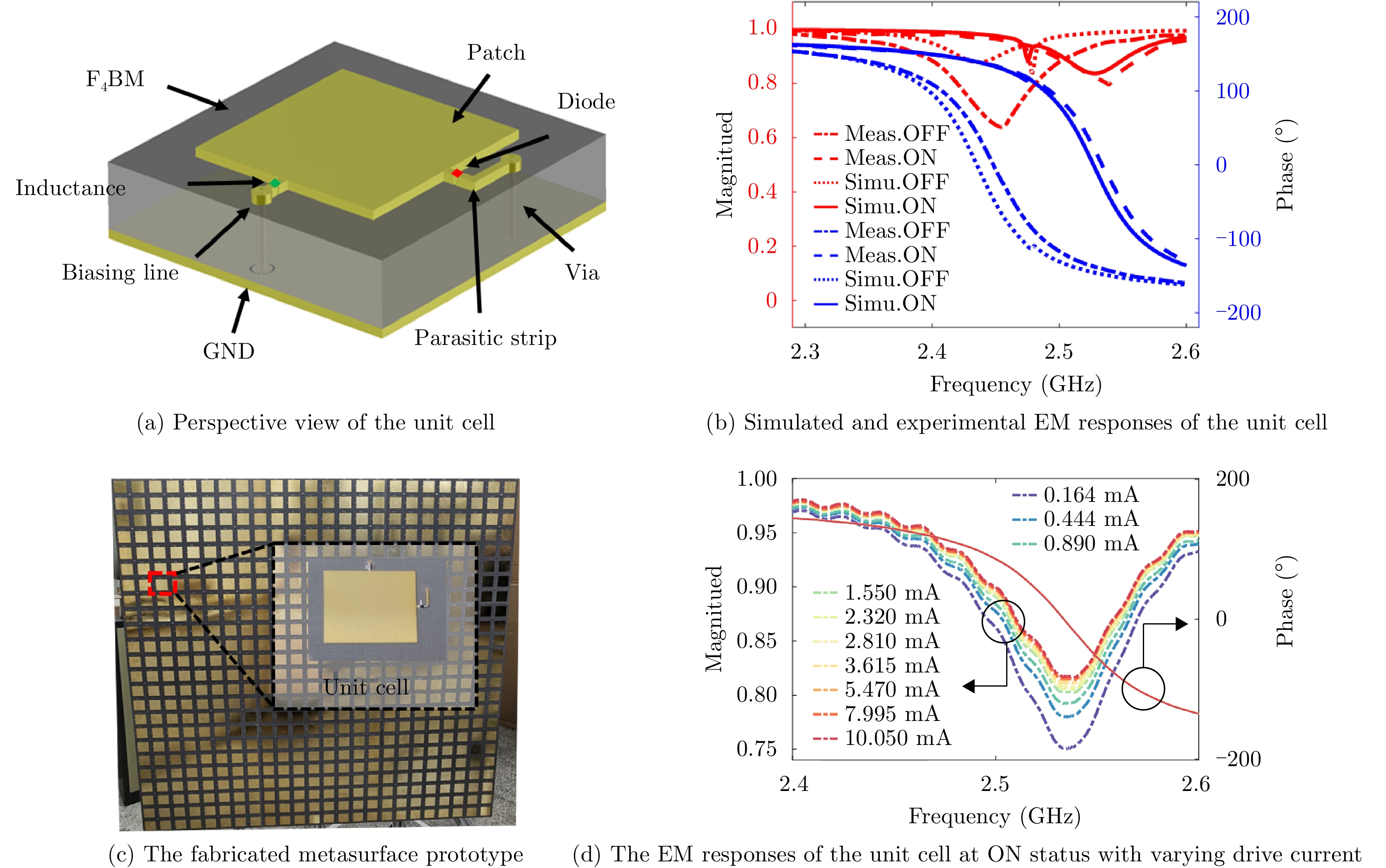
(%)–3 25.36 30.73 40.24 28.51 35.27 21.27 –6 37.42 45.19 59.32 41.81 51.96 38.65 Table 2. Comparing with the existing works dealing with EM waves manipulation using metasurface
Ref. f0 (GHz) Source type Working mode of metasurface Optimization
goal of algorithmWorking
regionThe shape
of energy
allocationReconfig-urability Maximum
focusing
efficiency[6] 6.9 Dedicated source Active Field’s amplitude pattern Near-field Point-like YES – [7] 10 Dedicated source Active Field’s amplitude pattern Near-field Point-like NO 57.8% [8] 5.75 Dedicated source Active Field’s amplitude pattern Near-field Point-like YES – [9] 10 Dedicated source Active Field’s amplitude pattern Near-field Point-like YES – [10] 20 Dedicated source Active Field’s amplitude pattern Near-field Point-like NO 52.3% [11] 10 Dedicated source Active Field’s amplitude pattern Near-field Point-like NO – [12] 5.8 Dedicated source Active Field’s amplitude pattern Near-field Point-like NO – [31] 14.3 Dedicated source Active Field’s amplitude pattern Far-field Single beam YES – [23] 5.8 Dedicated source Active Field’s amplitude pattern Near-field Point-like NO – [24] 2.3 Dedicated source Active Field’s amplitude pattern Far-field Single beam YES – [25] 10 Dedicated source Active Field’s amplitude pattern Far-field Single beam YES Proposed 2.4 Commodity wireless device Passive Field’s complex amplitude pattern Not limited Not limited YES 59.32% -
[1] YANG Huanhuan, CAO Xiangyu, YANG Fan, et al. A programmable metasurface with dynamic polarization, scattering and focusing control[J]. Scientific Reports, 2016, 6: 35692. doi: 10.1038/srep35692 [2] LI Lianlin, CUI Tiejun, JI Wei, et al. Electromagnetic reprogrammable coding-metasurface holograms[J]. Nature Communications, 2017, 8(1): 197. doi: 10.1038/s41467-017-00164-9 [3] LAROUCHE S, TSAI Y J, TYLER T, et al. Infrared metamaterial phase holograms[J]. Nature Materials, 2012, 11(5): 450–454. doi: 10.1038/nmat3278 [4] LI Lianlin, RUAN Hengxin, LIU Che, et al. Machine-learning reprogrammable metasurface imager[J]. Nature Communications, 2019, 10(1): 1082. doi: 10.1038/s41467-019-09103-2 [5] LI Lianlin and CUI Tiejun. Information metamaterials – from effective media to real-time information processing systems[J]. Nanophotonics, 2019, 8(5): 703–724. doi: 10.1515/nanoph-2019-0006 [6] CHEN Ke, FENG Yijun, MONTICONE F, et al. A reconfigurable active huygens’ metalens[J]. Advanced Materials, 2017, 29(17): 1606422. doi: 10.1002/adma.201606422 [7] WANG Yue, GUAN Chunsheng, DING Xumin, et al. Multi-focus hologram utilizing Pancharatnam-Berry phase elements based metamirror[J]. Optics Letters, 2019, 44(9): 2189–2192. doi: 10.1364/OL.44.002189 [8] WANG Zehao, LIAO Dashuang, ZHANG Ting, et al. Metasurface-based focus-tunable mirror[J]. Optics Express, 2019, 27(21): 30332–30339. doi: 10.1364/OE.27.030332 [9] ZHANG Kuang, YUAN Yueyi, DING Xumin, et al. High-efficiency metalenses with switchable functionalities in microwave region[J]. ACS Applied Materials & Interfaces, 2019, 11(31): 28423–28430. [10] GOWDA V R, IMANI M F, SLEASMAN T, et al. Focusing microwaves in the fresnel zone with a cavity-backed holographic metasurface[J]. IEEE Access, 2018, 6: 12815–12824. doi: 10.1109/ACCESS.2018.2802379 [11] ZHANG Pei, LI Long, ZHANG Xuanming, et al. Design, measurement and analysis of near-field focusing reflective metasurface for dual-polarization and multi-focus wireless power transfer[J]. IEEE Access, 2019, 7: 110387–110399. doi: 10.1109/ACCESS.2019.2934135 [12] YU Shixing, LIU Haixia, and LI Long. Design of near-field focused metasurface for high-efficient wireless power transfer with multifocus characteristics[J]. IEEE Transactions on Industrial Electronics, 2019, 66(5): 3993–4002. doi: 10.1109/TIE.2018.2815991 [13] ZHAO Jie, YANG Xi, DAI Junyan, et al. Programmable time-domain digital-coding metasurface for non-linear harmonic manipulation and new wireless communication systems[J]. National Science Review, 2019, 6(2): 231–238. doi: 10.1093/nsr/nwy135 [14] ZHANG Xu, GRAJAL J, VAZQUEZ-ROY J L, et al. Two-dimensional MoS2-enabled flexible rectenna for Wi-Fi-band wireless energy harvesting[J]. Nature, 2019, 566(7744): 368–372. doi: 10.1038/s41586-019-0892-1 [15] WANG Guanhua, ZOU Yongpan, ZHOU Zimu, et al. We can hear you with Wi-Fi![J]. IEEE Transactions on Mobile Computing, 2016, 15(11): 2907–2920. doi: 10.1109/TMC.2016.2517630 [16] ALI K, LIU A X, WANG Wei, et al. Keystroke recognition using WiFi signals[C]. The 21st Annual International Conference on Mobile Computing and Networking, Paris, France, 2015: 90–102. [17] WU Xuangou, CHU Zhaobin, YANG Panlong, et al. TW-see: Human activity recognition through the wall with commodity Wi-Fi devices[J]. IEEE Transactions on Vehicular Technology, 2019, 68(1): 306–319. doi: 10.1109/TVT.2018.2878754 [18] XU Qinyi, CHEN Yan, WANG Beibei, et al. Radio biometrics: Human recognition through a wall[J]. IEEE Transactions on Information Forensics and Security, 2017, 12(5): 1141–1155. doi: 10.1109/TIFS.2016.2647224 [19] HOLL P M and REINHARD F. Holography of Wi-Fi radiation[J]. Physical Review Letters, 2017, 118(18): 183901. doi: 10.1103/PhysRevLett.118.183901 [20] ZHONG Wei, HE W K, WANG Longgang, et al. Through-the-wall imaging using Wi-Fi signals[C]. The 2018 12th International Symposium on Antennas, Propagation and EM Theory, Hangzhou, China, 2018: 1–3. [21] LI Lianlin, SHUANG Ya, MA Qian, et al. Intelligent metasurface imager and recognizer[J]. Light: Science & Applications, 2019, 8: 97. [22] TANG Wankai, DAI Junyan, CHEN Mingzheng, et al. Programmable metasurface-based RF chain-free 8PSK wireless transmitter[J]. Electronics Letters, 2019, 55(7): 417–420. doi: 10.1049/el.2019.0400 [23] GOWDA V R, YURDUSEVEN O, LIPWORTH G, et al. Wireless power transfer in the radiative near field[J]. IEEE Antennas and Wireless Propagation Letters, 2016, 15: 1865–1868. doi: 10.1109/LAWP.2016.2542138 [24] DAI Linglong, WANG Bichai, WANG Min, et al. Reconfigurable intelligent surface-based wireless communications: Antenna design, prototyping, and experimental results[J]. IEEE Access, 2020, 8: 45913–45923. doi: 10.1109/ACCESS.2020.2977772 [25] RATNI B, DE LUSTRAC A, PIAU G P, et al. Reconfigurable meta-mirror for wavefronts control: Applications to microwave antennas[J]. Optics Express, 2018, 26(3): 2613–2624. doi: 10.1364/OE.26.002613 [26] XU Hexiu, SUN Shulin, TANG Shiwei, et al. Dynamical control on helicity of electromagnetic waves by tunable metasurfaces[J]. Scientific Reports, 2016, 6: 27503. doi: 10.1038/srep27503 [27] WANG Di, YIN Lizheng, HUANG Tiejun, et al. Design of a 1 bit broadband space-time-coding digital metasurface element[J]. IEEE Antennas and Wireless Propagation Letters, 2020, 19(4): 611–615. doi: 10.1109/LAWP.2020.2973424 [28] YANG Xue, XU Shenheng, YANG Fan, et al. A novel 2-bit reconfigurable reflectarray element for both linear and circular polarizations[C]. 2017 IEEE International Symposium on Antennas and Propagation & USNC/URSI National Radio Science Meeting, San Diego, USA, 2017: 2083–2084. [29] KAMODA H, IWASAKI T, TSUMOCHI J, et al. 60-GHz electronically reconfigurable large reflectarray using single-bit phase shifters[J]. IEEE Transactions on Antennas and Propagation, 2011, 59(7): 2524–2531. doi: 10.1109/TAP.2011.2152338 [30] LI Long, YANG Yang, and LIANG Changhong. A wide-angle polarization-insensitive ultra-thin metamaterial absorber with three resonant modes[J]. Journal of Applied Physics, 2011, 110(6): 063702. doi: 10.1063/1.3638118 [31] YANG Huanhuan, YANG Fan, CAO Xiangyu, et al. A 1600-element dual-frequency electronically reconfigurable reflectarray at X/Ku-Band[J]. IEEE Transactions on Antennas and Propagation, 2017, 65(6): 3024–3032. doi: 10.1109/TAP.2017.2694703 [32] WANG Ke, ZHAO Jie, CHENG Qiang, et al. Broadband and broad-angle low-scattering metasurface based on hybrid optimization algorithm[J]. Scientific Reports, 2014, 4: 5935. [33] GUAN Chunsheng, WANG Zhuochao, DING Xumin, et al. Coding Huygens’ metasurface for enhanced quality holographic imaging[J]. Optics Express, 2019, 27(5): 7108–7119. doi: 10.1364/OE.27.007108 -



 作者中心
作者中心 专家审稿
专家审稿 责编办公
责编办公 编辑办公
编辑办公
 下载:
下载: