面向近垂直场景的RD图多任务运动信息提取方法

刘子源; 王绍平; 何屹廷; 谷源涛

doi:10.12000/JR25259

面向近垂直场景的RD图多任务运动信息提取方法

DOI: 10.12000/JR25259 CSTR: 32380.14.JR25259

1.
清华大学电子工程系北京 100084
2.
清华大学深圳国际研究生院深圳 518055

基金项目: 国家自然科学基金(U2230201)

详细信息

作者简介:
刘子源，博士生，主要研究方向为SAR图像处理与雷达信号处理

王绍平，硕士，主要研究方向为电子与通信

何屹廷，硕士生，主要研究方向为雷达信号处理

谷源涛，博士，教授。主要研究方向为信号处理

通讯作者:
谷源涛 gyt@tsinghua.edu.cn

责任主编：丁一鹏 Corresponding Editor: DING Yipeng

中图分类号: TN957.52
计量
- 文章访问数:
- HTML全文浏览量:
- PDF下载量:
- 被引次数: 0
出版历程
- 收稿日期: 2025-12-01
- 修回日期: 2026-01-11

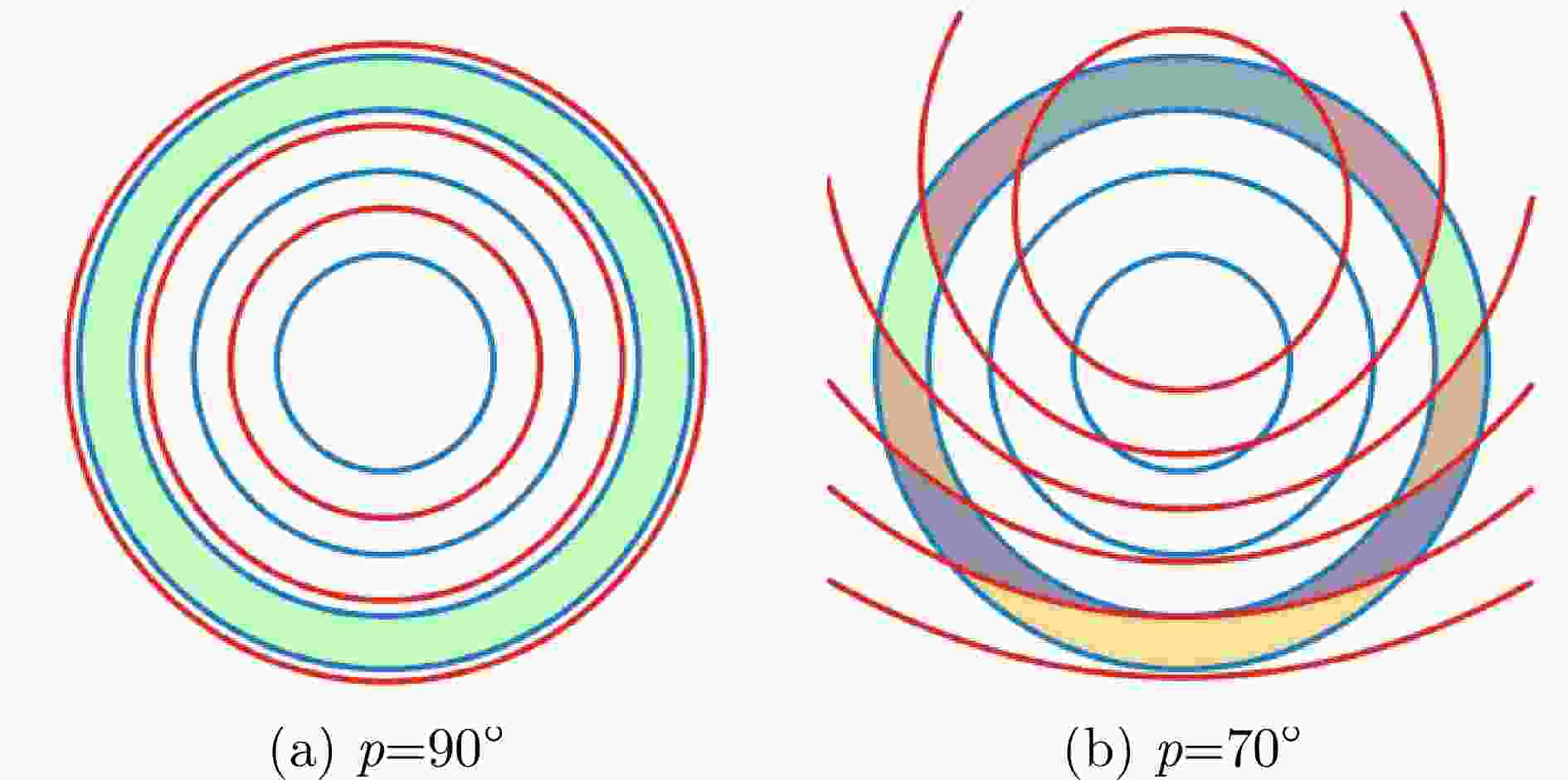
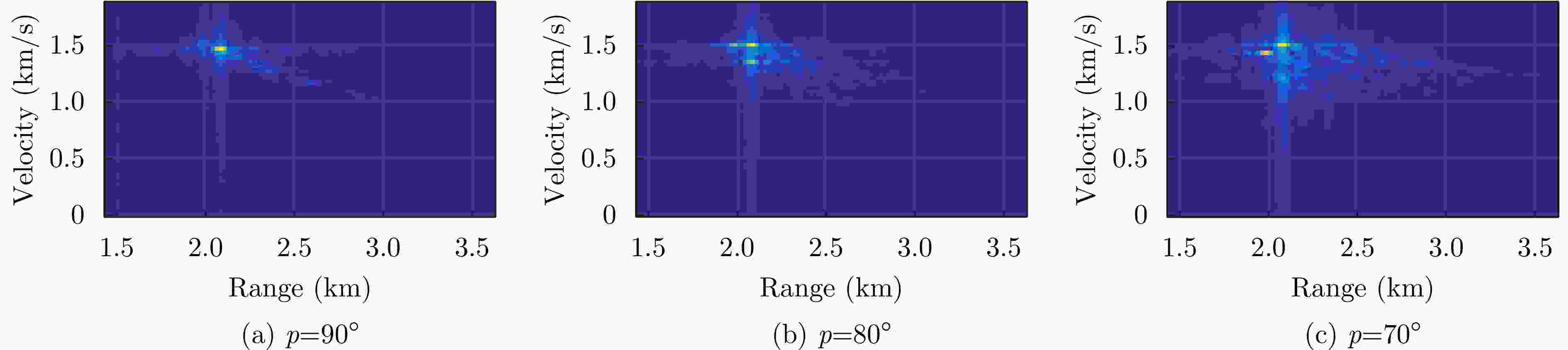
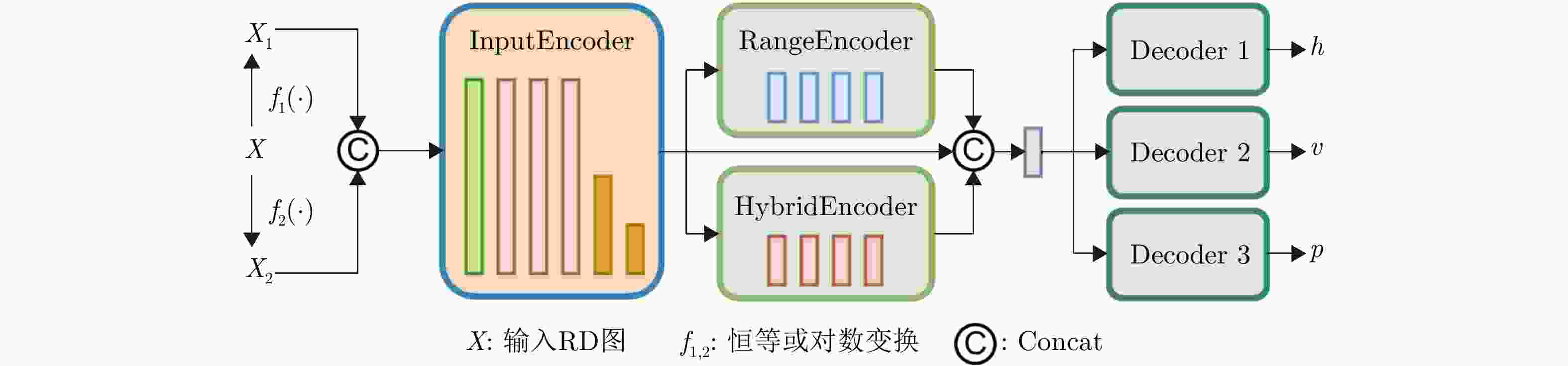
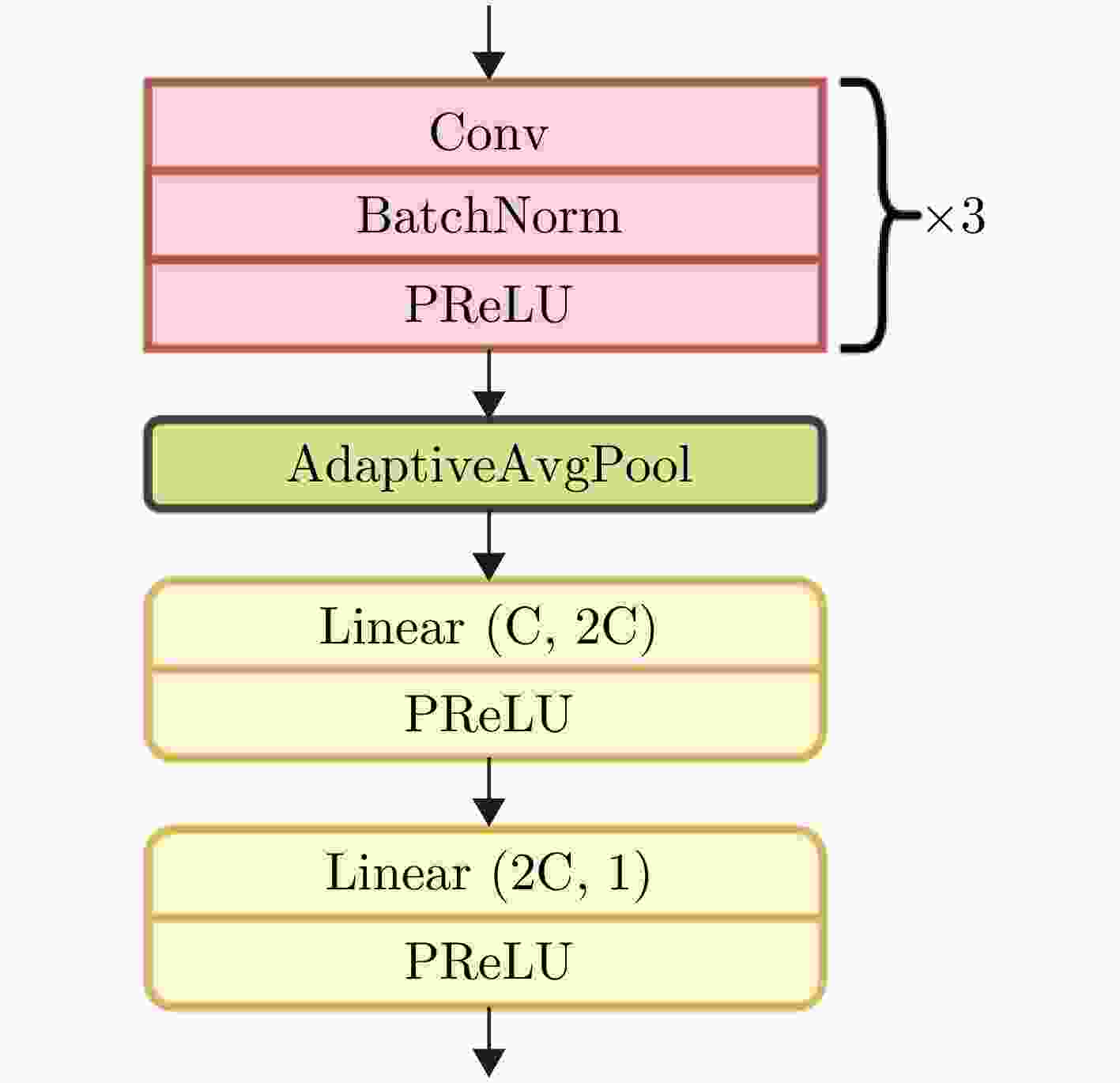
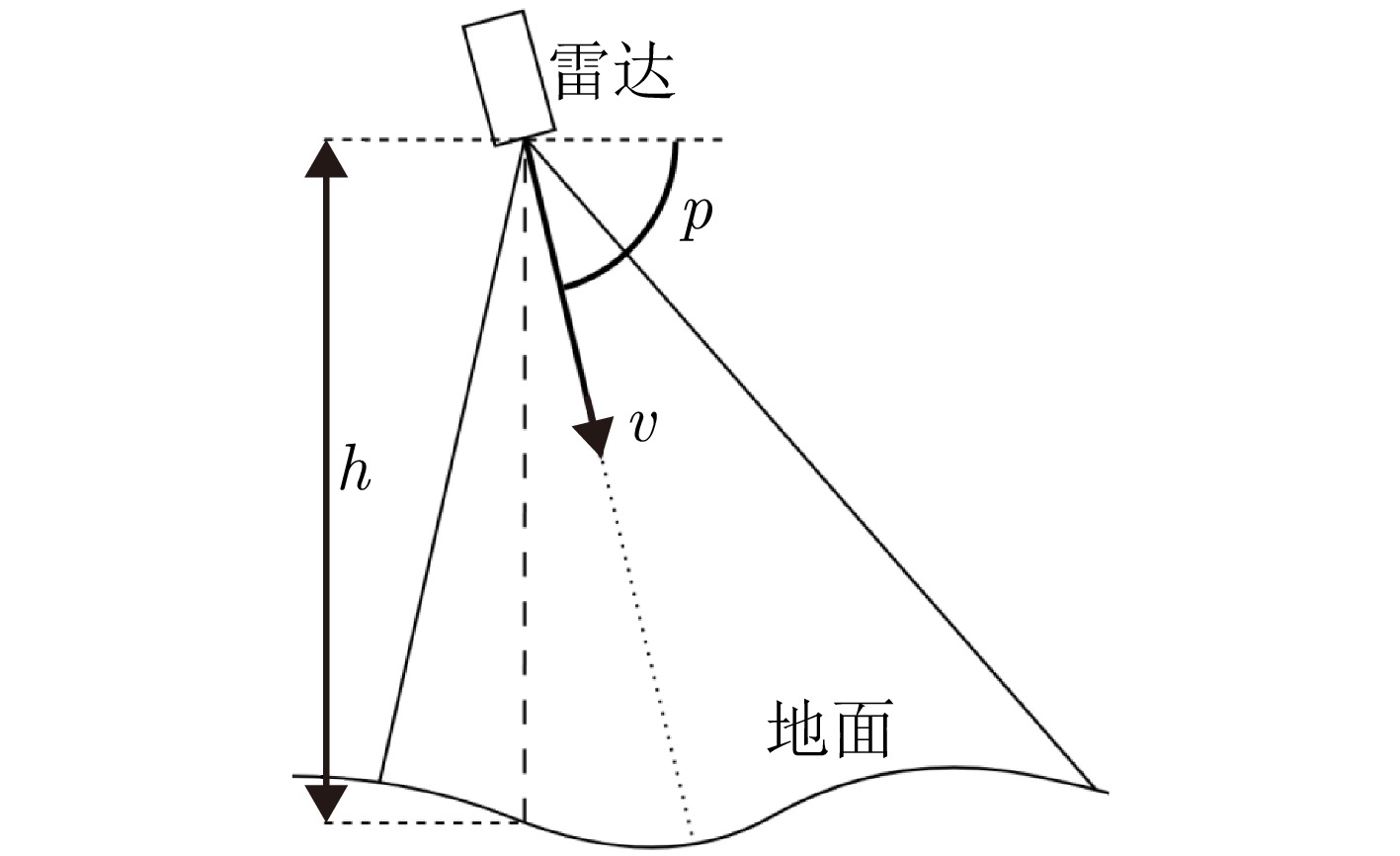
A MultiTask Motion Information Extraction Method Based on Range-Doppler Maps for Near-vertical Scenarios

1.
Department of Electronic Engineering, Tsinghua University, Beijing 100084, China
2.
Tsinghua Shenzhen International Graduate School, Shenzhen 518055, China

Funds: The National Natural Science Foundation of China (U2230201)

More Information

Corresponding author: GU Yuantao, gyt@tsinghua.edu.cn

摘要

摘要: 脉冲多普勒雷达具备全天候工作能力，可通过距离-多普勒(RD)图像同时获取目标的距离与速度信息。在近垂直飞行场景下，RD图的几何结构中蕴含飞行平台的高度、速度及俯仰角等关键运动参数，但这些参数在 RD 域中呈现明显耦合，传统信号处理方法在复杂地形和近垂直入射条件下难以实现有效解耦。近年来，深度学习在运动信息感知领域展现出显著优势，但多任务学习在该场景下仍难以同时满足实时性与高精度要求。为此，本文提出一种新型的网络结构——RDMFNet，通过共享编码器与并行解码器实现多表征信息融合，并采用两阶段渐进式训练策略，以提高参数估计的精度。实验表明，RDMFNet在高度、速度及俯仰角估计上的误差分别降低至14.447 m, 4.635 m/s和0.755°，展现了其在高精度实时感知中的优势。
- 运动参数估计 /
- 近垂直场景 /
- 距离-多普勒图 /
- 多任务学习 /
- 深度学习
Abstract: Pulse Doppler radar provides all-weather operational capability and enables simultaneous acquisition of target range and velocity through Range-Doppler (RD) maps. In near-vertical flight scenarios, the geometric structure of RD maps implicitly encodes key platform motion parameters, including altitude, velocity, and pitch angle. However, these parameters are strongly coupled in the RD domain, making effective decoupling difficult for traditional signal-processing-based inversion methods, particularly under complex terrain and near-vertical incidence conditions. Although recent advances in deep learning have shown strong potential for motion information sensing, multitask learning in this context still faces challenges in achieving both real-time performance and high estimation accuracy. To address these issues, this study proposes a novel network architecture, termed RDMFNet, that performs multirepresentation information fusion via shared encoders and parallel decoders, along with a two-stage progressive training strategy to enhance parameter estimation accuracy. Experimental results show that RDMFNet achieves estimation errors of 14.447 m for altitude, 4.635 m/s for velocity, and 0.755° for pitch angle, demonstrating its effectiveness for high-precision, real-time perception.
- Motion parameter estimation /
- Near-vertical scenario /
- Range-Doppler map /
- Multi-task learning /
- Deep learning

HTML全文

图 1 近垂直雷达场景示意

Figure 1. An illustration of a near-vertical radar scenario

下载: 全尺寸图片幻灯片

图 2 近垂直场景等距离线(蓝色)与等速度线(红色) 示意图

Figure 2. A schematic illustration depicting isorange contours (in blue) and isovelocity contours (in red) in a near-vertical scenari

下载: 全尺寸图片幻灯片

图 3 相同高度和速度，不同俯仰角下的仿真RD图

Figure 3. Simulated RD maps of the same altitude and velocity with different pitch angles

下载: 全尺寸图片幻灯片

图 4 RDMFNet 网络结构

Figure 4. Network architecture of RDMFNet

下载: 全尺寸图片幻灯片

图 5 解码器结构

Figure 5. The architecture of the decoders

下载: 全尺寸图片幻灯片

图 6 两阶段训练过程中验证集上误差曲线

Figure 6. RMSE curves on the validation set during the two-stage training process

下载: 全尺寸图片幻灯片

图 7 不同 SNR 设置下的误差比较

Figure 7. Comparison of RMSE under different SNR settings

下载: 全尺寸图片幻灯片

表 1 仿真中设定的雷达参数

Table 1. Radar parameters set in simulaiton

参数		取值
f_c	载频	1 GHz
T_r	脉冲发射间隔	4e-5s
f_s	采样率	6.25 MHz
T	发射信号时宽	5e-66s
B	发射信号带宽	2.5 MHz
M	相参积累脉冲数	101

下载: 导出CSV

表 2 RDMFNet 各卷积层参数

Table 2. Parameters of the Convolutional Layers in RDMFNet

参数	卷积 1	卷积 2	卷积 3	卷积 4	卷积 5
C_in, C_out	(2, C)	(C, C)	(C, C)	(C, C)	(3C, C)
ks (3, 3)	(3, 3)	(3, 3)	(3, 3)	(1, 3)	(1, 1)
stride	(1, 1)	(1, 1)	(2, 2)	(1, 1)	(1, 1)
pad	(1, 1)	(1, 1)	(1, 1)	(0, 1)	(1, 1)

下载: 导出CSV

表 3 各模型的参数量，计算复杂度和推理时间

Table 3. The parameter counts, MACs, and inference times for each model

模型	Params/M	MACs/G	Time/ms
ResNet	11.172	0.52	0.881
TSCNet	1.576	6.65	21.984
TSCNet-mini	0.288	1.48	8.141
RDMFNet	0.204	0.51	0.815

下载: 导出CSV

表 4 各方法的均方根误差

Table 4. The RMSE of each method

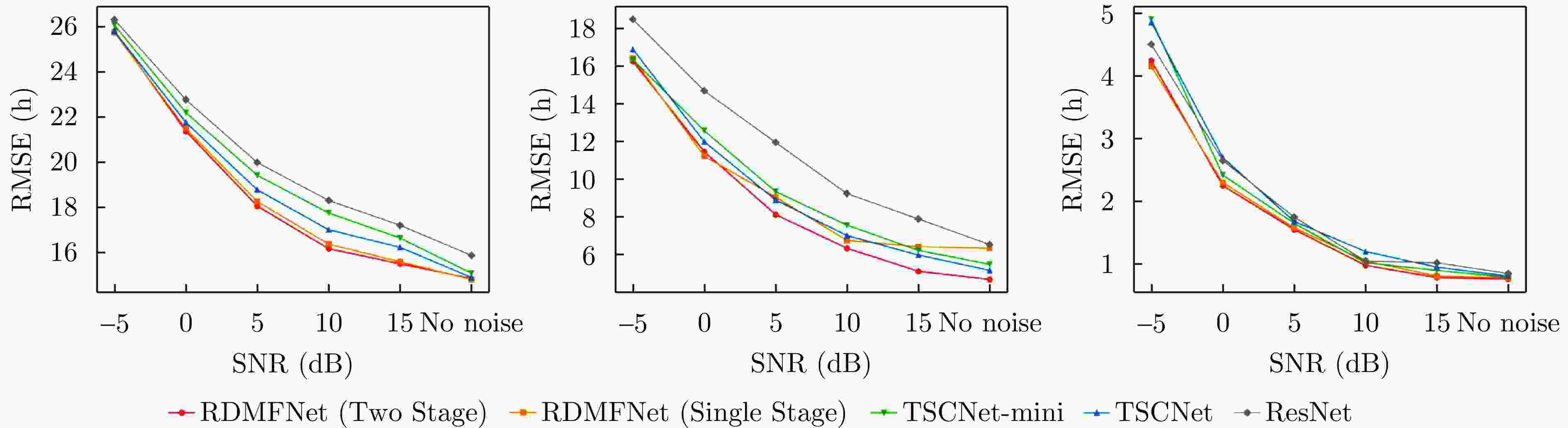
算法	Input	h (m)	v (m/s)	p (°)
传统方法	R	21.647	15.809	-
	R	15.928	9.205	0.991
ResNet	L	16.358	7.845	0.855
	R+L	15.886	6.530	0.851
	R	14.755	5.852	0.777
TSCNet	L	16.725	5.392	0.781
	R+L	14.911	5.167	0.810
	R	15.432	5.859	0.834
TSCNet-mini	L	16.737	5.417	0.768
	R+L	15.099	5.484	0.788
	R	36.407	9.509	1.098
RDMFNet	L	15.195	5.250	0.755
(单阶段)	R+L	14.820	6.341	0.780
	R	15.273	5.252	0.823
RDMFNet	L	14.447	4.635	0.755
(两阶段)	R+L	14.861	4.690	0.758
注：加粗数值表示最优性能，下划线数值表示第二优性能。

下载: 导出CSV

表 5 移除各个模块后RDMFNet的估计误差

Table 5. The RMSE of RDMFNet after the removal of each module

Range Encoder	Hybrid Encoder	Skip Connection	一阶段			两阶段
Range Encoder	Hybrid Encoder	Skip Connection	h (m)	v (m/s)	p (°)	h (m)	v (m/s)	p (°)
-	√	√	23.177	9.178	0.790	15.551	4.950	0.792
√	-	√	15.679	9.887	0.787	15.031	4.460	0.769
√	√	-	16.002	23.073	0.759	15.148	5.088	0.740
√	√	√	14.820	6.341	0.780	14.861	4.690	0.758
注：加粗数值表示最优性能，下划线数值表示第二优性能。“-”表示去除该模块，“√”表示添加该模块。

下载: 导出CSV

表 6 共享编码与独立编码下的误差结果比较

Table 6. Comparison of RMSE between shared encoding and independent encoding

编码策略	Params (M)	MACs (G)	Time (ms)	h (m)	v (m/s)	p (°)
共享编码	0.204	0.51	0.815	14.820	6.341	0.780
独立编码	0.315	1.17	1.554	15.123	6.440	0.792
注：加粗数值表示最优性能。

下载: 导出CSV

表 7 使用不同损失函数时各方法的均方根误差

Table 7. The RMSE of each method when using different loss functions

算法	Input	Loss	h/m	v/(m/s)	p/°
ResNet	R+L	UC	15.886	6.530	0.851
		DLS	17.365	6.943	0.986
		MSE	16.277	6.693	0.850
TSCNet	R+L	UC	15.099	5.484	0.788
		DLS	15.107	6.844	0.853
		MSE	15.234	6.651	0.795
RDMFNet (单阶段)	R+L	UC	14.820	6.341	0.780
		DLS	19.741	7.900	0.890
		MSE	21.471	8.329	0.787
	L	UC	15.195	5.250	0.755
		DLS	21.932	6.025	0.736
		MSE	20.906	5.958	0.742
RDMFNet (两阶段)	R+L	UC	14.861	4.690	0.758
		DLS	15.229	4.530	0.759
		MSE	14.767	4.861	0.755
	L	UC	14.447	4.635	0.755
		DLS	14.441	4.585	0.767
		MSE	14.432	4.525	0.742
注：加粗数值表示最优性能，下划线数值表示第二优性能。

下载: 导出CSV

表 8 不同训练策略的均方根误差

Table 8. The RMSE of different training strategies

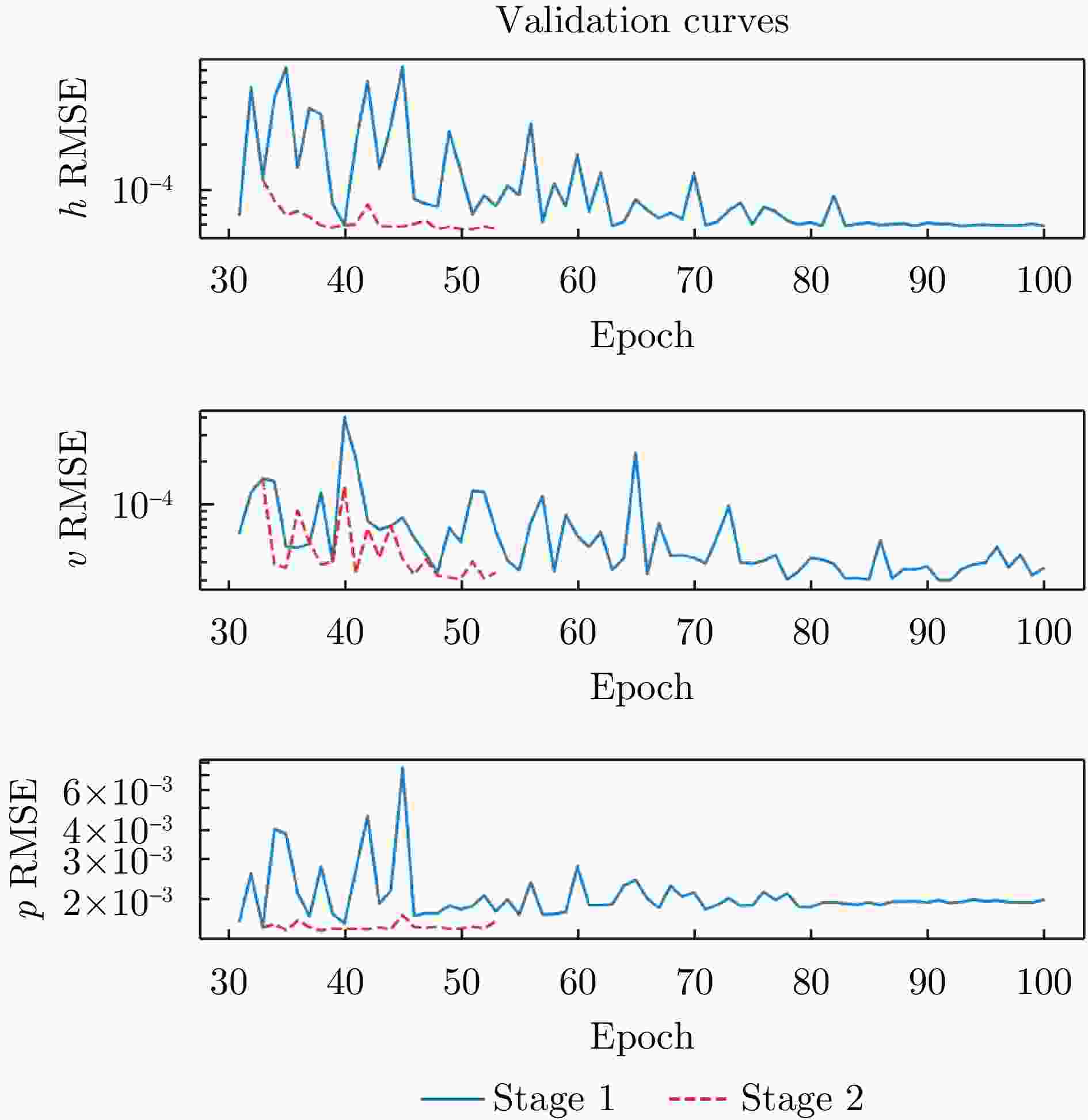
策略	epoch	h (m)	v (m/s)	p (°)
单阶段	100	14.820	6.341	0.780
p收敛+微调	33+53	14.861	4.690	0.758
过拟合+微调	100+48	15.362	7.097	0.811
欠拟合+微调	10+93	14.897	6.144	0.790
注：加粗数值表示最优性能，下划线数值表示第二优性能。

下载: 导出CSV

参考文献(18)

[1]	MILLER S D, MWAFFO V, and COSTELLO III D H. Deep learning-based relative bearing estimation between naval surface vessels and uas in challenging maritime environments[C]. 2025 International Conference on Unmanned Aircraft Systems (ICUAS), Charlotte, USA, 2025: 742–748. doi: 10.1109/ICUAS65942.2025.11007882.
[2]	毛军, 付浩, 褚超群, 等. 惯性/视觉/激光雷达SLAM技术综述[J]. 导航定位与授时, 2022, 9(4): 17–30. doi: 10.19306/j.cnki.2095-8110.2022.04.003. MAO Jun, FU Hao, CHU Chaoqun, et al. A review of simultaneous localization and mapping based on inertial-visual-lidar fusion[J]. Navigation Positioning and Timing, 2022, 9(4): 17–30. doi: 10.19306/j.cnki.2095-8110.2022.04.003.
[3]	NARASIMHAPPA M, MAHINDRAKAR A D, GUIZILINI V C, et al. MEMS-based IMU drift minimization: Sage Husa adaptive robust Kalman filtering[J]. IEEE Sensors Journal, 2020, 20(1): 250–260. doi: 10.1109/JSEN.2019.2941273.
[4]	李道京, 朱宇, 胡烜, 等. 衍射光学系统的激光应用和稀疏成像分析[J]. 雷达学报, 2020, 9(1): 195–203. doi: 10.12000/JR19081. LI Daojing, ZHU Yu, HU Xuan, et al. Laser application and sparse imaging analysis of diffractive optical system[J]. Journal of Radars, 2020, 9(1): 195–203. doi: 10.12000/JR19081.
[5]	王超, 王岩飞, 刘畅, 等. 基于参数估计的高分辨率SAR运动目标距离徙动校正方法[J]. 雷达学报, 2019, 8(1): 64–72. doi: 10.12000/JR18054. WANG Chao, WANG Yanfei, LIU Chang, et al. A new approach to range cell migration correction for ground moving targets in high-resolution SAR system based on parameter estimation[J]. Journal of Radars, 2019, 8(1): 64–72. doi: 10.12000/JR18054.
[6]	许京新. 基于深度学习的SAR图像舰船目标检测[D]. [硕士论文], 烟台大学, 2025. doi: 10.27437/d.cnki.gytdu.2025.000610. XU Jingxin. Deep learning-based ship target detection in SAR images[D]. [Master dissertation], Yantai University, 2025. doi: 10.27437/d.cnki.gytdu.2025.000610.
[7]	DE HOOP M V, LASSAS M, and WONG C A. Deep learning architectures for nonlinear operator functions and nonlinear inverse problems[J]. Mathematical Statistics and Learning, 2022, 4(1/2): 1–86. doi: 10.4171/MSL/28.
[8]	DARA S and TUMMA P. Feature extraction by using deep learning: A survey[C]. 2018 Second International Conference on Electronics, Communication and Aerospace Technology (ICECA), Coimbatore, India, 2018: 1795–1801. doi: 10.1109/ICECA.2018.8474912.
[9]	KWON H Y, YOON H G, LEE C, et al. Magnetic Hamiltonian parameter estimation using deep learning techniques[J]. Science Advances, 2020, 6(39): eabb0872. doi: 10.1126/sciadv.abb0872.
[10]	KOLLIAS D. ABAW: Learning from synthetic data & multi-task learning challenges[C]. European Conference on Computer Vision, Tel Aviv, Israel, 2023: 157–172. doi: 10.1007/978-3-031-25075-0_12.
[11]	CIPOLLA R, GAL Y, and KENDALL A. Multi-task learning using uncertainty to weigh losses for scene geometry and semantics[C]. IEEE/CVF Conference on Computer Vision and Pattern Recognition, Salt Lake City, USA, 2018: 7482–7491. doi: 10.1109/CVPR.2018.00781.
[12]	RICHARDS M A and MELVIN W L. Principles of Modern Radar: Basic Principles[M]. London: The Institution of Engineering and Technology, 2022: 360.
[13]	WANG Aiguo, ZHANG Wei, and CAO Jianshu. Terrain clutter modeling for airborne radar system using digital elevation model[C]. The 2012 International Workshop on Microwave and Millimeter Wave Circuits and System Technology, Chengdu, China, 2012: 1–4. doi: 10.1109/MMWCST.2012.6238182.
[14]	IOFFE S and SZEGEDY C. Batch normalization: Accelerating deep network training by reducing internal covariate shift[C]. The 32nd International Conference on International Conference on Machine Learning, Lille, France, 2015: 448–456.
[15]	HE Kaiming, ZHANG Xiangyu, REN Shaoqing, et al. Delving deep into rectifiers: Surpassing human-level performance on ImageNet classification[C]. The IEEE International Conference on Computer Vision, Santiago, Chile, 2015: 1026–1034. doi: 10.1109/ICCV.2015.123.
[16]	HE Kaiming, ZHANG Xiangyu, REN Shaoqing, et al. Deep residual learning for image recognition[C]. The IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, USA, 2016: 770–778. doi: 10.1109/CVPR.2016.90.
[17]	ABDULATIF S, CAO Ruizhe, and YANG Bin. CMGAN: Conformer-based metric-GAN for monaural speech enhancement[J]. IEEE/ACM Transactions on Audio, Speech, and Language Processing, 2024, 32: 2477–2493. doi: 10.1109/TASLP.2024.3393718.
[18]	RUDER S. An overview of multi-task learning in deep neural networks[J]. arXiv preprint arXiv: 1706.05098, 2017. doi: 10.48550/arXiv.1706.05098.