-
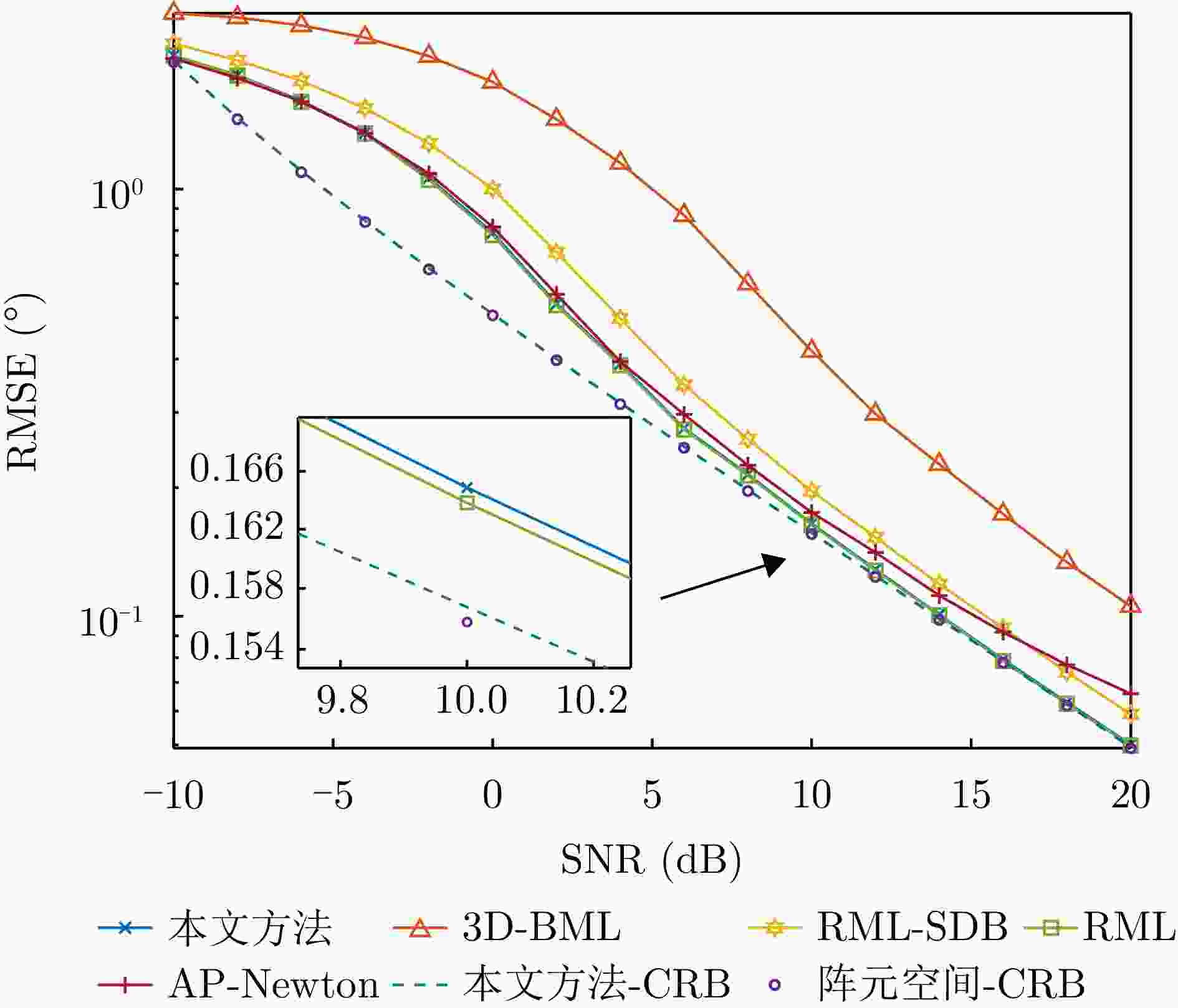
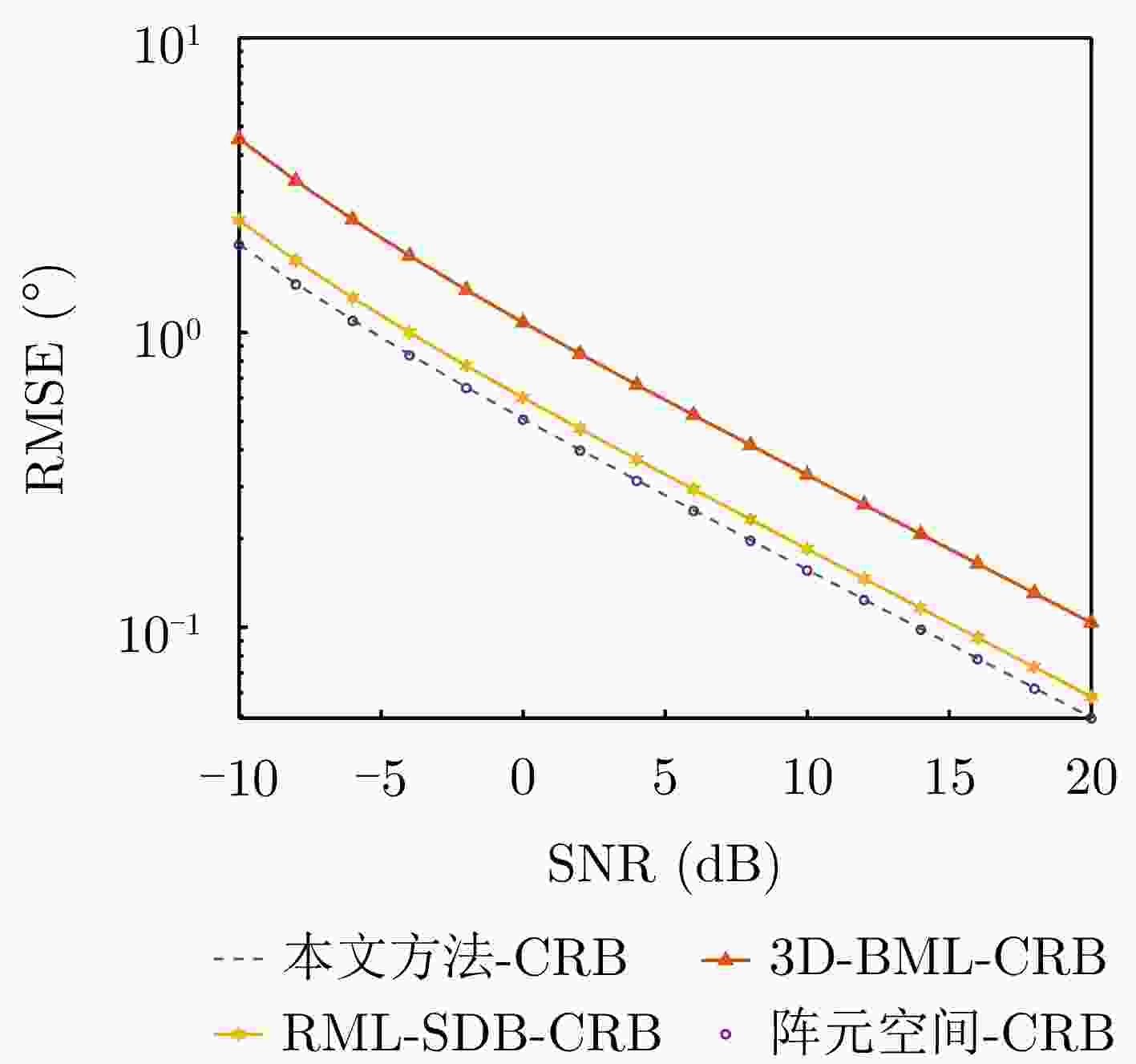
摘要: 低仰角目标波达方向(DOA)估计是米波雷达与全息凝视雷达中的关键问题,其估计误差直接影响目标的测高精度。传统波束空间方法通过构建波束形成器,将高维阵元空间数据映射至低维波束空间以降低计算复杂度。然而,该类方法的有损映射会造成部分目标信息丢失,使目标仰角估计精度显著低于阵元空间方法。为解决这一问题,该文提出了一种低仰角目标高精度波束空间DOA估计方法。首先,推导了阵元空间与波束空间中DOA估计的克拉美罗界(CRB),并分析了两者相等所需满足的充分条件。由于该条件在实际应用中难以严格满足,该文进一步提出一种基于近似条件的波束形成器设计方法。该方法在降低数据维度的同时,最大限度保留目标的有效信息。最后,基于最大似然准则实现了目标仰角的精确估计。仿真与实测结果表明,所提方法在显著降低处理数据维度的同时,能够在低仰角观测区域内保持与阵元空间方法相近的估计精度,并优于现有波束空间算法。
-
关键词:
- 低仰角目标 /
- 波达方向(DOA)估计 /
- 波束空间处理 /
- 克拉美罗界(CRB) /
- 多径效应 /
- 最大似然
Abstract: Direction of Arrival (DOA) estimation for low-elevation angle targets is a critical challenge in meter-wave and holographic staring radar systems, as its accuracy directly affects target height measurement performance. Traditional beamspace methods reduce computational complexity by projecting high-dimensional element-space data onto a low-dimensional beamspace using a beamformer. However, this lossy mapping leads to partial information loss, resulting in degraded elevation-angle estimation accuracy compared to that of element-space methods. To address this issue, this study proposes a high-accuracy beamspace DOA estimation method for low-elevation angle targets. First, the Cramér-Rao Bound (CRB) for both element-space and beamspace DOA estimation is derived, and the conditions under which these bounds are equal are analyzed. Since these conditions are difficult to satisfy in practical scenarios, an approximate-condition-based beamformer design strategy is developed to reduce data dimensionality while preserving effective target information. Finally, precise elevation-angle estimation is achieved using the maximum likelihood criterion. Simulation and experimental results show that the proposed method significantly reduces data dimensionality while maintaining estimation accuracy comparable to that of element-space methods at low-elevation angles, clearly outperforming existing beamspace algorithms. -
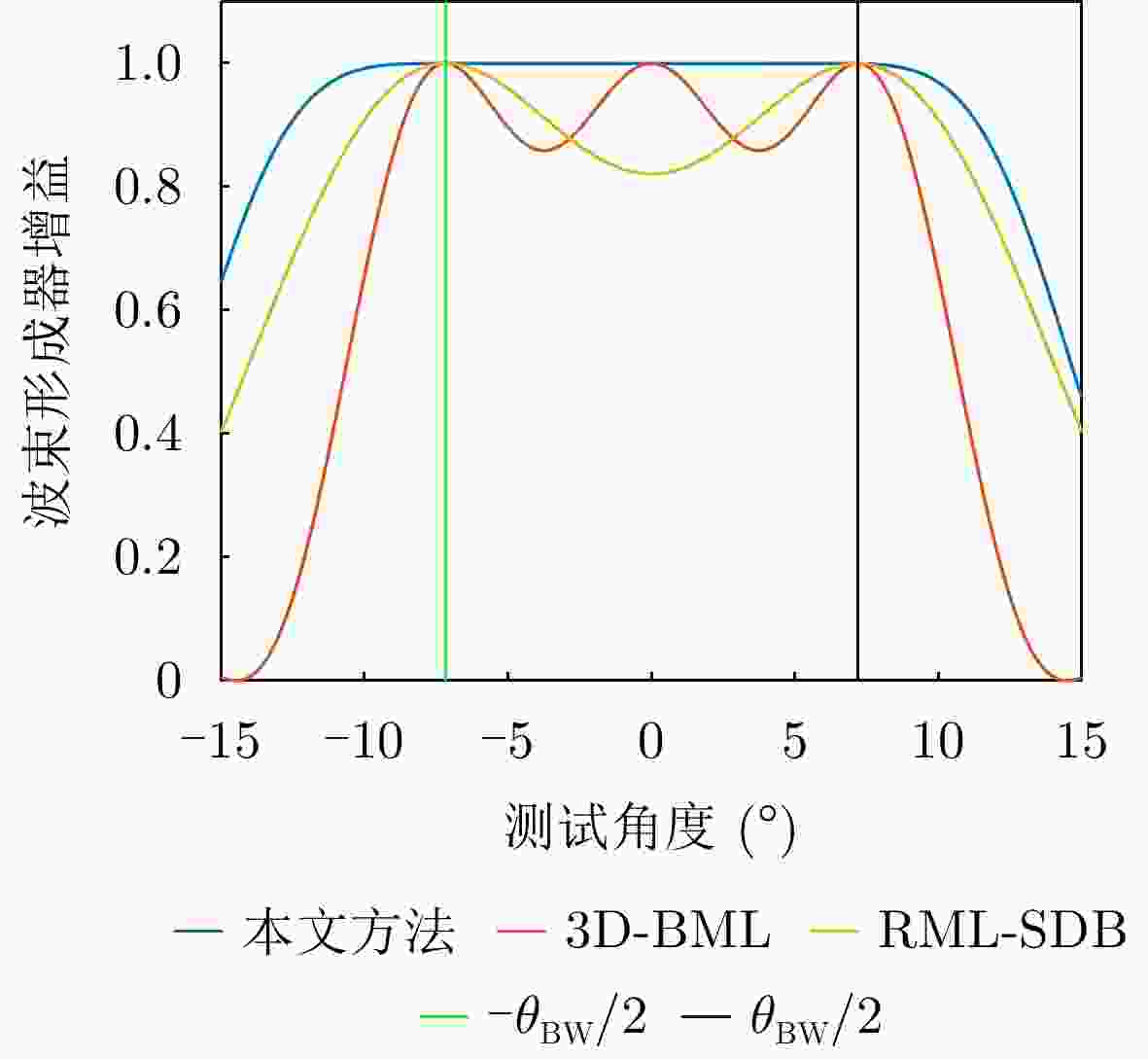
表 1 不同波束空间DOA估计算法波束形成器的波束指向角设置
Table 1. Beam steering angle configurations of beamformers in different beamspace DOA estimation algorithms
算法 波束指向角集合 3D-BML $ {\boldsymbol{\theta }}_{B}=\left[-{7.18}^{ \circ},{0}^{\circ},{7.18}^{ \circ}\right] $ RML-SDB $ {\boldsymbol{\theta }}_{B}=\left[-{7.18}^{ \circ},{7.18}^{ \circ}\right] $ 本文方法 $ {\boldsymbol{\theta }}_{B}=\left[-{6.73}^{ \circ},-{5.41}^{\circ},-{2.08}^{\circ},{5.06}^{ \circ},{5.78}^{ \circ}\right] $ 表 2 不同算法的计算复杂度
Table 2. Computational complexity of different algorithms
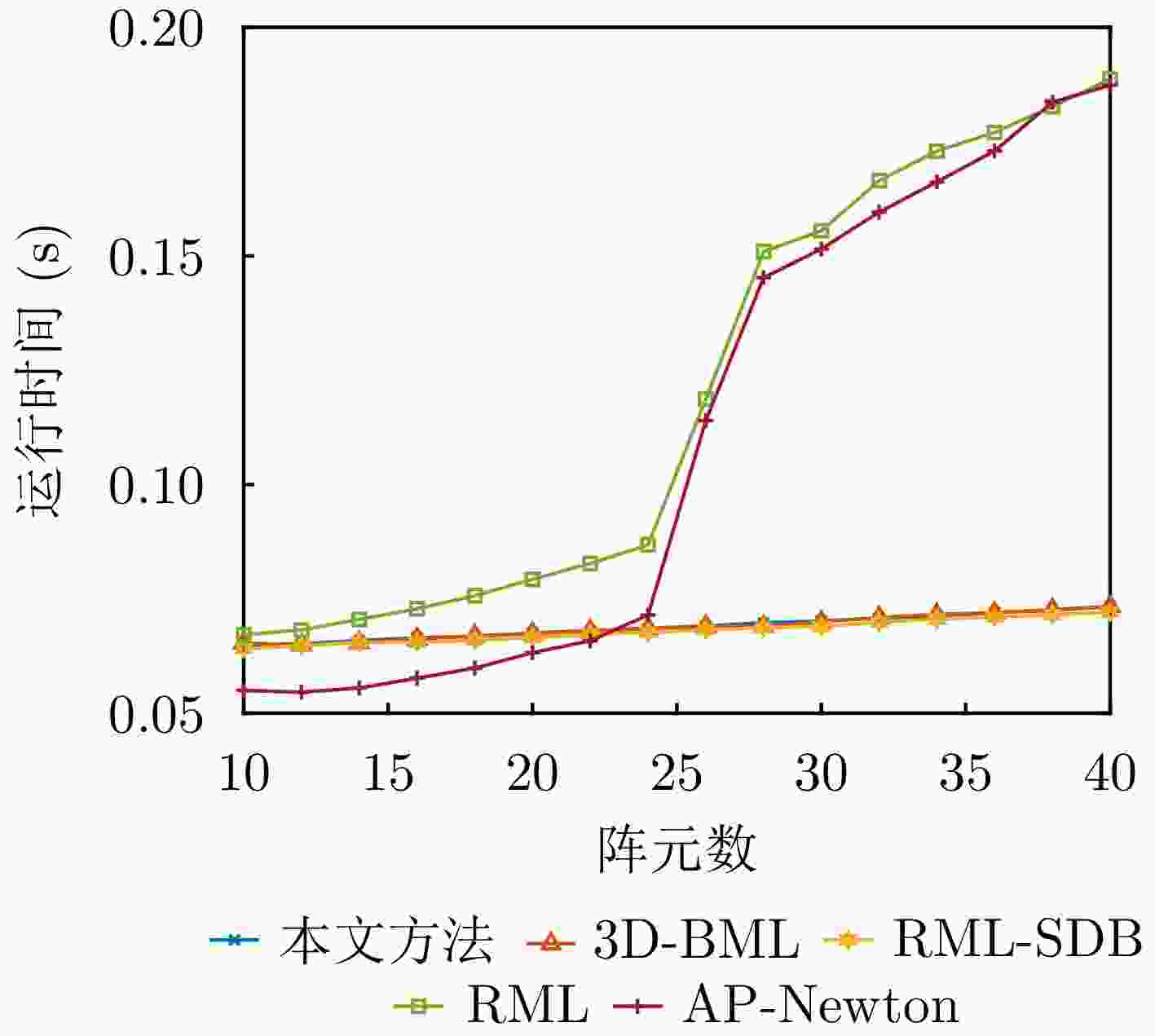
算法 在线计算复杂度 离线计算复杂度 3D-BML $ O\left(\overline{Q}{B}_{\text{3D}}M+\overline{Q}{({{B}_{\text{3D}}})}^{3}\right) $ $ O\left({B}_{\text{3D}}ML\right) $ RML-SDB $ O\left(\overline{Q}{B}_{\text{SDB}}M+\overline{Q}{({{B}_{\text{SDB}}})}^{3}\right) $ $ O\left({B}_{\text{SDB}}ML\right) $ 本文方法 $ O\left(\overline{Q}{B}_{\text{PM}}M+\overline{Q}{({{B}_{\text{PM}}})}^{3}\right) $ $ O \left( NKM{({{B}_{\text{PM}}})}^{2} \right) $ AP-Newton $ O \left({M}^{3} + \overline{Q}{M}^{2} + L{M}^{2} + {I}_{\text{AP}}M\right) $ — RML $ O\left(\overline{Q}{M}^{3}\right) $ — 表 3 L波段全息凝视雷达关键参数
Table 3. Key parameters of the L-Band holographic staring radar
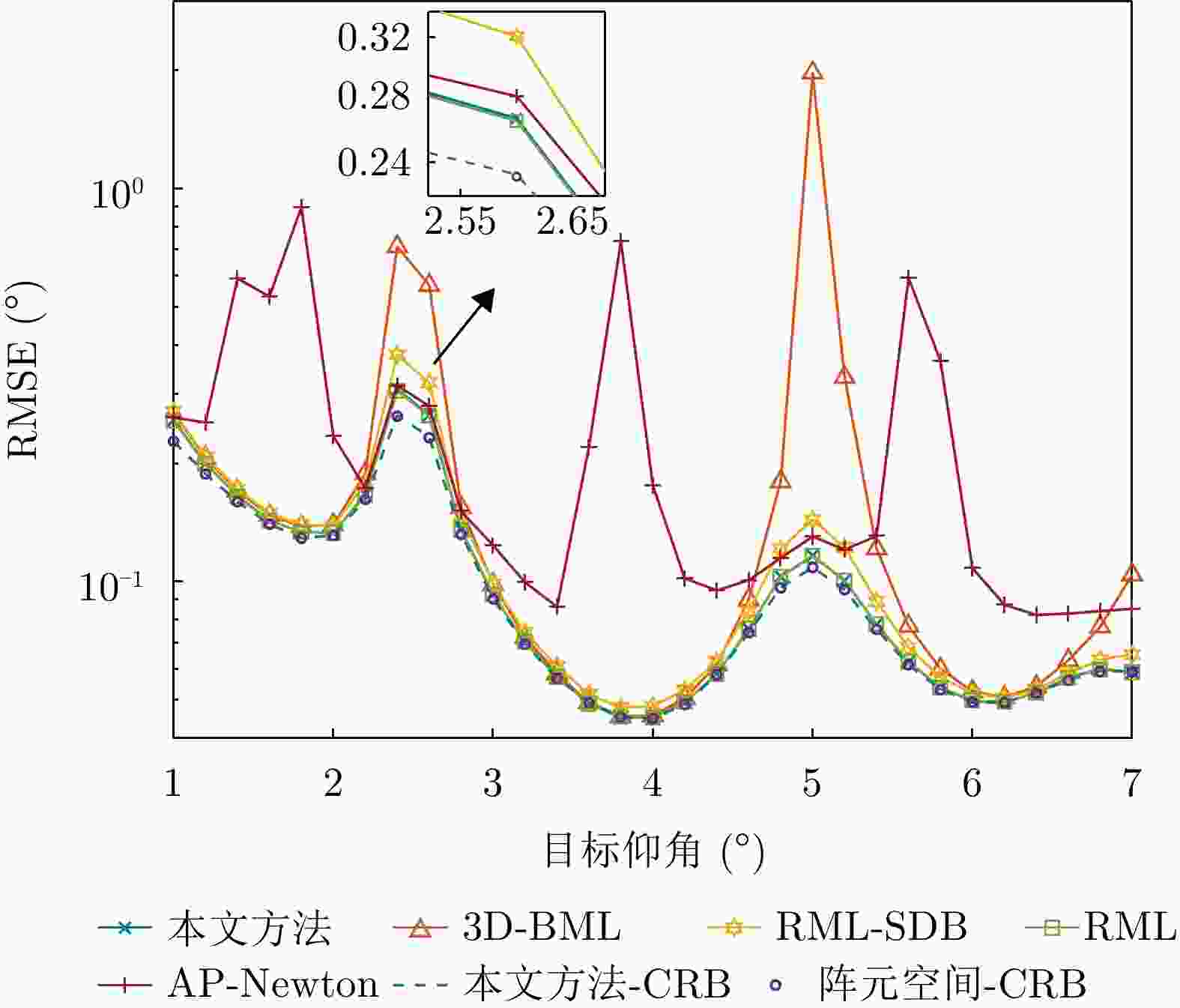
参数 数值 带宽 2~16 MHz 接收通道数 8×8 方位覆盖范围 90° 俯仰覆盖范围 22.5°, 30.0°, 45.0°, 60.0° (可设定) 脉冲重复频率 ~5 kHz 更新频率 ~1 s 探测距离 10 km (@RCS 0.01 m2) 表 4 不同算法对目标仰角估计的RMSE
Table 4. RMSE of target elevation angle estimation using different algorithms
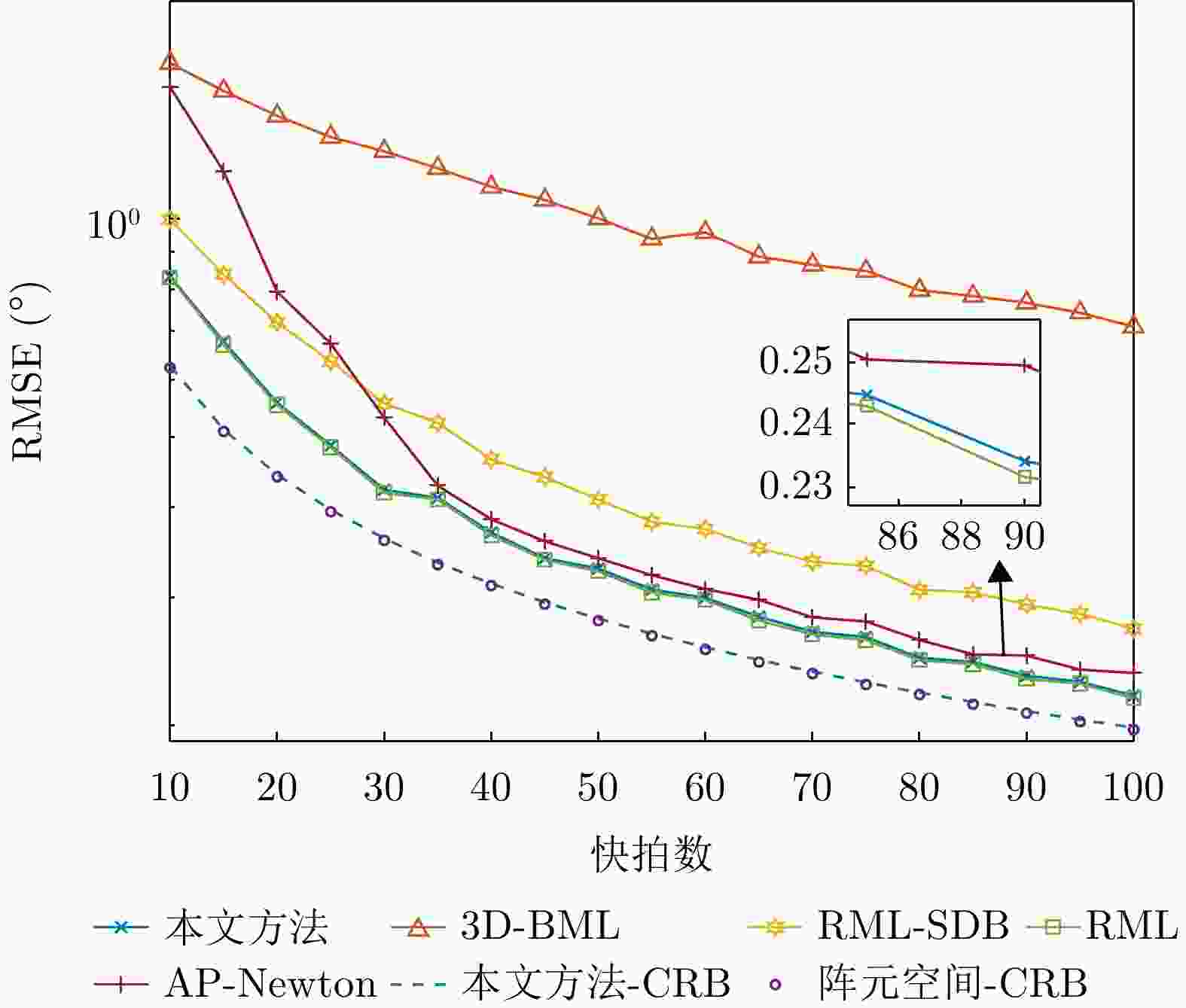
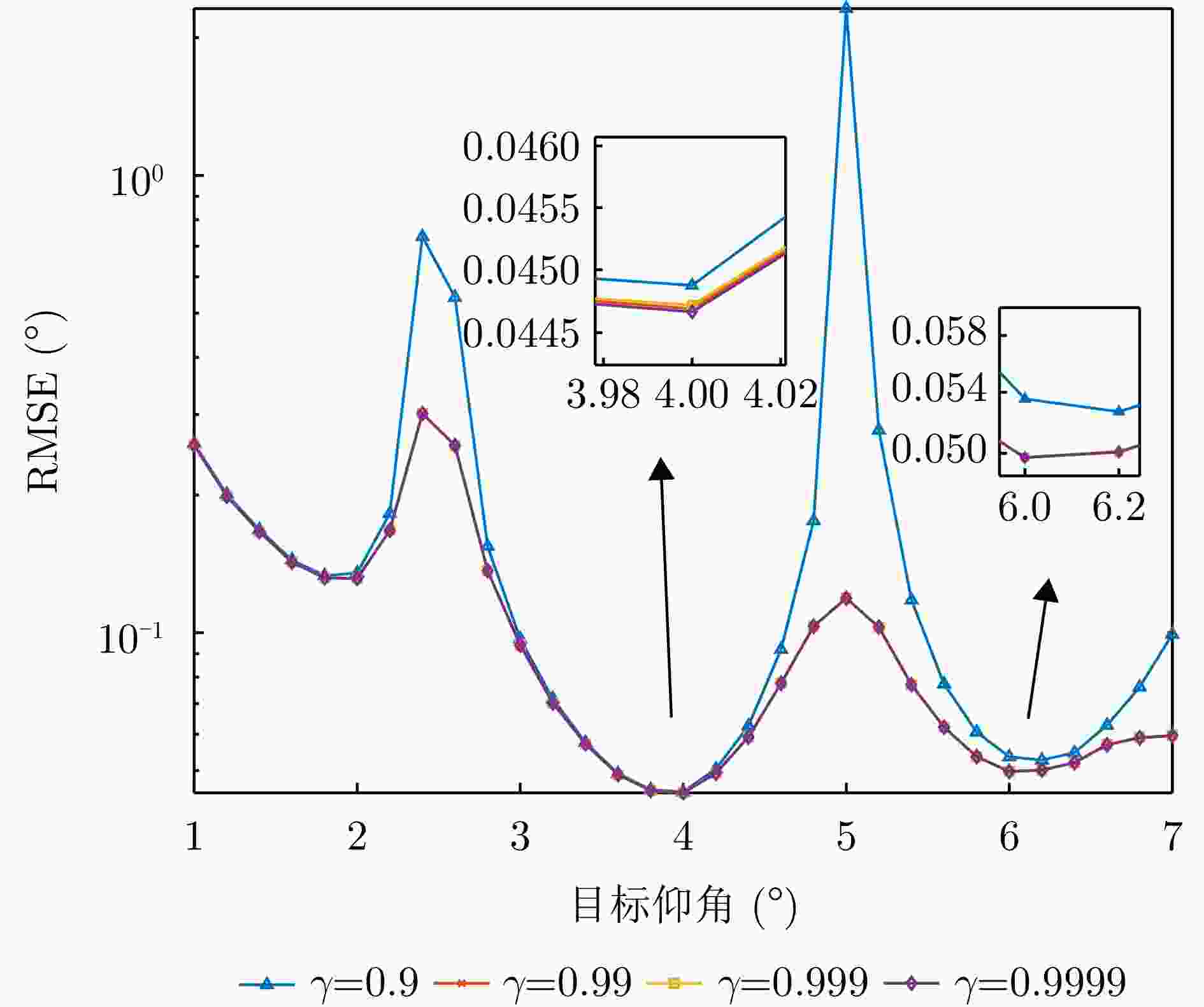
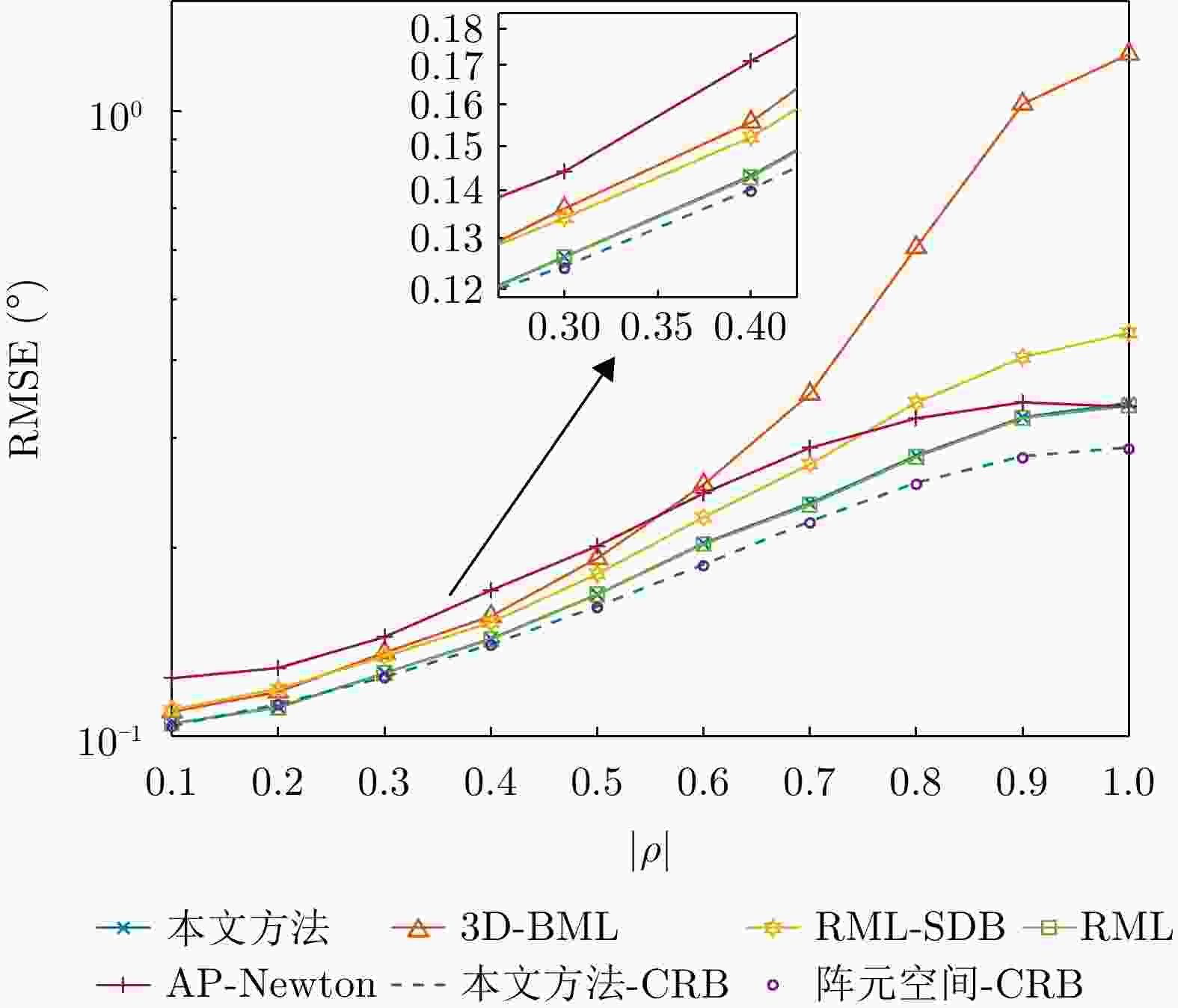
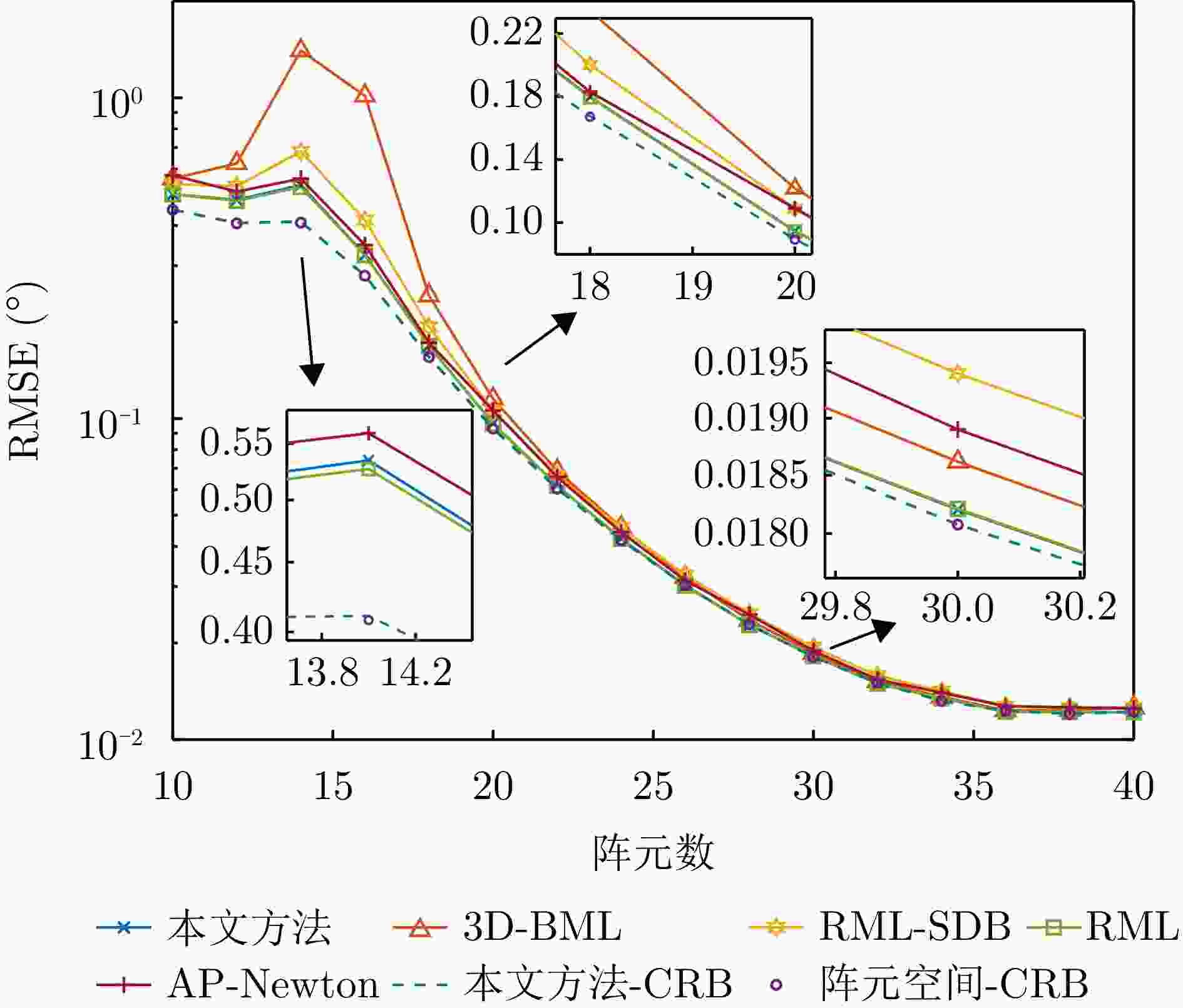
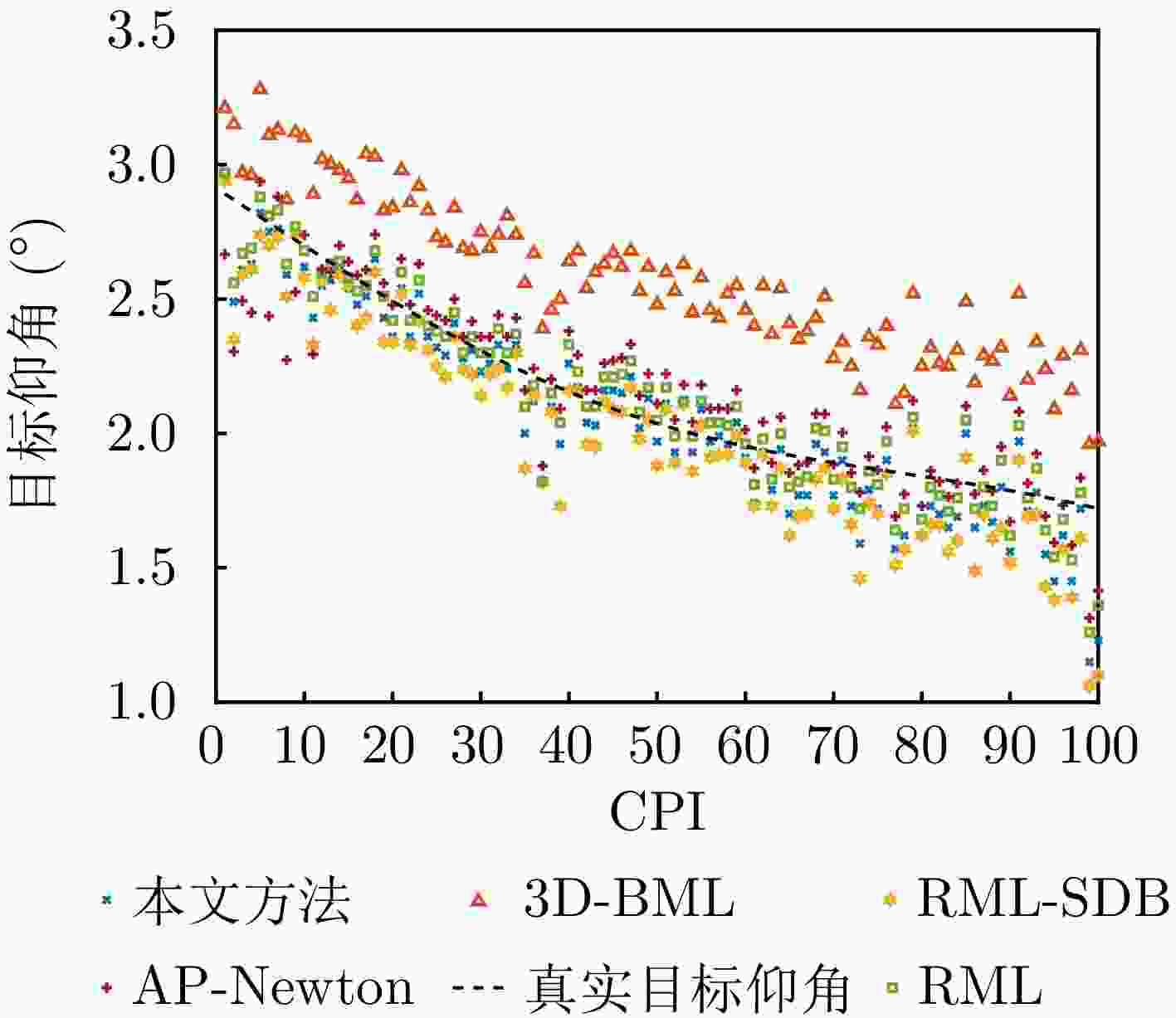
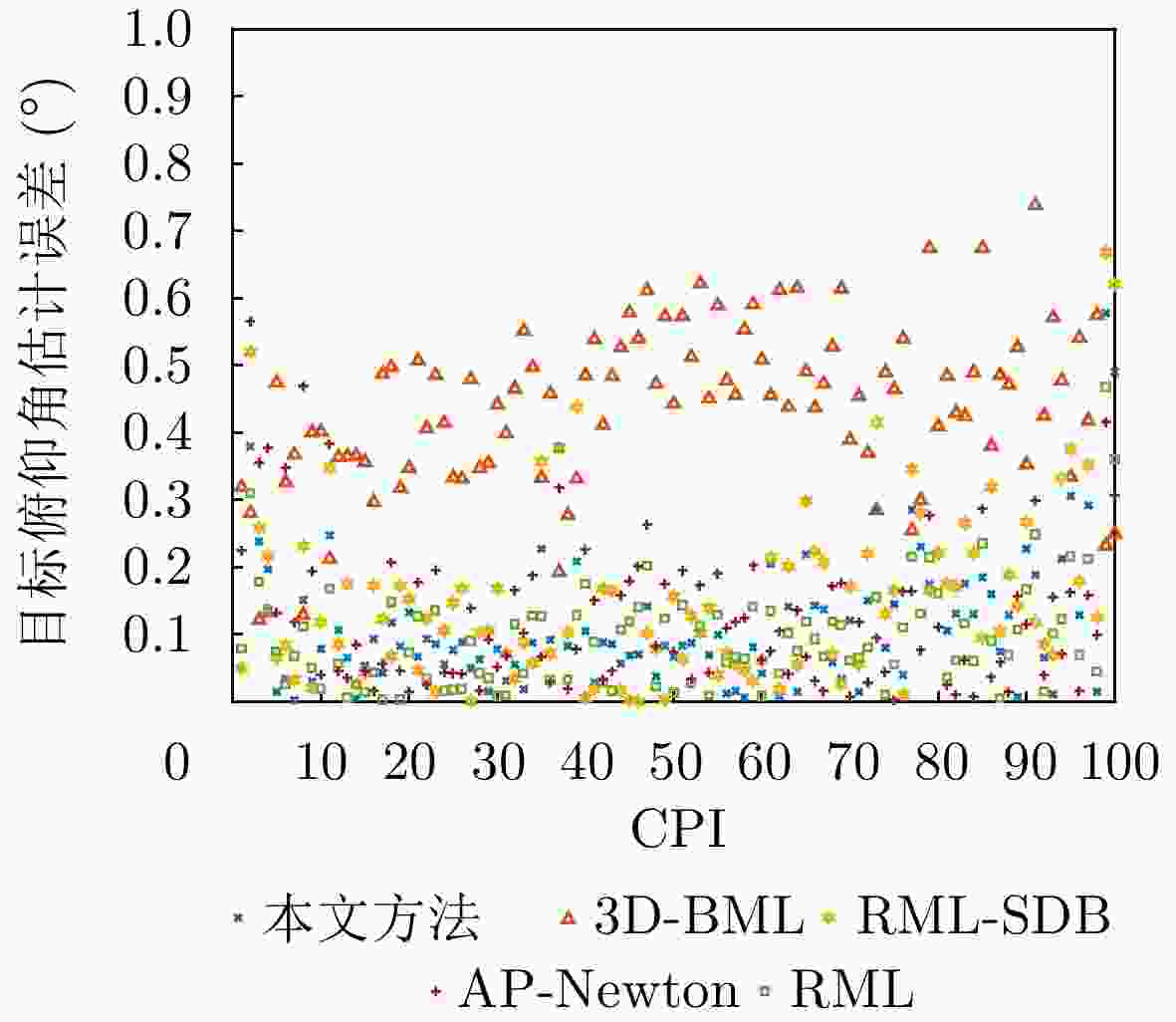
算法 RMSE (°) 3D-BML 0.4587 RML-SDB 0.1998 AP-Newton 0.1688 RML 0.1279 本文方法 0.1537 -
[1] 郭瑞, 张月, 田彪, 等. 全息凝视雷达系统技术与发展应用综述[J]. 雷达学报, 2023, 12(2): 389–411. doi: 10.12000/JR22153.GUO Rui, ZHANG Yue, TIAN Biao, et al. Review of the technology, development and applications of holographic staring radar[J]. Journal of Radars, 2023, 12(2): 389–411. doi: 10.12000/JR22153. [2] LAN Lan, ROSAMILIA M, AUBRY A, et al. Adaptive target detection and DOA estimation with uniform rectangular arrays in the presence of unknown mutual coupling[J]. IEEE Transactions on Radar Systems, 2023, 1: 325–338. doi: 10.1109/TRS.2023.3289991. [3] WEN Fangqing, WANG Han, GUI Guan, et al. Polarized intelligent reflecting surface aided 2D-DOA estimation for NLoS sources[J]. IEEE Transactions on Wireless Communications, 2024, 23(7): 8085–8098. doi: 10.1109/TWC.2023.3348520. [4] YU Canping, LI Yingsong, LI Liping, et al. Dual Lawson norm-based robust DOA estimation for RIS-Aided wireless communication systems[J]. IEEE Transactions on Aerospace and Electronic Systems, 2025, 61(1): 582–592. doi: 10.1109/TAES.2024.3446752. [5] WAN Liangtian, SUN Yuchen, SUN Lu, et al. Deep learning based autonomous vehicle super resolution DOA estimation for safety driving[J]. IEEE Transactions on Intelligent Transportation Systems, 2021, 22(7): 4301–4315. doi: 10.1109/TITS.2020.3009223. [6] XU He, LIU Wei, JIN Ming, et al. Positioning and contour extraction of autonomous vehicles based on enhanced DOA estimation by large-scale arrays[J]. IEEE Internet of Things Journal, 2023, 10(13): 11792–11803. doi: 10.1109/JIOT.2023.3244861. [7] 马健钧, 魏少鹏, 马晖, 等. 基于ADMM的低仰角目标二维DOA估计算法[J]. 电子与信息学报, 2022, 44(8): 2859–2866. doi: 10.11999/JEIT210582.MA Jianjun, WEI Shaopeng, MA Hui, et al. Two-dimensional DOA estimation for low-angle target based on ADMM[J]. Journal of Electronics & Information Technology, 2022, 44(8): 2859–2866. doi: 10.11999/JEIT210582. [8] LIU Qi, GUO Rui, WANG Jiajia, et al. Signal-level fusion-based height estimation of low-elevation target for distributed radar[J]. IEEE Transactions on Instrumentation and Measurement, 2025, 74: 6508114. doi: 10.1109/TIM.2025.3593573. [9] CHEN Sheng, ZHAO Yongbo, HU Yili, et al. A beamspace maximum likelihood algorithm for target height estimation for a bistatic MIMO radar[J]. Digital Signal Processing, 2022, 122: 103330. doi: 10.1016/j.dsp.2021.103330. [10] ZHENG Guimei, CHEN Chen, and SONG Yuwei. Height measurement for meter wave MIMO radar based on matrix pencil under complex terrain[J]. IEEE Transactions on Vehicular Technology, 2023, 72(9): 11844–11854. doi: 10.1109/TVT.2023.3268791. [11] TANG Derui, ZHAO Yongbo, NIU Ben, et al. Bistatic MIMO radar height estimation method based on adaptive beam-space RML data fusion[J]. Digital Signal Processing, 2024, 145: 104346. doi: 10.1016/j.dsp.2023.104346. [12] LIU Qi, GUO Rui, WANG Bo, et al. Direct altitude estimation of low-elevation target for bistatic holographic staring radar based on coprime array[J]. IEEE Sensors Journal, 2024, 24(11): 17926–17940. doi: 10.1109/JSEN.2024.3387534. [13] 刘源. 米波阵列雷达低仰角目标测高方法研究[D]. [博士论文], 西安电子科技大学, 2018: 1–146.LIU Yuan. Research on some issues of low-angle target height measurement for VHF array radar[D]. [Ph.D. dissertation], Xidian University, 2018: 1–146. [14] 谭俊. 米波雷达低仰角测角中多径效应影响抑制及关键技术研究[D]. [博士论文], 电子科技大学, 2019: 1–130.TAN Jun. Research on multipath effect suppression and key technologies in low-angle measurement of meter wave radar[D]. [Ph.D. dissertation], University of Electronic Science and Technology of China, 2019: 1–130. [15] 王鸿帧, 郑桂妹, 陈晨, 等. 米波雷达低仰角估计技术分析与展望[J]. 火力与指挥控制, 2023, 48(11): 6–16. doi: 10.3969/j.issn.1002-0640.2023.11.002.WANG Hongzhen, ZHENG Guimei, CHEN Chen, et al. Analysis and prospect of low elevation estimation technology for meter wave radar[J]. Fire Control & Command Control, 2023, 48(11): 6–16. doi: 10.3969/j.issn.1002-0640.2023.11.002. [16] GUO Rui, ZHANG Yue, TIAN Biao, et al. Height measurement of Micro-UAVs with L-Band staring radar[C]. 2021 IEEE International Geoscience and Remote Sensing Symposium IGARSS, Brussels, Belgium, 2021: 7967–7970. doi: 10.1109/IGARSS47720.2021.9553143. [17] MA Jianjun, LIU Hongwei, and MA Hui. Low-elevation target DOA estimation based on multi-scattering center equivalent model[J]. Remote Sensing, 2022, 14(15): 3533. doi: 10.3390/rs14153533. [18] CHEN Sheng, ZHAO Yongbo, and HU Yili. Beamspace phase solving algorithm for elevation angle estimation[J]. IEEE Signal Processing Letters, 2022, 29: 742–746. doi: 10.1109/LSP.2022.3154686. [19] XIANG Houhong, CHEN Baixiao, YANG Ting, et al. Improved de-multipath neural network models with self-paced feature-to-feature learning for DOA estimation in multipath environment[J]. IEEE Transactions on Vehicular Technology, 2020, 69(5): 5068–5078. doi: 10.1109/TVT.2020.2977894. [20] LIU Wei, HAARDT M, GRECO M S, et al. Twenty-five years of sensor array and multichannel signal processing: A review of progress to date and potential research directions[J]. IEEE Signal Processing Magazine, 2023, 40(4): 80–91. doi: 10.1109/MSP.2023.3258060. [21] SCHMIDT R. Multiple emitter location and signal parameter estimation[J]. IEEE Transactions on Antennas and Propagation, 1986, 34(3): 276–280. doi: 10.1109/TAP.1986.1143830. [22] PILLAI S U and KWON B H. Forward/backward spatial smoothing techniques for coherent signal identification[J]. IEEE Transactions on Acoustics, Speech, and Signal Processing, 1989, 37(1): 8–15. doi: 10.1109/29.17496. [23] ZOLTOWSKI M and HABER F. A vector space approach to direction finding in a coherent multipath environment[J]. IEEE Transactions on Antennas and Propagation, 1986, 34(9): 1069–1079. doi: 10.1109/TAP.1986.1143956. [24] LIU Yuan, LIU Hongwei, XIA Xianggen, et al. Projection techniques for altitude estimation over complex multipath condition-based VHF radar[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2018, 11(7): 2362–2375. doi: 10.1109/JSTARS.2018.2835448. [25] ZISKIND I and WAX M. Maximum likelihood localization of multiple sources by alternating projection[J]. IEEE Transactions on Acoustics, Speech, and Signal Processing, 1988, 36(10): 1553–1560. doi: 10.1109/29.7543. [26] LO T and LITVA J. Use of a highly deterministic multipath signal model in low-angle tracking[J]. IEE Proceedings F-Radar and Signal Processing, 1991, 138(2): 163–171. doi: 10.1049/Ip-f-2.1991.0022. [27] LIU Yuan, JIU Bo, XIA Xianggen, et al. Height measurement of low-angle target using MIMO radar under multipath interference[J]. IEEE Transactions on Aerospace and Electronic Systems, 2018, 54(2): 808–818. doi: 10.1109/TAES.2017.2767919. [28] MA Jianjun, MA Hui, LIU Hongwei, et al. A novel DOA estimation for low-elevation target method based on multiscattering center equivalent model[J]. IEEE Geoscience and Remote Sensing Letters, 2023, 20: 3501605. doi: 10.1109/LGRS.2023.3242977. [29] WU Jianqi, ZHU Wei, and CHEN Baixiao. Compressed sensing techniques for altitude estimation in multipath conditions[J]. IEEE Transactions on Aerospace and Electronic Systems, 2015, 51(3): 1891–1900. doi: 10.1109/TAES.2015.130841. [30] GUO Rui, PENG Xiangyu, and TIAN Biao. Low elevation target altitude measurement for ubiquitous radar based on known transmitted waveform and sparse representation[J]. IET Radar, Sonar & Navigation, 2022, 16(2): 346–355. doi: 10.1049/rsn2.12187. [31] LIU Yuan, LIU Hongwei, WANG Lu, et al. Target localization in high-coherence multipath environment based on low-rank decomposition and sparse representation[J]. IEEE Transactions on Geoscience and Remote Sensing, 2020, 58(9): 6197–6209. doi: 10.1109/TGRS.2020.2975218. [32] LIU Yuan, LIU Hongwei, JIU Bo, et al. Altitude measurement of low-angle target under complex terrain environment for meter-wave radar[C]. The 2018 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Calgary, Canada, 2018: 3464–3468. doi: 10.1109/ICASSP.2018.8462623. [33] ZOLTOWSKI M D and LEE T S. Maximum likelihood based sensor array signal processing in the beamspace domain for low angle radar tracking[J]. IEEE Transactions on Signal Processing, 1991, 39(3): 656–671. doi: 10.1109/78.80885. [34] CHEN Sheng, ZHAO Yongbo, HU Yili, et al. Beamspace maximum likelihood algorithm based on sum and difference beams for elevation estimation[J]. Journal of Systems Engineering and Electronics, 2024, 35(3): 589–598. doi: 10.23919/JSEE.2024.000057. [35] WEISS A J and FRIEDLANDER B. On the Cramer-Rao bound for direction finding of correlated signals[J]. IEEE Transactions on Signal Processing, 1993, 41(1): 495. doi: 10.1109/TSP.1993.193187. -



 作者中心
作者中心 专家审稿
专家审稿 责编办公
责编办公 编辑办公
编辑办公
 下载:
下载: