作者中心
专家审稿
责编办公
编辑办公
Super-Resolution Imaging for Vortex Electromagnetic Wave Radar Based on Mode Correlation Weighting and Adaptive Regularization
-
摘要: 涡旋电磁波雷达(VEWR)利用轨道角动量(OAM)模态的正交性，理论上为突破传统雷达的方位向分辨率限制提供了新的物理维度，从而也为目标微动感知与前视成像开辟了新途径。然而，实际应用中有限可用模态与复杂电磁噪声导致严重的模态混叠和分辨率退化，现有稀疏成像方法普遍存在精度-效率失衡、噪声鲁棒性不足等问题。该文提出一种融合模态相关性加权与自适应正则化(MCW-AR)的超分辨成像框架。首先构建VEWR前视成像几何与波前调制信号模型；进而设计OAM模态相关矩阵量化模态间辐射能量的非均匀分布特性，通过贝塞尔函数幅值加权调制强化主导模态的低秩约束；最终建立联合稀疏性与低秩性的复合优化模型，引入自适应权重机制动态平衡结构保持与噪声抑制，并设计基于交替方向乘子法(ADMM)与增广拉格朗日(ALM)的联合优化框架，其中核心图像更新子问题采用动量加速的二维共轭梯度最小二乘(2D-CGLS)法高效求解。数值仿真与电磁仿真实验表明：该方法在有限模态和强噪声下仍能保持目标结构完整性，计算效率与成像质量得到显著提升。Abstract: Vortex electromagnetic wave radar (VEWR) leverages the orthogonality of orbital angular momentum (OAM) modes, introducing a new physical dimension that theoretically overcomes the azimuth resolution limitations of conventional radar systems and enables enhanced micro-motion perception and forward-looking imaging. However, in practical engineering applications, the limited number of available OAM modes and the presence of complex electromagnetic noise often cause severe mode aliasing and resolution degradation. Existing sparse imaging methods face inherent trade-offs between accuracy and computational efficiency and exhibit limited robustness to noise. To address these issues, this paper proposes a super-resolution imaging framework that integrates mode correlation weighting and adaptive regularization. First, a forward-looking imaging geometry and a wavefront-modulated signal model for VEWR are established. Subsequently, an OAM mode correlation matrix is designed to characterize the nonuniform distribution of radiation energy among modes, where Bessel-function-modulated weights reinforce the low-rank constraints of dominant radiation components. Finally, a compound optimization model combining sparsity and low-rankness priors is developed, incorporating an adaptive weighting mechanism that dynamically balances structural preservation and noise suppression. A joint optimization framework based on the alternating direction method of multipliers and augmented Lagrange multiplier algorithms is constructed, in which the core image-updating subproblem is efficiently solved using a momentum-accelerated two-dimensional conjugate gradient least-squares method. Numerical simulations and electromagnetic experiments verify that the proposed method preserves target structural integrity under limited modes and strong noise, while effectively improving both imaging quality and computational efficiency.
-
图 1 涡旋电磁波雷达成像几何模型
Figure 1. Imaging geometry model of vortex electromagnetic wave radar
图 2 图像矩阵的奇异值分布与能量累积特性
Figure 2. Singular value distribution and energy accumulation characteristics of image matrix
图 5 不同带宽参数$ \eta $取值对成像性能的影响
Figure 5. The impact of different bandwidth parameter $ \eta $ values on imaging performance
图 7 传统CG与所提2D-CGLS的相对残差收敛曲线对比
Figure 7. Comparison of relative residual convergence between conventional CG and the proposed 2D-CGLS
图 8 传统CG与所提2D-CGLS的成像结果对比
Figure 8. Comparison of imaging results between conventional CG and the proposed 2D-CGLS
图 11 无噪环境情况下利用不同OAM模态范围获得的VEWR成像结果
Figure 11. VEWR imaging results with different OAM mode ranges in a noise-free environment
图 12 不同信噪比条件下通过OAM模态范围$ [ - 40,40] $获得的VEWR成像结果
Figure 12. VEWR imaging results with OAM modes $ [ - 40,40] $ under different SNRs
图 14 仿真点目标的图像相关系数曲线图
Figure 14. The image correlation value curve of simulated point target
图 15 各种算法的运行时间与方位网格数的关系
Figure 15. The running time of various algorithms vs. the number of azimuth grids
图 16 贝塞尔函数调制下各方法的成像对比
Figure 16. Imaging comparison of various methods under Bessel function modulation
图 18 SNR=0dB情况下利用不同OAM模态范围获得的电磁数据VEWR成像结果
Figure 18. VEWR imaging results of electromagnetic data with different OAM mode ranges at SNR=0 dB
图 19 电磁仿真数据的熵值对比
Figure 19. Comparison of entropy values for electromagnetic simulation data
1 所提MCW-AR算法的成像求解流程
1. The imaging procedure of the proposed MCW-AR algorithm
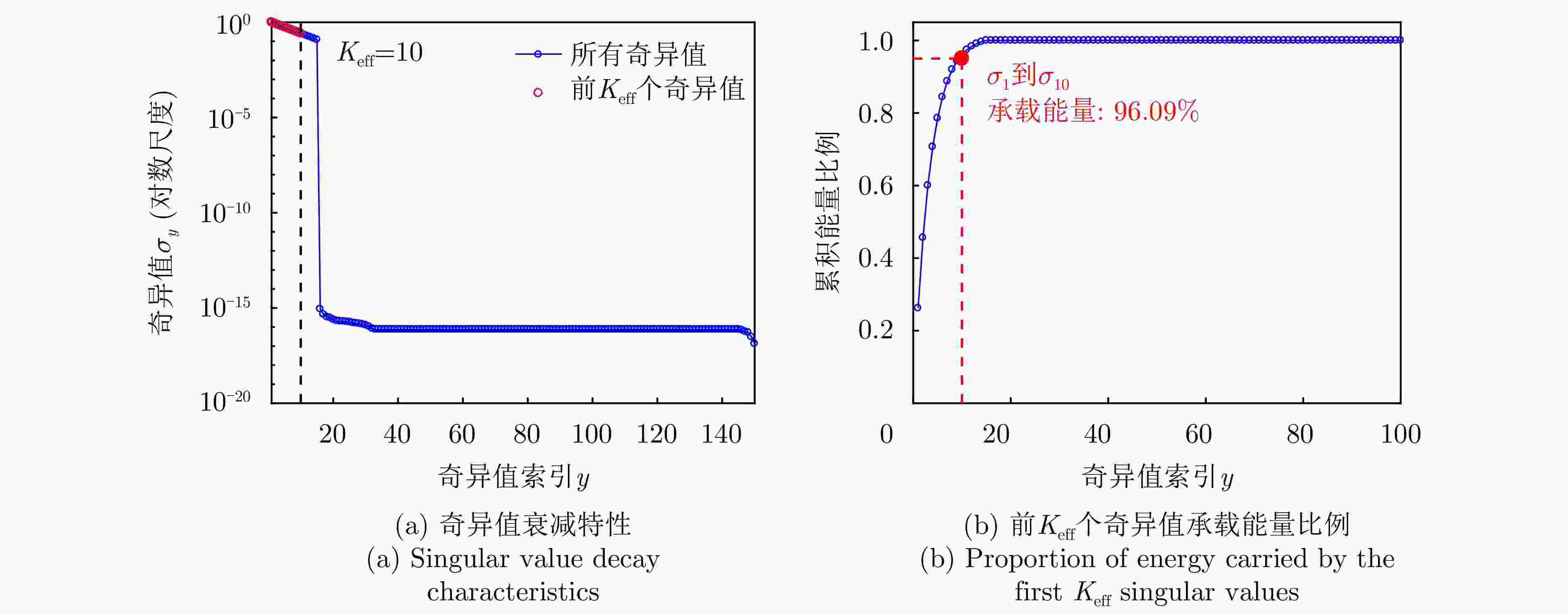
输入：观测矩阵$ {\boldsymbol{S}} $，字典$ {\boldsymbol{\Phi}} $，模态相关矩阵$ {\boldsymbol{C}} $，最大迭代次数$ {K_{{\max}}} $，容差$ \varepsilon $，参数$ \lambda _1 $, $ \lambda _2 $, $ \mu_1^0 $, $ \mu_2^0$, $ \mu_3^0 $, $ \rho $, $ \eta $ 初始化： 计算$ {\boldsymbol{G}} = {{\boldsymbol{\Phi}} ^{{\mathrm{H}}}}{\boldsymbol{S}} $ 对G进行SVD：$ {\boldsymbol{G}} = {{\boldsymbol{U}}_G}{{\boldsymbol{\Sigma}} _G}{\boldsymbol{V}}_G^{{\mathrm{H}}} $, $ {{\boldsymbol{\varSigma}} _G} = {\mathrm{diag}}({\sigma _{G,1}},{\sigma _{G,2}}, \cdots ,{\sigma _{G,{r_G}}}) $, $ {\sigma _{G,1}} \ge {\sigma _{G,2}} \ge \cdots \ge 0 $, $ {r_G} = \min ({N_{{\mathrm{r}}}},{N_{{\mathrm{a}}}}) $ 估计有效秩$ {K_{{{\mathrm{eff}}}}} $：$ {K_{{{\mathrm{eff}}}}} = \min \left\{ {q \in {\mathbb{Z}^ + }\left| {\displaystyle\sum\limits_{y = 1}^q {\sigma _y^2({\boldsymbol{X}}) \ge 0.95\displaystyle\sum\limits_{z = 1}^r {\sigma _z^2({\boldsymbol{X}})} } } \right.} \right\} $ 初始化$ {{\boldsymbol{X}}^0} $：$ {{\boldsymbol{X}}^0} = {{\boldsymbol{U}}_{G(:,1:{K_{{{\mathrm{eff}}}}})}}{{\boldsymbol{\varSigma}} _{G(1:{K_{{{\mathrm{eff}}}}},1:{K_{{{\mathrm{eff}}}}})}}{\boldsymbol{V}}_{G(:,1:{K_{{{\mathrm{eff}}}}})}^{{\mathrm{H}}} $，$ {{\boldsymbol{U}}_{G(:,1:{K_{{{\mathrm{eff}}}}})}} $表示$ {{\boldsymbol{U}}_G} $矩阵的前$ {K_{{{\mathrm{eff}}}}} $列，$ {{\boldsymbol{\varSigma}} _{G(1:{K_{{{\mathrm{eff}}}}},1:{K_{{{\mathrm{eff}}}}})}} $表示$ {{\boldsymbol{\varSigma}} _G} $左上角的
$ {K_{{{\mathrm{eff}}}}} \times {K_{{{\mathrm{eff}}}}} $子矩阵，$ {{\boldsymbol{V}}_{G(:,1:{K_{{{\mathrm{eff}}}}})}} $表示$ {{\boldsymbol{V}}_G} $矩阵的前$ {K_{{{\mathrm{eff}}}}} $列$ {{\boldsymbol{Z}}^0} = {{\boldsymbol{C}}^{ - 1/2}}{{\boldsymbol{X}}^0} $, $ {{\boldsymbol{J}}^0} = {{\boldsymbol{X}}^0} $, $ {\boldsymbol{E}}^0 = 0 $, $ {\boldsymbol{Q}}^0_1 = 0 $, $ {\boldsymbol{Q}}_2^0 = 0 $, ${\boldsymbol{Q}}_3^0 = 0 $, $ k = 0 $ 迭代：While $ k \lt {K_{{\max}}} $ and $ \Vert {{\boldsymbol{X}}}^{k}-{{\boldsymbol{X}}}^{k-1}{\Vert }_{\text{F}}/\Vert {{\boldsymbol{X}}}^{k-1}{\Vert }_{\text{F}} \gt \varepsilon $ do: 1. 更新自适应权重： 计算$ {{\boldsymbol{U}}^k} = {{\boldsymbol{C}}^{ - 1/2}}{{\boldsymbol{X}}^k} + {\boldsymbol{Q}}_2^k/\mu _2^k $ 对$ {{\boldsymbol{U}}^k} $进行SVD：$ {{\boldsymbol{U}}^k} = {\boldsymbol{U\varSigma}} {{\boldsymbol{V}}^{\mathrm{H}}} $，计算奇异值权重$ {{w_y} = {\sigma _y}({{\boldsymbol{U}}^k})/\sum\limits_{z = 1}^{{\mathrm{rank}}({{\boldsymbol{U}}^k})} {{\sigma _z}} ({{\boldsymbol{U}}^k})}\;\;{y = 1, \cdots ,{\mathrm{rank}}({{\boldsymbol{U}}^k})} $ 更新稀疏性参数：更新稀疏阈值$ \lambda _1^k = \lambda _1^0 \cdot \frac{{{{\left\| {{{\boldsymbol{J}}^k}} \right\|}_0}}}{{{N_{{\mathrm{r}}}}{N_{{\mathrm{a}}}}}} $ 2. 更新$ {\boldsymbol{Z}}^{k+1} $： $ {{\boldsymbol{Z}}^{k + 1}} = \mathcal{U} \cdot {\mathcal{D}_\alpha }({\boldsymbol{\varSigma}} ) \cdot {\mathcal{V}^{\mathrm{H}}} $，其中$ {\mathcal{D}_\alpha }({\boldsymbol{\varSigma}} ) = {\mathrm{diag}}\left( {\max\left( {{\sigma _y} - {\alpha _y},0} \right)} \right) $ 3. 更新$ {\boldsymbol{J}}^{k+1} $： $ {\boldsymbol{V}}^k={\boldsymbol{X}}^k+Q_3^k/\mu_3^k,\;\;{\boldsymbol{J}}^{k+1}={\mathrm{sign}}({\boldsymbol{V}}^k) \odot\max\left(|{\boldsymbol{V}}^k|-\dfrac{ \lambda_1^k}{\mu_3},0 \right) $ 4. 更新$ {\boldsymbol{X}}^{k+1} $： 构造线性算子$ \mathcal{H}({\boldsymbol{X}}) = \mu _1^k{\boldsymbol{\Phi}} _{{\mathrm{r}}}^{{\mathrm{H}}}({{\boldsymbol{\Phi}} _{{\mathrm{r}}}}{\boldsymbol{X\Phi}} _{{\mathrm{a}}}^{{\mathrm{H}}}){{\boldsymbol{\Phi}} _{{\mathrm{a}}}} + \mu _2^k{{\boldsymbol{C}}^{ - 1}}{\boldsymbol{X}} + \mu _3^k{\boldsymbol{X}} $及右端项$ {{\boldsymbol{B}}^k} $以$ {{\boldsymbol{X}}^k} $为初值，应用2D-CGLS算法求解$ \mathcal{H}({\boldsymbol{X}}) = {{\boldsymbol{B}}^k} $ 5. 更新${\boldsymbol{E}}^{k + 1} $： $ {\boldsymbol{W}}^k={\boldsymbol{S}}-{\boldsymbol{\Phi}}{\boldsymbol{X}}^{k+1}+{\boldsymbol{Q}}_1^k/\mu_1^k $，$ {\boldsymbol{E}}^{k + 1} = \dfrac{\mu_1}{ \lambda_2+\mu_1}{\boldsymbol{W}}^k $ 6. 更新乘子： $ {\boldsymbol{Q}}_1^{k + 1} = {\boldsymbol{Q}}_1^k + {\mu _1}({\boldsymbol{S}} - {\boldsymbol{\Phi }}{{\boldsymbol{X}}^{k + 1}} - {{\boldsymbol{E}}^{k + 1}}) $, $ {\boldsymbol{Q}}_2^{k + 1} = {\boldsymbol{Q}}_2^k + {\mu _2}({{\boldsymbol{C}}^{ - 1/2}}{{\boldsymbol{X}}^{k + 1}} - {{\boldsymbol{Z}}^{k + 1}}) $, $ {\boldsymbol{Q}}_3^{k + 1} = {\boldsymbol{Q}}_3^k + {\mu _3}({{\boldsymbol{X}}^{k + 1}} - {{\boldsymbol{J}}^{k + 1}}) $ 7. 更新惩罚系数：$ \mu_w^{k+1}=\rho\mu_w^k $ for $ w = 1,2,3 $ 8. $ k = k + 1 $ End While 输出：超分辨图像$ {\boldsymbol{X}} $ 
下载: 导出CSV
表 1 VEWR仿真参数
Table 1. Simulation parameters of VEWR
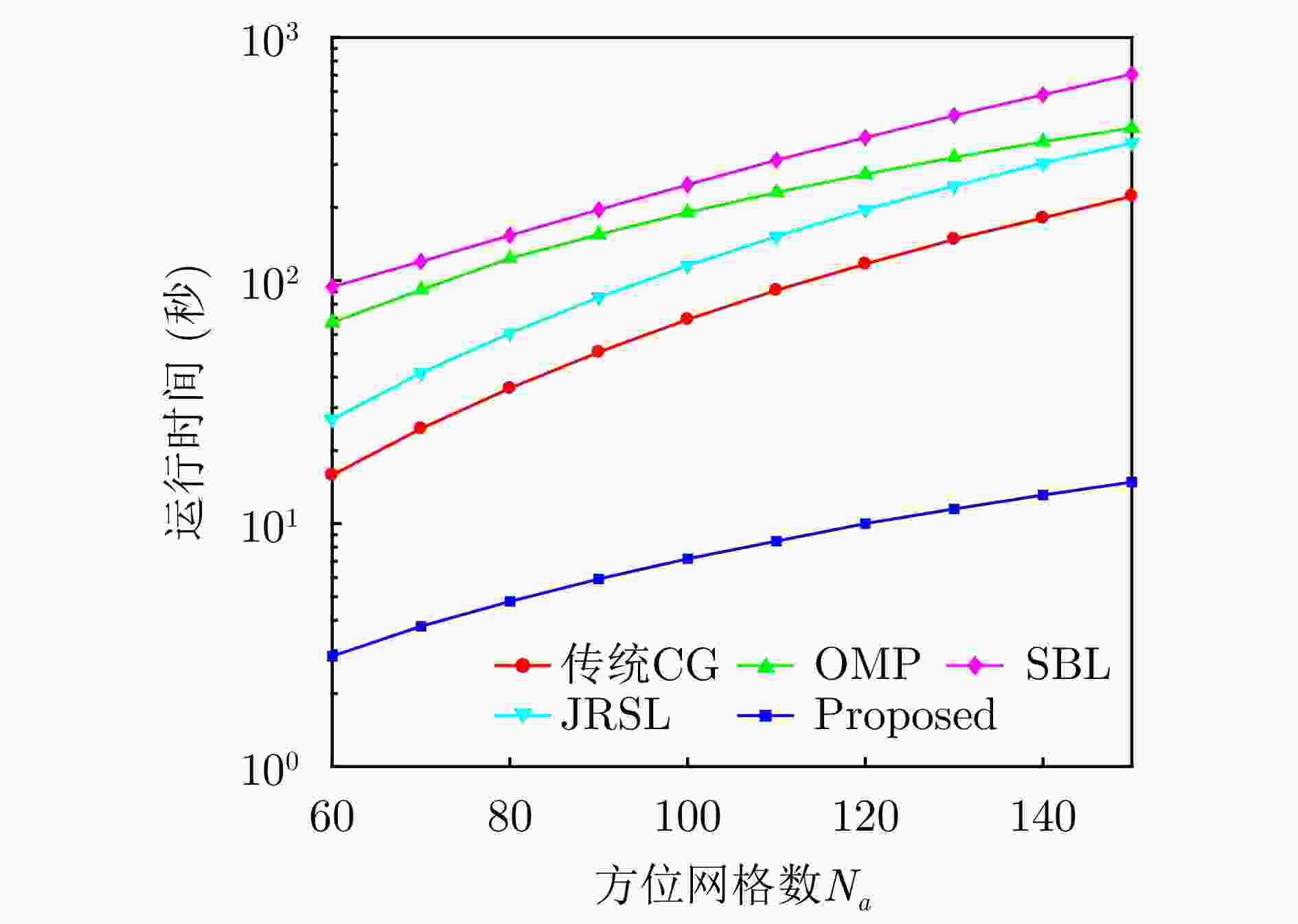
参数 数值 载频f0 10 GHz 带宽B 180 MHz 脉冲周期$ PR $ 50 μs 子脉冲数D 100 阵列半径a 0.5 m 目标俯仰角$ {\theta _0} $ $0.3 \pi $ 目标距离范围 (880, 920) m 目标方位角范围 ($0\pi $, $0.5\pi $) rad 距离单元数$ {N_{r}} $ 120 方位网格数$ {N_{{\mathrm{a}}}} $ 120
下载: 导出CSV
-
[1] 马晖, 胡敦法, 师竹雨, 等. 基于涡旋电磁波的雷达应用研究进展[J]. 现代雷达, 2023, 45(5): 27–41. doi: 10.16592/j.cnki.1004-7859.2023.05.003.MA Hui, HU Dunfa, SHI Zhuyu, et al. Research progress of radar applications based on vortex electromagnetic waves[J]. Modern Radar, 2023, 45(5): 27–41. doi: 10.16592/j.cnki.1004-7859.2023.05.003. [2] 王健, 王仲阳, 刘劲峰, 等. 基于涡旋电磁波的无线通信技术(特邀)[J]. 激光与光电子学进展, 2024, 61(7): 0706001. doi: 10.3788/LOP240754.WANG Jian, WANG Zhongyang, LIU Jinfeng, et al. Wireless communication technologies using vortex electromagnetic waves (Invited)[J]. Laser & Optoelectronics Progress, 2024, 61(7): 0706001. doi: 10.3788/LOP240754. [3] ZHANG Lingling, ZHU Yongzhong, CHEN Yijun, et al. Three-dimensional micro-Doppler parameter estimation of rotor target based on VEMW radar[J]. IEEE Sensors Journal, 2025, 25(6): 10155–10162. doi: 10.1109/JSEN.2025.3533009. [4] 吴丹, 李佳豪, 唐杰, 等. 基于轨道角动量编码的机载MDI-QKD系统性能分析方法研究[J]. 激光与光电子学进展, 2024, 61(15): 1506007. doi: 10.3788/LOP241377.WU Dan, LI Jiahao, TANG Jie, et al. Performance analysis of airborne MDI-QKD based on orbital angular momentum encoding[J]. Laser & Optoelectronics Progress, 2024, 61(15): 1506007. doi: 10.3788/LOP241377. [5] 袁航, 何其芳, 罗迎, 等. 涡旋电磁波雷达平动旋转目标三维微动参数提取方法[J]. 雷达学报, 2023, 12(4): 804–816. doi: 10.12000/JR23065.YUAN Hang, HE Qifang, LUO Ying, et al. Three-dimensional micro-motion parameters extraction of translational rotating targets based on vortex electromagnetic wave radar[J]. Journal of Radars, 2023, 12(4): 804–816. doi: 10.12000/JR23065. [6] LIU Kang, LIU Hongyan, LI Shuangxun, et al. Three-dimensional object imaging with vortex wave tomography[J]. Optics Express, 2025, 33(10): 20798–20806. doi: 10.1364/OE.563860. [7] 潘浩然, 马晖, 胡敦法, 等. 基于涡旋电磁波新体制的雷达前视三维成像[J]. 雷达学报(中英文), 2024, 13(5): 1109–1122. doi: 10.12000/JR24123.PAN Haoran, MA Hui, HU Dunfa, et al. Novel forward-looking three-dimensional imaging based on vortex electromagnetic wave radar[J]. Journal of Radars, 2024, 13(5): 1109–1122. doi: 10.12000/JR24123. [8] YANG Ting, SHI Hongyin, GUO Jianwen, et al. A fast and high-resolution imaging method for electromagnetic vortex radar using uniform concentric circular arrays[J]. IEEE Transactions on Microwave Theory and Techniques, 2025, 73(5): 3004–3015. doi: 10.1109/TMTT.2024.3484164. [9] LI Lianlin and LI Fang. Beating the Rayleigh limit: Orbital-angular-momentum-based super-resolution diffraction tomography[J]. Physical Review E, 2013, 88(3): 033205. doi: 10.1103/PhysRevE.88.033205. [10] 王建秋, 刘康, 王煜, 等. 涡旋电磁波雷达成像分辨力研究[J]. 雷达学报, 2021, 10(5): 680–690. doi: 10.12000/JR21054.WANG Jianqiu, LIU Kang, WANG Yu, et al. Resolution analysis of vortex electromagnetic radar imaging[J]. Journal of Radars, 2021, 10(5): 680–690. doi: 10.12000/JR21054. [11] QU Haiyou, LI Shiyuan, CHEN Chang, et al. High-resolution orbital angular momentum imaging with the removal of Bessel function modulation effect[J]. IEEE Transactions on Microwave Theory and Techniques, 2024, 72(4): 2577–2590. doi: 10.1109/TMTT.2023.3314107. [12] 屈海友, 程迪, 陈畅, 等. 涡旋雷达高分辨率稀疏自校正相位误差成像[J]. 雷达学报, 2021, 10(5): 699–717. doi: 10.12000/JR21094.QU Haiyou, CHENG Di, CHEN Chang, et al. High-resolution sparse self-calibration imaging for vortex radar with phase error[J]. Journal of Radars, 2021, 10(5): 699–717. doi: 10.12000/JR21094. [13] ZHAO Hao and WANG Kaizhi. Orbital-angular-momentum-based radar imaging by dice regularized orthogonal matching pursuit[C]. 2020 IEEE 5th International Conference on Signal and Image Processing (ICSIP), Nanjing, China, 2020: 446–450. doi: 10.1109/ICSIP49896.2020.9339258. [14] WEN Peng, HE Zi, DING Dazhi, et al. Vortex electromagnetic wave three-dimensional imaging based on OMP[C]. 2024 IEEE International Conference on Computational Electromagnetics (ICCEM), Nanjing, China, 2024: 1–3. doi: 10.1109/ICCEM60619.2024.10559065. [15] LIU Kang, LI Xiang, GAO Yue, et al. High-resolution electromagnetic vortex imaging based on sparse Bayesian learning[J]. IEEE Sensors Journal, 2017, 17(21): 6918–6927. doi: 10.1109/JSEN.2017.2754554. [16] YUAN Hang, CHEN Yijun, LUO Ying, et al. A resolution-improved imaging algorithm based on uniform circular array[J]. IEEE Antennas and Wireless Propagation Letters, 2022, 21(3): 461–465. doi: 10.1109/LAWP.2021.3135806. [17] LI Rui, MA Zhiqiang, ZHANG Qun, et al. Sparse-Bayesian-learning-based translational motion estimation of electromagnetic vortex imaging[J]. The Journal of Engineering, 2019, 2019(21): 8002–8005. doi: 10.1049/joe.2019.0667. [18] JIANG Ting, HU Jun, LUO Siqi, et al. A fast and super-resolution method of vortex-based imaging[J]. IEEE Antennas and Wireless Propagation Letters, 2023, 22(9): 2225–2229. doi: 10.1109/LAWP.2023.3281617. [19] LI Xue, ZHOU Ningning, ZHU Shitao, et al. Resolution analysis of coincidence imaging based on OAM beams with equal divergence angle[J]. IEEE Transactions on Antennas and Propagation, 2023, 71(3): 2891–2896. doi: 10.1109/TAP.2022.3233718. [20] YANG Ting, SHI Hongyin, GUO Jianwen, et al. 3D sparse ISAR imaging with multiple plane spiral OAM electromagnetic waves[J]. IEEE Sensors Journal, 2022, 22(15): 15082–15097. doi: 10.1109/JSEN.2022.3179925. [21] WANG Siyuan, CHEN Yijun, QU Yi, et al. Vortex electromagnetic radar imaging and adaptive resource scheduling based on uniform concentric circular arrays[J]. IEEE Sensors Journal, 2024, 24(14): 22658–22671. doi: 10.1109/JSEN.2024.3405969. [22] QIU Wei, ZHOU Jianxiong, and FU Qiang. Jointly using low-rank and sparsity priors for sparse inverse synthetic aperture radar imaging[J]. IEEE Transactions on Image Processing, 2020, 29: 100–115. doi: 10.1109/TIP.2019.2927458. [23] TANG Junkui, RAN Lei, LIU Zheng, et al. A weighted low-rank and sparse constraint-based multichannel radar forward-looking imaging method[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2025, 18: 12973–12987. doi: 10.1109/JSTARS.2025.3568783. [24] ZHOU Peng, ZHU Yanli, MA Mingyu, et al. ISAR super-resolution imaging approach based on low-rank sparse joint constraint under low SNR[J]. IEEE Sensors Journal, 2024, 24(3): 3191–3201. doi: 10.1109/JSEN.2023.3340150. [25] QU Haiyou, CHEN Chang, LIU Jun, et al. Enhanced vortex wavefront modulated radar forward-looking variational Bayesian hierarchical structural sparse imaging by leveraging the continuity of target scene[J]. IEEE Transactions on Aerospace and Electronic Systems, 2025, 61(3): 5962–5979. doi: 10.1109/TAES.2024.3524367. [26] REN Xiaozhen, CUI Jing, BAI Yanwen, et al. Low-rank and patch-based method for enhanced sparse ISAR imaging[J]. IEEE Sensors Journal, 2023, 23(9): 9560–9570. doi: 10.1109/JSEN.2023.3258504. [27] ZENG Chuangzhan, ZHU Weigang, JIA Xin, et al. Sparse aperture ISAR imaging method based on joint constraints of sparsity and low rank[J]. IEEE Transactions on Geoscience and Remote Sensing, 2021, 59(1): 168–181. doi: 10.1109/TGRS.2020.2994179. [28] TANG Junkui, LIU Zheng, RAN Lei, et al. Enhancing forward-looking image resolution: Combining low-rank and sparsity priors[J]. IEEE Transactions on Geoscience and Remote Sensing, 2023, 61: 5100812. doi: 10.1109/TGRS.2023.3237332. [29] YANG Ting, SHI Hongyin, GUO Jianwen, et al. Super-resolution performance studies for orbital-angular-momentum-based imaging radar[J]. International Journal of Remote Sensing, 2021, 42(21): 8185–8206. doi: 10.1080/01431161.2021.1975842. [30] 戴彧虹, 刘泽显. 非线性共轭梯度法研究进展[J]. 中国科学: 数学, 2025, 55(2): 427–450. doi: 10.1360/SSM-2024-0144.DAI Yuhong and LIU Zexian. Advances in nonlinear conjugate gradient methods[J]. Scientia Sinica Mathematica, 2025, 55(2): 427–450. doi: 10.1360/SSM-2024-0144. [31] LI Ting and WAN Zhong. New adaptive Barzilai-Borwein step size and its application in solving large-scale optimization problems[J]. The Anziam Journal, 2019, 61(1): 76–98. doi: 10.1017/S1446181118000263. [32] QIAN Fulan, YUAN Bei, CHEN Hai, et al. Enhancing the transferability of adversarial examples based on Nesterov momentum for recommendation systems[J]. IEEE Transactions on Big Data, 2023, 9(5): 1276–1287. doi: 10.1109/TBDATA.2023.3248626. [33] LIU Kang, CHENG Yongqiang, LI Xiang, et al. Microwave-sensing technology using orbital angular momentum: Overview of its advantages[J]. IEEE Vehicular Technology Magazine, 2019, 14(2): 112–118. doi: 10.1109/MVT.2018.2890673. [34] HASHEMPOUR H R. Sparsity-driven ISAR imaging based on two-dimensional ADMM[J]. IEEE Sensors Journal, 2020, 20(22): 13349–13356. doi: 10.1109/JSEN.2020.3006105. -
图(19) / 表(2)
计量
- 文章访问数:
- HTML全文浏览量:
- PDF下载量:
- 被引次数: 0
