作者中心
专家审稿
责编办公
编辑办公
Fast and Gridless Sparse Recovery STAP Method Based on Nonconvex Relaxation of Atomic Norm
-
摘要: 稀疏恢复空时自适应处理(SR-STAP)方法因其对训练样本的极低需求，在非均匀杂波环境下体现出显著优势。然而，由于需要对空时平面进行离散划分，大多数现有SR-STAP方法的性能均受到网格失配效应的约束。为了克服这个问题并提升杂波抑制性能，该文提出了一种基于非凸松弛原子范数的无网格SR-STAP方法。首先，该方法基于连续域内的原子构建无网格的杂波谱稀疏恢复模型，克服了传统基于离散字典方法的网格失配效应；其次，采用原子范数的非凸松弛形式并按照重加权策略迭代执行优化过程，有效突破了分辨率的限制；另外，针对半正定规划求解复杂度高的问题，该文提出了一种基于改进交替方向乘子法(ADMM)的快速求解方案。该方案在ADMM框架基础上，利用杂波协方差矩阵的低秩和block-Toeplitz特性，通过近似半正定投影技术进一步降低算法的复杂度，并采用基于超梯度下降的自适应惩罚系数加快算法的收敛速度。仿真和实测数据结果表明，与现有的SR-STAP方法相比，该文提出的方法能够以更高的计算效率获得更好的杂波抑制和目标检测性能。Abstract: Sparse Recovery-based Space-Time Adaptive Processing (SR-STAP) methods offer significant advantages in nonhomogeneous clutter environments owing to their minimal requirement for training samples. However, the performance of most existing SR-STAP methods is limited by the grid mismatch effect, which arises from the discretization of the space-time plane. To address this problem and enhance clutter suppression, this paper proposes a gridless SR-STAP method based on a nonconvex relaxation of atomic norm. The proposed method formulates a gridless sparse recovery model using atoms in the continuous domain, overcoming the grid mismatch effect inherent in traditional discrete dictionary-based methods. Furthermore, a nonconvex relaxation of atomic norm is employed, with optimization progress iteratively executed using a reweighting strategy, which effectively surpasses the resolution limit. In addition, to address the high computational complexity associated with solving semidefinite programming, a fast solution scheme based on an improved Alternating Direction Method of Multipliers (ADMM) is proposed. This scheme exploits the low-rank and block-Toeplitz properties of the clutter covariance matrix, reduces the algorithm’s complexity using an approximate positive semidefinite projection technique, and accelerates convergence with an adaptive penalty parameter based on hypergradient descent. Simulation results and real-measured data demonstrate that the proposed method achieves superior clutter suppression, robust target detection performance, and higher computational efficiency compared to existing SR-STAP methods.
-
图 3 不同迭代次数下估计的$ \mathcal{T}({\boldsymbol V}) $特征谱
Figure 3. Eigenspectra of estimated $ \mathcal{T}({\boldsymbol V}) $ against different number of iterations
图 4 不同参数设置下估计的$ \mathcal{T}({\boldsymbol V}) $特征谱
Figure 4. Eigenspectra of estimated $ \mathcal{T}({\boldsymbol V}) $ under different parameter settings
图 5 不同训练样本下的平均SCNR损失对比
Figure 5. Comparison of average SCNRloss against the number of training samples
图 6 $\delta = 0^\circ ,\beta = 0.8$时的杂波谱
Figure 6. Clutter spectra when $\delta = 0^\circ ,\beta = 0.8$
图 7 $\delta = 90^\circ ,\beta = 1.0$时的杂波谱
Figure 7. Clutter spectra when $\delta = 90^\circ ,\beta = 1.0$
图 8 不同方法重构CNCM的特征谱对比
Figure 8. Comparison of eigenspectra of CNCM reconstructed by different methods
图 10 存在幅相误差时不同方法的信杂噪比损失对比
Figure 10. Comparison of SCNRloss of different methods in the presence of amplitude and phase errors
1 基于RNLA的近似半正定投影流程表
1. The flow table of approximate PSD projection based on RNLA
输入：待投影矩阵${{\boldsymbol{P}}_{{\text{temp}}}}$，目标秩r，过采样数o，幂迭代次数q (1) 构造随机复高斯矩阵 ${\boldsymbol{\varOmega}} \in {\mathbb{C}^{(NK + L) \times (r + o)}}$ (2) 使用$ {{\boldsymbol{P}}_{{\text{temp}}}} $与$ {\boldsymbol{P}}_{{\text{temp}}}^{\rm H} $对$ {\boldsymbol{\varOmega }}$进行q次幂迭代 $ {\boldsymbol{X}} = {({{\boldsymbol{P}}_{{\text{temp}}}}{\boldsymbol{P}}_{{\text{temp}}}^{\rm H})^q}{{\boldsymbol{P}}_{{\text{temp}}}}{\boldsymbol{\varOmega}} $ (3) 利用经济QR分解获得X的正交基 $ {{\boldsymbol{Q}}_{{\boldsymbol{P}}},\sim} = {\text{qr}}( {\boldsymbol{X}} $,'econ') (4) 对低维矩阵$ {\boldsymbol{Q}}_{\boldsymbol{P}}^{\rm H}{{\boldsymbol{P}}_{{\text{temp}}}}{{\boldsymbol{Q}}_{\boldsymbol{P}}} $进行特征值分解 ${\boldsymbol{Q}}_{\boldsymbol{P}}^{\rm H}{{\boldsymbol{P}}_{{\text{temp}}}}{{\boldsymbol{Q}}_{\boldsymbol{P}}} = \displaystyle \sum \limits_i^{r + o} {\delta _i}{{\boldsymbol{\beta}} _i}{\boldsymbol{\beta}} _i^{\rm H}$ (5) 截断负特征值并重构近似PSD矩阵 $ \hat {\boldsymbol{P}} = \displaystyle\sum \limits_i^{r + o} {\text{max}}({\delta _i},0){{\boldsymbol{\beta }}_i}{\boldsymbol{\beta }}_i^{\rm H} $ 
下载: 导出CSV
2 FNCANM-STAP处理流程表
2. Flow table of FNCANM-STAP
输入：训练样本，ANM正则化参数$ \gamma $，非凸松弛参数a，p，衰
减因子${\delta _p}$，MM迭代次数${T_{{\text{MM}}}}$，初始惩罚系数$ {\rho _0} $，ADMM最大
迭代次数${T_{{\text{ADMM}}}}$，终止阈值$ {\varepsilon _A} $，超梯度下降步长$\kappa '$, 过采样数
o，幂迭代次数q(1) 初始化：$ {{\boldsymbol{V}}_0} ={\bf{ 0}} $ (2) for $i = 1:{T_{{\text{MM}}}}$ (迭代1) (3) 利用式(23)确定加权矩阵W (4) 初始化：${{\boldsymbol{P}}^0} = {\bf{0}}$，$ {{\boldsymbol Q}^0} = {\bf{0}} $ (5) for $t = 1:{T_{{\text{ADMM}}}}$ (迭代2) (6) 利用式(35)—式(37)，更新${\boldsymbol{Y}}_{\text{c}}^{t + 1},{\boldsymbol{V}}_i^{t + 1},{{\boldsymbol{C}}^{t + 1}}$ (7) 利用MaPP算法获取目标秩r (8) 利用算法1中的算法更新$ {{\boldsymbol{P}}^{t + 1}} $ (9) 利用式(48)更新${{\boldsymbol Q}^{t + 1}}$ (10) 利用式(47)更新$ {\rho ^{t + 1}} $ (11) if $ \parallel {\boldsymbol{V}}_i^{t + 1} - {\boldsymbol{V}}_i^t\parallel _{\text{F}}^2/\parallel {\boldsymbol{V}}_i^{t + 1}\parallel _{\text{F}}^2 \le {\varepsilon _A} $： (12) 停止迭代2 (13) end (14) 更新平滑系数：$p = p/{\delta _p}$ (15) end (16) 利用最后一次迭代获取的$ \hat {\mathcal{T}}({\boldsymbol{V}}) $及式(24)和式(25)，计算
CNCM的估计值$\hat {\boldsymbol{R}}_{{\text{cn}}}^{{\mathrm{NCANM}}}$(17) 利用式(26)计算空时滤波器权矢量${{\boldsymbol{w}}_{{\text{NCANM}}}}$
下载: 导出CSV
表 1 不同方法的计算复杂度
Table 1. Computational complexity of different methods
算法 复乘法次数 计算复杂度 FOCUSS-STAP $ O({T_{{\text{FOCUSS}}}}({(NK)^3}{({\rho _{\text{s}}}{\rho _{\text{d}}} + 1)^2} + {(NK)^2}{\rho _{\text{s}}}{\rho _{\text{d}}}L)) $ $ O({T_{{\text{FOCUSS}}}}{(NK)^3}{({\rho _{\text{s}}}{\rho _{\text{d}}})^2}) $ ANM-CVX-STAP $ O({\text{log(}}1/\varepsilon ){({L^2} + (2N - 1)(2K - 1) + NKL)^2}{(NK + L)^{2.5}}) $ $ O({\text{log(}}1/\varepsilon ){(NK)^{3.5}}) $ NCANM-CVX-STAP $ O({T_{{\text{MM}}}}({\text{log(}}1/\varepsilon ){({L^2} + (2N - 1)(2K - 1) + NKL)^2}{(NK + L)^2})) $ $ O({T_{{\text{MM}}}}{\text{log(}}1/\varepsilon ){(NK)^{3.5}}) $ FNCANM-STAP $ O({T_{{\text{MM}}}}{T_{{\text{FNCANM}}}}(({k_{\mathrm{r}}} + 1){(NK + L)^2} + k_{\mathrm{r}} + {(NK)^2}({N_{\mathrm{R}}} + 1) + 6NK + {L^2} + L)) $ $ O({T_{{\text{MM}}}}{T_{{\text{FNCANM}}}}{k_{\mathrm{r}}}{(NK)^2}) $
下载: 导出CSV
表 2 雷达系统仿真参数
Table 2. Simulation parameters of the radar system
参数 数值 雷达波长$\lambda $ 0.2 m 脉冲重复频率${f_{\text{r}}}$ 3000 Hz阵元间距d 0.1 m 平台高度H 5 km 距离R 20 km 杂噪比${\text{CNR}}$ 40 dB 阵元数目N 8 脉冲数目K 8
下载: 导出CSV
表 3 不同方法的平均运行时间(s)
Table 3. Average run time of different methods (s)
算法 $N = K = 8$ $N = K = 16$ FOCUSS-STAP (${\rho _{\mathrm{s}}} = {\rho _{\mathrm{d}}} = 4$) 1.8336 118.9174 FOCUSS-STAP (${\rho _{\mathrm{s}}} = {\rho _{\mathrm{d}}} = 6$) 12.0256 1198.5405 ANM-CVX-STAP 12.0123 484.6128 NCANM-CVX-STAP 33.2512 1421.3224 FNCANM-STAP 1.6231 19.0949
下载: 导出CSV
表 4 Monutain-Top数据集的主要参数
Table 4. The main parameter of Monutain-Top dataset
参数 数值 脉冲重复频率 625 Hz 阵元间距 0.033 m 阵元数目 14 脉冲数目 16 带宽 500 kHz 总距离单元数 403 目标所在距离单元数 147 目标多普勒频率 156 Hz 目标角度 275°
下载: 导出CSV
表 5 Monutain-Top数据处理结果
Table 5. The results of Monutain-Top dataset
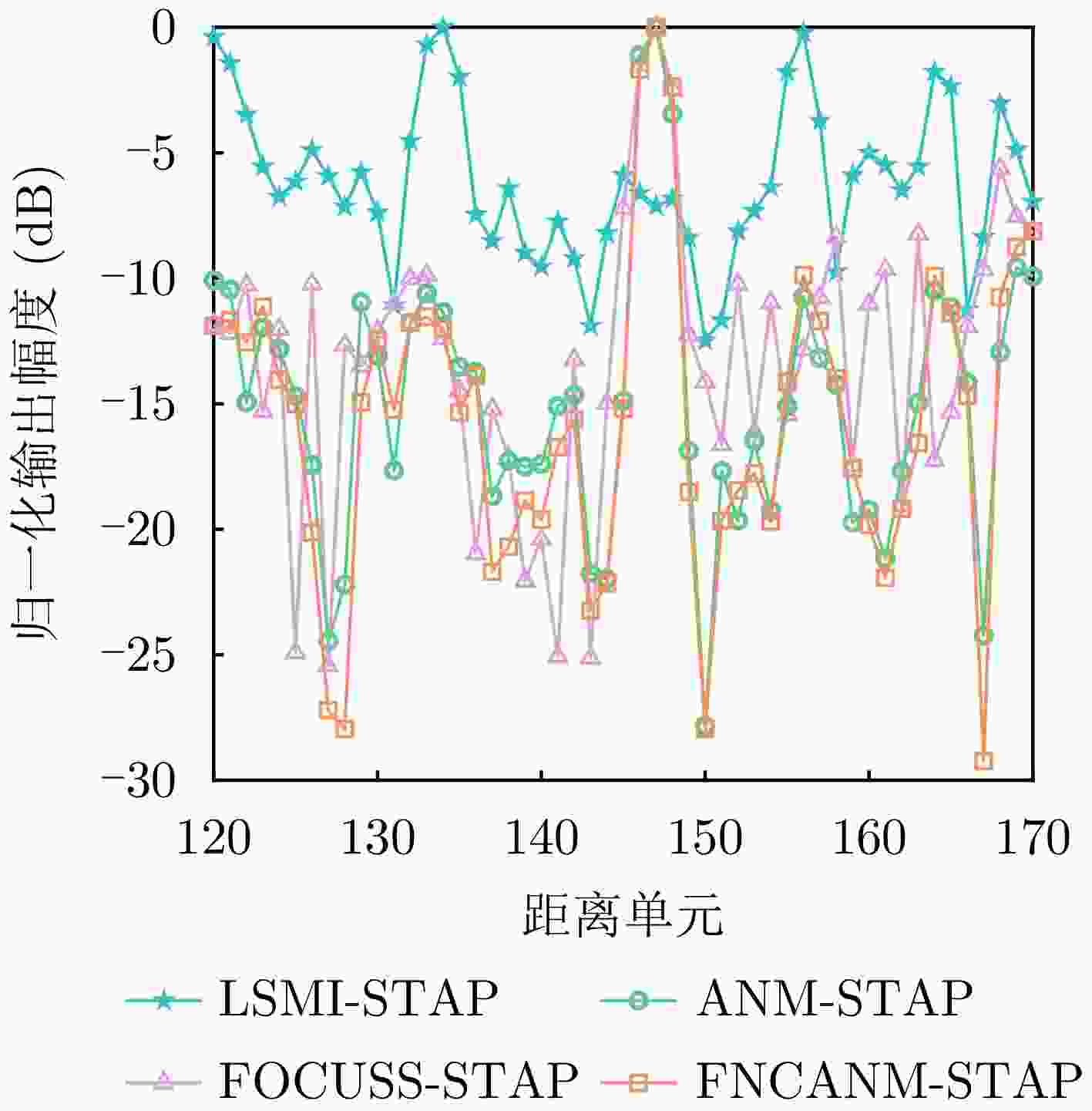
算法 输出功率差值(dB) 运行时间(s) FOCUSS-STAP 13.8295 83.2056 ANM-STAP 15.2041 175.5791 FNCANM-STAP 15.9341 15.4252
下载: 导出CSV
-
[1] 谢文冲, 段克清, 王永良. 机载雷达空时自适应处理技术研究综述[J]. 雷达学报, 2017, 6(6): 575–586. doi: 10.12000/JR17073.XIE Wenchong, DUAN Keqing, and WANG Yongliang. Space time adaptive processing technique for airborne radar: An overview of its development and prospects[J]. Journal of Radars, 2017, 6(6): 575–586. doi: 10.12000/JR17073. [2] REED I S, MALLETT J D, and BRENNAN L E. Rapid convergence rate in adaptive arrays[J]. IEEE Transactions on Aerospace and Electronic Systems, 1974, AES-10(6): 853–863. doi: 10.1109/TAES.1974.307893. [3] KLEMM R. Comparison between monostatic and bistatic antenna configurations for STAP[J]. IEEE Transactions on Aerospace and Electronic Systems, 2000, 36(2): 596–608. doi: 10.1109/7.845248. [4] MELVIN W L. A STAP overview[J]. IEEE Aerospace and Electronic Systems Magazine, 2004, 19(1): 19–35. doi: 10.1109/MAES.2004.1263229. [5] KLEMM R. Adaptive airborne MTI: An auxiliary channel approach[J]. IEE Proceedings F (Communications, Radar and Signal Processing), 1987, 134(3): 269–276. doi: 10.1049/ip-f-1.1987.0054. [6] HAIMOVICH A M and BAR-NESS Y. An eigenanalysis interference canceler[J]. IEEE Transactions on Signal Processing, 1991, 39(1): 76–84. doi: 10.1109/78.80767. [7] MELVIN W L and SHOWMAN G A. An approach to knowledge-aided covariance estimation[J]. IEEE Transactions on Aerospace and Electronic Systems, 2006, 42(3): 1021–1042. doi: 10.1109/TAES.2006.248216. [8] PILLAI S U, LIM Y L, and GUERCI J R. Generalized forward/backward subaperture smoothing techniques for sample starved STAP[J]. IEEE Transactions on Signal Processing, 2000, 48(12): 3569–3574. doi: 10.1109/78.887049. [9] DONOHO D L. Compressed sensing[J]. IEEE Transactions on Information Theory, 2006, 52(4): 1289–1306. doi: 10.1109/TIT.2006.871582. [10] MALLAT S G and ZHANG Zhifeng. Matching pursuits with time-frequency dictionaries[J]. IEEE Transactions on Signal Processing, 1993, 41(12): 3397–3415. doi: 10.1109/78.258082. [11] 马泽强, 王希勤, 刘一民, 等. 基于稀疏恢复的空时二维自适应处理技术研究现状[J]. 雷达学报, 2014, 3(2): 217–228. doi: 10.3724/SP.J.1300.2014.14002.MA Zeqiang, WANG Xiqin, LIU Yimin, et al. An overview on sparse recovery-based STAP[J]. Journal of Radars, 2014, 3(2): 217–228. doi: 10.3724/SP.J.1300.2014.14002. [12] SUN Ke, MENG Huadong, WANG Yongliang, et al. Direct data domain STAP using sparse representation of clutter spectrum[J]. Signal Processing, 2011, 91(9): 2222–2236. doi: 10.1016/j.sigpro.2011.04.006. [13] DUAN Keqing, WANG Zetao, XIE Wenchong, et al. Sparsity-based STAP algorithm with multiple measurement vectors via sparse Bayesian learning strategy for airborne radar[J]. IET Signal Processing, 2017, 11(5): 544–553. doi: 10.1049/iet-spr.2016.0183. [14] BAI Gatai, TAO Ran, ZHAO Juan, et al. Parameter-searched OMP method for eliminating basis mismatch in space-time spectrum estimation[J]. Signal Processing, 2017, 138: 11–15. doi: 10.1016/j.sigpro.2017.03.003. [15] TANG Gongguo, BHASKAR B N, SHAH P, et al. Compressed sensing off the grid[J]. IEEE Transactions on Information Theory, 2013, 59(11): 7465–7490. doi: 10.1109/TIT.2013.2277451. [16] YANG Zai and XIE Lihua. On gridless sparse methods for line spectral estimation from complete and incomplete data[J]. IEEE Transactions on Signal Processing, 2015, 63(12): 3139–3153. doi: 10.1109/TSP.2015.2420541. [17] CANDÈS E J and FERNANDEZ-GRANDA C. Towards a mathematical theory of super-resolution[J]. Communications on Pure and Applied Mathematics, 2014, 67(6): 906–956. doi: 10.1002/cpa.21455. [18] LI Yuanxin and CHI Yuejie. Off-the-grid line spectrum denoising and estimation with multiple measurement vectors[J]. IEEE Transactions on Signal Processing, 2016, 64(5): 1257–1269. doi: 10.1109/TSP.2015.2496294. [19] FENG Weike, GUO Yiduo, ZHANG Yongshun, et al. Airborne radar space time adaptive processing based on atomic norm minimization[J]. Signal Processing, 2018, 148: 31–40. doi: 10.1016/j.sigpro.2018.02.008. [20] YANG Zai and XIE Lihua. Enhancing sparsity and resolution via reweighted atomic norm minimization[J]. IEEE Transactions on Signal Processing, 2016, 64(4): 995–1006. doi: 10.1109/TSP.2015.2493987. [21] WU Xiaohuan, ZHU Weiping, and YAN Jun. A high-resolution DOA estimation method with a family of nonconvex penalties[J]. IEEE Transactions on Vehicular Technology, 2018, 67(6): 4925–4938. doi: 10.1109/TVT.2018.2817638. [22] 高一丁, 吴敏, 郝程鹏, 等. 无需信源数先验的快速稀疏增强DOA估计方法[J]. 海军航空大学学报, 2024, 39(5): 515–522. doi: 10.7682/j.issn.2097-1427.2024.05.001.GAO Yiding, WU Min, HAO Chengpeng, et al. Fast sparse enhanced DOA estimation method without source number priors[J]. Journal of Naval Aviation University, 2024, 39(5): 515–522. doi: 10.7682/j.issn.2097-1427.2024.05.001. [23] 黎子皓, 吴敏, 郝程鹏, 等. 使用重加权原子范数最小化的稀疏可重构直线阵列设计[J]. 声学学报, 2023, 48(6): 1174–1188. doi: 10.12395/0371-0025.2022071.LI Zihao, WU Min, HAO Chengpeng, et al. Design of sparse reconfigurable array using reweighted atomic norm minimization[J]. Acta Acustica, 2023, 48(6): 1174–1188. doi: 10.12395/0371-0025.2022071. [24] LI Zhongyue and WANG Tong. ADMM-based low-complexity off-grid space-time adaptive processing methods[J]. IEEE Access, 2020, 8: 206646–206658. doi: 10.1109/ACCESS.2020.3037652. [25] HALKO N, MARTINSSON P G, and TROPP J A. Finding structure with randomness: Probabilistic algorithms for constructing approximate matrix decompositions[J]. SIAM Review, 2011, 53(2): 217–288. doi: 10.1137/090771806. [26] CHANDRA K, XIE A, RAGAN-KELLEY J, et al. Gradient descent: The ultimate optimizer[C]. 36th International Conference on Neural Information Processing Systems, New Orleans, USA, 2022: 597. [27] CARLSON B D. Covariance matrix estimation errors and diagonal loading in adaptive arrays[J]. IEEE Transactions on Aerospace and Electronic Systems, 1988, 24(4): 397–401. doi: 10.1109/7.7181. [28] ZHOU Zhiyong and YU Jun. A new nonconvex sparse recovery method for compressive sensing[J]. Frontiers in Applied Mathematics and Statistics, 2019, 5: 14. doi: 10.3389/fams.2019.00014. [29] CHI Yuejie and FERREIRA DA COSTA M. Harnessing sparsity over the continuum: Atomic norm minimization for superresolution[J]. IEEE Signal Processing Magazine, 2020, 37(2): 39–57. doi: 10.1109/MSP.2019.2962209. [30] ECKSTEIN J and YAO Wang. Relative-error approximate versions of Douglas-Rachford splitting and special cases of the ADMM[J]. Mathematical Programming, 2018, 170(2): 417–444. doi: 10.1007/s10107-017-1160-5. [31] RONTSIS N, GOULART P, and NAKATSUKASA Y. Efficient semidefinite programming with approximate ADMM[J]. Journal of Optimization Theory and Applications, 2022, 192(1): 292–320. doi: 10.1007/s10957-021-01971-3. [32] YANG Zai, XIE Lihua, and STOICA P. Vandermonde decomposition of multilevel toeplitz matrices with application to multidimensional super-resolution[J]. IEEE Transactions on Information Theory, 2016, 62(6): 3685–3701. doi: 10.1109/TIT.2016.2553041. [33] BOYD S, PARIKH N, CHU E, et al. Distributed optimization and statistical learning via the alternating direction method of multipliers[J]. Foundations and Trends® in Machine Learning, 2010, 3(1): 1–122. doi: 10.1561/2200000016. [34] CHEN Tiancheng, MENG Yang, ZHOU Guoru, et al. An improved imaging method for highly-squinted SAR based on hyper-optimized admm[C]. 2023 IEEE International Geoscience and Remote Sensing Symposium, Pasadena, USA, 2023: 4548–4551. doi: 10.1109/IGARSS52108.2023.10281842. [35] LIU Weijian, XIE Wenchong, LI Rongfeng, et al. Adaptive detectors in the Krylov subspace[J]. Science China Information Sciences, 2014, 57(10): 1–11. doi: 10.1007/s11432-014-5080-1. [36] BRENNAN L E and REED L S. Theory of adaptive radar[J]. IEEE Transactions on Aerospace and Electronic Systems, 1973, AES-9(2): 237–252. doi: 10.1109/TAES.1973.309792. [37] ROBEY F C, FUHRMANN D R, KELLY E J, et al. A CFAR adaptive matched filter detector[J]. IEEE Transactions on Aerospace and Electronic Systems, 1992, 28(1): 208–216. doi: 10.1109/7.135446. [38] TITI G W and MARSHALL D F. The ARPA/NAVY mountaintop program: Adaptive signal processing for airborne early warning radar[C]. 1996 IEEE International Conference on Acoustics, Speech, and Signal Processing Conference Proceedings, Atlanta, USA, 1996: 1165–1168. doi: 10.1109/ICASSP.1996.543572. [39] AUBRY A, DE MAIO A, PALLOTTA L, et al. Covariance matrix estimation via geometric barycenters and its application to radar training data selection[J]. IET Radar, Sonar & Navigation, 2013, 7(6): 600–614. doi: 10.1049/iet-rsn.2012.0190. -
图(15) / 表(7)
计量
- 文章访问数:
- HTML全文浏览量:
- PDF下载量:
- 被引次数: 0
