作者中心
专家审稿
责编办公
编辑办公
A Moving Target Tracking Method Based on Adaptive Tensor Decomposition in Bistatic MIMO Radar
-
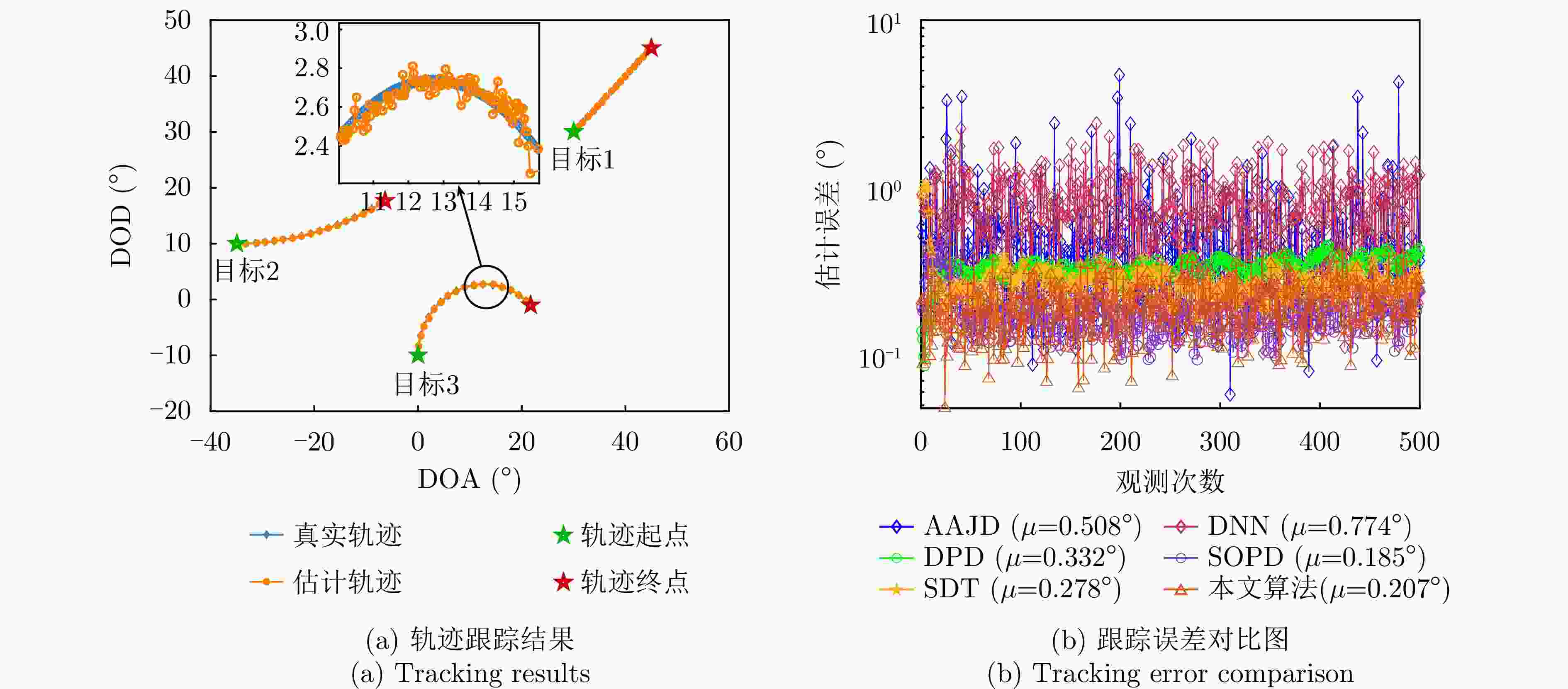
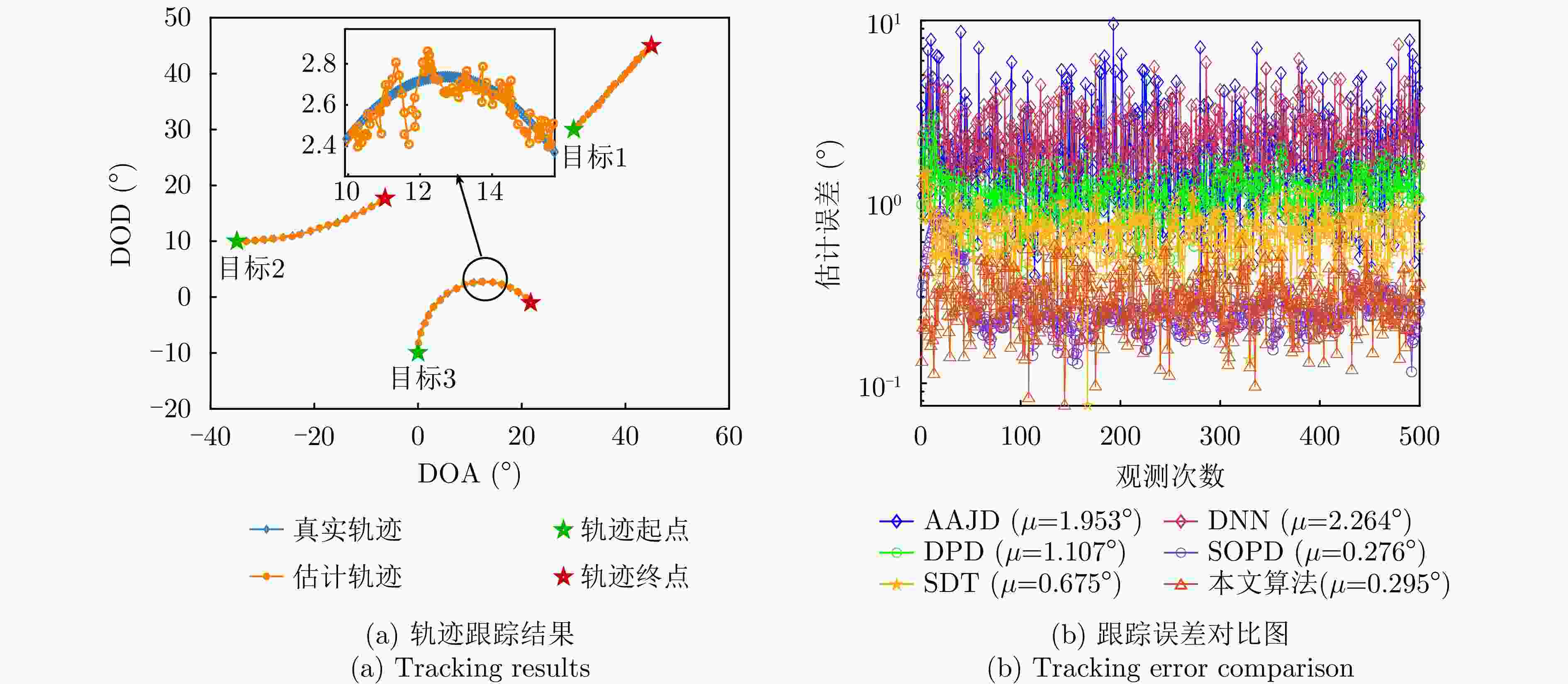
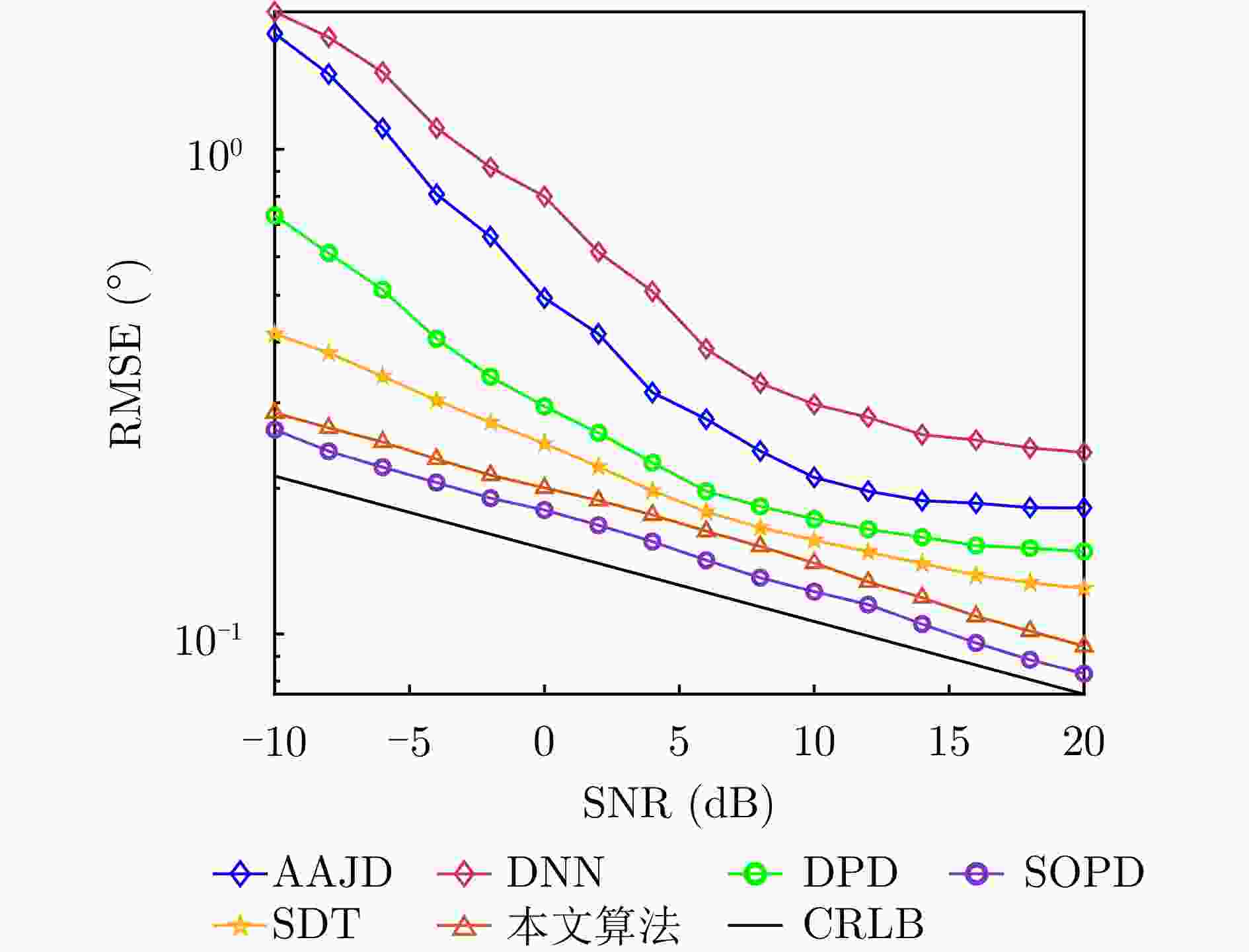
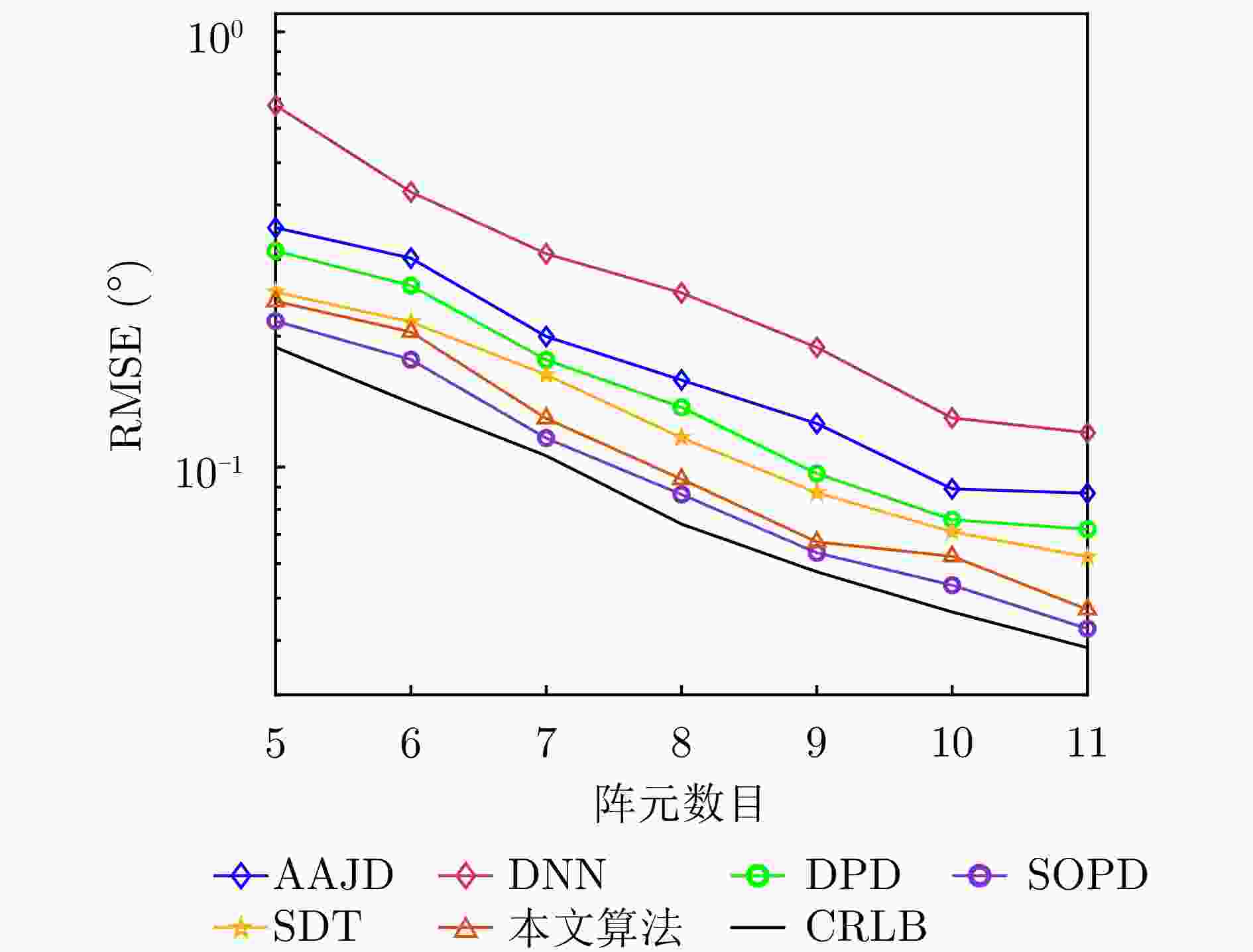
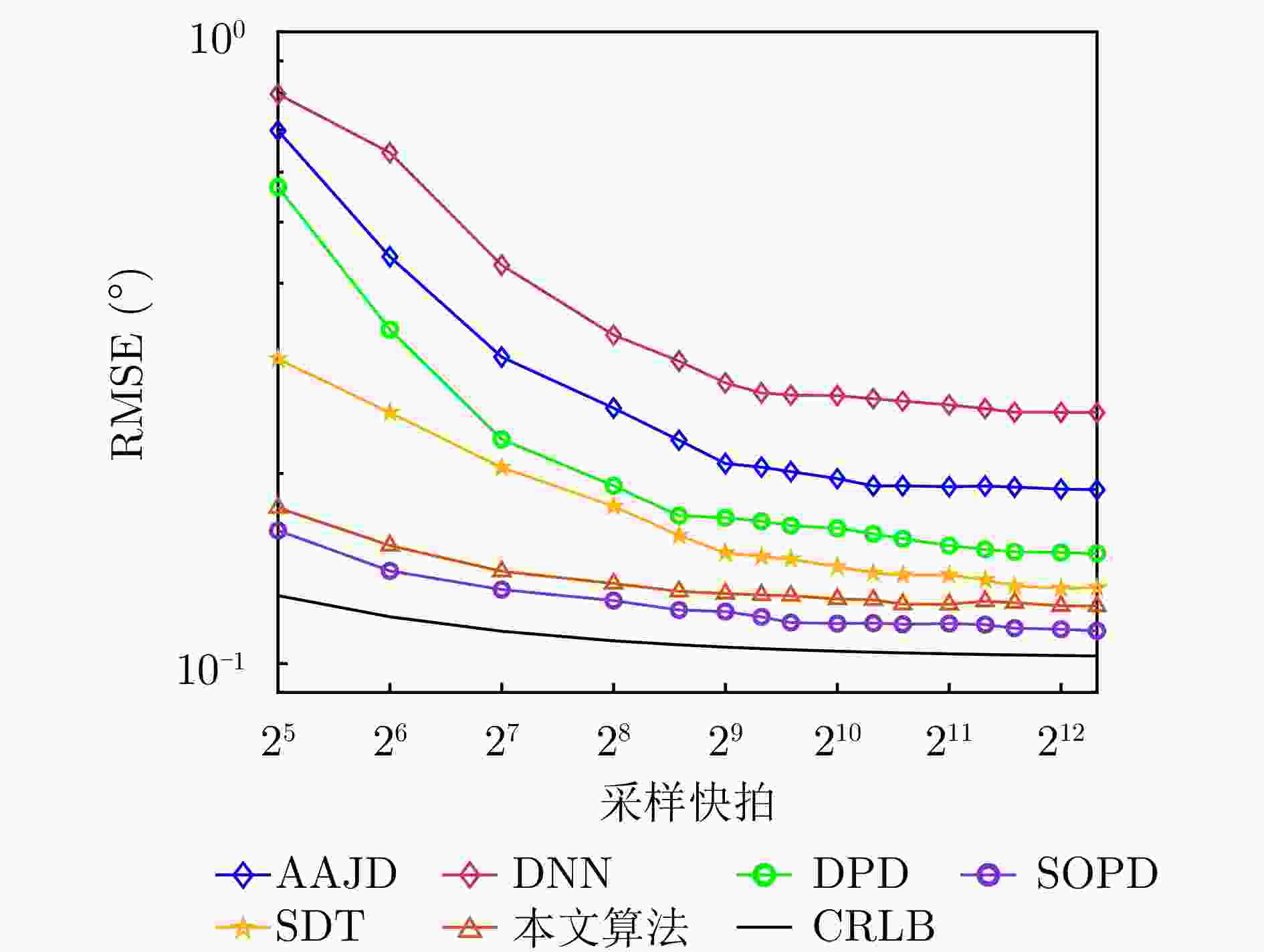
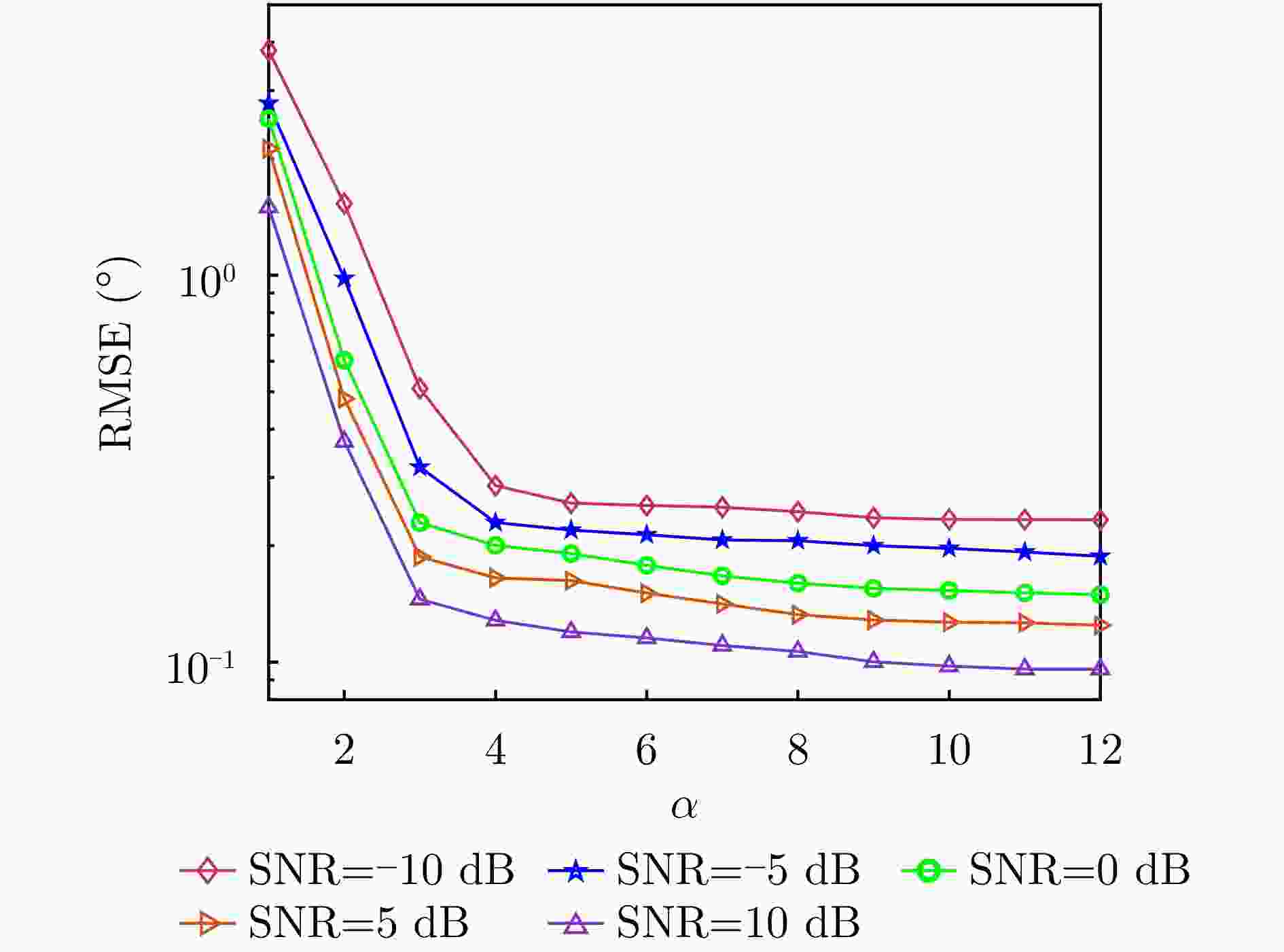
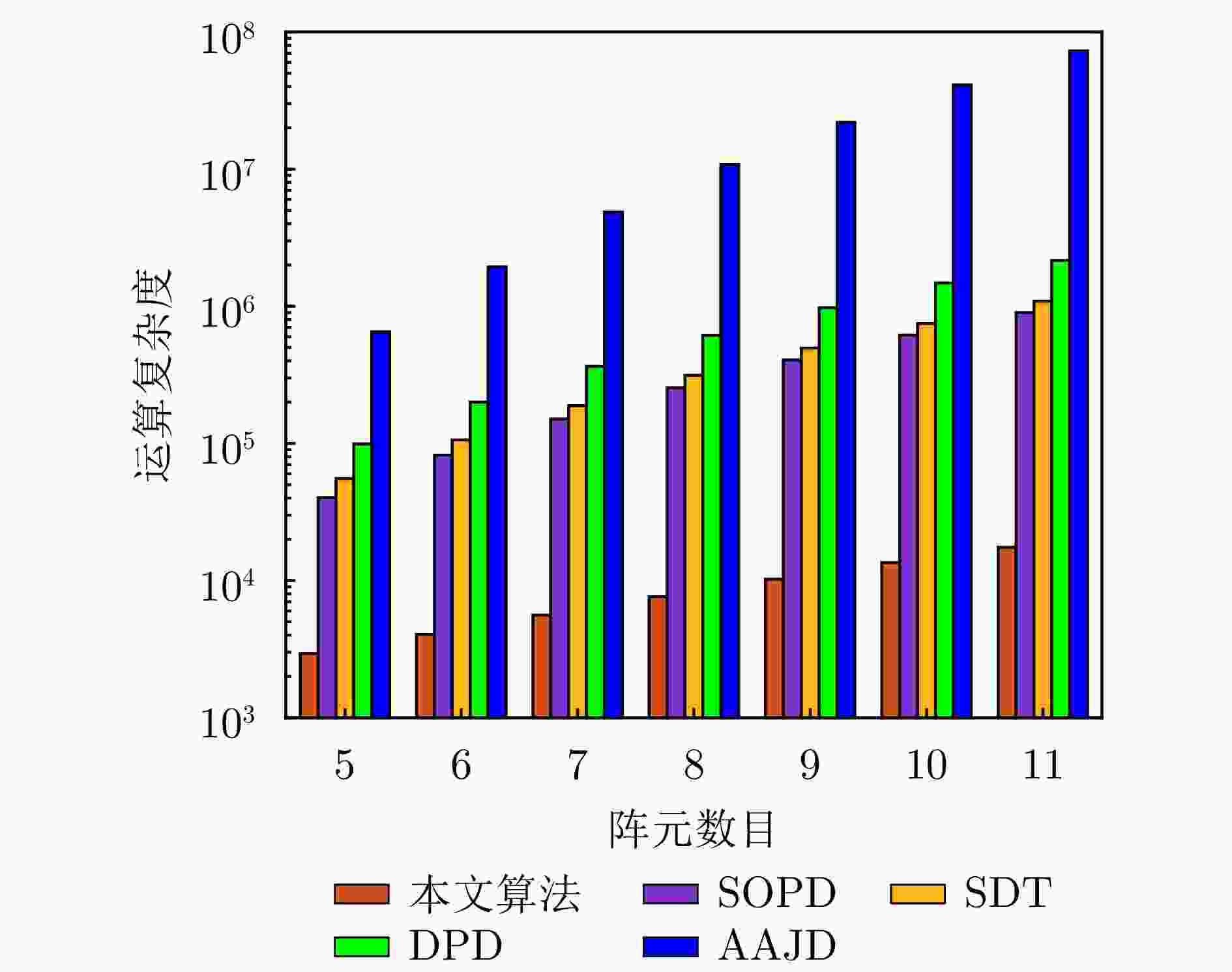
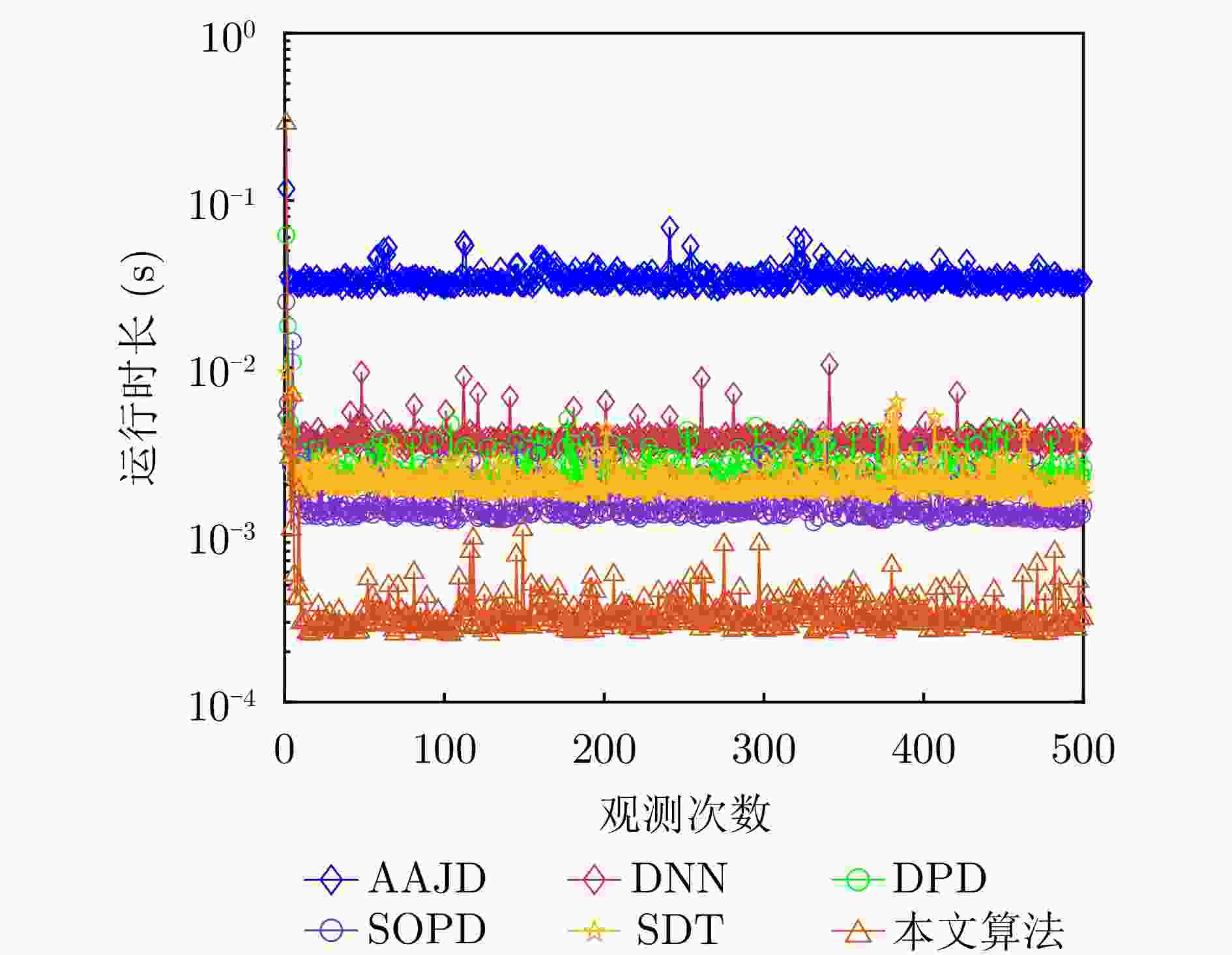
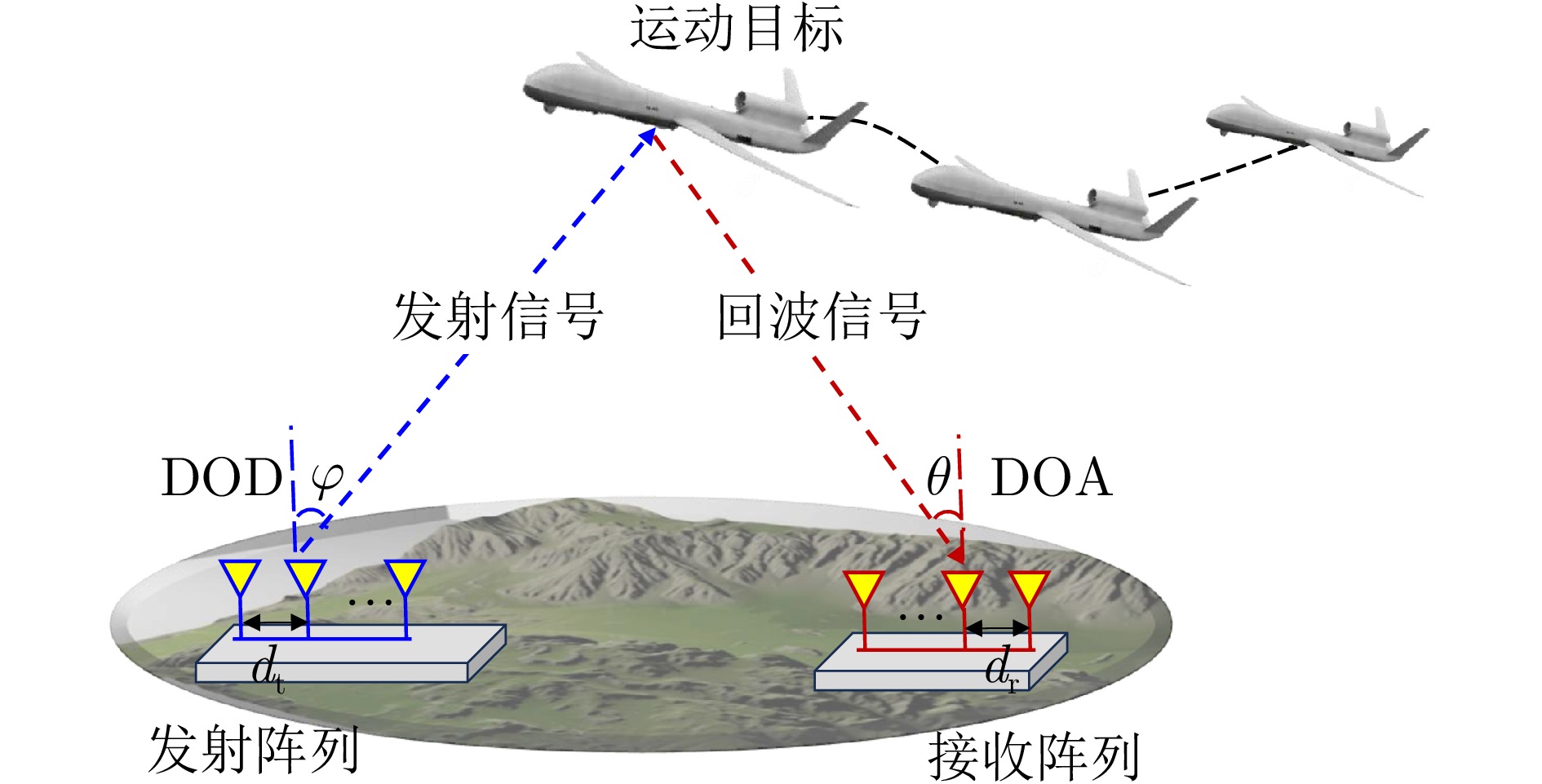
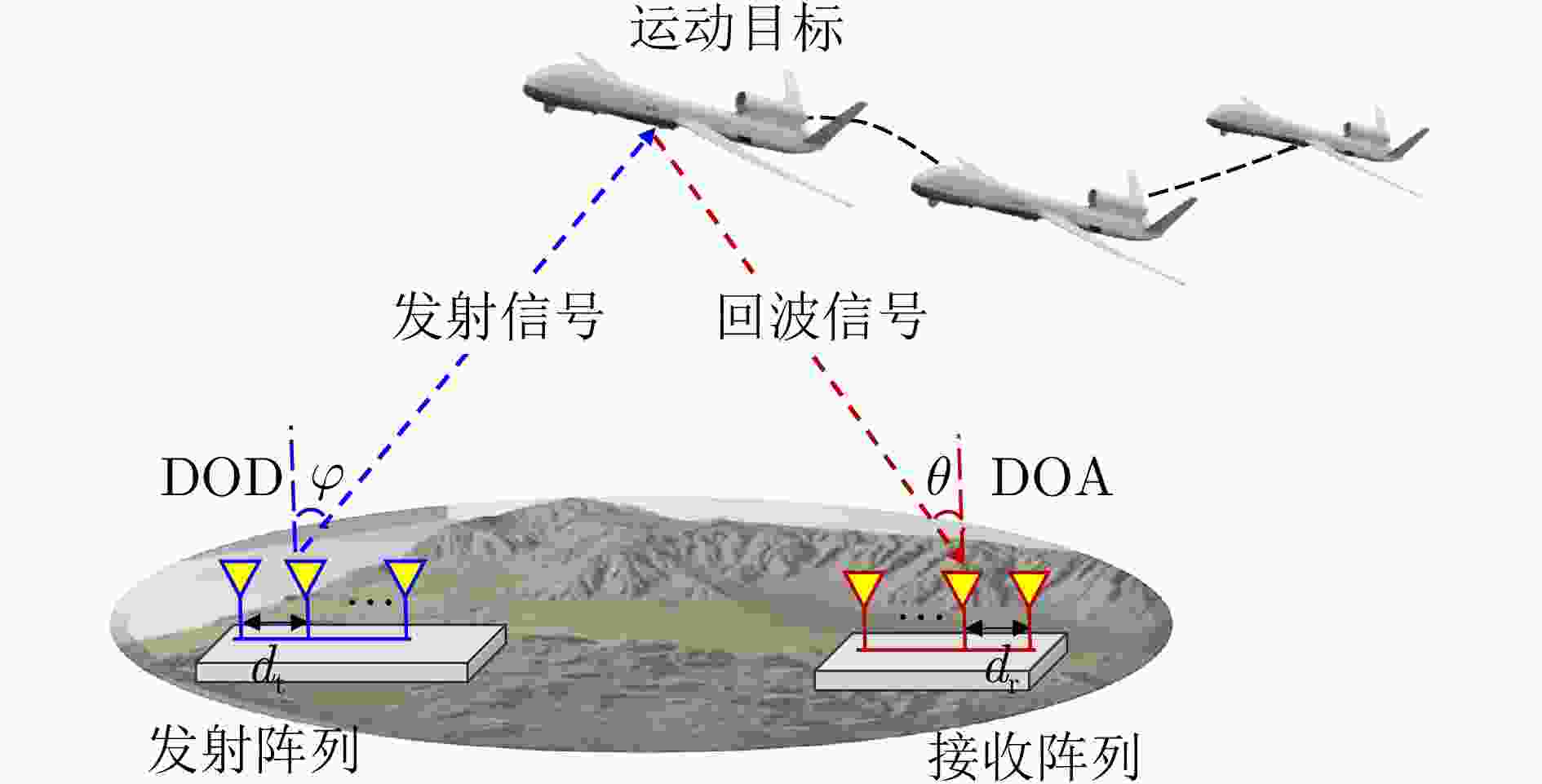
摘要: 动目标跟踪是双基地多输入多输出(MIMO)雷达系统的核心任务之一，对提升系统的目标感知精度与动态响应能力具有重要意义。针对复杂场景下动目标跟踪性能易受状态变化、高维数据耦合等因素制约的问题，该文提出一种基于自适应张量分解(ATD)的动目标跟踪算法。首先建立包含运动目标波离方向(DOD)和波达方向(DOA)信息的三阶动态张量信号模型，以表征接收信号中时、空多维数据的时变结构。基于所建立动态张量模型，构建运动目标空间位置与张量因子矩阵间的映射关系，采用矩阵随机降维策略设计自适应因子矩阵更新机制，迭代分解包含目标状态信息的阵列流形矩阵，以实现对目标方向的实时稳健跟踪。最后，通过仿真实验分析所提算法的跟踪性能。仿真结果表明，所提算法在低信噪比(SNR)场景下可实现动目标轨迹的持续稳定跟踪。与传统动目标跟踪算法相比，所提算法在保证跟踪精度的同时降低了计算复杂度，跟踪运算时长可缩短1～2个数量级，满足双基地MIMO雷达系统对动目标的实时跟踪需求。
-
关键词:
- 双基地多输入多输出雷达 /
- 阵列信号处理 /
- 动目标跟踪 /
- 自适应张量分解 /
- 并行因子
Abstract: Moving target tracking is a fundamental task in bistatic Multiple-Input Multiple-Output (MIMO) radar systems, as it is essential for improving sensing accuracy and real-time adaptability in dynamic environments. This paper proposes a tracking algorithm based on Adaptive Tensor Decomposition (ATD) to address accuracy degradation caused by target dynamics and high-dimensional data coupling. A third-order streaming tensor is first established to model the time-varying, multi-dimensional structure of received signals from moving targets, which jointly incorporates the Direction Of Departure (DOD) and Direction Of Arrival (DOA). A dynamic mapping is then derived from the tensor to characterize the relationship between the target’s spatial state and the factor matrices. Next, a random dimensionality reduction strategy is integrated into the adaptive tensor decomposition, which iteratively updates the factor matrices that contain target state information, thereby enabling real-time and robust tracking of target angles. Finally, numerical simulations are conducted to evaluate the tracking performance of the proposed method. The results demonstrate that it provides continuous and stable tracking of moving targets under low Signal-to-Noise Ratio (SNR) conditions. Compared to classical approaches, the proposed algorithm reduces computational time by one to two orders of magnitude, demonstrating its effectiveness and real-time applicability in complex and dynamic environments. -
图 4 基于自适应张量分解的动目标轨迹跟踪
Figure 4. Target tracking based on adaptive tensor decomposition
图 11 角度跟踪RMSE受降维系数影响对比
Figure 11. RMSE comparison v.s. dimensionality reduction coefficients
图 13 跟踪算法运行时长结果对比
Figure 13. Computing time comparison of different tracking algorithms
1 动目标跟踪算法流程
1. Moving target tracking algorithm
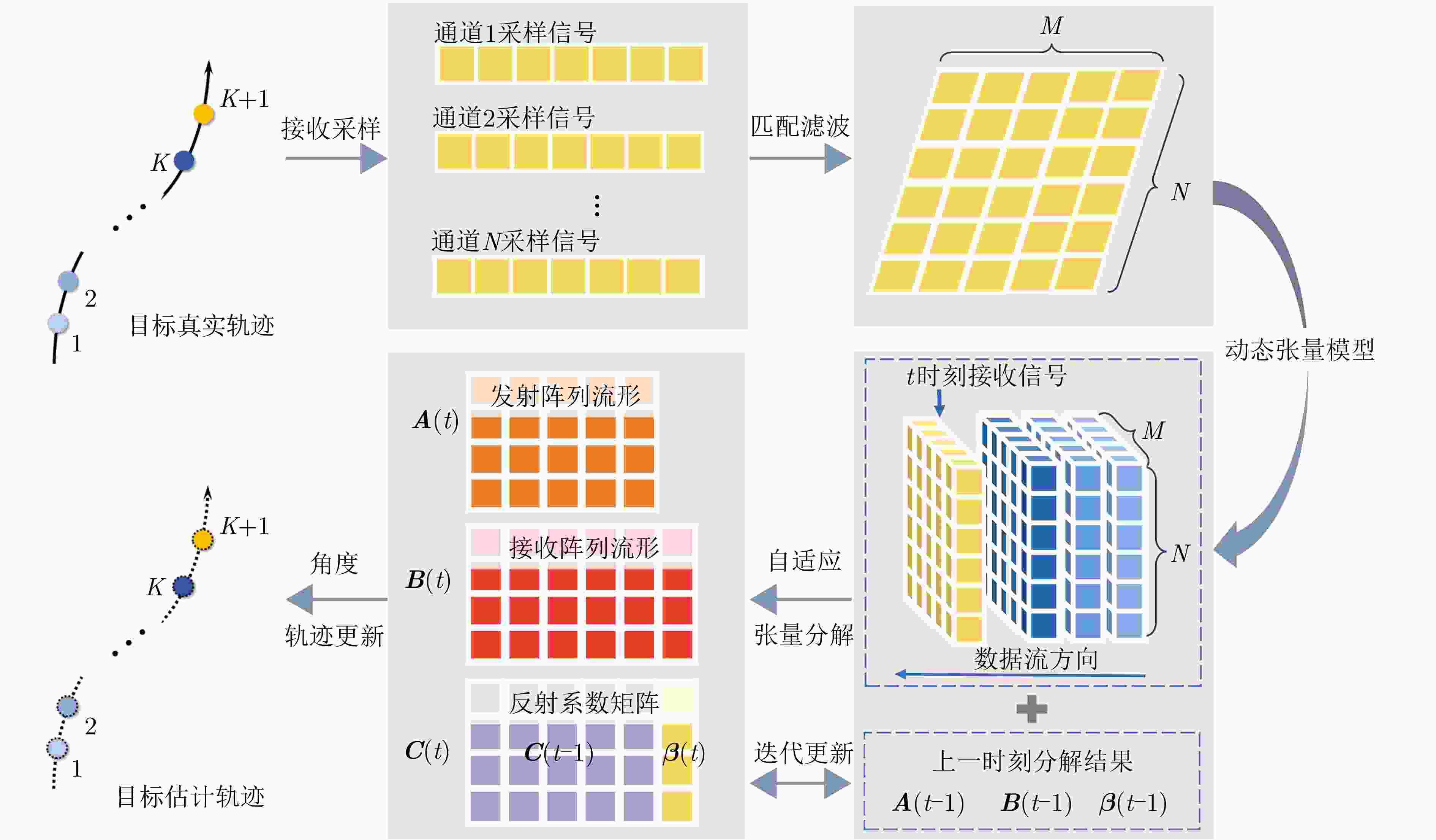
输入：接收端阵列原始采样信号$ {\boldsymbol{X}}(t) $ 步骤1：算法初始化 初始化$ {\boldsymbol{A}}(0) $,$ {\boldsymbol{B}}(0) $为独立同分布的高斯随机变量，并设置$ r \lt MN $。 步骤2：接收数据矢量化 根据式(10)和式(11)对$ {\boldsymbol{X}}(t) $匹配滤波和矢量化，得到接收信号$ {\boldsymbol{y}}(t) $。 步骤3：自适应张量分解 3.1：随机选取$ {\boldsymbol{\varPsi}} (t - 1) $和$ {\boldsymbol{y}}(t) $的r行得到$ \bar {\boldsymbol{\varPsi}} (t - 1) $和$ {\boldsymbol{\bar y}}(t) $； 3.2：构建关于$ {\boldsymbol{\beta}} (t) $求解的代价函数，根据式(38)计算$ \hat {\boldsymbol{\beta}} (t) $； 3.3：构建关于$ {\boldsymbol{B}}(t) $求解的代价函数，根据式(45)计算$ {{\hat {\boldsymbol B}}}(t) $； 3.4：构建关于$ {\boldsymbol{A}}(t) $求解的代价函数，根据式(48)计算$ {{\hat {\boldsymbol A}}}(t) $ 步骤4：角度更新 4.1：根据式(49)、式(50)计算$ {{\boldsymbol{\varTheta}} _q}(t) $, $ {{\boldsymbol{\varPhi}} _q}(t) $，进行特征值分解并构造噪声子空间$ {{\boldsymbol{U}}_\vartheta }(t) $, $ {{\boldsymbol{U}}_\upsilon }(t) $； 4.2：根据式(54)、式(55)，构造求根多项式$ {f_\vartheta }(z) $, $ {f_\upsilon }(z) $，求解并根据式(56)、式(57)计算目标发射角$ {\hat \varphi _q}(t) $和接收角$ {\hat \theta _q}(t) $。 步骤5：轨迹更新 对$ t + 1 $时刻接收信号$ {\boldsymbol{X}}(t + 1) $重复步骤2—步骤4； 输出：Q个目标的DOD和DOA。 
下载: 导出CSV
表 1 运算复杂度对比
Table 1. Comparison of computational complexity
算法名称 运算复杂度 AAJD $ O(4{M^3}{N^3}{Q^2} + 12{M^2}{N^2} + 5{M^3}{N^3} + 4{M^3}Q + 4{N^3}Q) $ DPD $ O(2{I_{\rm d}}{Q^3} + 4{I_{\rm d}}MN{Q^2} + 5{I_{\rm d}}{M^2}{N^2}Q + M{Q^2} + N{Q^2} + 2Q{M^3} + 2Q{N^3}) $ SOPD $ O(4{I_{\rm s}}{M^2}{N^2}Q + {I_{\rm s}}MN{Q^2} + M{Q^2} + N{Q^2} + 2Q{M^3} + 2Q{N^3}) $ SDT $ O[16{Q^3} + {Q^2}(31MN + 31{T_{\mathrm{W}}} + 40) + Q(32MN + 10N + 20) + 2{M^3}Q + 2{N^3}Q] $ 本文算法 $ O(8r{Q^2} + 4rQ + M{Q^2} + N{Q^2} + 2{M^3}Q + 2{N^3}Q) $
下载: 导出CSV
-
[1] 何子述, 程子扬, 李军, 等. 集中式MIMO雷达研究综述[J]. 雷达学报, 2022, 11(5): 805–829. doi: 10.12000/JR22128.HE Zishu, CHENG Ziyang, LI Jun, et al. A survey of collocated MIMO radar[J]. Journal of Radars, 2022, 11(5): 805–829. doi: 10.12000/JR22128. [2] BJÖRNSON E, SANGUINETTI L, WYMEERSCH H, et al. Massive MIMO is a reality—What is next?: Five promising research directions for antenna arrays[J]. Digital Signal Processing, 2019, 94: 3–20. doi: 10.1016/j.dsp.2019.06.007. [3] 刘德顺, 夏德平, 陈露, 等. 基于神经网络的FDA-MIMO低截获发射波形和接收波束形成联合设计[J]. 雷达学报(中英文), 2024, 13(6): 1239–1251. doi: 10.12000/JR24140.LIU Deshun, XIA Deping, CHEN Lu, et al. Joint design of LPI transmit waveform and receive beamforming based on neural networks for FDA-MIMO[J]. Journal of Radars, 2024, 13(6): 1239–1251. doi: 10.12000/JR24140. [4] DONG Fuwang, WANG Wei, LI Xin, et al. Joint beamforming design for dual-functional MIMO radar and communication systems guaranteeing physical layer security[J]. IEEE Transactions on Green Communications and Networking, 2023, 7(1): 537–549. doi: 10.1109/TGCN.2022.3233863. [5] HU Qiang, GAO Feifei, ZHANG Hao, et al. Understanding deep MIMO detection[J]. IEEE Transactions on Wireless Communications, 2023, 22(12): 9626–9639. doi: 10.1109/TWC.2023.3272525. [6] BUZZI S, GROSSI E, LOPS M, et al. Foundations of MIMO radar detection aided by reconfigurable intelligent surfaces[J]. IEEE Transactions on Signal Processing, 2022, 70: 1749–1763. doi: 10.1109/TSP.2022.3157975. [7] 国月皓, 王咸鹏, 兰翔, 等. 张量框架下双基地FDA-MIMO雷达参数估计算法[J]. 电子学报, 2024, 52(6): 2103–2111. doi: 10.12263/DZXB.20230172.GUO Yuehao, WANG Xianpeng, LAN Xiang, et al. Parameter estimation algorithm for bistatic FDA-MIMO radar based on tensor framework[J]. Acta Electronica Sinica, 2024, 52(6): 2103–2111. doi: 10.12263/DZXB.20230172. [8] 肖炯, 唐波, 王海. 互耦条件下基于稀疏重构的MIMO雷达角度估计[J]. 雷达学报(中英文), 2024, 13(5): 1123–1133. doi: 10.12000/JR24061.XIAO Jiong, TANG Bo, and WANG Hai. Sparse reconstruction-based direction of arrival estimation for MIMO radar in the presence of unknown mutual coupling[J]. Journal of Radars, 2024, 13(5): 1123–1133. doi: 10.12000/JR24061. [9] 于文启, 陈建文, 李雪. 基于双迭代MVDR波束形成的MIMO-OTHR多模扩展多普勒杂波抑制算法[J]. 电子与信息学报, 2018, 40(11): 2667–2675. doi: 10.11999/JEIT180101.YU Wenqi, CHEN Jianwen, and LI Xue. Multi-mode spread doppler clutter suppression algorithm of MIMO-OTHR based on bi-iterative MVDR beamformer[J]. Journal of Electronics & Information Technology, 2018, 40(11): 2667–2675. doi: 10.11999/JEIT180101. [10] GOMES P R B, DE ALMEIDA A L F, DA COSTA J P C L, et al. A nested-PARAFAC based approach for target localization in bistatic MIMO radar systems[J]. Digital Signal Processing, 2019, 89: 40–48. doi: 10.1016/j.dsp.2019.02.005. [11] 郑志东. 互耦条件下基于4阶累积量的双基地MIMO雷达角度估计[J]. 电子与信息学报, 2021, 43(9): 2720–2727. doi: 10.11999/JEIT200692.ZHENG Zhidong. A four cumulant-based direction finding method for bistatic MIMO radar with mutual coupling[J]. Journal of Electronics & Information Technology, 2021, 43(9): 2720–2727. doi: 10.11999/JEIT200692. [12] 田丰, 刘万, 符渭波, 等. 重叠阵元时分复用MIMO雷达多目标参数估计方法研究[J]. 电子与信息学报, 2024, 46(1): 229–239. doi: 10.11999/JEIT230039.TIAN Feng, LIU Wan, FU Weibo, et al. Research on multi-target parameter estimation method for overlapping-element time division multiplexing MIMO radar[J]. Journal of Electronics & Information Technology, 2024, 46(1): 229–239. doi: 10.11999/JEIT230039. [13] MÉRIAUX B, ZHANG Xin, EL KORSO M N, et al. Iterative marginal maximum likelihood DOD and DOA estimation for MIMO radar in the presence of SIRP clutter[J]. Signal Processing, 2019, 155: 384–390. doi: 10.1016/j.sigpro.2018.09.034. [14] 张正言, 张剑云, 周青松. 目标个数未知时双基地MIMO雷达多目标角度跟踪算法研究[J]. 电子与信息学报, 2018, 40(10): 2491–2497. doi: 10.11999/JEIT171174.ZHANG Zhengyan, ZHANG Jianyun, and ZHOU Qingsong. Study on multi-target angle tracking algorithm of bistatic MIMO radar with unknown target number[J]. Journal of Electronics & Information Technology, 2018, 40(10): 2491–2497. doi: 10.11999/JEIT171174. [15] 张正言, 张剑云, 郑志东, 等. 低信噪比双基地MIMO雷达目标角度跟踪算法[J]. 电子学报, 2019, 47(12): 2480–2487. doi: 10.3969/j.issn.0372-2112.2019.12.005.ZHANG Zhengyan, ZHANG Jianyun, ZHENG Zhidong, et al. Target angle tracking algorithm of bistatic MIMO radar with low signal-to-noise ratio[J]. Acta Electronica Sinica, 2019, 47(12): 2480–2487. doi: 10.3969/j.issn.0372-2112.2019.12.005. [16] CONG Jingyu, WANG Xianpeng, HUANG Mengxing, et al. Robust DOA estimation method for MIMO radar via deep neural networks[J]. IEEE Sensors Journal, 2021, 21(6): 7498–7507. doi: 10.1109/JSEN.2020.3046291. [17] MA Yugang, ZENG Yonghong, and SUN Sumei. A deep learning based super resolution DOA estimator with single snapshot MIMO radar data[J]. IEEE Transactions on Vehicular Technology, 2022, 71(4): 4142–4155. doi: 10.1109/TVT.2022.3151674. [18] LI Yifan, SHU Feng, SONG Yaoliang, et al. A novel tree model-based DNN to achieve a high-resolution DOA estimation via massive MIMO receive array[J]. Radioengineering, 2024, 33(4): 563–570. doi: 10.13164/re.2024.0563. [19] LIU Qing, XIE Jian, ZHANG Zhaolin, et al. Tensor-based passive localization of multiple wideband emitters using PARAFAC decomposition[J]. Digital Signal Processing, 2025, 164: 105290. doi: 10.1016/j.dsp.2025.105290. [20] GUO Yuehao, WANG Xianpeng, SHI Jinmei, et al. Fast real-valued tensor decomposition framework for parameter estimation in FDA-MIMO radar[J]. Digital Signal Processing, 2024, 145: 104309. doi: 10.1016/j.dsp.2023.104309. [21] WANG Linwei, LI Bo, YU Changjun, et al. PARAFAC-Direct: A joint parameters estimation method for slow-time MIMO[J]. IEEE Signal Processing Letters, 2022, 29: 732–736. doi: 10.1109/LSP.2022.3154285. [22] NION D and SIDIROPOULOS N D. Adaptive algorithms to track the PARAFAC decomposition of a third-order tensor[J]. IEEE Transactions on Signal Processing, 2009, 57(6): 2299–2310. doi: 10.1109/TSP.2009.2016885. [23] THANH L T, ABED-MERAIM K, TRUNG N L, et al. A contemporary and comprehensive survey on streaming tensor decomposition[J]. IEEE Transactions on Knowledge and Data Engineering, 2023, 35(11): 10897–10921. doi: 10.1109/TKDE.2022.3230874. [24] WANG Wenshuai, WANG Xianpeng, GUO Yuehao, et al. Parameter estimation with bistatic MIMO radar: A coarray tensor decomposition framework[J]. IEEE Transactions on Aerospace and Electronic Systems, 2025, 61(2): 4450–4465. doi: 10.1109/TAES.2024.3505112. [25] CICHOCKI A, MANDIC D, DE LATHAUWER L, et al. Tensor decompositions for signal processing applications: From two-way to multiway component analysis[J]. IEEE Signal Processing Magazine, 2015, 32(2): 145–163. doi: 10.1109/MSP.2013.2297439. [26] 潘步年, 谭睿, 汪兵, 等. 分布式雷达多域张量分解抗复合干扰方法[J]. 太赫兹科学与电子信息学报, 2024, 22(10): 1117–1126. doi: 10.11805/TKYDA2023066.PAN Bunian, TAN Rui, WANG Bing, et al. Joint multi-domain tensor decomposition method for compound jamming in distributed radars[J]. Journal of Terahertz Science and Electronic Information Technology, 2024, 22(10): 1117–1126. doi: 10.11805/TKYDA2023066. [27] STEGEMAN A and SIDIROPOULOS N D. On Kruskal’s uniqueness condition for the Candecomp/Parafac decomposition[J]. Linear Algebra and its Applications, 2007, 420(2/3): 540–552. doi: 10.1016/j.laa.2006.08.010. [28] 潘小义, 谢前朋, 孟晓明, 等. 基于差分阵列的双基地EMVS-MIMO雷达高分辨多维参数估计[J]. 电子与信息学报, 2023, 45(11): 3860–3867. doi: 10.11999/JEIT221259.PAN Xiaoyi, XIE Qianpeng, MENG Xiaoming, et al. High resolution multidimensional parameters estimation for bistatic EMVS-MIMO radar: From the difference coarray perspective[J]. Journal of Electronics & Information Technology, 2023, 45(11): 3860–3867. doi: 10.11999/JEIT221259. [29] XU Baoqing and ZHAO Yongbo. Joint transmit-receive B-PARAFAC method for angle estimation in bistatic MIMO radar[J]. Digital Signal Processing, 2019, 92: 54–61. doi: 10.1016/j.dsp.2019.03.001. [30] KASAI H. Fast online low-rank tensor subspace tracking by CP decomposition using recursive least squares from incomplete observations[J]. Neurocomputing, 2019, 347: 177–190. doi: 10.1016/j.neucom.2018.11.030. [31] RASKUTTI G and MAHONEY M W. A statistical perspective on randomized sketching for ordinary least-squares[J]. The Journal of Machine Learning Research, 2016, 17(1): 7508–7538. [32] TROPP J A, YURTSEVER A, UDELL M, et al. Practical sketching algorithms for low-rank matrix approximation[J]. SIAM Journal on Matrix Analysis and Applications, 2017, 38(4): 1454–1485. doi: 10.1137/17M1111590. [33] MAHONEY M W. Randomized algorithms for matrices and data[J]. Foundations and Trends® in Machine Learning, 2011, 3(2): 123–224. doi: 10.1561/2200000035. [34] BATTAGLINO C, BALLARD G, and KOLDA T G. A practical randomized CP tensor decomposition[J]. SIAM Journal on Matrix Analysis and Applications, 2018, 39(2): 876–901. doi: 10.1137/17M1112303. [35] SIDIROPOULOS N D, BRO R, and GIANNAKIS G B. Parallel factor analysis in sensor array processing[J]. IEEE Transactions on Signal Processing, 2000, 48(8): 2377–2388. doi: 10.1109/78.852018. [36] ZHENG Hang, ZHOU Chengwei, SHI Zhiguo, et al. Coarray tensor direction-of-arrival estimation[J]. IEEE Transactions on Signal Processing, 2023, 71: 1128–1142. doi: 10.1109/TSP.2023.3260559. [37] XU Feng, MORENCY M W, and VOROBYOV S A. DOA estimation for transmit beamspace MIMO radar via tensor decomposition with Vandermonde factor matrix[J]. IEEE Transactions on Signal Processing, 2022, 70: 2901–2917. doi: 10.1109/TSP.2022.3176092. [38] WEN Fangqing, SHI Junpeng, and ZHANG Zijing. Joint 2D-DOD, 2D-DOA, and polarization angles estimation for bistatic EMVS-MIMO radar via PARAFAC analysis[J]. IEEE Transactions on Vehicular Technology, 2020, 69(2): 1626–1638. doi: 10.1109/TVT.2019.2957511. [39] GAO Sizhe, MA Hui, LIU Hongwei, et al. DOD and DOA estimation from incomplete data based on PARAFAC and atomic norm minimization method[J]. IEEE Transactions on Geoscience and Remote Sensing, 2023, 61: 5100314. doi: 10.1109/TGRS.2023.3234576. -
图(13) / 表(2)
计量
- 文章访问数:
- HTML全文浏览量:
- PDF下载量:
- 被引次数: 0
