作者中心
专家审稿
责编办公
编辑办公
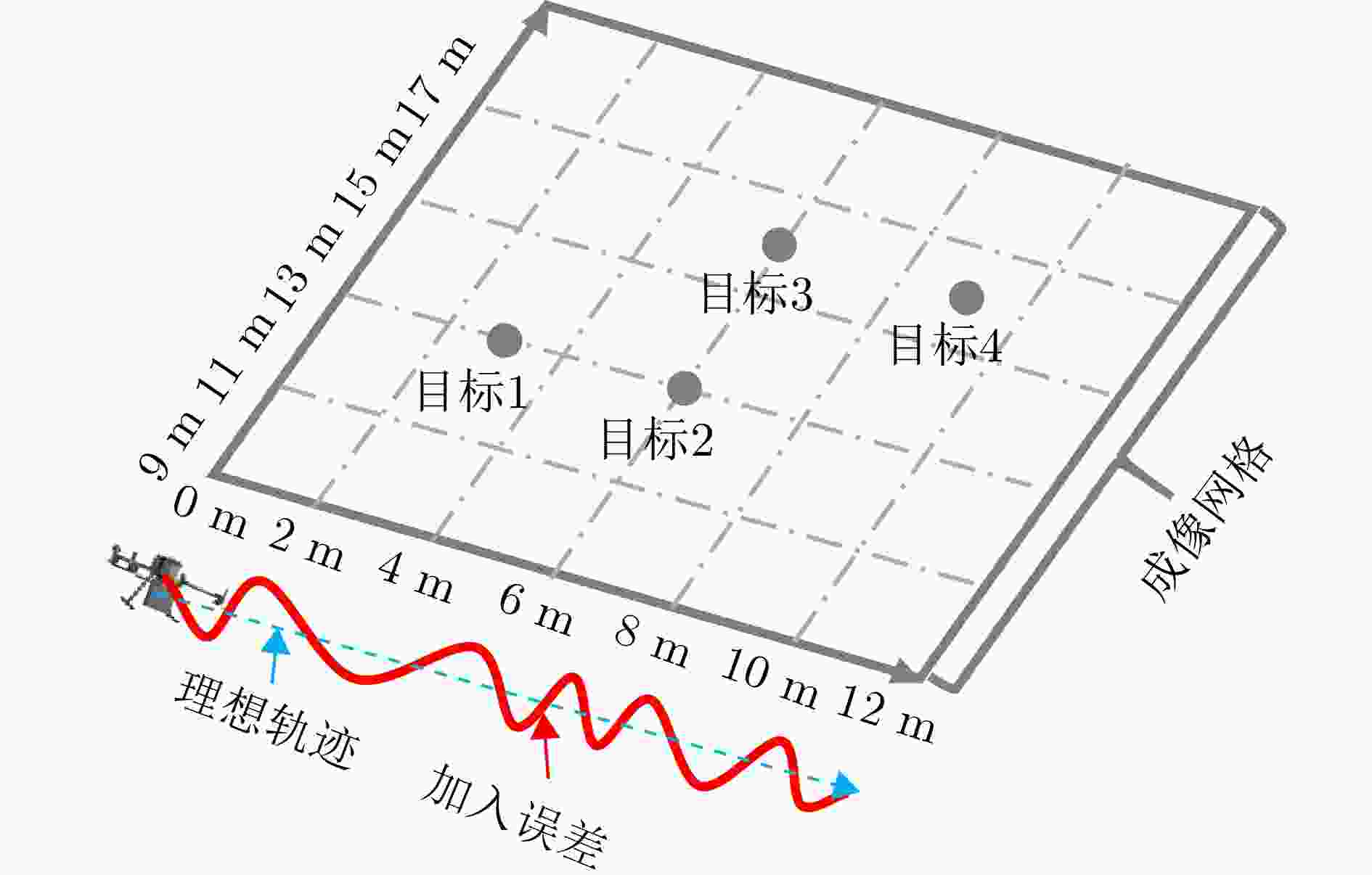
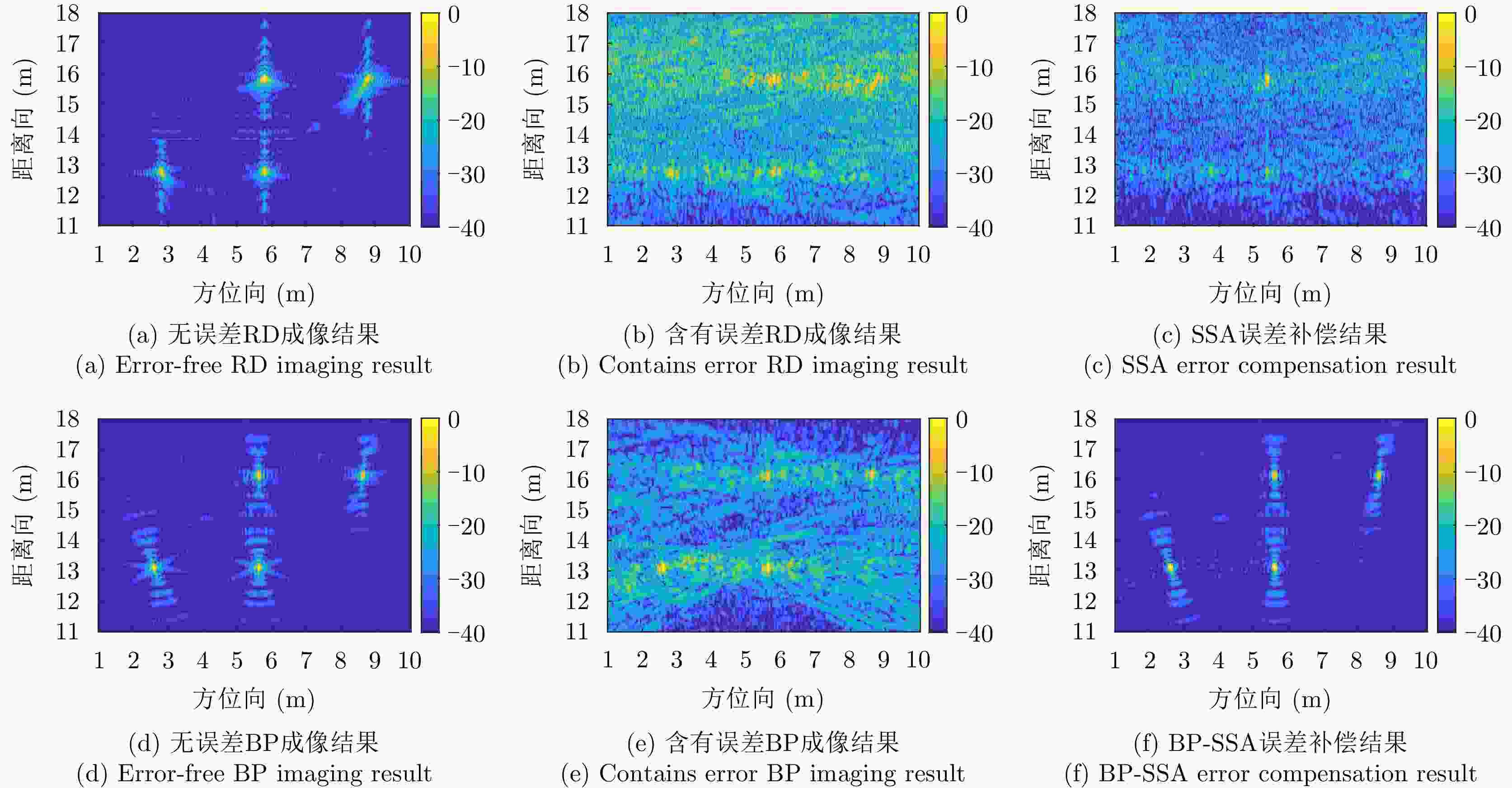
Space-varying Motion Error Compensation for UAV-mounted through-the-wall SAR Based on SSA Algorithm
-
摘要: 小型旋翼无人机由于其体积小、重量轻、机动性优异等特点，常作为合成孔径雷达(SAR)搭载平台，在低空复杂环境探测中具有广阔应用前景。然而，由于小型旋翼无人机低空飞行过程运动误差随机性强，且受限于旋翼无人机载重限制，无法搭载高精度定位设备，导致运动误差成为影响小型旋翼无人机载穿墙SAR成像精度的关键问题。传统基于逐步逼近(SSA)方法的误差补偿算法基于聚束SAR提出，假设场景中所有像素点的相位误差相同，条带宽波束条件下明显不适用。该文提出一种基于SSA算法的宽波束穿墙SAR空变运动误差补偿方法，该方法结合后向投影(BP)算法对旋翼无人机运动误差的雷达回波进行建模，在SAR图像熵评估准则下，利用SSA优化算法估计天线相位中心对成像场景中每个像素点的相位误差，通过BP算法可对每个像素点进行高精度相位补偿，解决了宽波束穿墙SAR运动误差空变问题。仿真与实测数据处理结果表明，该算法能够在宽波束情况下，对空变运动误差完成精确补偿，使场景中多目标均完成良好聚焦，有效解决了宽波束穿墙SAR运动误差空变问题。Abstract: Small rotorcraft Unmanned Aerial Vehicles (UAVs), owing to their compact size, lightweight nature, and excellent maneuverability, are often used as platforms for Synthetic Aperture Radar (SAR) systems. These UAVs exhibit great potential in complex environment detection at low altitudes. However, the operation of small rotorcraft UAVs involves sharp, random motion errors during flight at low altitudes. Additionally, the limited payload capacity of these vehicles further limits their capacity to carry high-precision positioning equipment. The abovementioned motion errors observed during the operation of UAVs become a key factor that affects the imaging accuracy in UAV-mounted through-the-wall SAR imaging. To address this drawback, a conventional error compensation algorithm based on the Stage by Stage Approaching (SSA) algorithm has been proposed. This approach is based on the bunching SAR imaging mechanism, assuming that the phase error of all the pixels in the scene is the same; this approach is not applicable under the condition of a bandwidth beam. Therefore, this paper presents a wide-beam motion error compensation method for through-the-wall SAR imaging based on the SSA algorithm. The method employs the Back Projection (BP) algorithm to model the motion errors of the radar echo of the rotorcraft UAVs. Using the image entropy evaluation criterion of SAR, the SSA optimization algorithm was applied in this study to estimate the phase errors of the antenna phase center for each pixel in the imaging scene. Subsequently, the BP algorithm was used to perform high-precision phase compensation for each pixel, thereby addressing the spatial variations of motion errors in the wide-beam through-the-wall SAR system. The results of the simulation and experimental data processing reveal that the proposed algorithm can accurately compensate for spatially varying motion errors in wide-beam scenarios. It enables good focusing of multiple targets in the scene and effectively resolves the problem of spatially varying motion errors in wide-beam through-the-wall SAR imaging.
-
图 8 不同信噪比条件下算法聚焦性能对比
Figure 8. Comparison of the focusing performance of algorithms under different signal-to-noise ratio conditions
图 9 旋翼无人机载宽波束穿墙雷达
Figure 9. Wide beam through-the-wall radar equipped on rotorcraft UAV
图 17 穿墙场景目标2距离向与方位向剖面
Figure 17. Through-the-wall scene range and azimuth profile of target 2
1 BP-SSA算法流程
1. BP-SSA algorithm flow
输入：初始化参数，搜索阶段$i = 1$，搜索步长${\varDelta _i} = 0.02$，
APC位置$\Delta {\tilde {\boldsymbol{P}}}$，终止迭代门限${T_1}$，终止算法门限${T_2}$输出：APC位置误差估计值$\Delta {{\tilde {\boldsymbol{P}}}_{i,k}}$ 1：while ${D_1} > {T_1}$ do 2： while ${D_2} > {T_2}$ do 3： for $k \leftarrow 1,K$ do 4： 当前无人机位置候选位置误差 5： $ \begin{gathered} \Delta {{{\tilde {\boldsymbol{P}}}}_1} = \Delta {{{\tilde {\boldsymbol{P}}}}_{i,k}} \\ \Delta {{{\tilde {\boldsymbol{P}}}}_2} = \Delta {{{\tilde {\boldsymbol{P}}}}_{i,k}} + {\varDelta _i} \\ \Delta {{{\tilde {\boldsymbol{P}}}}_3} = \Delta {{{\tilde {\boldsymbol{P}}}}_{i,k}} - {\varDelta _i} \\ \end{gathered} $ 6： 更新无人机位置，并进行BP成像 7： $ \Delta {{\tilde {\boldsymbol{P}}}_{i,k}} = \mathop {\arg \min }\limits_{\Delta {{{\tilde {\boldsymbol{P}}}}_j}} [{H} (\Delta {{\tilde {\boldsymbol{P}}}_j})] \cdots j = 1,2,3 $ 8： end 9： $ {D_1} = \left| {\dfrac{{{H} (\Delta {{{\tilde {\boldsymbol{P}}}}_{i,1}}) - {H} (\Delta {{{\tilde {\boldsymbol{P}}}}_{i,k}})}}{{{H} (\Delta {{{\tilde {\boldsymbol{P}}}}_{i,1}})}}} \right| $ 10： end 11： $ {D_2} = \left| {\dfrac{{{H} (\Delta {{{\tilde {\boldsymbol{P}}}}_{i - 1,K}}) - {H} (\Delta {{{\tilde {\boldsymbol{P}}}}_{i,k}})}}{{{H} (\Delta {{{\tilde {\boldsymbol{P}}}}_{i - 1,K}})}}} \right| $ 12： $ i = i + 1{\text{, }}{\varDelta _i} = \dfrac{{{\varDelta _{i - 1}}}}{2} $ 13：end 
下载: 导出CSV
表 1 雷达系统仿真参数设置
Table 1. Radar system simulation parameter setting
参数 数值 信号带宽 500 MHz 雷达起始频率 2.7 GHz 调频斜率 $0.927 \times {10^{12}}{\text{ Hz/s}}$ 脉冲重复频率 50 Hz 平台飞行速度 1 m/s
下载: 导出CSV
表 2 目标1与目标4的PSLR
Table 2. The PSLR of target 1 and target 4
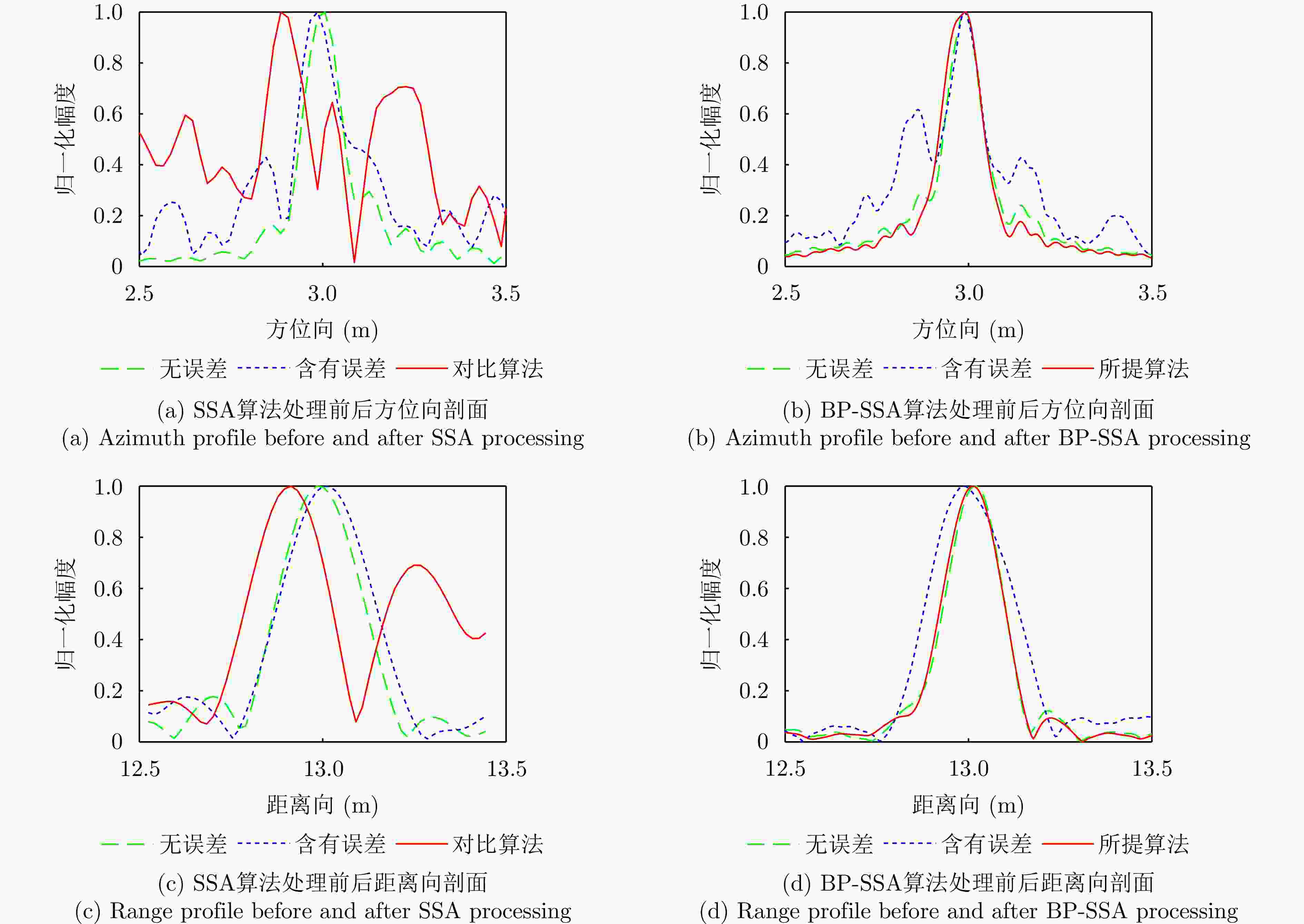
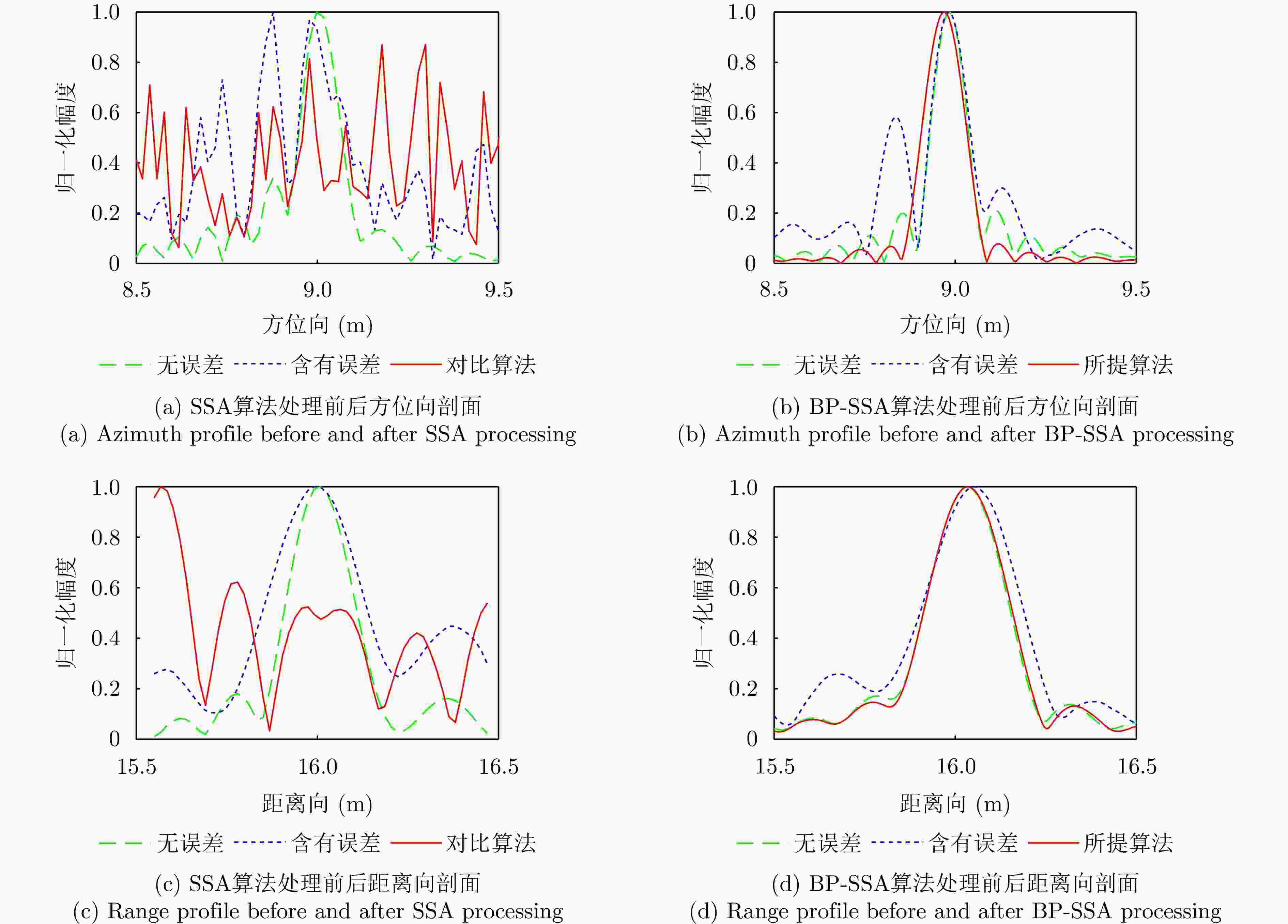
误差补偿 目标1
PSLR (dB)目标4
PSLR (dB)无误差 –23.91 –20.13 含有误差 –9.32 –8.53 所提算法补偿后 –21.82 –20.41
下载: 导出CSV
表 3 成像质量与效率
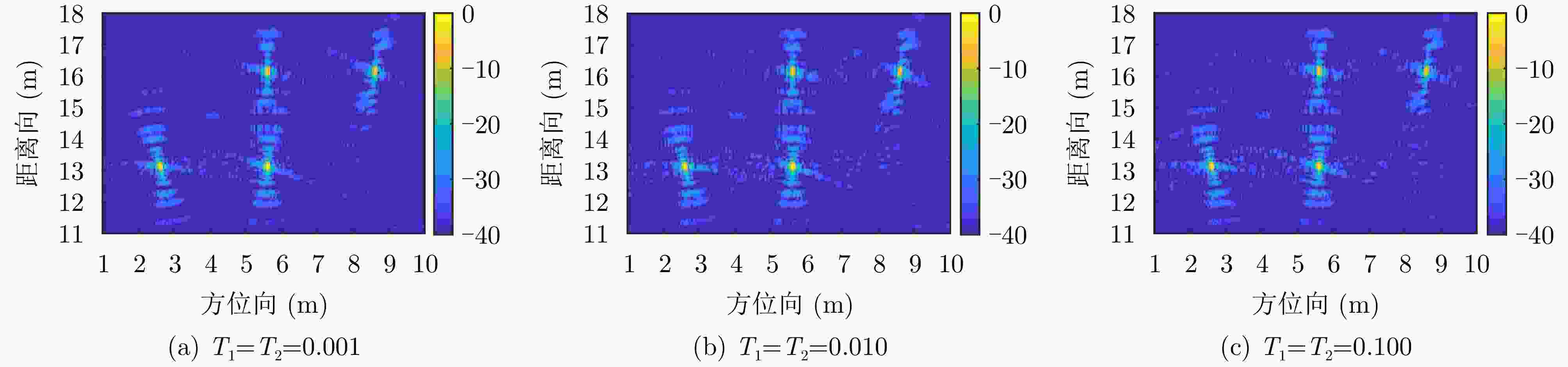
Table 3. Imaging quality and efficiency
参数 数值 T1, T2 0.001 0.010 0.100 图像熵 5.4152 5.6293 5.6409 迭代次数 10 5 2 迭代时间(s) 10646 8816 2709
下载: 导出CSV
表 4 雷达系统参数
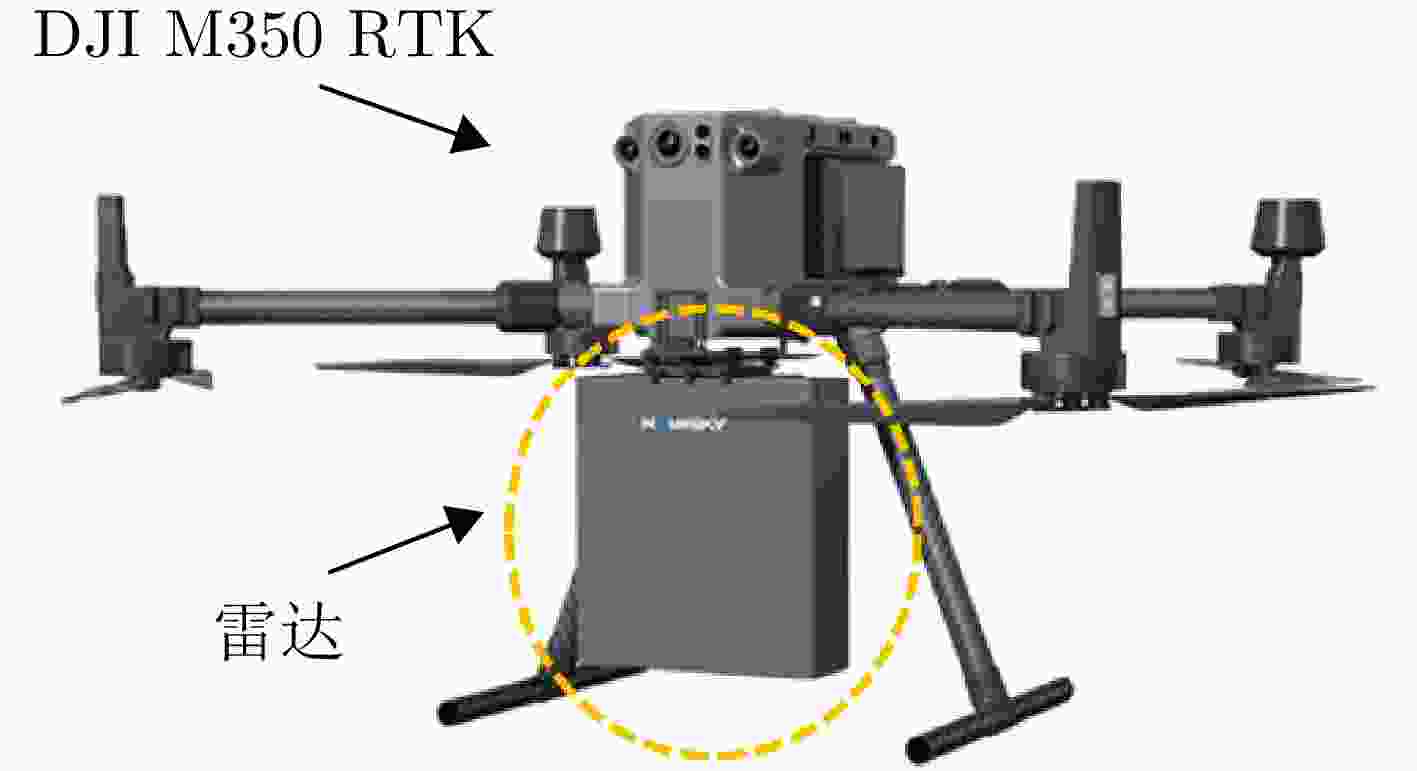
Table 4. Radar system parameter
参数 数值 信号带宽 408 MHz 雷达起始频率 2.67 GHz 调频斜率 $1.136 \times {10^{12}}{\text{ Hz/s}}$ 脉冲重复频率 1923 Hz 平台飞行速度 约1.3 m/s 采样率 10 MHz 收发天线间距 0.12 m
下载: 导出CSV
-
[1] CUMMING I G and WONG F H. Digital Processing of Synthetic Aperture Radar Data[M]. Boston: Artech House Publishers, 2005: 108–110. [2] 金秋, 王雨晗, 杨果, 等. 高速平台SAR脉内多普勒效应误差分析和校正[J]. 雷达科学与技术, 2023, 21(3): 237–246. doi: 10.3969/j.issn.1672-2337.2023.03.001.JIN Qiu, WANG Yuhan, YANG Guo, et al. Error analysis and correction of Doppler effect for SAR on high-speed platform[J]. Radar Science and Technology, 2023, 21(3): 237–246. doi: 10.3969/j.issn.1672-2337.2023.03.001. [3] 张健丰. 微小型无人机载FMCW SAR成像技术研究与系统实现[D]. 长沙: 国防科技大学, 2021. doi: 10.27052/d.cnki.gzjgu.2021.000036.ZHANG Jianfeng. Imaging technology research and system implementation for microminiature UAV FMCW SAR[D]. Changsha: National University of Defense Technology, 2021. doi: 10.27052/d.cnki.gzjgu.2021.000036. [4] 李嘉诚, 马彦恒, 董健, 等. 小型无人机载战场侦察雷达关键技术研究[J]. 飞航导弹, 2015(8): 37–41. doi: 10.16338/j.issn.1009-1319.2015.08.07.LI Jiacheng, MA Yanheng, DONG Jian, et al. Research on key technology of battlefield reconnaissance radar carried by small UAV[J]. Aerospace Technology, 2015(8): 37–41. doi: 10.16338/j.issn.1009-1319.2015.08.07. [5] 褚丽娜, 郭利, 马彦恒, 等. 小型旋翼无人机载圆周SAR成像研究综述[J]. 兵器装备工程学报, 2015, 46(2): 303–316.CHU Lina, GUO Li, MA Yanheng, et al. Review of circular SAR imaging by a small rotor unmanned aerial vehicle[J]. Journal of Ordnance Equipment Engineering, 2015, 46(2): 303–316. [6] 李悦丽, 李泽森, 王建, 等. 多旋翼无人机载SAR的视线运动误差修正与补偿[J]. 雷达学报, 2022, 11(6): 1061–1080. doi: 10.12000/JR22082.LI Yueli, LI Zesen, WANG Jian, et al. Modification and compensation of the line-of-sight motion error for multirotor UAV SAR[J]. Journal of Radars, 2022, 11(6): 1061–1080. doi: 10.12000/JR22082. [7] WANG Zhanze, LIU Feifeng, ZENG Tao, et al. A novel motion compensation algorithm based on motion sensitivity analysis for Mini-UAV-based BiSAR system[J]. IEEE Transactions on Geoscience and Remote Sensing, 2022, 60: 5205813. doi: 10.1109/TGRS.2021.3071460. [8] JOYO M K, HAZRY D, FAIZ AHMED S, et al. Altitude and horizontal motion control of quadrotor UAV in the presence of air turbulence[C]. 2013 IEEE Conference on Systems, Process & Control, Kuala Lumpur, Malaysia, 2013: 16–20. doi: 10.1109/SPC.2013.6735095. [9] CHENG Yao, QIU Xiaolan, and MENG Dadi. Precise motion compensation of multi-rotor UAV-borne SAR based on improved PTA[J]. Remote Sensing, 2024, 16(14): 2678. doi: 10.3390/rs16142678. [10] CHEN Jianlai, XING Mengdao, YU Hanwen, et al. Motion compensation/autofocus in airborne synthetic aperture radar: A review[J]. IEEE Geoscience and Remote Sensing Magazine, 2022, 10(1): 185–206. doi: 10.1109/MGRS.2021.3113982. [11] RAN Lei, LIU Zheng, ZHANG Lei, et al. An autofocus algorithm for estimating residual trajectory deviations in synthetic aperture radar[J]. IEEE Transactions on Geoscience and Remote Sensing, 2017, 55(6): 3408–3425. doi: 10.1109/TGRS.2017.2670785. [12] ZHANG Tao, LIAO Guisheng, LI Yachao, et al. An improved time-domain autofocus method based on 3-D motion errors estimation[J]. IEEE Transactions on Geoscience and Remote Sensing, 2022, 60: 5223816. doi: 10.1109/TGRS.2021.3137422. [13] CALLOWAY T M and DONOHOE G W. Subaperture autofocus for synthetic aperture radar[J]. IEEE Transactions on Aerospace and Electronic Systems, 1994, 30(2): 617–621. doi: 10.1109/7.272285. [14] WAHL D E, EICHEL P H, GHIGLIA D C, et al. Phase gradient autofocus-a robust tool for high resolution SAR phase correction[J]. IEEE Transactions on Aerospace and Electronic Systems, 1994, 30(3): 827–835. doi: 10.1109/7.303752. [15] 蒋锐, 朱岱寅, 朱兆达. 一种用于条带模式SAR成像的自聚焦算法[J]. 航空学报, 2010, 31(12): 2385–2392.JIANG Rui, ZHU Daiyin, and ZHU Zhaoda. A novel approach to strip-map SAR autofocus[J]. Acta Aeronauticaet Astronautica Sinica, 2010, 31(12): 2385–2392. [16] ASH J N. An autofocus method for backprojection imagery in synthetic aperture radar[J]. IEEE Geoscience and Remote Sensing Letters, 2012, 9(1): 104–108. doi: 10.1109/LGRS.2011.2161456. [17] LI Xi, LIU Guosui, and NI Jinlin. Autofocusing of ISAR images based on entropy minimization[J]. IEEE Transactions on Aerospace and Electronic Systems, 1999, 35(4): 1240–1252. doi: 10.1109/7.805442. [18] ZHANG Lei, WANG Guanyong, QIAO Zhijun, et al. Azimuth motion compensation with improved subaperture algorithm for airborne SAR imaging[J] IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2017, 10(1): 184–193. doi: 10.1109/JSTARS.2016.2577588. [19] 张法桐, 付耀文, 杨威, 等. 微小型无人机载FMCW SAR宽波束运动补偿算法[J]. 系统工程与电子技术, 2024, 46(10): 3303–3311. doi: 10.12305/j.issn.1001-506X.2024.10.08.ZHANG Fatong, FU Yaowen, YANG Wei, et al. Wide-beam motion compensation algorithm for micro-UAV FMCW SAR[J]. Systems Engineering and Electronics, 2024, 46(10): 3303–3311. doi: 10.12305/j.issn.1001-506X.2024.10.08. [20] 胡克彬, 张晓玲, 师君, 等. 基于图像强度最优的SAR高精度运动补偿方法[J]. 雷达学报, 2015, 4(1): 60–69. doi: 10.12000/JR15007.HU Kebin, ZHANG Xiaoling, SHI Jun, et al. A high-precision motion compensation method for SAR based on image intensity optimization[J]. Journal of Radars, 2015, 4(1): 60–69. doi: 10.12000/JR15007. -
图(17) / 表(5)
计量
- 文章访问数:
- HTML全文浏览量:
- PDF下载量:
- 被引次数: 0
