作者中心
专家审稿
责编办公
编辑办公
-
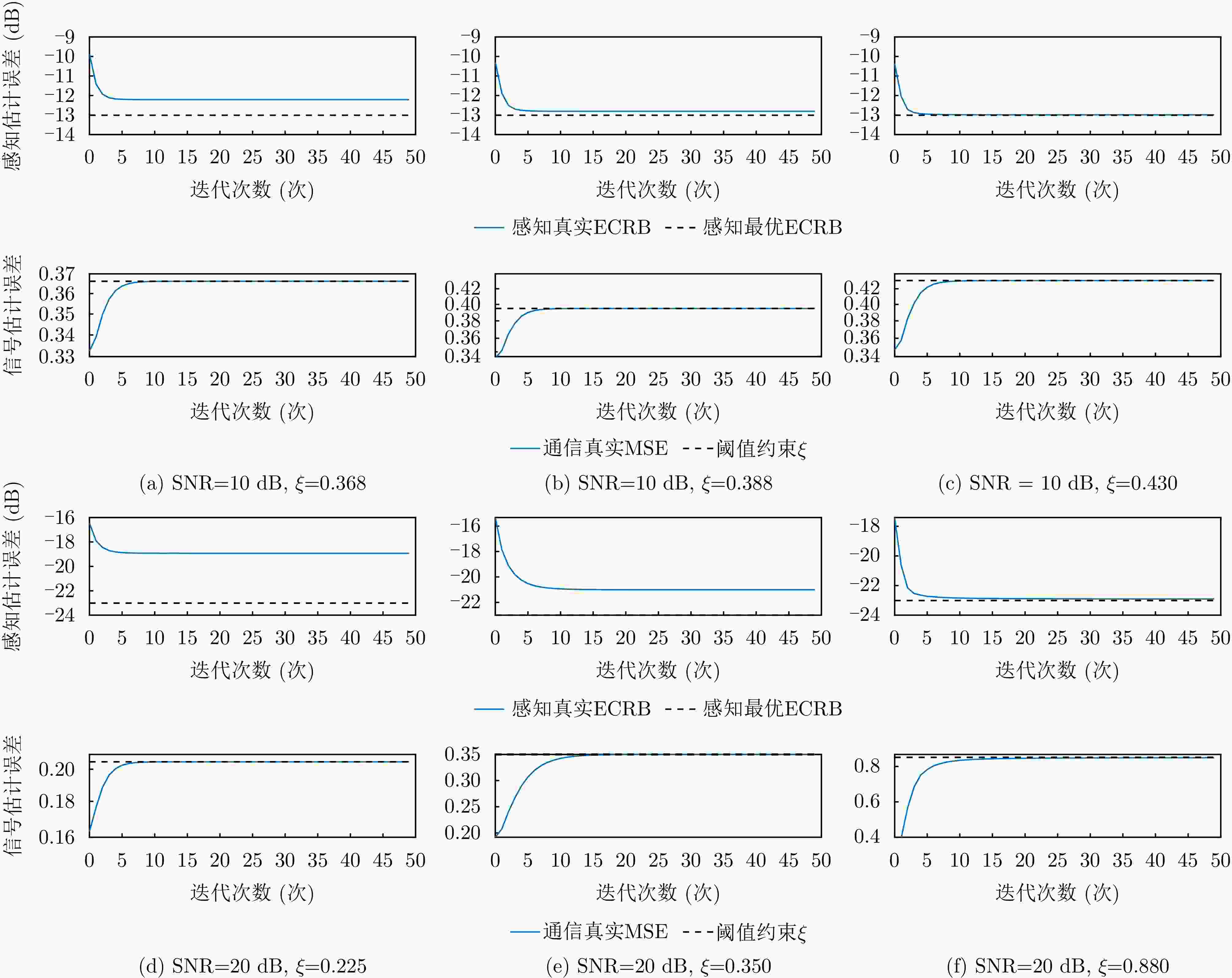
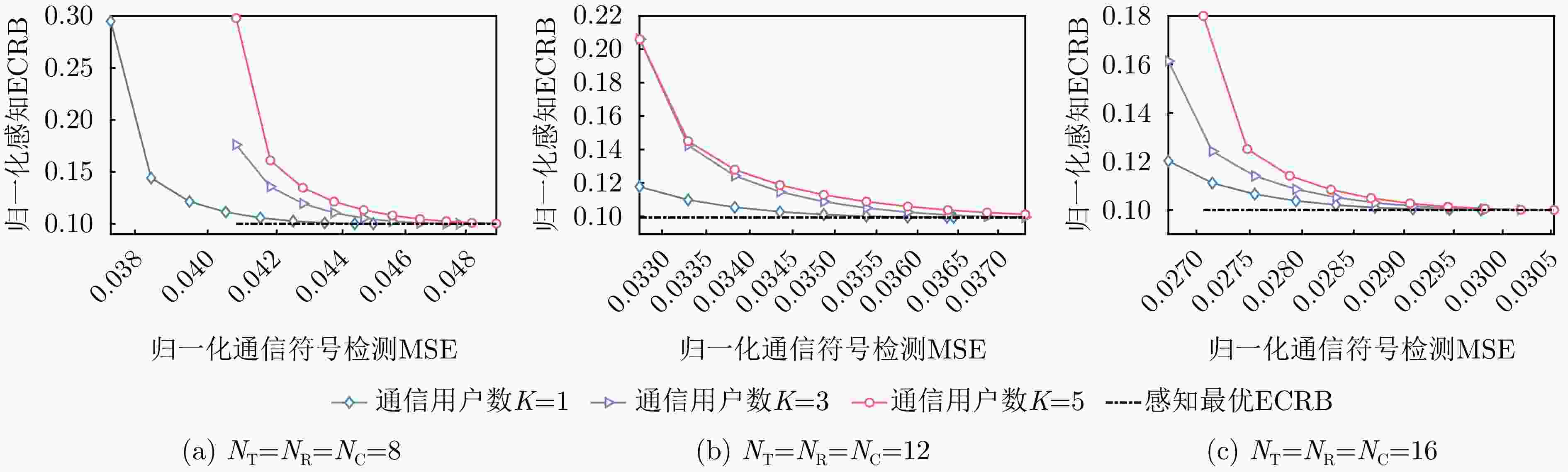
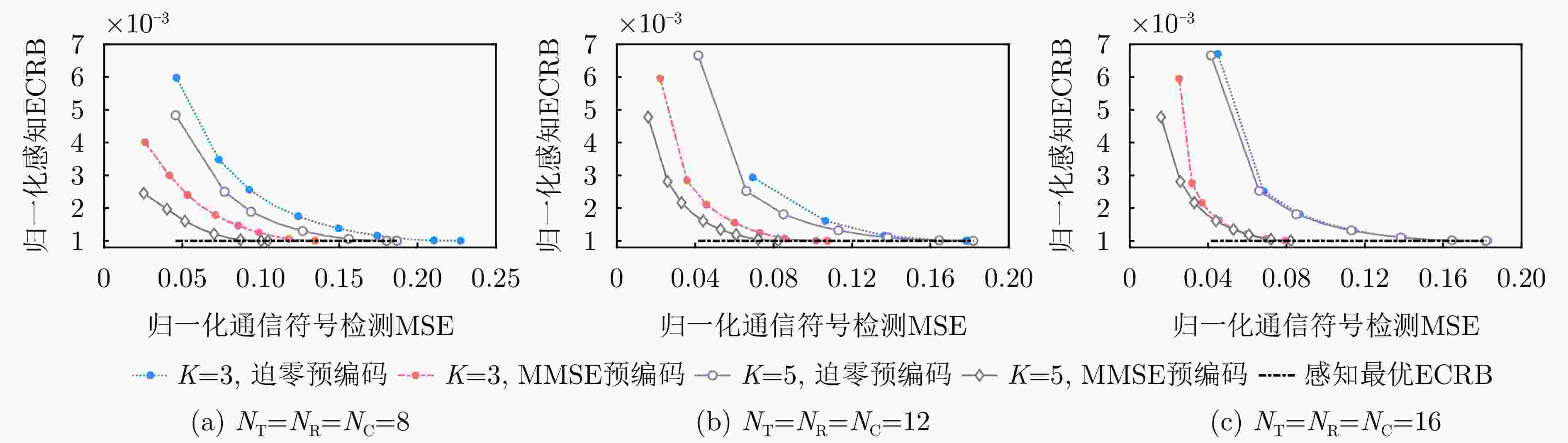
摘要: 通过复用随机通信信号，并基于现网中的通信架构实现通信感知一体化(ISAC)，能够显著降低ISAC实现成本、加速感知功能融入现有通信网络。然而，通信数据的随机性将会使得感知功能出现随机起伏，造成感知性能不稳定。为了获得稳健的感知性能，该文研究了随机通感一体空域信号处理方法，提出了多输入多输出通感一体(MIMO-ISAC)系统收发预编码联合优化设计方案。具体而言，考虑对目标响应矩阵的估计，该文首先定义了随机信号下感知系统的遍历克拉美罗界(ECRB)，并基于复逆Wishart矩阵的分布推导了ECRB的闭合表达式，从理论上说明了使用随机信号进行感知相较于传统使用确定性正交信号的性能损失。进一步地，该文分别考虑了ECRB最小化的感知最优问题以及多天线多用户信号估计的通信最优问题，并获得了感知最优预编码设计和通信最优预编码设计方案。接着，该文将上述收发预编码优化设计思路扩展至通信感知一体化场景。最后，该文通过大量仿真验证了所提方法的有效性，相关结果表明所提出的联合收发预编码设计方案能够支持高精度目标响应矩阵估计，同时能够实现通信信号估计误差与目标响应矩阵估计误差的灵活折衷。Abstract: Integrated Sensing And Communications (ISAC) based on reusing random communication signals within the existing network architecture may drastically reduce implementation costs, thereby accelerating the integration of sensing functionalities into current communication networks. However, the randomness of communication data introduces fluctuations in sensing performance across different signal realizations, leading to unstable sensing accuracy. To address this issue, we delve into random ISAC signal processing methods and propose a joint transceiver precoding optimization design for Multiple-Input Multiple-Output ISAC (MIMO-ISAC) systems. Specifically, considering target impulse response matrix estimation, we first define the Ergodic Cramér-Rao Bound (ECRB) as an average sensing performance metric under random signaling. By deriving the closed-form expression of the ECRB based on the distribution of complex inverse Wishart matrices, we theoretically reveal the performance loss arising when using random signals for sensing compared to the conventional deterministic orthogonal signals. Furthermore, we formulate the sensing-optimal subproblem by minimizing the ECRB and the communication-optimal subproblem of multiantenna multiuser signal estimation and derive the corresponding sensing-optimal and communication-optimal precoding designs. Subsequently, we extend the proposed transceiver precoding optimization framework to ISAC scenarios by explicitly constraining the communication requirements. Finally, through numerous simulations, we validate the effectiveness of the proposed method. The results demonstrate that the joint transceiver precoding design may allow high-accuracy target response matrix estimation while enabling flexible trade-offs between communication signal estimation and target response matrix estimation errors.
-
图 1 随机通感一体信号体制下的MIMO-ISAC系统示意图
Figure 1. The illustration of considered MIMO-ISAC systems under random signaling
图 2 感知最优场景下采用确定信号和采用随机信号下性能对比
Figure 2. Performance comparisons under deterministic and random signals in sensing-optimal scenarios
图 3 通信最优场景下算法1的收敛性能
Figure 3. The convergence behaviors of Alg. 1 in communication-optimal scenarios
图 4 通信最优场景下用户信号估计误差MSE
Figure 4. The normalized MSE of communication users in communication-optimal scenarios
图 5 通信最优场景下用户归一化信号估计误差MSE随信噪比变化
Figure 5. The normalized MSE versus SNR in communication-optimal scenarios
图 6 不同通信信号检测阈值下算法2的收敛性能对比
Figure 6. The convergence behaviors of Alg. 2 in ISAC scenarios, under different MSE thresholds
图 7 不同天线数下通感一体场景性能折衷(SNR=10 dB)
Figure 7. The performance tradeoffs of S&C in ISAC scenarios, under different numbers of antennas (SNR=10 dB)
图 8 通感一体场景对比基线方案(SNR=30 dB)
Figure 8. The performance tradeoffs of S&C in ISAC scenario (SNR=30 dB)
表 1 波形设计方案对比
Table 1. Comparisons of waveform design methods
设计思路 实现方法与典型用例 技术优势 技术挑战 以雷达为中心 雷达波形调制通信信息
(例如：FMCW, PMCW)对感知功能影响较小
感知性能稳健频谱效率低
与现网体制不兼容以通信为中心 基于通信波形实现感知
(例如：OFDM)与现网体制完全兼容
不影响通信性能随机信号影响感知性能
随机信号处理方法不明联合波形设计 基于优化方法设计波形
(例如：CRB-SINR优化问题)可实现通信与感知性能灵活折衷 复杂度高
难以适应未来6G空口
下载: 导出CSV
1 通信最优场景收发联合预编码设计
1. Joint transmit and receive precoding design in communication-optimal scenarios
输入：系统参数：$ \mathcal{K}, {\{ }{{\boldsymbol{H}}_k}{\} }_{k = 1}^K, {\sigma}_k^2,{N_{\rm T}},{N_{\rm R}},{N_{\rm C}},{P_{\rm T}},L $，
算法参数：最大迭代次数$ {{{r}}_{{\max}}} $和收敛误差$ {{\varepsilon }} $输出：收发机预编码矩阵$ {\{ }{{\boldsymbol{B}}_k}{\} }_{k = 1}^K, {\boldsymbol{P}} $ 初始化参数：$ {{r}} = 1, {{\boldsymbol{P}}^{\left( {{r}} \right)}} $ 1. 重复以下步骤 2. 根据$ {{\boldsymbol{P}}^{\left( {{r}} \right)}} $计算得到MMSE接收预编码$ {\{ }{\boldsymbol{B}}_k^{\left( {{r}} \right)}{\} }_{k = 1}^K $ 3. 根据$ {\{ }{\boldsymbol{B}}_k^{\left( {{r}} \right)}{\} }_{k = 1}^K $求解优化问题(P3.1)，获得最优解$ {{\boldsymbol{P}}^ \star } $ 4. 代入$ {{\boldsymbol{P}}^{\left( {{r}} \right)}}\xleftarrow{{}}{{\boldsymbol{P}}^ \star },r = r + 1 $ 5. 继续执行2 6. 直到最大迭代次数$ {{{r}}_{{\max}}} $或者目标函数变化值低于误差$ {{\varepsilon }} $
下载: 导出CSV
2 通感一体场景收发联合预编码设计
2. Joint transmit and receive precoding design in ISAC scenarios
输入：系统参数：$ \mathcal{K}, {\{ }{{\boldsymbol{H}}_k}{\} }_{k = 1}^K, {\sigma}_k^2,{N_{\rm T}},{N_{\rm R}},{N_{\rm C}},{P_{\rm T}},L $，
算法参数：最大迭代次数$ {{{m}}_{{\max}}} $和收敛误差$ {\delta} $输出：收发机预编码矩阵$ {\{ }{{\boldsymbol{B}}_k}{\} }_{k = 1}^K, {\boldsymbol{P}} $ 初始化参数：$ {{m}} = 1, {{\boldsymbol{P}}^{\left( m \right)}} $ 1. 重复以下步骤 2. 根据$ {{\boldsymbol{P}}^{\left( m \right)}} $求解(P4.1)并计算得到MMSE接收预编码
$ {\{ }{\boldsymbol{B}}_k^{\left( m \right)}{\} }_{k = 1}^K $3. 根据$ {{\boldsymbol{P}}^{\left( m \right)}},{\{ }{\boldsymbol{B}}_k^{\left( m \right)}{\} }_{k = 1}^K $代入(P4.4)，求解获得最优解$ {{\boldsymbol{P}}^\prime } $ 4. 根据Armijo步长搜索算法寻找$ {{\lambda}^{\left( m \right)}} $并更新
$ {{\boldsymbol{P}}^{\left( {m + 1} \right)}} = {{\boldsymbol{P}}^{\left( m \right)}} + {\lambda}{(}{{\boldsymbol{P}}^\prime } - {{\boldsymbol{P}}^{\left( m \right)}}{)} $5. $ m = m + 1 $，继续执行2 6. 直到最大迭代次数$ {{{m}}_{{\text{max}}}} $或者目标函数变化值低于误差$ {\delta} $
下载: 导出CSV
表 2 仿真参数设置
Table 2. Simulation parameter settings
参数 数值 参数 数值 基站发射天线数 16 通信噪声功率 0 dBm 基站接收天线数 16 感知噪声功率 0 dBm 用户接收天线数 16 信号相干长度 32 仿真最大迭代数 50 目标函数误差 1E–5
下载: 导出CSV
-
[1] 马丁友, 刘祥, 黄天耀, 等. 雷达通信一体化: 共用波形设计和性能边界[J]. 雷达学报, 2022, 11(2): 198–212. doi: 10.12000/JR21146.MA Dingyou, LIU Xiang, HUANG Tianyao, et al. Joint radar and communications: Shared waveform designs and performance bounds[J]. Journal of Radars, 2022, 11(2): 198–212. doi: 10.12000/JR21146. [2] LIU Fan, ZHENG Le, CUI Yuanhao, et al. Seventy years of radar and communications: The road from separation to integration[J]. IEEE Signal Processing Magazine, 2023, 40(5): 106–121. doi: 10.1109/MSP.2023.3272881. [3] LU Shihang, LIU Fan, LI Yunxin, et al. Integrated sensing and communications: Recent advances and ten open challenges[J]. IEEE Internet of Things Journal, 2024, 11(11): 19094–19120. doi: 10.1109/JIOT.2024.3361173. [4] XIE Lei, SONG Shenghui, ELDAR Y C, et al. Collaborative sensing in perceptive mobile networks: Opportunities and challenges[J]. IEEE Wireless Communications, 2023, 30(1): 16–23. doi: 10.1109/MWC.005.2200214. [5] 尹浩, 黄宇红, 韩林丛, 等. 6G通信-感知-计算融合网络的思考[J]. 中国科学: 信息科学, 2023, 53(9): 1838–1842. doi: 10.1360/SSI-2023-0135.YIN Hao, HUANG Yuhong, HAN Lincong, et al. Thoughts on 6G integrated communication, sensing and computing networks[J]. Scientia Sinica Informationis, 2023, 53(9): 1838–1842. doi: 10.1360/SSI-2023-0135. [6] WEI Zhiqing, XU Ruizhong, FENG Zhiyong, et al. Symbol-level integrated sensing and communication enabled multiple base stations cooperative sensing[J]. IEEE Transactions on Vehicular Technology, 2024, 73(1): 724–738. doi: 10.1109/TVT.2023.3304856. [7] ITU-R. Recommendation ITU-R M.2160-0: Framework and overall objectives of the future development of IMT for 2030 and beyond[EB/OL]. https://www.itu.int/rec/R-REC-M.2160, 2023. [8] ANTIPOLIS S. ETSI launches a new group for integrated sensing and communications, a candidate technology for 6G[EB/OL]. https://www.etsi.org/committee?id=2291, 2023. [9] 通信世界网. 5G-A先行者计划成功!中国移动实现低空无人机感知重大突破[EB/OL]. http://www.cww.net.cn/article?id=578106, 2023.Communication World Network. 5G-A pioneer program success! China mobile achieves low-altitude UAV sensing[EB/OL]. http://www.cww.net.cn/article?id=578106, 2023. [10] IMT-2030(6G)推进组. 通信感知一体化技术研究报告[EB/OL], https://www.imt2030.org.cn/html//default/zhongwen/chengguofabu/yanjiubaogao/index.html?index=2, 2022.IMT-2030 (6G) Promotion Group. Research report on ISAC technologies[EB/OL], https://www.imt2030.org.cn/html//default/zhongwen/chengguofabu/yanjiubaogao/index.html?index=2, 2022. [11] 华为. 6G太赫兹通信感知一体化, 开启无线新可能[EB/OL]. https://www.huawei.com/cn/huaweitech/future-technologies/6g-isac-thz, 2022.Huawei. 6G terahertz ISAC: New opportunities for wireless systems[EB/OL]. https://www.huawei.com/cn/huaweitech/future-technologies/6g-isac-thz, 2022. [12] ISAC-ETI & Huawei. Wi-Fi sensing white paper[R]. 2022. [13] 中国移动. 5G-A通感一体典型场景技术解决方案白皮书[R]. 2024.China Mobile. White paper on 5G-A ISAC systems: Typical scenarios and technology Solutions[R]. 2024. [14] 中国联通. 6G通感智算一体化无线网络白皮书[R]. 2023.China Unicom. White paper on 6G integrated sensing, communication, and intelligent computation[R]. 2023. [15] ZHAO Yajun, DAI Linglong, ZHANG Jianhua, et al. 6G near-field technologies white paper[EB/OL]. FuTURE Forum, Nanjing, China, https://www.g6gconference.com/index/Lists/index.html?id=9, 2024. [16] LIU Fan, CUI Yuanhao, MASOUROS C, et al. Integrated sensing and communications: Toward dual-functional wireless networks for 6G and beyond[J]. IEEE Journal on Selected Areas in Communications, 2022, 40(6): 1728–1767. doi: 10.1109/JSAC.2022.3156632. [17] LIU An, HUANG Zhe, LI Min, et al. A survey on fundamental limits of integrated sensing and communication[J]. IEEE Communications Surveys & Tutorials, 2022, 24(2): 994–1034. doi: 10.1109/COMST.2022.3149272. [18] XIONG Yifeng, LIU Fan, WAN Kai, et al. From torch to projector: Fundamental tradeoff of integrated sensing and communications[J]. IEEE BITS the Information Theory Magazine, 2024, 4(1): 73–90. doi: 10.1109/MBITS.2024.3376638. [19] WEI Zhiqing, QU Hangyang, WANG Yuan, et al. Integrated sensing and communication signals toward 5G-A and 6G: A survey[J]. IEEE Internet of Things Journal, 2023, 10(13): 11068–11092. doi: 10.1109/JIOT.2023.3235618. [20] MENG Kaitao, MASOUROS C, PETROPULU A P., et al. Cooperative ISAC networks: Opportunities and challenges[J]. IEEE Wireless Communications, 2024, in press. doi: 10.1109/MWC.008.2400151. [21] HASSANIEN A, AMIN M G, ZHANG Y D, et al. Signaling strategies for dual-function radar communications: An overview[J]. IEEE Aerospace and Electronic Systems Magazine, 2016, 31(10): 36–45. doi: 10.1109/MAES.2016.150225. [22] HUA Haocheng, XU Jie, and HAN T X. Optimal transmit beamforming for integrated sensing and communication[J]. IEEE Transactions on Vehicular Technology, 2023, 72(8): 10588–10603. doi: 10.1109/TVT.2023.3262513. [23] CHEN Li, WANG Zhiqing, DU Ying, et al. Generalized transceiver beamforming for DFRC with MIMO radar and MU-MIMO communication[J]. IEEE Journal on Selected Areas in Communications, 2022, 40(6): 1795–1808. doi: 10.1109/JSAC.2022.3155515. [24] HUA Meng, WU Qingqing, CHEN Wen, et al. Secure intelligent reflecting surface-aided integrated sensing and communication[J]. IEEE Transactions on Wireless Communications, 2024, 23(1): 575–591. doi: 10.1109/TWC.2023.3280179. [25] XIAO Zichao, LIU Rang, LI Ming, et al. A novel joint angle-range-velocity estimation method for MIMO-OFDM ISAC systems[J]. IEEE Transactions on Signal Processing, 2024, 72: 3805–3818. doi: 10.1109/TSP.2024.3442886. [26] ZHANG Yumeng, ADITYA S, and CLERCKX B. Input distribution optimization in OFDM dual-function radar-communication systems[J]. IEEE Transactions on Signal Processing, 2024, 72: 5258–5273. doi: 10.1109/TSP.2024.3491899. [27] LI Yunxin, LIU Fan, DU Zhen, et al. Frame structure and protocol design for sensing-assisted NR-V2X communications[J]. IEEE Transactions on Mobile Computing, 2024, 23(12): 11045–11060. doi: 10.1109/TMC.2024.3389697. [28] LU Shihang, LIU Fan, DONG Fuwang, et al. Random ISAC signals deserve dedicated precoding[J]. IEEE Transactions on Signal Processing, 2024, 72: 3453–3469. doi: 10.1109/TSP.2024.3427373. [29] LIU Fan, LIU Yafeng, LI Ang, et al. Cramér-Rao bound optimization for joint radar-communication beamforming[J]. IEEE Transactions on Signal Processing, 2022, 70: 240–253. doi: 10.1109/TSP.2021.3135692. [30] SONG Xianxin, XU Jie, LIU Fan, et al. Intelligent reflecting surface enabled sensing: Cramér-Rao bound optimization[J]. IEEE Transactions on Signal Processing, 2023, 71: 2011–2026. doi: 10.1109/TSP.2023.3280715. [31] CHENG Gaoyuan, FANG Yuan, XU Jie, et al. Optimal coordinated transmit beamforming for networked integrated sensing and communications[J]. IEEE Transactions on Wireless Communications, 2024, 23(8): 8200–8214. doi: 10.1109/TWC.2023.3346457. [32] WEN Cai, HUANG Yan, ZHENG Le, et al. Transmit waveform design for dual-function radar-communication systems via hybrid linear-nonlinear precoding[J]. IEEE Transactions on Signal Processing, 2023, 71: 2130–2145. doi: 10.1109/TSP.2023.3278858. [33] XIONG Yifeng, LIU Fan, CUI Yuanhao, et al. On the fundamental tradeoff of integrated sensing and communications under Gaussian channels[J]. IEEE Transactions on Information Theory, 2023, 69(9): 5723–5751. doi: 10.1109/TIT.2023.3284449. [34] LIU Fan, ZHANG Ying, XIONG Yifeng, et al. OFDM achieves the lowest ranging sidelobe under random ISAC signaling[J]. arXiv: 2407.06691, 2024. doi: 10.48550/arXiv.2407.06691. [35] KESKIN M F, MOJAHEDIAN M M, LACRUZ J O, et al. Fundamental trade-offs in monostatic ISAC: A holistic investigation towards 6G[J]. arXiv: 2401.18011, 2024. doi: 10.48550/arXiv.2401.18011. [36] DU Zhen, LIU Fan, XIONG Yifeng, et al. Reshaping the ISAC tradeoff under OFDM signaling: A probabilistic constellation shaping approach[J]. IEEE Transactions on Signal Processing, 2024, 72: 4782–4797. doi: 10.1109/TSP.2024.3465499. [37] LU Shihang, LIU Fan, DONG Fuwang, et al. Optimal precoding toward random ISAC signals[J]. IEEE Transactions on Vehicular Technology, 2024, 73(12): 19884–19889. doi: 10.1109/TVT.2024.3446821. [38] XIE Lei, LIU Fan, LUO Jiajin, et al. Sensing mutual information with random signals in gaussian channels: Bridging sensing and communication metrics[J]. arXiv: 2402.03919, 2024. [39] XIE Lei, LIU Fan, XIE Zhanyuan, et al. Sensing mutual information with random signals in Gaussian channels[C]. IEEE International Conference on Communications, Denver, CO, USA, 2024: 2228–2233. doi: 10.1109/ICC51166.2024.10622618. [40] DONG Fuwang, LIU Fan, LU Shihang, et al. Rethinking estimation rate for wireless sensing: A rate-distortion perspective[J]. IEEE Transactions on Vehicular Technology, 2023, 72(12): 16876–16881. doi: 10.1109/TVT.2023.3298005. [41] MAIWALD D and KRAUS D. On moments of complex Wishart and complex inverse Wishart distributed matrices[C]. 1997 IEEE International Conference on Acoustics, Speech, and Signal Processing, Munich, Germany, 1997: 3817–3820. doi: 10.1109/ICASSP.1997.604712. [42] MARSHALL A W, OLKIN I, and ARNOLD B C. Inequalities: Theory of Majorization and Its Applications[M]. New York: Academic Press, 1979: 340–341. [43] KHANDAKER M R A and RONG Yue. Precoding design for MIMO relay multicasting[J]. IEEE Transactions on Wireless Communications, 2013, 12(7): 3544–3555. doi: 10.1109/TWC.2013.060413.121817. [44] CHEN Guangji, WU Qingqing, HE Chong, et al. Active IRS aided multiple access for energy-constrained IoT systems[J]. IEEE Transactions on Wireless Communications, 2023, 22(3): 1677–1694. doi: 10.1109/TWC.2022.3206332. [45] CHEN Guangji, WU Qingqing, CHEN Wen, et al. IRS-aided wireless powered MEC systems: TDMA or NOMA for computation offloading?[J]. IEEE Transactions on Wireless Communications, 2023, 22(2): 1201–1218. doi: 10.1109/TWC.2022.3203158. [46] WU Tuo, PAN Cunhua, ZHI Kangda, et al. Exploit high-dimensional ris information to localization: What is the impact of faulty element?[J]. IEEE Journal on Selected Areas in Communications, 2024, 42(10): 2803–2819. doi: 10.1109/JSAC.2024.3414582. [47] WU Tuo, ZHI Kangda, YAO Junteng, et al. Fluid antenna systems enabling 6G: Principles, applications, and research directions[J]. arXiv: 2412.03839, 2024. [48] YU Xianghao, SHEN J C, ZHANG Jun, et al. Alternating minimization algorithms for hybrid precoding in millimeter wave MIMO systems[J]. IEEE Journal of Selected Topics in Signal Processing, 2016, 10(3): 485–500. doi: 10.1109/JSTSP.2016.2523903. -
图(8) / 表(4)
计量
- 文章访问数:
- HTML全文浏览量:
- PDF下载量:
- 被引次数: 0
