-
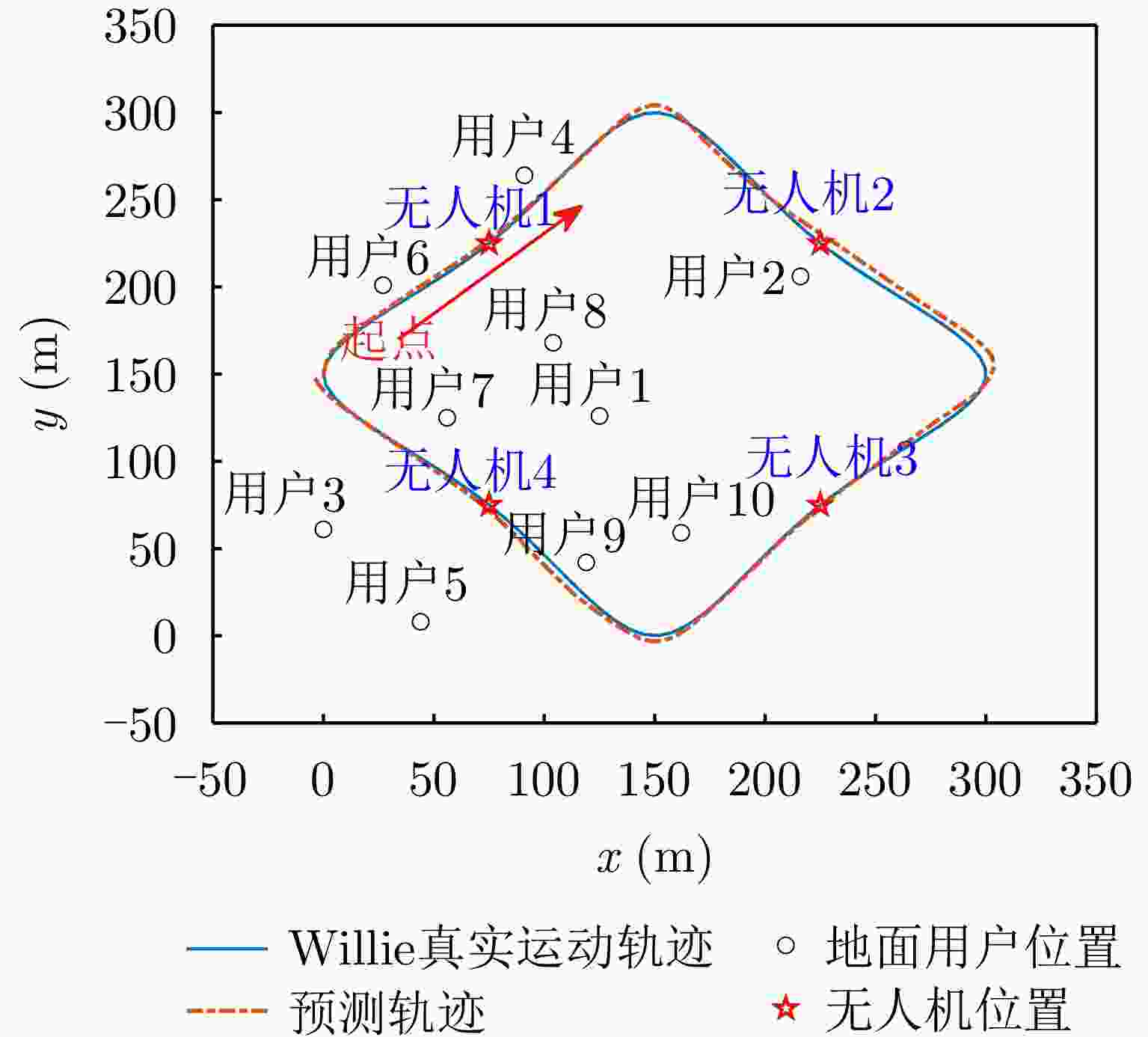
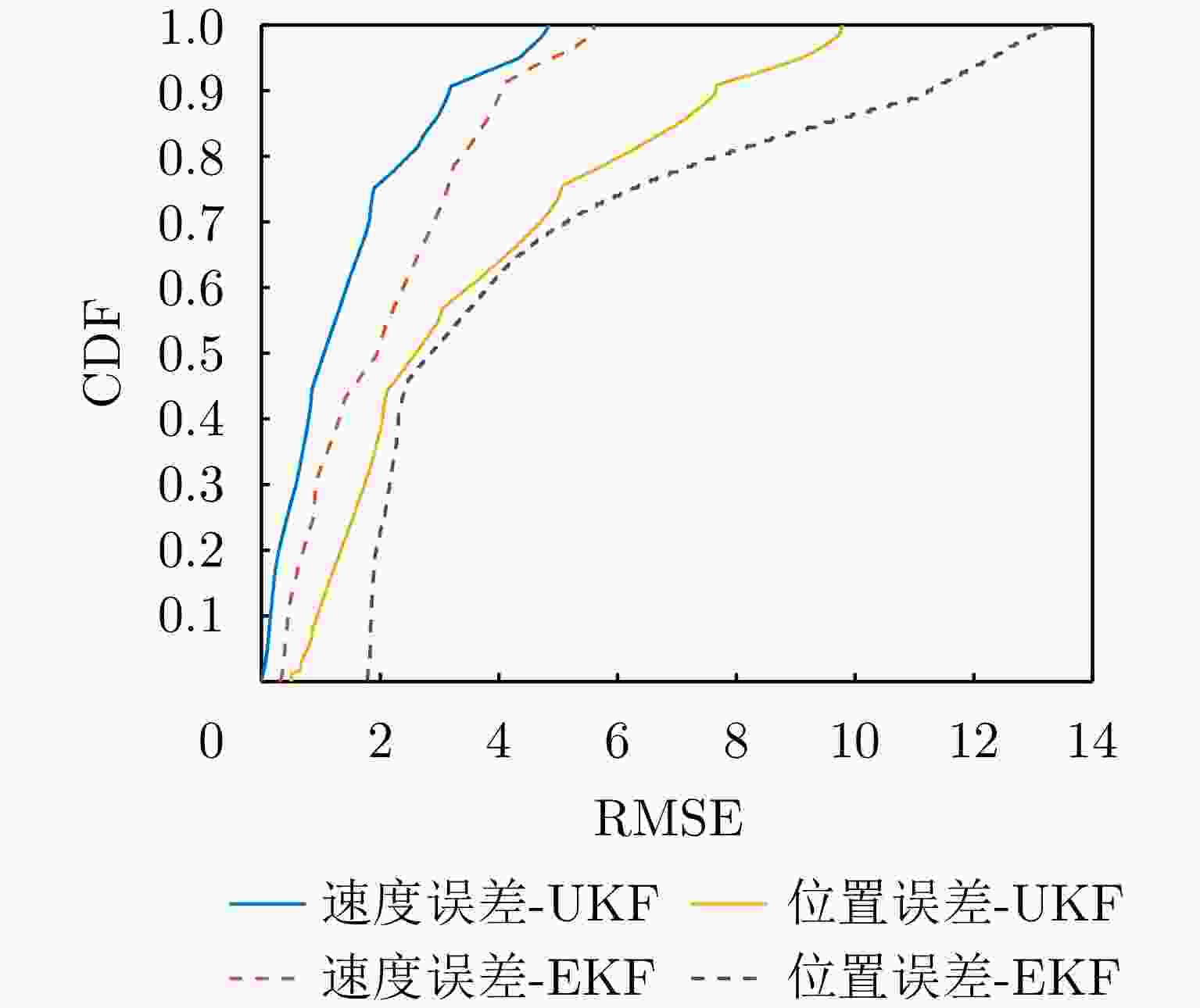
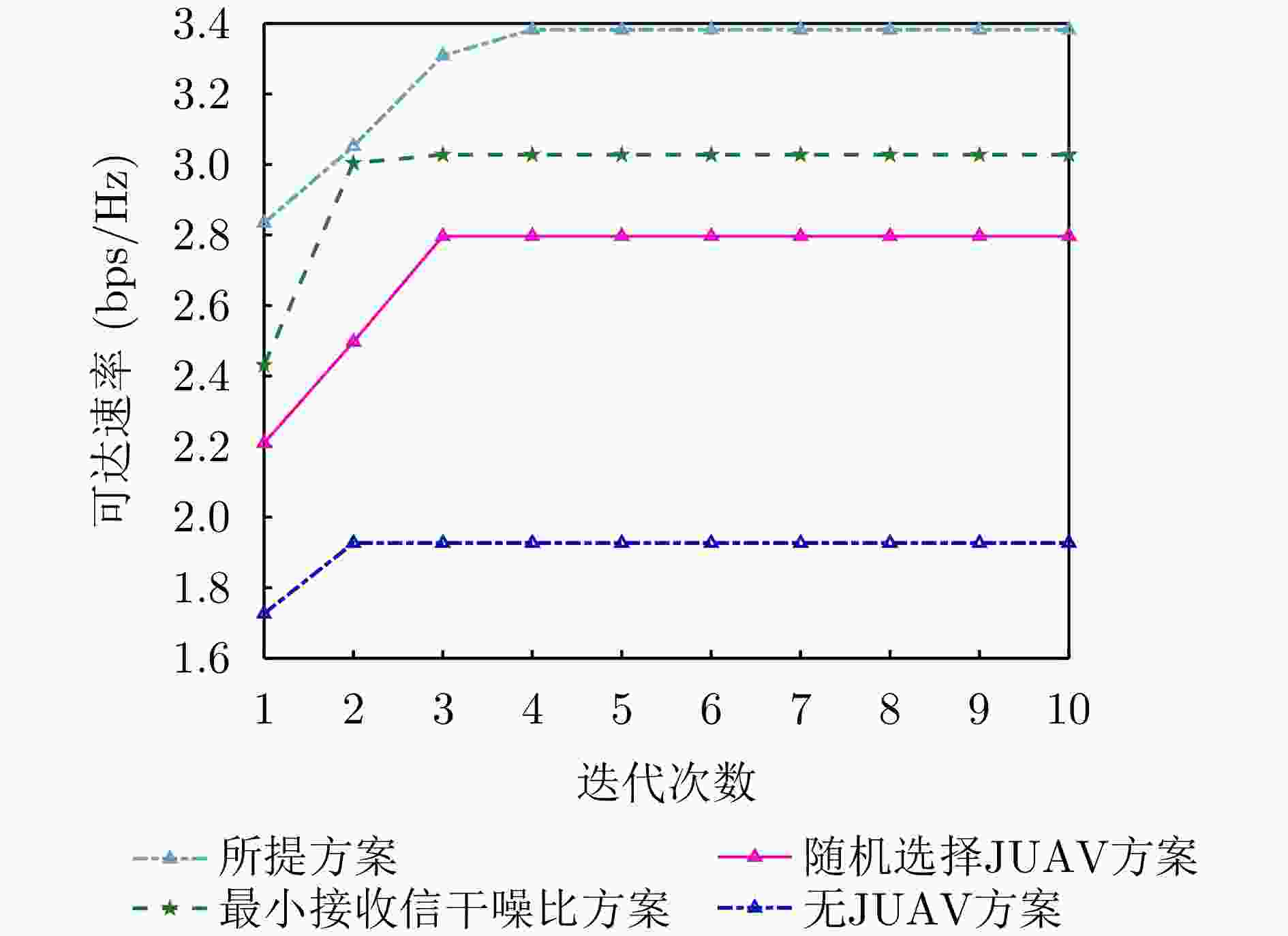
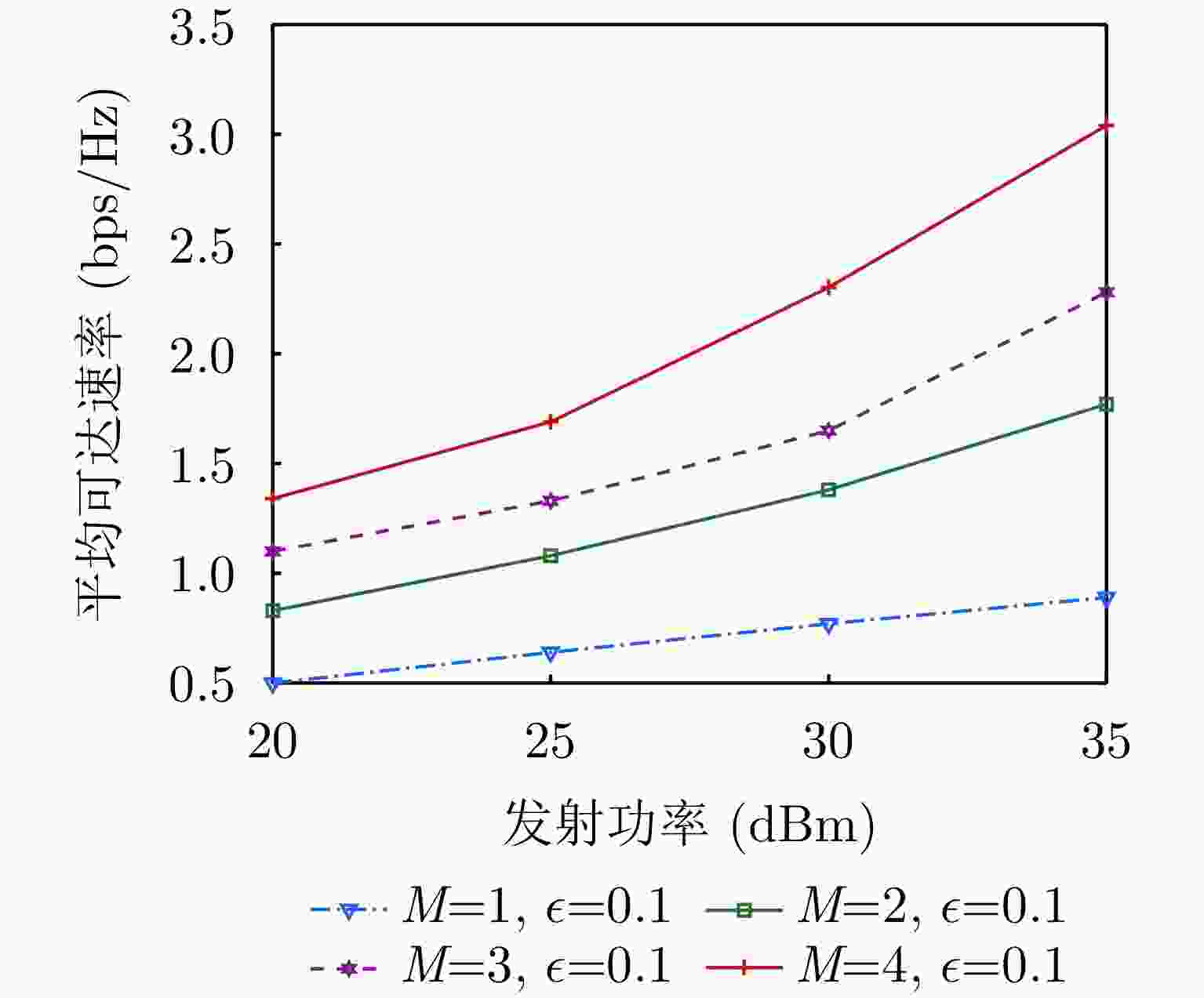
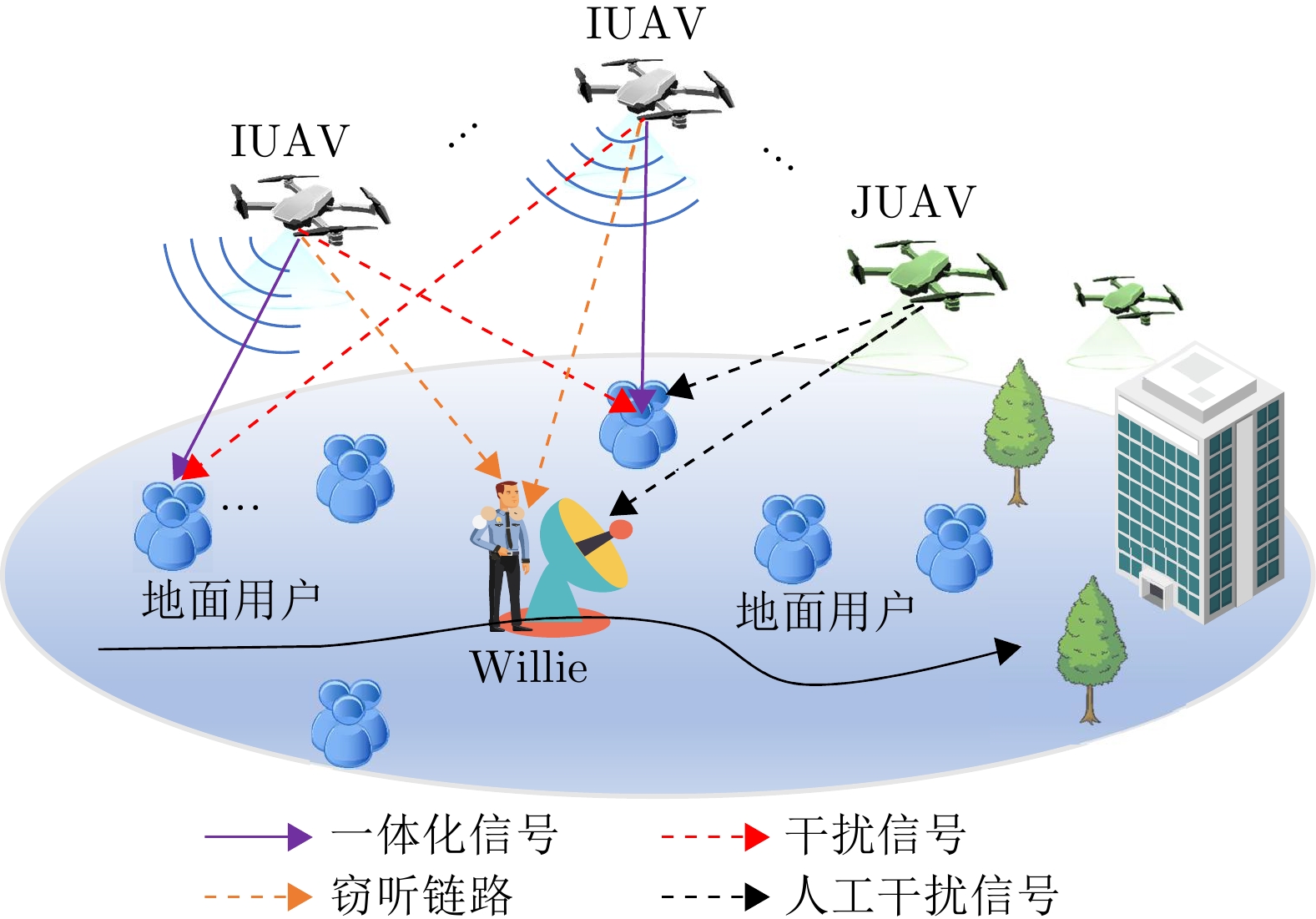
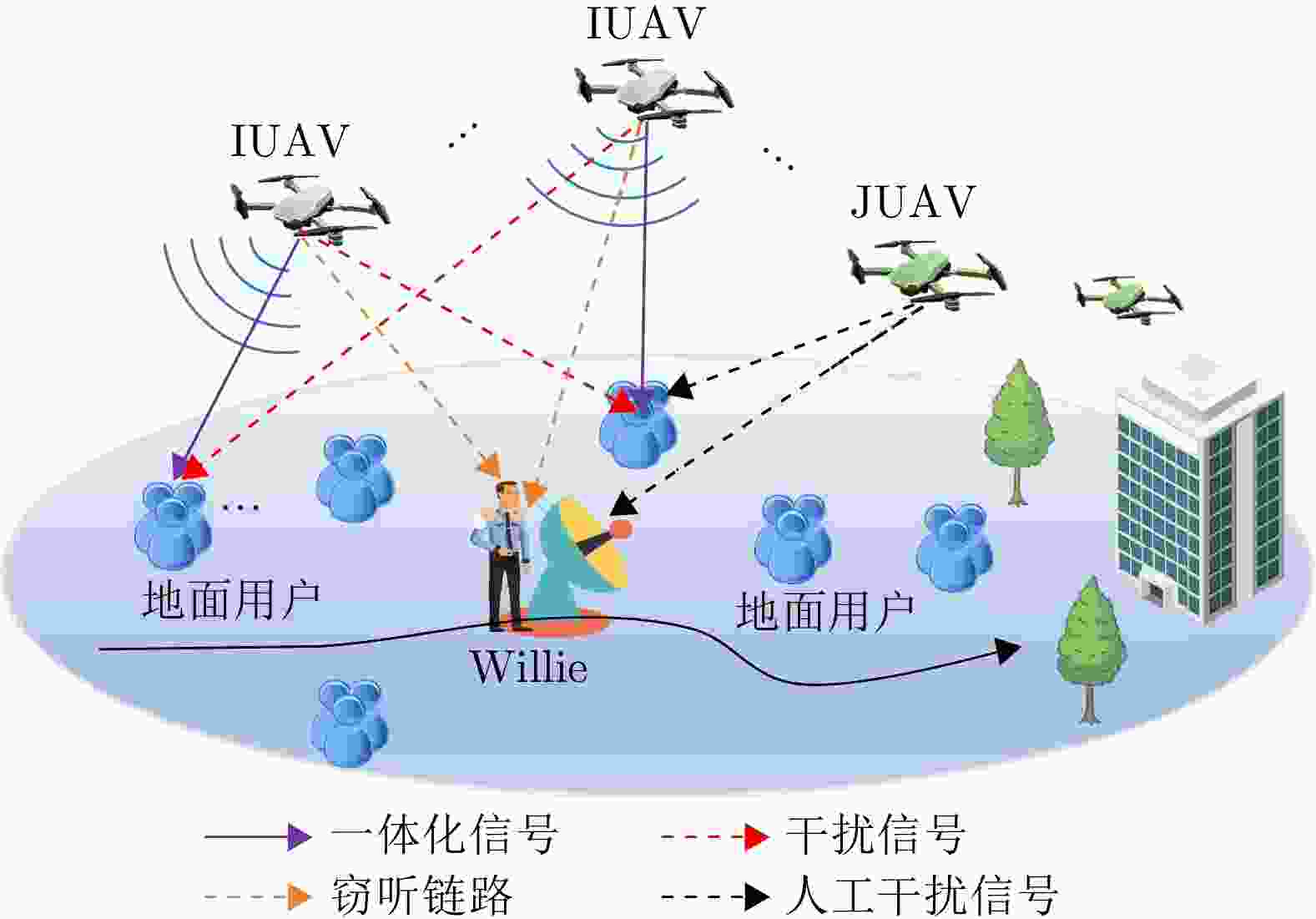
摘要: 无人机隐蔽通信在实现可持续低空经济方面引起了相当大的关注。该文基于通感一体化(ISAC)框架,研究了多无人机协作隐蔽通信网络的系统策略和资源分配,其中多个无人机进行协作感知并在移动监管者(Willie)存在的情况下同时向多个地面用户(GUs)隐蔽传输下行信息。为了提高通信隐蔽性,无人机在干扰无人机(JUAV)模式和信息无人机(IUAV)模式之间自适应切换。为了应对Willie的移动性,采用基于无迹卡尔曼滤波的方法,利用从ISAC回波中提取的时延和多普勒频移来预测和跟踪Willie的位置。通过联合优化JUAV选择策略、IUAV-GU调度、通信/干扰功率分配,该文提出了一个实时公平性传输最大化问题。采用交替优化方法,将原始问题分解为一系列子问题,从而获得有效的次优解。仿真结果表明,所提出的方案能够准确跟踪Willie并有效保证下行隐蔽传输。Abstract: Covert Unmanned Aerial Vehicle (UAV) communication has garnered considerable attention for realizing a sustainable Low-Altitude Economy (LAE). Based on the Integrated Sensing And Communication (ISAC) framework, this paper studies the system strategies and resource allocation for a cooperative multi-UAV covert communication network, where multiple UAVs are employed to simultaneously conduct cooperative sensing and covert downlink transmissions to multiple Ground Users (GUs) in the presence of a mobile warden (Willie). To improve communication covertness, UAVs adaptively switch between Jamming Unmanned Aerial Vehicle (JUAV) mode and Information Unmanned Aerial Vehicle (IUAV) mode. To cope with the mobility of Willie, an Unscented Kalman Filtering (UKF)-based method is employed to track and predict Willie's location using delay and Doppler measurements extracted from ISAC echoes. By jointly optimizing the JUAV selection strategy, IUAV-GU scheduling, and communication/jamming power allocation, a real-time fairness transmission maximization problem is formulated. The Alternating Optimization (AO) approach is adopted to decompose the original problem into a series of sub-problems, resulting in an efficient sub-optimal solution. Simulation results demonstrate that the proposed scheme can accurately track Willie and effectively ensure covert downlink transmission.
-
1 多无人机联合干扰策略优化算法
1. Jamming strategy optimization algorithm
输入:迭代索引${r_1} = 0$, ${r_{1,\max }}$, ${\kappa _{\max }}$和可行点
$ \left\{ {{\mathcal{B}^0},{\mathcal{P}^0},{{\tilde {\mathcal{P}}}}^0},{\mu ^0} \right\} $输出:$\left\{ {{\mathcal{B}^*},{\mathcal{P}^{J,*}},{{\tilde {\mathcal{P}}}^{J,*}},{\mu ^*}} \right\}$ 1.给定$\left\{ {{\mathcal{B}^{{r_1}}},{\mathcal{P}^{J,{r_1}}},{{\tilde {\mathcal{P}}}^{J,{r_1}}},{\mu ^{{r_1}}}} \right\}$,求解(P1-1),并将解表示
为$\left\{ {{\mathcal{B}^*},{\mathcal{P}^{J,*}},{{\tilde {\mathcal{P}}}^{J,*}},{\mu ^*}} \right\}$2.令$\left\{ {{\mathcal{B}^{{r_1}}},{\mathcal{P}^{J,{r_1}}},{{\tilde {\mathcal{P}}}^{J,{r_1}}},{\mu ^{{r_1}}}} \right\} = \left\{ {{\mathcal{B}^*},{\mathcal{P}^{J,*}},{{\tilde {\mathcal{P}}}^{J,*}},{\mu ^*}} \right\}$ 3.更新 ${\kappa ^{{r_1} + 1}} = \min \{ {a_0}{\kappa ^{{r_1}}},{\kappa _{\max }}\} $ 4.更新 ${r_1} = {r_1} + 1$ 5.重复上述步骤直到收敛 2 多无人机隐蔽通信总体设计算法
2. Overall algorithm of multi-UAV-based covert communications
输入:$n = 2,$$\ell = 0,{{\boldsymbol{\hat x}}_{\rm w}}[1],{{\hat {\boldsymbol C}}}[1]$,最大迭代次数为${\ell _{\max }}$和
$\left\{ {{\mathcal{A}^0},{\mathcal{P}^{I,0}}} \right\}$输出:$\left\{ {\mathcal{A},{\mathcal{P}^I},\mathcal{B},{\mathcal{P}^\mathcal{J}}} \right\}$ 1. 计算预测值${{\boldsymbol{\hat x}}_{\rm w}}[n\mid n - 1]$和${{\hat {\boldsymbol C}}}[n\mid n - 1]$ 2. 解问题(P1-1)来确定干扰策略$\left\{ {{\mathcal{B}^{\ell + 1}},{\mathcal{P}^{\mathcal{J},\ell + 1}}} \right\}$ 3. 基于$\left\{ {{\mathcal{B}^{\ell + 1}},{\mathcal{P}^{\mathcal{J},\ell + 1}}} \right\}$,解(P2-1)和(P3-1)确定
$\left\{ {{\mathcal{A}^{\ell + 1}},{\mathcal{P}^{I,\ell + 1}}} \right\}$4. 更新$\ell = \ell + 1$并重复步骤2、步骤3,直到收敛或者$\ell \ge {\ell _{{\text{max }}}}$ 5. 更新$n = n + 1$,并重复上述步骤,直到$n > N$ -
[1] JIANG Yihang, LI Xiaoyang, ZHU Guangxu, et al. 6G non-terrestrial networks enabled low-altitude economy: Opportunities and challenges[EB/OL]. https://arxiv.org/abs/2311.09047, 2024. [2] MOTLAGH N H, TALEB T, and AROUK O. Low-altitude unmanned aerial vehicles-based internet of things services: Comprehensive survey and future perspectives[J]. IEEE Internet of Things Journal, 2016, 3(6): 899–922. doi: 10.1109/JIOT.2016.2612119. [3] ZHANG Ruizhi, ZHANG Ying, TANG Rui, et al. A joint UAV trajectory, user association, and beamforming design strategy for multi-UAV-assisted ISAC systems[J]. IEEE Internet of Things Journal, 2024, 11(18): 29360–29374. doi: 10.1109/JIOT.2024.3430390. [4] CAI Yuanxin, WEI Zhiqiang, LI Ruide, et al. Joint trajectory and resource allocation design for energy-efficient secure UAV communication systems[J]. IEEE Transactions on Communications, 2020, 68(7): 4536–4553. doi: 10.1109/TCOMM.2020.2982152. [5] WU Jun, YUAN Weijie, and BAI Lin. Multi-UAV enabled sensing: Cramér-Rao bound optimization[C]. 2023 IEEE International Conference on Communications Workshops, Rome, Italy, 2023: 925–930. doi: 10.1109/ICCWorkshops57953.2023.10283770. [6] WEI Zhiqiang, LIU Fan, LIU Chang, et al. Integrated sensing, navigation, and communication for secure UAV networks with a mobile eavesdropper[J]. IEEE Transactions on Wireless Communications, 2024, 23(7): 7060–7078. doi: 10.1109/TWC.2023.3337148. [7] WU Jun, YUAN Weijie, and HANZO L. When UAVs meet ISAC: Real-time trajectory design for secure communications[J]. IEEE Transactions on Vehicular Technology, 2023, 72(12): 16766–16771. doi: 10.1109/TVT.2023.3290033. [8] CHEN Xinying, AN Jianping, XIONG Zehui, et al. Covert communications: A comprehensive survey[J]. IEEE Communications Surveys & Tutorials, 2023, 25(2): 1173–1198. doi: 10.1109/COMST.2023.3263921. [9] 白恒志, 王海超, 李国鑫, 等. 无人机隐蔽通信网络研究综述[J]. 电信科学, 2023, 39(8): 1–16. doi: 10.11959/j.issn.1000-0801.2023162.BAI Hengzhi, WANG Haichao, LI Guoxin, et al. Review on unmanned aerial vehicle covert communication network[J]. Telecommunications Science, 2023, 39(8): 1–16. doi: 10.11959/j.issn.1000-0801.2023162. [10] BASH B A, GOECKEL D, and TOWSLEY D. Limits of reliable communication with low probability of detection on AWGN channels[J]. IEEE Journal on Selected Areas in Communications, 2013, 31(9): 1921–1930. doi: 10.1109/JSAC.2013.130923. [11] JIANG Xu, CHEN Xinying, TANG Jie, et al. Covert communication in UAV-assisted air-ground networks[J]. IEEE Wireless Communications, 2021, 28(4): 190–197. doi: 10.1109/MWC.001.2000454. [12] HE Biao, YAN Shihao, ZHOU Xiangyun, et al. On covert communication with noise uncertainty[J]. IEEE Communications Letters, 2017, 21(4): 941–944. doi: 10.1109/LCOMM.2016.2647716. [13] CHEN Xinying, ZHANG Ning, TANG Jie, et al. UAV-aided covert communication with a multi-antenna jammer[J]. IEEE Transactions on Vehicular Technology, 2021, 70(11): 11619–11631. doi: 10.1109/TVT.2021.3112121. [14] ZHENG Tongxing, YANG Ziteng, WANG Chao, et al. Wireless covert communications aided by distributed cooperative jamming over slow fading channels[J]. IEEE Transactions on Wireless Communications, 2021, 20(11): 7026–7039. doi: 10.1109/TWC.2021.3080382. [15] HE Rongrong, CHEN Jin, LI Guoxin, et al. Channel-aware jammer selection and power control in covert communication[J]. IEEE Transactions on Vehicular Technology, 2024, 73(2): 2266–2279. doi: 10.1109/TVT.2023.3317638. [16] WANG Huiming, ZHANG Yan, ZHANG Xu, et al. Secrecy and covert communications against UAV surveillance via multi-hop networks[J]. IEEE Transactions on Communications, 2020, 68(1): 389–401. doi: 10.1109/TCOMM.2019.2950940. [17] WANG Chao, LI Zan, and NG D W K. Covert rate optimization of millimeter wave full-duplex communications[J]. IEEE Transactions on Wireless Communications, 2022, 21(5): 2844–2861. doi: 10.1109/TWC.2021.3116106. [18] 刘学敏, 钱玉文, 宋耀良, 等. 一种基于无人机与智能反射面的隐蔽通信系统研究[J]. 电子与信息学报, 2025, 47(2): 386–396. doi: 10.11999/JEIT240663.LIU Xuemin, QIAN Yuwen, SONG Yaoliang, et al. An intelligent reflecting surface assisted covert communication system with a cooperative unmanned aerial vehicle[J]. Journal of Electronics & Information Technology, 2025, 47(2): 386–396. doi: 10.11999/JEIT240663. [19] WU Jun, YUAN Weijie, WEI Zhiqiang, et al. Optimal BER minimum precoder design for OTFS-Based ISAC systems[C]. 2024 IEEE International Conference on Acoustics, Speech and Signal Processing, Seoul, Korea, Republic of, 2024: 12966–12970. doi: 10.1109/ICASSP48485.2024.10446140. [20] ZHANG Xiaoqi, YUAN Weijie, LIU Chang, et al. Predictive beamforming for vehicles with complex behaviors in ISAC systems: A deep learning approach[J]. IEEE Journal of Selected Topics in Signal Processing, 2024, 18(5): 828–841. doi: 10.1109/JSTSP.2024.3405856. [21] LIU Yulin, SHI Yuye, ZHANG Xiaoqi, et al. Reinforcement learning-based car-following control for autonomous vehicles with OTFS[C]. 2024 IEEE Wireless Communications and Networking Conference, Dubai, United Arab Emirates, 2024: 1–6. doi: 10.1109/WCNC57260.2024.10570722. [22] LU Shihang, LIU Fan, LI Yunxin, et al. Integrated sensing and communications: Recent advances and ten open challenges[J]. IEEE Internet of Things Journal, 2024, 11(11): 19094–19120. doi: 10.1109/JIOT.2024.3361173. [23] WU Jun, YUAN Weijie, WEI Zhiqiang, et al. Low-complexity minimum BER precoder design for ISAC systems: A delay-Doppler perspective[J]. IEEE Transactions on Wireless Communications, 2025, 24(2): 1526–1540. doi: 10.1109/TWC.2024.3509973. [24] 杨小鹏, 马忠杰, 钟世超, 等. 基于遗传算法的无人机载穿墙三维SAR航迹规划方法[J]. 雷达学报(中英文), 2024, 13(4): 731–746. doi: 10.12000/JR24068.YANG Xiaopeng, MA Zhongjie, ZHONG Shichao, et al. Trajectory planning method for UAV-through-the-wall 3D SAR based on a genetic algorithm[J]. Journal of Radars, 2024, 13(4): 731–746. doi: 10.12000/JR24068. [25] WU Jun, YUAN Weijie, and BAI Lin. On the interplay between sensing and communications for UAV trajectory design[J]. IEEE Internet of Things Journal, 2023, 10(23): 20383–20395. doi: 10.1109/JIOT.2023.3287991. [26] WANG Xinyi, FEI Zesong, LIU Peng, et al. Sensing-aided covert communications: Turning interference into allies[J]. IEEE Transactions on Wireless Communications, 2024, 23(9): 10726–10739. doi: 10.1109/TWC.2024.3374775. [27] XIONG Kaiqi, ZHANG H Y, and CHAN C W. Performance evaluation of UKF-based nonlinear filtering[J]. Automatica, 2006, 42(2): 261–270. doi: 10.1016/j.automatica.2005.10.004. [28] LI Ruide, WEI Zhiqiang, YANG Lei, et al. Resource allocation for secure multi-UAV communication systems with multi-eavesdropper[J]. IEEE Transactions on Communications, 2020, 68(7): 4490–4506. doi: 10.1109/TCOMM.2020.2983040. [29] CHENG Gaoyuan, FANG Yuan, XU Jie, et al. Optimal coordinated transmit beamforming for networked integrated sensing and communications[J]. IEEE Transactions on Wireless Communications, 2024, 23(8): 8200–8214. doi: 10.1109/TWC.2023.3346457. [30] CHEN Xinying, SHENG Min, ZHAO Nan, et al. UAV-relayed covert communication towards a flying warden[J]. IEEE Transactions on Communications, 2021, 69(11): 7659–7672. doi: 10.1109/TCOMM.2021.3106354. -



 作者中心
作者中心 专家审稿
专家审稿 责编办公
责编办公 编辑办公
编辑办公
 下载:
下载: