基于变分边缘化粒子滤波的车载雷达扩展目标跟踪

周浩文; 王奇

doi:10.12000/JR25005

基于变分边缘化粒子滤波的车载雷达扩展目标跟踪

DOI: 10.12000/JR25005 CSTR: 32380.14.JR25005

周浩文^1, ,,
王奇²

1.
南京楚航科技有限公司南京 211800
2.
海拉南京研发中心南京 211106

详细信息

作者简介:
周浩文，博士，主要研究方向为车载毫米波雷达数据处理、信息融合、非线性估计与滤波

王　奇，硕士，主要研究方向为车载毫米波雷达数据处理

通讯作者:
周浩文 zhouhaowen@nuaa.edu.cn

责任主编：黄岩 Corresponding Editor: HUANG Yan
中图分类号: TN911.7
计量
- 文章访问数:
- HTML全文浏览量:
- PDF下载量:
- 被引次数: 0
出版历程
- 收稿日期: 2025-01-03
- 修回日期: 2025-05-01

Extended Object Tracking Based on Variational Marginalized Particle Filter for Automotive Radar

ZHOU Haowen^{1
, ,},
WANG Qi²

1.
Nanjing ChuHang Technology Co., Ltd., Nanjing 211800, China
2.
Hella Nanjing Technology Center, Nanjing 211106, China

More Information

Corresponding author: ZHOU Haowen, zhouhaowen@nuaa.edu.cn

摘要

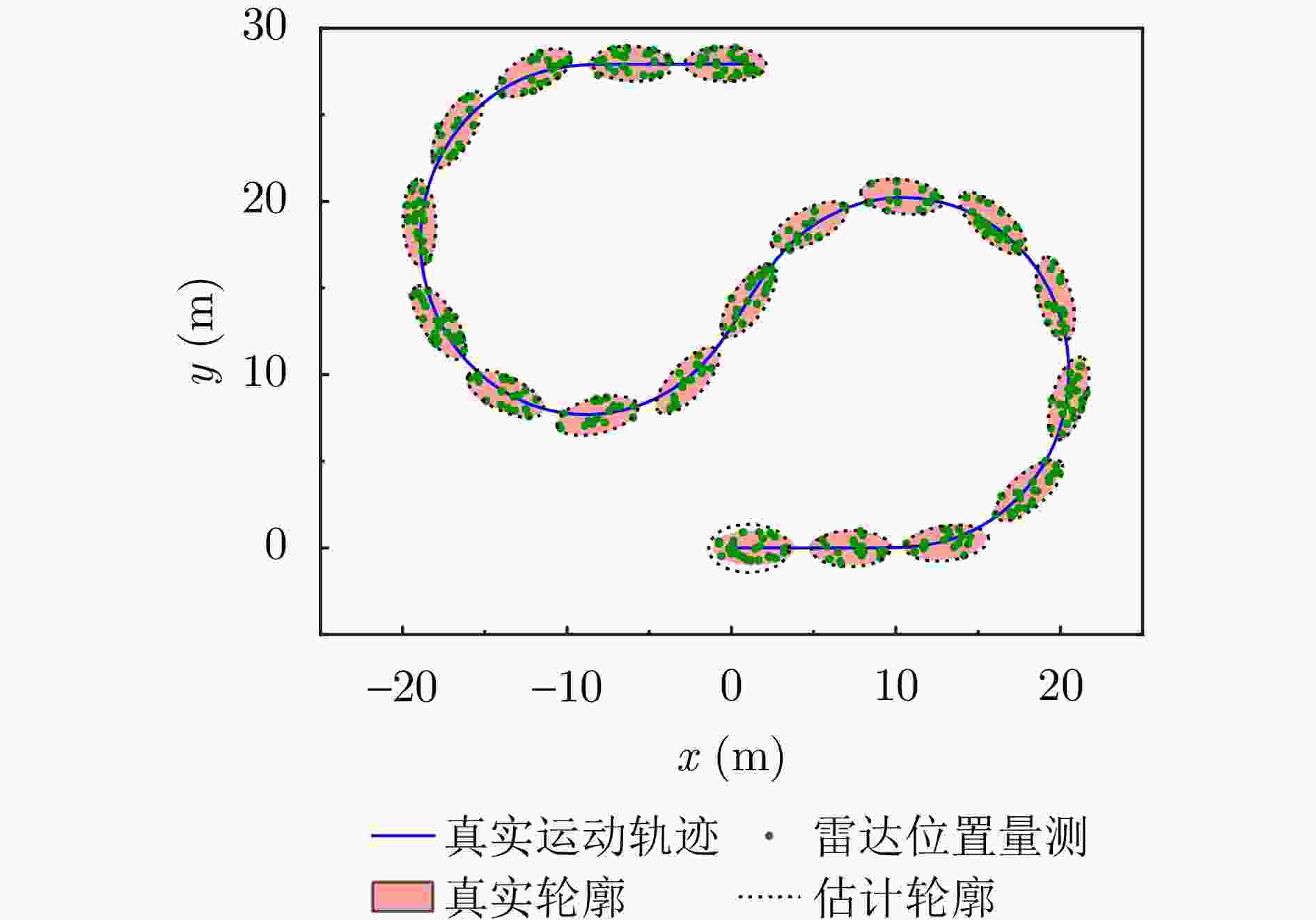
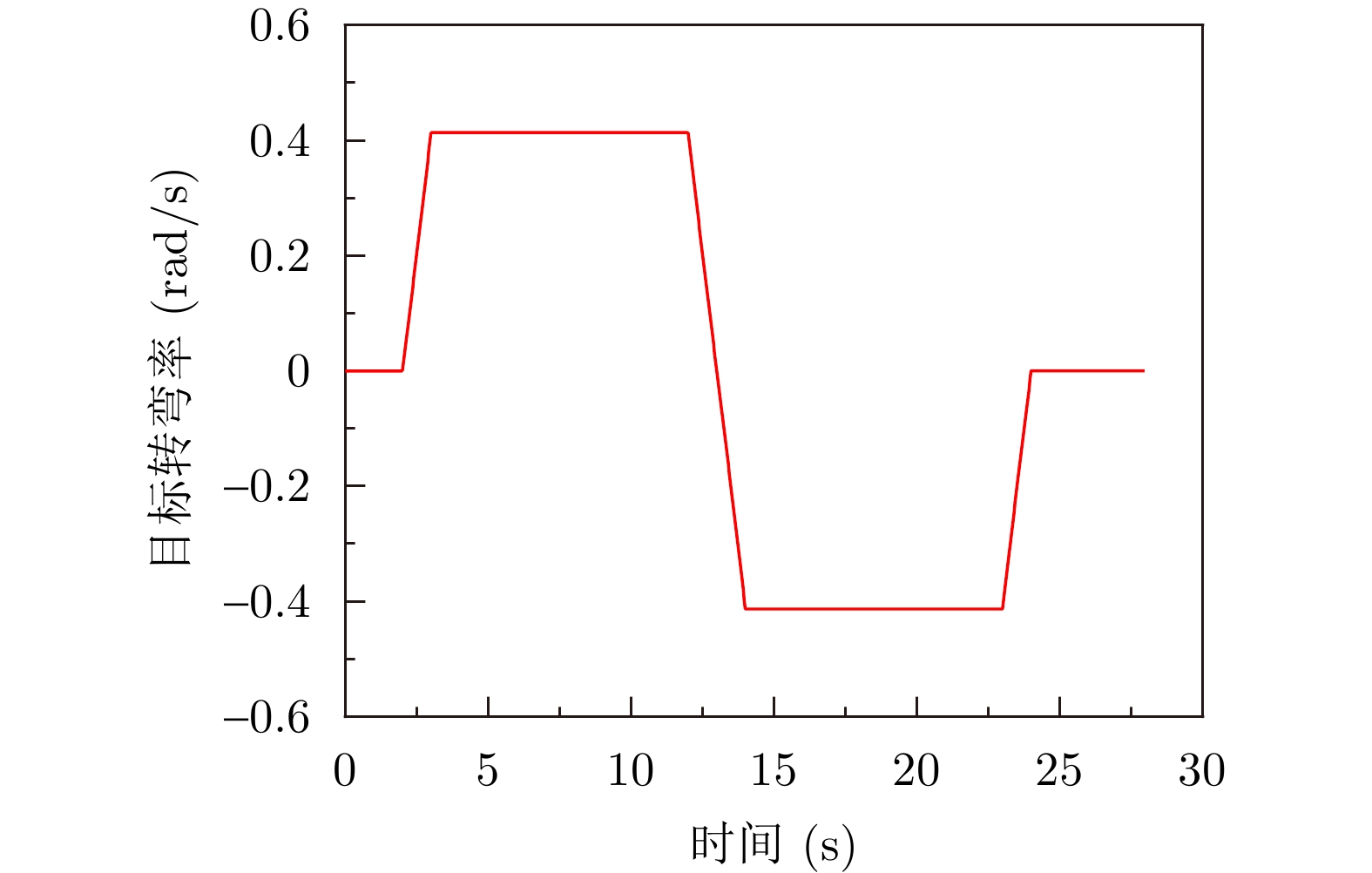
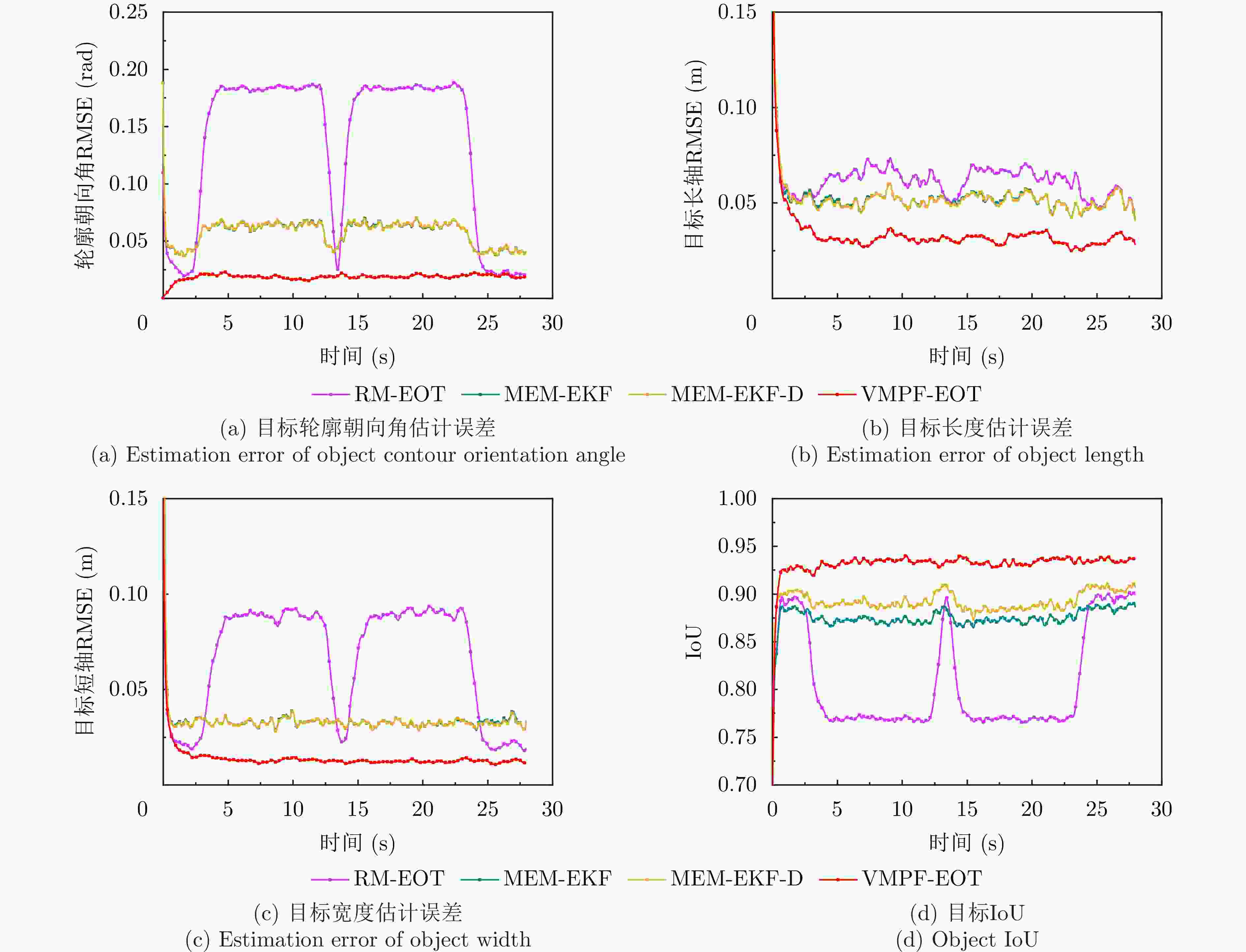
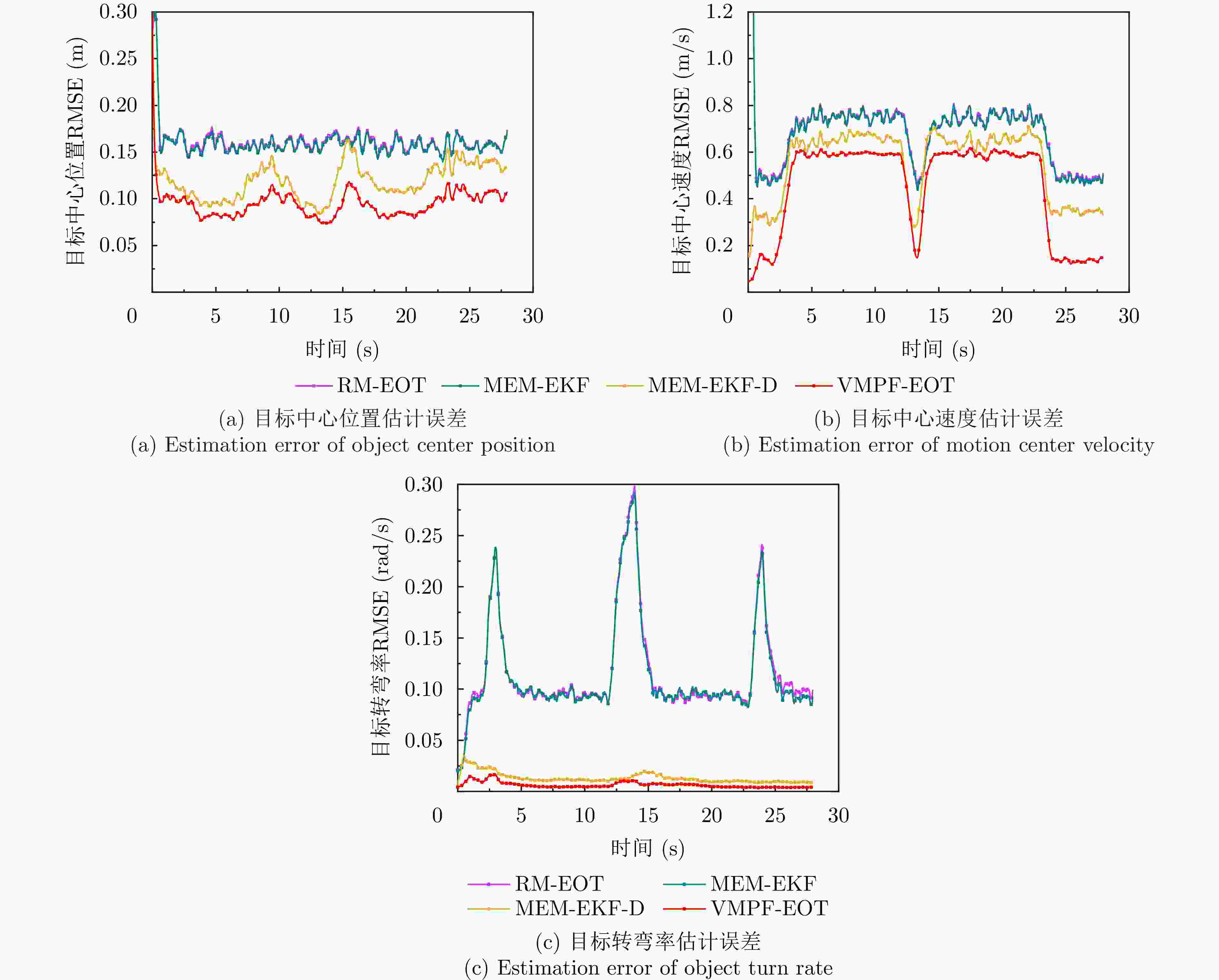
摘要: 车载毫米波雷达量测由极坐标系下的位置坐标与多普勒速度组成，其与笛卡儿坐标系下建模的扩展目标状态具有复杂的非线性关系。针对以上非线性状态估计问题，提出一种基于变分边缘化粒子滤波的扩展目标跟踪算法。首先，采用椭圆对目标二维平面轮廓建模，显式定义轮廓朝向角，构建参数化的逆伽马分布作为轮廓尺寸的共轭先验分布；其次，引入量测源位置作为辅助变量，建立适用于毫米波雷达的扩展目标量测模型；然后，为了改善复杂机动目标轮廓估计性能，基于边缘化思想，利用粒子滤波算法独立估计轮廓朝向角的后验分布，并在变分贝叶斯推断框架内，迭代求解剩余状态变量(包括目标中心运动状态、轮廓尺寸)后验分布的近似解析表达式。仿真实验结果表明，所提算法相比于已有算法能够获得更高的状态估计精度，在跟踪机动目标时，对轮廓朝向角与尺寸的估计性能优势更加明显。
- 车载雷达 /
- 扩展目标跟踪 /
- 多普勒速度 /
- 变分贝叶斯 /
- 边缘化粒子滤波
Abstract: The measurement from automotive millimeter-wave radar consists of position coordinates in the polar coordinate system and doppler velocity, which has a complex, nonlinear relationship with the extended object state modeled in the Cartesian coordinate system. To address this nonlinear state estimation problem, a Variational Marginalized Particle Filter–based Extended Object Tracking (VMPF-EOT) algorithm is proposed. First, the object’s two-dimensional planar contour is modeled as an ellipse with an explicitly defined orientation angle. A parameterized inverse gamma distribution is constructed as the conjugate prior distribution for the contour size. Second, the measurement source position is introduced as an auxiliary variable to establish a measurement model for extended objects detected by automotive millimeter-wave radar. To enhance the contour estimation performance for maneuvering objects, the joint distribution of the extended object state is marginalized with respect to the contour orientation angle. The posterior distribution of the contour orientation angle is estimated independently using a particle filter. The approximate analytical solution for the posterior distributions of the remaining state variables—including the target’s center motion state and contour size—is derived using the variational Bayesian inference. The simulation results demonstrate that the proposed algorithm achieves higher state estimation accuracy than existing algorithms. In tracking maneuvering targets, the proposed algorithm offers a more significant advantage in terms of estimating the contour orientation angle and contour size.
- Automotive radar /
- Extended object tracking /
- Doppler velocity /
- Variational inference /
- Marginalized particle filter

HTML全文

图 1 基于车载毫米波雷达的扩展目标

Figure 1. Extended object tracking based on automotive millimeter-wave radar

下载: 全尺寸图片幻灯片

图 2 基于VMPF-EOT算法的扩展目标跟踪

Figure 2. Extended object tracking based on VMPF-EOT

下载: 全尺寸图片幻灯片

图 3 目标真实转弯率

Figure 3. True object turn rate

下载: 全尺寸图片幻灯片

图 4 目标轮廓估计结果

Figure 4. Estimation results of object contour state

下载: 全尺寸图片幻灯片

图 5 目标运动估计结果

Figure 5. Estimation results of object motion state

下载: 全尺寸图片幻灯片

图 6 VMPF-EOT算法在粒子数不同时的轮廓估计精度

Figure 6. Contour estimation accuracy of VMPF-EOT algorithm with different particle numbers

下载: 全尺寸图片幻灯片

图 7 VMPF-EOT算法在迭代次数不同时的估计结果

Figure 7. Estimation results of VMPF-EOT algorithm with different iteration numbers

下载: 全尺寸图片幻灯片

1 基于变分边缘化粒子滤波的扩展目标跟踪算法

1. Variational marginalized particle filtering based extended object tracking algorithm

输入：分布参数$\{{\bar{\boldsymbol{x}}}_{k-1\left\|k-1\right.}^{\left(i\right)},{\boldsymbol{P}}_{k-1\left\|k-1\right.}^{\left(i\right)},\{{\alpha }_{k-1\left\|k-1\right.}^{t,\left(i\right)} $, 　$ {\beta }_{k-1\left\|k-1\right.}^{t,\left(i\right)}\}_{t=1}^{{n}_{\boldsymbol{y}}^{p}},\;{\theta }_{k-1}^{\left(i\right)},\;{w}_{k-1}^{\left(i\right)}\}_{i=1}^{N} $，量测 $ {\boldsymbol{Y}}_{k} $.
输出：分布参数$ \{{\bar{\boldsymbol{x}}}_{k\left\|k\right.}^{\left(i\right)},{\boldsymbol{P}}_{k\left\|k\right.}^{\left(i\right)},{\{{\alpha }_{k\left\|k\right.}^{t,\left(i\right)},{\beta }_{k\left\|k\right.}^{t,\left(i\right)}\}}_{t=1}^{{n}_{\boldsymbol{y}}^{p}}, $ 　$ {\theta }_{k}^{\left(i\right)},{w}_{k}^{\left(i\right)}\}_{i=1}^{N} $.
步骤1　状态预测：
(1) 轮廓朝向角预测：根据式(17)，采样新粒子集　　　　 $ {\left\{{\theta }_{k}^{\left(i\right)}\right\}}_{k=1}^{N} $；
(2) 运动状态与轮廓尺寸预测：
for i = 1, 2, ···, N
根据式(20)和式(21)，计算$ p\left({\boldsymbol{x}}_{k}\left\|{\theta }_{k}^{\left(i\right)},{\boldsymbol{Y}}_{1:k-1}\right.\right) $；
根据式(23)和式(24)，计算$ p\left({\boldsymbol{X}}_{k}\left\|{\theta }_{k}^{\left(i\right)},{\boldsymbol{Y}}_{1:k-1}\right.\right) $；
end for
步骤2　量测更新：
(1) 运动状态与轮廓尺寸更新：
for i = 1, 2, ···, N
初始化：
$ {\bar{\boldsymbol{x}}}_{k\left\|k\right.}^{\left(i\right),0}={\bar{\boldsymbol{x}}}_{k\left\|k-1\right.}^{\left(i\right)},{\boldsymbol{P}}_{k\left\|k\right.}^{\left(i\right),0}={\boldsymbol{P}}_{k\left\|k-1\right.}^{\left(i\right)} $;
$ {\alpha }_{k\left\|k\right.}^{t,\left(i\right),0}={\alpha }_{k\left\|k\right.-1}^{t,\left(i\right)},{\beta }_{k\left\|k\right.}^{t,\left(i\right),0}={\beta }_{k\left\|k\right.-1}^{t,\left(i\right)}(t=1,2,\cdots, {n}_{\boldsymbol{y}}^{p}) $;
$ {\bar{\boldsymbol{z}}}_{k}^{p,\left(i\right),j,0}={\boldsymbol{y}}_{k}^{p,j},{\boldsymbol{\varSigma }}_{k}^{{\boldsymbol{z}}^{p},\left(i\right),j,0}=s{\bar{\boldsymbol{X}}}_{k}(j=1,2,\cdots ,{m}_{k}) $;
for l = 1, 2,···, $\ell_{\max} $
根据式(35)—式(37)，计算$ {q}_{\boldsymbol{x}}^{\left(i\right),\ell }\left({\boldsymbol{x}}_{k}\right) $；
根据式(42)—式(44)，计算$ {q}_{{\boldsymbol{X}}}^{\left(i\right),\ell }\left({\boldsymbol{X}}_{k}\right)； $
根据式(47)—式(49)，计算$ {q}_{{\boldsymbol{Z}}^{p}}^{\left(i\right),\ell }\left({\boldsymbol{Z}}_{k}^{p}\right)； $
end for
end for
(2) 轮廓朝向角更新：
for i = 1, 2,···, N
根据式(63)，计算$ p\left({\boldsymbol{Y}}_{k}\|{\theta }_{k}^{\left(i\right)},{\boldsymbol{Y}}_{1:k}\right)； $
根据式(60)，计算$ {w}_{k}^{\left(i\right)}； $
end for
根据式(67)，归一化权值；
若$ {N}_{e} $低于阈值，对粒子重采样.

下载: 导出CSV

表 1 仿真参数

Table 1. Simulation parameters

参数	数值
粒子数N	10
最大迭代次数$ {\ell }_{\max} $	5
过程噪声参数$ {q}_{1} $	0.1
过程噪声参数$ {q}_{2} $	0.1
轮廓朝向角过程噪声方差$ {Q}_{k}^{\theta } $	0.005
遗忘因子$ {\rho }_{k} $	0.99
重采样阈值$ {N}_{{\mathrm{thr}}} $	$ 0.2N $
轮廓缩放系数s	$ 1/4 $

下载: 导出CSV

表 2 各算法的平均单步长运行时间

Table 2. Average single-step running time of various algorithms

算法	运行时间(ms)
RM-EOT	0.0653
MEM-EKF	0.3274
MEM-EKF-D	0.4659
VMPF-EOT	0.7238
VMPF-EOT(并行计算)	0.2587

下载: 导出CSV

参考文献(48)

[1]	PANDHARIPANDE A, CHENG C H, DAUWELS J, et al. Sensing and machine learning for automotive perception: A review[J]. IEEE Sensors Journal, 2023, 23(11): 11097–11115. doi: 10.1109/JSEN.2023.3262134.
[2]	张新钰, 卢毅果, 高鑫, 等. 面向智能网联汽车的车路协同感知技术及发展趋势[J]. 自动化学报, 2025, 51(2): 233–248. doi: 10.16383/j.aas.c230575. ZHANG Xinyu, LU Yiguo, GAO Xin, et al. Vehicle-road collaborative perception technology and development trend for intelligent connected vehicles[J]. Acta Automatica Sinica, 2025, 51(2): 233–248. doi: 10.16383/j.aas.c230575.
[3]	ZHANG Yuxiao, CARBALLO A, YANG Hanting, et al. Perception and sensing for autonomous vehicles under adverse weather conditions: A survey[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2023, 196: 146–177. doi: 10.1016/j.isprsjprs.2022.12.021.
[4]	SRIVASTAV A and MANDAL S. Radars for autonomous driving: A review of deep learning methods and challenges[J]. IEEE Access, 2023, 11: 97147–97168. doi: 10.1109/ACCESS.2023.3312382.
[5]	黄岩, 张慧, 兰吕鸿康, 等. 汽车毫米波雷达信号处理技术综述[J]. 雷达学报, 2023, 12(5): 923–970. doi: 10.12000/JR23119. HUANG Yan, ZHANG Hui, LAN Lyuhongkang, et al. Overview of signal processing techniques for automotive millimeter-wave radar[J]. Journal of Radars, 2023, 12(5): 923–970. doi: 10.12000/JR23119.
[6]	PATOLE S M, TORLAK M, WANG Dan, et al. Automotive radars: A review of signal processing techniques[J]. IEEE Signal Processing Magazine, 2017, 34(2): 22–35. doi: 10.1109/MSP.2016.2628914.
[7]	ZHUANG Yuan, WANG Binliang, HUAI Jianzhu, et al. 4D iRIOM: 4D imaging radar inertial odometry and mapping[J]. IEEE Robotics and Automation Letters, 2023, 8(6): 3246–3253. doi: 10.1109/LRA.2023.3266669.
[8]	MEYER F and WILLIAMS J L. Scalable detection and tracking of geometric extended objects[J]. IEEE Transactions on Signal Processing, 2021, 69: 6283–6298. doi: 10.1109/TSP.2021.3121631.
[9]	XIA Yuxuan, GARCÍA-FERNÁNDEZ Á F, MEYER F, et al. Trajectory PMB filters for extended object tracking using belief propagation[J]. IEEE Transactions on Aerospace and Electronic Systems, 2023, 59(6): 9312–9331. doi: 10.1109/TAES.2023.3317233.
[10]	GRANSTRÖM K, FATEMI M, and SVENSSON L. Poisson multi-bernoulli mixture conjugate prior for multiple extended target filtering[J]. IEEE Transactions on Aerospace and Electronic Systems, 2020, 56(1): 208–225. doi: 10.1109/TAES.2019.2920220.
[11]	GRANSTRÖM K, BAUM M, and REUTER S. Extended object tracking: Introduction, overview, and applications[J]. Journal of Advances in Information Fusion, 2017, 12(2): 139–174.
[12]	YURDAKUL O C, ÇETINKAYA M, ÇELEBI E, et al. A rao-blackwellized particle filter for superelliptical extended target tracking[C]. The 2024 27th International Conference on Information Fusion, Venice, Italy, 2024: 1–8. doi: 10.23919/FUSION59988.2024.10706504.
[13]	KOCH J W. Bayesian approach to extended object and cluster tracking using random matrices[J]. IEEE Transactions on Aerospace and Electronic Systems, 2008, 44(3): 1042–1059. doi: 10.1109/TAES.2008.4655362.
[14]	LAN Jian and LI Xiaorong. Tracking of extended object or target group using random matrix: New model and approach[J]. IEEE Transactions on Aerospace and Electronic Systems, 2016, 52(6): 2973–2989. doi: 10.1109/TAES.2016.130346.
[15]	FELDMANN M, FRÄNKEN D, and KOCH W. Tracking of extended objects and group targets using random matrices[J]. IEEE Transactions on Signal Processing, 2011, 59(4): 1409–1420. doi: 10.1109/TSP.2010.2101064.
[16]	ORGUNER U. A variational measurement update for extended target tracking with random matrices[J]. IEEE Transactions on Signal Processing, 2012, 60(7): 3827–3834. doi: 10.1109/TSP.2012.2192927.
[17]	YANG Shishan and BAUM M. Tracking the orientation and axes lengths of an elliptical extended object[J]. IEEE Transactions on Signal Processing, 2019, 67(18): 4720–4729. doi: 10.1109/TSP.2019.2929462.
[18]	GRAMSCH C, YANG Shishan, and ALQADERI H. A batch update using multiplicative noise modelling for extended object tracking[C]. The 2024 27th International Conference on Information Fusion, Venice, Italy, 2024: 1–8. doi: 10.23919/FUSION59988.2024.10706375.
[19]	ZHANG Le and LAN Jian. Tracking of extended object using random matrix with non-uniformly distributed measurements[J]. IEEE Transactions on Signal Processing, 2021, 69: 3812–3825. doi: 10.1109/TSP.2021.3090946.
[20]	STEUERNAGEL S, THORMANN K, and BAUM M. Random matrix-based tracking of rectangular extended objects with contour measurements[C]. The 2024 27th International Conference on Information Fusion, Venice, Italy, 2024: 1–8. doi: 10.23919/FUSION59988.2024.10706288.
[21]	CAO Xiaomeng, LAN Jian, LIU Yushuang, et al. Tracking of rectangular object using key points with regionally concentrated measurements[J]. IEEE Transactions on Intelligent Transportation Systems, 2024, 25(6): 5312–5327. doi: 10.1109/TITS.2023.3332606.
[22]	XIA Yuxuan, WANG Pu, BERNTORP K, et al. Learning-based extended object tracking using hierarchical truncation measurement model with automotive radar[J]. IEEE Journal of Selected Topics in Signal Processing, 2021, 15(4): 1013–1029. doi: 10.1109/JSTSP.2021.3058062.
[23]	TUNCER B, ORGUNER U, and ÖZKAN E. Multi-ellipsoidal extended target tracking with variational bayes inference[J]. IEEE Transactions on Signal Processing, 2022, 70: 3921–3934. doi: 10.1109/TSP.2022.3192617.
[24]	BAUM M and HANEBECK U D. Extended object tracking with random hypersurface models[J]. IEEE Transactions on Aerospace and Electronic Systems, 2014, 50(1): 149–159. doi: 10.1109/TAES.2013.120107.
[25]	WAHLSTRÖM N and ÖZKAN E. Extended target tracking using Gaussian processes[J]. IEEE Transactions on Signal Processing, 2015, 63(16): 4165–4178. doi: 10.1109/TSP.2015.2424194.
[26]	郭云飞, 李勇, 任昕, 等. 基于高斯过程的多机动扩展目标跟踪[J]. 自动化学报, 2020, 46(11): 2392–2403. doi: 10.16383/j.aas.c180849. GUO Yunfei, LI Yong, REN Xin, et al. Multiple maneuvering extended target tracking based on Gaussian process[J]. Acta Automatica Sinica, 2020, 46(11): 2392–2403. doi: 10.16383/j.aas.c180849.
[27]	陈辉, 边斌超, 连峰, 等. 基于Transformer复杂运动辨识的机动星凸形扩展目标跟踪方法[J]. 雷达学报, 2024, 13(3): 629–645. doi: 10.12000/JR24031. CHEN Hui, BIAN Binchao, LIAN Feng, et al. A novel method for tracking complex maneuvering star convex extended targets using Transformer network[J]. Journal of Radars, 2024, 13(3): 629–645. doi: 10.12000/JR24031.
[28]	LAN Jian. Extended object tracking using random matrix with extension-dependent measurement numbers[J]. IEEE Transactions on Aerospace and Electronic Systems, 2023, 59(4): 4464–4477. doi: 10.1109/TAES.2023.3241888.
[29]	ŞAHIN K K, BALCI A E, and ÖZKAN E. Random matrix extended target tracking for trajectory-aligned and drifting targets[J]. IET Radar, Sonar & Navigation, 2024, 18(11): 2247–2263. doi: 10.1049/rsn2.12628.
[30]	WEN Zheng, LAN Jian, ZHENG Le, et al. Velocity-dependent orientation estimation using variance adaptation for extended object tracking[J]. IEEE Signal Processing Letters, 2024, 31: 3109–3113. doi: 10.1109/LSP.2024.3492718.
[31]	李佳彤, 杨金龙. 基于PMBM滤波的机动非椭圆扩展目标跟踪算法[J]. 信号处理, 2023, 39(6): 1108–1119. doi: 10.16798/j.issn.1003-0530.2023.06.016. LI Jiatong and YANG Jinlong. A maneuvering non-ellipsoidal extended target tracking algorithm based on PMBM filter[J]. Journal of Signal Processing, 2023, 39(6): 1108–1119. doi: 10.16798/j.issn.1003-0530.2023.06.016.
[32]	LI Guchong, LI Gang, and HE You. PMBM-based unresolved-group object tracking[J]. IEEE Transactions on Aerospace and Electronic Systems, 2024, 60(4): 4229–4240. doi: 10.1109/TAES.2024.3373561.
[33]	GARCÍA-FERNÁNDEZ Á F, XIA Yuxuan, and SVENSSON L. Poisson multi-bernoulli mixture filter with general target-generated measurements and arbitrary clutter[J]. IEEE Transactions on Signal Processing, 2023, 71: 1895–1906. doi: 10.1109/TSP.2023.3278944.
[34]	陈辉, 张丁丁, 连峰, 等. 扩展目标跟踪Student’s t逆Wishart平滑算法[J]. 电子与信息学报, 2024, 46(8): 3353–3362. doi: 10.11999/JEIT231145. CHEN Hui, ZHANG Dingding, LIAN Feng, et al. Student’s t inverse Wishart smoothing algorithm for extended target tracking[J]. Journal of Electronics & Information Technology, 2024, 46(8): 3353–3362. doi: 10.11999/JEIT231145.
[35]	GRANSTRÖM K, NATALE A, BRACA P, et al. Gamma Gaussian inverse Wishart probability hypothesis density for extended target tracking using X-band marine radar data[J]. IEEE Transactions on Geoscience and Remote Sensing, 2015, 53(12): 6617–6631. doi: 10.1109/TGRS.2015.2444794.
[36]	LAN Jian and LI Xiaorong. Extended-object or group-target tracking using random matrix with nonlinear measurements[J]. IEEE Transactions on Signal Processing, 2019, 67(19): 5130–5142. doi: 10.1109/TSP.2019.2935866.
[37]	THORMANN K and BAUM M. Incorporating range rate measurements in EKF-based elliptical extended object tracking[C]. The 2021 IEEE International Conference on Multisensor Fusion and Integration for Intelligent Systems, Karlsruhe, Germany, 2021: 1–6. doi: 10.1109/MFI52462.2021.9591170.
[38]	KELLNER D, BARJENBRUCH M, KLAPPSTEIN J, et al. Tracking of extended objects with high-resolution Doppler radar[J]. IEEE Transactions on Intelligent Transportation Systems, 2016, 17(5): 1341–1353. doi: 10.1109/TITS.2015.2501759.
[39]	SCHON T, GUSTAFSSON F, and NORDLUND P J. Marginalized particle filters for mixed linear/nonlinear state-space models[J]. IEEE Transactions on Signal Processing, 2005, 53(7): 2279–2289. doi: 10.1109/TSP.2005.849151.
[40]	MUSTIERE F, BOLIC M, and BOUCHARD M. Rao-blackwellised particle filters: Examples of applications[C]. The 2006 Canadian Conference on Electrical and Computer Engineering, Ottawa, ON, Canada, 2006: 1196–1200. doi: 10.1109/CCECE.2006.277461.
[41]	DOUCET A, DE FREITAS N, MURPHY K, et al. Rao-blackwellised particle filtering for dynamic Bayesian networks[C]. The Sixteenth Conference on Uncertainty in Artificial Intelligence, Stanford, California, 2000: 176–183. doi: 10.5555/2073946.2073968.
[42]	CHENG Cheng, TOURNERET J Y, and LU Xiaodong. A marginalised particle filter with variational inference for non-linear state-space models with Gaussian mixture noise[J]. IET Radar, Sonar & Navigation, 2022, 16(2): 238–248. doi: 10.1049/rsn2.12179.
[43]	BADAR T, SÄRKKÄ S, ZHAO Zheng, et al. Rao-blackwellized particle filter using noise adaptive kalman filter for fully mixing state-space models[J]. IEEE Transactions on Aerospace and Electronic Systems, 2024, 60(5): 6972–6982. doi: 10.1109/TAES.2024.3409644.
[44]	CHENG Cheng and TOURNERET J Y. A variational marginalized particle filter for jump Markov nonlinear systems with unknown transition probabilities[J]. Signal Processing, 2021, 188: 108226. doi: 10.1016/j.sigpro.2021.108226.
[45]	TZIKAS D G, LIKAS A C, and GALATSANOS N P. The variational approximation for Bayesian inference[J]. IEEE Signal Processing Magazine, 2008, 25(6): 131–146. doi: 10.1109/MSP.2008.929620.
[46]	BISHOP C M. Pattern Recognition and Machine Learning[M]. New York: Springer, 2006: 462–465.
[47]	ARULAMPALAM M S, MASKELL S, GORDON N, et al. A tutorial on particle filters for online nonlinear/non-Gaussian Bayesian tracking[J]. IEEE Transactions on Signal Processing, 2002, 50(2): 174–188. doi: 10.1109/78.978374.
[48]	胡玉梅, 潘泉, 胡振涛, 等. 基于自然梯度的噪声自适应变分贝叶斯滤波算法[J]. 自动化学报, 2023, 49(10): 2094–2108. doi: 10.16383/j.aas.c210964. HU Yumei, PAN Quan, HU Zhentao, et al. A novel noise adaptive variational Bayesian filter using natural gradient[J]. Acta Automatica Sinica, 2023, 49(10): 2094–2108. doi: 10.16383/j.aas.c210964.