动态海面SAR成像高精度仿真方法及其典型应用

王小青; 祁瑞; 姚晓楠; 徐诚极; 晁小朋

doi:10.12000/JR24255

动态海面SAR成像高精度仿真方法及其典型应用

DOI: 10.12000/JR24255 CSTR: 32380.14.JR24255

1.
中山大学电子与通信工程学院深圳 518107
2.
中山大学系统科学与工程学院广州 510275
3.
大连海事大学信息科学技术学院大连 116026

基金项目: 国家重点研发计划(2023YFB3904905)

详细信息

作者简介:
王小青，博士，教授，博士生导师，主要研究方向为海洋微波遥感、雷达信号处理等

祁　瑞，博士生，主要研究方向为SAR海洋遥感

姚晓楠，博士，讲师，主要研究方向为海洋微波遥感、雷达信号处理等

徐诚极，博士生，主要研究方向为SAR海洋遥感

晁小朋，博士生，主要研究方向为SAR海洋遥感

通讯作者:
姚晓楠 yaoxn@dlmu.edu.cn

责任主编：吴尚蓉 Corresponding Editor: WU Shangrong
中图分类号: TN955
计量
- 文章访问数:
- HTML全文浏览量:
- PDF下载量:
- 被引次数: 0
出版历程
- 收稿日期: 2024-12-22
- 修回日期: 2025-03-23

High-precision Simulation of Dynamic Oceans Synthetic Aperture Radar Imaging and its Typical Application

1.
School of Electronic and Communication Engineering, Sun Yat sen University, Shenzhen 518107, China
2.
School of Systems Science and Engineering, Sun Yat sen University, Guangzhou 510275, China
3.
Information Science and Technology College, Dalian Maritime University, Dalian 116026, China

Funds: The National Key R&D Program of China (2023YFB3904905)

More Information

Corresponding author: YAO Xiaonan, yaoxn@dlmu.edu.cn

摘要

摘要: 合成孔径雷达(SAR)海洋遥感仿真是面向海洋应用的SAR系统设计的重要分析工具，同时也可以为复杂海洋现象SAR图像的检测、识别提供训练样本，为海洋参数反演提供正演模型，因此在SAR海洋遥感的SAR系统设计和应用中扮演着非常重要的角色。海面的运动特性、时变特性、去相干特性使得SAR海洋遥感的仿真难度和计算量要远远大于陆地固定目标的仿真，如何在保证仿真精度的情况下提升仿真效率是实现SAR海洋成像高精度、高效率仿真的关键。该文介绍了动态海面SAR成像仿真的主要方法以及发展现状和主要问题，给出了动态海面SAR成像高精度仿真中若干关键问题的实现方法，该仿真方法在保证较高的逼真度情况下(典型工况下仿真SAR图像谱谱峰误差3%，谱宽误差4%)，能在10分钟内完成4 m分辨率情况下400 km²场景的仿真。实现并介绍了动态海面SAR成像仿真在波浪谱反演、基于深度对消网络的海浪纹理抑制以及基于Wake2Wake网络的舰船尾迹检测方面的典型应用。这些应用案例一方面验证了该文给出的动态海面SAR成像高精度仿真的逼真度能够达到智能化仿真训练的要求，另一方面也说明了高精度仿真在SAR海洋图像智能化应用有很好的前景，可以成为解决SAR海洋遥感智能化应用中样本数据瓶颈的重要手段。
- 动态海面 /
- SAR回波仿真 /
- 波浪纹理抑制 /
- 舰船尾迹检测 /
- 波浪谱反演
Abstract: Synthetic Aperture Radar (SAR) ocean remote sensing simulation is an important analytical tool for designing SAR systems for ocean applications. It can also provide training samples for detecting and recognizing SAR images of complex ocean phenomena. Therefore, it plays an important role in the design and application of SAR ocean remote sensing systems. The motion, time-varying, and decoherence characteristics of the sea surface caused the simulation difficulty and calculation amount of SAR ocean remote sensing to be much larger than those of fixed land targets. Therefore, improving the simulation efficiency while ensuring the simulation accuracy is key to achieving high-precision and high-efficiency simulation of SAR ocean imaging. This study introduces the main methods, development status, and main problems of dynamic ocean SAR imaging simulation and provides methods for realizing key problems in high-precision simulation of dynamic ocean SAR imaging. The method can complete the simulation of a 4 m resolution at a 400 km² scene within 10 min while ensuring high fidelity. Under typical working conditions, the spectral peak error of a simulated SAR image is 3%, and the spectral width error is 4%. The typical applications of dynamic ocean surface SAR imaging simulation in wave spectrum inversion, wave texture suppression based on depth cancellation networks, and ship wake detection based on the Wake2Wake network are introduced. On the one hand, these applications verify that the fidelity of the high-precision simulation of dynamic sea SAR imaging presented in this study can satisfy the requirements of intelligent simulation training. On the other hand, the high-precision simulation offers a good prospect for intelligent application of SAR ocean images and can be an important method for providing samples for intelligent application of SAR ocean remote sensing.
- Dynamic ocean /
- SAR echo simulation /
- Wave texture suppression /
- Ship wake detection /
- Wave spectrum inversion

HTML全文

图 1 SAR海面回波模块组成示意图

Figure 1. Diagram of components of SAR ocean echo simulation

下载: 全尺寸图片幻灯片

图 2 考虑和不考虑海面时变性的交叉谱对比

Figure 2. Comparison of the cross spectrum with and without sea surface variability

下载: 全尺寸图片幻灯片

图 3 流场拟合结果和M4S仿真结果对比

Figure 3. Comparison between current field fitting results and M4S simulation results

下载: 全尺寸图片幻灯片

图 4 ZMNL方法示意图

Figure 4. diagram of ZMNL method

下载: 全尺寸图片幻灯片

图 5 BAS算法框架示意图(图中不同颜色代表不同模式信号处理流程)

Figure 5. Diagram of BAS framework (different colors in the figure represent different mode signal processing processes)

下载: 全尺寸图片幻灯片

图 6 基于全链路仿真的SAR海浪方向谱反演方法示意图

Figure 6. Schematic diagram of SAR wave directional spectrum inversion method based on full-link simulation

下载: 全尺寸图片幻灯片

图 7 3种条件下仿真SAR图像与Sentinel-1观测SAR图像的比较

Figure 7. Comparison of simulated SAR images and Sentinel-1 observed SAR images under three conditions

下载: 全尺寸图片幻灯片

图 8 与图7对应的SAR图像谱

Figure 8. SAR image spectrum corresponding to Fig. 7

下载: 全尺寸图片幻灯片

图 9 基于浮标谱仿真的SAR图像谱与MPI解析化谱和真实SAR图像谱对比

Figure 9. Comparison of SAR image spectrum based on buoy spectrum simulation with MPI analytical spectrum and real SAR image spectrum

下载: 全尺寸图片幻灯片

图 10 反演得到的海浪参数和相应的浮标数据数据对比

Figure 10. Comparison between the inverted wave parameters and the corresponding buoy data

下载: 全尺寸图片幻灯片

图 11 有/无海浪杂波干扰SAR图像样本对比

Figure 11. Comparison of SAR image samples with/without wave clutter interference

下载: 全尺寸图片幻灯片

图 12 对消器网络结构

Figure 12. Network structure of the eliminator

下载: 全尺寸图片幻灯片

图 13 海浪纹理抑制效果对比

Figure 13. Comparison of wave clutter suppression effects

下载: 全尺寸图片幻灯片

图 14 典型尾迹示意图及典型尾迹SAR图像

Figure 14. Typical wake diagram and typical wake SAR image

下载: 全尺寸图片幻灯片

图 15 典型开尔文尾迹特征

Figure 15. Typical Kelvin wake characteristics

下载: 全尺寸图片幻灯片

图 16 湍流定常等效示意图

Figure 16. Steady equivalent diagram of turbulence

下载: 全尺寸图片幻灯片

图 17 典型尾迹仿真图像与真实图像对比

Figure 17. Comparison between typical wake simulation images and real images

下载: 全尺寸图片幻灯片

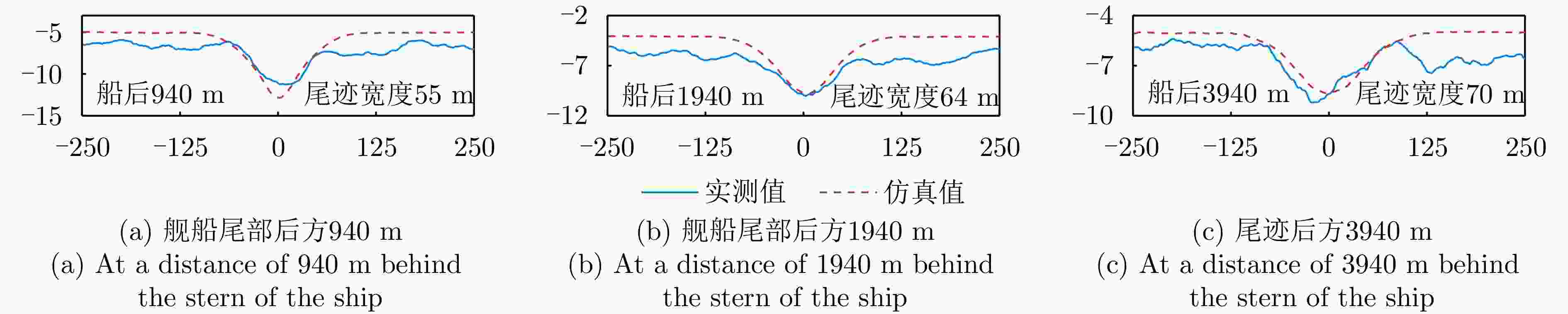
图 18 距离舰船尾部不同位置处的湍流尾迹切面图像强度值对比，对应图17(a)和图17(b)

Figure 18. Comparison of intensity values of turbulent wake section images at variant positions behind the ship tail corresponding to Fig. 17 (a) and Fig. 17(b)

下载: 全尺寸图片幻灯片

图 19 距离舰船尾部后方不同位置处的湍流尾迹切面图像强度值对比，对应图17(c)和图17(d)

Figure 19. Comparison of intensity values of turbulent wake section images at variant positions behind the ship tail corresponding to Fig. 17 (c) and Fig. 17(d)

下载: 全尺寸图片幻灯片

图 20 Wake2Wake检测网络结构示意图

Figure 20. Schematic diagram of Wake2Wake detection network structure

下载: 全尺寸图片幻灯片

表 1 流场调制系数拟合精度表

Table 1. Current field modulation coefficient fitting accuracy table

参数	数值
R²	0.74
RMSE	0.06
MAE	0.04
Bias	0

下载: 导出CSV

表 2 基于全链路仿真反演结果与MPI方法反演结果对比

Table 2. Comparison of inversion results based on full link simulation and MPI method

方法	RMSE (Bias)			平均运行时间
方法	波向(°)	波周期(s)	有效波高(m)	平均运行时间
本研究的反演方法	7.646(–1.873)	0.691(0.078)	0.273(–0.049)	8 h
MPI方法	12.774(0.065)	0.978(0.198)	0.453(0.396)	2 min

下载: 导出CSV

表 3 对应图17中3个尾迹的仿真参数

Table 3. Simulation parameters for the three wakes in Fig. 17

参数	参数/名称
参数	尾迹1	尾迹2	尾迹3
SAR平台	TerraSAR-X	TerraSAR-X	Sentinel-1
雷达波段	X	X	C
风速(m/s)	8.9	14.6	7.5
舰长(m)	100	60	220
船宽(m)	17.0	16.5	32.0
吃水(m)	2.7	2.2	8.3
船速(m/s)	17.0	14.5	19.6

下载: 导出CSV

表 4 不同类型旋转目标检测器在实测数据集以及本文所提出的混合数据集上的检测性能

Table 4. Detection performance of different types of rotating object detectors on measured datasets and the hybrid dataset proposed in this paper

数据集	旋转目标检测器(召回率/mAp)
数据集	Rotated RepPoints	S2A-Net	Oriented R-CNN
OpenSARWake	57.4/39.9	46.4/34.0	48.7/35.6
OpenSARWake & Simulated Wake	59.1/41.1	48.9/36.4	50.2/37.9

下载: 导出CSV

参考文献(71)

[1]	HOLTZMAN J C, FROST V S, and ABBOTT J L, et al. Radar image simulation[J]. IEEE Transactions on Geoscience Electronics, 1978, 16(4): 296–303. doi: 10.1109/TGE.1978.294587.
[2]	KAUPP V H, WAITE W P, and MACDONALD H C. Incidence angle considerations for spacecraft imaging radar[J]. IEEE Transactions on Geoscience and Remote Sensing, 1982, GE-20(3): 384–390. doi: 10.1109/TGRS.1982.350459.
[3]	WU C, LIU K Y, and JIN M. Modeling and a correlation algorithm for spaceborne SAR signals[J]. IEEE Transactions on Aerospace and Electronic Systems, 1982, AES-18(5): 563–575. doi: 10.1109/TAES.1982.309269.
[4]	汪丙南, 张帆, 向茂生. 基于混合域的SAR回波快速算法[J]. 电子与信息学报, 2011, 33(3): 690–695. doi: 10.3724/SP.J.1146.2010.00555. WANG Bingnan, ZHANG Fan, and XIANG Maosheng. SAR raw signal fast algorithm in mixed domain[J]. Journal of Electronics & Information Technology, 2011, 33(3): 690–695. doi: 10.3724/SP.J.1146.2010.00555.
[5]	FRANCESCHETTI G and SCHIRINZI G. A SAR processor based on two-dimensional FFT codes[J]. IEEE Transactions on Aerospace and Electronic Systems, 1990, 26(2): 356–366. doi: 10.1109/7.53462.
[6]	FRANCESCHETTI G, MIGLIACCIO M, RICCIO D, et al. SARAS: A synthetic aperture radar (SAR) raw signal simulator[J]. IEEE Transactions on Geoscience and Remote Sensing, 1992, 30(1): 110–123. doi: 10.1109/36.124221.
[7]	陈杰, 周荫清, 李春升. 星载SAR自然地面场景仿真方法研究[J]. 电子学报, 2001, 29(9): 1202–1205. doi: 10.3321/j.issn:0372-2112.2001.09.014. CHEN Jie, ZHOU Yinqing, and LI Chunsheng. Spaceborne synthetic aperture radar image simulation of natural ground scene[J]. Acta Electronica Sinica, 2001, 29(9): 1202–1205. doi: 10.3321/j.issn:0372-2112.2001.09.014.
[8]	张朋, 张超, 郭陈江, 等. 建筑物的SAR回波信号模拟方法[J]. 系统仿真学报, 2006, 18(7): 1742–1744. doi: 10.3969/j.issn.1004-731X.2006.07.003. ZHANG Peng, ZHANG Chao, GUO Chenjiang, et al. SAR raw signal simulation for building[J]. Journal of System Simulation, 2006, 18(7): 1742–1744. doi: 10.3969/j.issn.1004-731X.2006.07.003.
[9]	KENT S, KARTAL M, KASAPOGLU N G, et al. Synthetic aperture radar raw data simulation for microwave remote sensing applications[C]. 2007 3rd International Conference on Recent Advances in Space Technologies, Istanbul, Turkey, 2007: 389–392. doi: 10.1109/RAST.2007.4284018.
[10]	CHRISTOPHE E, MICHEL J, and INGLADA J. Remote sensing processing: From multicore to GPU[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2011, 4(3): 643–652. doi: 10.1109/JSTARS.2010.2102340.
[11]	ZHANG Fan, HU Chen, LI Wei, et al. Accelerating time-domain SAR raw data simulation for large areas using multi-GPUs[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2014, 7(9): 3956–3966. doi: 10.1109/JSTARS.2014.2330333.
[12]	ZHANG Fan, HU Chen, LI Wei, et al. A deep collaborative computing based SAR raw data simulation on multiple CPU/GPU platform[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2017, 10(2): 387–399. doi: 10.1109/JSTARS.2016.2594272.
[13]	ZHANG Fan, YAO Xiaojie, TANG Hanyuan, et al. Multiple mode SAR raw data simulation and parallel acceleration for Gaofen-3 mission[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2018, 11(6): 2115–2126. doi: 10.1109/JSTARS.2017.2787728.
[14]	ALPERS W R, ROSS D B, and RUFENACH C L. On the detectability of ocean surface waves by real and synthetic aperture radar[J]. Journal of Geophysical Research: Oceans, 1981, 86(C7): 6481–6498. doi: 10.1029/JC086iC07p06481.
[15]	HASSELMANN K and HASSELMANN S. On the nonlinear mapping of an ocean wave spectrum into a synthetic aperture radar image spectrum and its inversion[J]. Journal of Geophysical Research: Oceans, 1991, 96(C6): 10713–10729. doi: 10.1029/91JC00302.
[16]	ENGEN G and JOHNSEN H. SAR-ocean wave inversion using image cross spectra[J]. IEEE Transactions on Geoscience and Remote Sensing, 1995, 33(4): 1047–1056. doi: 10.1109/36.406690.
[17]	ALPERS W. Monte Carlo simulations for studying the relationship between ocean wave and synthetic aperture radar image spectra[J]. Journal of Geophysical Research: Oceans, 1983, 88(C3): 1745–1759. doi: 10.1029/JC088iC03p01745.
[18]	RIZAEV I G, KARAKUŞ O, HOGAN S J, et al. Modeling and SAR imaging of the sea surface: A review of the state-of-the-art with simulations[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2022, 187: 120–140. doi: 10.1016/j.isprsjprs.2022.02.017.
[19]	HARGER R O. The side-looking radar image of time-variant scenes[J]. Radio Science, 1980, 15(4): 749–756. doi: 10.1029/RS015i004p00749.
[20]	HARGER R O and KORMAN C E. Comparisons of simulated and actual synthetic aperture radar gravity wave images[J]. Journal of Geophysical Research: Oceans, 1988, 93(C11): 13867–13882. doi: 10.1029/JC093iC11p13867.
[21]	VACHON P W, RANEY R K, and EMERGY W J. A simulation for spaceborne SAR imagery of a distributed, moving scene[J]. IEEE Transactions on Geoscience and Remote Sensing, 1989, 27(1): 67–78. doi: 10.1109/36.20276.
[22]	FRANCESCHETTI G, MIGLIACCIO M, and RICCIO D. On ocean SAR raw signal simulation[J]. IEEE Transactions on Geoscience and Remote Sensing, 1998, 36(1): 84–100. doi: 10.1109/36.655320.
[23]	NUNZIATA F, GAMBARDELLA A, and MIGLIACCIO M. An educational SAR sea surface waves simulator[J]. International Journal of Remote Sensing, 2008, 29(11): 3051–3066. doi: 10.1080/01431160701469008.
[24]	YOSHIDA T and RHEEM C K. SAR image simulation in the time domain for moving ocean surfaces[J]. Sensors, 2013, 13(4): 4450–4467. doi: 10.3390/s130404450.
[25]	SANTOS F M, SANTOS A L C, VIOLANTE-CARVALHO N, et al. A simulator of synthetic aperture radar (SAR) image spectra: The applications on oceanswell waves[J]. International Journal of Remote Sensing, 2021, 42(8): 2981–3001. doi: 10.1080/01431161.2020.1847352.
[26]	王运华, 于越, 张彦敏. 海面风浪SAR成像仿真研究[J]. 海洋湖沼通报, 2019(6): 41–47. doi: 10.13984/j.cnki.cn37-1141.2019.06.005. WANG Yunhua, YU Yue, and ZHANG Yanmin. Investigation on synthetic aperture radar imaging simulation of oceanic wind waves[J]. Transactions of Oceanology and Limnology, 2019(6): 41–47. doi: 10.13984/j.cnki.cn37-1141.2019.06.005.
[27]	ROMEISER R. M4S 3.2.0 user’s manual[R]. 2008. ftp://ftp.ifm.zmaw.de/outgoing/romeiser/M4S320/.
[28]	FRANCESCHETTI G, IODICE A, RICCIO D, et al. SAR raw signal simulation of oil slicks in ocean environments[J]. IEEE Transactions on Geoscience and Remote Sensing, 2002, 40(9): 1935–1949. doi: 10.1109/TGRS.2002.803798.
[29]	MARULL-PARETAS G. Development of a multi-channel SAR simulator for open-oceans: OASIS[D]. [Master dissertation], Delft University of Technology, 2013.
[30]	LIU Baochang and HE Yijun. SAR raw data simulation for ocean scenes using inverse Omega-K algorithm[J]. IEEE Transactions on Geoscience and Remote Sensing, 2016, 54(10): 6151–6169. doi: 10.1109/TGRS.2016.2582525.
[31]	LI Qian, ZHANG Yanmin, WANG Yunhua, et al. Numerical simulation of SAR image for sea surface[J]. Remote Sensing, 2022, 14(3): 439. doi: 10.3390/rs14030439.
[32]	PLANT W J. A stochastic, multiscale model of microwave backscatter from the ocean[J]. Journal of Geophysical Research: Oceans, 2002, 107(C9): 3120. doi: 10.1029/2001JC000909.
[33]	FUNG A and LEE K. A semi-empirical sea-spectrum model for scattering coefficient estimation[J]. IEEE Journal of Oceanic Engineering, 1982, 7(4): 166–176. doi: 10.1109/JOE.1982.1145535.
[34]	ROMEISER R, SCHMIDT A, and ALPERS W. A three-scale composite surface model for the ocean wave-radar modulation transfer function[J]. Journal of Geophysical Research: Oceans, 1994, 99(C5): 9785–9801. doi: 10.1029/93JC03372.
[35]	余颖, 王小青, 朱敏慧, 等. 基于二阶散射的海面三尺度雷达后向散射模型[J]. 电子学报, 2008, 36(9): 1771–1775. doi: 10.3321/j.issn:0372-2112.2008.09.022. YU Ying, WANG Xiaoqing, ZHU Minhui, et al. Three-Scale radar backscattering model of the ocean surface based on second-order scattering[J]. Acta Electronica Sinica, 2008, 36(9): 1771–1775. doi: 10.3321/j.issn:0372-2112.2008.09.022.
[36]	KUDRYAVTSEV V, HAUSER D, CAUDAL G, et al. A semiempirical model of the normalized radar cross section of the sea surface, 2. Radar modulation transfer function[J]. Journal of Geophysical Research: Oceans, 2003, 108(C3): 8055. doi: 10.1029/2001JC001004.
[37]	JIN T and OH Y. An improved semi-empirical model for radar backscattering from rough sea surfaces at X-band[J]. Journal of Electromagnetic Engineering and Science, 2018, 18(2): 136–140. doi: 10.26866/jees.2018.18.2.136.
[38]	DU Yanlei, YANG Xiaofeng, CHEN Kunshan, et al. A L-band semi-empirical ocean backscattering model[C]. 2017 IEEE International Geoscience and Remote Sensing Symposium, Fort Worth, USA, 2017: 4915–4918. doi: 10.1109/IGARSS.2017.8128106.
[39]	SHIMADA T, KAWAMURA H, and SHIMADA M. An L-band geophysical model function for SAR wind retrieval using JERS-1 SAR[J]. IEEE Transactions on Geoscience and Remote Sensing, 2003, 41(3): 518–531. doi: 10.1109/TGRS.2003.808836.
[40]	ISOGUCHI O and SHIMADA M. An L-band ocean geophysical model function derived from PALSAR[J]. IEEE Transactions on Geoscience and Remote Sensing, 2009, 47(6): 1925–1936. doi: 10.1109/TGRS.2008.2010864.
[41]	STOFFELEN A and ANDERSON D. Scatterometer data interpretation: Estimation and validation of the transfer function CMOD4[J]. Journal of Geophysical Research: Oceans, 1997, 102(C3): 5767–5780. doi: 10.1029/96JC02860.
[42]	HERSBACH H, STOFFELEN A, and DE HAAN S. An improved C-band scatterometer ocean geophysical model function: CMOD5[J]. Journal of Geophysical Research: Oceans, 2007, 112(C3): C03011. doi: 10.1029/2006JC003743.
[43]	HERSBACH H. Comparison of C-band scatterometer CMOD5.N equivalent neutral winds with ECMWF[J]. Journal of Atmospheric and Oceanic Technology, 2010, 27(4): 721–736. doi: 10.1175/2009JTECHO698.1.
[44]	VERSPEEK J, STOFFELEN A, VERHOEF A, et al. Improved ASCAT wind retrieval using NWP ocean calibration[J]. IEEE Transactions on Geoscience and Remote Sensing, 2012, 50(7): 2488–2494. doi: 10.1109/TGRS.2011.2180730.
[45]	STOFFELEN A, VERSPEEK J A, VOGELZANG J, et al. The CMOD7 geophysical model function for ASCAT and ERS wind retrievals[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2017, 10(5): 2123–2134. doi: 10.1109/JSTARS.2017.2681806.
[46]	LU Yiru, ZHANG Biao, PERRIE W, et al. A C-band geophysical model function for determining coastal wind speed using synthetic aperture radar[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2018, 11(7): 2417–2428. doi: 10.1109/JSTARS.2018.2836661.
[47]	ZHANG Biao, MOUCHE A, LU Yiru, et al. A geophysical model function for wind speed retrieval from C-band HH-polarized synthetic aperture radar[J]. IEEE Geoscience and Remote Sensing Letters, 2019, 16(10): 1521–1525. doi: 10.1109/LGRS.2019.2905578.
[48]	LI Xiaoming and LEHNER S. Algorithm for sea surface wind retrieval from TerraSAR-X and TanDEM-X data[J]. IEEE Transactions on Geoscience and Remote Sensing, 2014, 52(5): 2928–2939. doi: 10.1109/TGRS.2013.2267780.
[49]	SHAO Weizeng, ZHANG Zheng, LI Xiaoming, et al. Sea surface wind speed retrieval from TerraSAR-X HH polarization data using an improved polarization ratio model[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2016, 9(11): 4991–4997. doi: 10.1109/JSTARS.2016.2590475.
[50]	WENTZ F J and SMITH D K. A model function for the ocean-normalized radar cross section at 14 GHz derived from NSCAT observations[J]. Journal of Geophysical Research: Oceans, 1999, 104(C5): 11499–11514. doi: 10.1029/98JC02148.
[51]	SOISUVARN S, JELENAK Z, CHANG P S, et al. Scatsat-1 high winds geophysical model function and its winds application in operational marine forecasting and warning[C]. 2020 IEEE International Geoscience and Remote Sensing Symposium, Waikoloa, USA, 2020: 5794–5797. doi: 10.1109/IGARSS39084.2020.9324328.
[52]	YUROVSKY Y Y, KUDRYAVTSEV V N, GRODSKY S A, et al. Ka-band dual copolarized empirical model for the sea surface radar cross section[J]. IEEE Transactions on Geoscience and Remote Sensing, 2017, 55(3): 1629–1647. doi: 10.1109/TGRS.2016.2628640.
[53]	POLVERARI F, WINETEER A, RODRIGUEZ E, et al. A Ka-band wind geophysical model function using Doppler scatterometer measurements from the air-sea interaction tower experiment[J]. Remote Sensing, 2022, 14(9): 2067. doi: 10.3390/rs14092067.
[54]	FEINDT F, SCHRÖTER J, and ALPERS W. Measurement of the ocean wave-radar modulation transfer function at 35 GHz from a sea-based platform in the North Sea[J]. Journal of Geophysical Research: Oceans, 1986, 91(C8): 9701–9708. doi: 10.1029/JC091iC08p09701.
[55]	SCHULZ-STELLENFLETH J, LEHNER S, and HOJA D. Global ocean wave measurements using complex synthetic aperture radar data[C]. Ocean Wave Measurement and Analysis, San Francisco, USA, 2001: 173–182. doi: 10.1061/40604(273)18.
[56]	ALPERS W and HENNINGS I. A theory of the imaging mechanism of underwater bottom topography by real and synthetic aperture radar[J]. Journal of Geophysical Research: Oceans, 1984, 89(C6): 10529–10546. doi: 10.1029/JC089iC06p10529.
[57]	PRATS P, SCHEIBER R, MITTERMAYER J, et al. Processing of sliding spotlight and TOPS SAR data using baseband azimuth scaling[J]. IEEE Transactions on Geoscience and Remote Sensing, 2010, 48(2): 770–780. doi: 10.1109/TGRS.2009.2027701.
[58]	DAVIDSON G W, CUMMING I G, and ITO M R. A chirp scaling approach for processing squint mode SAR data[J]. IEEE Transactions on Aerospace and Electronic Systems, 1996, 32(1): 121–133. doi: 10.1109/7.481254.
[59]	GOMMENGINGER C, CHAPRON B, HOGG A, et al. SEASTAR: A mission to study ocean submesoscale dynamics and small-scale atmosphere-ocean processes in coastal, shelf and polar seas[J]. Frontiers in Marine Science, 2019, 6: 457. doi: 10.3389/fmars.2019.00457.
[60]	MASTENBROEK C and DE VALK C F. A semiparametric algorithm to retrieve ocean wave spectra from synthetic aperture radar[J]. Journal of Geophysical Research: Oceans, 2000, 105(C2): 3497–3516. doi: 10.1029/1999JC900282.
[61]	何宜军. 合成孔径雷达提取海浪方向谱的参数化方法[J]. 科学通报, 1999, 44(4): 428–433. doi: 10.3321/j.issn:0023-074X.1999.04.022. HE Yijun. Parameterization method for extracting wave directional spectrum using synthetic aperture radar[J]. Chinese Science Bulletin, 1999, 44(4): 428–433. doi: 10.3321/j.issn:0023-074X.1999.04.022.
[62]	SUN Jian and GUAN Changlong. Parameterized first-guess spectrum method for retrieving directional spectrum of swell-dominated waves and huge waves from SAR images[J]. Chinese Journal of Oceanology and Limnology, 2006, 24(1): 12–20. doi: 10.1007/BF02842769.
[63]	BRÜNING C, HASSELMANN K, HASSELMANN S, et al. A first evaluation of ERS-1 synthetic aperture radar wave mode data[J]. The Global Atmosphere and Ocean System, 1994, 2: 61–98.
[64]	WANG Anqi, WANG Xiaoqing, CHEN Jian et al. Wave spectrum retrieval method based on full-link ocean surface SAR imaging simulation[J]. IEEE Transactions on Geoscience and Remote Sensing, 2023, 61: 5219120. doi: 10.1109/TGRS.2023.3324812.
[65]	高骥超, 王小青, 种劲松. 一种基于序列SAR图像的海浪对消方法[J]. 国外电子测量技术, 2016, 35(9): 57–60. doi: 10.3969/j.issn.1002-8978.2016.09.014. GAO Jichao, WANG Xiaoqing, and CHONG Jinsong. Ocean wave clutter cancellation method based on series of SAR images[J]. Foreign Electronic Measurement Technology, 2016, 35(9): 57–60. doi: 10.3969/j.issn.1002-8978.2016.09.014.
[66]	CHAO Xiaopeng, WANG Qingsong, WANG Xiaoqing, et al. Ocean-wave suppression for synthetic aperture radar images by depth counteraction method[J]. Remote Sensing of Environment, 2024, 305: 114086. doi: 10.1016/j.rse.2024.114086.
[67]	ZHANG Min, ZHAO Yanwei, CHEN Hui, et al. SAR imaging simulation for composite model of ship on dynamic ocean scene[J]. Progress in Electromagnetics Research, 2011, 113: 395–412. doi: 10.2528/PIER10121102.
[68]	TUCK E O. Wave resistance of thin ships and catamarans[R]. Applied Mathematics Report T8701, 1987.
[69]	TUCK E O, LAZAUSKAS L, and SCULLEN D C. Sea wave pattern evaluation[R]. 1999. HTTPS://SCULLEN.COM.AU/DSC/PUBLICATIONS/TUCK_SCULLEN_LAZAUSKAS_99.PDF.
[70]	XU Chengji, QI Rui, WANG Xiaoqing, et al. Instability of energy spectrum disturbance for ship turbulent wakes: SAR imaging simulation and analysis[J]. Ocean Engineering, 2024, 292: 116502. doi: 10.1016/j.oceaneng.2023.116502.
[71]	XU Chengji, WANG Qingsong, WANG Xiaoqing, et al. Wake2Wake: Feature-guided self-supervised wave suppression method for SAR ship wake detection[J]. IEEE Transactions on Geoscience and Remote Sensing, 2024, 62: 5108114. doi: 10.1109/TGRS.2024.3422803.