Full-waveform Small-footprint LiDAR Multi-target Echo Waveform Lightweight Detection by Spatio-temporal Coupling Models
-
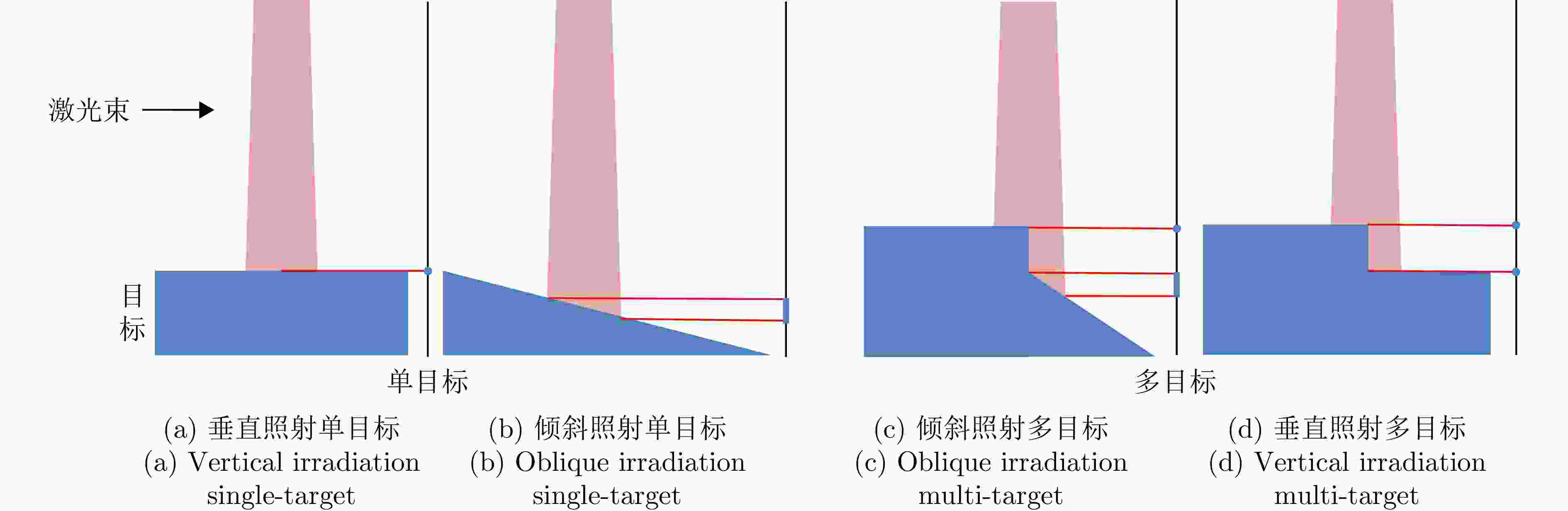
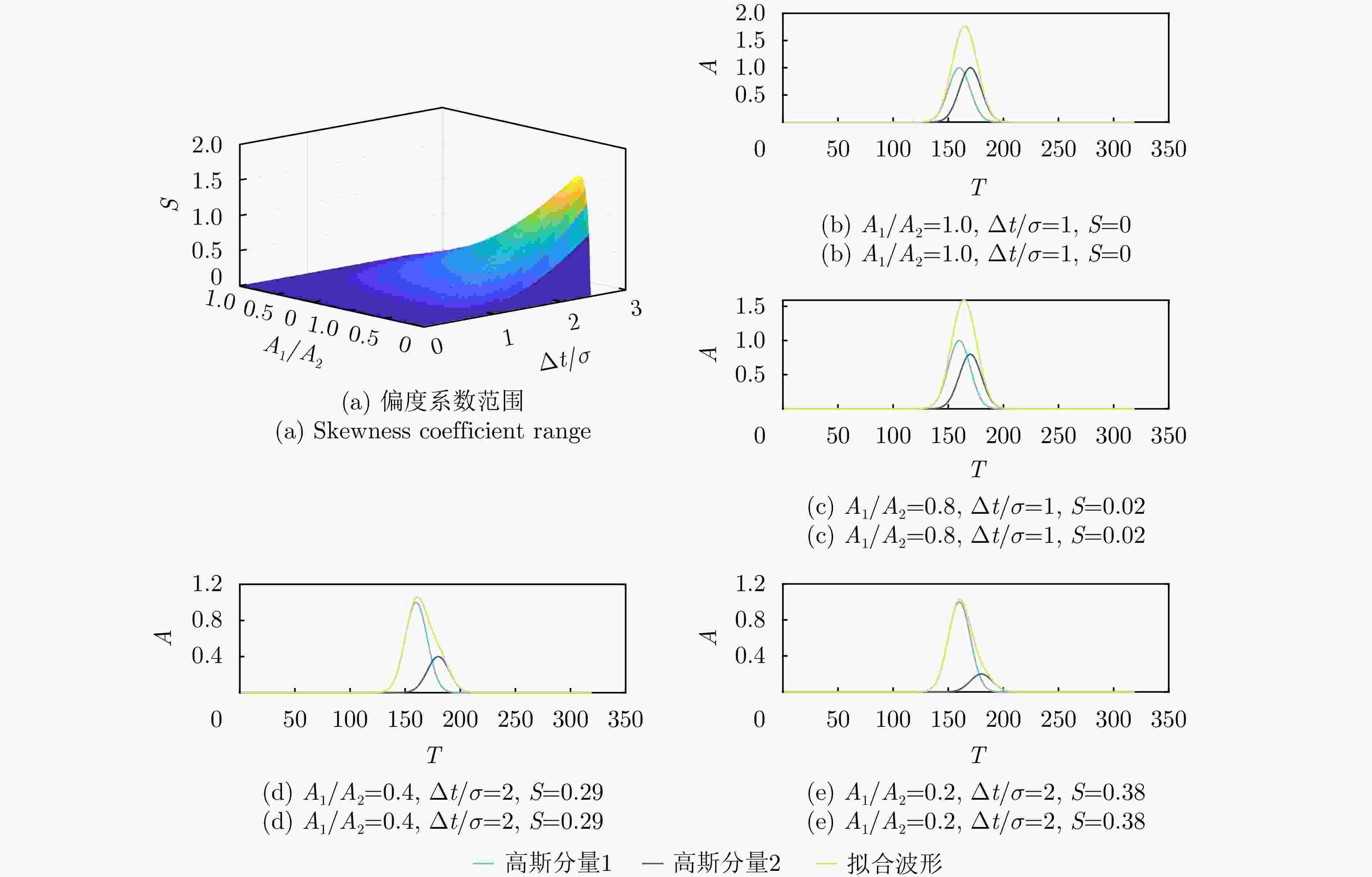
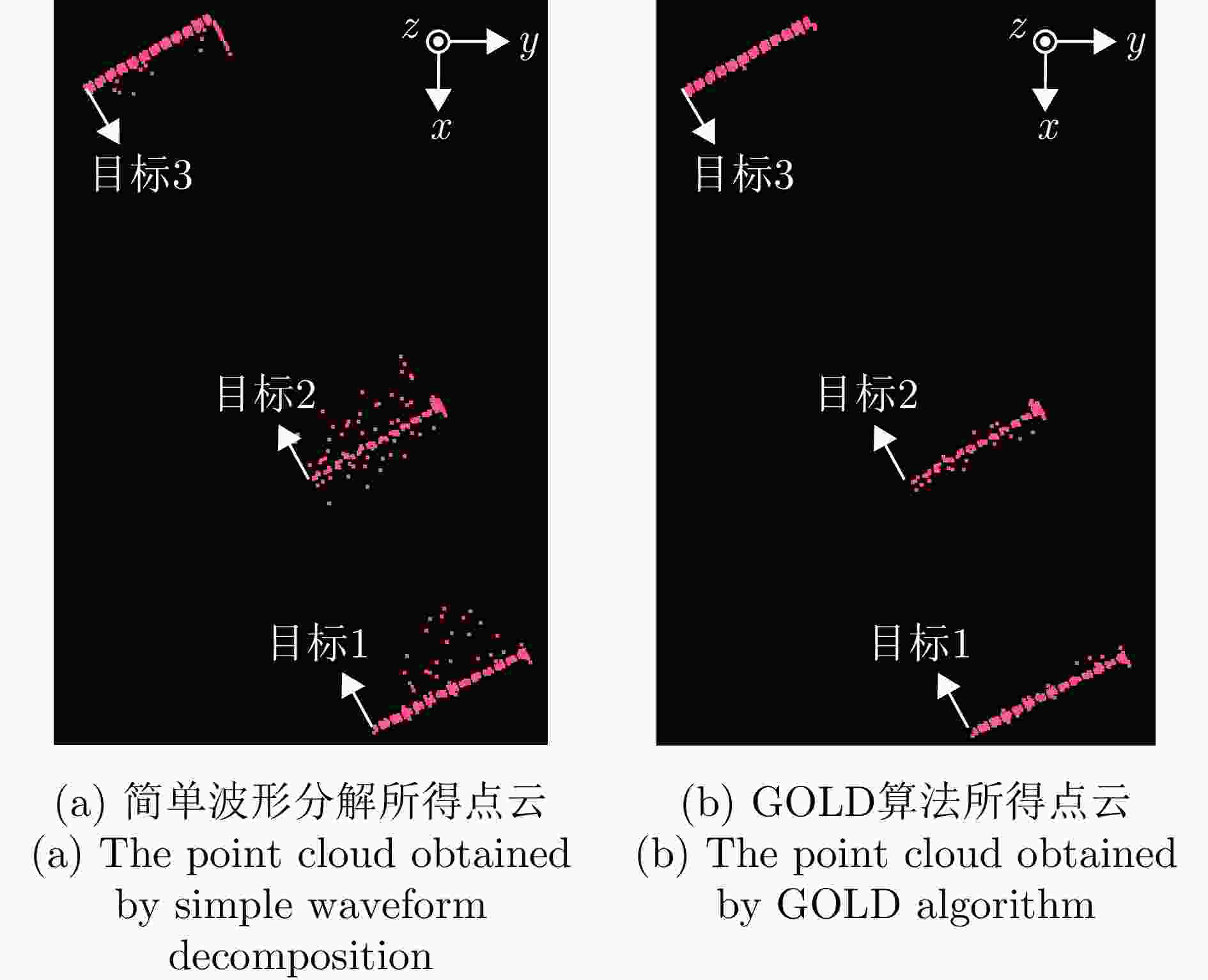
摘要: 小光斑全波形激光雷达凭借高穿透、完整回波获取能力而蕴含巨大应用潜力。高效精准处理海量回波信号是全波形激光雷达实际应用前提,成为波形分解技术前沿性挑战。对于小光斑全波形激光雷达系统,单目标回波占比高且仅多目标回波需要精细波形分解处理,然而现有方案通常以牺牲精度为代价而采用简单快速波形分解算法,或将全部回波信号无差别进行波形分解而导致效率低下,难以兼顾精度和效率。该研究面向小光斑全波形激光雷达,提出一种时空耦合模型驱动的多目标回波轻量化检测算法,首次实现从未知回波次数的波形数据中高效精准检测多目标回波,有效避免波形分解算法无差别处理单目标回波而引入冗余计算,显著减少波形分解次数。具体地,(1)该算法构建了激光雷达时空耦合回波信号模型,以揭示回波传输的时空特性;(2)基于该模型驱动双高斯函数叠加拟合方式,轻量化估计波形参数;(3)根据信噪比引入自适应相关性判别方法。结合系统发射脉冲一致性,所提方法能够轻量化且准确检测多目标回波信号,在地基和机载波形数据实验结果证明,该研究提出的轻量化多目标回波检测算法检测准确率高达98.4%,召回率93.1%。利用4种波形分解方法结合多目标回波检测,效率显著提高2~3倍,且在单目标回波数量占比增大情况下效率提升更显著。Abstract: Small-footprint full-waveform Light Detection And Ranging (LiDAR) exhibits significant application potential owing to its high penetration capability and ability to capture complete echo data. However, the efficient and accurate processing of massive echo signals remains a crucial challenge for practical use, particularly in advancing waveform decomposition technology. In small-footprint full-waveform LiDAR systems, most echoes are single-target, while only multi-target echoes require detailed decomposition. Current solutions often sacrifice precision by employing simplified rapid waveform decomposition algorithms or process all echoes indiscriminately, resulting in low efficiency and the inability to balance accuracy and speed effectively. This study proposes a spatiotemporal coupling model-driven lightweight algorithm for detecting multi-target echoes in small-footprint full-waveform LiDAR. For the first time, it achieves efficient and accurate detection of multi-target echoes from waveform data with unknown echo counts. The proposed method eliminates redundant computations caused by indiscriminate processing of single-target echoes, significantly reducing waveform decomposition iterations. The technical contributions include constructing a spatiotemporal coupling echo signal model that captures the spatiotemporal characteristics of echo transmission, implementing model-driven lightweight waveform parameter estimation through double Gaussian function superposition fitting, and introducing an adaptive correlation discrimination method based on a signal-to-noise ratio approach. By leveraging the consistency of system-emitted pulses, the proposed method enables lightweight yet accurate multi-target echo detection. Experimental results on terrestrial and airborne waveform datasets demonstrate that our algorithm achieves 98.4% detection accuracy with a 93.1% recall rate. When integrated with four waveform decomposition methods, it improves processing efficiency by 2–3 times. The efficiency gain becomes even more pronounced as the proportion of single-target echoes increases.
-
表 1 VZ 2000激光雷达关键指标
Table 1. VZ 2000 LiDAR key indicators
参数 数值 发射脉宽 4 ns 采样率 500 MHz 激光束发散角 0.3 mrad 表 2 数据采集分组
Table 2. Data acquisition and grouping
数据组 目标1
(°)间隔1
(cm)目标2
(°)间隔2
(cm)目标3
(°)W1 0 45 0 105 0 W2 0 60 0 90 0 W3 0 75 0 75 0 W4 0 90 0 60 0 W5 0 105 0 45 0 W6 –15 75 15 75 0 W7 –30 75 30 75 0 W8 –15 75 30 75 0 W9 –30 75 15 75 0 W10 0 45 0 105 0 W11 0 60 0 90 0 W12 0 75 0 75 0 W13 0 90 0 60 0 W14 0 105 0 45 0 表 3 Optech Gemini激光雷达关键指标
Table 3. Optech Gemini LiDAR key indicators
参数 数值 发射脉宽 14 ns 采样率 1 GHz 激光束发散角 0.8 mrad 表 4 发射脉冲拟合结果
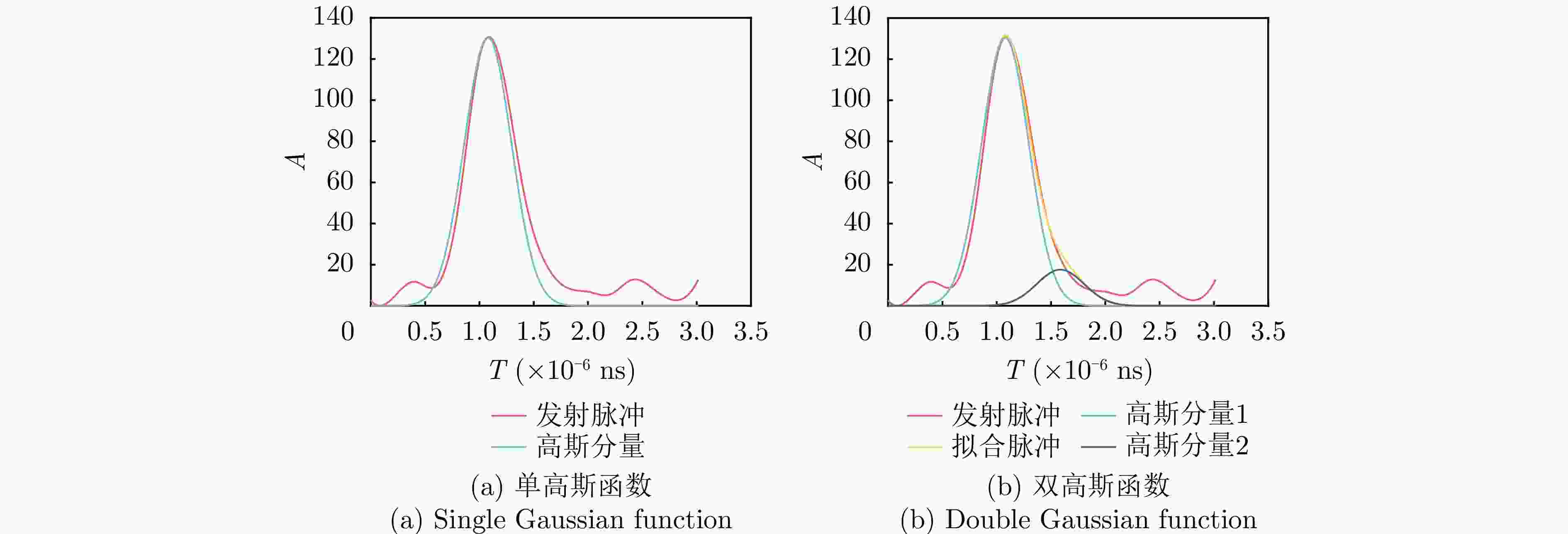
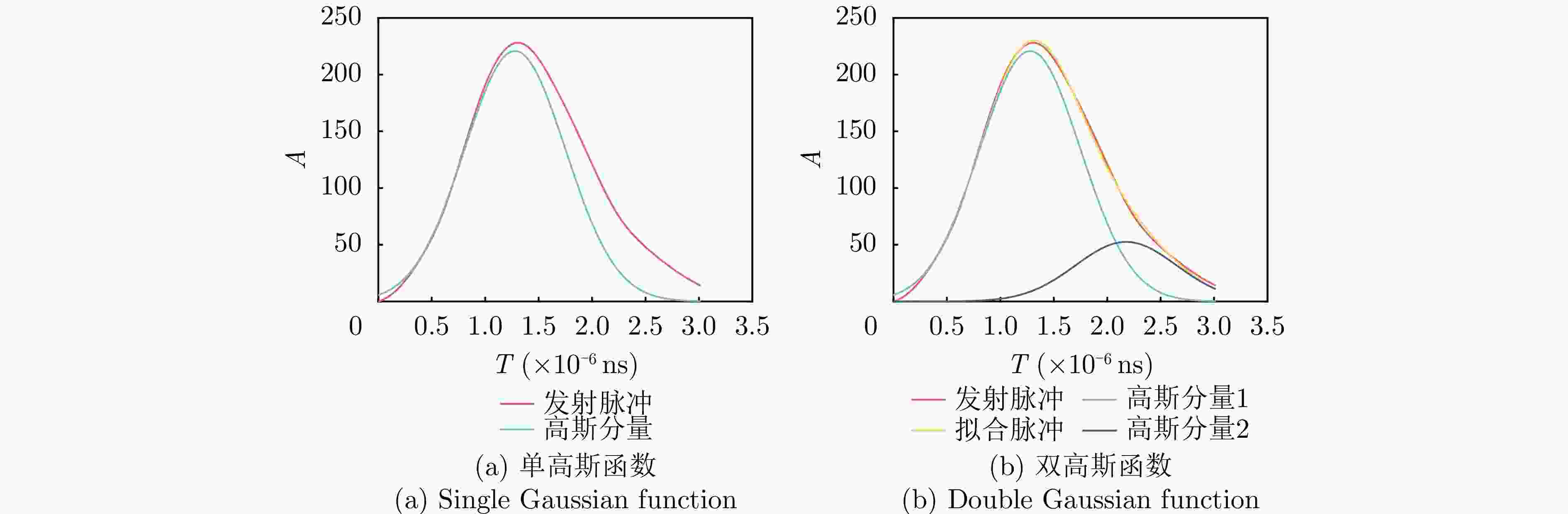
Table 4. Results of transmitting pulse fitting
拟合方法 R2 VZ 2000 Optech Gemini 单高斯拟合 0.986 0.973 双高斯拟合 0.997 0.999 表 5 地面数据轻量化多目标回波检测结果
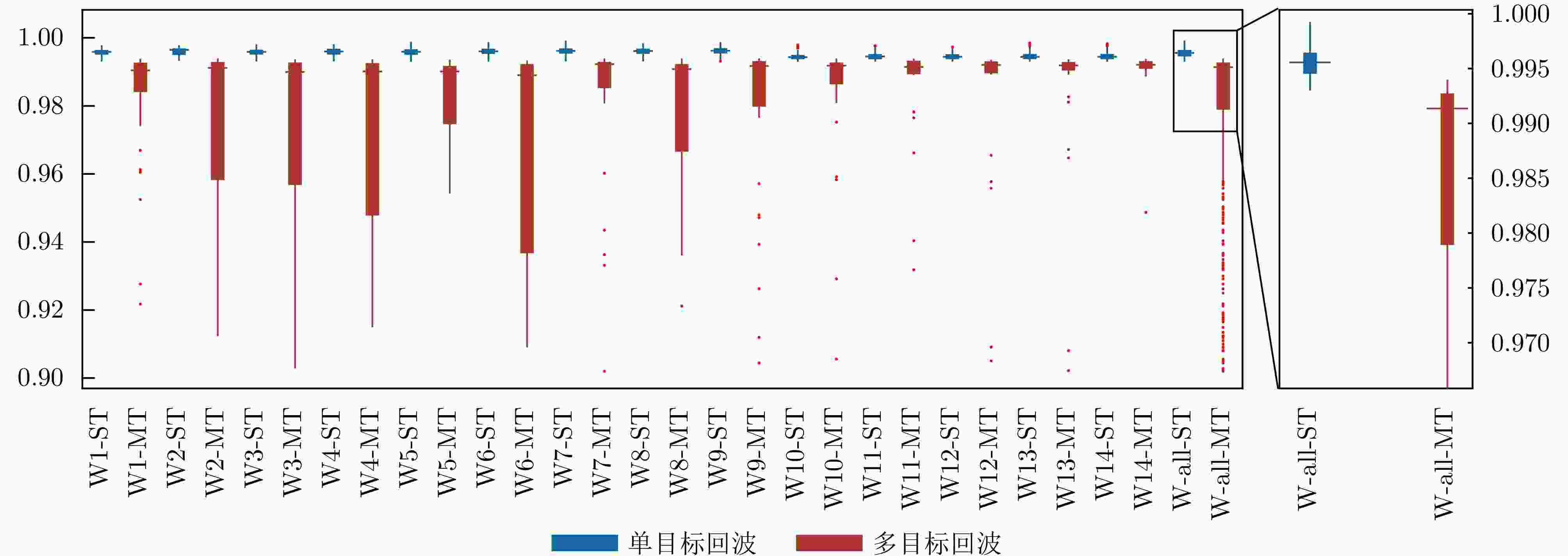
Table 5. Results of lightweight multi-target waveforms detection for terrain data
数据组 TP FP FN TF 准确率(%) 召回率(%) W1 43 6 3 781 98.9 93.5 W2 22 2 3 119 97.2 91.7 W3 35 5 3 494 98.5 92.1 W4 32 6 3 389 97.9 91.4 W5 34 8 1 404 98.0 97.1 W6 47 4 0 489 99.3 100 W7 38 4 2 454 98.8 95.0 W8 35 7 3 618 98.5 92.1 W9 33 4 2 492 98.9 94.3 W10 30 4 3 370 98.3 90.9 W11 29 5 4 312 97.4 87.9 W12 28 4 1 345 98.7 96.6 W13 39 6 4 404 97.8 90.7 W14 16 7 3 369 97.5 84.2 W-all 461 72 34 6040 98.4 93.1 表 6 错误检测波形数据的波形分解结果
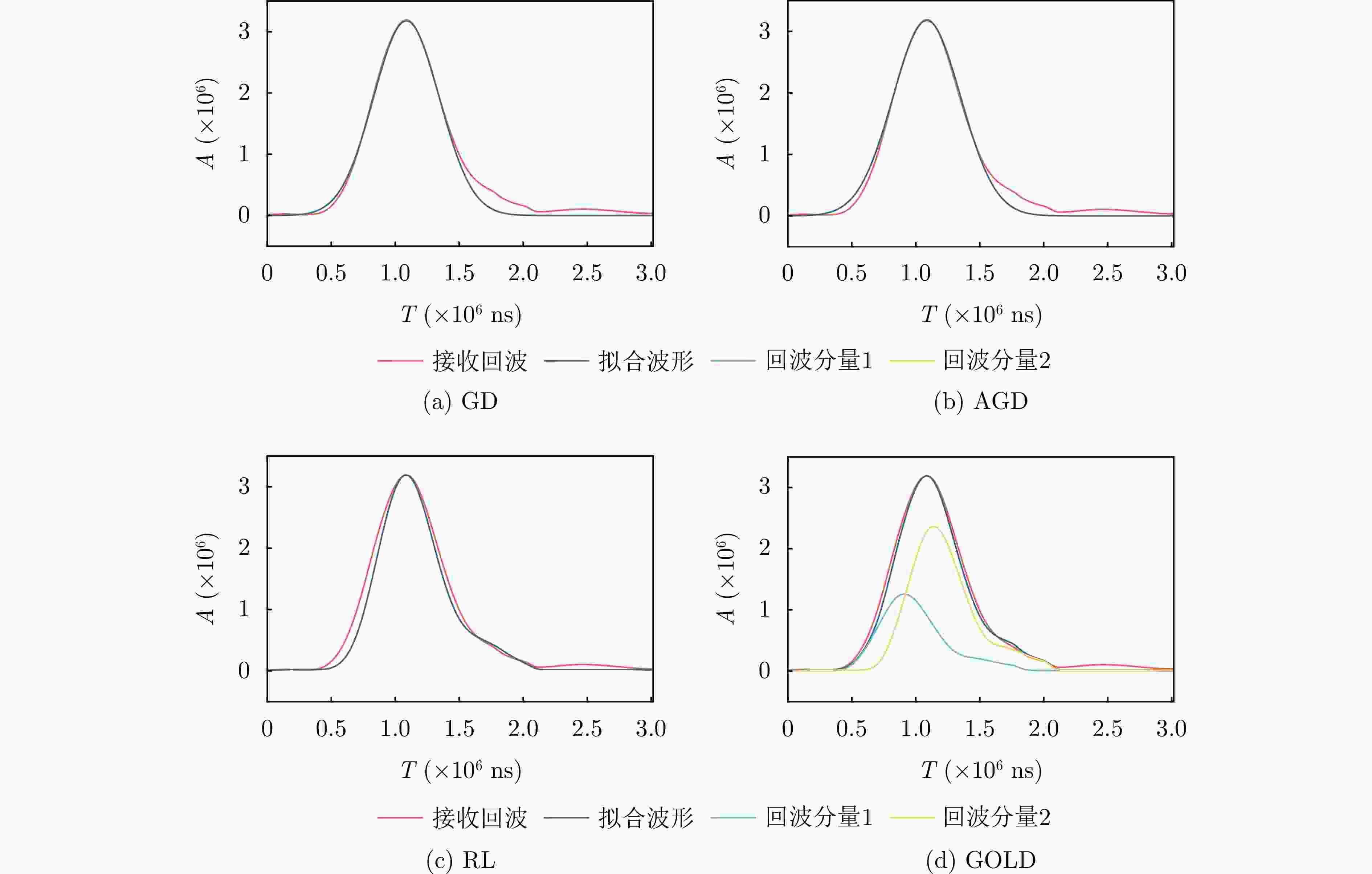
Table 6. Waveform decomposition results of error detection waveform data
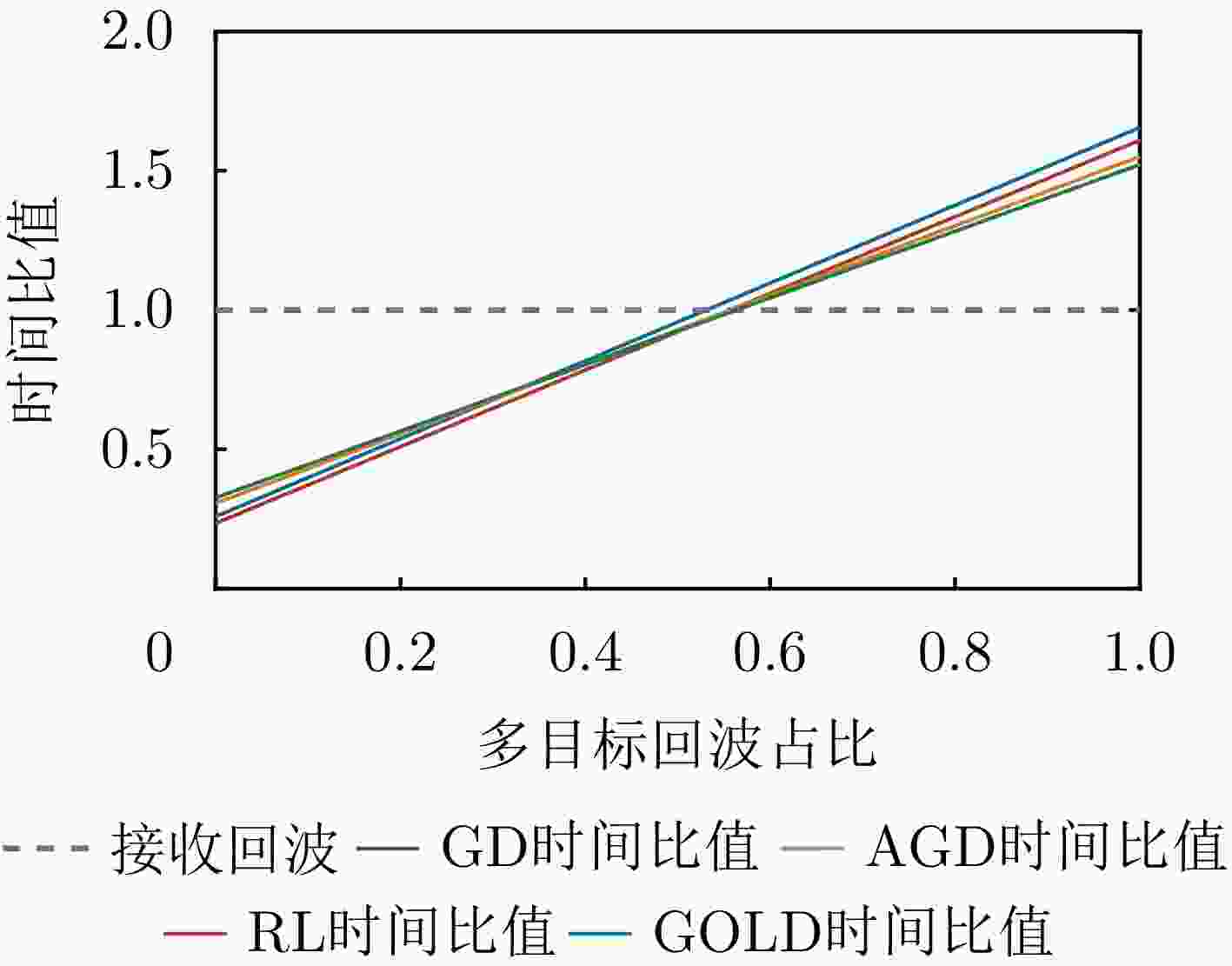
数据组 FP+FN GD AGD RL GOLD W1 9 2 1 2 2 W2 4 1 1 1 1 W3 8 1 0 2 3 W4 9 1 1 1 1 W5 9 0 0 0 1 W6 4 0 0 0 0 W7 6 1 1 1 0 W8 10 1 1 0 0 W9 6 0 1 3 3 W10 7 1 1 1 1 W11 9 2 3 3 2 W12 5 0 0 0 1 W13 10 3 3 3 3 W14 10 1 0 1 1 W-all 106 14 13 18 19 表 7 机载数据波形分解结果
Table 7. Waveform decomposition results of airborne data
回波数 GD|GD* AGD|AGD* RL|RL* GOLD|GOLD* 1 46972|47294 47236|47613 46144|46361 46056|46335 2 1323|1134 1240|1032 1594|1508 1595|1462 3 940|807 907|738 1269|1137 1155|1009 4 365|365 421|421 536|536 663|663 5 309|309 138|138 224|224 317|317 >5 91|91 58|58 233|234 214|214 注:*表示进行多目标回波检测 表 8 地面数据波形分解效率对比表
Table 8. Terrain data waveform decomposition efficiency comparison table
方法 检测 波形分解 检测+波形分解 时间(s)|数量 平均时间(s) 时间(s)|数量 平均时间(s) 时间(s)|数量 平均时间(s) GD* 83.3|6112 0.014 27.2|533 0.051 110.5|6112 0.018 GD —— —— 281.2|6112 0.046 281.2|6112 0.046 AGD* 83.3|6112 0.014 30.2|533 0.057 113.5|6112 0.019 AGD —— —— 299.5|6112 0.049 299.5|6112 0.049 RL* 83.3|6112 0.014 43.6|533 0.082 126.9|6112 0.021 RL —— —— 391.2|6112 0.064 391.2|6112 0.064 GOLD* 83.3|6112 0.014 40.1|533 0.075 123.4|6112 0.020 GOLD —— —— 354.5|6112 0.058 354.5 |6112 0.058 注:*表示进行多目标回波检测,加粗数值表示效率最优方法。 表 9 机载数据波形分解效率对比表
Table 9. Airborne data waveform decomposition efficiency comparison table
方法 检测 波形分解 检测+波形分解 时间(s)|数量 平均时间(s) 时间(s)|数量 平均时间(s) 时间(s)|数量 平均时间(s) GD* 652|50000 0.013 202|3746 0.054 854|50000 0.017 GD —— —— 2118|50000 0.042 2118|50000 0.042 AGD* 652|50000 0.013 225|3746 0.060 877|50000 0.018 AGD —— —— 2243|50000 0.045 2243|50000 0.045 RL* 652|50000 0.013 326|3746 0.087 978|50000 0.020 RL —— —— 2953|50000 0.059 2953|50000 0.059 GOLD* 652|50000 0.013 296|3746 0.079 948|50000 0.019 GOLD —— —— 2659|50000 0.053 2659|50000 0.053 注:*表示进行多目标回波检测,加粗数值表示效率最优方法。 -
[1] GOETZ A F H. Imaging spectrometry for remote sensing: Vision to reality in 15 years[C]. The SPIE 2480, Imaging Spectrometry, Orlando, FL, United States, 1995: 2–13. doi: 10.1117/12.210867. [2] WEHR A and LOHR U. Airborne laser scanning—an introduction and overview[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 1999, 54(2): 68–82. doi: 10.1016/S0924-2716(99)00011-8. [3] YOU R J and LIN B C. A quality prediction method for building model reconstruction using LiDAR data and topographic maps[J]. IEEE Transactions on Geoscience and Remote Sensing, 2011, 49(9): 3471–3480. doi: 10.1109/TGRS.2011.2128326. [4] GONZALEZ-AGUILERA D, CRESPO-MATELLAN E, HERNANDEZ-LOPEZ D, et al. Automated urban analysis based on LiDAR-derived building models[J]. IEEE Transactions on Geoscience and Remote Sensing, 2013, 51(3): 1844–1851. doi: 10.1109/TGRS.2012.2205931. [5] GUAN Hongcan, SU Yanjun, HU Tianyu, et al. A novel framework to automatically fuse multiplatform LiDAR data in forest environments based on tree locations[J]. IEEE Transactions on Geoscience and Remote Sensing, 2020, 58(3): 2165–2177. doi: 10.1109/TGRS.2019.2953654. [6] JI Xue, YANG Bisheng, WANG Yuan, et al. Full-waveform classification and segmentation-based signal detection of single-wavelength bathymetric LiDAR[J]. IEEE Transactions on Geoscience and Remote Sensing, 2022, 60: 1–14. doi: 10.1109/TGRS.2022.3198168. [7] GROLLIUS S, LIGGES M, RUSKOWSKI J, et al. Concept of an automotive LiDAR target simulator for direct time-of-flight LiDAR[J]. IEEE Transactions on Intelligent Vehicles, 2023, 8(1): 825–835. doi: 10.1109/TIV.2021.3128808. [8] MALLET C and BRETAR F. Full-waveform topographic LiDAR: State-of-the-art[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2009, 64(1): 1–16. doi: 10.1016/j.isprsjprs.2008.09.007. [9] 沈俊, 尚建华, 贺岩. 全波形机载激光雷达数据处理技术的研究进展[J]. 激光技术, 2018, 42(3): 295–299. doi: 10.7510/jgjs.issn.1001-3806.2018.03.002.SHEN Jun, SHANG Jianhua, and HE Yan. Research process of data processing technology of full-waveform airborne laser radars[J]. Laser Technology, 2018, 42(3): 295–299. doi: 10.7510/jgjs.issn.1001-3806.2018.03.002. [10] ZHANG Zhengnan, CAO Lin, LIU Hao, et al. Assessing the 3-D structure of bamboo forests using an advanced pseudo-vertical waveform approach based on airborne full-waveform LiDAR data[J]. IEEE Transactions on Geoscience and Remote Sensing, 2021, 59(12): 10647–10670. doi: 10.1109/TGRS.2020.3042790. [11] GAO Shuai, NIU Zheng, SUN Gang, et al. Height extraction of maize using airborne full-waveform LIDAR data and a deconvolution algorithm[J]. IEEE Geoscience and Remote Sensing Letters, 2015, 12(9): 1978–1982. doi: 10.1109/LGRS.2015.2441655. [12] YANG Fanlin, CHAO Qi, SU Dianpeng, et al. An airborne LiDAR bathymetric waveform decomposition method in very shallow water: A case study around Yuanzhi Island in the South China Sea[J]. International Journal of Applied Earth Observation and Geoinformation, 2022, 109: 102788. doi: 10.1016/j.jag.2022.102788. [13] RiUNITE[OL]. http://www.riegl.com/products/software-packages/riunite/. [14] WANG Zining, XU Lijun, LI Duan, et al. Online multi-target laser ranging using waveform decomposition on FPGA[J]. IEEE Sensors Journal, 2021, 21(9): 10879–10889. doi: 10.1109/JSEN.2021.3060158. [15] LIU Gangping and KE Jun. End-to-end full-waveform echo decomposition based on self-attention classification and U-Net decomposition[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2022, 15: 7978–7987. doi: 10.1109/JSTARS.2022.3203130. [16] WANG Cheng, YANG Xuebo, XI Xiaohuan, et al. Introduction to LiDAR Remote Sensing[M]. Boca Raton: CRC Press, 2024: 26–29. doi: 10.1201/9781032671512. [17] MOUNTRAKIS G and LI Yuguang. A linearly approximated iterative Gaussian decomposition method for waveform LiDAR processing[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2017, 129: 200–211. doi: 10.1016/j.isprsjprs.2017.05.009. [18] ZHOU Guoqing, LONG Shuhua, XU Jiasheng, et al. Comparison analysis of five waveform decomposition algorithms for the airborne LiDAR echo signal[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2021, 14: 7869–7880. doi: 10.1109/JSTARS.2021.3096197. [19] ZHOU Guoqing, DENG Ronghua, ZHOU Xiang, et al. Gaussian inflection point selection for LiDAR hidden echo signal decomposition[J]. IEEE Geoscience and Remote Sensing Letters, 2022, 19: 1–5. doi: 10.1109/LGRS.2021.3107438. [20] ZHOU Tan, POPESCU S C, KRAUSE K, et al. Gold—A novel deconvolution algorithm with optimization for waveform LiDAR processing[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2017, 129: 131–150. doi: 10.1016/j.isprsjprs.2017.04.021. [21] LIU Chang, XU Lijun, SI Lin, et al. A robust deconvolution method of airborne LiDAR waveforms for dense point clouds generation in forest[J]. IEEE Transactions on Geoscience and Remote Sensing, 2022, 60: 1–14. doi: 10.1109/TGRS.2021.3061166. [22] XIAO Zhen, GU Yanfeng, LI Xian, et al. Application of landweber with optimization for small footprint waveform lidar decomposition[C]. IGARSS 2024 - 2024 IEEE International Geoscience and Remote Sensing Symposium, Athens, Greece, 2024: 6408–6411. doi: 10.1109/IGARSS53475.2024.10640890. [23] WANG Binhui, SONG Shalei, SHI Shuo, et al. Multichannel interconnection decomposition for hyperspectral LiDAR waveforms detected from over 500 m[J]. IEEE Transactions on Geoscience and Remote Sensing, 2022, 60: 5515714. doi: 10.1109/TGRS.2021.3108160. [24] SONG Shalei, WANG Binhui, GONG Wei, et al. A new waveform decomposition method for multispectral LiDAR[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2019, 149: 40–49. doi: 10.1016/j.isprsjprs.2019.01.014. [25] BAI Jie, NIU Zheng, BI Kaiyi, et al. Toward an advanced method for full-waveform hyperspectral LiDAR data processing[J]. IEEE Transactions on Geoscience and Remote Sensing, 2024, 62: 5702516. doi: 10.1109/TGRS.2024.3382481. [26] BAI Jie, NIU Zheng, HUANG Yanru, et al. Full-waveform hyperspectral LiDAR data decomposition via ranking central locations of natural target echoes (Rclonte) at different wavelengths[J]. Remote Sensing of Environment, 2024, 310: 114227. doi: 10.1016/j.rse.2024.114227. [27] XIA Yuhao, XU Shilong, SHAO Hui, et al. Range resolution enhanced method with spectral properties for hyperspectral LiDAR[J]. IEEE Transactions on Geoscience and Remote Sensing, 2023, 61: 5703517. doi: 10.1109/TGRS.2023.3301896. [28] XU Fan, LI Fenfang, and WANG Yuanqing. Modified levenberg-marquardt-based optimization method for LiDAR waveform decomposition[J]. IEEE Geoscience and Remote Sensing Letters, 2016, 13(4): 530–534. doi: 10.1109/LGRS.2016.2522387. -



 作者中心
作者中心 专家审稿
专家审稿 责编办公
责编办公 编辑办公
编辑办公
 下载:
下载: