Terahertz Communication and Sensing Framework Based on Orthogonal Delay-Doppler Division Multiplexing Modulation
-
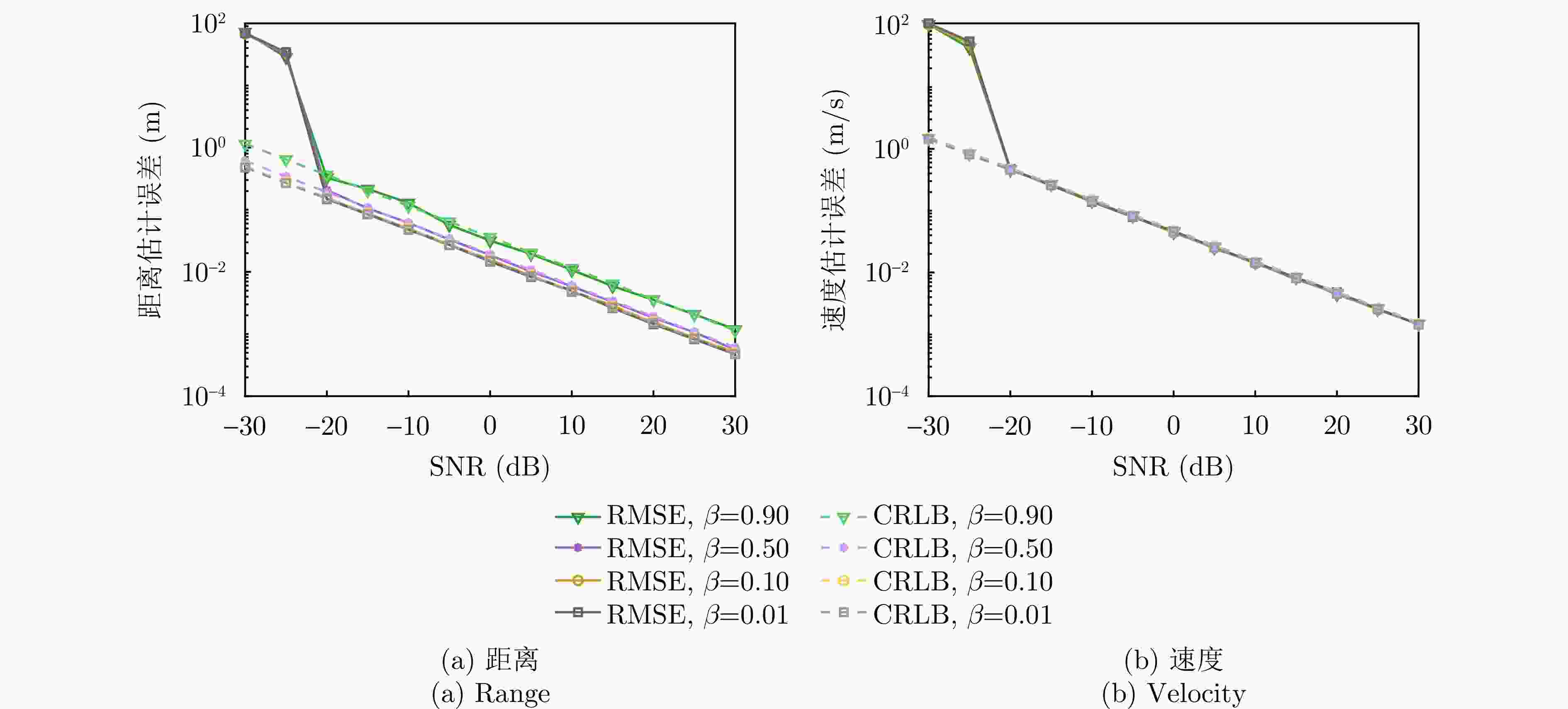
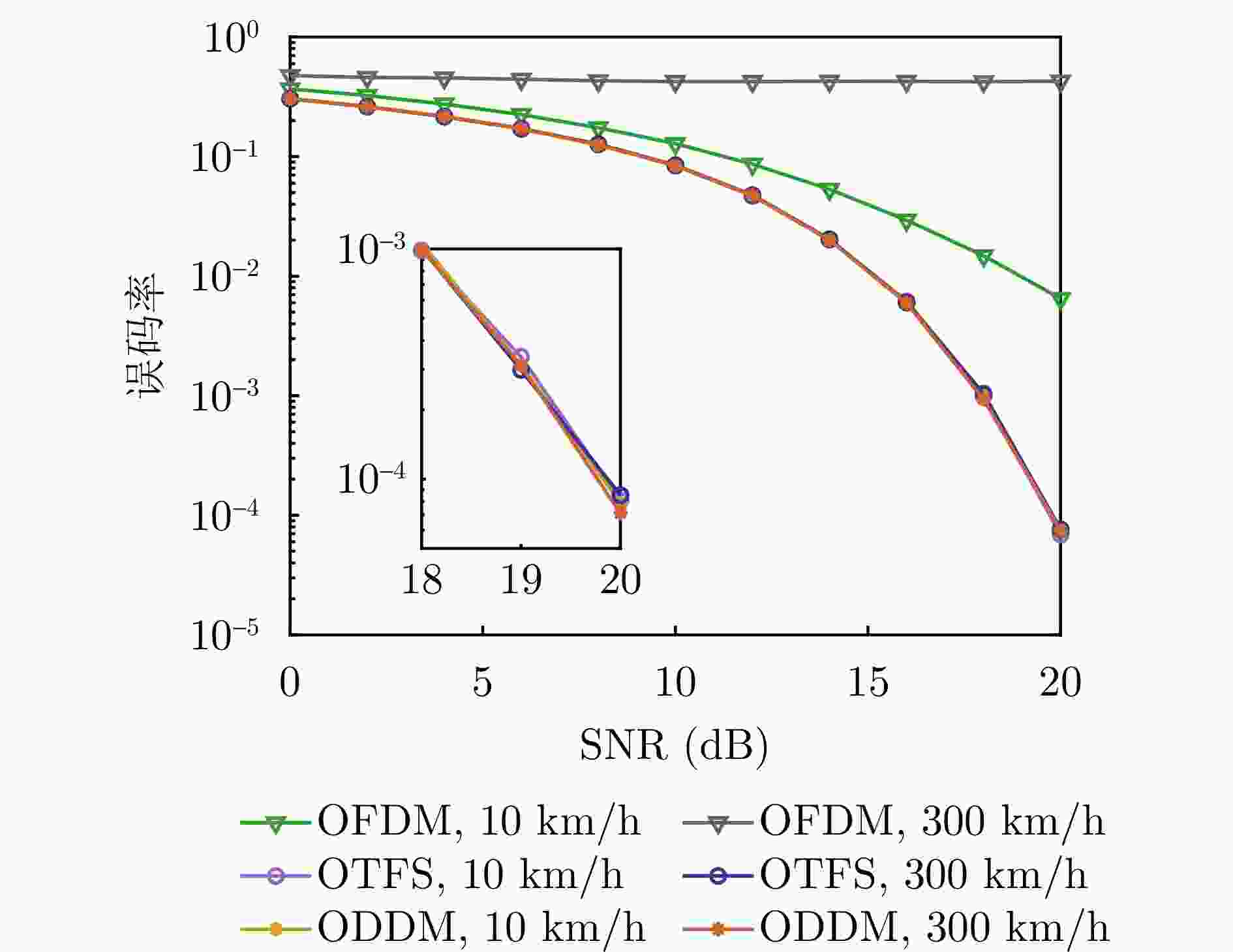
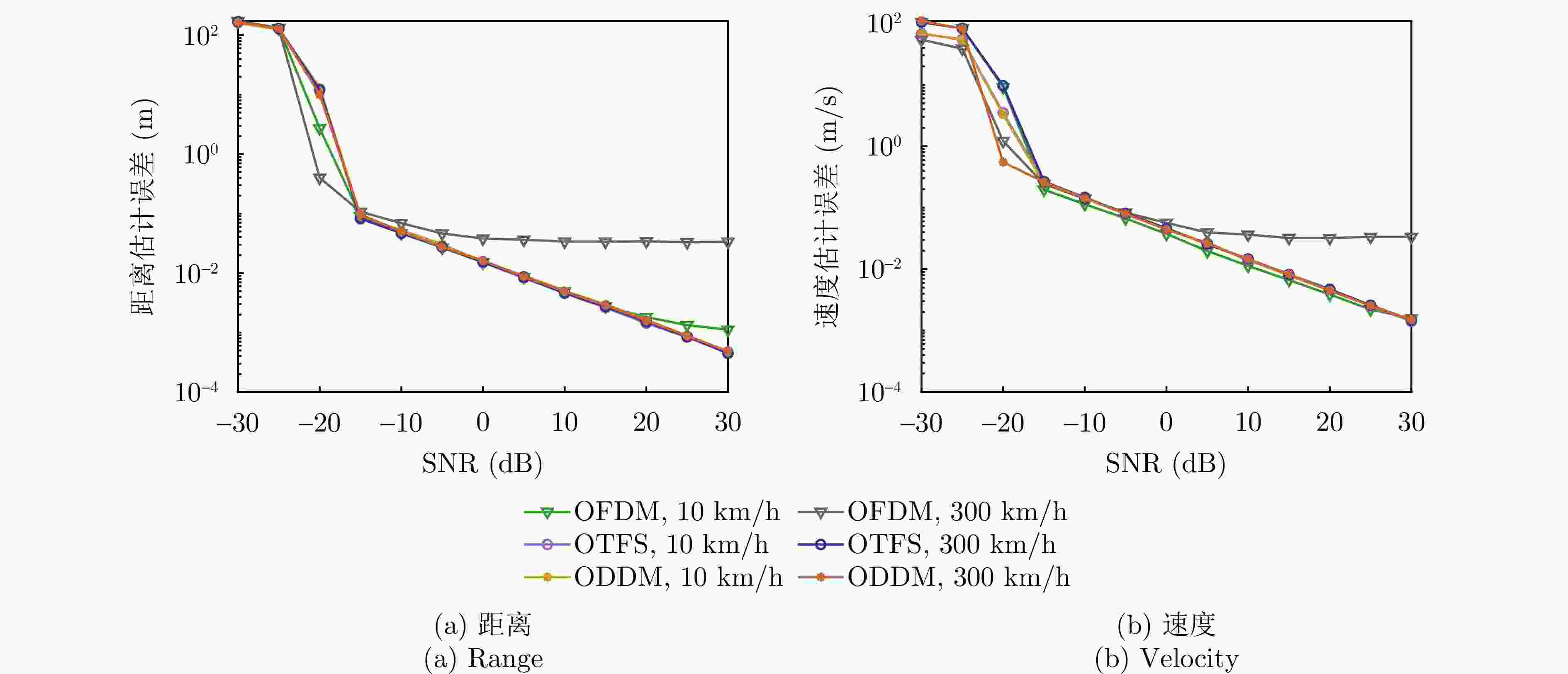
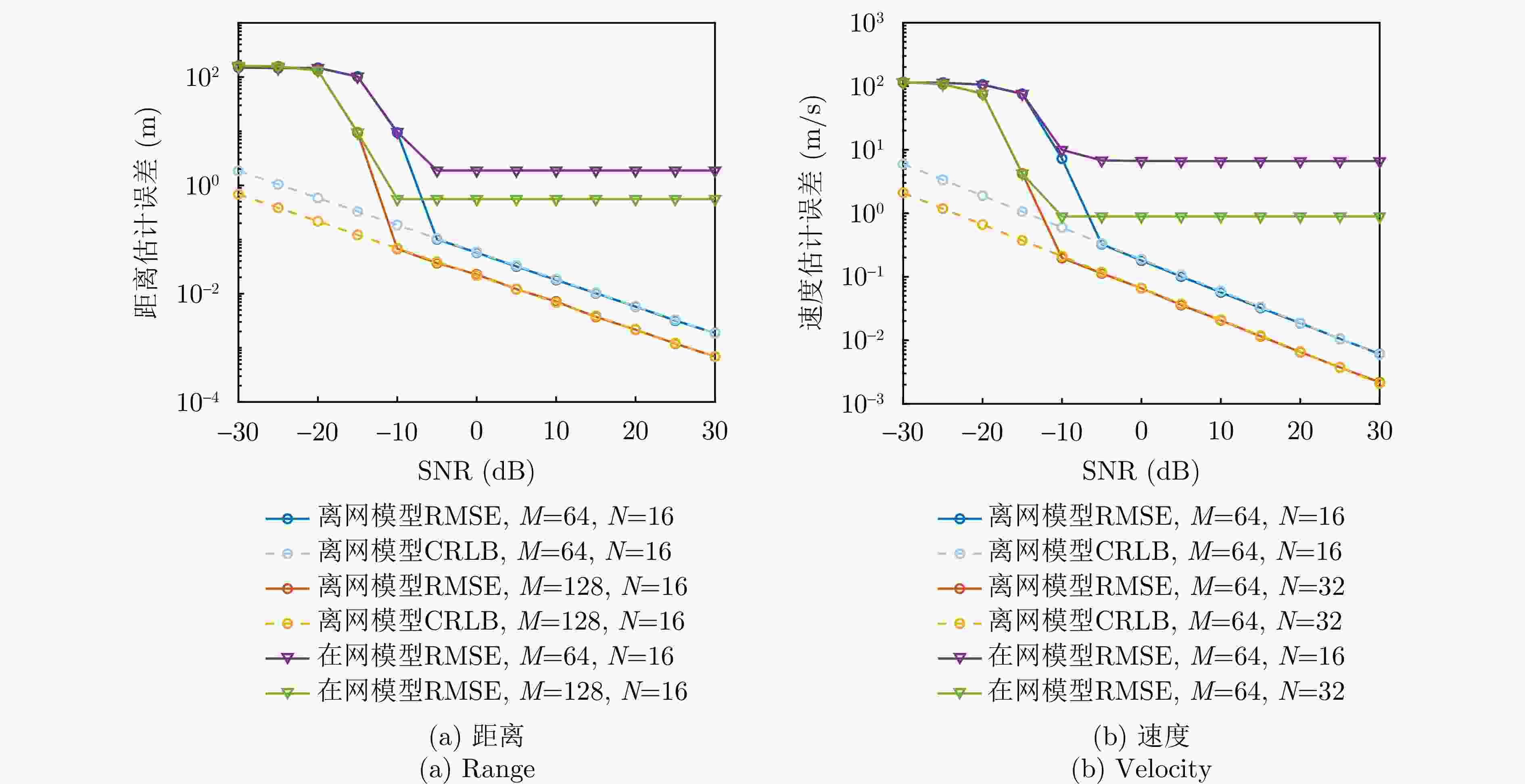
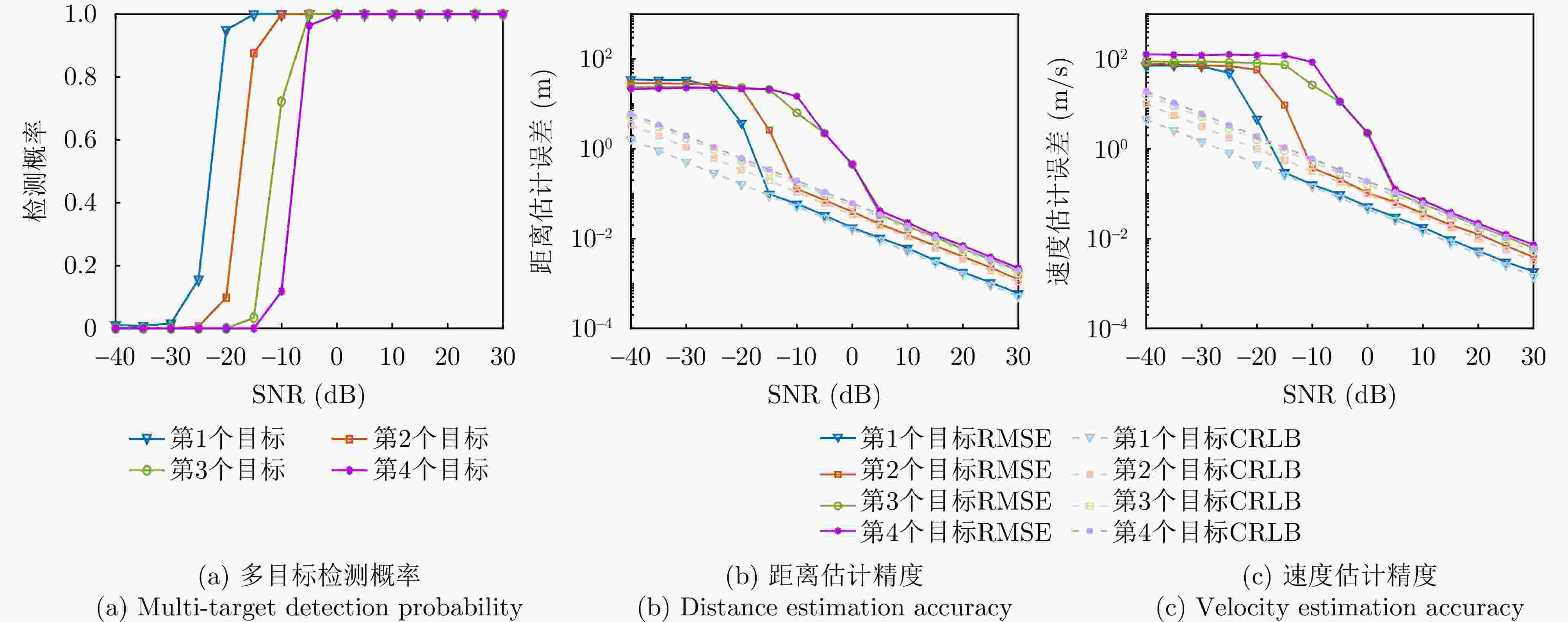
摘要: 太赫兹频段被认为可实现太比特每秒的通信速率并实现高精度感知,因此太赫兹通信感知一体化是未来无线通信系统的关键技术。该文聚焦于一种时延多普勒域波形——正交时延多普勒分路复用(ODDM)调制,提出了一种基于ODDM的太赫兹通信感知一体化传输方案。针对现有信号模型的局限性,该文推导了一种更为通用的离网ODDM调制输入/输出关系,突破了信道路径时延和多普勒频移必须为其分辨率整数倍的假设限制。针对ODDM符号检测问题,该文基于共轭梯度的时域信道均衡器优化计算复杂度,发现ODDM相比OFDM具有针对多普勒效应更高的鲁棒性。最后,该文设计了一种多目标感知估计算法,该算法能够在低复杂度下实现高精度估计,其多目标估计精度与克拉美罗下界相近。
-
关键词:
- 通信感知一体化 /
- 太赫兹频段 /
- 正交时延多普勒分路复用调制 /
- 时延多普勒域波形 /
- 感知估计
Abstract: Because the Terahertz (THz) band is capable of achieving terabit-per-second communication rates and high-precision sensing, THz Integrated Sensing And Communication (ISAC) has become a key technology for future wireless systems. We propose a THz ISAC framework based on a delay-Doppler waveform, i.e., the Orthogonal Delay-Doppler Multiplexing (ODDM) modulation. A more general off-grid ODDM modulation input/output relationship is derived to eliminate the assumption that channel path delays and Doppler frequency shifts are integer multiples of their resolutions. For ODDM symbol detection, a time-domain channel equalizer based on the conjugate gradient method is proposed to optimize the computational complexity. Compared with orthogonal frequency division multiplexing, ODDM demonstrates higher Doppler robustness against the Doppler effect. A sensing estimation algorithm is designed to achieve high-precision estimates with low complexity. The results show that the multi-target estimation accuracy approaches Cramér-Rao Lower Bounds (CRLB). -
1 基于共轭梯度的信道均衡迭代算法
1. Conjugate gradient based iterative algorithm for channel equalization
输入:时域接收向量r,信道参数$ \boldsymbol{\alpha },\boldsymbol{\tau },\boldsymbol{\nu } $,信号模型函数
$ {\boldsymbol{h}}_{\mathrm{1,2}}\left(\boldsymbol{s}|\boldsymbol{\alpha },\boldsymbol{\tau },\boldsymbol{\nu }\right) $,信噪比的倒数$ \lambda $输出:基带时间域传输向量$ \hat{\boldsymbol{s}} $ 初始化: $ {\boldsymbol{s}}_{0}={0}_{MN\times 1},{\boldsymbol{r}}_{0}=\boldsymbol{r}-{\boldsymbol{h}}_{1}\left({\boldsymbol{s}}_{0}|\boldsymbol{\alpha },\boldsymbol{\tau },\boldsymbol{\nu }\right) $,
${x}_{0}={p}_{0}={\boldsymbol{h}}_{2}\left({\boldsymbol{r}}_{0}|\boldsymbol{\alpha },\boldsymbol{\tau },\boldsymbol{\nu }\right),{\mathrm{\gamma }}_{0}=|{\boldsymbol{x}}_{0}{|}^{2},t=0 $重复以下操作:
$ {\boldsymbol{q}}_{t}={\boldsymbol{h}}_{1}\left({\boldsymbol{p}}_{t}|\boldsymbol{\alpha },\boldsymbol{\tau },\boldsymbol{\nu }\right),\text{}{\mathrm{\beta }}_{t}=\dfrac{{\mathrm{\gamma }}_{t}}{\left|\right|{\boldsymbol{q}}_{t}{\left|\right|}^{2}+\mathrm{\lambda }\left|\right|{\boldsymbol{p}}_{t}{\left|\right|}^{2}} $$ {\boldsymbol{s}}_{t+1}={\boldsymbol{s}}_{t}+{\mathrm{\beta }}_{t}{\boldsymbol{p}}_{t},\text{}{\boldsymbol{r}}_{t+1}={\boldsymbol{r}}_{t}-{\mathrm{\beta }}_{t}{\boldsymbol{q}}_{t} $ $ {x}_{t+1}={\boldsymbol{h}}_{2}\left({\boldsymbol{r}}_{t+1}|\boldsymbol{\alpha },\boldsymbol{\tau },\boldsymbol{\nu }\right)-\mathrm{\lambda }{\boldsymbol{s}}_{t+1} $ $ {\mathrm{\gamma }}_{t+1}=\left|\right|{\boldsymbol{x}}_{t+1}{\left|\right|}^{2} $ $ {\boldsymbol{p}}_{t+1}={\boldsymbol{x}}_{t+1}+\dfrac{{\mathrm{\gamma }}_{t+1}}{{\mathrm{\gamma }}_{t}}{\boldsymbol{p}}_{t} $ $ t=t+1 $ 直到收敛 返回: $ \hat{\boldsymbol{s}}={\boldsymbol{s}}_{t} $ 表 1 仿真参数
Table 1. Simulation paramters
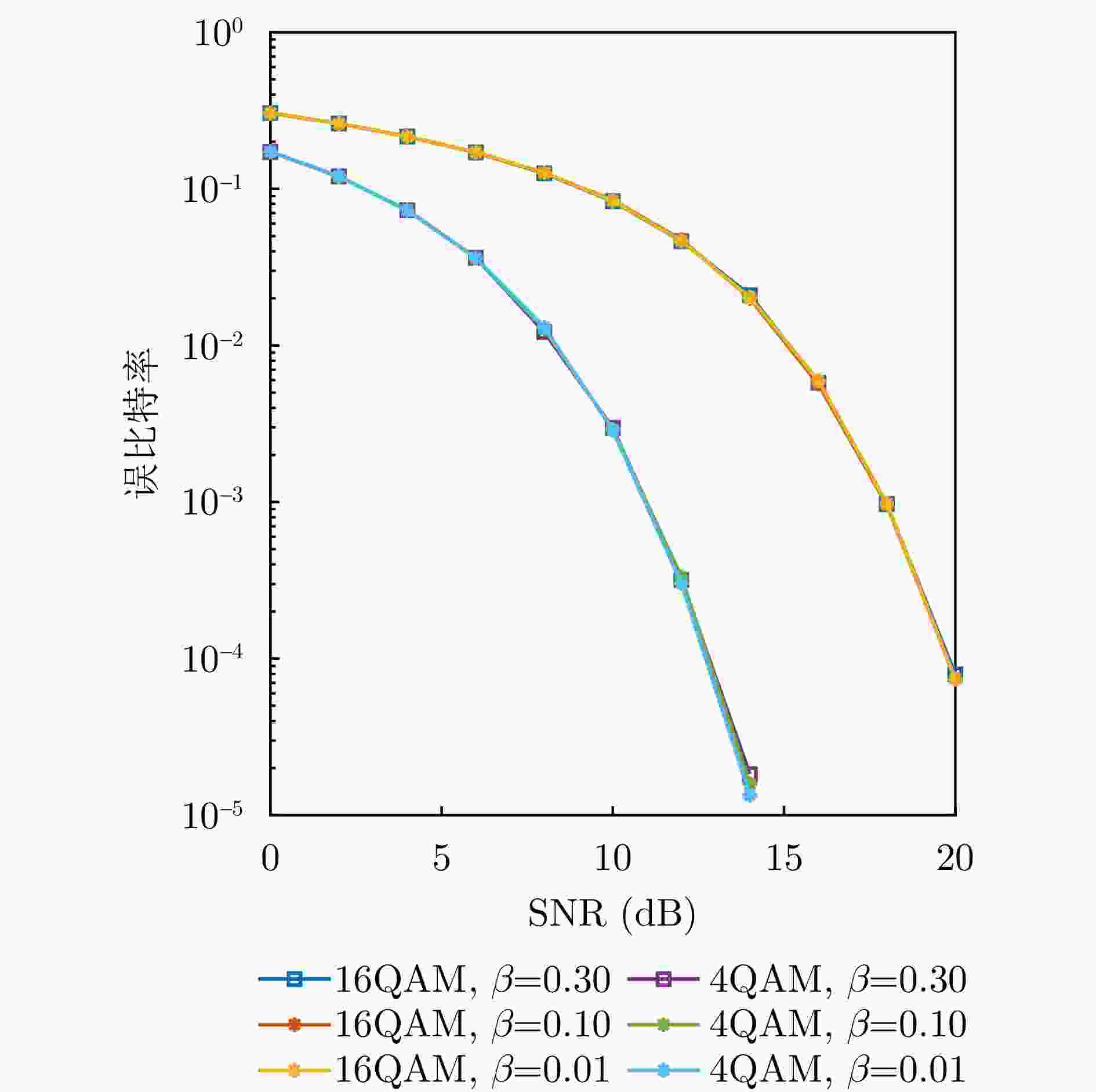
参数 数值 载波频率$ {f}_{\mathrm{{c}}} $ 0.3 THz 子载波间隔$ \Delta f $ 480 kHz 时延区间的数量M 128 多普勒区间的数量N 32 滚降因子$ \beta $ 0.1 -
[1] LIU Fan, CUI Yuanhao, MASOUROS C, et al. Integrated sensing and communications: Toward dual-functional wireless networks for 6G and beyond[J]. IEEE Journal on Selected Areas in Communications, 2022, 40(6): 1728–1767. doi: 10.1109/JSAC.2022.3156632. [2] YUAN Weijie, ZHOU Lin, DEHKORDI S K, et al. From OTFS to DD-ISAC: Integrating sensing and communications in the delay Doppler domain[J]. IEEE Wireless Communications, 2024, 31(6): 152–160. doi: 10.1109/MWC.018.2300607. [3] ZHANG Hongqi, YANG Zuomin, LYU Zhidong, et al. 300 GHz photonic-wireless transmission with aggregated 1.034 Tbit/s data rate over 100 m wireless distance[C]. Optical Fiber Communication Conference 2024, San Diego, USA, 2024: M2F.1. doi: 10.1364/OFC.2024.M2F.1. [4] ZHANG Hongqi, ZHANG Lu, WANG Shiwei, et al. Tbit/s multi-dimensional multiplexing THz-over-fiber for 6G wireless communication[J]. Journal of Lightwave Technology, 2021, 39(18): 5783–5790. doi: 10.1109/JLT.2021.3093628. [5] CHEN Zhi, HAN Chong, WU Yongzhi, et al. Terahertz wireless communications for 2030 and beyond: A cutting-edge frontier[J]. IEEE Communications Magazine, 2021, 59(11): 66–72. doi: 10.1109/MCOM.011.2100195. [6] HAN Chong, WU Yongzhi, CHEN Zhi, et al. THz ISAC: A physical-layer perspective of terahertz integrated sensing and communication[J]. IEEE Communications Magazine, 2024, 62(2): 102–108. doi: 10.1109/MCOM.001.2200404. [7] WEI Zhiqing, PIAO Jinghui, YUAN Xin, et al. Waveform design for MIMO-OFDM integrated sensing and communication system: An information theoretical approach[J]. IEEE Transactions on Communications, 2024, 72(1): 496–509. doi: 10.1109/TCOMM.2023.3317258. [8] XIANG Yang, GAO Yuxing, YANG Xinru, et al. An ESPRIT-based moving target sensing method for MIMO-OFDM ISAC systems[J]. IEEE Communications Letters, 2023, 27(12): 3205–3209. doi: 10.1109/LCOMM.2023.3325531. [9] MAO Tianqi, CHEN Jiaxuan, WANG Qi, et al. Waveform design for joint sensing and communications in millimeter-wave and low terahertz bands[J]. IEEE Transactions on Communications, 2022, 70(10): 7023–7039. doi: 10.1109/TCOMM.2022.3196685. [10] ROU H S, DE ABREU G T F, CHOI J, et al. From OTFS to AFDM: A comparative study of next-generation waveforms for ISAC in doubly-dispersive channels[EB/OL]. https://arxiv.org/abs/2401.07700, 2024. [11] WU Yongzhi and HAN Chong. Time-frequency-space transmit design and signal processing with dynamic subarray for terahertz integrated sensing and communication[EB/OL]. https://arxiv.org/abs/2307.04440v1, 2023. [12] TOM A, ŞAHIN A, and ARSLAN H. Suppressing alignment: Joint PAPR and out-of-band power leakage reduction for OFDM-based systems[J]. IEEE Transactions on Communications, 2016, 64(3): 1100–1109. doi: 10.1109/TCOMM.2015.2512603. [13] WANG Tiejun, PROAKIS J G, MASRY E, et al. Performance degradation of OFDM systems due to Doppler spreading[J]. IEEE Transactions on Wireless Communications, 2006, 5(6): 1422–1432. doi: 10.1109/TWC.2006.1638663. [14] HADANI R, RAKIB S, TSATSANIS M, et al. Orthogonal time frequency space modulation[C]. 2017 IEEE Wireless Communications and Networking Conference (WCNC), San Francisco, USA, 2017: 1–6. doi: 10.1109/WCNC.2017.7925924. [15] LIN Hai and YUAN Jinhong. Orthogonal delay-Doppler division multiplexing modulation[J]. IEEE Transactions on Wireless Communications, 2022, 21(12): 11024–11037. doi: 10.1109/TWC.2022.3188776. [16] WEI Zhiqiang, YUAN Weijie, LI Shuangyang, et al. Orthogonal time-frequency space modulation: A promising next-generation waveform[J]. IEEE Wireless Communications, 2021, 28(4): 136–144. doi: 10.1109/MWC.001.2000408. [17] RAVITEJA P, PHAN K T, HONG Yi, et al. Interference cancellation and iterative detection for orthogonal time frequency space modulation[J]. IEEE Transactions on Wireless Communications, 2018, 17(10): 6501–6515. doi: 10.1109/TWC.2018.2860011. [18] RAVITEJA P, HONG Yi, VITERBO E, et al. Practical pulse-shaping waveforms for reduced-cyclic-prefix OTFS[J]. IEEE Transactions on Vehicular Technology, 2019, 68(1): 957–961. doi: 10.1109/TVT.2018.2878891. [19] LI Shuangyang, YUAN Weijie, LIU Chang, et al. A novel ISAC transmission framework based on spatially-spread orthogonal time frequency space modulation[J]. IEEE Journal on Selected Areas in Communications, 2022, 40(6): 1854–1872. doi: 10.1109/JSAC.2022.3155538. [20] WEI Xinyuan, ZHANG Lingyan, YUAN Weijie, et al. SDR system design and implementation on delay-Doppler communications and sensing[C]. 2023 IEEE Wireless Communications and Networking Conference (WCNC), Glasgow, UK, 2023: 1–6. doi: 10.1109/WCNC55385.2023.10118889. [21] WU Yongzhi, HAN Chong, and CHEN Zhi. DFT-spread orthogonal time frequency space system with superimposed pilots for terahertz integrated sensing and communication[J]. IEEE Transactions on Wireless Communications, 2023, 22(11): 7361–7376. doi: 10.1109/TWC.2023.3250267. [22] HUANG Kehan, QIU Min, TONG Jun, et al. Performance of ODDM with imperfect channel estimation[C]. 2023 IEEE 24th International Workshop on Signal Processing Advances in Wireless Communications (SPAWC), Shanghai, China, 2023: 561–565. doi: 10.1109/SPAWC53906.2023.10304518. [23] CHENG Qingqing, SHI Zhenguo, YUAN Jinhong, et al. A novel environmentally robust ODDM detection approach using contrastive learning[J]. IEEE Transactions on Communications, 2023, 71(9): 5274–5286. doi: 10.1109/TCOMM.2023.3282959. [24] TONG Jun and XI Jiantao. Super-resolution estimation of delay-Doppler-angle parameters of doubly selective channels in hybrid MIMO systems[C]. 2023 IEEE International Conference on Communications Workshops (ICC Workshops), Rome, Italy, 2023: 800–806. doi: 10.1109/ICCWorkshops57953.2023.10283616. [25] HAN Chong, BICEN A O, and AKYILDIZ I F. Multi-ray channel modeling and wideband characterization for wireless communications in the terahertz band[J]. IEEE Transactions on Wireless Communications, 2015, 14(5): 2402–2412. doi: 10.1109/TWC.2014.2386335. [26] TONG Jun, XI Jiangtao, YUAN Jinhong, et al. On the input-output relation of ODDM modulation over general physical channels[C]. 2023 IEEE International Conference on Communications Workshops (ICC Workshops), Rome, Italy, 2023: 289–294. doi: 10.1109/ICCWorkshops57953.2023.10283746. -



 作者中心
作者中心 专家审稿
专家审稿 责编办公
责编办公 编辑办公
编辑办公
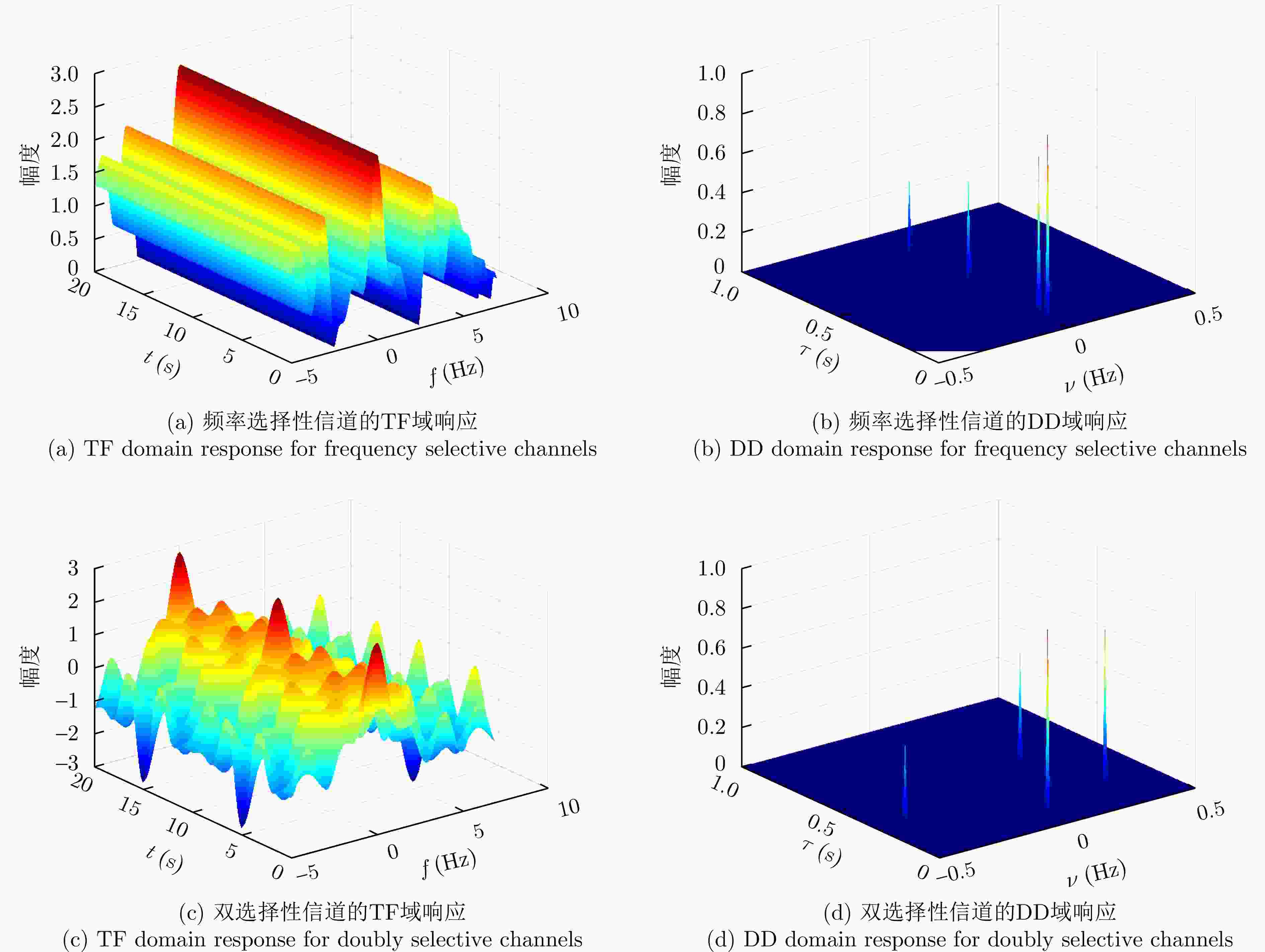
 下载:
下载: