作者中心
专家审稿
责编办公
编辑办公
Integrated Transmission Resource Management Scheme for Multifunctional Radars in Dynamic Electromagnetic Environments
-
摘要: 传统多功能雷达仅面向目标特性优化发射资源，在动态电磁环境下面临干扰智能时变、优化模型失配的问题。因此，该文提出一种基于数据驱动的一体化发射资源管理方案，旨在通过对动态干扰信息在线感知与利用提升多功能雷达在动态电磁环境下的多目标跟踪(MTT)性能。该方案首先建立马尔可夫决策过程，数学化描述雷达被敌方截获和干扰的风险。而后将该马尔可夫决策过程感知的干扰信息耦合进MTT精度计算，一体化发射资源管理方法被设计为具有约束动作空间的优化问题。最后提出一种贪婪排序回溯算法对其进行求解。仿真结果表明，所提方法在面向动态干扰环境时不仅可以降低敌方截获概率，还能在被干扰时降低干扰对雷达的影响，改善MTT性能。Abstract: Traditional multifunctional radar systems optimize transmission resources solely based on target characteristics. However, this approach poses challenges in dynamic electromagnetic environments owing to the intelligent time-varying nature of jamming and the mismatch between traditional optimization models and real-world scenarios. To address these limitations, this paper proposes a data-driven integrated transmission resource management scheme designed to enhance the Multiple Target Tracking (MTT) performance of multifunctional radars in complex and dynamic electromagnetic environments. The proposed scheme achieves this by enabling online perception and utilization of dynamic jamming information. The scheme initially establishes a Markov Decision Process (MDP) to mathematically model the risks associated with radar interception and adversarial jamming. This MDP provides a structured approach to perceive jamming information, which is then integrated into the calculation of MTT. The integrated resource management challenge is formulated as an optimization problem with constraints on the action space. To solve this problem effectively, a greedy sorting backtracking algorithm is introduced. Simulation results demonstrate the efficacy of the proposed method, demonstrating its ability to significantly reduce the probability of radar interception in dynamic jamming environments. Furthermore, the method mitigates the impact of jamming on radar performance during adversarial interference, thereby improving MTT performance.
-
图 4 一体化发射资源管理方案的发射方案以及目标干扰动作
Figure 4. Transmit scheme of the integrated transmit resource management scheme and jamming actions of targets
图 5 抗干扰发射资源管理方案的发射方案以及目标干扰动作
Figure 5. Transmit scheme of the anti-jamming transmit resource management scheme and jamming actions of targets
1 贪婪排序回溯算法流程
1. The flow of greedy sort backtracking algorithm
步骤1 输入在第k帧状态${{\boldsymbol{s}}_k}$、动作空间$\mathcal{A}$。初始化$ \mathcal{D}_{q}=\varnothing $、迭代次数$j = 1$以及动作索引${n_q} = 1$, $\forall q$。 步骤2 评估每一个目标与动作空间$\mathcal{A}$相关的成本函数： ${{\boldsymbol{C}}_q} = \left[ {c({\boldsymbol{s}}_k^q,{{\boldsymbol{a}}_1}), c({\boldsymbol{s}}_k^q,{{\boldsymbol{a}}_2}), \cdots ,c({\boldsymbol{s}}_k^q,{{\boldsymbol{a}}_{{N_\mathcal{A}}}})} \right]$, $ \forall q $ 步骤3 将成本函数${{\boldsymbol{C}}_q}$按升序排序，形成索引${\bf{I}}{{\bf{X}}_q}$： $ {{\boldsymbol{C}}_q}({\bf{I}}{{\bf{X}}_q}(1)) \lt{{\boldsymbol{C}}_q}({\bf{I}}{{\bf{X}}_q}(2)) \lt \cdots \lt {{\boldsymbol{C}}_q}({\bf{I}}{{\bf{X}}_q}({N_\mathcal{A}})) $, $\forall q$ 步骤4 当至少存在一个目标的动作索引${n_q}{\text{ \lt }}{N_\mathcal{A}}$，进入步骤5。 步骤5 形成一个联合发射方案并提取其中的驻留时间信息，进入步骤6。 ${{\boldsymbol{a}}_j} = \left[ {{\mathcal{A}_1}({\bf{I}}{{\bf{X}}_1}({n_1})),{\mathcal{A}_2}({\bf{I}}{{\bf{X}}_2}({n_2})), \cdots ,{\mathcal{A}_Q}({\bf{I}}{{\bf{X}}_Q}({n_Q}))} \right] \Rightarrow {{\boldsymbol{t}}_j} = \left[ {{t_1},{t_2}, \cdots ,{t_Q}} \right]$ 步骤6 计算联合发射方案${{\boldsymbol{a}}_j}$对应的成本函数$ {{\boldsymbol{c}}_j} = \left[ {{c_j}(1), {c_j}(2), \cdots ,{c_j}(Q)} \right] $： $ {c}_{j}\left(q\right)=\left\{\begin{aligned}& {{\boldsymbol{C}}}_{q}({\bf{IX}}_{q}({n}_{q}^{})),\quad{t}_{q}^{} \gt {t}_{\text{min}}\text{ }或者{n}_{q}\text{ \lt }{N}_{\mathcal{A}}\text{ }\\ & +\infty, \quad\qquad\quad \text{ }其他\end{aligned}\right. $ 步骤7 如果$\displaystyle\sum\nolimits_{q = 1}^Q {{t_q}} \le {t_{{\text{total}}}}$，进入到步骤9；否则进入到步骤8。 步骤8 获得${{\boldsymbol{c}}_j}$中具有最小成本函数的目标索引${\rm{I}}{{\rm{X}}_{\min }}$，将对应的驻留时间方案$ {t_{{\rm{I}}{{\rm{X}}_{{\text{min}}}}}} $存储进$ \mathcal{D}_{\mathrm{IX}_{\mathrm{min}}} $(目标${\rm{I}}{{\rm{X}}_{\min }}$已遍历过的动作，
$ \left|{\mathcal{D}}_{{\text{IX}}_{\mathrm{min}}}\right|={n}_{{\text{IX}}_{\mathrm{min}}} $)。然后执行$ j = j + 1 $，${n_{{\rm{I}}{{\rm{X}}_{{\text{min}}}}}} = {n_{{\rm{I}}{{\rm{X}}_{{\text{min}}}}}} + 1$，进入到步骤4。步骤9 在$ \mathcal{D}_{q} $中回溯寻找具有相同驻留时间参数($ {t}_{q}\in {\mathcal{D}}_{q} $)的最小索引$ {\text{IX}}_{{\mathcal{D}}_{q}} $，同时更新动作索引： $ {n}_{q}^{*}=\left\{\begin{array}{llllllllllllll}{\text{IX}}_{{\mathcal{D}}_{q}},& {\text{ IX}}_{{\mathcal{D}}_{q}}\ne \varnothing \text{ }\\ {n}_{q},& 其他\end{array} \right.$ 然后形成最优发射方案$ {\boldsymbol{a}}_k^* = \left[ {{\mathcal{A}_1}({\bf{I}}{{\bf{X}}_1}(n_1^*)),{\mathcal{A}_2}({\bf{I}}{{\bf{X}}_2}(n_2^*)), \cdots ,{\mathcal{A}_Q}({\bf{I}}{{\bf{X}}_Q}(n_Q^*))} \right] $，进入步骤10。 步骤10 输出最终的发射方案$ {\boldsymbol{a}}_k^* $。 
下载: 导出CSV
表 1 雷达参数
Table 1. Radar parameters
参数 设定值 ${G_{{\text{R,R}}}}$ 80 dB ${B_{{\text{R,r}}}}$ 1 MHz ${\eta _{\text{R}}}$ –141 dBW ${B_{{\text{R,r}}}}$ 0.5°
下载: 导出CSV
表 2 目标参数
Table 2. Target parameters
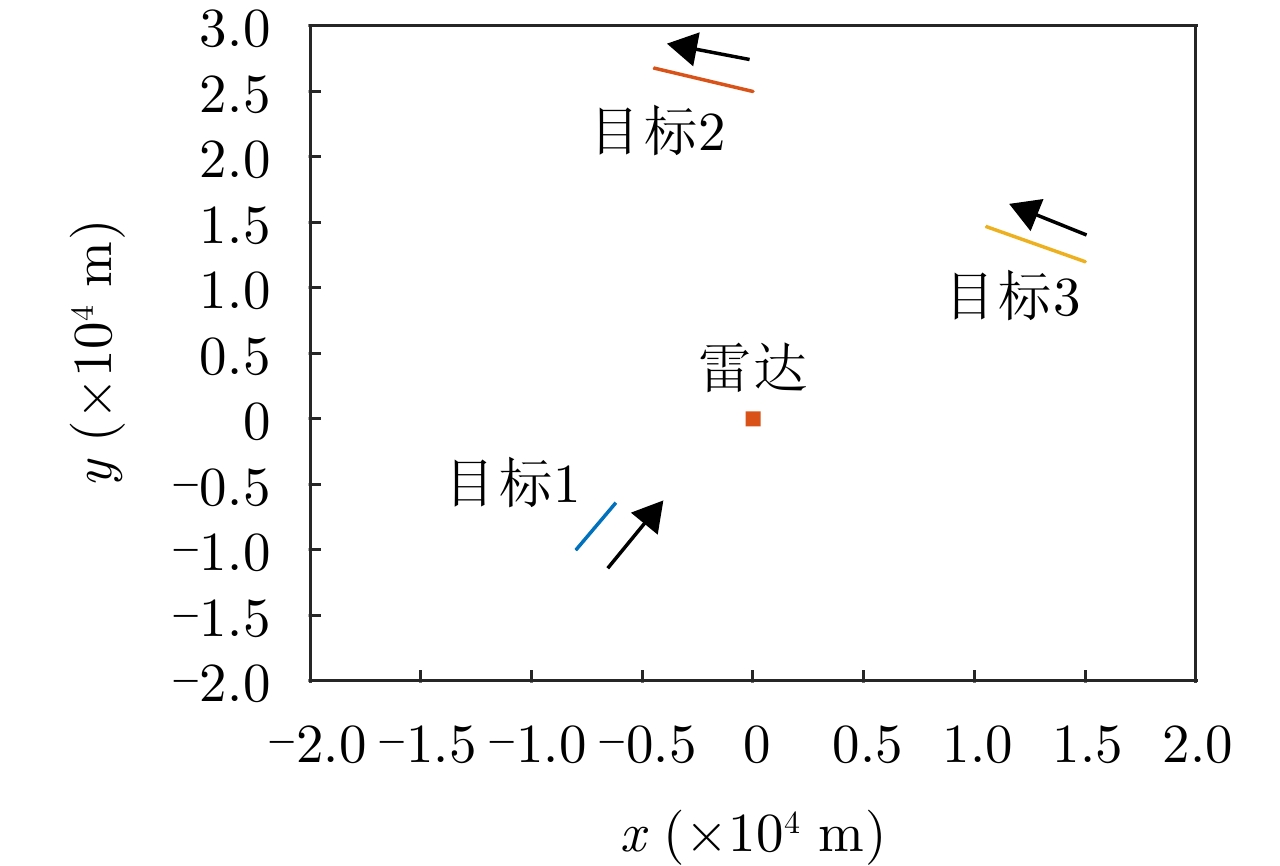
目标索引 位置(km) 速度(m/s) ${\bar \sigma _q}$(${{\text{m}}^2}$) 1 (–8, –10) (10, 20) [9, 6, 3] 2 (0, 25) (–25, 10) [7, 4, 2] 3 (15, 12) (–25, 15) [8, 5, 2]
下载: 导出CSV
表 3 动态电磁环境参数
Table 3. Parameters of dynamic electromagnetic environments
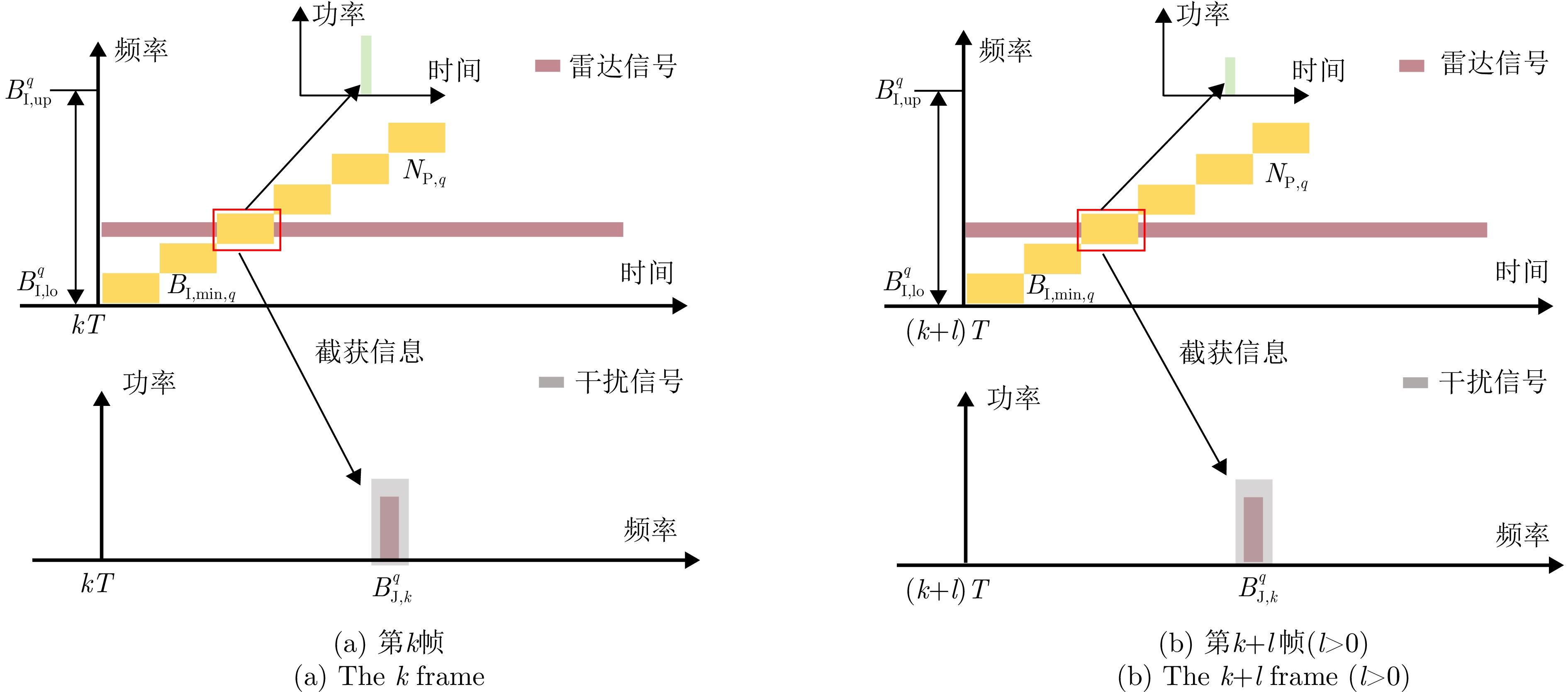
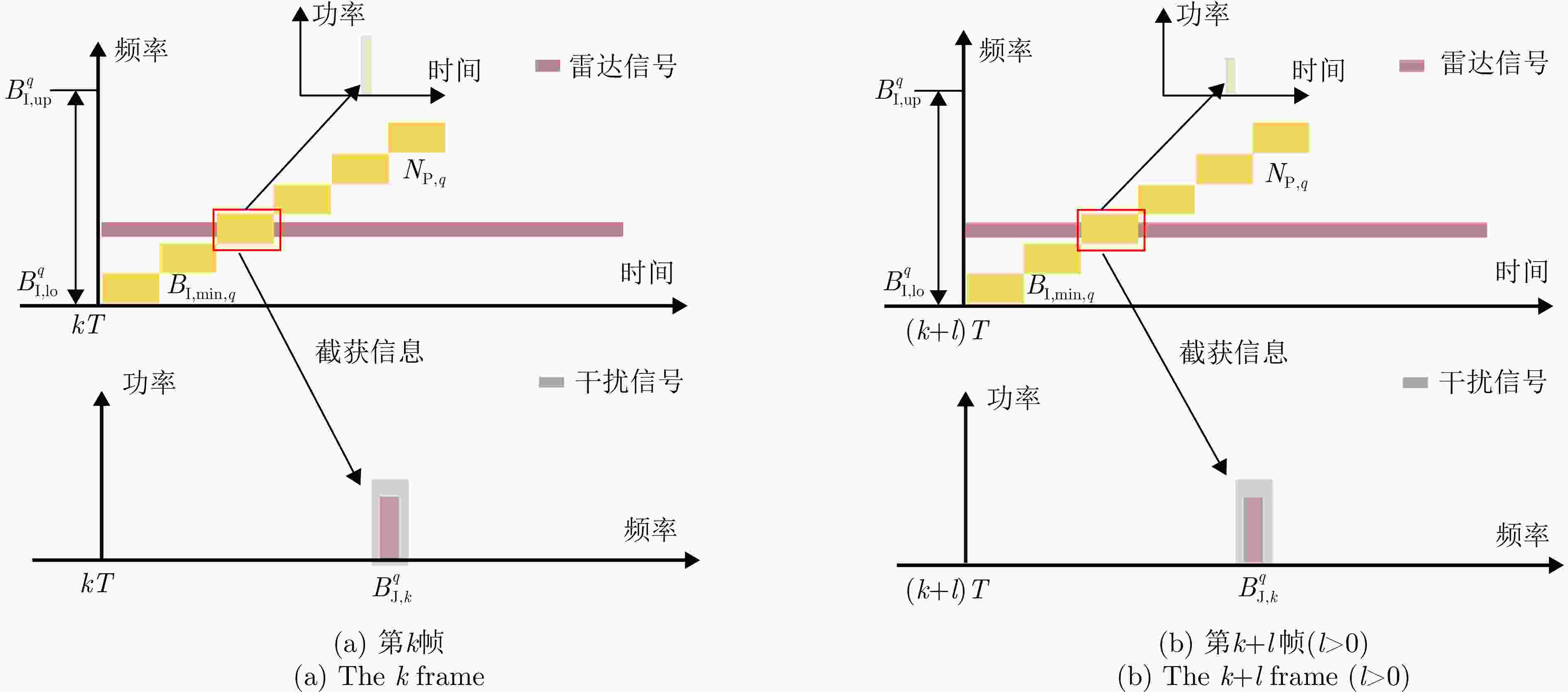
目标索引 截获模式 $\left[ {B_{{\text{I,lo}}}^q,B_{{\text{I,up}}}^q} \right]$ $G_{{\text{R,I}}}^q$ ${N_{{\text{P,}}q}}$ $B_{{\text{I,min}}}^q$ 干扰策略 ${P_{{\text{J}},q}}$ $G_{{\text{J,R}}}^q$ $B_{{\text{J,k}}}^q$ 1 弱 $ \left[ {0.5,6.5} \right] $ GHz –3 dB 5 0.2 GHz 2 30 W 43 dB 2 MHz 2 弱 $ \left[ {0.5,3.5} \right] $ GHz 0 dB 7 0.1 GHz 1 30 W 43 dB 2 MHz 3 强 $ \left[ {0.5,4.5} \right] $ GHz 14 dB 5 0.3 GHz 1 30 W 43 dB 2 MHz
下载: 导出CSV
表 4 不同优化算法运行时间
Table 4. Running time of different optimization algorithms
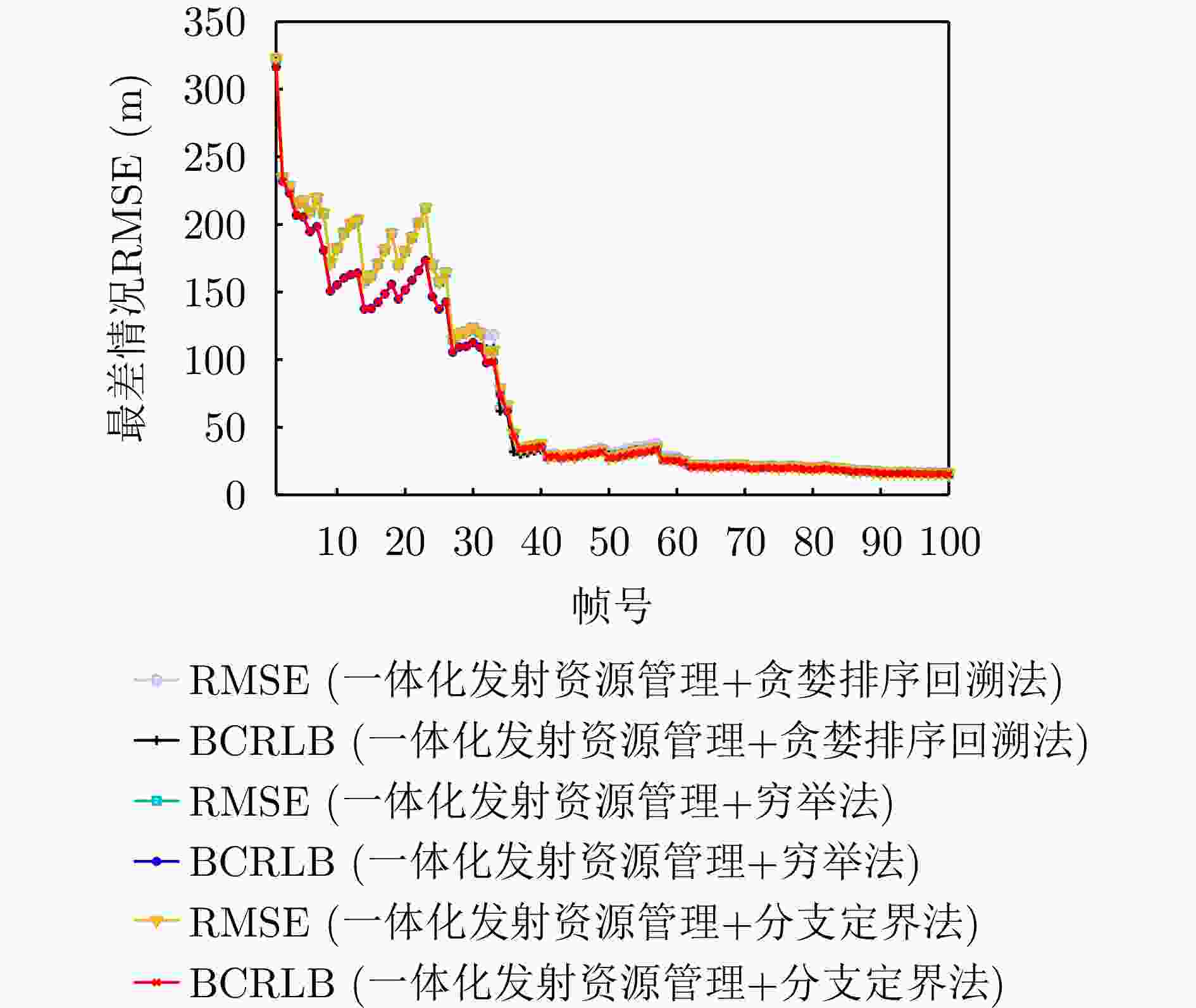
优化算法 运行时间(s) 贪婪排序回溯算法 0.00074 穷举法 0.01790 分支定界法 0.01660
下载: 导出CSV
-
[1] MORELANDE M R, KREUCHER C M, and KASTELLA K. A Bayesian approach to multiple target detection and tracking[J]. IEEE Transactions on Signal Processing, 2007, 55(5): 1589–1604. doi: 10.1109/TSP.2006.889470. [2] BLACKMAN S S. Multiple-Target Tracking with Radar Applications[M]. Dedham: Artech House, 1986: 1–449. [3] STONE L D, STREIT R L, CORWIN T L, et al. Bayesian Multiple Target Tracking[M]. 2nd ed. Boston: Artech House, 2014: 107–160. [4] HUE C, LE CADRE J P, and PÉREZ P. Sequential Monte Carlo methods for multiple target tracking and data fusion[J]. IEEE Transactions on Signal Processing, 2002, 50(2): 309–325. doi: 10.1109/78.978386. [5] WANG Xiangli, YI Wei, XIE Mingchi, et al. A joint beam and dwell time allocation strategy for multiple target tracking based on phase array radar system[C]. 2017 20th International Conference on Information Fusion (Fusion), Xi’an, China, 2017: 1–5. doi: 10.23919/ICIF.2017.8009856. [6] 戴金辉, 严俊坤, 王鹏辉, 等. 基于目标容量的网络化雷达功率分配方案[J]. 电子与信息学报, 2021, 43(9): 2688–2694. doi: 10.11999/JEIT200873.DAI Jinhui, YAN Junkun, WANG Penghui, et al. Target capacity based power allocation scheme in radar network[J]. Journal of Electronics & Information Technology, 2021, 43(9): 2688–2694. doi: 10.11999/JEIT200873. [7] YUAN Ye, YI Wei, and KONG Lingjiang. Joint tracking sequence and dwell time allocation for multi-target tracking with phased array radar[J]. Signal Processing, 2022, 192: 108374. doi: 10.1016/j.sigpro.2021.108374. [8] NARYKOV A S, KRASNOV O A, and YAROVOY A. Algorithm for resource management of multiple phased array radars for target tracking[C]. 2013 16th International Conference on Information Fusion, Istanbul, Turkey, 2013: 1258–1264. [9] YUAN Ye, YI Wei, HOSEINNEZHAD R, et al. Robust power allocation for resource-aware multi-target tracking with colocated MIMO radars[J]. IEEE Transactions on Signal Processing, 2021, 69: 443–458. doi: 10.1109/TSP.2020.3047519. [10] SCHLEHER D C. Electronic Warfare in the Information Age[M]. Boston: Artech House, 1999: 1–60. [11] SHI Chenguang, WANG Yijie, SALOUS S, et al. Joint transmit resource management and waveform selection strategy for target tracking in distributed phased array radar network[J]. IEEE Transactions on Aerospace and Electronic Systems, 2022, 58(4): 2762–2778. doi: 10.1109/TAES.2021.3138869. [12] ZHANG Haowei, LIU Weijian, ZHANG Qiliang, et al. Joint resource optimization for a distributed MIMO radar when tracking multiple targets in the presence of deception jamming[J]. Signal Processing, 2022, 200: 108641. doi: 10.1016/j.sigpro.2022.108641. [13] AILIYA, YI Wei, and VARSHNEY P K. Adaptation of frequency hopping interval for radar anti-jamming based on reinforcement learning[J]. IEEE Transactions on Vehicular Technology, 2022, 71(12): 12434–12449. doi: 10.1109/TVT.2022.3197425. [14] LI Kang, JIU Bo, WANG Penghui, et al. Radar active antagonism through deep reinforcement learning: A way to address the challenge of mainlobe jamming[J]. Signal Processing, 2021, 186: 108130. doi: 10.1016/j.sigpro.2021.108130. [15] ZHANG Peng, YAN Junkun, PU Wenqiang, et al. Multi-dimensional resource management scheme for multiple target tracking under dynamic electromagnetic environment[J]. IEEE Transactions on Signal Processing, 2024, 72: 2377–2393. doi: 10.1109/TSP.2024.3390119. [16] YAN Junkun, LIU Hongwei, JIU Bo, et al. Simultaneous multibeam resource allocation scheme for multiple target tracking[J]. IEEE Transactions on Signal Processing, 2015, 63(12): 3110–3122. doi: 10.1109/TSP.2015.2417504. [17] YAN Junkun, LIU Hongwei, PU Wenqiang, et al. Joint beam selection and power allocation for multiple target tracking in netted colocated MIMO radar system[J]. IEEE Transactions on Signal Processing, 2016, 64(24): 6417–6427. doi: 10.1109/TSP.2016.2607147. [18] LI Nengjing and ZHANG Yiting. A survey of radar ECM and ECCM[J]. IEEE Transactions on Aerospace and Electronic Systems, 1995, 31(3): 1110–1120. doi: 10.1109/7.395232. [19] VAN TREES H L. Detection, Estimation, and Modulation Theory, Part III: Radar-Sonar Signal Processing and Gaussian Signals in Noise[M]. New York: John Wiley & Sons, 2001: 294–307. [20] SKOLNIK M I. Radar Handbook[M]. New York: McGraw-Hill, 2008: 313–370. [21] SUKHAREVSKY O I, VASILETS V A, and ZALEVSKY G S. Electromagnetic wave scattering by aerial and ground radar objects[C]. 2015 IEEE Radar Conference (RadarCon), Arlington, USA, 2015: 162–167. DOI: 10.1109/RADAR.2015.7130989. [22] BERTSEKAS D P. Reinforcement Learning and Optimal Control[M]. Nashua: Athena Scientific, 2019: 1–40. [23] SUTTON R S and BARTO A G. Reinforcement Learning: An Introduction[M]. 2nd ed. Cambridge: MIT Press, 2018: 37–58. [24] NERI F. Introduction to Electronic Defense Systems[M]. 2nd ed. Henderson: SciTech Publishing, 2006: 259–368. [25] STINCO P, GRECO M, GINI F, et al. Cognitive radars in spectrally dense environments[J]. IEEE Aerospace and Electronic Systems Magazine, 2016, 31(10): 20–27. doi: 10.1109/MAES.2016.150193. [26] SELVI E, BUEHRER R M, MARTONE A, et al. Reinforcement learning for adaptable bandwidth tracking radars[J]. IEEE Transactions on Aerospace and Electronic Systems, 2020, 56(5): 3904–3921. doi: 10.1109/TAES.2020.2987443. [27] KOCHENDERFER M J, WHEELER T A, and WRAY K H. Algorithms for Decision Making[M]. Cambridge: MIT Press, 2022: 311–326. [28] 严俊坤, 纠博, 刘宏伟, 等. 一种针对多目标跟踪的多基雷达系统聚类与功率联合分配算法[J]. 电子与信息学报, 2013, 35(8): 1875–1881. doi: 10.3724/SP.J.1146.2012.01470.YAN Junkun, JIU Bo, LIU Hongwei, et al. Joint cluster and power allocation algorithm for multiple targets tracking in multistatic radar systems[J]. Journal of Electronics & Information Technology, 2013, 35(8): 1875–1881. doi: 10.3724/SP.J.1146.2012.01470. [29] LISI F, FORTUNATI S, GRECO M S, et al. Enhancement of a state-of-the-art RL-based detection algorithm for massive MIMO radars[J]. IEEE Transactions on Aerospace and Electronic Systems, 2022, 58(6): 5925–5931. doi: 10.1109/TAES.2022.3168033. -
图(6) / 表(5)
计量
- 文章访问数:
- HTML全文浏览量:
- PDF下载量:
- 被引次数: 0
