一种调频连续波体制微型多基SAR相位同步方法

周涛; 金国栋; 陆萍萍; 朱岱寅

doi:10.12000/JR24198

一种调频连续波体制微型多基SAR相位同步方法

DOI: 10.12000/JR24198

周涛¹,
金国栋^{1, 2, ,},
陆萍萍^{3, 4},
朱岱寅^{1, 2}

1.
南京航空航天大学电子信息工程学院雷达成像与微波光子技术教育部重点实验室南京 211106
2.
南京航空航天大学深圳研究院深圳 518000
3.
中国科学院空天信息创新研究院北京 100190
4.
微波成像全国重点实验室北京 100190

基金项目: 国家自然科学基金(62101248)，江苏省自然科学基金(BK20210282)，广东省基础与应用基础研究基金(2020B1515120060)，深圳市科技计划项目(JCYJ20230807142000001)，中央高校基本科研业务费专项基金(NT2023008)

详细信息

作者简介:
周　涛，博士生，主要研究方向为雷达信号处理和雷达成像技术

金国栋，博士，副研究员，博士生导师，主要研究方向为雷达信号处理、雷达波形设计与优化和雷达成像技术

陆萍萍，博士，研究员，博士生导师，主要研究方向为微波遥感成像技术、遥感图像智能解译和人工智能应用

朱岱寅，博士，教授，博士生导师，主要研究方向为合成孔径雷达/逆合成孔径雷达(SAR/ISAR)成像以及自聚焦算法、干涉SAR成像、SAR地面动目标指示、以及机载雷达动目标指示技术

通讯作者:
金国栋 jinguodong@nuaa.edu.cn

责任主编：禹卫东 Corresponding Editor: YU Weidong
中图分类号: TN951
计量
- 文章访问数:
- HTML全文浏览量:
- PDF下载量:
- 被引次数: 0
出版历程
- 收稿日期: 2024-10-08
- 修回日期: 2024-11-11
- 网络出版日期: 2024-11-27

A Phase Synchronization Method for Miniature Multistatic FMCW SAR

ZHOU Tao¹,
JIN Guodong^{1, 2
, ,},
LU Pingping^{3, 4},
ZHU Daiyin^{1, 2}

1.
Key Laboratory of Radar Imaging and Microwave Photonics, Ministry of Education, College of Electronic Information Engineering, Nanjing University of Aeronautics and Astronautics, Nanjing 211106, China
2.
Nanjing University of Aeronautics and Astronautics Shenzhen Research Institute, Shenzhen 518000, China
3.
Aerospace Information Research Institute, Chinese Academy of Sciences, Beijing 100190, China
4.
National Key Laboratory of Microwave Imaging, Beijing 100190, China

Funds: The National Natural Science Foundation of China (62101248), The Natural Science Foundation of Jiangsu Province (BK20210282), The Guangdong Basic and Applied Basic Research Foundation (2020B1515120060), The Shenzhen Science and Technology Program (JCYJ20230807142000001), The Fundamental Research Funds for the Central Universities (NT2023008)

More Information

Corresponding author: JING Guodong, jinguodong@nuaa.edu.cn

摘要

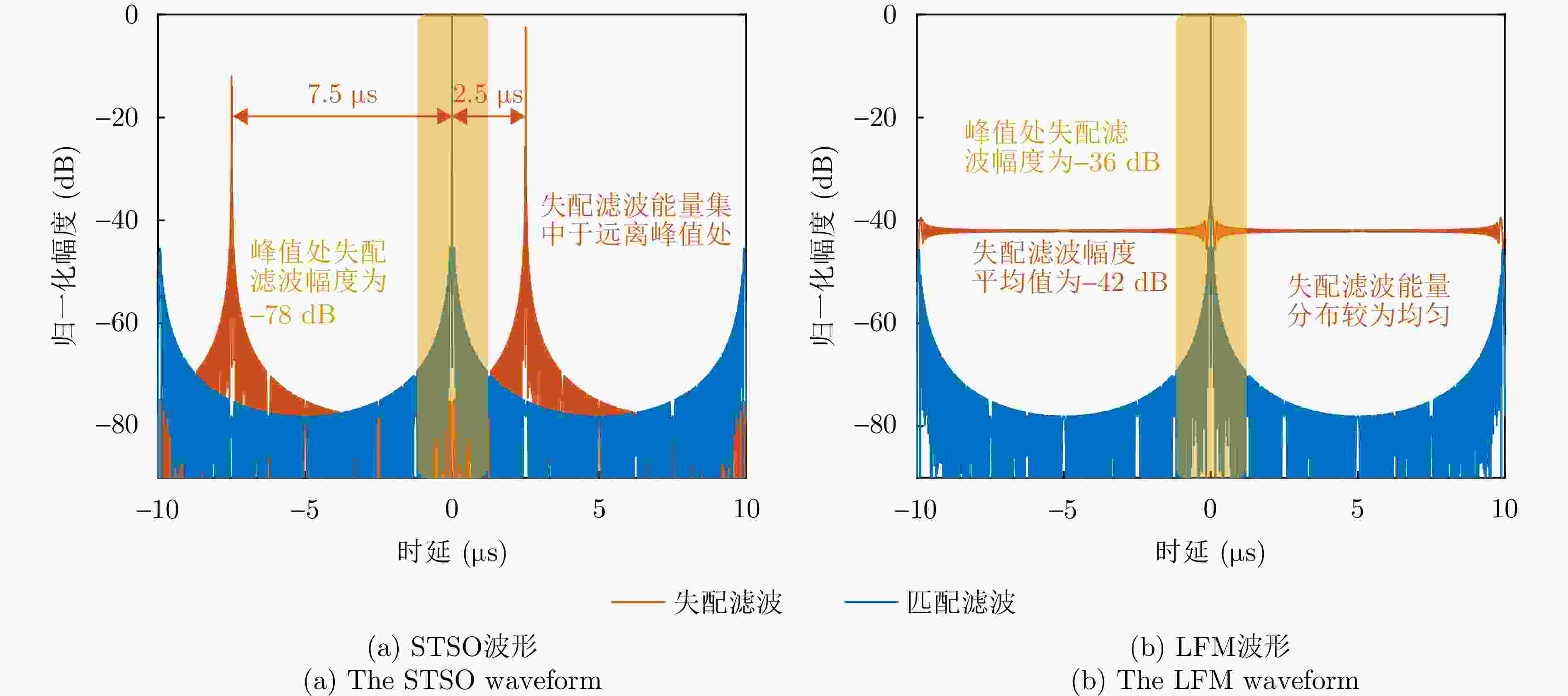
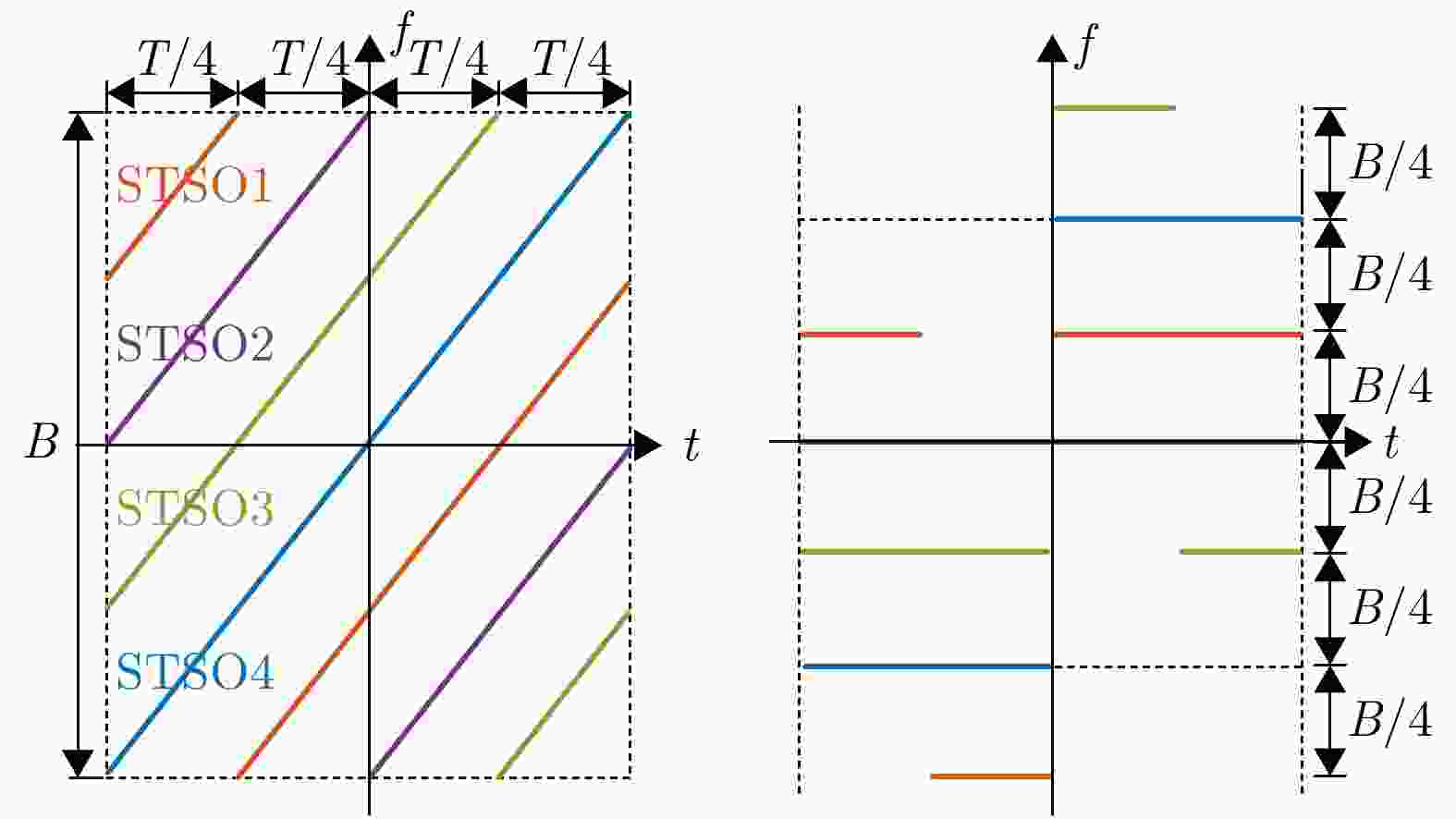
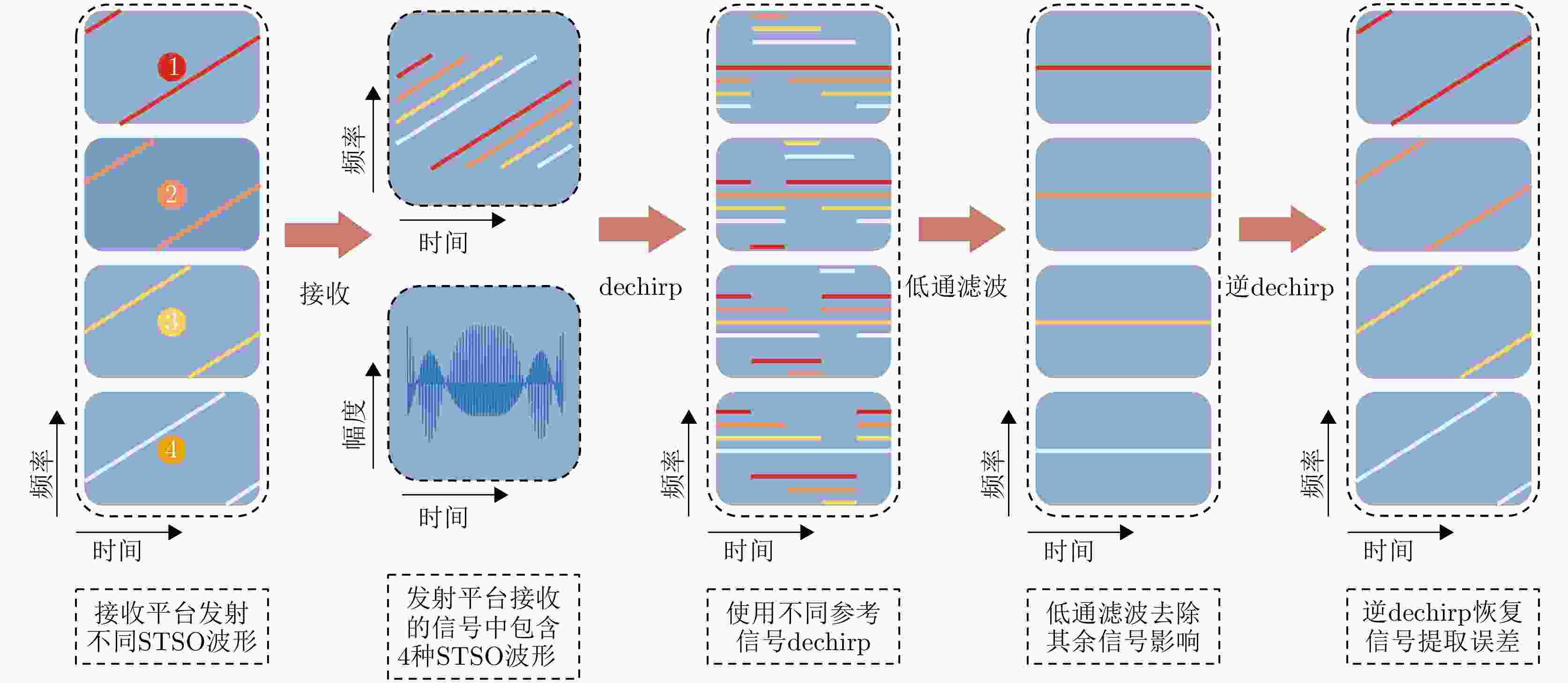
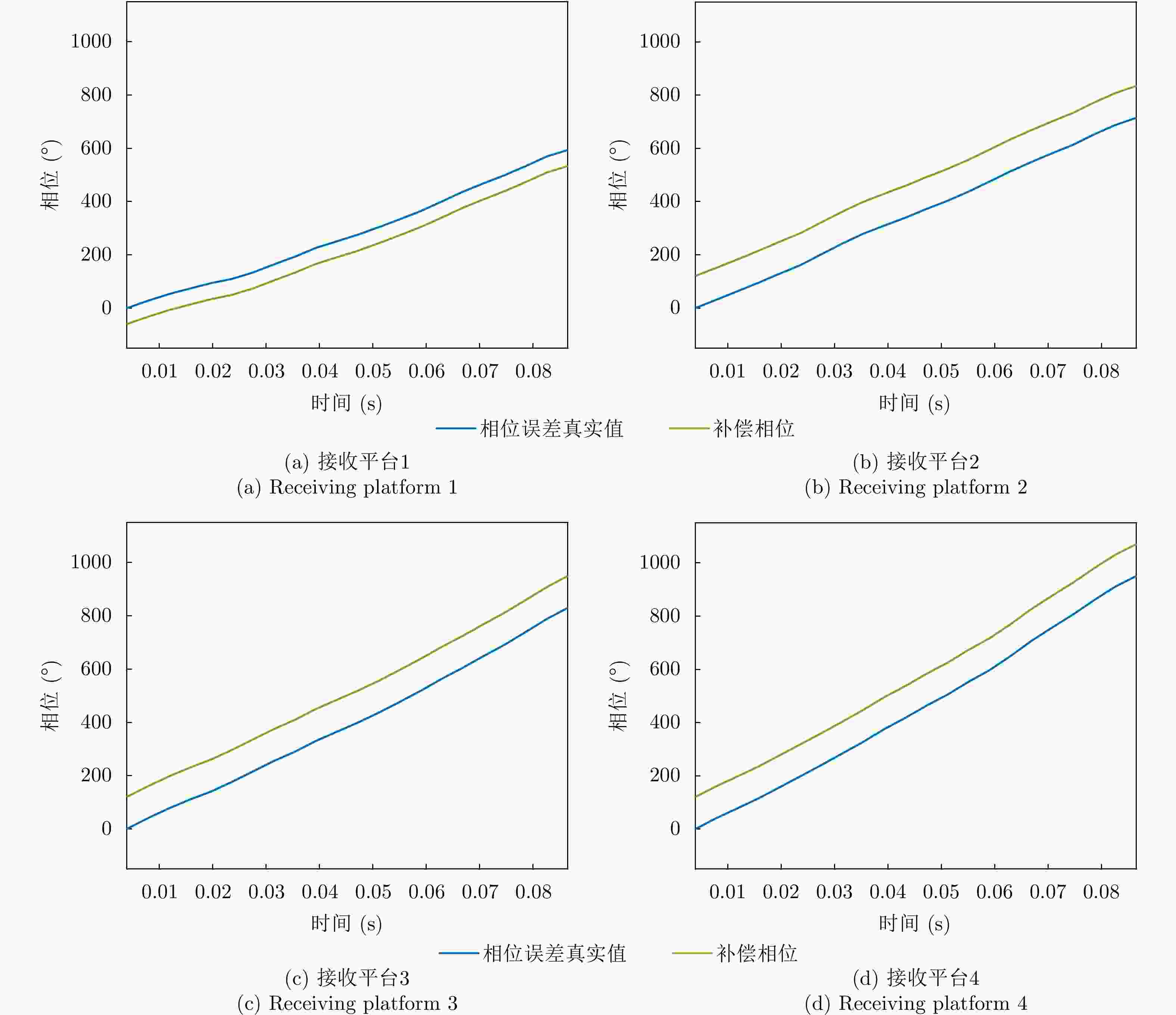
摘要: 相比于微型单基SAR系统，微型多基SAR系统采用收发分置的灵活构型，具备多角度成像等优势。然而，由于微型多基SAR系统需要采用相互独立的振荡源，相位同步是实现微型多基SAR高精度成像的必要条件。当前双基SAR相位同步方案的研究已相对成熟，但这些方案主要基于脉冲体制SAR系统，针对调频连续波(FMCW)体制微型多基SAR系统的相位同步研究仍较为匮乏。与脉冲体制SAR系统相比，FMCW SAR系统的信号连续发射，脉冲间不存在时间间隙，因此部分脉冲体制SAR的相位同步方案无法直接应用于FMCW SAR系统。为此，该文提出了一种适用于FMCW微型多基SAR相位同步方法，旨在有效解决FMCW SAR系统所面临的相位同步难题。该方法采用广义短时正交波形作为不同雷达平台的相位同步信号，通过脉冲压缩技术提取出雷达平台间的相位误差，进而实现相位同步。与传统线性调频波形相比，广义短时正交(STSO)波形在经过相同的脉冲压缩函数处理后，干扰信号的能量会集中于远离匹配信号峰值的位置，从而提高了相位同步的精度。此外，所提方法还适应了FMCW微型多基SAR系统dechirp接收的特点，并通过地面和数值仿真实验验证，所提方法具有较高的同步精度。
- 调频连续波体制微型多基SAR /
- 相位同步 /
- 短时正交信号 /
- 去斜处理 /
- 相位误差补偿
Abstract: The miniature multistatic Synthetic Aperture Radar (SAR) system uses a flexible configuration of transceiver division compared with the miniature monostatic SAR system, thereby affording the advantages of multi-angle imaging. As the transceiver-separated SAR system uses mutually independent oscillator sources, phase synchronization is necessary for high-precision imaging of the miniature multistatic SAR. Although current research on phase synchronization schemes for bistatic SAR is relatively mature, these schemes are primarily based on the pulse SAR system. However, a paucity of research exists on phase synchronization for the miniature multistatic Frequency Modulated Continuous Wave (FMCW) SAR. In comparison with the pulse SAR, the FMCW SAR system lacks a temporal interval between the transmitted pulses. Consequently, some phase synchronization schemes developed for the pulse SAR system cannot be directly applied to the FMCW SAR system. To this end, this study proposes a novel phase synchronization method for the miniature multistatic FMCW SAR, effectively resolving the problem of the FMCW SAR. This method uses the generalized Short-Time Shift-Orthogonal (STSO) waveform as the phase synchronization signal of disparate radar platforms. The phase error between the radar platforms can be effectively extracted through pulse compression to realize phase synchronization. Compared with the conventional linear frequency-modulated waveform, after the generalized STSO waveform is pulsed by the same pulse compression function, the interference signal energy is concentrated away from the peak of the matching signal and the phase synchronization accuracy is enhanced. Furthermore, the proposed method is adapted to the characteristics of dechirp reception in FMCW miniature multistatic SAR systems, and ground and numerical simulation experiments verify that the proposed method has high synchronization accuracy.
- Miniature multistatic FMCW SAR /
- Phase synchronization /
- Short-time shift-orthogonal waveform /
- Dechirp /
- Phase error compensation

HTML全文

图 1 微型双基SAR系统

Figure 1. Miniature bistatic SAR system

下载: 全尺寸图片幻灯片

图 2 本文提出的调频连续波体制微型多基SAR相位同步方法时序图

Figure 2. Timing diagram of the miniature multistatic FMCW SAR phase synchronization method

下载: 全尺寸图片幻灯片

图 3 波形相关属性

Figure 3. The correlation property of waveform

下载: 全尺寸图片幻灯片

图 4 干扰相位同步信号的相位对所需相位同步信号的影响

Figure 4. The influence of the interfering synchronization signal phase on the desired synchronization signal

下载: 全尺寸图片幻灯片

图 5 相位同步精度受雷达平台数目的影响

Figure 5. The influence of the number of radar platforms on the accuracy of phase synchronization

下载: 全尺寸图片幻灯片

图 6 4个STSO波形经$ {s_{{\text{STSO2}}}}(t) $的参考信号dechirp处理结果

Figure 6. The dechirp results of four STSO waveforms processed by $ {s_{{\text{STSO2}}}}(t) $’s reference signal

下载: 全尺寸图片幻灯片

图 7 调频连续波体制微型多基SAR相位同步方法系统框图

Figure 7. Diagram of miniature multistatic FMCW SAR phase synchronization method

下载: 全尺寸图片幻灯片

图 8 试验设备

Figure 8. Experimental setup

下载: 全尺寸图片幻灯片

图 9 各接收平台的误差相位和补偿相位

Figure 9. The error phase and compensation phase for each receiving platform

下载: 全尺寸图片幻灯片

表 1 双基SAR系统参数

Table 1. The parameters of miniature bistatic SAR system

参数	数值
雷达信号载频	9.7 GHz
雷达信号带宽	1800 MHz
脉冲重复频率	525 Hz
最大作用距离	3 km
雷达系统重量	1.6 kg

下载: 导出CSV

表 2 试验参数

Table 2. Simulation parameters

参数	数值
相位同步信号带宽	800 MHz
相位同步信号脉冲宽度	10 μs
发射平台频率偏移	1 Hz
接收平台频率偏移	2 Hz
雷达载频	9.7 GHz
同步频率	525 Hz
收发平台间距	2 km
相位同步信号信噪比	60 dB

下载: 导出CSV

参考文献(26)

[1]	CARRARA W G, GOODMAN R S, and MAJEWSKI R M. Spotlight Synthetic Aperture Radar: Signal Processing Algorithms[M]. Boston: Artech House, 1995.
[2]	杨建宇. 双基地合成孔径雷达技术[J]. 电子科技大学学报, 2016, 45(4): 482–501. doi: 10.3969/j.issn.1001-0548.2016.04.001. YANG Jianyu. Bistatic synthetic aperture radar technology[J]. Journal of University of Electronic Science and Technology of China, 2016, 45(4): 482–501. doi: 10.3969/j.issn.1001-0548.2016.04.001.
[3]	武俊杰, 孙稚超, 杨建宇, 等. 基于GF-3照射的星机双基SAR成像及试验验证[J]. 雷达科学与技术, 2021, 19(3): 241–247. doi: 10.3969/j.issn.1672-2337.2021.03.002. WU Junjie, SUN Zhichao, YANG Jianyu, et al. Spaceborne-airborne bistatic SAR using GF-3 illumination—technology and experiment[J]. Radar Science and Technology, 2021, 19(3): 241–247. doi: 10.3969/j.issn.1672-2337.2021.03.002.
[4]	武俊杰, 孙稚超, 吕争, 等. 星源照射双/多基地SAR成像[J]. 雷达学报, 2023, 12(1): 13–35. doi: 10.12000/JR22213. WU Junjie, SUN Zhichao, LV Zheng, et al. Bi/multi-static synthetic aperture radar using spaceborne illuminator[J]. Journal of Radars, 2023, 12(1): 13–35. doi: 10.12000/JR22213.
[5]	邓云凯, 禹卫东, 张衡, 等. 未来星载SAR技术发展趋势[J]. 雷达学报, 2020, 9(1): 1–33. doi: 10.12000/JR20008. DENG Yunkai, YU Weidong, ZHANG Heng, et al. Forthcoming spaceborne SAR development[J]. Journal of Radars, 2020, 9(1): 1–33. doi: 10.12000/JR20008.
[6]	何友, 蔡复青, 唐小明, 等. 双/多基地SAR发展评述[J]. 雷达科学与技术, 2008, 6(1): 1–8. doi: 10.3969/j.issn.1672-2337.2008.01.001. HE You, CAI Fuqing, TANG Xiaoming, et al. An overview of the development of bistatic/multistatic SAR[J]. Radar Science and Technology, 2008, 6(1): 1–8. doi: 10.3969/j.issn.1672-2337.2008.01.001.
[7]	KRIEGER G. MIMO-SAR: Opportunities and pitfalls[J]. IEEE Transactions on Geoscience and Remote Sensing, 2014, 52(5): 2628–2645. doi: 10.1109/TGRS.2013.2263934.
[8]	杨建宇. 双基合成孔径雷达[M]. 北京: 国防工业出版社, 2017. YANG Jianyu. Bistatic Synthetic Aperture Radar[M]. Beijing: National Defense Industry Press, 2017.
[9]	王燕宇, 张长耀, 王金根. GEO星机双/多基地SAR系统同步探讨[J]. 雷达科学与技术, 2007, 5(5): 353–357, 364. doi: 10.3969/j.issn.1672-2337.2007.05.008. WANG Yanyu, ZHANG Changyao, and WANG Jin'gen. Study on synchronization of bistatic and multistatic SAR systems using GEO and airplane[J]. Radar Science and Technology, 2007, 5(5): 353–357, 364. doi: 10.3969/j.issn.1672-2337.2007.05.008.
[10]	DING Zegang, LI Zhe, WANG Yan, et al. Joint master-slave yaw steering for bistatic spaceborne SAR with an arbitrary configuration[J]. IEEE Geoscience and Remote Sensing Letters, 2021, 18(8): 1426–1430. doi: 10.1109/LGRS.2020.3003334.
[11]	周鹏, 皮亦鸣. 一种新的星机双基地SAR空间同步方法[J]. 遥感技术与应用, 2008, 23(4): 440–445. ZHOU Peng and PI Yiming. A new approach for spatial synchronization in spaceborne/airborne hybrid Bi-static SAR[J]. Remote Sensing Technology and Application, 2008, 23(4): 440–445.
[12]	D’ERRICO M. Distributed Space Missions for Earth System Monitoring[M]. New York: Springer, 2012. doi: 10.1007/978-1-4614-4541-8.
[13]	遆晶晶, 索志勇, 王婷婷, 等. 导航卫星星地双基SAR时频同步误差估计方法[J]. 西安电子科技大学学报, 2023, 50(2): 42–53. doi: 10.19665/j.issn1001-2400.2023.02.005. TI Jingjing, SUO Zhiyong, WANG Tingting, et al. Time-frequency synchronization error estimation method for the satellite-to-ground bistatic SAR for a navigation satellite[J]. Journal of Xidian University, 2023, 50(2): 42–53. doi: 10.19665/j.issn1001-2400.2023.02.005.
[14]	JIN Guodong, LIU Kaiyu, LIU Dacheng, et al. An advanced phase synchronization scheme for LT-1[J]. IEEE Transactions on Geoscience and Remote Sensing, 2020, 58(3): 1735–1746. doi: 10.1109/TGRS.2019.2948219.
[15]	POURRANJBAR A, BANIASADI M, ABBASFAR A, et al. A novel distributed algorithm for phase synchronization in unmanned aerial vehicles[J]. IEEE Communications Letters, 2020, 24(10): 2260–2264. doi: 10.1109/LCOMM.2020.3002859.
[16]	俞根苗, 方志红, 陈仁元, 等. Dechirp及频谱分析技术的目标分辨率分析[J]. 雷达与对抗, 2003, 23(1): 8–12. doi: 10.19341/j.cnki.issn.1009-0401.2003.01.003. YU Genmiao, FANG Zhihong, CHEN Renyuan, et al. Analysis of resolution of Dechirp and spectral analysis technology[J]. Radar & ECM, 2003, 23(1): 8–12. doi: 10.19341/j.cnki.issn.1009-0401.2003.01.003.
[17]	YOUNIS M, METZIG R, and KRIEGER G. Performance prediction of a phase synchronization link for bistatic SAR[J]. IEEE Geoscience and Remote Sensing Letters, 2006, 3(3): 429–433. doi: 10.1109/LGRS.2006.874163.
[18]	YOUNIS M, METZIG R, KRIEGER G, et al. Performance prediction and verification for the synchronization link of TanDEM-X[C]. 2007 IEEE International Geoscience and Remote Sensing Symposium, Barcelona, Spain, 2007: 5206–5209. doi: 10.1109/IGARSS.2007.4424035.
[19]	LIANG Da, LIU Kaiyu, ZHANG Heng, et al. The processing framework and experimental verification for the noninterrupted synchronization scheme of LuTan-1[J]. IEEE Transactions on Geoscience and Remote Sensing, 2021, 59(7): 5740–5750. doi: 10.1109/TGRS.2020.3024561.
[20]	LIANG Da, LIU Kaiyu, YUE Haixia, et al. An advanced non-interrupted synchronization scheme for bistatic synthetic aperture radar[C]. IGARSS 2019 - 2019 IEEE International Geoscience and Remote Sensing Symposium, Yokohama, Japan, 2019: 1116–1119. doi: 10.1109/IGARSS.2019.8900103.
[21]	LIANG Da, ZHANG Heng, LIU Kaiyu, et al. Phase synchronization techniques for bistatic and multistatic synthetic aperture radar: Accounting for frequency offset[J]. IEEE Geoscience and Remote Sensing Magazine, 2022, 10(3): 153–167. doi: 10.1109/MGRS.2022.3189005.
[22]	LIANG Da, ZHANG Heng, CAI Yonghua, et al. An advanced phase synchronization scheme based on coherent integration and waveform diversity for bistatic SAR[J]. Remote Sensing, 2021, 13(5): 981. doi: 10.3390/rs13050981.
[23]	RUTMAN J. Characterization of phase and frequency instabilities in precision frequency sources: Fifteen years of progress[J]. Proceedings of the IEEE, 1978, 66(9): 1048–1075. doi: 10.1109/PROC.1978.11080.
[24]	KRIEGER G, CASSOLA M R, YOUNIS M, et al. Impact of oscillator noise in bistatic and multistatic SAR[C]. 2005 IEEE International Geoscience and Remote Sensing Symposium, Seoul, Korea (South), 2005: 1043–1046. doi: 10.1109/IGARSS.2005.1525293.
[25]	JIN Guodong, ZHANG Xifeng, HUANG Jingkai, et al. High freedom parameterized FM (HFPFM) code: Model, correlation function, and advantages[J]. IEEE Transactions on Aerospace and Electronic Systems, 2024, 60(5): 6284–6298. doi: 10.1109/TAES.2024.3405449.
[26]	LIU Jiafang, ZHANG Yunhua, and DONG Xiao. Dechirping compression method for nonlinear frequency modulation waveforms[J]. IEEE Geoscience and Remote Sensing Letters, 2019, 16(3): 377–381. doi: 10.1109/LGRS.2018.2875893.