作者中心
专家审稿
责编办公
编辑办公
Transient Interference Suppression Algorithm Based on Time Frequency Sparse Prior for Skywave OTHR
-
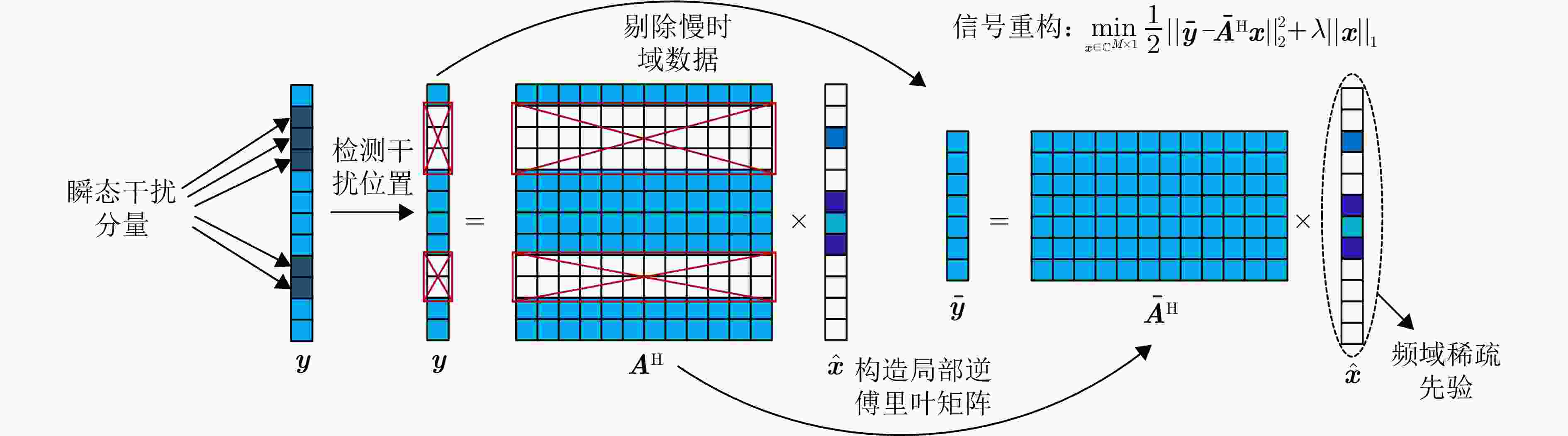
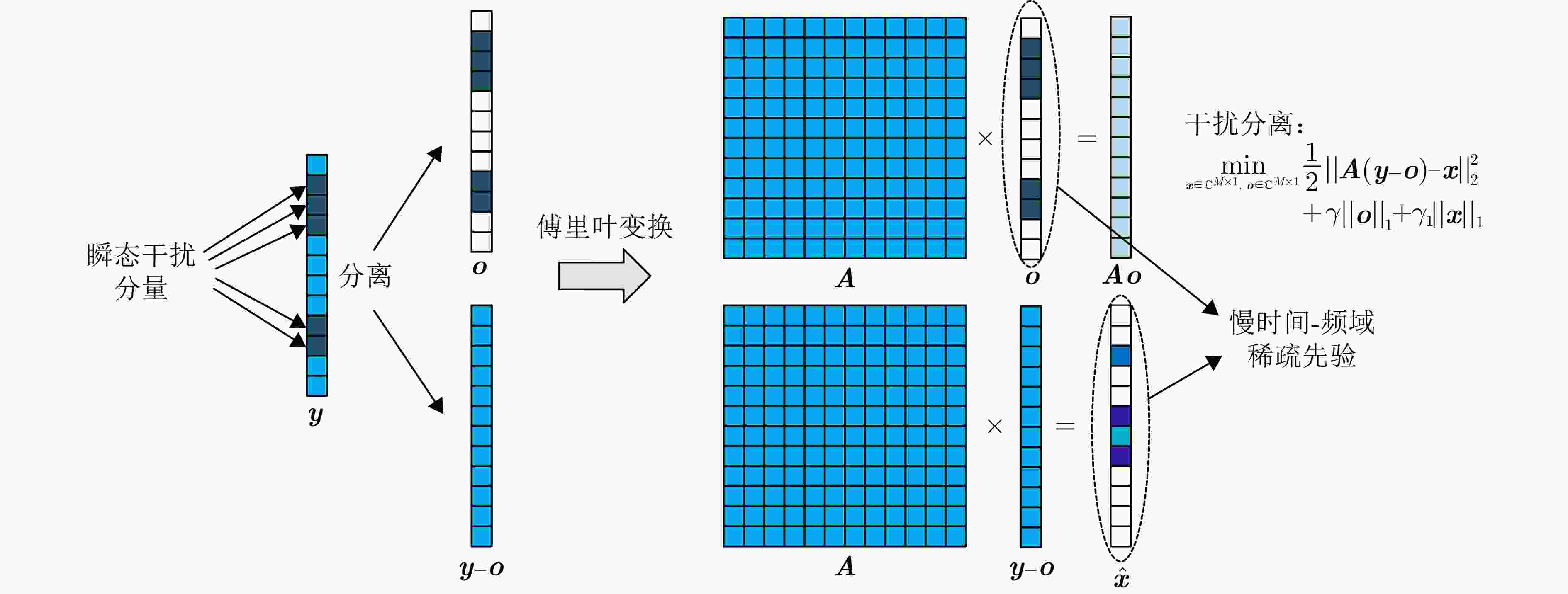
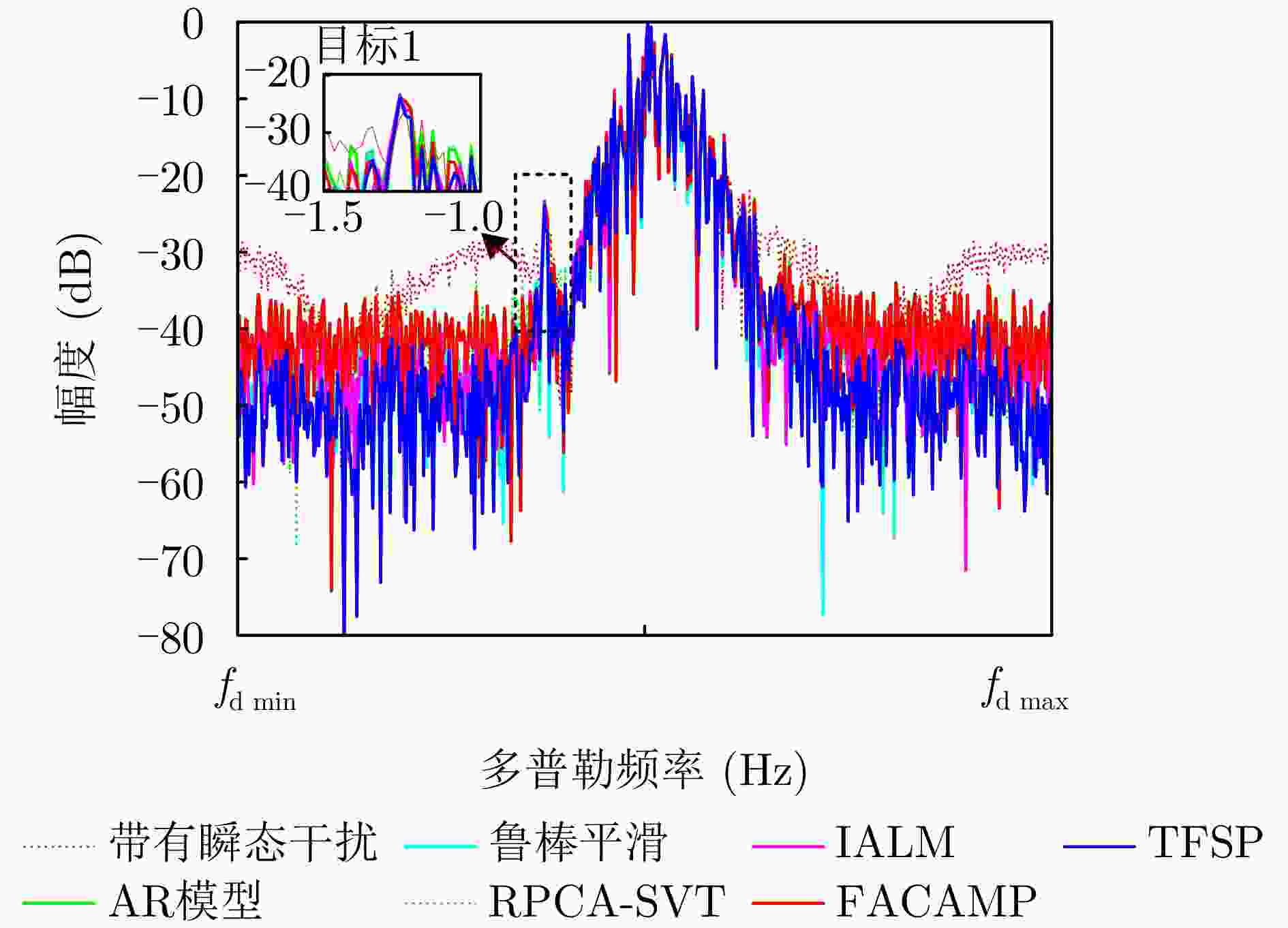
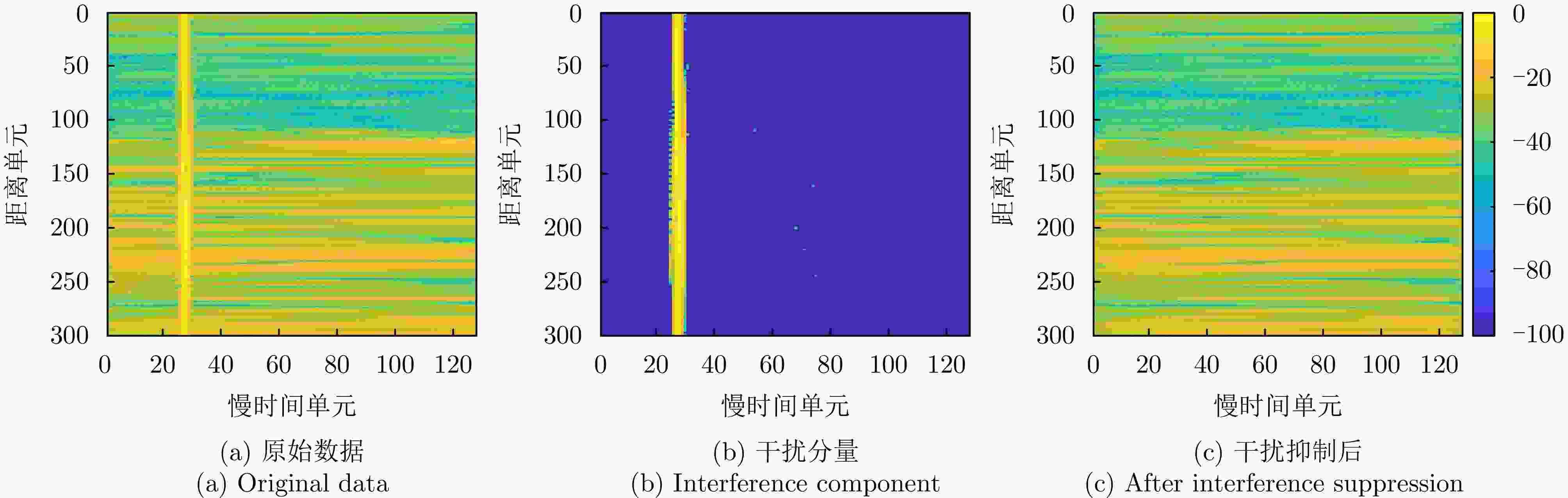
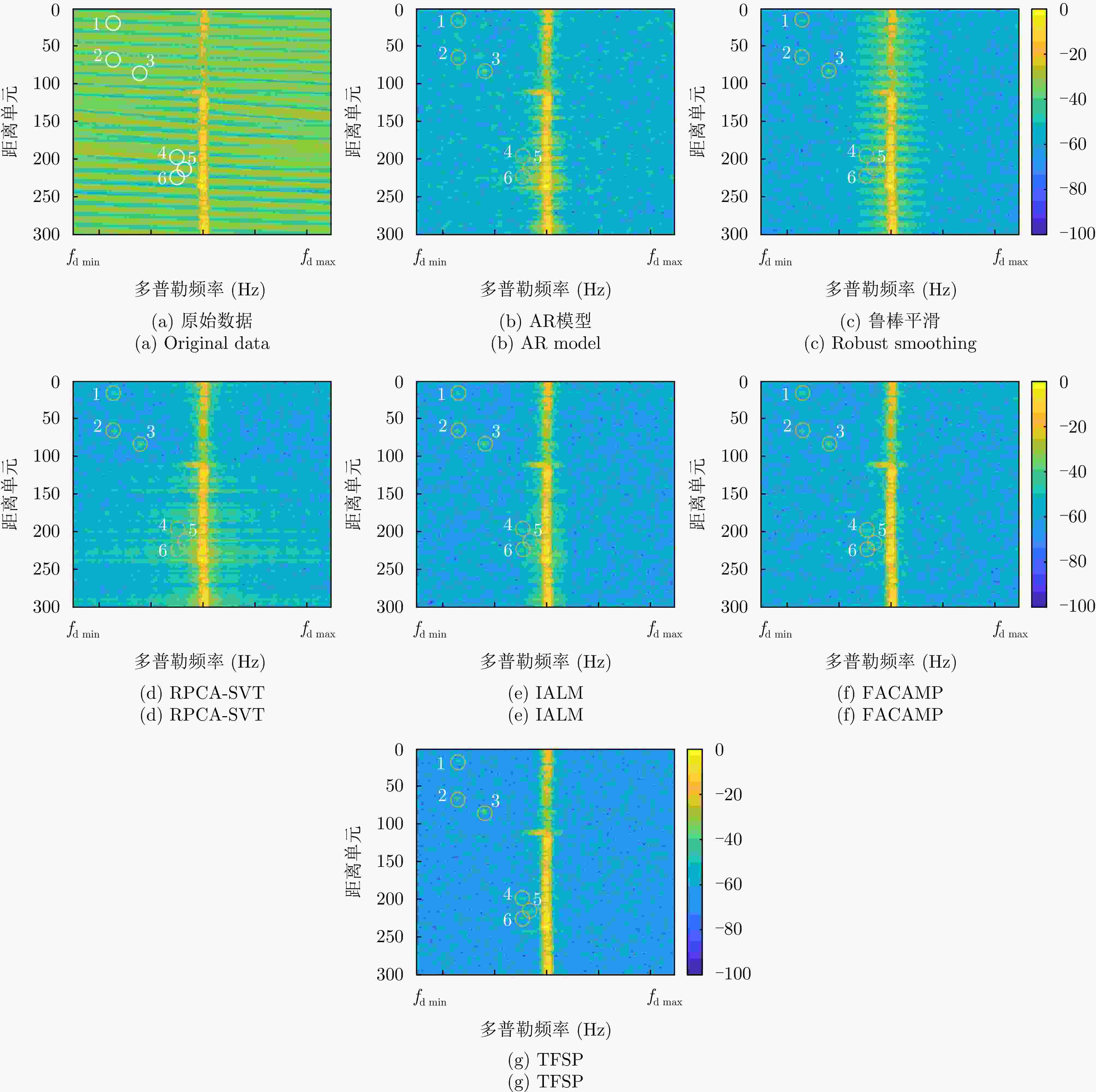
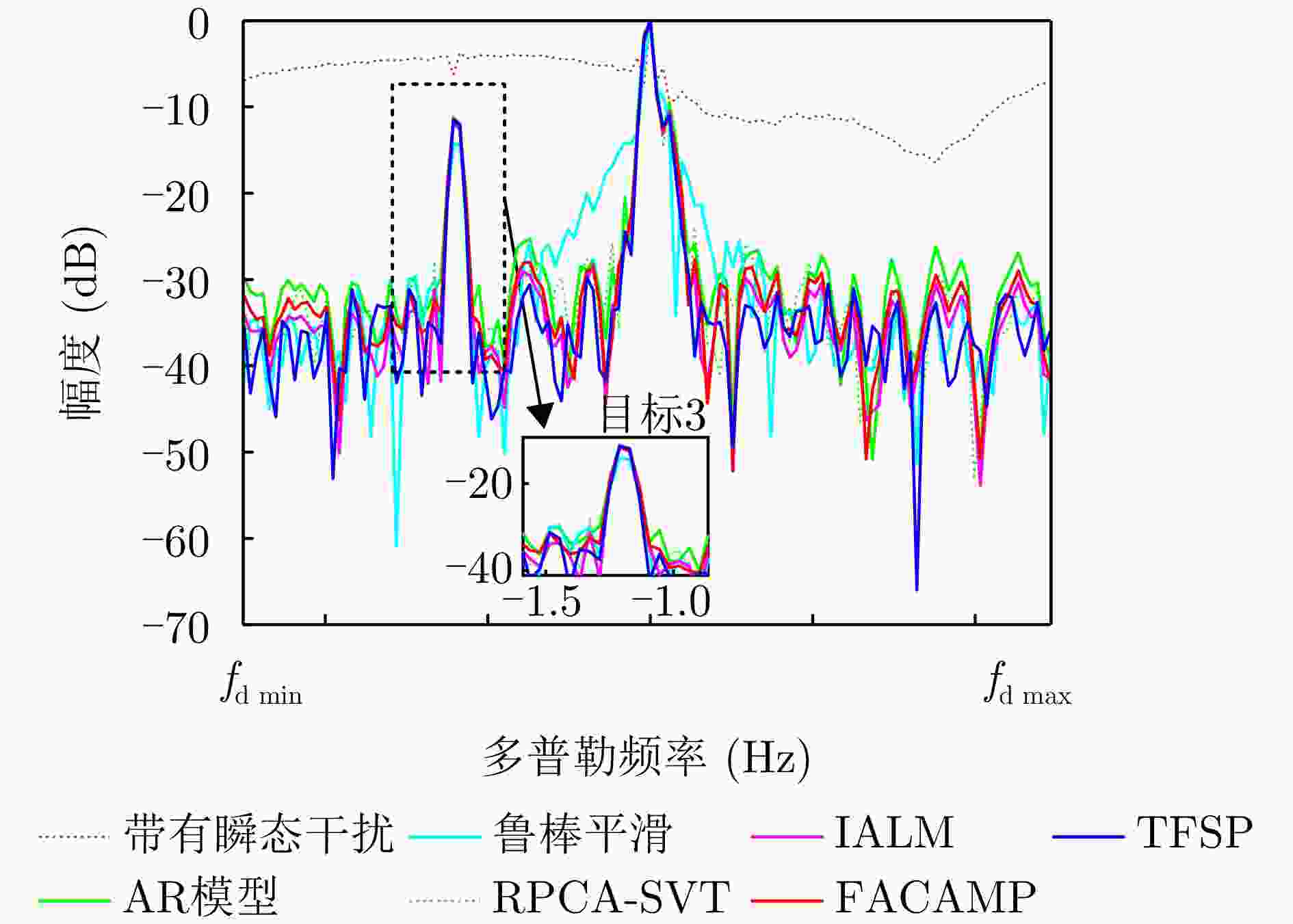
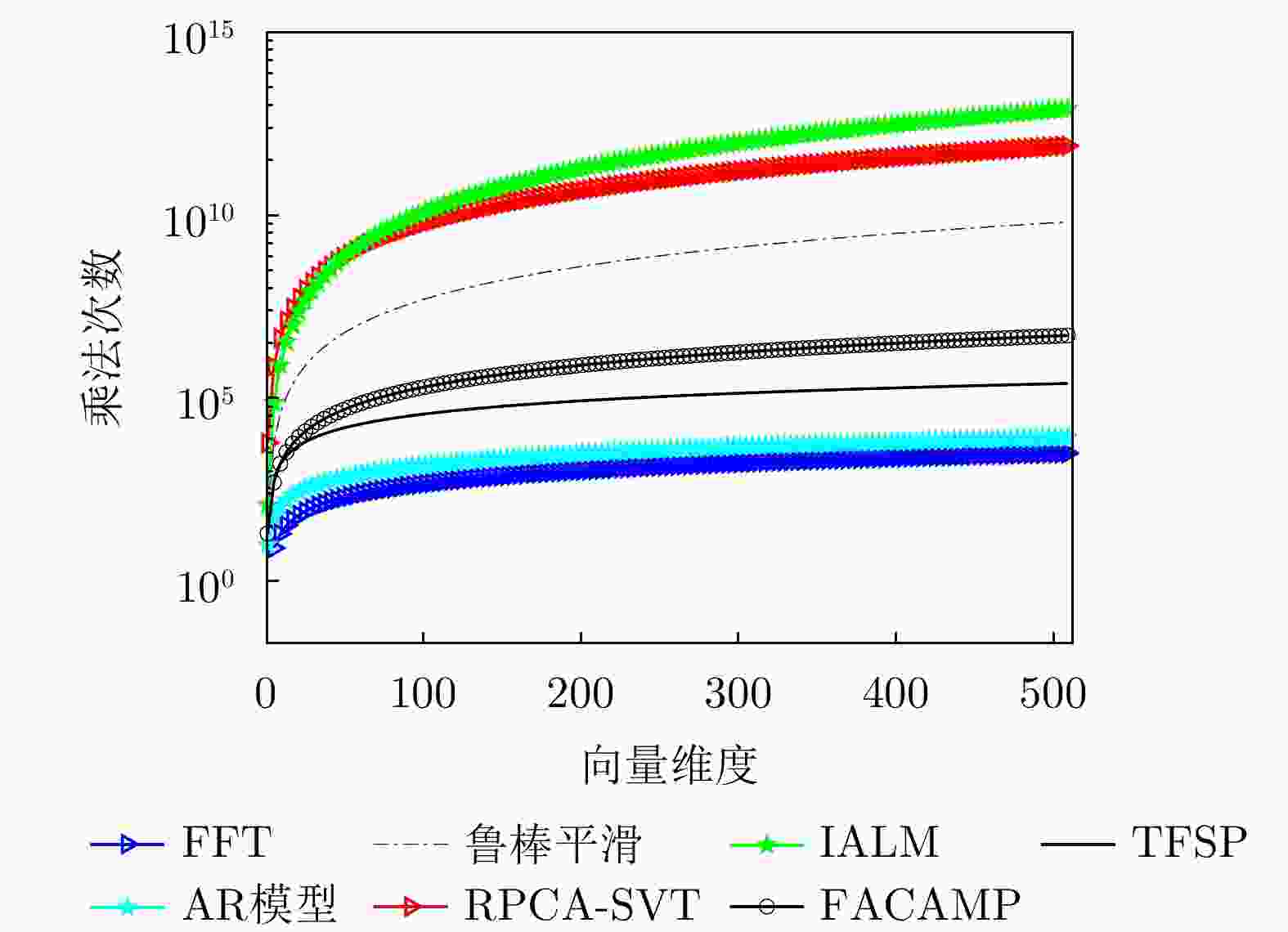
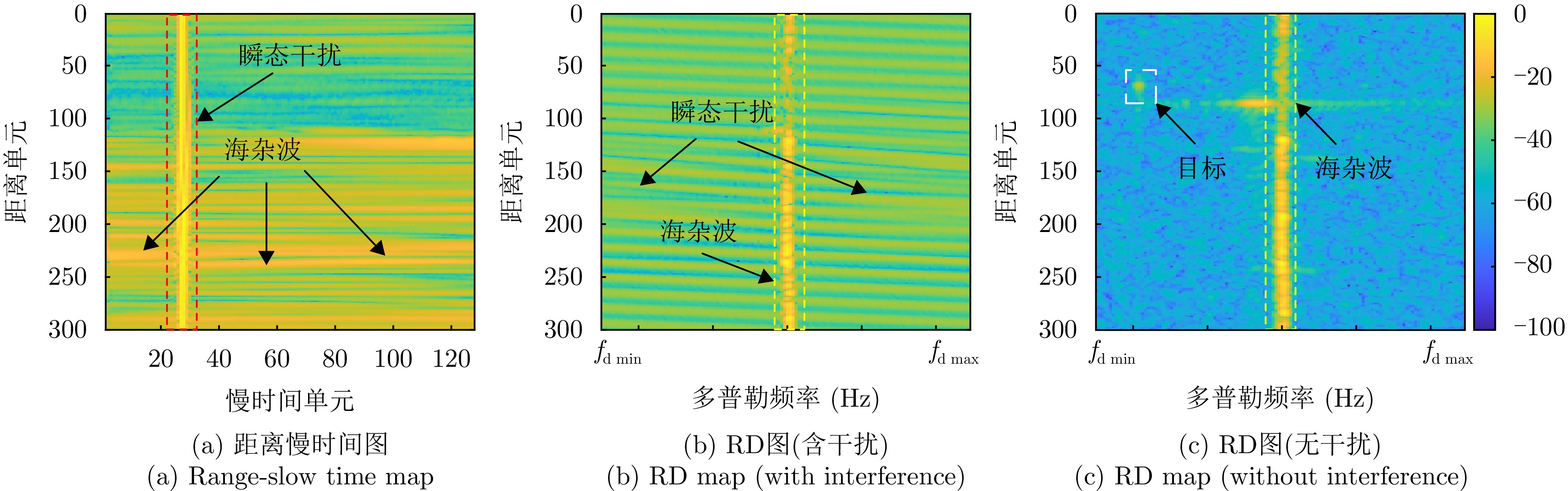
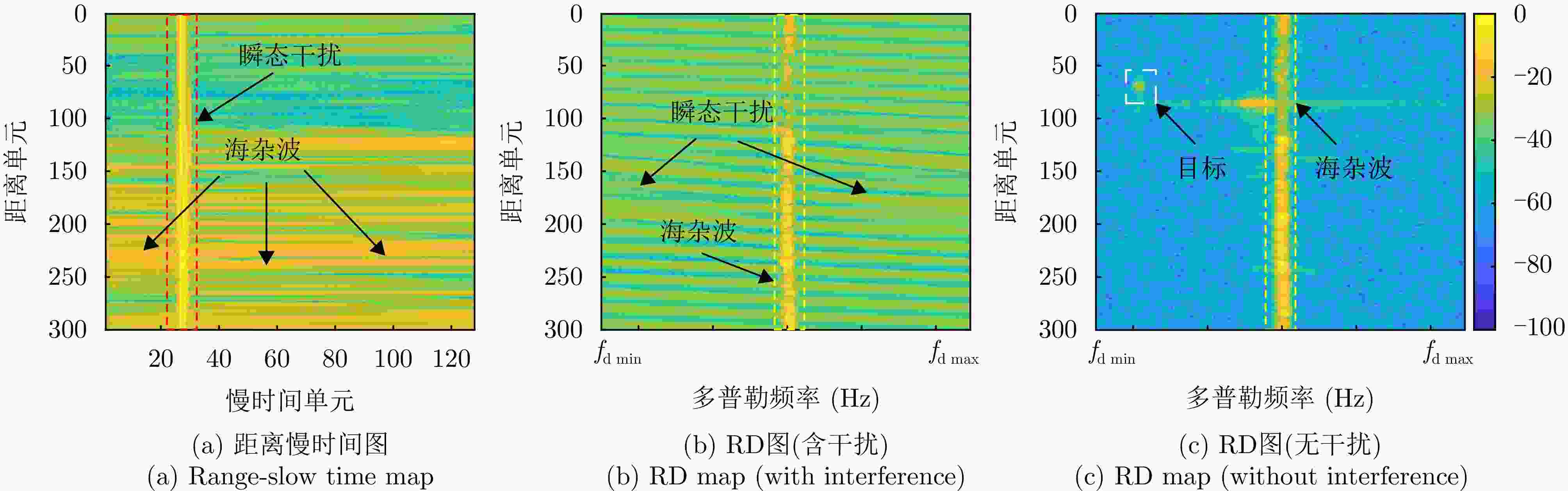
摘要: 针对瞬态干扰严重影响天波超视距雷达(OTHR)目标检测性能的问题，提出了一种基于时频稀疏先验(TFSP)的瞬态干扰抑制算法。TFSP同时利用了瞬态干扰在慢时域的稀疏先验以及海杂波和目标在多普勒频域的稀疏先验构造目标函数，通过交替方向乘子法(ADMM)进行最优化以实现瞬态干扰抑制。不同于现有算法“干扰定位—剔除—数据恢复”的处理步骤，TFSP能够直接分离瞬态干扰分量并恢复无干扰频谱。最后，通过OTHR实测数据实验验证了TFSP在对海和对空模式下均能得到良好的瞬态干扰抑制结果，相比于多数现有方法，TFSP具有更高的输出信噪比(SNR)以及更高的运算效率，其输出SNR增加了3～5 dB，运算复杂度仅为线性对数阶。Abstract: The target detection performance of skywave Over-the-Horizon Radar (OTHR) often struggles with transient interference. To address this issue, we have developed a transient interference suppression algorithm that uses Time Frequency Sparsity Prior (TFSP). TFSP uses the sparse nature of transient interference in the slow-time domain along with the sparse prior of sea clutter and targets in the Doppler frequency domain to construct an objective function, that is optimized using the Alternating Direction Method of Multipliers (ADMM) to effectively suppress transient interference. Unlike traditional methods that focus on locating and eliminating interference before recovering data, TFSP can directly separate transient interference components and restore an interference-free Doppler spectrum. Experimental results from OTHR data confirm that TFSP effectively suppresses transient interference in sea and air modes. TFSP offers a higher output Signal-to-Noise Ratio (SNR) and higher computational efficiency than most existing methods. In particular, it increases the output SNR by approximately 3～5 dB while maintaining computational complexity at a linear logarithmic order.
-
图 2 CS瞬态干扰抑制方法示意图
Figure 2. Schematic diagram of CS transient interference suppression method
图 3 TFSP瞬态干扰抑制方法示意图
Figure 3. Schematic diagram of TFSP transient interference suppression method
图 4 两种探测模式下改变$ {\gamma _1} $与$ \gamma $的NMSE
Figure 4. NMSE when changing $ {\gamma _1} $ and $ \gamma $ in two detection modes
图 5 对海模式下慢时域TFSP瞬态干扰抑制结果
Figure 5. Sea mode TFSP interference suppression result in slow time domain
图 6 对海模式下各算法RD域瞬态干扰抑制结果
Figure 6. Sea mode transient interference suppression results of each algorithm in RD domain
图 7 对海模式下各算法多普勒域瞬态干扰抑制结果
Figure 7. Sea mode transient interference suppression results of each algorithm in Doppler domain
图 8 对空模式下慢时域TFSP瞬态干扰抑制结果
Figure 8. Air mode TFSP interference suppression result in slow time domain
图 9 对空模式下各算法RD域瞬态干扰抑制结果
Figure 9. Air mode transient interference suppression results of each algorithm in RD domain
图 10 对空模式下各算法多普勒域瞬态干扰抑制结果
Figure 10. Air mode transient interference suppression results of each algorithm in Doppler domain
图 11 乘法次数随向量维度变化的曲线
Figure 11. The curve of multiplication times changing with vector dimension
1 TFSP算法
1. TFSP algorithm
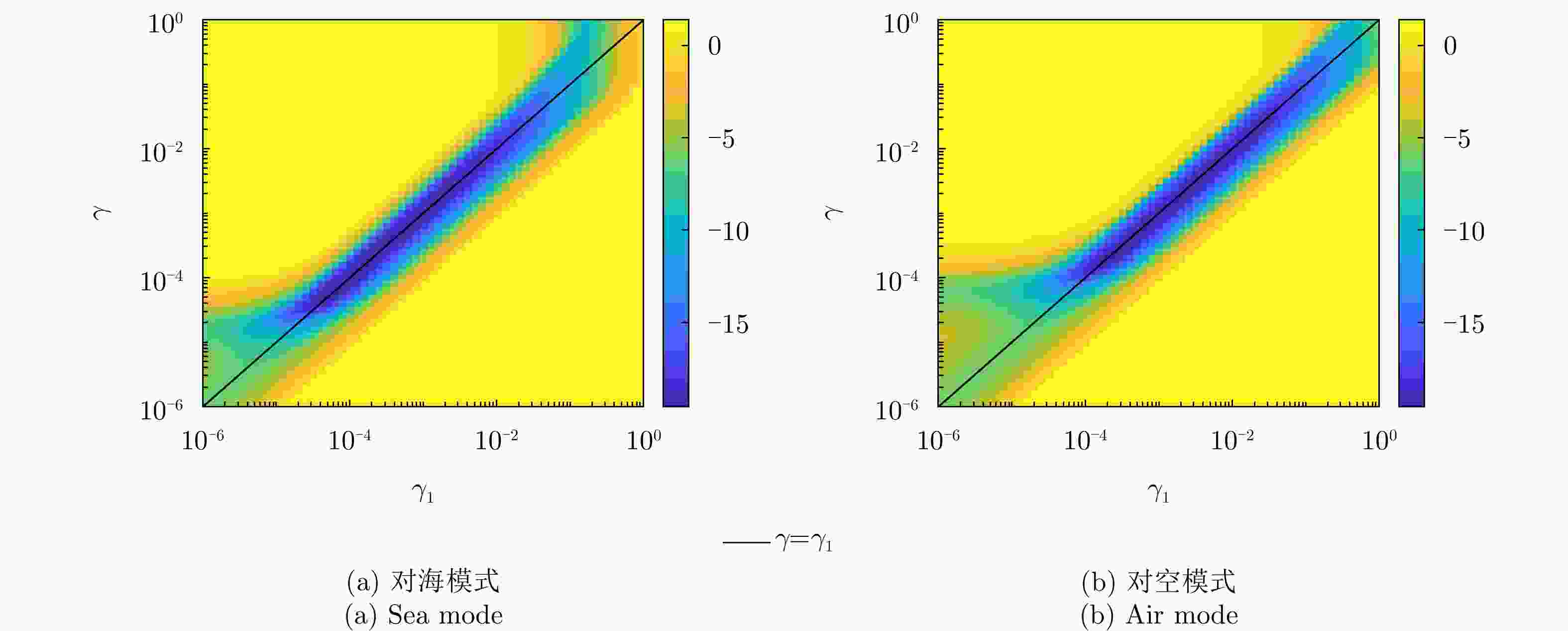
输入：受瞬态干扰的慢时域信号y、参数$\gamma $, ${\gamma _1}$, $\rho = 0.1$，最大
迭代次数$K = 100$；输出：慢时域瞬态干扰分量o、纯净频谱x； 初始化：初始向量$ {\boldsymbol{o}} = {\bf{0}} $, $ {\boldsymbol{x}} = {\bf{0}} $, $ {\boldsymbol{n}} = {\bf{0}} $, $ {\boldsymbol{b}} = {\bf{0}} $，中间变量
$ {\boldsymbol{u}} = {\bf{0}} $，初始化迭代次数$k = 1$；执行迭代$k = 1,2, \cdots ,K$ 计算梯度$ \nabla {g^k}\left( {\boldsymbol{o}} \right) = {{\boldsymbol{o}}^k} - {\boldsymbol{y}} + \sqrt M {\mathrm{IFFT}}\left( {{{\boldsymbol{x}}^k} + {{\boldsymbol{n}}^k} - {{\boldsymbol{b}}^k}/\rho } \right) $； 通过式(18)更新$ {{\boldsymbol{o}}^{k + 1}} $； 更新中间变量$ {{\boldsymbol{u}}^{k + 1}} = {\mathrm{FFT}}\left( {{\boldsymbol{y}} - {{\boldsymbol{o}}^{k + 1}}} \right)/\sqrt M $ 更新$ {{\boldsymbol{x}}^{k + 1}} = {\mathcal{P}_{\left( {{\gamma _1}/\rho } \right){\ell _1}}}\left( {{{\boldsymbol{u}}^{k + 1}} - {{\boldsymbol{n}}^k} + {{\boldsymbol{b}}^k}/\rho } \right) $； 更新$ {{\boldsymbol{n}}^{k + 1}} = \left( {{{\boldsymbol{b}}^k} + \rho \left( {{{\boldsymbol{u}}^{k + 1}} - {{\boldsymbol{x}}^{k + 1}}} \right)} \right)/\left( {\rho + 1} \right) $； 更新$ {{\boldsymbol{b}}^{k + 1}} = {{\boldsymbol{b}}^k} + \tau \rho \left( {{{\boldsymbol{u}}^{k + 1}} - {{\boldsymbol{x}}^{k + 1}} - {\boldsymbol{{n}}^{k + 1}}} \right) $； 更新迭代次数$k = k + 1$； 当满足$k > K$或$\left\| {{{\boldsymbol{x}}^{k + 1}} - {{\boldsymbol{x}}^k}} \right\|_2^2/\left\| {{{\boldsymbol{x}}^k}} \right\|_2^2 < {10^{ - 6}}$时； 停止迭代 
下载: 导出CSV
表 1 各算法的运行时间(s)
Table 1. Running time of each algorithm (s)
算法 对海模式的运行时间 对空模式的运行时间 FFT(对比) 0.021 0.007 AR模型 0.13 0.05 鲁棒平滑 572.51 3.27 PRCA-SVT 3252.78 42.03 IALM 15521.43 73.24 FACAMP 17.51 0.87 TFSP 3.42 0.72
下载: 导出CSV
-
[1] 周文瑜, 焦培南. 超视距雷达技术[M]. 北京: 电子工业出版社, 2008: 6–10.ZHOU Wenyu and JIAO Peinan. Technology for Over the Horizon Radar[M]. Beijing: Publishing House of Electronics Industry, 2008: 6–10. [2] FABRIZIO G, HOLDSWORTH D, WARD B, et al. Evolution of over-the-horizon radar in Australia from humble origins to operational capabilities[J]. IEEE Aerospace and Electronic Systems Magazine, 2023, 38(1): 38–52. doi: 10.1109/MAES.2022.3224095. [3] CHEN Zirui, CHEN Alei, LIU Weijian, et al. A sea clutter suppression algorithm for over-the-horizon radar based on dictionary learning and subspace estimation[J]. Digital Signal Processing, 2023, 140: 104131. doi: 10.1016/j.dsp.2023.104131. [4] CHEN Zirui, CHEN Alei, LIU Weijian, et al. CFAR detection in nonhomogeneous Weibull sea clutter for skywave OTHR[J]. IEEE Geoscience and Remote Sensing Letters, 2023, 20: 3508005. doi: 10.1109/LGRS.2023.3313179. [5] 陈希信. 天波雷达后多普勒自适应波束形成[J]. 雷达学报, 2016, 5(4): 373–377. doi: 10.12000/JR15124.CHEN Xixin. Post-Doppler adaptive digital beamforming of skywave radar[J]. Journal of Radars, 2016, 5(4): 373–377. doi: 10.12000/JR15124. [6] 阳云龙, 毛兴鹏, 董英凝, 等. 高频地波雷达电离层杂波的空域极化域协同抑制方法[J]. 雷达学报, 2016, 5(6): 673–680. doi: 10.12000/JR16024.YANG Yunlong, MAO Xingpeng, DONG Yingning, et al. Space-polarization collaborative suppression method for ionospheric clutter in HFSWR[J]. Journal of Radars, 2016, 5(6): 673–680. doi: 10.12000/JR16024. [7] LIU Ziwei, SU Hongtao, HU Qinzhen, et al. Computationally efficient transient interference excision method for skywave over-the-horizon radar[J]. IEEE Geoscience and Remote Sensing Letters, 2016, 13(7): 1017–1021. doi: 10.1109/LGRS.2016.2560943. [8] LEI Zhenshuo, ZHANG Zhaojian, ZHOU Bilei, et al. Transient interference suppression method based on an improved TK energy operator and fuzzy reasoning[J]. IEEE Transactions on Geoscience and Remote Sensing, 2023, 61: 5106214. doi: 10.1109/TGRS.2023.3287280. [9] ZHANG Beiqiang, XIE Junhao, SUN Minglei, et al. Impulsive noise excision using robust smoothing[J]. IEEE Geoscience and Remote Sensing Letters, 2022, 19: 8015205. doi: 10.1109/LGRS.2021.3093257. [10] 刘子威, 苏洪涛, 胡勤振. 天波超视距雷达中瞬态干扰定位方法研究[J]. 电子与信息学报, 2016, 38(10): 2482–2487. doi: 10.11999/JEIT151475.LIU Ziwei, SU Hongtao, and HU Qinzhen. Transient interference localization method in the skywave over-the-horizon radar[J]. Journal of Electronics & Information Technology, 2016, 38(10): 2482–2487. doi: 10.11999/JEIT151475. [11] 邢孟道, 保铮, 强勇. 天波超视距雷达瞬态干扰抑制[J]. 电子学报, 2002, 30(6): 823–826. doi: 10.3321/j.issn:0372-2112.2002.06.014.XING Mengdao, BAO Zheng, and QIANG Yong. Transient interference excision in OTHR[J]. Acta Electronica Sinica, 2002, 30(6): 823–826. doi: 10.3321/j.issn:0372-2112.2002.06.014. [12] TURLEY M. Impulsive noise rejection in HF radar using a linear prediction technique[C]. 2003 Proceedings of the International Conference on Radar, Adelaide, Australia, 2003: 358–362. doi: 10.1109/RADAR.2003.1278767. [13] LUO Zhongtao, SONG Tiecheng, HE Zishu, et al. Approach for transient interference detection based on straight line extraction for high-frequency sky-wave radar[J]. Electronics Letters, 2017, 53(9): 618–620. doi: 10.1049/el.2016.4125. [14] GUO Xin, SUN Hongbo, and YEO T S. Transient interference excision in over-the-horizon radar using adaptive time-frequency analysis[J]. IEEE Transactions on Geoscience and Remote Sensing, 2005, 43(4): 722–735. doi: 10.1109/TGRS.2005.844291. [15] 权太范, 李健巍, 于长军, 等. 高频雷达抑制冲击干扰的研究与实验[J]. 电子学报, 1999, 27(12): 23–25. doi: 10.3321/j.issn:0372-2112.1999.12.007.QUAN Taifan, LI Jianwei, YU Changjun, et al. An approach and experiment of suppressing burst interference in high-frequency radar[J]. Acta Electronica Sinica, 1999, 27(12): 23–25. doi: 10.3321/j.issn:0372-2112.1999.12.007. [16] ZHANG Baiqiang, XIE Junhao, and ZHOU Wei. Robust low-rank Hankel matrix recovery for skywave radar slow-time samples[J]. IET Radar, Sonar & Navigation, 2021, 15(6): 581–591. doi: 10.1049/rsn2.12074. [17] AI Xiaofan, LUO Yongjiang, and ZHAO Guoqing. Transient interference excision in over-the-horizon radar by robust principal component analysis with a structured matrix[J]. IEEE Geoscience and Remote Sensing Letters, 2016, 13(1): 48–52. doi: 10.1109/LGRS.2015.2496223. [18] LI Mao, HE Zishu, and LI Wencai. Transient interference mitigation via supervised matrix completion[J]. IEEE Geoscience and Remote Sensing Letters, 2016, 13(7): 907–911. doi: 10.1109/LGRS.2016.2553082. [19] 李茂, 何子述. 基于矩阵补全的天波雷达瞬态干扰抑制算法[J]. 电子与信息学报, 2015, 37(5): 1031–1037. doi: 10.11999/JEIT140973.LI Mao and HE Zishu. Sky-wave radar transient interference suppression based on matrix completion[J]. Journal of Electronics & Information Technology, 2015, 37(5): 1031–1037. doi: 10.11999/JEIT140973. [20] 全英汇, 张磊, 邢孟道, 等. 天波超视距雷达缺损信号的频谱重构[J]. 系统工程与电子技术, 2011, 33(8): 1732–1737. doi: 10.3969/j.issn.1001-506X.2011.08.11.QUAN Yinghui, ZHANG Lei, XING Mengdao, et al. Optimal reconstruction of spectrum with partial samples in OTHR[J]. Systems Engineering and Electronics, 2011, 33(8): 1732–1737. doi: 10.3969/j.issn.1001-506X.2011.08.11. [21] 陈子睿, 陈阿磊, 刘维建, 等. 天波超视距雷达非均匀采样信号频谱重构[J]. 系统工程与电子技术, 2024, 46(4): 1236–1246. doi: 10.12305/j.issn.1001-506X.2024.04.12.CHEN Zirui, CHEN Alei, LIU Weijian, et al. Spectrum reconstruction of nonuniformly sampled signals for over-the-horizon radar[J]. Systems Engineering and Electronics, 2024, 46(4): 1236–1246. doi: 10.12305/j.issn.1001-506X.2024.04.12. [22] CHEN Zirui, CHEN Alei, LIU Weijian, et al. An improved fast adaptive complex approximation message passing algorithm[J]. Digital Signal Processing, 2023, 137: 104016. doi: 10.1016/j.dsp.2023.104016. [23] CHEN Zirui, CHEN Alei, LIU Weijian, et al. Transient interference suppression based on minimax concave penalty for OTHR[J]. IEEE Geoscience and Remote Sensing Letters, 2024, 21: 3500905. doi: 10.1109/LGRS.2023.3342935. [24] CROMBIE D D. Doppler spectrum of sea echo at 13.56 Mc./s.[J]. Nature, 1955, 175(4459): 681–682. doi: 10.1038/175681a0. [25] AHMED A, ZHANG Y D, and HIMED B. Joint target and ionosphere parameter estimation in over-the-horizon radar[J]. IEEE Transactions on Aerospace and Electronic Systems, 2022, 58(5): 4361–4376. doi: 10.1109/TAES.2022.3161396. [26] XU Huan, CARAMANIS C, and SANGHAVI S. Robust PCA via outlier pursuit[J]. IEEE Transactions on Information Theory, 2012, 58(5): 3047–3064. doi: 10.1109/TIT.2011.2173156. [27] YANG Junfeng and ZHANG Yin. Alternating direction algorithms for ${\ell _1}$-problems in compressive sensing[J]. SIAM Journal on Scientific Computing, 2011, 33(1): 250–278. doi: 10.1137/090777761. [28] ZHANG Xiaoqun, BURGER M, and OSHER S. A unified primal-dual algorithm framework based on Bregman iteration[J]. Journal of Scientific Computing, 2011, 46(1): 20–46. doi: 10.1007/s10915-010-9408-8. -
计量
- 文章访问数: 89
- HTML全文浏览量: 34
- PDF下载量: 22
- 被引次数: 0
