作者中心
专家审稿
责编办公
编辑办公
Sparse DOA Estimation Method Based on Riemann Averaging under Strong Intermittent Jamming
-
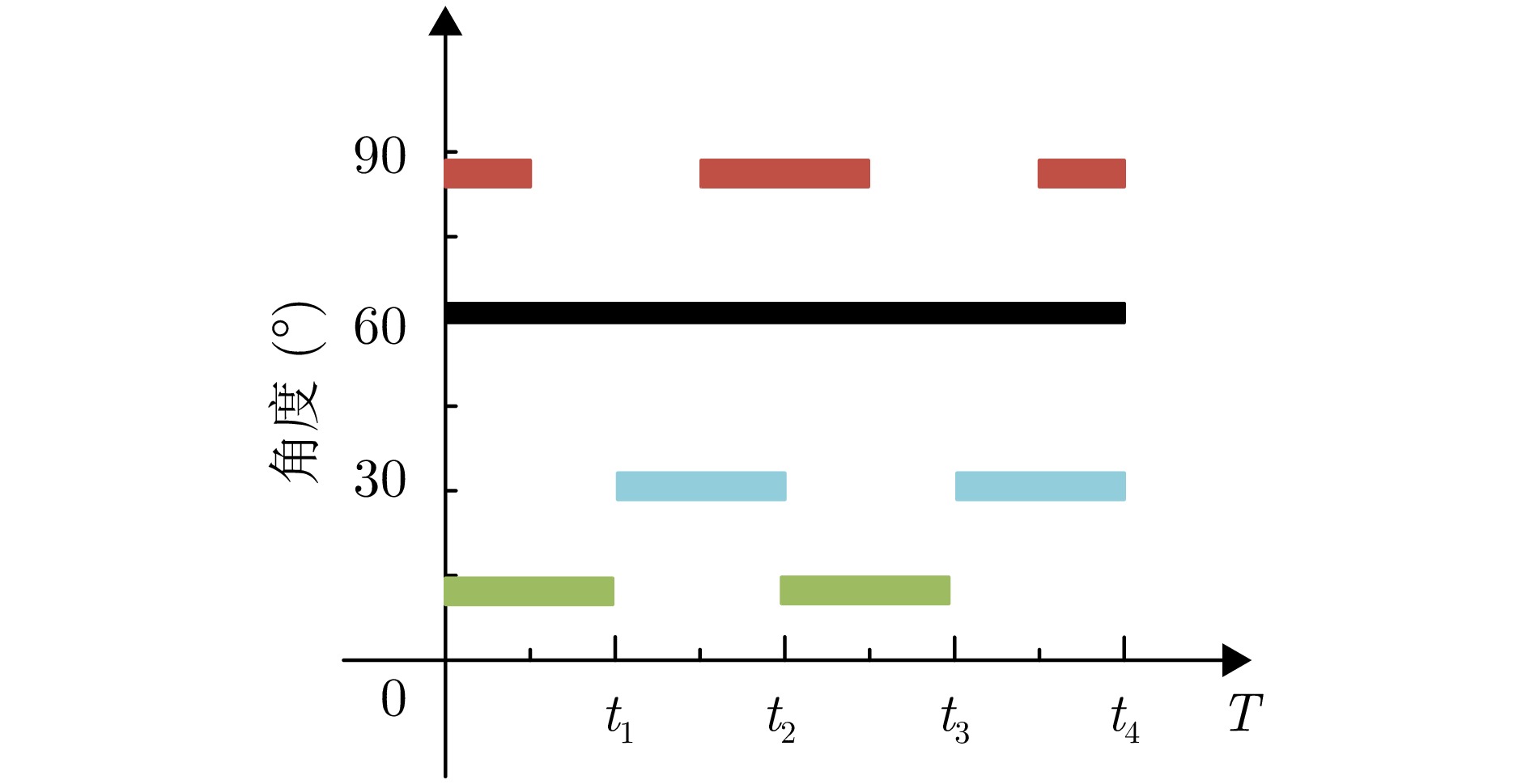
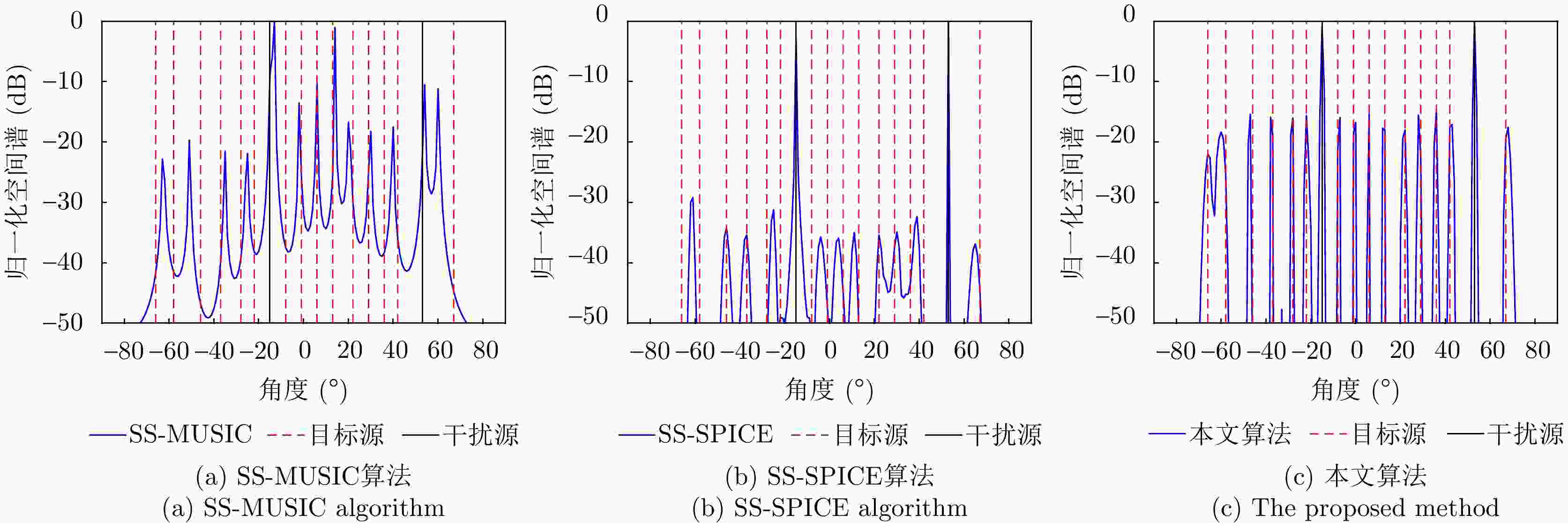
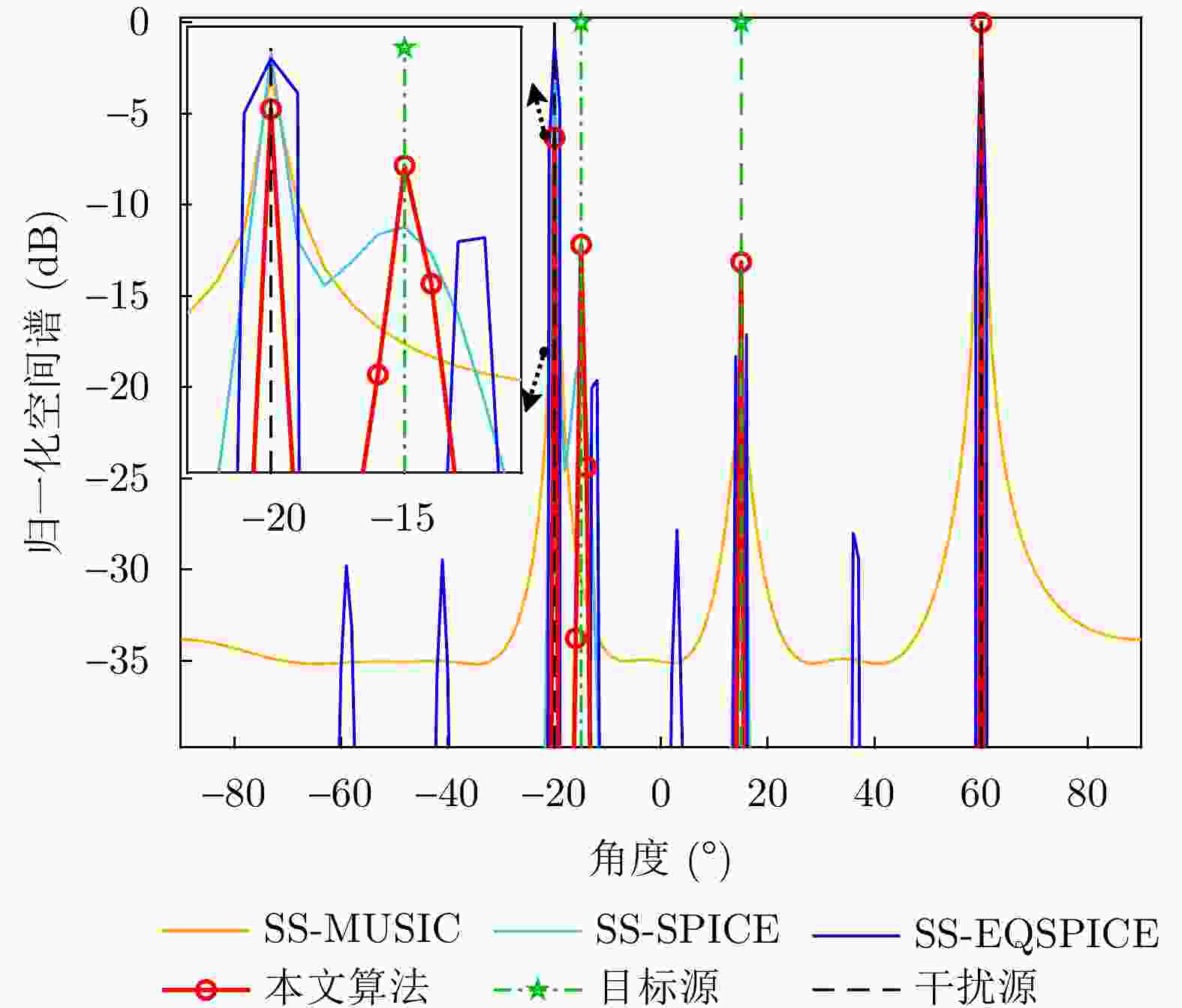
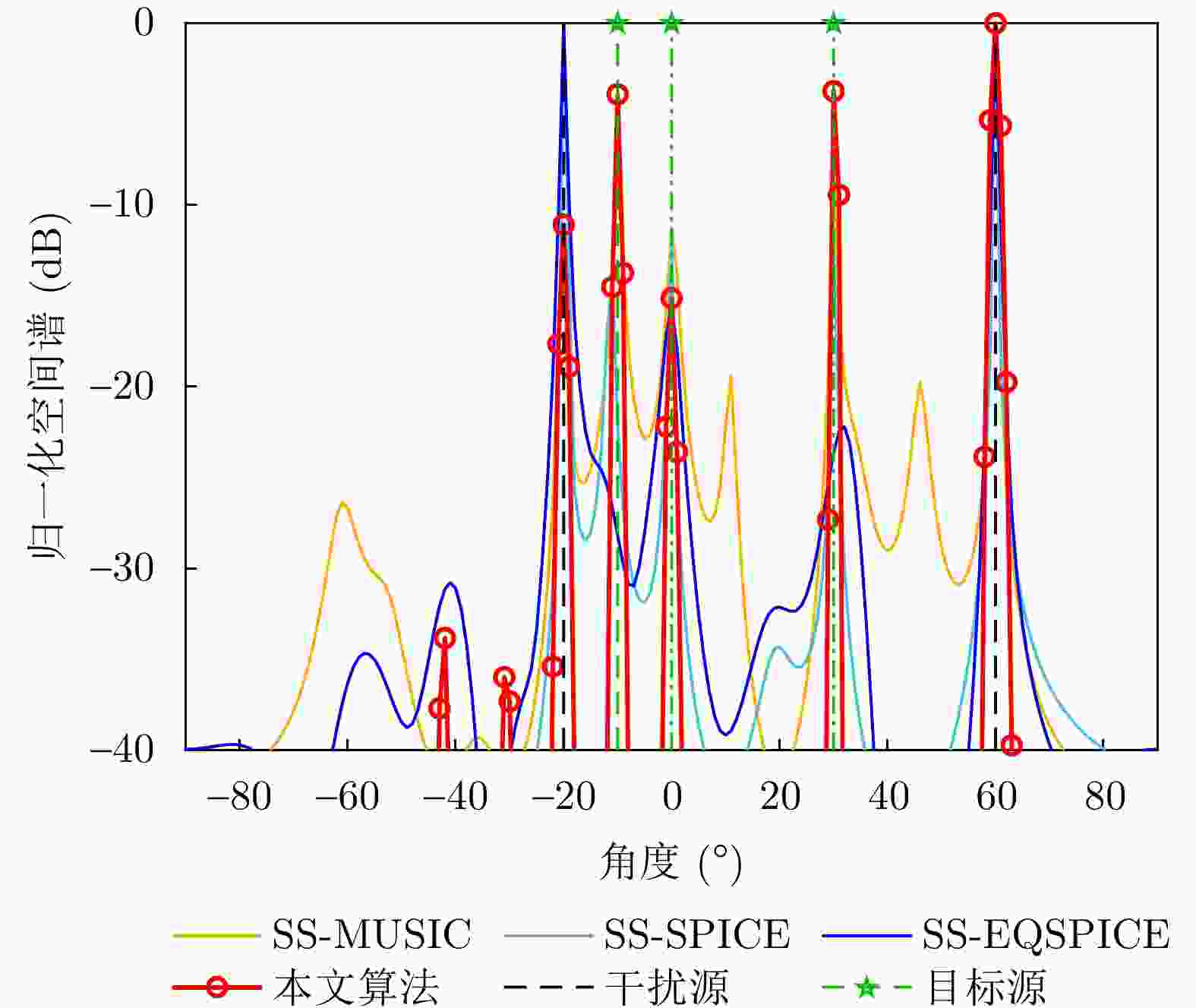
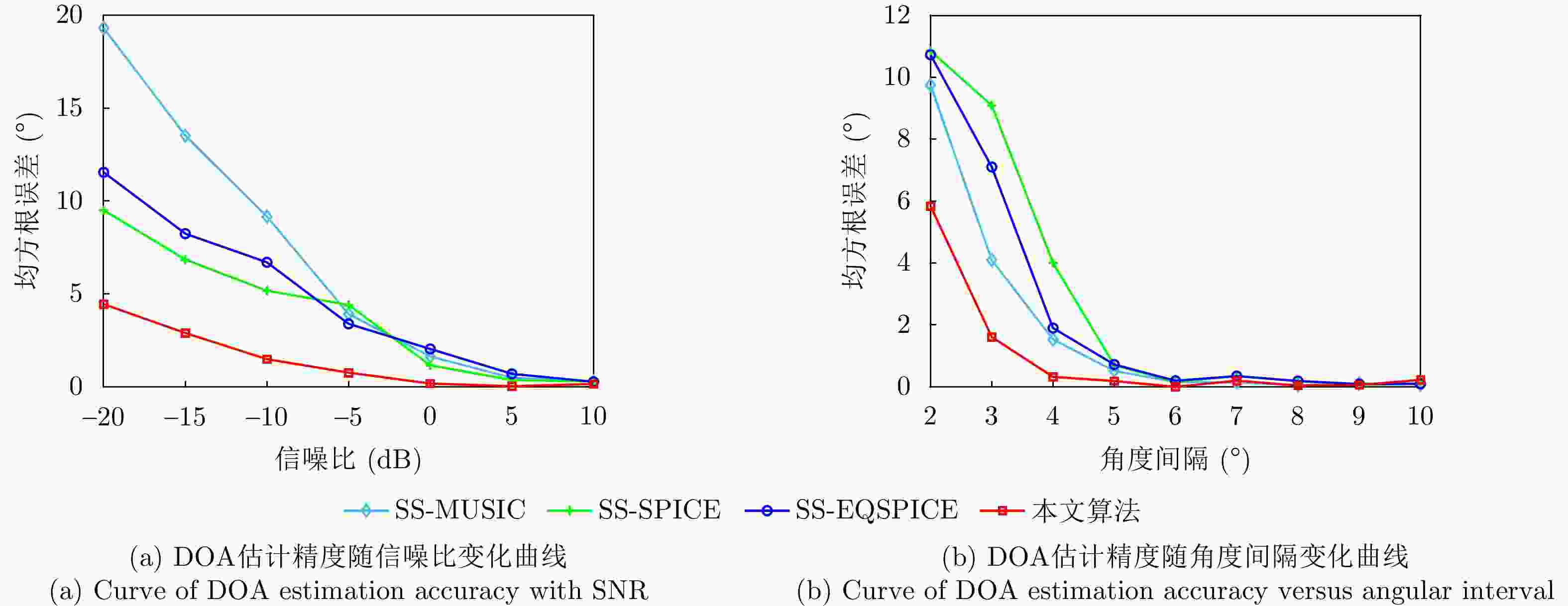
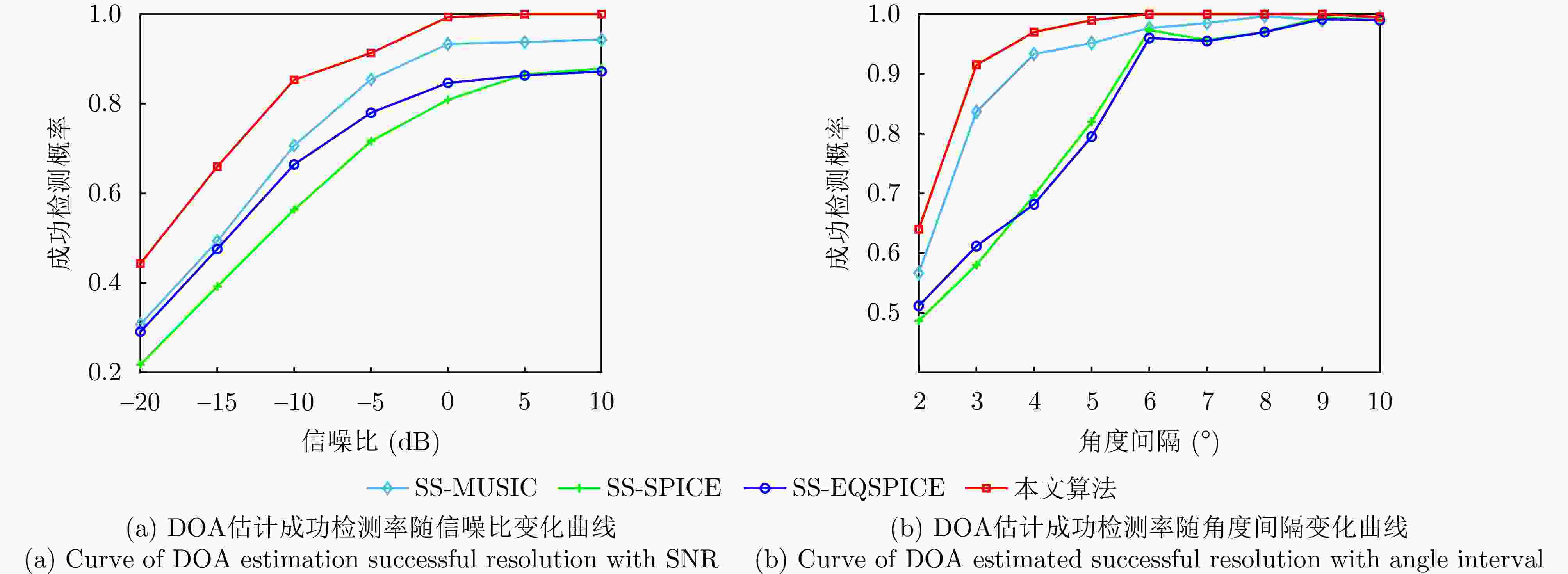
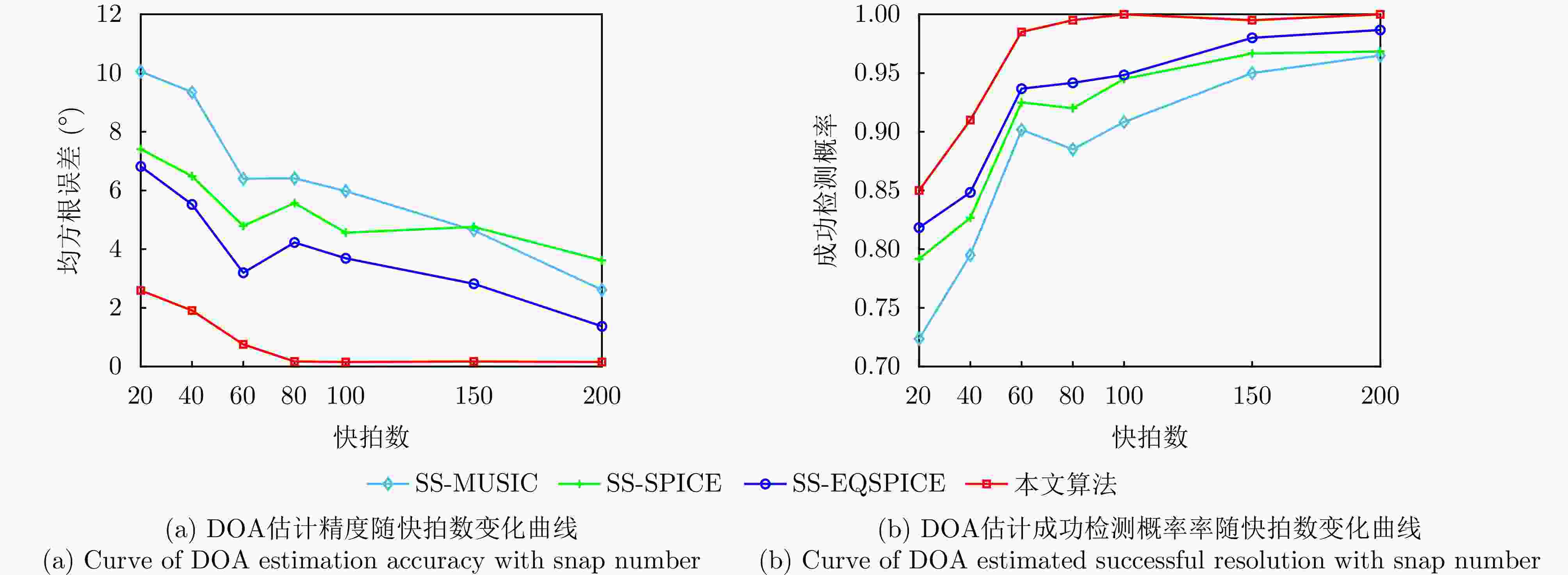
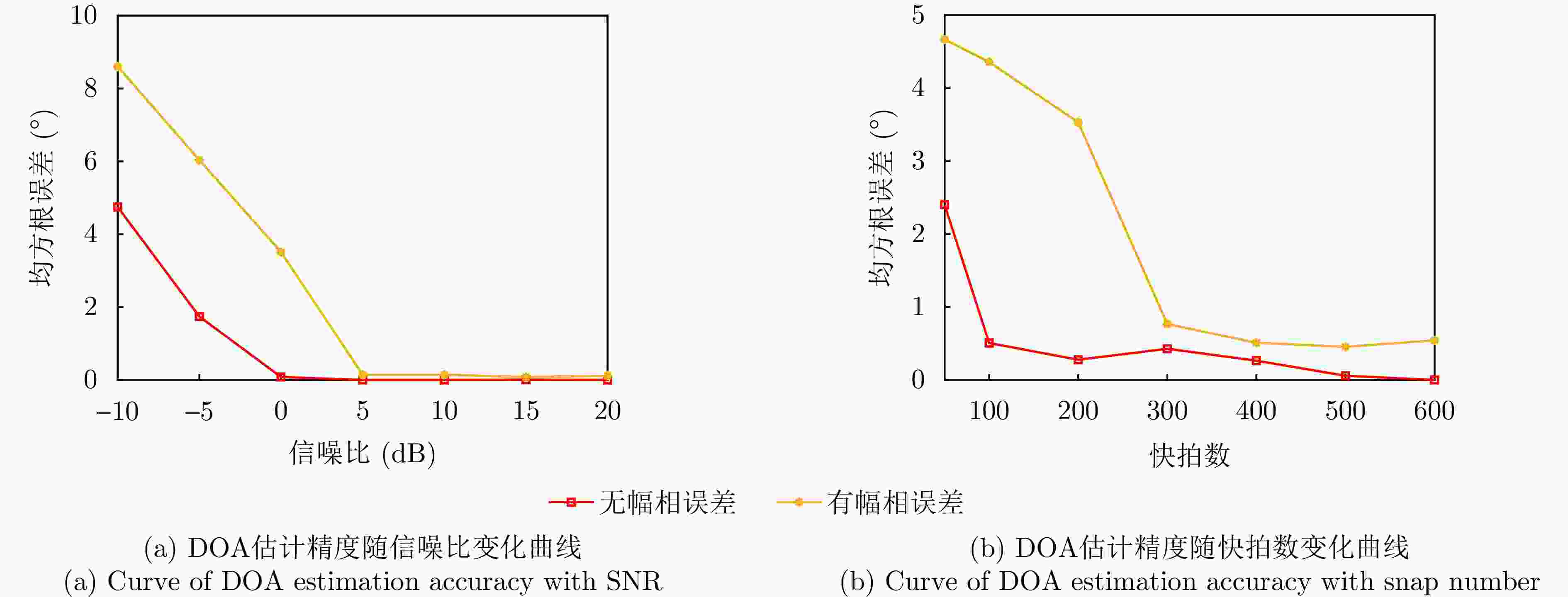
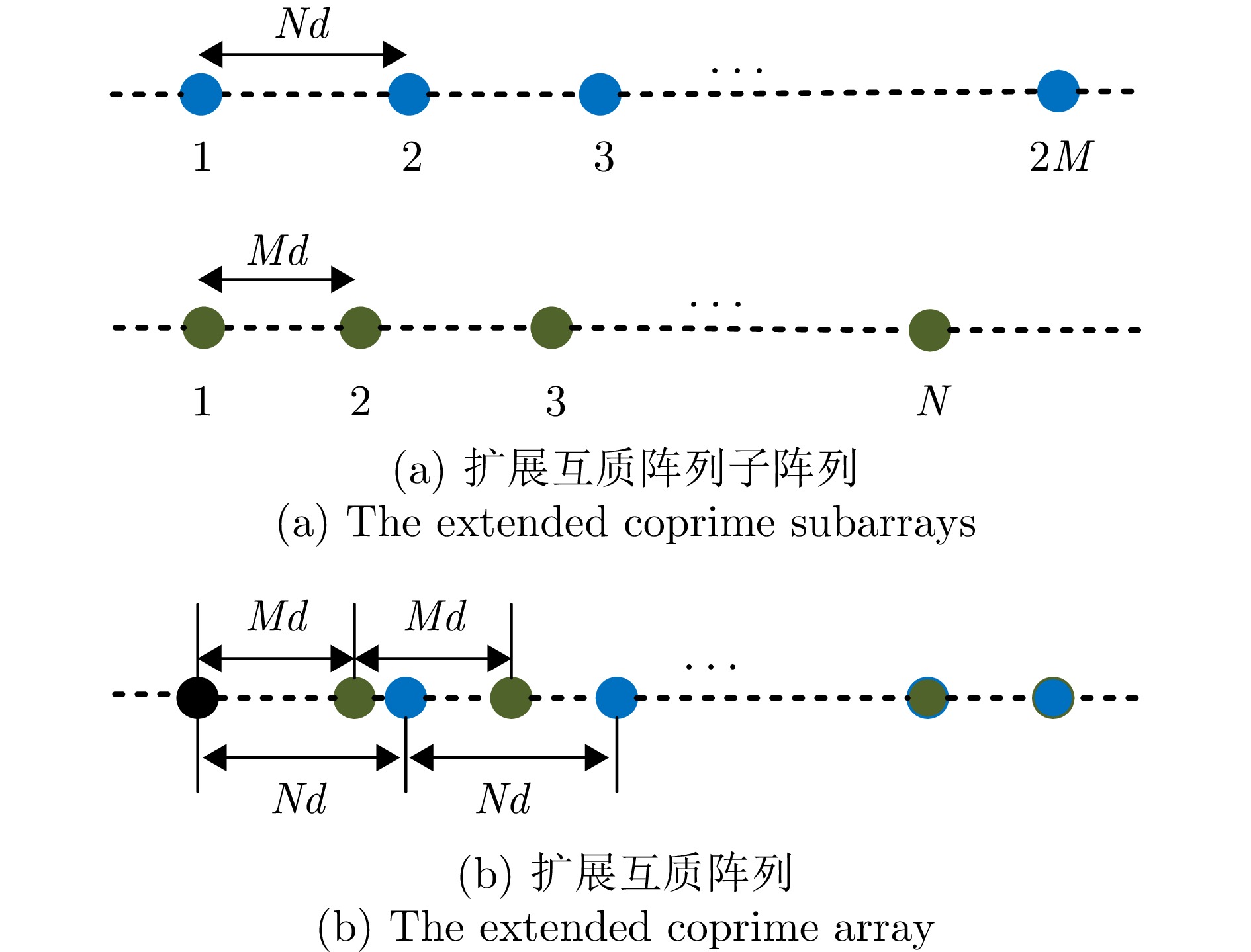
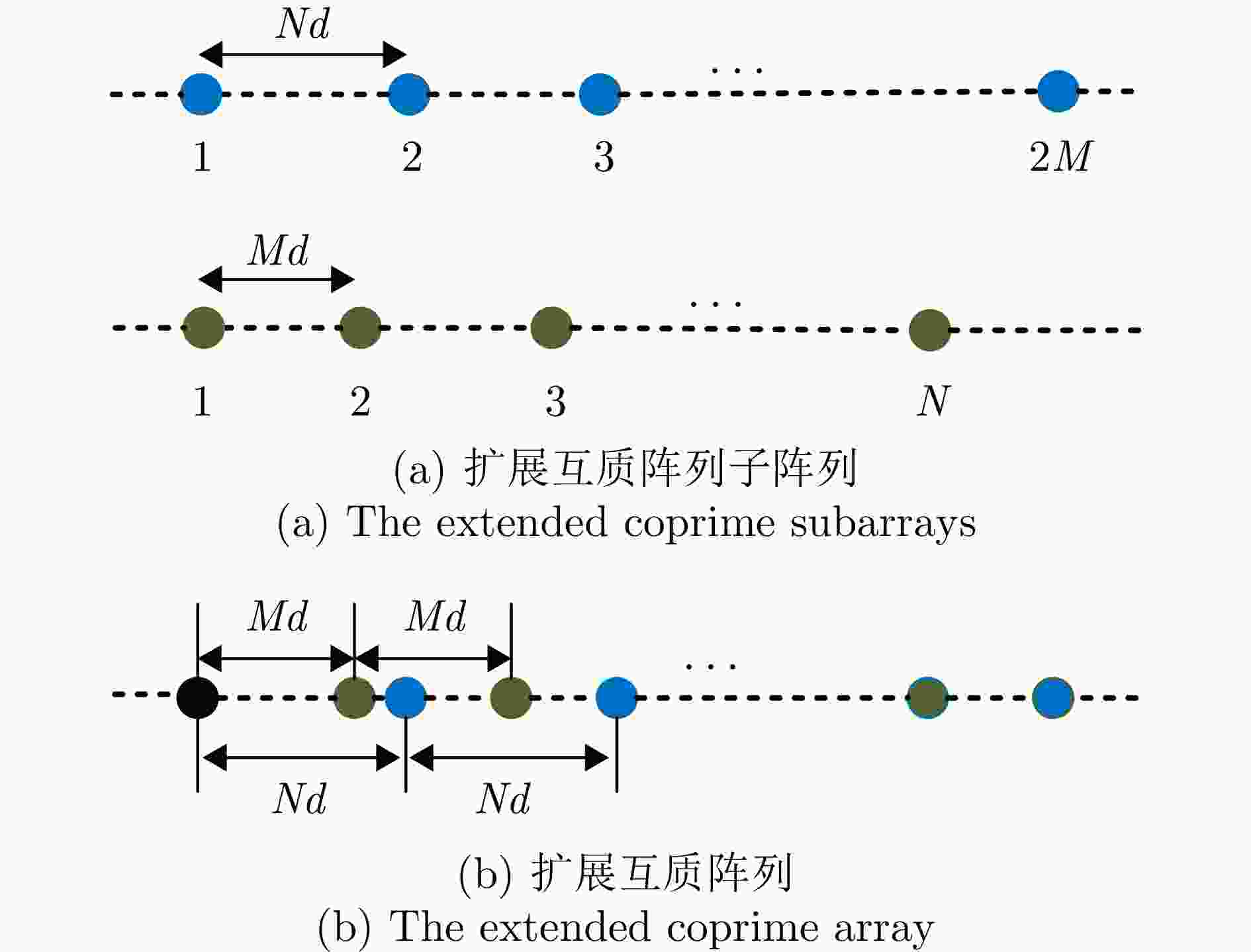
摘要: 针对复杂电磁环境下雷达干扰增多且靠近强干扰信号的目标信号难以准确估计的问题，该文提出了一种强间歇干扰下基于黎曼平均的稀疏波达方向(DOA)估计方法。首先，在扩展互质阵列接收数据模型下，利用在整个采样周期内目标信号持续活动而强干扰信号间歇性活动的特性，引入黎曼平均对干扰信号进行抑制；然后，将经过处理的数据协方差矩阵向量化，得到虚拟阵列接收数据；最后，在虚拟域中运用稀疏迭代协方差估计(SPICE)算法对稀疏信号进行重构，得到目标信号的DOA估计。仿真结果表明，在信号源数目未知的情况下，该方法可以对角度与强干扰信号紧密相邻的弱目标信号进行高精度的DOA估计。与现有子空间算法和稀疏重构类算法相比，所提算法在较小快拍数和低信噪比下具有更高的估计精度和角度分辨力。Abstract: Aiming to address the problem of increased radar jamming in complex electromagnetic environments and the difficulty of accurately estimating the target signal close to a strong jamming signal, this paper proposes a sparse Direction of Arrival (DOA) estimation method based on Riemann averaging under strong intermittent jamming. First, under the extended coprime array data model, the Riemann averaging is introduced to suppress the jamming signal by leveraging the property that the target signal is continuously active while the strong jamming signal is intermittently active. Then, the covariance matrix of the processed data is vectorized to obtain virtual array reception data. Finally, the sparse iterative covariance-based estimation method, which is used for estimating the DOA under strong intermittent interference, is employed in the virtual domain to reconstruct the sparse signal and estimate the DOA of the target signal. The simulation results show that the method can provide highly accurate DOA estimation for weak target signals whose angles are closely adjacent to strong interference signals when the number of signal sources is unknown. Compared with existing subspace algorithms and sparse reconstruction class algorithms, the proposed algorithm has higher estimation accuracy and angular resolution at a smaller number of snapshots, as well as a lower signal-to-noise ratio.
-
图 2 连续信号和间歇性干扰信号活动示意图
Figure 2. Schematic diagram of continuous and intermittent interfering signal activity
图 4 不同算法分辨性能对比
Figure 4. Comparison of the resolution performance of different algorithms
图 5 不同算法下相干信号空间谱对比
Figure 5. Comparison of spatial spectrum of coherent signals under different algorithms
图 6 不同参数条件下的DOA估计精度
Figure 6. Accuracy of DOA estimation under different parameter conditions
图 7 不同参数条件下的成功检测概率
Figure 7. Successful resolution under different parameter conditions
图 8 算法估计精度和分辨率随快拍数的变化
Figure 8. Algorithmic estimation of accuracy and resolution as a function of number of snapshots
图 9 所提算法在不同参数条件下的DOA估计精度
Figure 9. Accuracy of DOA estimation of the proposed algorithm under different parameter conditions
1 基于黎曼平均的虚拟域SPICE算法
1. A virtual domain SPICE algorithm based on Riemann averaging
输入：协方差矩阵的黎曼均值${\hat {\boldsymbol{R}}_{\mathrm{R}}}$，过完备网格点${\boldsymbol{\varTheta}} $，迭代终止阈值${\delta _{\min }}$，最大迭代次数Q； 输出：空间谱${\boldsymbol{P}}_{\mathrm{S}}^{(i)}$ 1 根据式(22)得到虚拟阵列数据r并通过式(23)剔除r中重复元素得到$\tilde {\boldsymbol{r}}$； 2 初始化：初始迭代次数$i = 1$，初始阈值${\delta _0} = 1$，分别根据式(35)、式(36)、式(24)和式(34)依次初始化$p_c^{(0)}$, ${\boldsymbol{P}}_{\mathrm{S}}^{(i)}$, R和${\rho ^0}$，$\sigma _n^2$初始化为
$ \sigma _n^2 = \min \left\{ {p_c^{(0)}} \right\} $；3 迭代开始：根据式(32)和式(33)更新$p_c^{(i + 1)}$和$\sigma _n^{(i + 1)}$； 4 根据式(36)、式(24)和式(34)依次更新${\boldsymbol{P}}_{\mathrm{S}}^{(i)}$, ${{\boldsymbol{R}}^{(i)}}$和${\rho ^{(i)}}$； 5 根据式(37)更新$\delta $，如果$\delta > {\delta _{\min }}$且$i < Q$，则返回步骤3； 迭代结束 
下载: 导出CSV
表 1 算法计算复杂度对比表
Table 1. Comparison table of computational complexity of algorithms
算法 复杂度 SS-MUSIC算法 $ O(L{G^2} + 2{(MN + 1)^3} + C{(MN + 1)^2} - CK(MN + 1)) $ SS-SPICE算法 $ O({G^3}CQ + G{C^{^2}}Q + L{G^2}) $ SS-EQSPICE算法 $ O({G^3}CQ' + G{C^{^2}}Q' + L{G^2}) $ 本文所提算法 $ O({G^3}CQ + G{C^{^2}}Q + L{G^2} + {G^3} + {G^2}) $
下载: 导出CSV
-
[1] MERKOFER J P, REVACH G, SHLEZINGER N, et al. DA-MUSIC: Data-driven DOA estimation via deep augmented MUSIC algorithm[J]. IEEE Transactions on Vehicular Technology, 2024, 73(2): 2771–2785. doi: 10.1109/TVT.2023.3320360. [2] MAO Zihuan, LIU Shengheng, ZHANG Y D, et al. Joint DoA-range estimation using space-frequency virtual difference coarray[J]. IEEE Transactions on Signal Processing, 2022, 70: 2576–2592. doi: 10.1109/TSP.2022.3173150. [3] CHEN Feng, YANG Desen, and MO Shiqi. A DOA estimation algorithm based on eigenvalues ranking problem[J]. IEEE Transactions on Instrumentation and Measurement, 2023, 72: 9501315. doi: 10.1109/TIM.2022.3232095. [4] OSMAN A, MOUSSA M M E, TAMAZIN M, et al. DOA elevation and azimuth angles estimation of GPS jamming signals using fast orthogonal search[J]. IEEE Transactions on Aerospace and Electronic Systems, 2020, 56(5): 3812–3821. doi: 10.1109/TAES.2020.2988424. [5] MOFFET A. Minimum-redundancy linear arrays[J]. IEEE Transactions on Antennas and Propagation, 1968, 16(2): 172–175. doi: 10.1109/TAP.1968.1139138. [6] PAL P and VAIDYANATHAN P P. Nested arrays: A novel approach to array processing with enhanced degrees of freedom[J]. IEEE Transactions on Signal Processing, 2010, 58(8): 4167–4181. doi: 10.1109/TSP.2010.2049264. [7] 周成伟, 郑航, 顾宇杰, 等. 互质阵列信号处理研究进展: 波达方向估计与自适应波束成形[J]. 雷达学报, 2019, 8(5): 558–577. doi: 10.12000/JR19068.ZHOU Chengwei, ZHENG Hang, GU Yujie, et al. Research progress on coprime array signal processing: Direction-of-arrival estimation and adaptive beamforming[J]. Journal of Radars, 2019, 8(5): 558–577. doi: 10.12000/JR19068. [8] QIN Si, ZHANG Y D, and AMIN M G. Generalized coprime array configurations for direction-of-arrival estimation[J]. IEEE Transactions on Signal Processing, 2015, 63(6): 1377–1390. doi: 10.1109/TSP.2015.2393838. [9] 陈小龙, 关键, 何友, 等. 高分辨稀疏表示及其在雷达动目标检测中的应用[J]. 雷达学报, 2017, 6(3): 239–251. doi: 10.12000/JR16110.CHEN Xiaolong, GUAN Jian, HE You, et al. High-resolution sparse representation and its applications in radar moving target detection[J]. Journal of Radars, 2017, 6(3): 239–251. doi: 10.12000/JR16110. [10] 陈辉, 苏海军. 强干扰/信号背景下的DOA估计新方法[J]. 电子学报, 2006, 34(3): 530–534. doi: 10.3321/j.issn:0372-2112.2006.03.033.CHEN Hui and SU Haijun. A new approach to estimate DOA in presence of strong jamming/signal suppression[J]. Acta Electronica Sinica, 2006, 34(3): 530–534. doi: 10.3321/j.issn:0372-2112.2006.03.033. [11] 张静, 廖桂生, 张洁. 强信号背景下基于噪声子空间扩充的弱信号DOA估计方法[J]. 系统工程与电子技术, 2009, 31(6): 1279–1283. doi: 10.3321/j.issn:1001-506X.2009.06.003.ZHANG Jing, LIAO Guisheng, and ZHANG Jie. DOA estimation based on extended noise subspace in the presence of strong signals[J]. Systems Engineering and Electronics, 2009, 31(6): 1279–1283. doi: 10.3321/j.issn:1001-506X.2009.06.003. [12] LIN Bin, HU Guoping, ZHOU Hao, et al. Coherent signal DOA estimation for MIMO radar under composite background of strong interference and non-uniform noise[J]. Sensors, 2022, 22(24): 9833. doi: 10.3390/s22249833. [13] 夏楠, 马昕昕, 王思琦. 强干扰下基于三阶互累积量的FMCW雷达信号DOA估计算法[J]. 电子学报, 2024, 52(2): 510–517. doi: 10.12263/DZXB.20230258.XIA Nan, MA Xinxin, and WANG Siqi. FMCW radar signal DOA estimation method based on the third-order cross cumulant under high interference[J]. Acta Electronica Sinica, 2024, 52(2): 510–517. doi: 10.12263/DZXB.20230258. [14] FANG Qingyuan, JIN Mengzhe, LIU Weidong, et al. DOA estimation for sources with large power differences[J]. International Journal of Antennas and Propagation, 2021, 2021: 8862789. doi: 10.1155/2021/8862789. [15] STOICA P, BABU P, and LI Jian. SPICE: A sparse covariance-based estimation method for array processing[J]. IEEE Transactions on Signal Processing, 2011, 59(2): 629–638. doi: 10.1109/TSP.2010.2090525. [16] 张赫, 陈华伟. 一种强干扰环境下的离格稀疏贝叶斯DOA估计方法[J]. 数据采集与处理, 2019, 34(6): 1019–1029. doi: 10.16337/j.1004-9037.2019.06.008.ZHANG He and CHEN Huawei. Off-grid sparse Bayesian DOA estimation method in strong interference environment[J]. Journal of Data Acquisition & Processing, 2019, 34(6): 1019–1029. doi: 10.16337/j.1004-9037.2019.06.008. [17] GENG Jiwen, YU Ze, and LI Chunsheng. Synthetic aperture radar increment imaging based on compressed sensing[J]. IEEE Geoscience and Remote Sensing Letters, 2022, 19: 4013705. doi: 10.1109/LGRS.2021.3076451. [18] ZUO Ming and XIE Shuguo. A novel DOA estimation method for an antenna array under strong interference[J]. EURASIP Journal on Advances in Signal Processing, 2022, 2022(1): 111. doi: 10.1186/s13634-022-00930-y. [19] LI Chenmu, LIANG Guolong, QIU Longhao, et al. An efficient sparse method for direction-of-arrival estimation in the presence of strong interference[J]. The Journal of the Acoustical Society of America, 2023, 153(2): 1257–1271. doi: 10.1121/10.0017256. [20] BESSON O, STOICA P, and KAMIYA Y. Direction finding in the presence of an intermittent interference[J]. IEEE Transactions on Signal Processing, 2002, 50(7): 1554–1564. doi: 10.1109/TSP.2002.1011196. [21] 王解, 刘文祥, 陈飞强, 等. 分布式间歇干扰下基于SMI的GNSS空时自适应处理器性能分析[J]. 国防科技大学学报, 2023, 45(6): 90–99. doi: 10.11887/j.cn.202306013.WANG Jie, LIU Wenxiang, CHEN Feiqiang, et al. Performance analysis of SMI based GNSS space-time adaptive processing under distributed intermittent interferences[J]. Journal of National University of Defense Technology, 2023, 45(6): 90–99. doi: 10.11887/j.cn.202306013. [22] AKDEMIR Ş B and CANDAN Ç. Maximum-likelihood direction of arrival estimation under intermittent jamming[J]. Digital Signal Processing, 2021, 113: 103028. doi: 10.1016/j.dsp.2021.103028. [23] BAR A and TALMON R. On interference-rejection using riemannian geometry for direction of arrival estimation[J]. IEEE Transactions on Signal Processing, 2024, 72: 260–274. doi: 10.1109/TSP.2023.3322779. [24] HIAI F and PETZ D. Riemannian metrics on positive definite matrices related to means[J]. Linear Algebra and its Applications, 2009, 430(11/12): 3105–3130. doi: 10.1016/j.laa.2009.01.025. [25] BARACHANT A, BONNET S, CONGEDO M, et al. Classification of covariance matrices using a Riemannian-based kernel for BCI applications[J]. Neurocomputing, 2013, 112: 172–178. doi: 10.1016/j.neucom.2012.12.039. [26] LI Yongtao, GU Xianming, and ZHAO Jianxing. The weighted arithmetic mean–geometric mean inequality is equivalent to the hölder inequality[J]. Symmetry, 2018, 10(9): 380. doi: 10.3390/sym10090380. [27] LIM Y and PÁLFIA M. Matrix power means and the Karcher mean[J]. Journal of Functional Analysis, 2012, 262(4): 1498–1514. doi: 10.1016/j.jfa.2011.11.012. [28] YANG Zai, XIE Lihua, and ZHANG Cishen. A discretization-free sparse and parametric approach for linear array signal processing[J]. IEEE Transactions on Signal Processing, 2014, 62(19): 4959–4973. doi: 10.1109/TSP.2014.2339792. [29] CHEN Peng, CAO Zhenxin, CHEN Zhimin, et al. Off-grid DOA estimation using sparse Bayesian learning in MIMO radar with unknown mutual coupling[J]. IEEE Transactions on Signal Processing, 2019, 67(1): 208–220. doi: 10.1109/TSP.2018.2881663. [30] DONG Feibiao, JIANG Ye, LIU Jian, et al. Experimental study on the performance of DOA estimation algorithm using a coprime acoustic sensor array without a priori knowledge of the source number[J]. Applied Acoustics, 2022, 186: 108502. doi: 10.1016/j.apacoust.2021.108502. [31] LIU Lutao, XIAO Yue, and WU Yanan. An iterative Lq-norm based optimization algorithm for generalized SPICE[J]. Digital Signal Processing, 2022, 123: 103389. doi: 10.1016/j.dsp.2022.103389. [32] 孙兵, 阮怀林, 吴晨曦, 等. 幅度相位误差条件下的互质阵列DOA估计方法[J]. 系统工程与电子技术, 2021, 43(12): 3488–3494. doi: 10.12305/j.issn.1001-506X.2021.12.09.SUN Bing, RUAN Huailin, WU Chenxi, et al. DOA estimation method for coprime array under gain and phase error[J]. Systems Engineering and Electronics, 2021, 43(12): 3488–3494. doi: 10.12305/j.issn.1001-506X.2021.12.09. -
图(9) / 表(2)
计量
- 文章访问数: 95
- HTML全文浏览量: 26
- PDF下载量: 10
- 被引次数: 0
