Three-dimensional Reconstruction Method for Detecting Small Targets within Walls Based on a Multistage Cascade U-Net Approach Using Ground Penetrating Radars
-
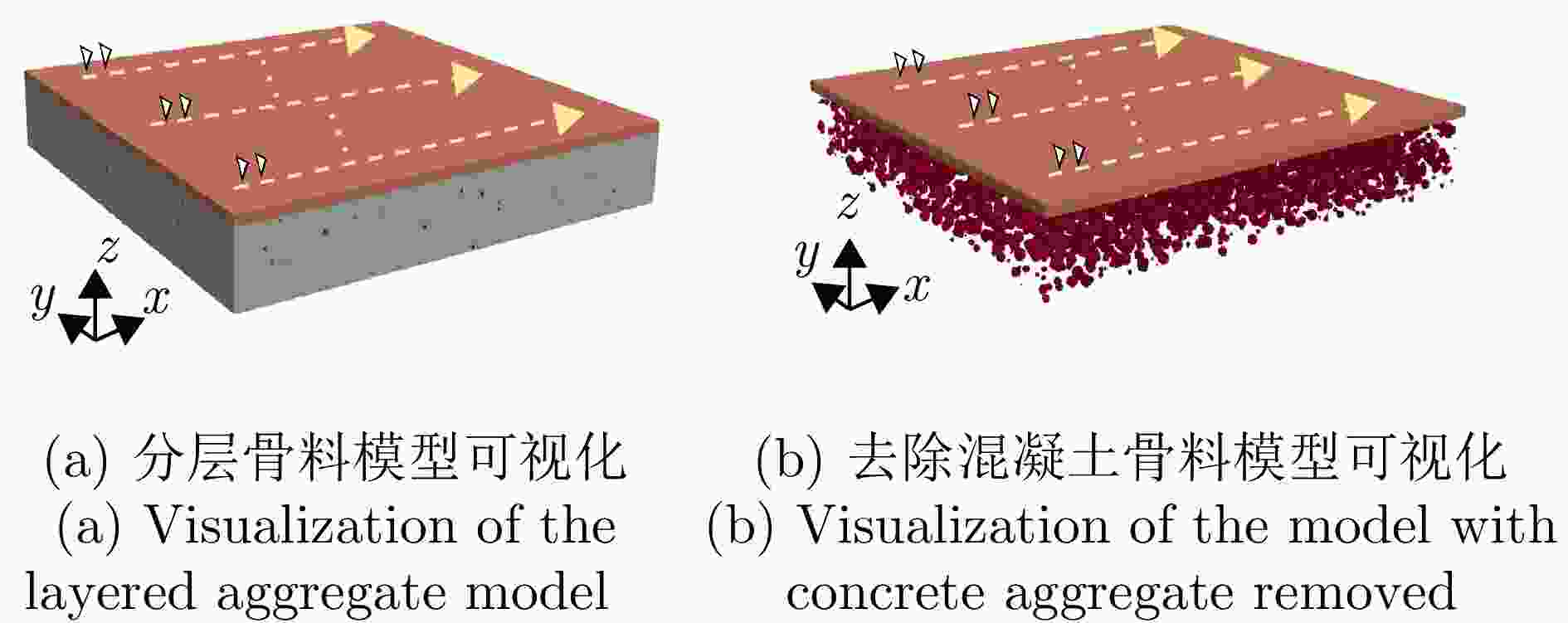
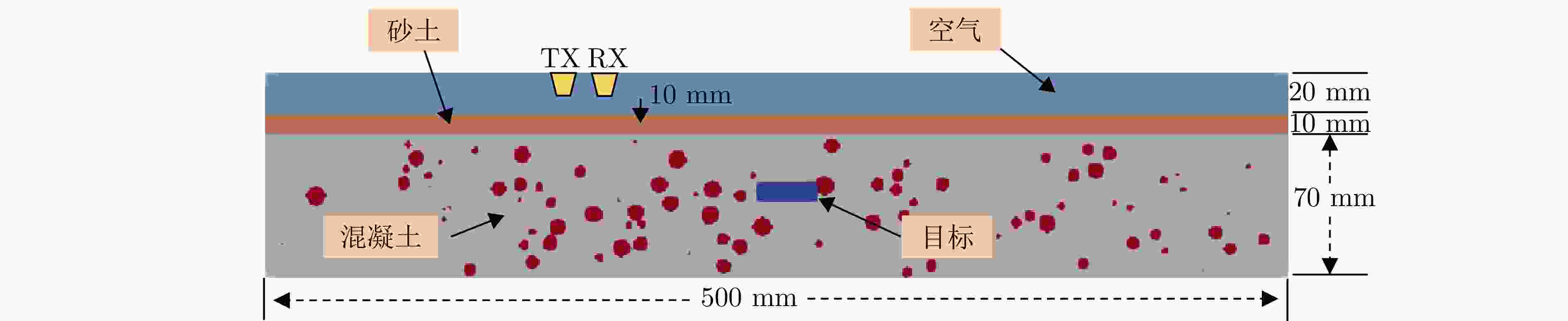
摘要: 探地雷达(GPR)在对掩埋目标的探测中发挥着至关重要的作用,尤其在墙体内小目标检测及重建方面。由于墙体结构及材质的复杂性,墙内小目标精准重建面临极大挑战。针对墙内小目标重建难题,该文提出了一种多阶段级联U-Net方法,用于墙内小目标的三维重建。首先,通过蒙特卡罗抽样生成符合级配要求的物理三维骨料散射模型,构建了复杂墙体场景的高分辨率探测模型和数据集,以提高模拟的真实性和准确性;其次,多阶段网络结构的设计能够有效抑制C扫描数据中的噪声和非均质杂波,从而提升信号质量;最后,预处理后的数据用于重建小目标三维分布。此外,该文还引入了一种自适应多尺度模块和级联网络训练策略,优化了复杂场景中小目标信息的拟合性能。通过模拟与实测数据的对比,验证所提方法的有效性和泛化能力。相比现有技术,该方法成功重建了三维墙体内小目标,显著提高了峰值信噪比,为小目标的准确探测提供了重要技术支持。Abstract: Ground Penetrating radars (GPR) are essential for detecting buried targets in civilian and military applications, especially given the increasing demand for detecting and imaging small targets within walls. The complex structures and materials of walls pose substantial challenges for precisely reconstructing small targets. To address this issue, this study proposes a multistage cascaded U-Net approach for the three-dimensional reconstruction of small targets within walls. First, we developed a high-resolution detection model and a dataset tailored to handle complex wall scenes. Thereafter, using the Monte Carlo sampling method, we sampled aggregate particle sizes to create a physical three-dimensional aggregate scattering model that satisfies grading requirements, thus enhancing the realism and accuracy of the simulated scenes. Our multistage network design effectively suppresses noise and inhomogeneous clutter in C-scan data, thereby improving signal quality. The preprocessed data are then fed into subsequent network stages to reconstruct the distribution of three-dimensional reconstruction values. In addition, we proposed an adaptive multiscale module and a cascaded network training strategy to better fit small target information in complex scenes. Through comparisons with simulated and measured data, we confirmed the effectiveness and generalizability of our method. Unlike existing techniques, our approach successfully reconstructs small targets within three-dimensional walls, thereby considerably enhancing the peak signal-to-noise ratio and providing critical technical support for accurately detecting small targets within walls.
-
表 1 仿真数据集预设置参数
Table 1. Simulation data set preset parameters
目标参数 设置范围 数量 1~2 形状 圆柱体和长方体 位置 随机 介质类型 金属 掩埋深度 40~60 mm 圆柱体厚度 10~20 mm 圆柱体半径 10~20 mm 长方体长、宽、高 15~30 mm 表 2 不同方法下的降噪评估指标对比
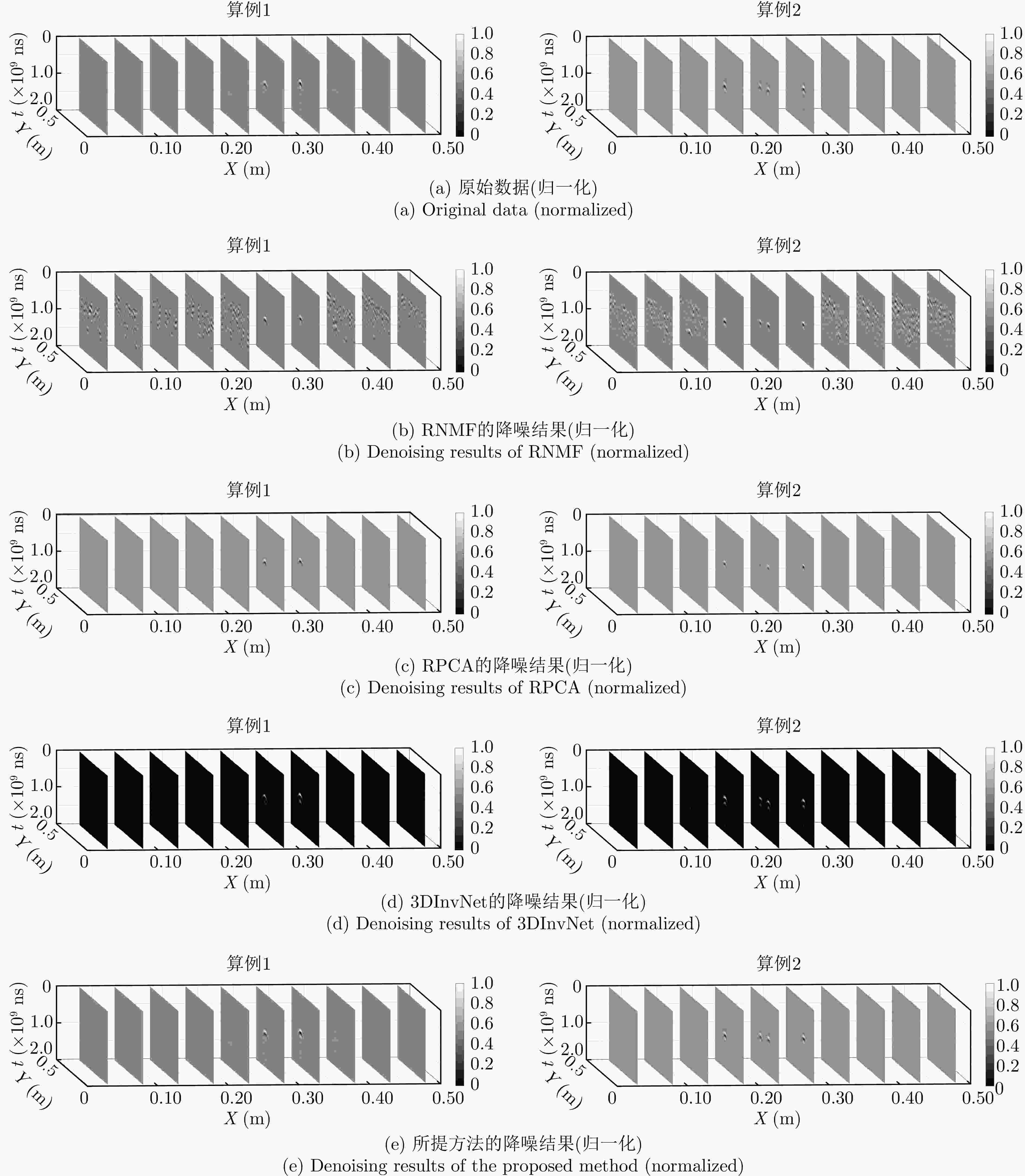
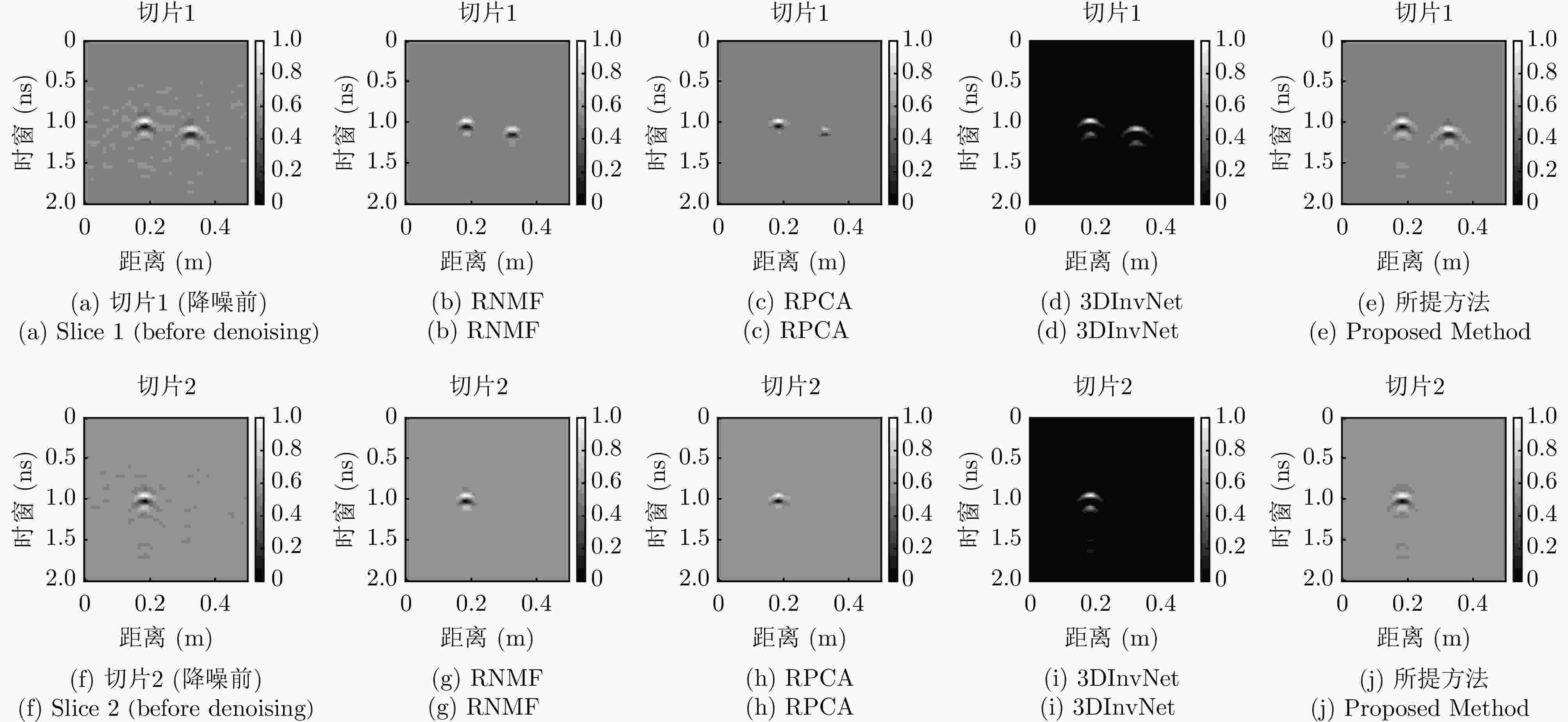
Table 2. Comparison of denoising evaluation indicators under different methods
方法 骨料配级比(%) 骨料配级比(%) 骨料配级比(%) 2 4 6 8 10 2 4 6 8 10 2 4 6 8 10 PSNR (dB)↑ RMSE↓ MAE↓ RNMF 33.21 34.43 33.61 33.35 33.94 0.5355 0.4913 0.5836 0.4581 0.5636 0.0929 0.0859 0.0937 0.0881 0.0905 RPCA 38.22 39.05 38.49 38.36 38.93 0.2992 0.2881 0.3373 0.2562 0.3158 0.0761 0.0709 0.0773 0.0722 0.0741 3DInvNet[24] 35.92 37.13 36.23 35.90 36.52 0.3931 0.3611 0.4351 0.3383 0.4199 0.0429 0.0375 0.0432 0.0412 0.0418 所提方法 56.18 56.90 55.04 53.01 54.62 0.0368 0.0357 0.0472 0.0476 0.0495 0.0183 0.0168 0.0196 0.0201 0.0205 表 3 不同方法下的重建评估指标对比
Table 3. Comparison of reconstruction evaluation indicators under different methods
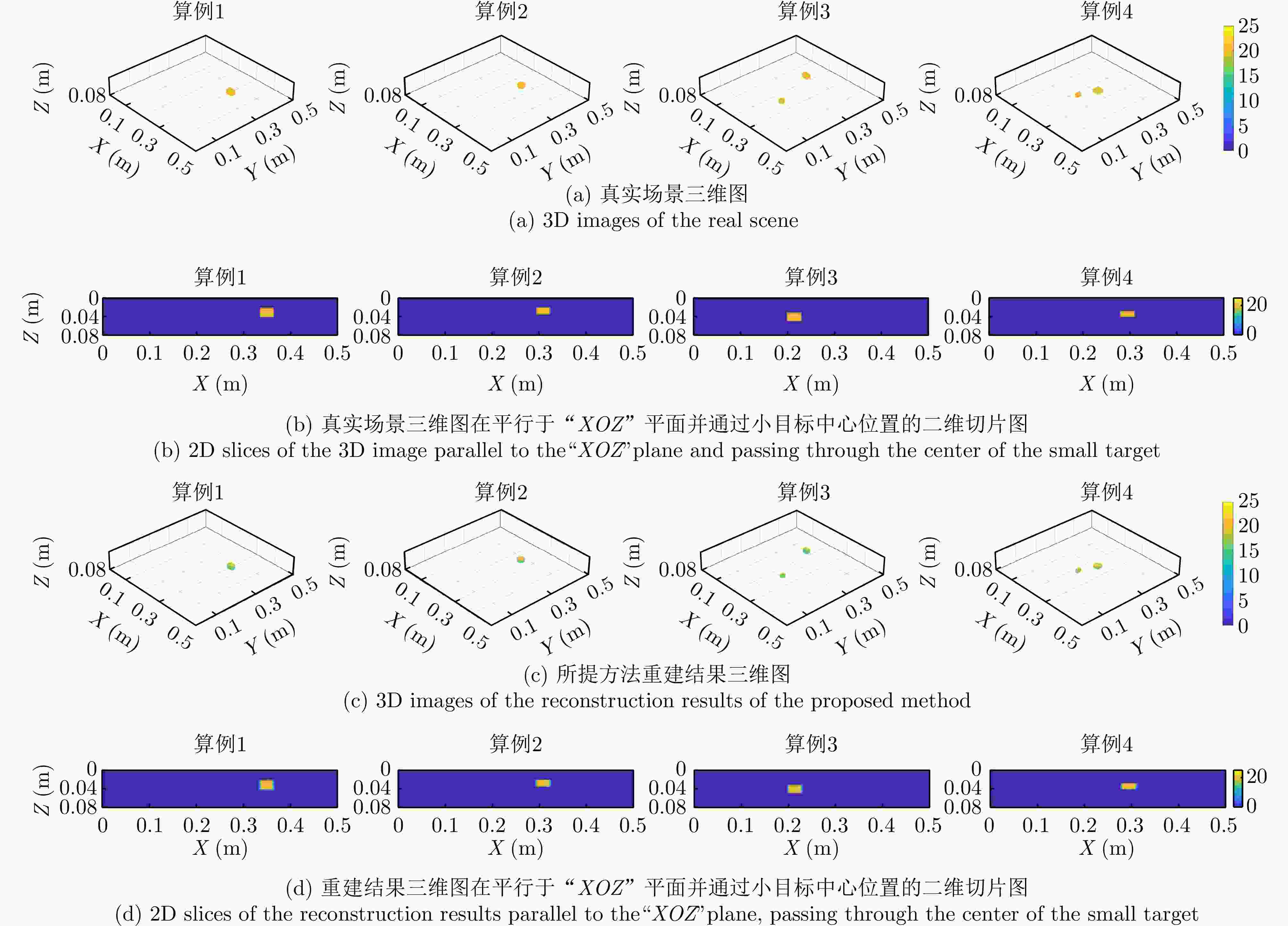
指标 PSNR (dB)↑ SSIM↑ RMSE↓ MAE↓ OR AR 均值 3DInvNet[24] 34.78 0.9969 0.1629 0.0092 0 0 – 0.0001 所提方法 52.17 0.9986 0.0074 0.0071 0.9241 4.0985 17.5678 表 4 所提方法在不同测试集上的评估指标
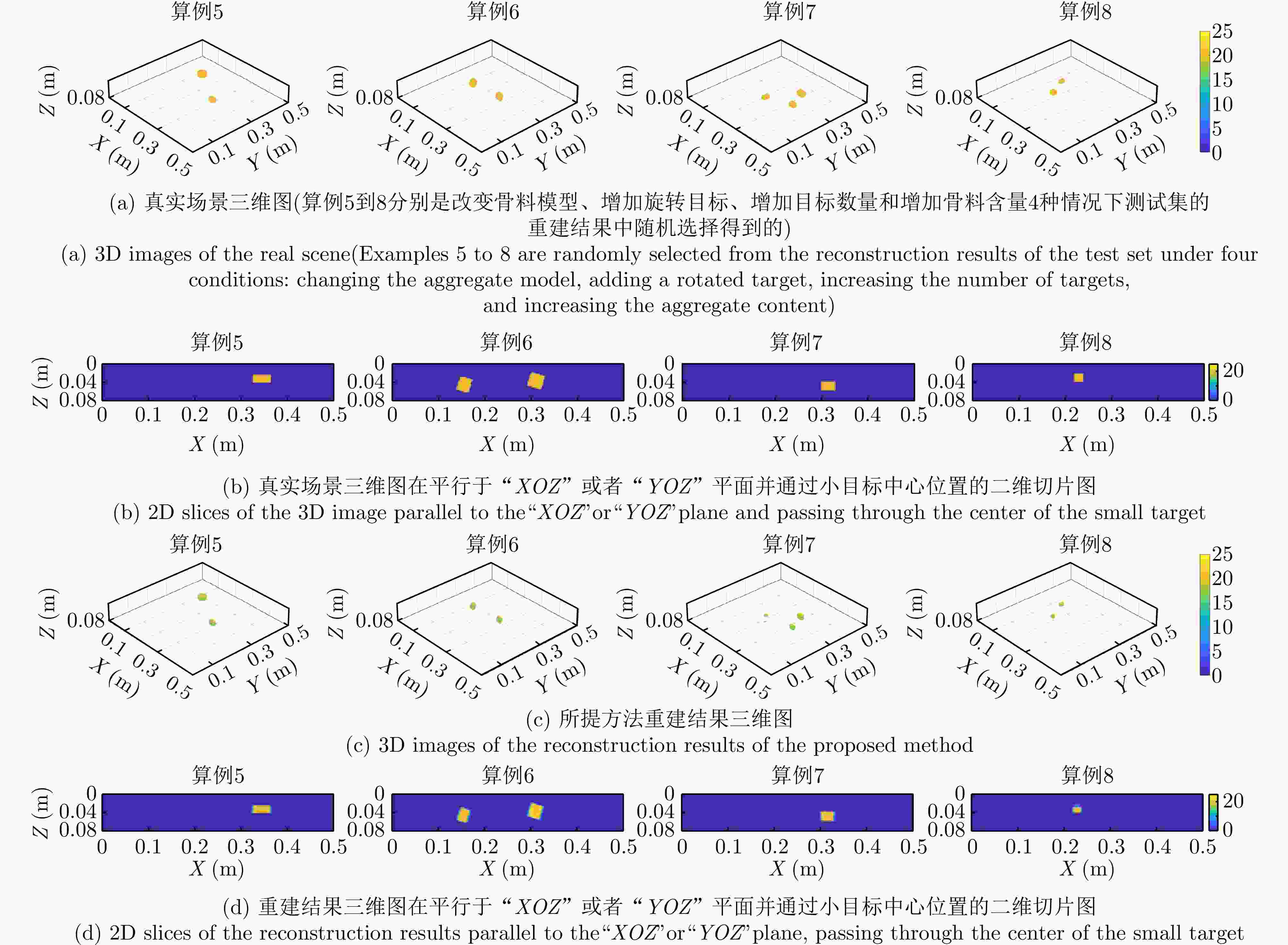
Table 4. Evaluation indicators of the proposed scheme on different test sets
测试集 PSNR (dB)↑ SSIM↑ RMSE↓ MAE↓ 改变
骨料模型48.63 0.9974 0.0081 0.0115 增加
旋转目标46.74 0.9978 0.0209 0.0101 增加
目标数量36.83 0.9945 0.0983 0.0199 增加
骨料含量43.77 0.9962 0.0309 0.1443 表 5 所提方法在不同背景材质下的重建指标对比
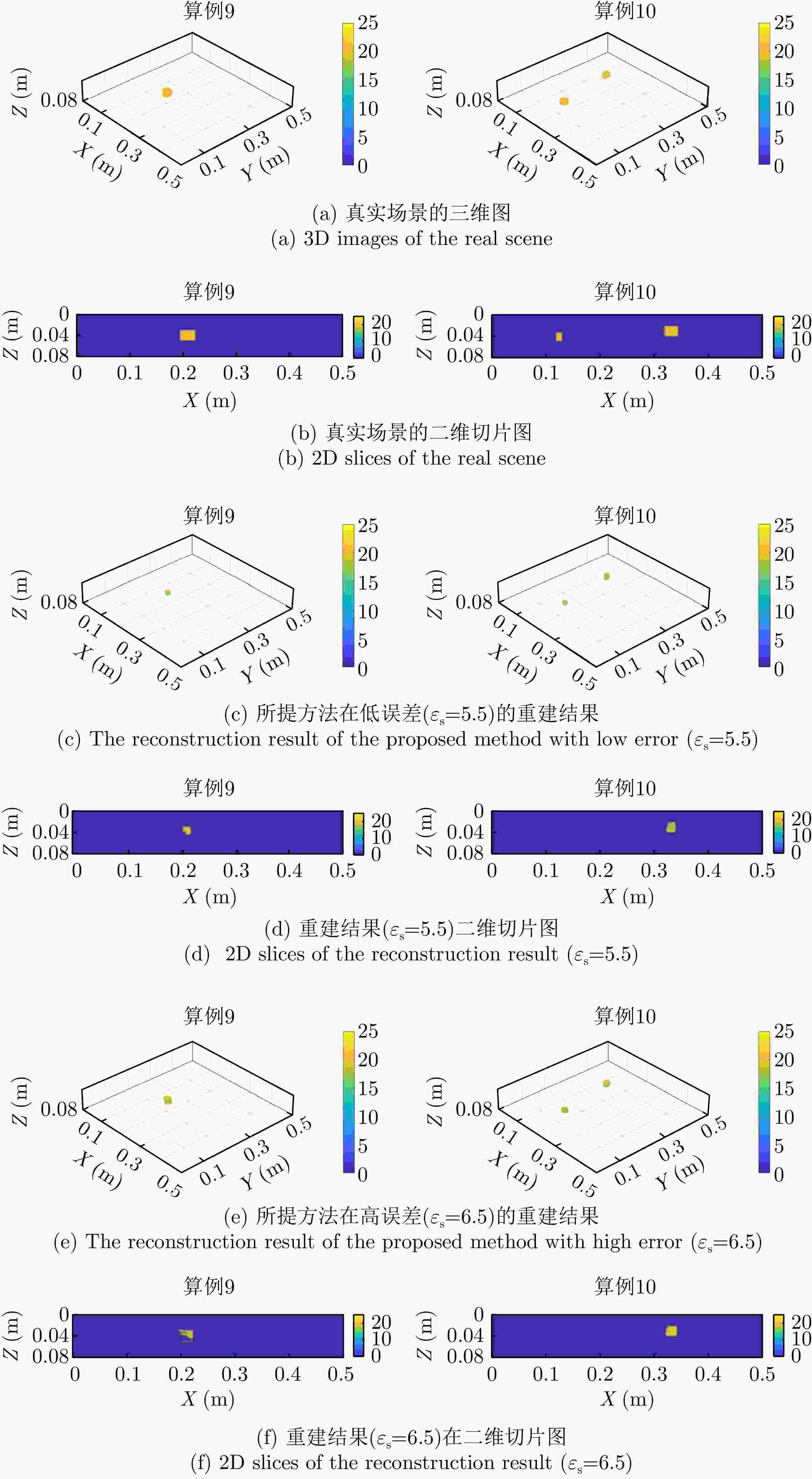
Table 5. Comparison of reconstruction indicators of the proposed scheme under different background materials
背景介电常数值 PSNR (dB)↑ SSIM↑ RMSE↓ MAE↓ 5.50 42.15 0.9945 0.0338 0.0161 5.75 45.70 0.9969 0.0157 0.0124 6.00 48.63 0.9974 0.0086 0.0115 6.25 48.14 0.9968 0.0086 0.0123 6.50 45.10 0.9949 0.0159 0.0151 表 6 消融实验
Table 6. Ablation experiment
实验 PSNR (dB)↑ SSIM↑ RMSE↓ MAE↓ (1) 44.85 0.9976 0.0219 0.0108 (2) 50.34 0.9976 0.0129 0.0079 (3) 31.07 0.6391 0.3735 0.2388 (4) 51.29 0.9981 0.0081 0.0097 (5) 52.17 0.9986 0.0074 0.0071 表 7 所提方法在实测算例的重建评估指标对比
Table 7. Comparison of reconstruction evaluation indicators of the proposed method in the measured example
指标 数值 PSNR (dB)↑ 36.49 SSIM↑ 0.9805 RMSE↓ 0.1033 MAE↓ 0.04155 OR 0.5708 AR 4.5737 均值 13.5055 -
[1] ZHANG Ju, HU Qingwu, ZHOU Yemei, et al. A multi-level robust positioning method for three-dimensional ground penetrating radar (3D GPR) road underground imaging in dense urban areas[J]. Remote Sensing, 2024, 16(9): 1559. doi: 10.3390/rs16091559. [2] DANIELS D J. A review of GPR for landmine detection[J]. Sensing and Imaging: An International Journal, 2006, 7(3): 90–123. doi: 10.1007/s11220-006-0024-5. [3] XUE Fangxiu, ZHANG Xiaowei, WANG Zepeng, et al. Analysis of imaging internal defects in living trees on irregular contours of tree trunks using ground-penetrating radar[J]. Forests, 2021, 12(8): 1012. doi: 10.3390/f12081012. [4] ZHOU Huawei, HU Hao, ZOU Zhihui, et al. Reverse time migration: A prospect of seismic imaging methodology[J]. Earth-Science Reviews, 2018, 179: 207–227. doi: 10.1016/j.earscirev.2018.02.008. [5] ZOU Lilong, WANG Yan, GIANNAKIS I, et al. Mapping and assessment of tree roots using ground penetrating radar with low-cost GPS[J]. Remote Sensing, 2020, 12(8): 1300. doi: 10.3390/rs12081300. [6] WEN Jian, LI Zhaoxi, and XIAO Jiang. Noise removal in tree radar B-scan images based on shearlet[J]. Wood Research, 2020, 65(1): 1–12. doi: 10.37763/wr.1336-4561/65.1.001012. [7] FENG Deshan, DING Siyuan, WANG Xun, et al. Wavefield reconstruction inversion of GPR data for permittivity and conductivity models in the frequency domain based on modified total variation regularization[J]. IEEE Transactions on Geoscience and Remote Sensing, 2022, 60: 5903314. doi: 10.1109/TGRS.2021.3077476. [8] KLOTZSCHE A, VEREECKEN H, and VAN DER KRUK J. Review of crosshole ground-penetrating radar full-waveform inversion of experimental data: Recent developments, challenges, and pitfalls[J]. Geophysics, 2019, 84(6): H13–H28. doi: 10.1190/geo2018-0597.1. [9] LIU Yuxin, FENG Deshan, XIAO Yougan, et al. Full-waveform inversion of multifrequency GPR data using a multiscale approach based on deep learning[J]. IEEE Transactions on Geoscience and Remote Sensing, 2024, 60: 5910212. doi: 10.1109/TGRS.2024.3382331. [10] FENG Deshan, LI Bingchao, WANG Xun, et al. An efficient dual-parameter full waveform inversion for GPR data using data encoding[J]. IEEE Transactions on Geoscience and Remote Sensing, 2023, 61: 5920011. doi: 10.1109/TGRS.2023.3321059. [11] 雷林林, 刘四新, 傅磊, 等. 基于全波形反演的探地雷达数据逆时偏移成像[J]. 地球物理学报, 2015, 58(9): 3346–3355. doi: 10.6038/cjg20150927.LEI Linlin, LIU Sixin, FU Lei, et al. Reverse time migration applied to GPR data based on full wave inversion[J]. Chinese Journal of Geophysics, 2015, 58(9): 3346–3355. doi: 10.6038/cjg20150927. [12] WANG Xun and FENG Deshan. Multiparameter full-waveform inversion of 3-D on-ground GPR with a modified total variation regularization scheme[J]. IEEE Geoscience and Remote Sensing Letters, 2021, 18(3): 466–470. doi: 10.1109/LGRS.2020.2976146. [13] 国运东, 孟凡冰, 秦广胜, 等. 基于动态平面波的三维多尺度全波形反演方法[J]. 石油物探, 2022, 61(4): 616–624. doi: 10.3969/j.issn.1000-1441.2022.04.005.GUO Yundong, MENG Fanbing, QIN Guangsheng, et al. 3D multi-scale full waveform inversion based on the dynamic plane-wave encoding method[J]. Geophysical Prospecting for Petroleum, 2022, 61(4): 616–624. doi: 10.3969/j.issn.1000-1441.2022.04.005. [14] DENG Jian, RENDERS J, MEENAKETAN B L P, et al. Imaging algorithm and optimal measurement protocol for 3-D impedance tomography on 2-D high-density microelectrode array[J]. IEEE Sensors Journal, 2024, 24(15): 24452–24465. doi: 10.1109/JSEN.2024.3417289. [15] LI Shucai, LIU Bin, REN Yuxiao, et al. Deep-learning inversion of seismic data[J]. IEEE Transactions on Geoscience and Remote Sensing, 2020, 58(3): 2135–2149. doi: 10.1109/TGRS.2019.2953473. [16] LIU Bin, REN Yuxiao, LIU Hanchi, et al. GPRInvNet: Deep learning-based ground-penetrating radar data inversion for tunnel linings[J]. IEEE Transactions on Geoscience and Remote Sensing, 2021, 59(10): 8305–8325. doi: 10.1109/TGRS.2020.3046454. [17] JI Yintao, ZHANG Fengkai, WANG Jing, et al. Deep neural network-based permittivity inversions for ground penetrating radar data[J]. IEEE Sensors Journal, 2021, 21(6): 8172–8183. doi: 10.1109/JSEN.2021.3050618. [18] SUN Haoran, YANG Xiaopeng, GONG Junbo, et al. Joint physics and data driven full-waveform inversion for underground dielectric targets imaging[J]. IEEE Transactions on Geoscience and Remote Sensing, 2022, 60: 4513311. doi: 10.1109/TGRS.2022.3219138. [19] DAI Qiqi, LEE Y H, SUN Haihan, et al. DMRF-UNet: A two-stage deep learning scheme for GPR data inversion under heterogeneous soil conditions[J]. IEEE Transactions on Antennas and Propagation, 2022, 70(8): 6313–6328. doi: 10.1109/TAP.2022.3176386. [20] WANG Mengjun, HU Da, CHEN Junjie, et al. Underground infrastructure detection and localization using deep learning enabled radargram inversion and vision based mapping[J]. Automation in Construction, 2023, 154: 105004. doi: 10.1016/j.autcon.2023.105004. [21] XIE Longhao, ZHAO Qing, MA Chunguang, et al. Ü-Net: Deep-learning schemes for ground penetrating radar data inversion[J]. Journal of Environmental and Engineering Geophysics, 2020, 25(2): 287–292. doi: 10.2113/JEEG19-074. [22] PANDA S L, SAHOO U K, MAITI S, et al. An attention U-Net-based improved clutter suppression in GPR images[J]. IEEE Transactions on Instrumentation and Measurement, 2024, 73: 8502511. doi: 10.1109/TIM.2024.3378267. [23] GE Junkai, SUN Huaifeng, SHAO Wei, et al. GPR-TransUNet: An improved transunet based on self-attention mechanism for ground penetrating radar inversion[J]. Journal of Applied Geophysics, 2024, 222: 105333. doi: 10.1016/j.jappgeo.2024.105333. [24] DAI Qiqi, LEE Y H, SUN Haihan, et al. 3DInvNet: A deep learning-based 3D ground-penetrating radar data inversion[J]. IEEE Transactions on Geoscience and Remote Sensing, 2023, 61: 5105016. doi: 10.1109/TGRS.2023.3275306. [25] XU Tianjia, YUAN Da, WANG Ping, et al. Improved 3-D representation of GPR pipelines B-scan sequences using a neural network framework[J]. IEEE Transactions on Geoscience and Remote Sensing, 2024, 62: 4502416. doi: 10.1109/TGRS.2024.3360101. [26] ZOUBIR A M, CHANT I J, BROWN C L, et al. Signal processing techniques for landmine detection using impulse ground penetrating radar[J]. IEEE Sensors Journal, 2002, 2(1): 41–51. doi: 10.1109/7361.987060. [27] XUE Wei, LUO Yan, YANG Yue, et al. Noise suppression for GPR data based on SVD of window-length-optimized hankel matrix[J]. Sensors, 2019, 19(17): 3807. doi: 10.3390/s19173807. [28] BI Wenda, ZHAO Yonghui, AN Cong, et al. Clutter elimination and random-noise denoising of GPR signals using an svd method based on the hankel matrix in the local frequency domain[J]. Sensors, 2018, 18(10): 3422. doi: 10.3390/s18103422. [29] KUMLU D and ERER I. Improved clutter removal in GPR by robust nonnegative matrix factorization[J]. IEEE Geoscience and Remote Sensing Letters, 2020, 17(6): 958–962. doi: 10.1109/LGRS.2019.2937749. [30] SONG Xiaoji, XIANG Deliang, ZHOU Kai, et al. Improving RPCA-based clutter suppression in GPR detection of antipersonnel mines[J]. IEEE Geoscience and Remote Sensing Letters, 2017, 14(8): 1338–1342. doi: 10.1109/LGRS.2017.2711251. [31] NI Zhikang, YE Shengbo, SHI Cheng, et al. Clutter suppression in GPR B-scan images using robust autoencoder[J]. IEEE Geoscience and Remote Sensing Letters, 2022, 19: 3500705. doi: 10.1109/LGRS.2020.3026007. [32] CAO Yanjie, YANG Xiaopeng, GUO Conglong, et al. Subspace projection attention network for GPR heterogeneous clutter removal[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2024, 17: 3917–3926. doi: 10.1109/JSTARS.2024.3355213. [33] NI Zhikang, SHI Cheng, PAN Jun, et al. Declutter-GAN: GPR B-scan data clutter removal using conditional generative adversarial nets[J]. IEEE Geoscience and Remote Sensing Letters, 2022, 19: 4023105. doi: 10.1109/LGRS.2022.3159788. [34] KAYACAN Y E and ERER I. A vision-transformer-based approach to clutter removal in GPR: DC-ViT[J]. IEEE Geoscience and Remote Sensing Letters, 2024, 21: 3505105. doi: 10.1109/LGRS.2024.3385694. [35] ZHANG Yan, DIAO Enmao, HUSTON D, et al. A data-efficient deep learning method for rough surface clutter reduction in GPR images[J]. IEEE Transactions on Geoscience and Remote Sensing, 2024, 62: 5104610. doi: 10.1109/TGRS.2024.3382545. [36] LI Boyang, YUAN Da, YANG Gexing, et al. Flexibility-residual BiSeNetV2 for GPR image decluttering[J]. IEEE Transactions on Geoscience and Remote Sensing, 2023, 61: 5106812. doi: 10.1109/TGRS.2023.3296722. [37] WARREN C, GIANNOPOULOS A, and GIANNAKIS I. gprMax: Open source software to simulate electromagnetic wave propagation for ground penetrating radar[J]. Computer Physics Communications, 2016, 209: 163–170. doi: 10.1016/j.cpc.2016.08.020. -



 作者中心
作者中心 专家审稿
专家审稿 责编办公
责编办公 编辑办公
编辑办公
 下载:
下载: