作者中心
专家审稿
责编办公
编辑办公
Integrated Jamming Perception and Parameter Estimation Method for Anti-Interrupted Sampling Repeater Jamming
-
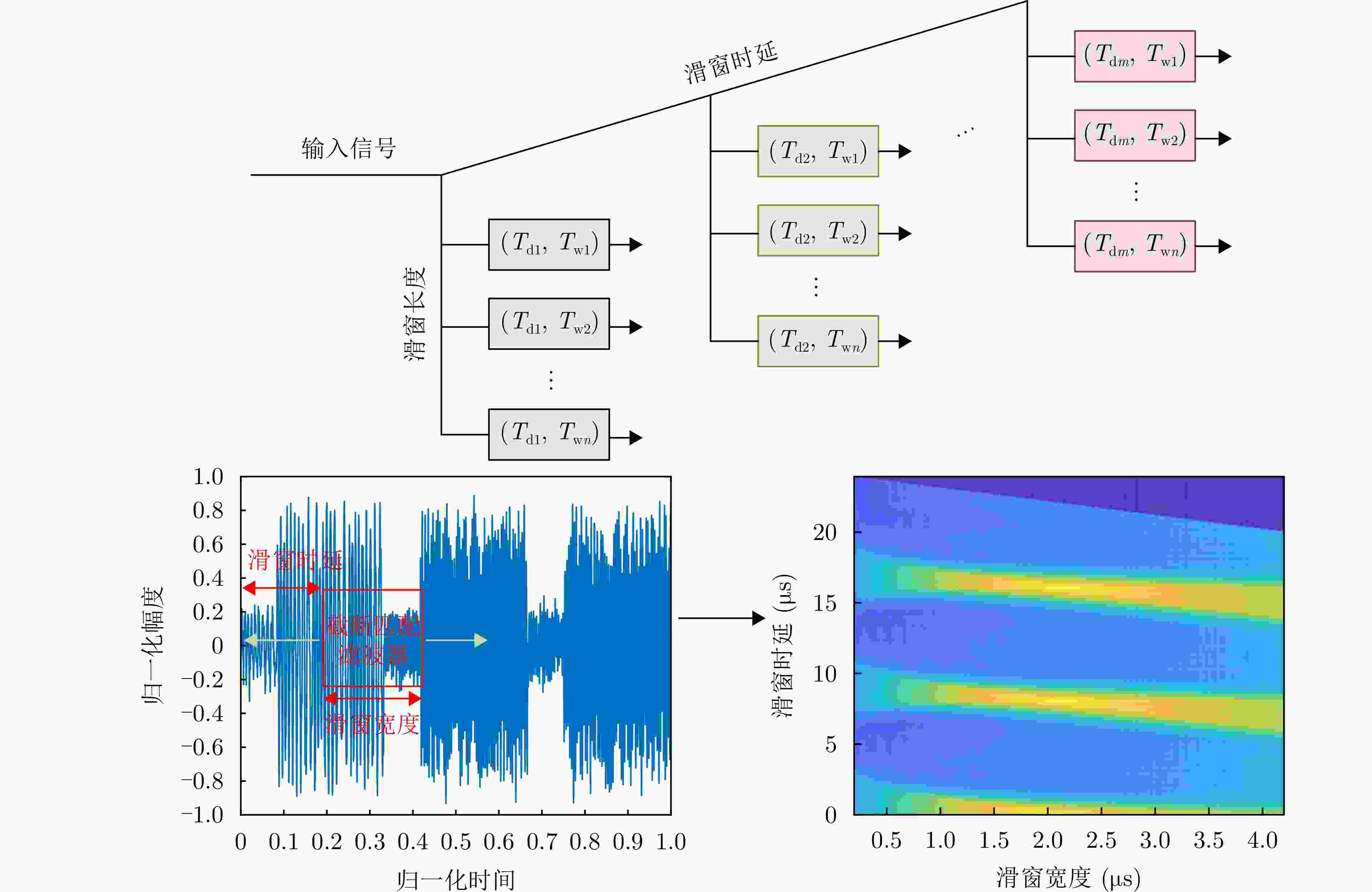
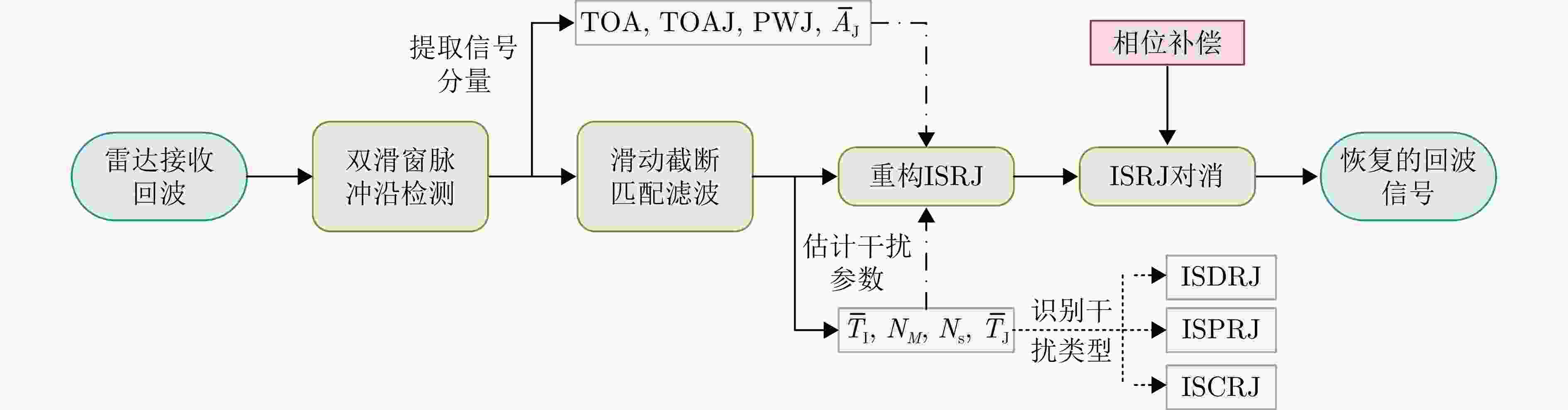
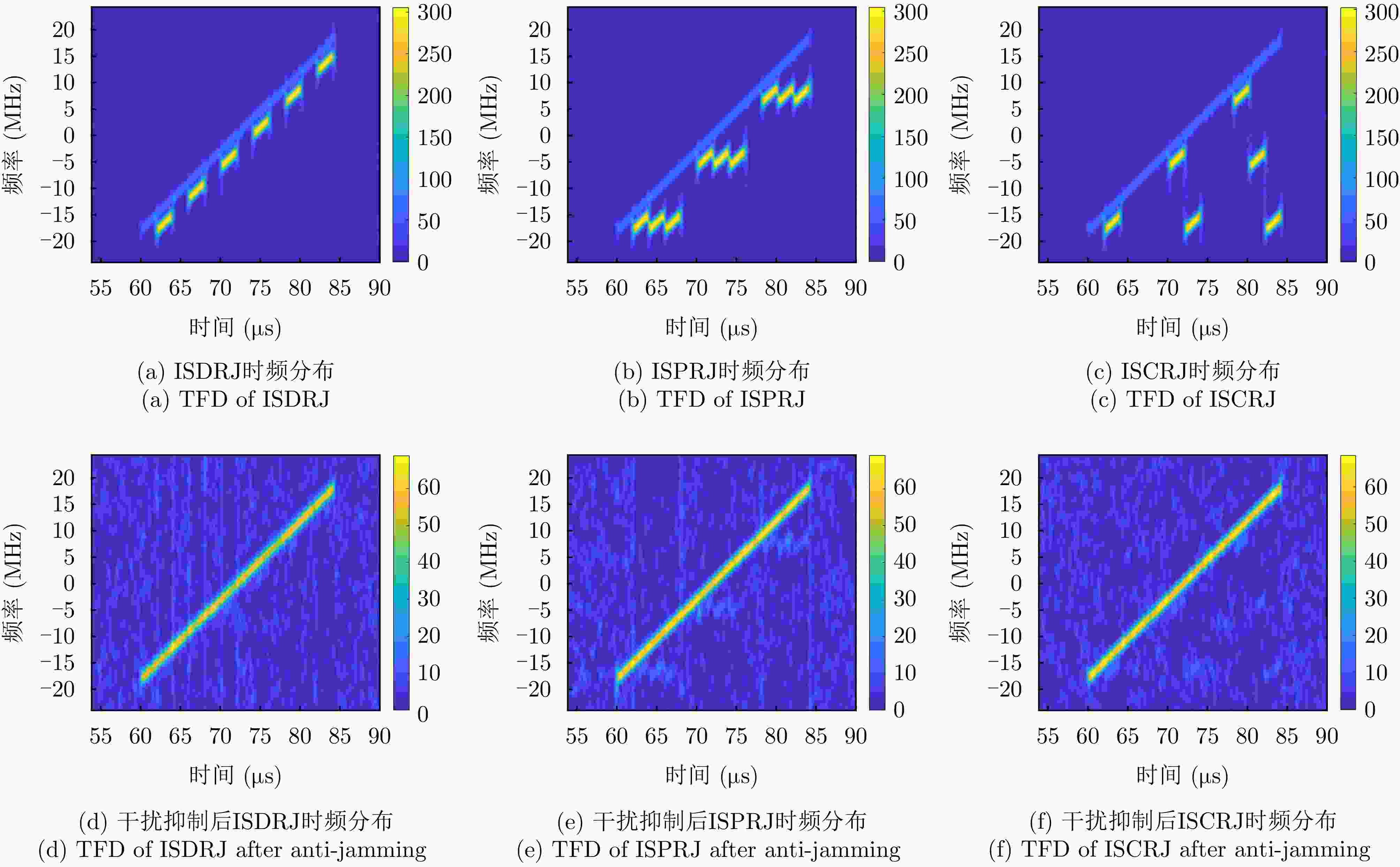
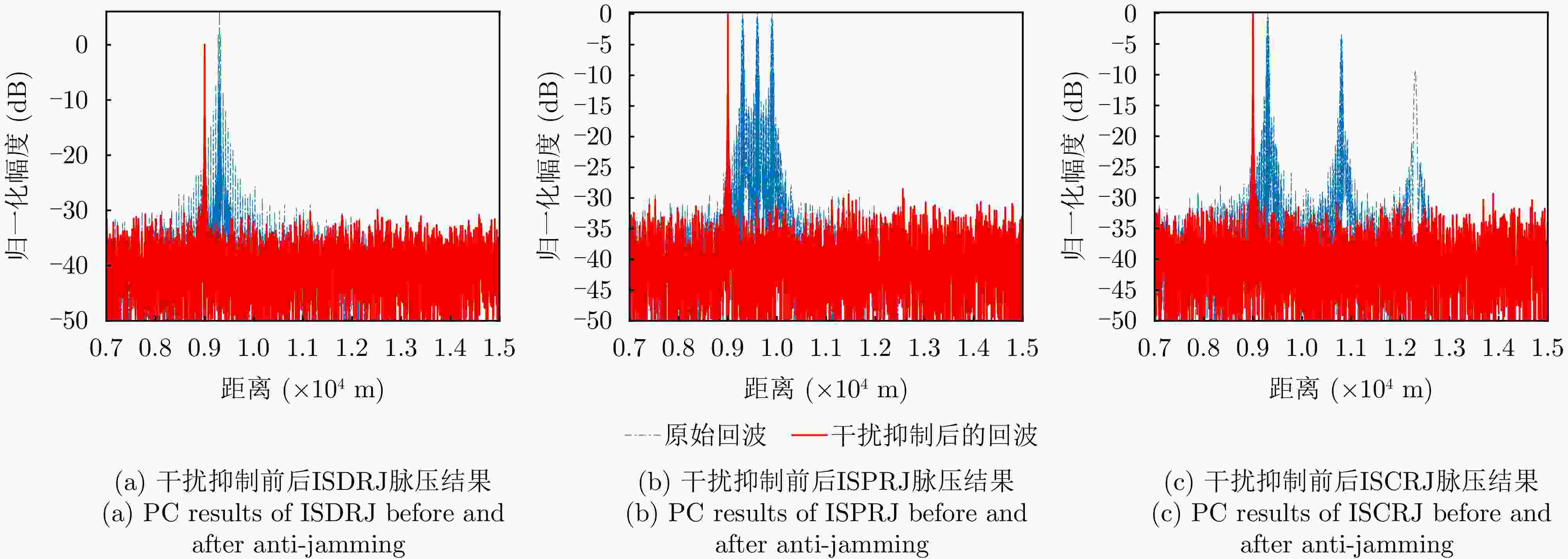
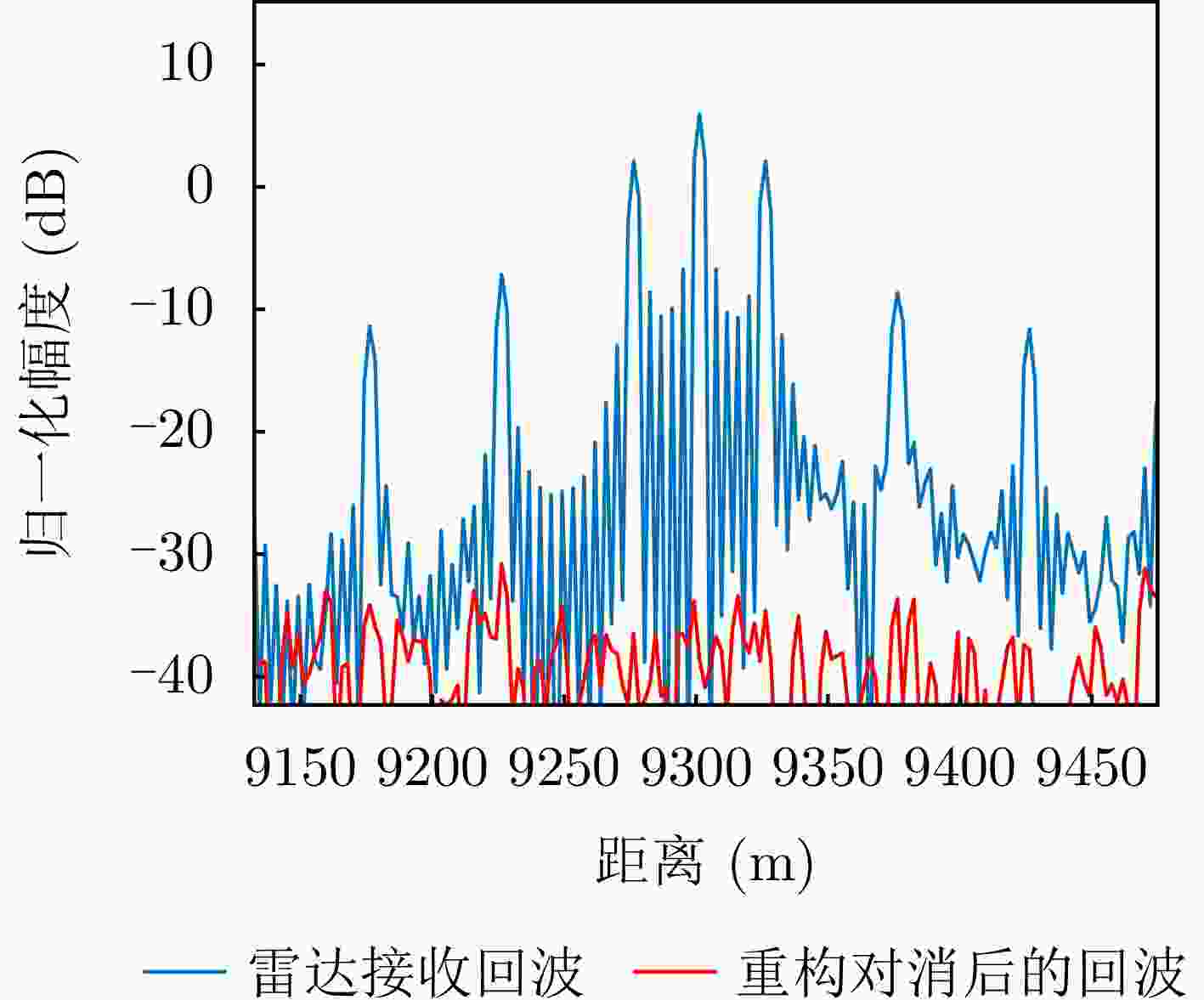
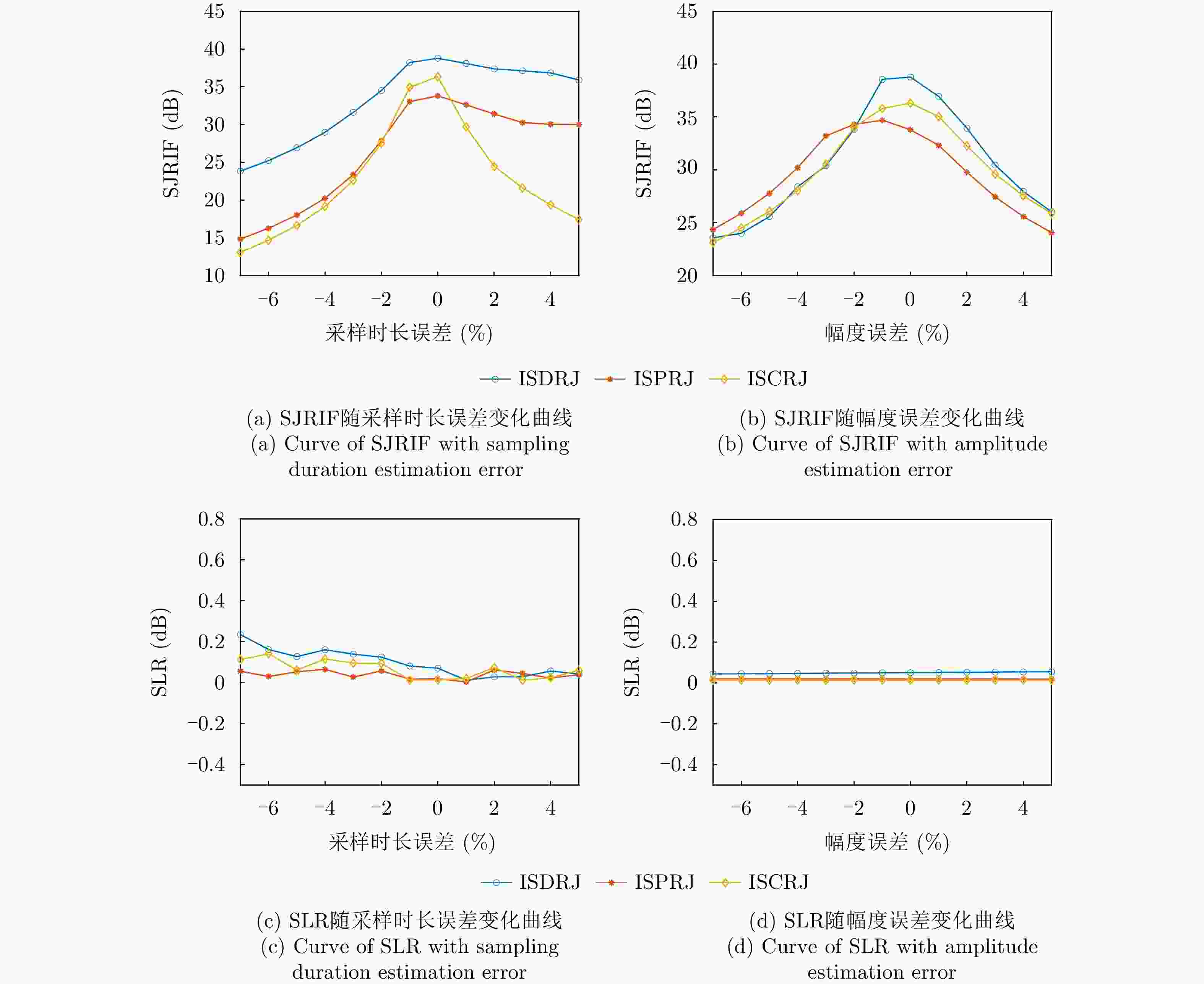
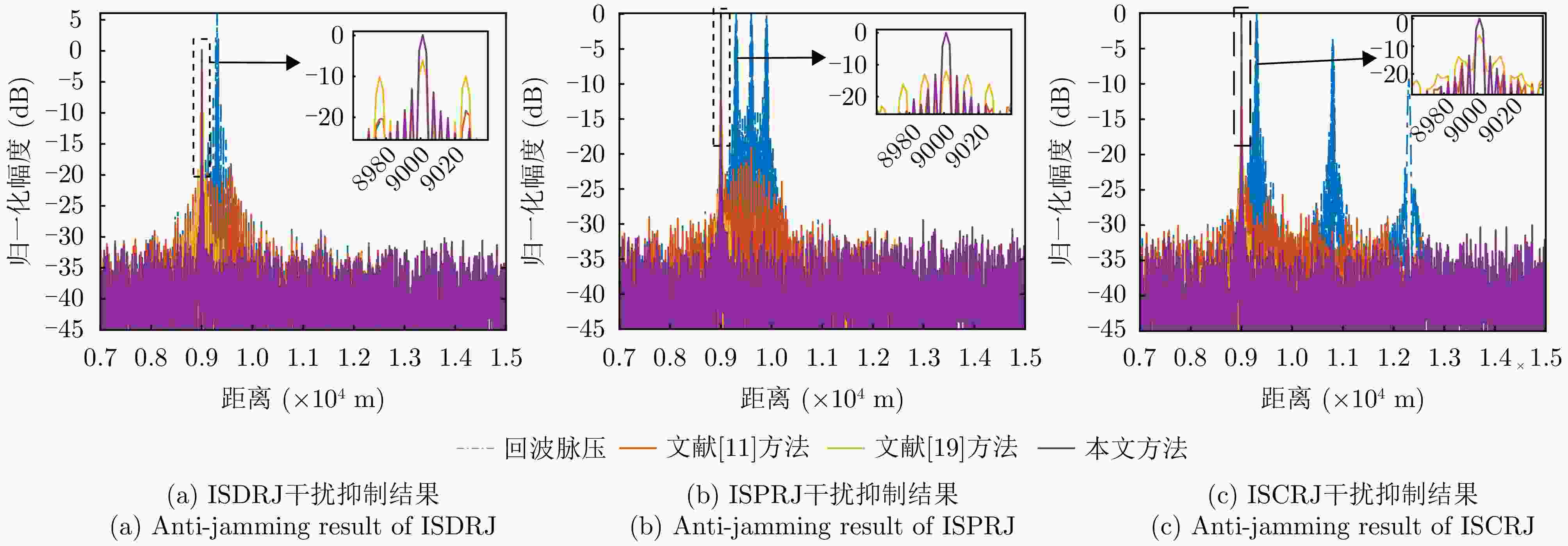
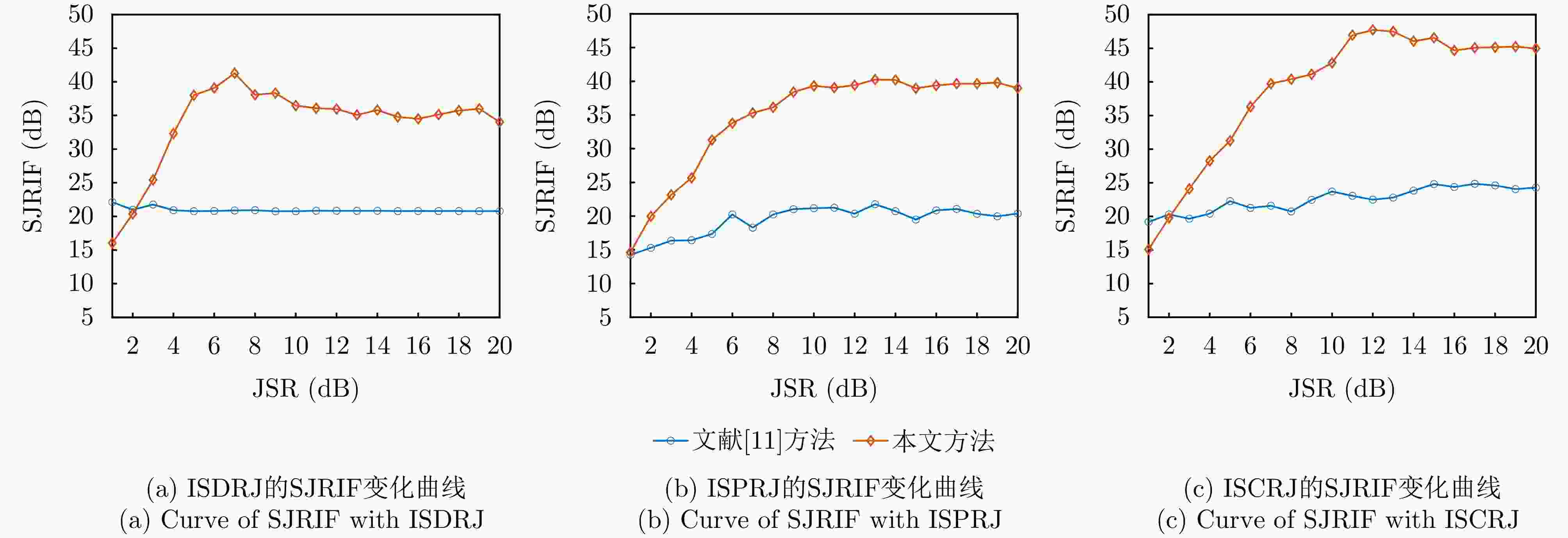
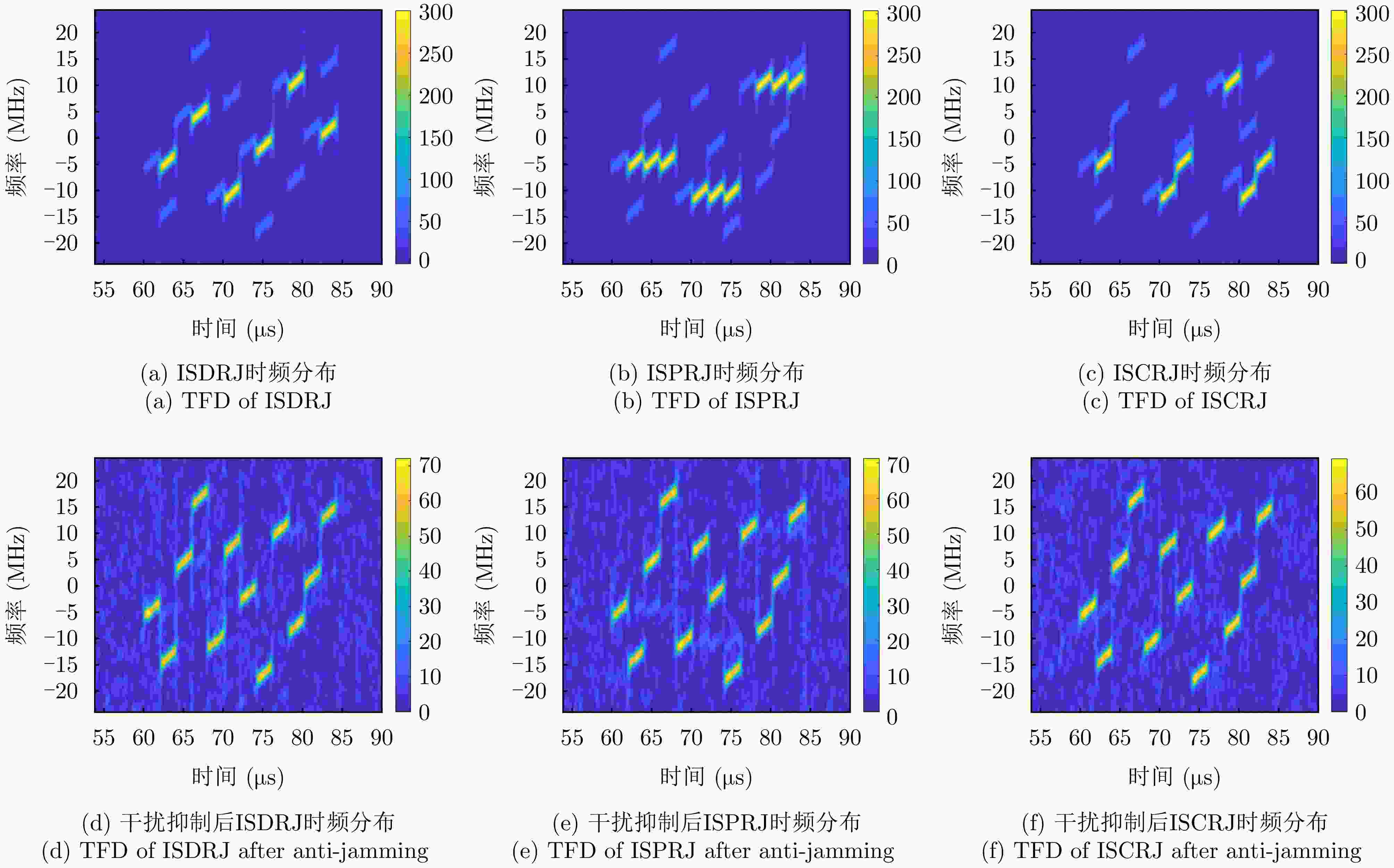
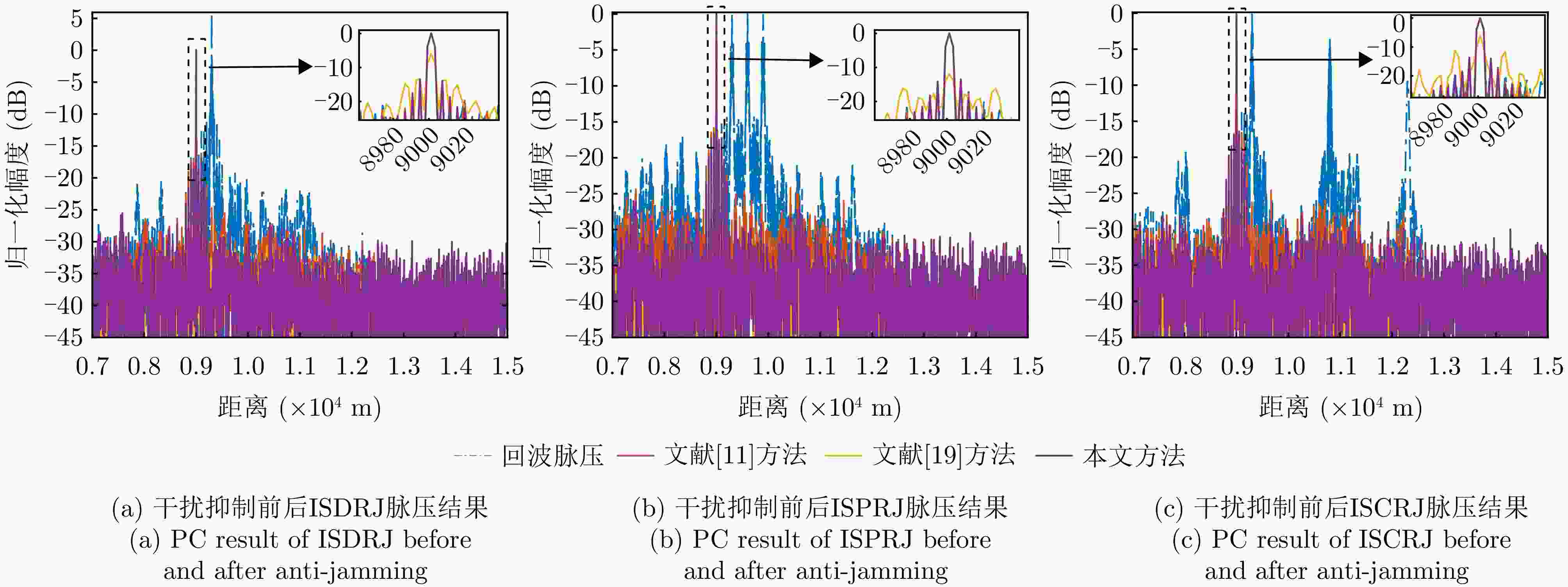
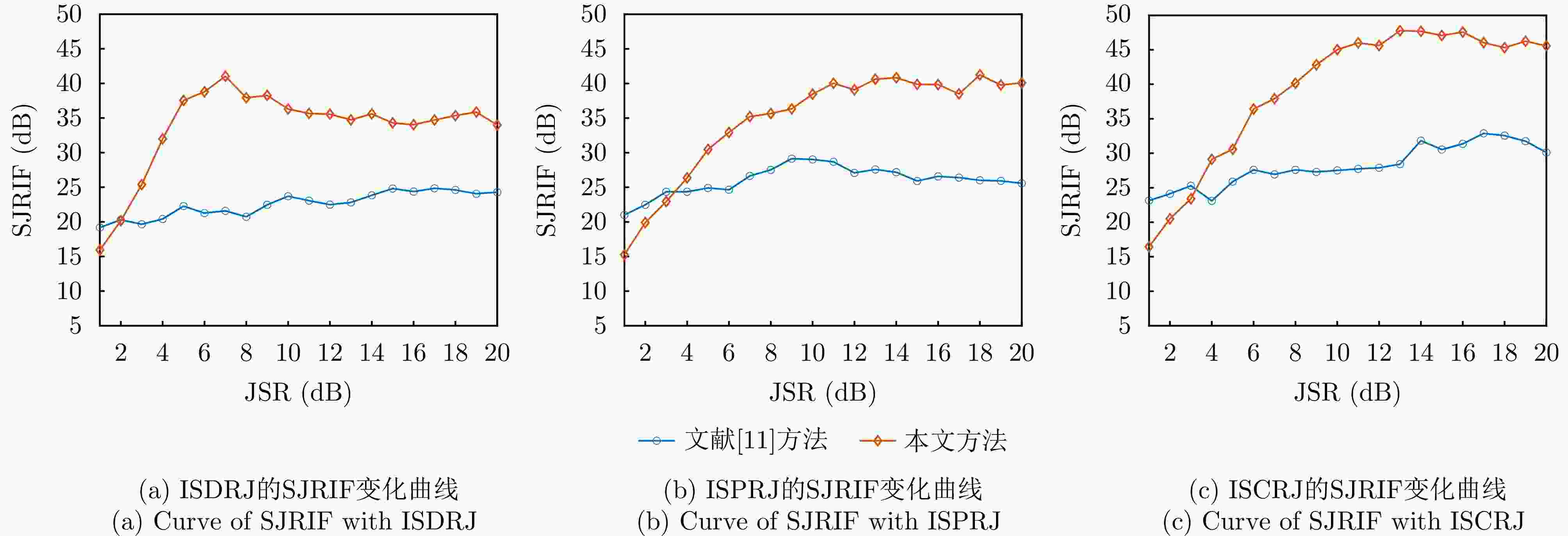
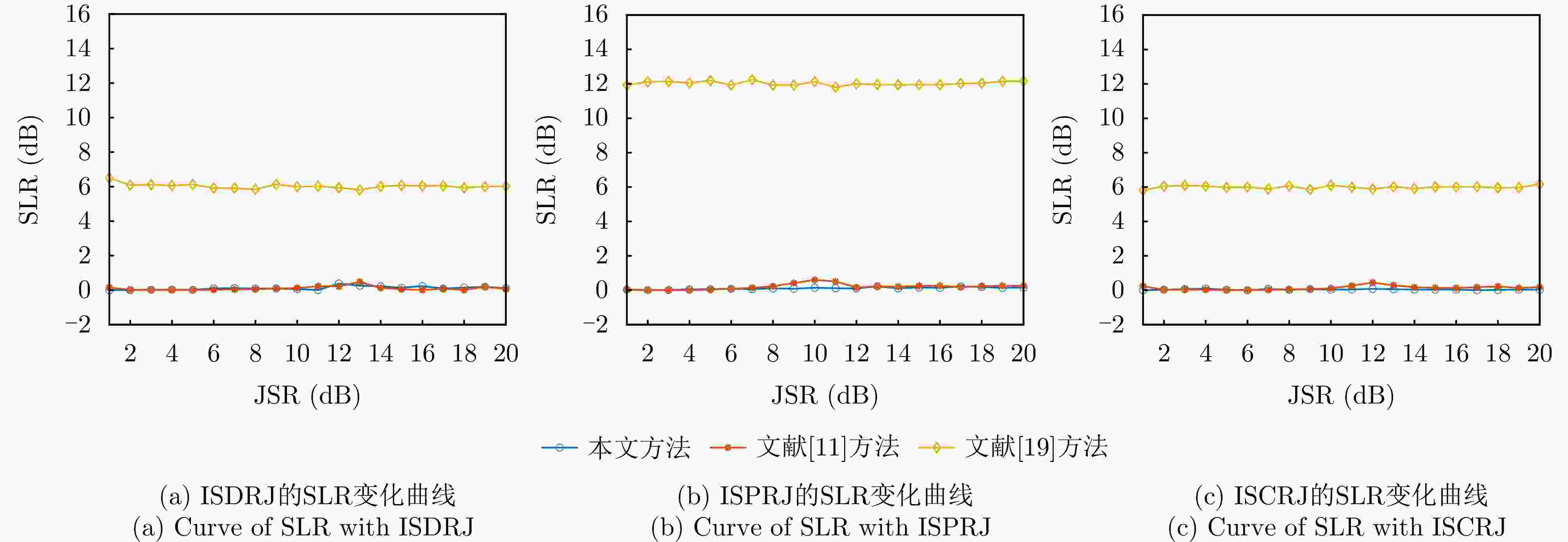
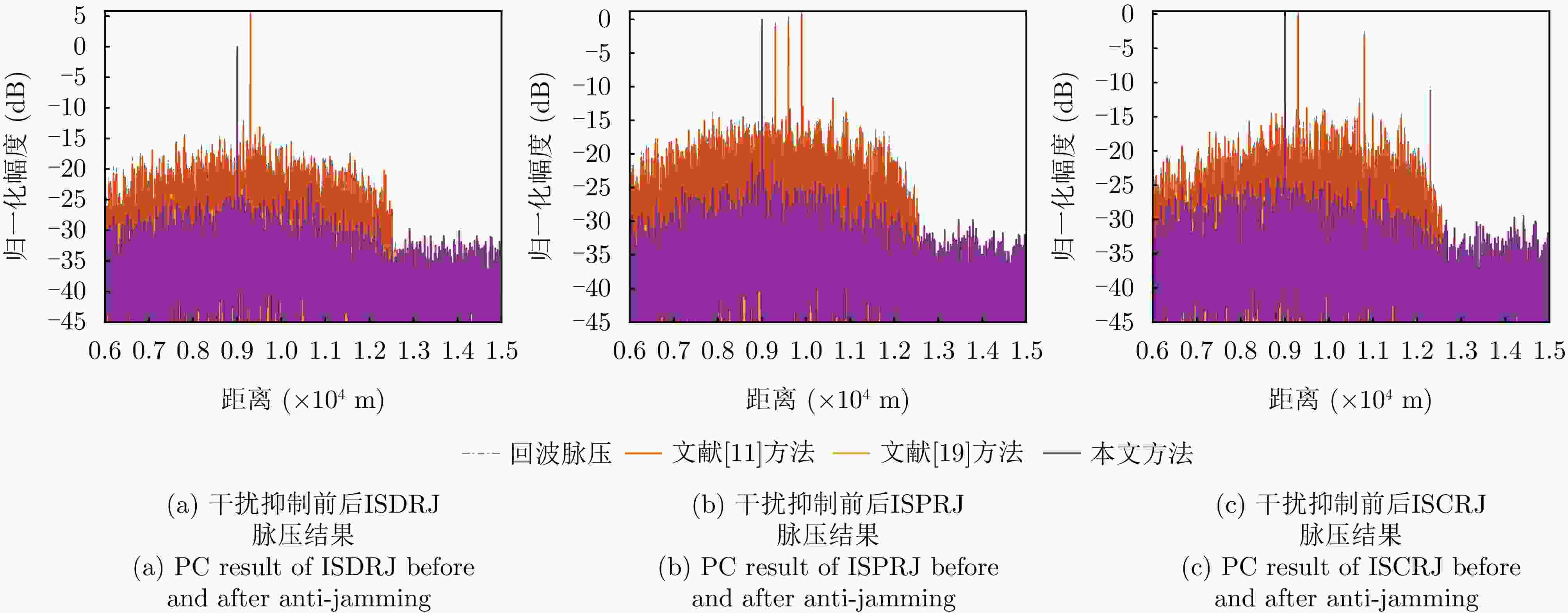
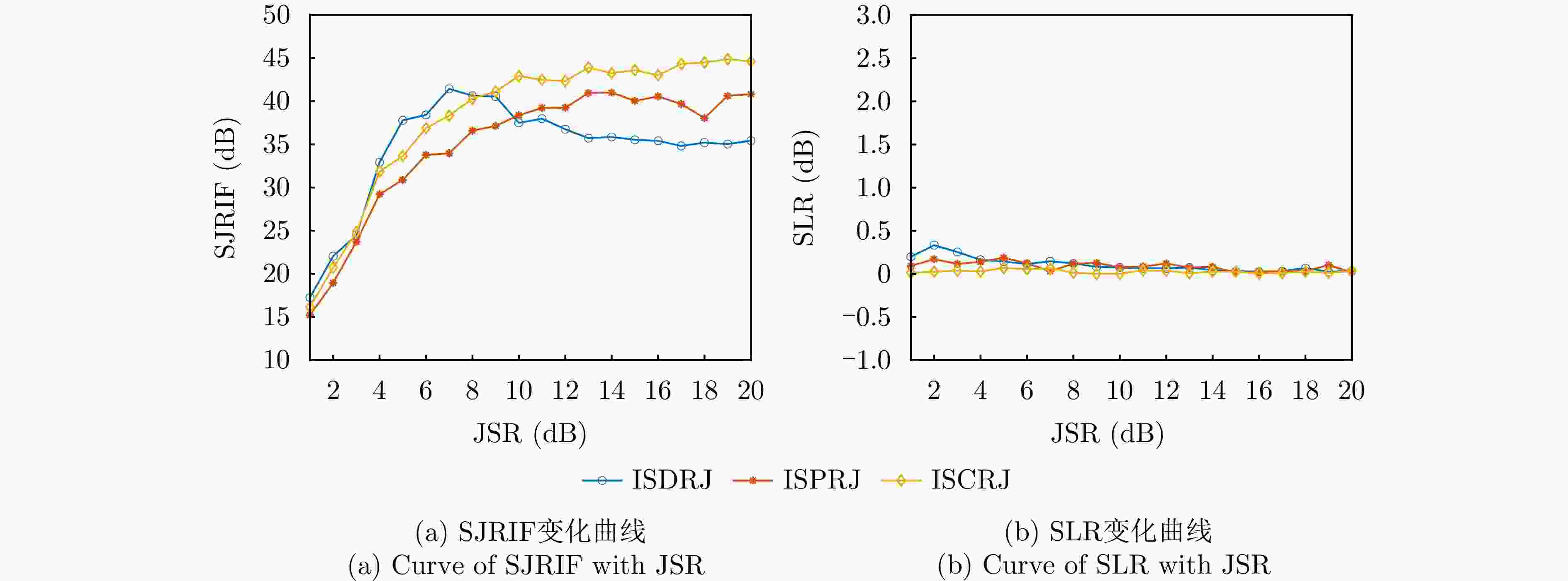
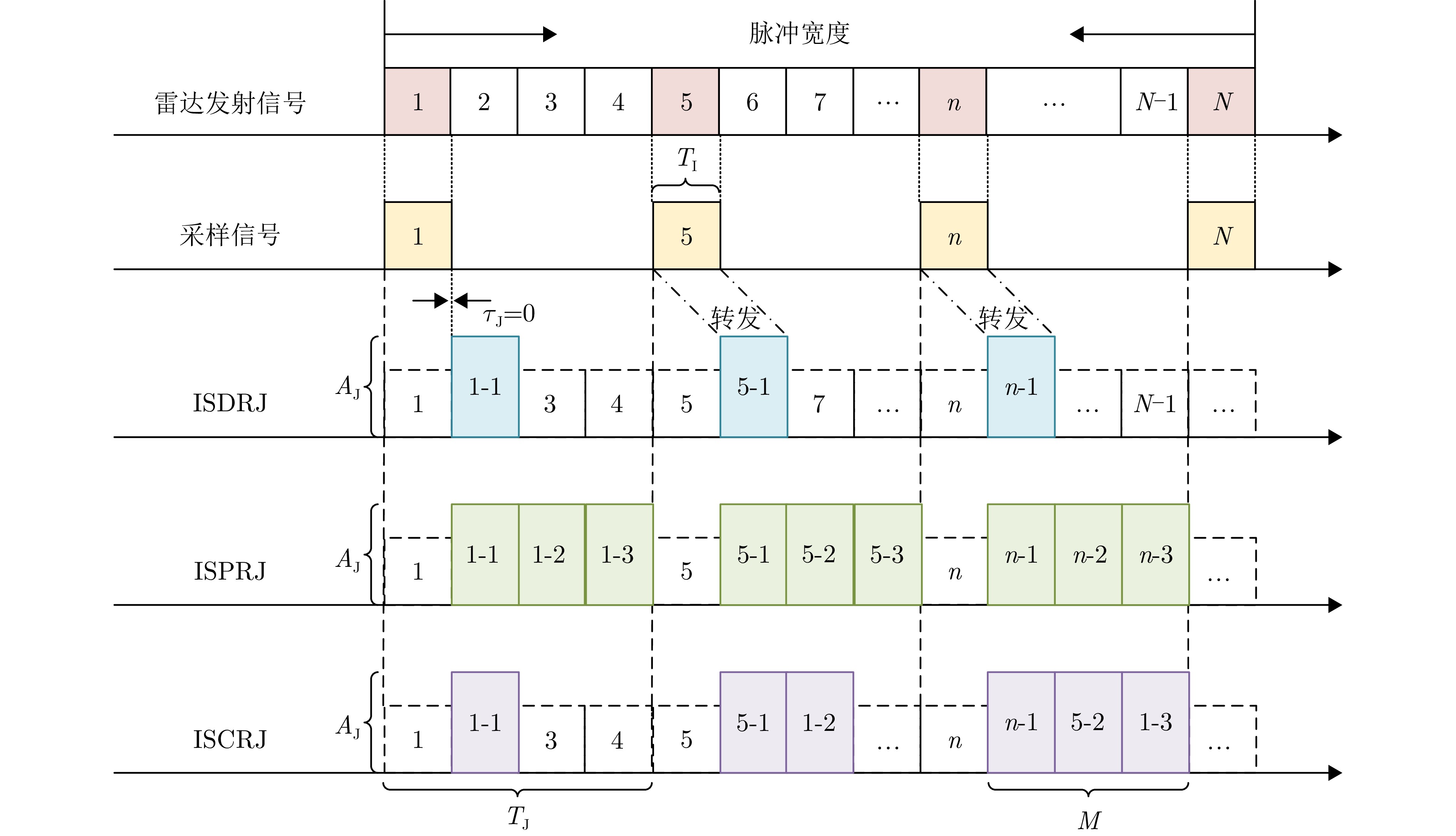
摘要: 间歇采样转发干扰是一种脉内相干干扰，其形成的电子假目标与真实目标高度相似，对雷达目标检测造成了严重威胁。传统抗干扰方法较为被动，且没有考虑到干扰机策略的变化，在干扰抑制时难免会出现干扰残留以及信号损失的情况。为了提升雷达抗干扰性能，该文提出一种联合“干扰感知-参数估计-干扰抑制”的抗干扰方案。首先，利用双向-双滑窗脉冲沿检测和滑动截断匹配滤波方法，准确提取接收回波中的干扰分量并估计采样时长和周期等参数。在此基础上，重构出干扰信号分量并将其从回波中剔除，从而确保准确有效的目标检测。仿真实验表明，所提方法在不损失信号能量的情况下，对于不同调制方式下的间歇采样转发干扰都具有较好的抑制效果。当干噪比为9 dB时，干扰抑制后信干比提升大于33 dB，保证了雷达稳健的抗干扰性能。Abstract: Interrupted Sampling Repeater Jamming (ISRJ) is a type of intra-pulse coherent jamming that can easily generate false targets resembling real ones, thus posing a severe threat to radar systems. Traditional methods for countering ISRJ techniques are relatively passive and often fail to adapt to evolving jamming techniques, leading to residual jamming effects and signal loss. To improve radar’s anti-jamming capabilities, a novel scheme integrating “jamming perception, parameter estimation, and jamming suppression” has been developed in this study. This method begins by using a bidirectional double sliding window pulse edge detector and a sliding truncated matched filter. These devices are used to extract the ISRJ components of received radar signals and accurately estimate the parameters such as sampling duration and period. The jamming components are then reconstructed and eliminated, allowing for effective target detection. Simulation experiments demonstrate that the proposed method effectively overcomes ISRJ across different modulation modes with almost no loss of signal energy. When the jamming-to-noise ratio is 9 dB, the method boosts the signal-to-jamming ratio by over 33 dB after jamming suppression, ensuring robust anti-ISRJ performance.
-
图 3 双向-双滑窗脉冲检测示意图
Figure 3. Schematic diagram of bidirectional dual-window pulse edge detection
图 7 ISPRJ脉冲检测与参数估计结果
Figure 7. Pulse edge detection and parameter estimation results of echo with ISPRJ
图 9 LFM波形干扰抑制前后回波时频分布情况
Figure 9. TFD of received echo before and after anti-jamming of LFM waveform
图 10 LFM波形干扰抑制前后回波脉压结果
Figure 10. PC results of received echo before and after anti-jamming of LFM waveform
图 12 性能指标随参数估计误差变化曲线
Figure 12. The variation curves of performance index with parameter estimation error
图 13 LFM波形不同方法干扰抑制后脉压结果对比图
Figure 13. Comparison of PC results after anti-jamming by different methods of LFM waveform
图 14 LFM波形下SJRIF随JSR变化曲线
Figure 14. The variation curves of SJRIF with JSR for LFM waveform
图 15 LFM波形下SLR随JSR变化曲线
Figure 15. The variation curves of SLR with JSR for LFM waveform
图 16 捷变波形干扰抑制前后回波时频分布情况
Figure 16. TFD of received echo before and after anti-jamming of agile waveform
图 17 捷变波形干扰抑制前后回波脉压结果
Figure 17. PC results of received echo before and after anti-jamming of agile waveform
图 18 捷变波形下SJRIF随JSR变化曲线
Figure 18. The variation curves of SJRIF with JSR for agile waveform
图 19 捷变波形下SLR随JSR变化曲线
Figure 19. The variation curves of SLR with JSR for agile waveform
图 20 相位编码波形干扰抑制前后回波脉压结果
Figure 20. PC results of received echo before and after anti-jamming of phase-coded waveform
图 21 相位编码波形下性能指标随JSR变化曲线
Figure 21. The variation curves of performance index with JSR for phase-coded waveform
表 1 雷达与目标参数
Table 1. Radar and target parameters
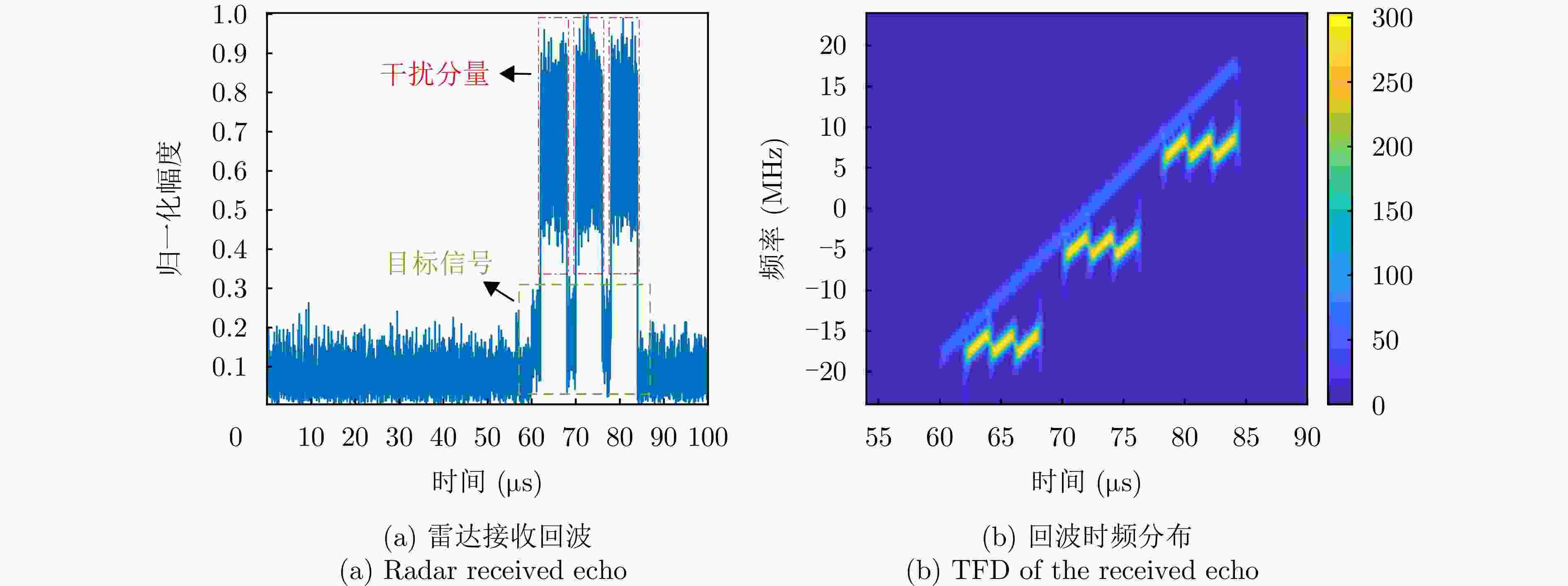
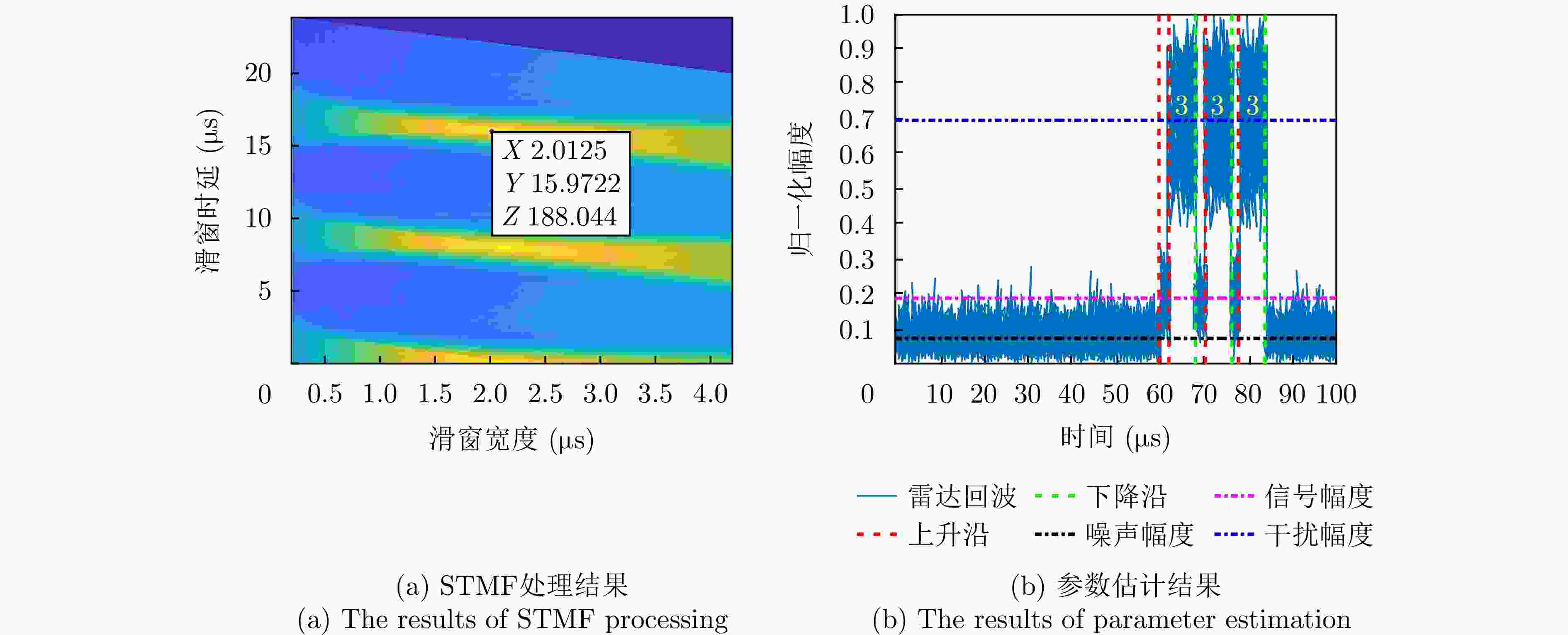
参数 数值 脉冲宽度T 24 μs 信号带宽B 36 MHz 采样率${f_{\text{s}}}$ 72 MHz 脉冲重复周期${\text{PRI}}$ 100 μs 中心载频${f_{\text{c}}}$ 3 GHz 目标距离R 9 km 
下载: 导出CSV
表 2 干扰机参数
Table 2. Jammer parameters
参数 数值 干扰转发时延${\tau _{\text{J}}}$ 0 μs 干扰采样时长${T_{\text{I}}}$ 2 μs 干扰采样周期${T_{\text{J}}}$ 8 μs 转发次数M 3 信噪比SNR 3 dB 干信比JSR 6 dB
下载: 导出CSV
-
[1] ARIK M and AKAN O B. Enabling cognition on electronic countermeasure systems against next-generation radars[C]. MILCOM 2015-2015 IEEE Military Communications Conference, Tampa, USA, 2015: 1103–1108. doi: 10.1109/MILCOM.2015.7357593. [2] HEAGNEY C P. Digital radio frequency memory synthetic instrument enhancing US navy automated test equipment mission[J]. IEEE Instrumentation & Measurement Magazine, 2018, 21(4): 41–63. doi: 10.1109/MIM.2018.8423745. [3] LEWIS G K, BAHL I J, GRIFFIN E L, et al. GaAs MMIC’s for digital radio frequency memory (DRFM) subsystems[J]. IEEE Transactions on Microwave Theory and Techniques, 1987, 35(12): 1477–1485. doi: 10.1109/TMTT.1987.1133878. [4] WANG Xuesong, LIU Jiancheng, ZHANG Wenming, et al. Mathematic principles of interrupted-sampling repeater jamming (ISRJ)[J]. Science in China Series F: Information Sciences, 2007, 50(1): 113–123. doi: 10.1007/s11432-007-2017-y. [5] OLIVIER K, CILLIERS J E, and DU PLESSIS M. Design and performance of wideband DRFM for radar test and evaluation[J]. Electronics Letters, 2011, 47(14): 824–825. doi: 10.1049/el.2011.0362. [6] 张建中, 穆贺强, 文树梁, 等. 基于脉内LFM-Costas频率步进的抗间歇采样干扰方法[J]. 系统工程与电子技术, 2019, 41(10): 2170–2177. doi: 10.3969/j.issn.1001-506X.2019.10.03.ZHANG Jianzhong, MU Heqiang, WEN Shuliang, et al. Anti-intermittent sampling jamming method based on intra-pulse LFM-Costas frequency stepping[J]. Systems Engineering and Electronics, 2019, 41(10): 2170–2177. doi: 10.3969/j.issn.1001-506X.2019.10.03. [7] ZHANG Yang, YU Lei, and WEI Yinsheng. Interrupted sampling repeater jamming countermeasure technology based on random interpulse frequency coding LFM signal[J]. Digital Signal Processing, 2022, 131: 103755. doi: 10.1016/j.dsp.2022.103755. [8] 周畅, 汤子跃, 余方利, 等. 基于脉内正交的抗间歇采样转发干扰方法[J]. 系统工程与电子技术, 2017, 39(2): 269–276. doi: 10.3969/j.issn.1001-506X.2017.02.06.ZHOU Chang, TANG Ziyue, YU Fangli, et al. Anti intermittent sampling repeater jamming method based on intrapulse orthogonality[J]. Systems Engineering and Electronics, 2017, 39(2): 269–276. doi: 10.3969/j.issn.1001-506X.2017.02.06. [9] ZHANG Jiaxiang and ZHOU Chao. Interrupted sampling repeater jamming suppression method based on hybrid modulated radar signal[C]. 2019 IEEE International Conference on Signal, Information and Data Processing (ICSIDP), Chongqing, China, 2019: 1–4. doi: 10.1109/ICSIDP47821.2019.9173093. [10] ZHANG Yang, WEI Yinsheng, and YU Lei. Interrupted sampling repeater jamming recognition and suppression based on phase-coded signal processing[J]. Signal Processing, 2022, 198: 108596. doi: 10.1016/j.sigpro.2022.108596. [11] 刘智星, 杜思予, 吴耀君, 等. 脉间-脉内捷变频雷达抗间歇采样干扰方法[J]. 雷达学报, 2022, 11(2): 301–312. doi: 10.12000/JR22001.LIU Zhixing, DU Siyu, WU Yaojun, et al. Anti-interrupted sampling repeater jamming method for interpulse and intrapulse frequency-agile radar[J]. Journal of Radars, 2022, 11(2): 301–312. doi: 10.12000/JR22001. [12] LIU Zhixing, QUAN Yinghui, DU Siyu, et al. A novel ECCM scheme against interrupted-sampling repeater jamming using intra-pulse dual-parameter agile waveform[J]. Digital Signal Processing, 2022, 129: 103652. doi: 10.1016/j.dsp.2022.103652. [13] ZHOU Kai, LI Dexin, SU Yi, et al. Joint design of transmit waveform and mismatch filter in the presence of interrupted sampling repeater jamming[J]. IEEE Signal Processing Letters, 2020, 27: 1610–1614. doi: 10.1109/LSP.2020.3021667. [14] ZHOU Kai, LI Dexin, QUAN Sinong, et al. SAR waveform and mismatched filter design for countering interrupted-sampling repeater jamming[J]. IEEE Transactions on Geoscience and Remote Sensing, 2022, 60: 5214514. doi: 10.1109/TGRS.2021.3107328. [15] WANG Fulai, LI Nanjun, PANG Chen, et al. Complementary sequences and receiving filters design for suppressing interrupted sampling repeater jamming[J]. IEEE Geoscience and Remote Sensing Letters, 2022, 19: 4022305. doi: 10.1109/LGRS.2022.3156164. [16] 盖季妤, 姜维, 张凯翔, 等. 基于差分特征的间歇采样转发干扰辨识与抑制方法[J]. 雷达学报, 2023, 12(1): 186–196. doi: 10.12000/JR22058.GAI Jiyu, JIANG Wei, ZHANG Kaixiang, et al. A method for interrupted-sampling repeater jamming identification and suppression based on differential features[J]. Journal of Radars, 2023, 12(1): 186–196. doi: 10.12000/JR22058. [17] CHEN Jian, WU Wenzhen, XU Shiyou, et al. Band pass filter design against interrupted-sampling repeater jamming based on time-frequency analysis[J]. IET Radar, Sonar & Navigation, 2019, 13(10): 1646–1654. doi: 10.1049/iet-rsn.2018.5658. [18] 周超, 刘泉华, 胡程. 间歇采样转发式干扰的时频域辨识与抑制[J]. 雷达学报, 2019, 8(1): 100–106. doi: 10.12000/JR18080.ZHOU Chao, LIU Quanhua, and HU Cheng. Time-frequency analysis techniques for recognition and suppression of interrupted sampling repeater jamming[J]. Journal of Radars, 2019, 8(1): 100–106. doi: 10.12000/JR18080. [19] 张建中, 穆贺强, 文树梁, 等. 基于脉内步进LFM时频分析的抗间歇采样干扰方法[J]. 北京理工大学学报, 2020, 40(5): 543–551. doi: 10.15918/j.tbit1001-0645.2018.202.ZHANG Jianzhong, MU Heqiang, WEN Shuliang, et al. Anti-intermittent sampling repeater jamming method based on stepped LFM joint time-frequency analysis[J]. Transactions of Beijing Institute of Technology, 2020, 40(5): 543–551. doi: 10.15918/j.tbit1001-0645.2018.202. [20] 杜思予, 刘智星, 吴耀君, 等. 频率捷变波形联合时频滤波器抗间歇采样转发干扰[J]. 系统工程与电子技术, 2023, 45(12): 3819–3827. doi: 10.12305/j.issn.1001-506X.2023.12.11.DU Siyu, LIU Zhixing, WU Yaojun, et al. Frequency agility waveform combined with time-frequency filter to suppress interrupted-sampling repeater jamming[J]. Systems Engineering and Electronics, 2023, 45(12): 3819–3827. doi: 10.12305/j.issn.1001-506X.2023.12.11. [21] ZHENG Hao, JIU Bo, and LIU Hongwei. Waveform design based ECCM scheme against interrupted sampling repeater jamming for wideband MIMO radar in multiple targets scenario[J]. IEEE Sensors Journal, 2022, 22(2): 1652–1669. doi: 10.1109/JSEN.2021.3131491. [22] WEI Zhenhua, LIU Zhen, PENG Bo, et al. ECCM scheme against interrupted sampling repeater jammer based on parameter-adjusted waveform design[J]. Sensors, 2018, 18(4): 1141. doi: 10.3390/s18041141. [23] ZHOU Chao, LIU Quanhua, and CHEN Xinliang. Parameter estimation and suppression for DRFM-based interrupted sampling repeater jammer[J]. IET Radar, Sonar & Navigation, 2018, 12(1): 56–63. doi: 10.1049/iet-rsn.2017.0114. [24] LU Lu and GAO Meiguo. A truncated matched filter method for interrupted sampling repeater jamming suppression based on jamming reconstruction[J]. Remote Sensing, 2022, 14(1): 97. doi: 10.3390/rs14010097. [25] 周超, 刘泉华, 曾涛. DRFM间歇采样转发式干扰辨识算法研究[J]. 信号处理, 2017, 33(7): 911–917. doi: 10.16798/j.issn.1003-0530.2017.07.002.ZHOU Chao, LIU Quanhua, and ZENG Tao. Research on DRFM repeater jamming recognition[J]. Journal of Signal Processing, 2017, 33(7): 911–917. doi: 10.16798/j.issn.1003-0530.2017.07.002. -
计量
- 文章访问数: 204
- HTML全文浏览量: 63
- PDF下载量: 258
- 被引次数: 0
