1.   引言

通过非接触式的心率呼吸等生理参数的实时检测，将改变传统医疗的研究范式。相对于传统的穿戴式检测，非接触式方法可以在用户的自然状态下，实现全方位监测，因此更有利于获取海量的数据，为医疗研究与健康应用提供基础。比如慢病的长期管理，通过非接触式传感，进行远程监测和诊断，及时调整治疗方案，实现远程医疗，让慢病患者减少入院次数，节约医疗资源；又比如通过非接触式传感，可以长期收集个体的数据，使得个性医疗成为可能，利用个体的长期数据可以建立个性化的健康模型，从而更有针对性地提供医疗健康服务。

在非接触式的监测手段中，相较于采用成像技术(比如摄像头^[1]，红外线成像^[2]等)，使用雷达的方法，由于其输出信号无法被人类直接解读，因此更有利于保护用户的隐私。同时，由于雷达具有穿透性，不像成像技术会受到不同光线强度的影响以及遮挡的影响。

在早期的研究中通常使用连续波(Continuous Wave, CW)雷达^[3−6]，作为非接触式监测呼吸心跳的简单可靠设备，并通过感知胸腔心前区的位移获取多普勒心肺图(Doppler Cardiopulmonary Diagram, DCD)信号。使用CW雷达的研究提出了几种方法来提高心率估计准确性^[7−10]。其中复数解调无法完全消除强烈的谐波和互调制项(Inter modulation terms)，从而难以获得高信噪比(Signal-to-Noise Ratio, SNR)的多普勒心跳图(Doppler Heartbeat Diagram, DHD)信号^[11]。通过使用反正切解调，实现了完美的相位提取，从而直接获取DCD信号^[12]。然而，完美的相位解调依赖于精确的直流偏置补偿^[13]。此外，传统连续波雷达在获取绝对距离位置上存在局限，这导致在实际场景中不同距离的目标和杂波容易混淆。为此，研究者提出了其他调制的雷达设计方案，如调频连续波(Frequency Modulated Continuous Wave, FMCW)雷达^[14−19]、谐波雷达和超宽带(Ultra-WideBand, UWB)雷达^[20]，以应对更加复杂的应用场景。比如文献[21]通过不同的距离仓区分不同的用户与环境反射，实现了室内的多人体征检测。又比如文献[22]利用FMCW的距离分辨率在行驶的汽车内提取了多人的呼吸信号以及驾驶员的心跳信号。另外一些研究利用FMCW不同位置的位移信号恢复出不同的生理信号^[23,24]。比如文献[24]通过在选取在心跳频带能量最大的角度距离仓的信号，恢复出同步采集的心脏振动描记图(Seismocardiogram, SCG)信号。又如文献[25]利用FMCW MIMO雷达通过距离DTFT和角度DTFT，整合人体不同距离和角度位置的振动以及域变换，恢复出心电图(Electrocardiogram, ECG)信号。

传统上，在从FMCW雷达信号中提取生命体征信号的流程中，第1步是通过I和Q通道组成雷达复信号^{[18,19,26,27]}。这与CW雷达相似。IQ通道的不正交也可以通过文献[13]方法进行补偿，但在现实的噪声环境中无法保证最佳校正。第2步是使用快速傅里叶变换(Fast Fourier Transform, FFT)算法对雷达复信号获取距离-时间图。然后根据该图进行人体的定位。文献[18]根据距离-时间图的强度进行手动定位，但需要提前知道要监视的对象数量及其与雷达的真实距离。在文献[26]中，选择了具有最大平均功率的距离仓。文献[21]中，作者减去连续时间测量值以消除静态物体的反射。正确找到与人体相关的信号后，根据相位信息提取胸部振动模式。第3步，通常通过反正切解调算法^[28]提取相位信息，然后进行体征提取。为了补偿反正切函数的边界限制，文献[29]使用了基于反正切函数导数的微分和交叉相乘(Differentiate and Cross-Multiply, DACM)算法。然而，它对噪声高度比较敏感。获取相位之后，估计生命体征最常用的方法是离散傅里叶变换(Discrete Fourier Transform, DFT)频谱，假设静息状态下心跳和呼吸频带不重叠^{[18,19,21,26,30,31]}。

为了可以更精确地提取感兴趣区域的信号，与环境杂波之间实现更好的分离，使用的带宽越来越高，从而使得距离仓宽度变小。对于7 GHz带宽的雷达，距离仓宽度仅2.1 cm。因此，受试者在静止状态下的呼吸幅度，很可能会超过距离仓宽度。导致胸腔的运动跨越距离仓的边界，影响从固定距离仓提取到的信号质量，进而使得部分相位信息无法正确解调。即使目标的呼吸运动范围没有跨越距离仓，也导致雷达复信号受到呼吸的幅度调制，不利于相位信息的提取以及高精确度的波形恢复。

基于上述分析，我们提出了基于距离导向矢量重构的相位提取算法。通过借鉴天线阵列波束形成的思想，根据实际场景中的信号，自适应地生成距离维度上的空间滤波器，实现基于现实场景中距离分布的目标生理信号提取算法。算法的具体架构如图1所示。

图  1  距离抽头重构与动态解调算法

Figure  1.  Range tapper refactoring and dynamic demodulation algorithms

下载: 全尺寸图片 幻灯片

本文的主要贡献如下：

(1) 深入分析了当目标跨越距离仓的条件以及距离FFT引发的幅度调制后对于目标生理信号提取的影响，以及该影响会随着未来雷达带宽的提升日益严峻。

(2) 基于分析提出了基于距离抽头重构的相位提取算法以应对各种跨越距离仓的情况，改善幅度调制，为未来更高带宽的雷达做准备。

(3) 提出了一种基于现实场景中距离分布的生理信号提取算法架构，解决了传统的距离FFT算法在信号提取方面面临的主要问题。

2.   方法

2.1   信号模型

FMCW线性调频连续波雷达的发射信号，频率在一个啁啾(Chirp)内随着时间线性增加：

其中，${A}_{{\mathrm{T}}}$是传输功率，$\phi \left(t\right)$是发射器的相位噪声，${f}_{\mathrm{c}}$和$K=\mathrm{B}\mathrm{W}/{T}_{{\mathrm{s}}}$分别是FMCW信号的起始频率和啁啾斜率。$\mathrm{B}\mathrm{W}$为雷达带宽；t为快时间变量；${T}_{\mathrm{s}}$为一个啁啾的持续时间(Chirp duration)。假设探测空间中只有一个目标，信号被胸腔反射后的接收信号为

其中，α是路径损失，c为光速；R为目标与雷达之间的距离，在一个啁啾之内的变化可忽略不计。然后使用I/Q混频器消除接收信号中的载波，得到信号中频(Intermediate Frequency, IF)。s(t)为

在式(3)中高阶项已被忽略。其中，${f}_{\mathrm{b}}=2KR/\mathrm{c}$代表拍频。拍频信号$s\left(t\right)$在经过I/Q采样后，一个啁啾内的第m个快时间采样信号为

每个啁啾之内共M个快时间采样点, $m=0, 1, \cdots ,{M}-1$，采样间隔为${T}_{\mathrm{f}}$，一个时间窗内收发N个啁啾后，第n个啁啾的慢时间采样为

其中，${T}_{\mathrm{s}}$为啁啾间隔(chirp interval)。在这里，值得注意的是$R\left(n{T}_{\mathrm{s}}\right)$是随着慢时间变化的，反应在中频信号中的相位值$4{\pi }R\left(n{T}_{\mathrm{s}}\right)/\lambda$ ，以及中频信号的频率${f}_{\mathrm{b}}\left(n{T}_{\mathrm{s}}\right)=2KR\left(n{T}_{\mathrm{s}}\right)/\mathrm{c}$。然后从慢时间维度提取相位信息：IQ平衡以及DC，并对比相邻时间上的相位变化${\Delta }\phi$：

继而可以得到胸腔的微小位移与相位变化的关系：

为了从$s[m,n]$样本分离拍频${f}_{\mathrm{b}}\left(n{T}_{\mathrm{s}}\right)$与微小位移$R\left(n{T}_{\mathrm{s}}\right)$，通常需要先在快时间维度进行FFT，确定目标的距离仓，每个距离仓对目标运动的响应为

这里令$x(k,n)=2\pi {(f}_{\mathrm{b}}\left(n{T}_{\mathrm{s}}\right){T}_{\mathrm{f}}-{k}/{{M}})=2\pi (R\left(n{T}_{\mathrm{s}}\right)/ {R}_{\mathrm{m}\mathrm{a}\mathrm{x}}-{k}/{{M}})$，其中，${R}_{\mathrm{m}\mathrm{a}\mathrm{x}}={M}\mathrm{c}/(2\mathrm{B}\mathrm{W})$为雷达最大探测距离，雷达距离分辨度或距离仓的宽度为

信号与目标位置的幅度响应为

相位响应为

2.2   距离FFT问题分析

从式(9)可以得到，对于一个拥有4 GHz带宽的毫米波雷达^[32]，距离仓宽度约为3.75 cm，而最近新发布的一些雷达可以达到7 GHz^[33]，对应的距离仓宽度约为2.14 cm。而人的静息呼吸所引起的胸腔外壁移动2～3 cm，而深呼吸则可以达到5 cm^[34]。2.2.1节将量化分析距离FFT导致的幅度调制，以及幅度调制对信号解调的影响；2.2.2节将探讨反射面跨越距离仓的发生条件；2.3节将探讨跨越距离仓对于信号完整性的影响。

2.2.1   距离FFT导致的幅度调制问题

图2展示了距离FFT引发信号幅度调制以及跨距离仓的问题，图2(a)显示了距离仓10和距离仓11 对目标位置R的幅度响应，如式(10)：图中蓝线为$S\left(10,R\left(n{T}_{\mathrm{s}}\right)\right)$ ，橙线为$S\left(11,R\left(n{T}_{\mathrm{s}}\right)\right)$。假设$R\left({{n}{T}}_{\mathrm{s}}\right)$在距离仓10.5附近做往复运动，幅度为$\mathrm{a}\mathrm{m}\mathrm{p}$，为了简洁，这里的幅度计量单位为距离仓宽度${R}_{\mathrm{r}\mathrm{e}\mathrm{s}}$，且$0 < \mathrm{a}\mathrm{m}\mathrm{p} < 0.5$，则目标位置为$R\left(n{T}_{\mathrm{s}}\right)/{R}_{\mathrm{r}\mathrm{e}\mathrm{s}}=10.5+ \mathrm{a}\mathrm{m}\mathrm{p}\,\mathrm{sin}\left({\omega }_{\mathrm{B}}n{T}_{\mathrm{s}}\right)$。那么距离仓10所提取的信号的幅度会如图2(a)中蓝色方框所示变化：当目标向距离仓11运动时，生理复信号幅度变小，幅度在$R\left(n{T}_{\mathrm{s}}\right)/ {R}_{\mathrm{r}\mathrm{e}\mathrm{s}}=10.5{R}_{\mathrm{r}\mathrm{e}\mathrm{s}}\,+\,\mathrm{a}\mathrm{m}\mathrm{p}$时取得最小值${S}_{\mathrm{m}\mathrm{i}\mathrm{n}}= \alpha {A}_{\mathrm{T}} \cdot\mathrm{sin} \left({\pi }\left(0.5+\mathrm{a}\mathrm{m}\mathrm{p}\right)\right)/\mathrm{sin}\left({\pi }\left(0.5+\mathrm{a}\mathrm{m}\mathrm{p}\right)/{M}\right)$。当目标向距离仓10运动时，信号幅度变大，幅度在$R\left(n{T}_{\mathrm{s}}\right)/{R}_{\mathrm{r}\mathrm{e}\mathrm{s}}=10.5-\mathrm{a}\mathrm{m}\mathrm{p}$时取得最大值：${S}_{\min}= \alpha {A}_{{\mathrm{T}}}\mathrm{sin}\left({\pi }\left(0.5-\mathrm{a}\mathrm{m}\mathrm{p}\right)\right)/\mathrm{sin}\left({\pi }\left(0.5+\mathrm{a}\mathrm{m}\mathrm{p}\right)/M\right)$。将调制系数定义为

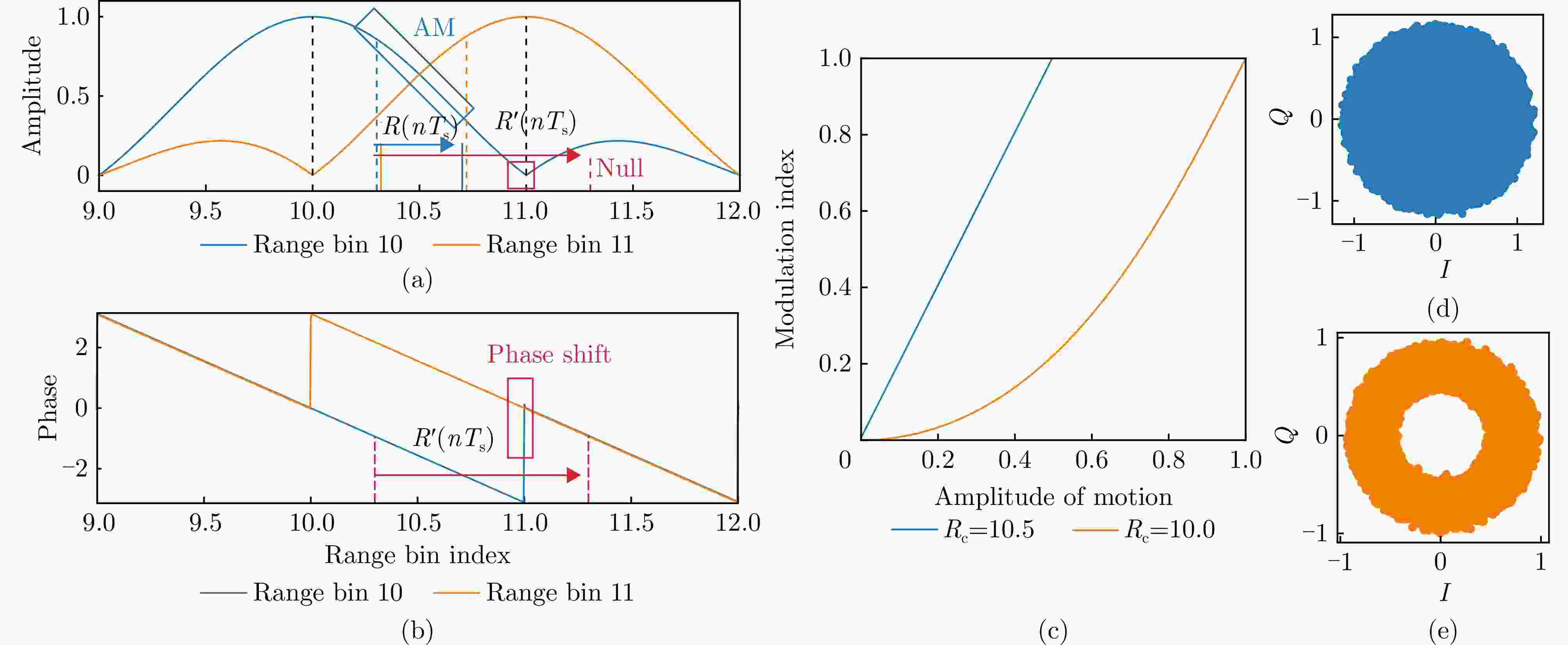
图  2  距离FFT引发的幅度信号幅度调制以及跨距离仓的问题 (a) 距离仓10和距离仓11对目标的幅度响应；(b) 距离仓10和距离仓11对目标的相位响应；(c) 当目标运动的中心点分别位于距离仓10.5和距离仓10.0时幅度调制系数与运动幅度的关系；(d) 当目标运动的中心点分别位于距离仓10.5且位移达到一个距离仓宽度时的星座图；(e) 当目标运动的中心点分别位于距离仓10.0且位移达到一个距离仓宽度时的星座图

Figure  2.  Amplitude modulation of the signal caused by range FFT and the problem of spanning range bins (a) Amplitude response of range bin 10 and range bin 11; (b) Phase response of range bin 10 and range bin 11; (c) Relationship between the amplitude modulation coefficient and the motion amplitude when the center point of the target motion is located in the range bin 10.5 and the range bin 10.0 respectively; (d) Constellation diagram when the center point of the target motion is located in the range bin 10.5 and the displacement reaches the width of one range bin; (e) Constellation diagram when the center point of the target motion is located in the range bin 10.0 and the displacement reaches the width of one range bin

下载: 全尺寸图片 幻灯片

图2(d)展示了幅度达到0.5${R}_{\mathrm{r}\mathrm{e}\mathrm{s}}$时的星座图，可以看到信号的分布呈实心圆形，而不是理想中的圆弧或者圆环，这是因为信号受到的严重的幅度调制，导致幅度的不断变化使得信号的半径不断变化，最终分布呈实心的圆形。在解调过程中，当信号幅度较小时，容易引发相位解调错误，将在2.3节展开。图2(e)展示了当目标运动的中心点分别位于距离仓10.0，运动幅度为0.5${R}_{\mathrm{r}\mathrm{e}\mathrm{s}}$时，从距离仓10提取信号的星座图。目标在$R\left(n{T}_{\mathrm{s}}\right)/{R}_{\mathrm{r}\mathrm{e}\mathrm{s}}=10$时幅度达到最大值，形成图中圆环的外沿。在$R\left(n{T}_{{\mathrm{s}}}\right)/{R}_{\mathrm{r}\mathrm{e}\mathrm{s}}=10\pm \mathrm{a}\mathrm{m}\mathrm{p}$ 时取得极小值。形成图中圆环的内沿。

图2(c)中展示了调制系数与运动幅度的关系，其中蓝线为运动中心点在距离仓10.5的场景，信号最容易受到幅度调制的影响，因为对于相邻的两个距离仓10和11来说在这里的幅度响应都有比较大的斜率，当目标运动的中心偏向10或者11一方时，对应距离仓的幅度响应都将更大。同理运动中心点恰好在整数个距离仓宽度时，比如10，信号最不容易受到幅度调制的影响，其调制系数与运动幅度的关系如图中黄线所示。(需要幅度响应的斜率以进一步说明。)其他情况下的调制系数与运动幅度应介于两条线之间。

对于4 GHz带宽的雷达，距离仓宽度约为3.75 cm，而人的静息呼吸导致的胸腔外壁2～3 cm，为$0.26～ 0.40{R}_{\mathrm{r}\mathrm{e}\mathrm{s}}$。当胸壁的位移中心点恰好在两个距离仓中间时，对应的调制系数为0.52～0.80，星座图上的圆弧或圆环较粗。当胸壁的位移中心点恰好在某个距离仓中间时，对应的调制系数为0.05～0.14，幅度调制影响可以接受。但在深呼吸的情况下，胸壁运动幅度约为0.67${R}_{\mathrm{r}\mathrm{e}\mathrm{s}}$，幅度调制可能达到1以上。对于7 GHz 带宽的雷达，距离仓宽度约为2.14 cm，而人的静息呼吸导致的胸壁运动幅度为$0.47～ 0.71{R}_{\mathrm{r}\mathrm{e}\mathrm{s}}$。当胸壁的位移中心点恰好在两个距离仓中间时，对应的调制系数约为0.94以上，当胸壁的位移中心点恰好在某个距离仓中间时，对应的调制系数为0.19～0.49。而在深呼吸情况下，胸壁运动幅度约为1.16${R}_{\mathrm{r}\mathrm{e}\mathrm{s}}$，跨越两个距离仓。跨越距离仓的问题在2.2.2节分析。

2.2.2   距离FFT导致的跨距离仓问题

当目标的最大位移覆盖两个连续的距离仓的中心时，对于那两个距离仓来说，目标位置都会跨越幅度响应的零点，那么从任意的距离仓提取的信号幅度都会在某时刻归零，这种情况定义为目标的运动跨越距离仓。

接下来讨论跨越距离仓出现的条件。如果要使得目标的区间内跨越至少两个距离仓中心，如图3的浅蓝色框，则首先要求目标的振动运动峰峰值${\Delta }R\left(n{T}_{\mathrm{s}}\right)=\mathrm{max}R\left(n{T}_{\mathrm{s}}\right)-\mathrm{min}R\left(n{T}_{\mathrm{s}}\right)$，至少要大于距离仓跨宽度${\Delta }R\left(n{T}_{\mathrm{s}}\right) > {R}_{\mathrm{r}\mathrm{e}\mathrm{s}}$。而当振动运动峰峰值大于两倍距离分辨度时，${\Delta }R\left(n{T}_{{\mathrm{s}}}\right) > {2R}_{\mathrm{r}\mathrm{e}\mathrm{s}}$，则必然跨越距离仓。另外，当振动运动峰峰值大于一倍距离分辨度但小于两倍距离分辨度时，${2R}_{\mathrm{r}\mathrm{e}\mathrm{s}} > {\Delta }R\left(n{T}_{{\mathrm{s}}}\right) > {R}_{\mathrm{r}\mathrm{e}\mathrm{s}}$，要使得目标位移跨越两个距离仓中心，目标运动距离雷达最近的位置$\mathrm{min}R\left(n{T}_{{\mathrm{s}}}\right)$，距离下一个距离仓的中心如果大于$\Delta R\left(n{T}_{{\mathrm{s}}}\right)-$ ${R}_{\mathrm{r}\mathrm{e}\mathrm{s}}$，如图3中深蓝色框，则也不会发生跨越距离仓的情况。因此在${\Delta }R\left(n{T}_{{\mathrm{s}}}\right) < 2{R}_{\mathrm{r}\mathrm{e}\mathrm{s}}$的情况下，假设目标运动距离雷达最近的位置$\mathrm{min}R\left(n{T}_{{\mathrm{s}}}\right)$满足均匀分布，发生跨越距离仓的概率为

图  3  跨越距离仓的条件

Figure  3.  The conditions of crossing range bin

下载: 全尺寸图片 幻灯片

对于4 GHz带宽的雷达，大部分人的静息呼吸胸壁位移小于距离分辨${\Delta }R\left(n{T}_{{\mathrm{s}}}\right) < {R}_{{\mathrm{res}}}$，不会跨越距离仓，只有在深呼吸的情况下，${\Delta }R\left(n{T}_{{\mathrm{s}}}\right)\approx 1.33{R}_{{\mathrm{res}}}$，可能跨越距离仓。但是对于7 GHz 带宽的雷达，静息呼吸胸壁位移在距离分辨度附近${\Delta }R\left(n{T}_{{\mathrm{s}}}\right)\approx {R}_{{\mathrm{res}}}$，有跨越距离仓的风险，而在深呼吸的情况下，${\Delta }R\left(n{T}_{{\mathrm{s}}}\right) > 2{R}_{{\mathrm{res}}}$，总会跨越距离仓。

2.3   跨距离仓和幅度调制的影响

在DCD信号中，有两个主要的心肺信号：DRD (Doppler Respiration Diagram)信号和DHD信号。实际的DRD信号可以简化为由3个单音信号(基频：${A}_{\mathrm{r}}\mathrm{s}\mathrm{i}\mathrm{n}\left(2{\pi }{f}_{\mathrm{r}}t\right)$，二次谐波：${A}_{2\mathrm{n}\mathrm{d}}\mathrm{s}\mathrm{i}\mathrm{n}\left(2{\pi }2{f}_{\mathrm{r}}t\right)$，和三次谐波：${A}_{3\mathrm{r}\mathrm{d}}\mathrm{s}\mathrm{i}\mathrm{n}\left(2{\pi }3{f}_{\mathrm{r}}t\right))$组成的混合信号^[11]。相比之下，DHD信号的复杂性远超DRD，因为它反映了心脏运动期间心室和心房体积的变化^[35]。DHD和BCG信号都是空间机械运动，是物理信号而非电信号，由心跳产生。BCG信号的能量主要集中在6～16 Hz的频段内^[36]。因此，DHD信号是一个包含6～16 Hz频带内丰富心脏信息的复杂信号。在模拟实验中，DHD信号同样简化为由3个不同频率的单音信号(${f}_{1\mathrm{h}}$= 9 Hz, ${f}_{2\mathrm{h}}$=12 Hz, ${f}_{3\mathrm{h}}$=15 Hz)组成的混合信号。综上，$\mathrm{D}\mathrm{C}\mathrm{D}=\mathrm{D}\mathrm{R}\mathrm{D}+\mathrm{D}\mathrm{H}\mathrm{D}$，其表达式为

其中，$N(0,\sigma )$为高斯噪声，使得$R\left(n{T}_{\mathrm{s}}\right)$信噪比为15 dB。另外，我们在雷达I/Q接收通道上也分别加入独立的白噪声，信噪比为3 dB。

图4展示了使用MATLAB仿真的信号，仿真中$R\left(n{T}_{{\mathrm{s}}}\right)$的幅度约为1 cm，峰峰值约为2 cm，距离仓宽度约为1 cm。图4(a)展示了从最大反射距离仓提取的生理复信号$S\left(k,n\right)$。图4(b)展示了经过反正切解调的DCD信号与源位移信号$R\left(n{T}_{{\mathrm{s}}}\right)$；图4(c) 展示了经过DACM (Differentiate and Cross-Multiply)解调后的DCD信号与源位移信号。图中目标在1 s, 5 s, 9 s时靠近距离仓边界，可以看到图4(a)中信号能量急剧减小，导致SNR攀升；进而导致图4(b)中的解相位过程中在相应的时间点无法解调信号，比如橘色的线在峰点附近应该是如同蓝色线弧线，但是由于信号能量变小，相对于存在一定误差的直流估计而言，信号的相位近乎不发生变化，因此在峰值区域出现平台，导致信号的不完整。在该情况下，由于信噪比降低，图4(c)中的DACM在峰值区域解相位也出现了解调错误。

图  4  幅度调制信号经过不同解调算法提取的DCD

Figure  4.  DCD extracted from amplitude modulated signals using different demodulation algorithms

下载: 全尺寸图片 幻灯片

图5展示了通过反正切解调获取的DCD信号功率谱密度(Power Spectral Density, PSD)。值得注意的是，由于幅度调制的非线性相位解调会产生高阶谐波和互调制项，这会降低DRD和DHD信号的信噪比(SNR)。尽管DRD信号本身含有高阶谐波，但幅度调制会引入新的谐波和交叉项。此外，由于幅度调制导致直流偏置补偿不精确也会独立地引入了这些谐波和交叉项。

图  5  幅度调制生理复信号解调后的功率谱密度

Figure  5.  Power spectral density of amplitude modulated physiological complex signal after arctan demodulation

下载: 全尺寸图片 幻灯片

图6展示经本文算法处理后，提取到DCD信号的功率谱密度。可以发现高阶谐波和互调制项被有效地抑制了，进而提高了DHD信号的信噪比。算法的具体实现将在2.4节展开。

图  6  本文算法处理后DCD信号的功率谱密度

Figure  6.  Power spectral density of DCD signal after processed by the proposed algorithm

下载: 全尺寸图片 幻灯片

2.4   距离抽头重构的相位提取算法

提出的方法主要由以下步骤构成：第1步是估计目标反射面(如胸腔)的位置与运动范围。第2步是依据目标的位置与范围重构距离导向矢量，提取该目标生理复信号。第3步是对复信号进行解调。之后，是通过相位信号可以用于估计生理参数。信号处理流程如图7所示。

图  7  信号处理流程

Figure  7.  Data processing chain

下载: 全尺寸图片 幻灯片

2.4.1   目标运动范围估计

在提取信号之前，首先需要精确估计反射面的运动范围，依据该范围设计距离滤波器，避免出现反射面运动距离过大导致的幅度调制，甚至超出滤波器的主瓣范围。为了提高距离维度的采样率，来更精确地估计目标的运动中心和运动幅度，先对雷达采样信号在快时间维度补零。雷达信号采样矩阵为

其中，M为快时间采样总数，m为快时间采样，N为一个窗长内的慢时间采样总数，n为慢时间采样；

其中，(·)^T代表矩阵转置。对雷达采样信号在快时间维度补零：${\boldsymbol{S}}_{{n}}={\left[s\left[1,n\right],s\left[2,n\right],\cdots ,s\left[{M},n\right],0,0,\cdots \right]}^{\mathrm{T}}$，补零的长度记为L，然后通过FFT计算距离谱：

其中，${k}^{{\prime}}$为补零后的距离谱序数，然后通过积累观察窗口内的反射能量，估计环境中的静态反射：

将距离谱去除静态反射杂波后，求取能量：

最后，通过阈值检测确定目标的运动范围${R}_{{\mathrm{amp}}}$，运动范围的中心记为${R}_{{\mathrm{c}}}$。

2.4.2   距离抽头重构

距离滤波器的设计有两个要求，首先是抽头的增益主瓣平整且范围覆盖目标的整个呼吸幅度，其次，主瓣内的相位响应必须是连续的，否则相位信息会有间断点以及偏差过大。基于此，我们通过递归IFT方法合成新的距离抽头：

(1) 初始化W = [$1,\mathrm{e}\mathrm{x}\mathrm{p}\left(1\mathrm{j}*{\omega }_{{\mathrm{Rc}}}\right),\cdots , \mathrm{e}\mathrm{x}\mathrm{p}\left(1\mathrm{j}* \left(M-1\right) {\omega }_{{\mathrm{Rc}}}\right)$]，为指向${\omega }_{{\mathrm{Rc}}}$的M点距离导向矢量：

(2) 使用O点逆 FFT 从W计算归一化距离抽头幅度响应F，其中O>M。

(3) 调整主瓣附近${\omega }_{\mathrm{R}\mathrm{c}}\pm {\omega }_{\mathrm{a}\mathrm{m}\mathrm{p}}/2$的范围内的增益，以及其他需要范围的增益。

(4) 使用O点直接 FFT 计算调整后的距离抽头的${\boldsymbol{W}}_{\mathrm{O}}$。

(5) 通过将距离采样外的所有样本设为零，将${\boldsymbol{W}}_{\mathrm{O}}$从O个样本截断为M个样本。

(6) 重复步骤2—步骤5，直到满足规定的约束要求，或达到允许的迭代次数。

具体而言，获取目标位置之后依据目标的距离中心点，转换得到中心点位置所对应的距离频率：

其中，${R}_{\mathrm{m}\mathrm{a}\mathrm{x}}$为雷达最大探测距离。初始话距离抽头为主瓣中心对准目标运动的中心的距离导向矢量：

此时，距离抽头在距离谱上的幅度相应$F\left(\omega \right)$的主瓣可能无法覆盖目标运动的范围。因此，在后续的迭代过程中扩大主瓣宽度，使其覆盖${\omega }_{\mathrm{R}\mathrm{c}}$的附近${\omega }_{\mathrm{a}\mathrm{m}\mathrm{p}}$：

在具体的迭代过程中，通过设置$F\left({\omega }_{{\mathrm{Rc}}}\right)$附近的小于一定阈值(比如0.7)的位置，为该阈值，使得主瓣覆盖目标的活动范围，并抑制幅度调制系数小于$1-\mathrm{t}\mathrm{h}\mathrm{r}\mathrm{e}\mathrm{s}\mathrm{h}\mathrm{o}\mathrm{l}\mathrm{d}$。对于单F(m)的约束条件为

然后通过逆变换获取新的距离抽头。通过计算超出约束的$F\left(\omega \right)$的数量来监控合成的进度。当此数字变为零时，即获得最佳合成结果。为了充分利用雷达的带宽，M为雷达采样点数，以确保充分利用雷达的原始数据。O决定了合成的精度，建议将O设定为M的10倍左右。另外，如果在旁瓣中存在干扰项时，需要对干扰区间进行抑制，使其小于一定的约束$\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{s}\mathrm{t}\mathrm{r}\mathrm{a}\mathrm{i}\mathrm{n}$(比如–71 dB)：

当上述范围内的幅度响应不满足要求时，将其幅度响应设置为约束值，然后通过逆变换求取距离抽头。

2.4.3   信号解调

理论上，可以直接求取复信号的相位，得到DCD信号^[28]。但是由于静止目标的回波杂波以及电路设计的不完备性等影响因素，接收到的雷达回波信号中会含有直流偏置分量，这可能会影响相位提取的结果。此外，在实际测量环境中，还会有其他静止物体产生直流回波。电路设计的不完备性主要包括天线的不完全匹配和本振与射频端口的隔离等。用于相位提取的直流偏置数据可能会产生误差。因此，有必要去除直流分量。

理想情况下，复数域中的信号轨迹形成围绕圆心的曲线；圆弧的半径为回波信号的幅值，圆弧的角度为回波信号与皮肤微小位移对应的相移，圆弧的中心为直流偏移量的大小。仅考虑相位误差和白噪声，可以通过复平面中的圆拟合来估计 DC(中心)。最小化以${\mathrm{DC}}$为圆心，$\beta$为半径的圆和第i个窗的数据点${V}_{i}\left(n\right)$之间的距离平方和，${d}_{i}^{2}=\displaystyle\sum\nolimits_{n=1}^{N} \left(\left|{{\mathrm{DC}}}_{i}- {V}_{i}\left(n\right)\right|-{\beta }_{i}\right)^{2}$：

然而，由于信号的中心不是静态的，我们提出了一种动态方法来解决这个时变问题。首先，将信号分为20 s的滑动窗口，重叠度为50%。 对于第1个滑动窗口内的信号，应用上述方法。 对于后续的滑动窗口信号，以先前获得的圆的中心$\widehat{{\mathrm{DC}}}$作为寻找新圆心的起点。 获取下一次圆拟合半径的范围受前一次RMSE ${\epsilon}_{i}={( {{d}_{i}^{2}}/{N})}^{0.5}$和上一次半径${\hat{\beta }}_{i}$的限制，以保证快速收敛：

随后可以使用相位展开来提取生命信号波形：

不连续的相位信号被拼接在一起，两段信号拼接的差值为前段信号最后的差值与后段信号第1个差值的均值。

3.   实验与结果

本文使用德州仪器公司的两款雷达：IWR6843 和WRL6432 FMCW雷达，参数设置表1、表2所示：

表  1  毫米波雷达IWR6843的主要参数

Table  1.  Key parameters of millimeter-wave radar IWR6843

参数	数值
载波频率	60 GHz
带宽	3.8 GHz
帧周期	4 ms
啁啾采样点数	100
距离仓宽度	3.94 cm

下载: 导出CSV 

| 显示表格

表  2  毫米波雷达WRL6432的主要参数

Table  2.  Key parameters of millimeter-wave radar IWR6432

参数	数值
载波频率	60 GHz
带宽	6.63 GHz
帧周期	4 ms
啁啾采样点数	512
距离仓宽度	2.26 cm

下载: 导出CSV 

| 显示表格

(1) 慢时间轴采样率：实验选择的慢时间采样率为250 Hz。慢轴采样率(啁啾/秒)应满足奈奎斯特准则，即采样率应为信号最大频率的两倍，并防止噪声混叠。由于DCD信号的复杂性，实验选取了和大部分标准ECG设备相同的采样率。

(2) 啁啾持续时间：这些实验选择的啁啾持续时间为50 μs。

(3) 带宽：众所周知，啁啾的带宽与系统的距离分辨率直接相关。虽然带宽不会直接影响生命体征估计的准确性，但它可以显著影响整体性能，因为更高的距离分辨率系统可以将感兴趣的区域(例如胸部)与其他肢体运动区分开，也可以更好地将一个人的生命体征与另一个人的生命体征区分开来。

(4) 观察时间：观察时间$N{T}_{{\mathrm{s}}}$越大，频率和幅度估计越好。根据Cramer Rao下限，频率估计的改进量级为${\left(N{T}_{{\mathrm{s}}}\right)}^{3}$，幅度估计的改进量级为$N{T}_{{\mathrm{s}}}$。然而，由于生命体征信号是非平稳的，由于固有的时间频率权衡，观察时间通常限制在8～15 s。

图8展示了实验的设置框图以及实验照片。雷达用于收集受试者心前区的位移信息并通过数据采集板卡DCA1000^[37]连接至PC，受PC段控制，并通过PC端获取时间戳。另外，还有一数据采集器，可以通过ADC同步采集目标的ECG信号与从放置在床垫下的压电传感器采集的BCG信号。该采集器配备无线网卡以获取网络时间戳。两个时间戳存在一定的差异，但通常不会超过一个心拍，因此雷达DHD与参考信号分别计算心拍间隔序列相互匹配。

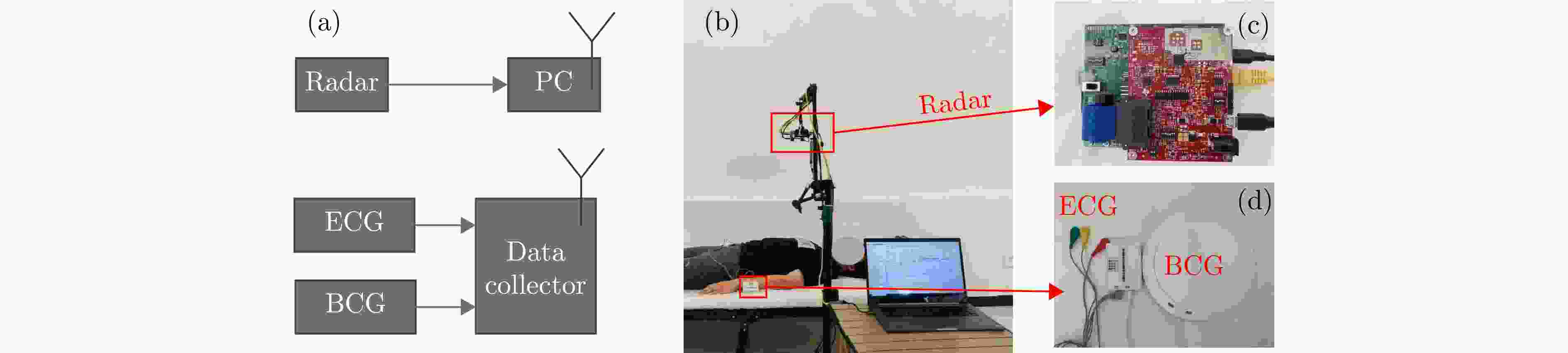
图  8  实验设置框图与实验设置 (a) 实验设置框图；(b) 实验设置照片；(c) 雷达传感器通过数据采集板连接到PC并通过无线网获取时间戳；(d) 数据采集器通过ADC同步采集ECG和BCG并通过无线网获取时间戳

Figure  8.  Block diagram of the experimental setup and the experimental setup (a) Block diagram of the experimental setup; (b) Photo of the experimental setup; (c) The radar sensor is connected to the PC through the data acquisition board and obtains timestamps through the wireless network; (d) The data collector synchronously collects ECG and BCG through ADC and obtains timestamps through the wireless network

下载: 全尺寸图片 幻灯片

仿真配置的参数如表3。

表  3  仿真主要参数

Table  3.  Key parameters of simulation

参数	数值
载波频率	60 GHz
带宽	3.8 GHz
帧周期	10 ms
啁啾采样点数	128
距离仓宽度	3.94 cm

下载: 导出CSV 

| 显示表格

3.1   算法性能

为了验证算法的性能，定量分析了目标在不同位置以及不同的运动幅度下，算法的有效性。将距离仓的位置从近到远定义为0到1，距离仓中心为0.5，呼吸的最大幅度也以距离仓宽度为单位，幅度包括0.25, 0.50, 1.00距离仓宽度(0.99 cm，1.97 cm和3.94 cm)，位置包括0, 0.25以及0.50距离仓，共8种模式。DHD的SNR定义为信号在${f}_{1{\mathrm{h}}}, {f}_{2{\mathrm{h}}}$和${f}_{3{\mathrm{h}}}$的能量之和与8～16 Hz其他频带能量之和的比值。图9(a)显示了8种不同情况下，通过距离FFT以及解调后得到的频谱图。图9(c)显示了频谱图从8～16 Hz的细节，可以看到，当出现目标接近距离仓边缘时(${\mathrm{Amp}}\ge {\mathrm{Pos}}$)，互调制项以及噪声都较为显著。相对的图9(b)显示了通过距离抽头重构之后的结果，与图9(a)相比呼吸谐波得到了有效的抑制；图9(d)显示了从8～16 Hz的细节，与图9(c)相比，可以看到互调制项的影响被完全消除，SNR得到了有效提升。具体提升效果如表4所示，可以看到，信噪比普遍有12 dB以上的提升。值得注意的是，在实际场景中，呼吸与心跳信号的频谱分布会更发散，因此互调制项的影响会更严重。

图  9  仿真结果

Figure  9.  Simulation results

下载: 全尺寸图片 幻灯片

表  4  距离FFT与本文算法处理信号的SNR对比

Table  4.  4 SNR comparison of the signal processed by range FFT and the proposed algorithm

Pos	Amp	SNR before (dB)	SNR after (dB)
0	1.00	24.69	42.05
0.25	1.00	23.50	35.60
0.50	1.00	24.29	36.87
0	0.50	22.91	43.44
0.25	0.50	27.73	42.16
0	0.25	26.54	45.66
0.50	0.50	29.84	43.04
0.25	0.25	32.28	44.69

下载: 导出CSV 

| 显示表格

3.2   跨距离仓实验

为了验证跨距离仓时算法的性能，我们使用WRL6432雷达，采集了受试者信号。雷达配置带宽为6.63 GHz，距离仓宽度为2.26 cm，其他具体参数如表2。

从图10(a)和图10(d)雷达距离-时间图中可以看出，目标在距离仓30～距离仓31之间发生了跨越，图10(b)中展示了从距离仓31提取的信号，可以看到，信号的幅度被调制，且幅度会减小到0；图10(c)展示了该信号解调得到的相位信号，解调错误频发，无法反映生理事件。图10(e)展示了通过距离抽头重构提取的信号的星座图，幅度调整较小，因此相位可以正确解调，相位如图10(f)。相位变化最大范围达到约47 rad，对应位移为2.35 cm。

图  10  跨距离仓实验相位解调结果

Figure  10.  Cross range bin phase demodulation results

下载: 全尺寸图片 幻灯片

图11(a)展示了滤波后的DHD信号与同步ECG信号的对比。图11(b)展示了雷达DHD信号提取的心拍间隔IBI (Interbeat interval)与ECG信号R-R间隔的对比。DHD信号IBI使用了文献[14]中的算法计算，R-R间隔使用了Pan-Tompkins^[38]算法。图片中的片段两者心拍间隔RMSE为10.53 ms。

图  11  跨距离仓实验结果

Figure  11.  Cross range bin results

下载: 全尺寸图片 幻灯片

3.3   DHD信号提取

为了验证所提算法的有效性，本文收集了8名受试者收集了信号，受试者平躺在床上，IWR6843雷达正对胸口。图12(a)分别显示了使用重构距离抽头和FFT获取的信号在I/Q 平面上的轨迹，可以看到，使用重构距离抽头得到的信号轨迹更加接近正圆，幅度调制更小，而FFT提取的信号轨迹类似螺旋线，因此是受到幅度调制的。图12(b)展示了算法处理前后的DCD信号解调结果。经过算法处理后的DCD信号波形相比原始信号更为平滑，这表明算法具有显著抑制高阶谐波和交叉项的能力。图12(c)显示，通过应用带宽为0.1～1.0 Hz和7～16 Hz的FIR滤波器，从DCD信号中提取出DRD和DHD信号。图12(d)比较了检测到的DHD信号与BCG信号之间不同特征峰值的细节。

图  12  DHD信号提取过程

Figure  12.  DHD signal extraction procedure

下载: 全尺寸图片 幻灯片

图13展示了使用本文算法获取的8名受试者的DHD信号。此外，为了定量分析通过本文算法获取的DHD信号与BCG信号的一致性，我们计算了8名受试者DHD和BCG信号的拍间间隔，如图14所示。我们还分析了DHD信号的心拍间隔(C-C间隔)与BCG信号的心拍间隔(J-J间隔)的RMSE，结果见表5。

图  13  检测到的8名受试者的DHD信号(滤波器通带为8～20 Hz以及每段信号3～5 s的DHD信号细节)

Figure  13.  Detected DHD signals for each eight subjects (details of the DHD signals between 3 and 5 s where the filter passband is 8～20 Hz)

下载: 全尺寸图片 幻灯片

图  14  DHD信号中C-C间隔与BCG信号中J-J间隔的关系

Figure  14.  Relationship between C-C interval in DHD signal and J-J interval in BCG signal

下载: 全尺寸图片 幻灯片

4.   讨论

生物雷达传感器，通常先使用距离FFT，分离不同距离的反射，然后使用反正切解调，面临的主要挑战主要有两方面，一方面是随时间变化的幅度调制，另一方面是随时间变化的直流偏置。首先距离FFT固有的频谱泄露，在目标接近距离仓边界时，会导致复信号的幅度调制，导致反正切解调结果中出现大量的高次谐波和互调项，如图4所示。我们建议的合理步骤是先减小幅度调制，然后进行补偿以恢复固有的直流成分。其次，由于生物雷达传感器的应用场景中目标位置的不固定且存在一定的浮动，通常存在随时间变化的目标位置变化。此外，传感器的I和Q分支中通道环境和组件特性不同，直流偏置也会随时间变化。因此，不应假设补偿和校正值恒定。此外，直流偏置和幅度调制都会引入不希望的谐波和交叉项。因此，需要同时进行直流偏置补偿和距离再分配。

4.1   DHD 信号的提取

DHD信号的临床意义已得到广泛认可。DHD信号和BCG信号都是由心跳产生的物理信号，而非电信号。DHD信号通过生物雷达传感器捕获，而BCG信号则通过压电陶瓷传感器记录。如图8所示，通过计算DHD信号的C-C间隔和BCG信号的J-J间隔，可以用于心率变异性(Heart Rate Variability, HRV)分析。计算心跳节奏的目的是定量评估DHD信号是否能像BCG信号一样用于HRV分析。对于8名受试者，与BCG信号的相对RMSE为21.58±13.26 ms (3.40%±2.08%)，如表5所示。

表  5  DHD信号的C-C间隔相对于BCG信号的 J-J间隔的RMSE

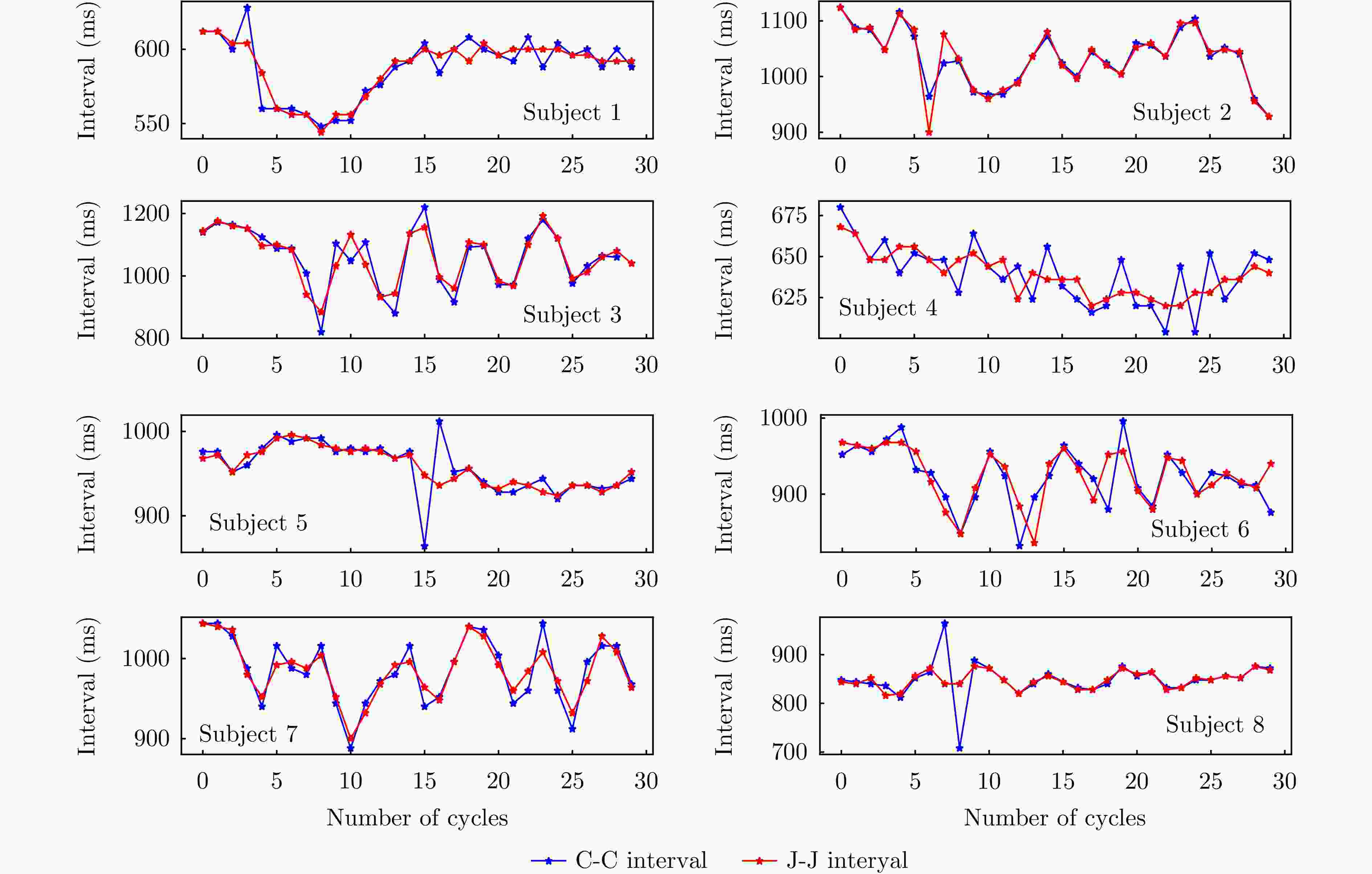
Table  5.  RMSE of the C-C interval of the DHD signal relative to the J-J interval of the BCG signal

人员	RMSE (ms)	平均偏差(%)
Subject 1	8.32	0.96
Subject 2	15.90	0.77
Subject 3	34.85	2.36
Subject 4	22.15	2.07
Subject 5	21.92	1.07
Subject 6	28.28	2.07
Subject 7	12.97	1.01
Subject 8	19.12	1.22

下载: 导出CSV 

| 显示表格

此外，通过计算C-C间隔可以确定DHD信号的心率(HR)。因此，DRD信号的高次谐波的存在不影响测量DHD信号HR的准确性。先前的研究假设DHD信号的基频(静息心率)在0.83～1.50 Hz (50～90 次/min)，而DRD信号的基频(静息呼吸频率)在0.15～0.40 Hz (9～24 次/min)，这是不合理的。这是因为DRD信号的能量主要集中在0.13～0.40 Hz，而DHD信号的能量并不集中在0.83～1.50 Hz。与心电图(ECG)和BCG信号类似，0.83～1.50 Hz代表心率转化为频率值的频率范围，而ECG和BCG信号的能量主要集中在5～15 Hz和6～16 Hz。

4.2   局限

本研究针对实验室环境下，从健康受试者收集的短时数据集对DHD信号进行了分析，这些受试者在实验过程中尽可能保持静止。这限制了这些结果在实际医疗应用中的普适性。因此，需要进行广泛的实际验证，以证明所提出算法在不同场景下的有效性。

5.   结语

本研究提出了一种基于距离再分配的动态解调算法。该算法通过自适应地生成距离滤波器，以及动态直流(DC)估计，防止了目标位置跨越距离仓导致的解调错误。仿真和实验结果均表明，该算法展现出良好的噪声抑制性能，并能实现高信噪比(SNR)的DHD信号获取。 未来的研究将聚焦于从不同生理状态的更大人群，包括心血管疾病患者群体中收集数据。