作者中心
专家审稿
责编办公
编辑办公
-
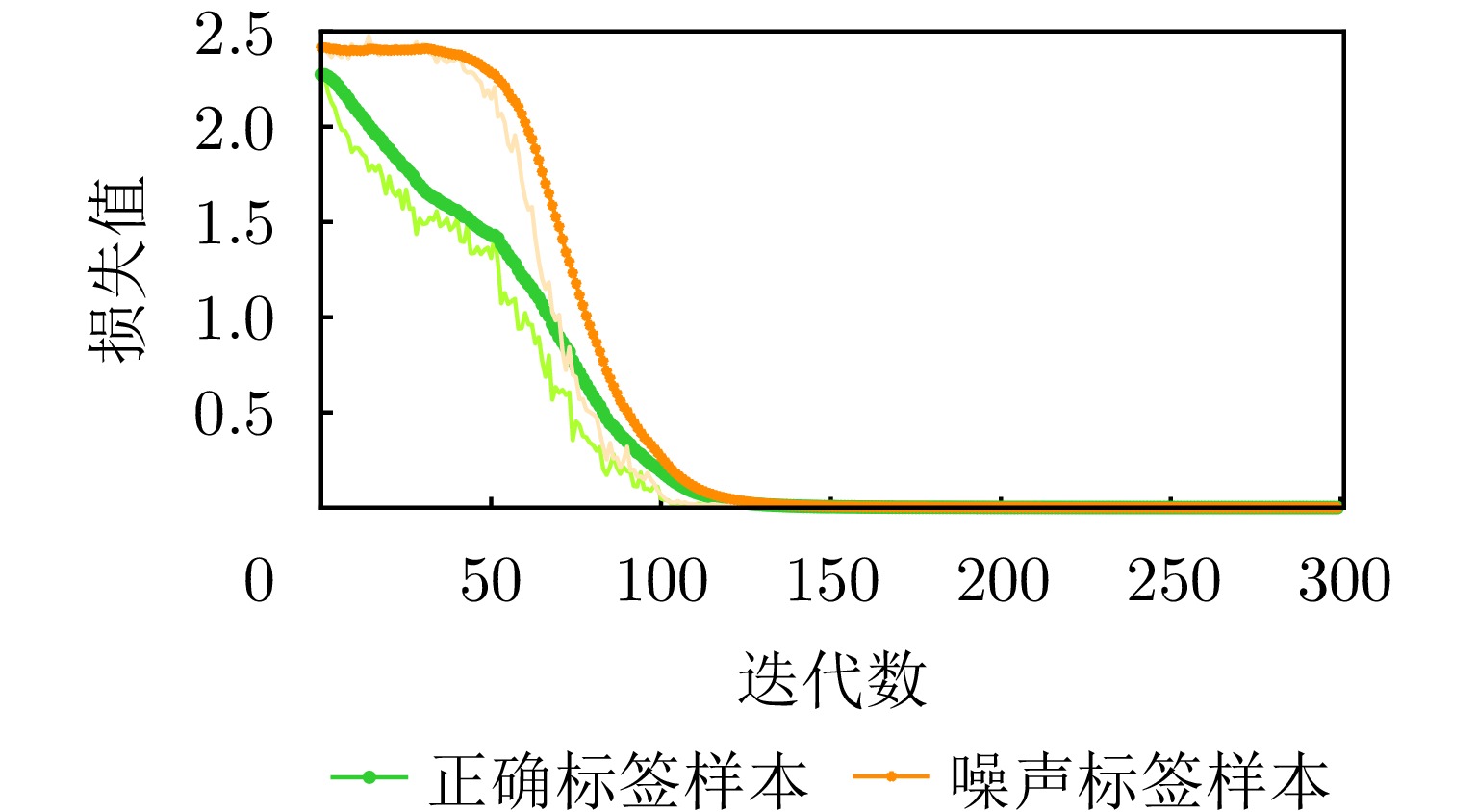
摘要: 深度监督学习在合成孔径雷达自动目标识别任务中的成功依赖于大量标签样本。但是，在大规模数据集中经常存在错误(噪声)标签，很大程度降低网络训练效果。该文提出一种基于损失曲线拟合的标签噪声不确定性建模和基于噪声不确定度的纠正方法：以损失曲线作为判别特征，应用无监督模糊聚类算法获得聚类中心和类别隶属度以建模各样本标签噪声不确定度；根据样本标签噪声不确定度将样本集划分为噪声标签样本集、正确标签样本集和模糊标签样本集，以加权训练损失方法分组处理训练集，指导分类网络训练实现纠正噪声标签。在MSTAR数据集上的实验证明，该文所提方法可处理数据集中混有不同比例标签噪声情况下的网络训练问题，有效纠正标签噪声。当训练数据集中标签噪声比例较小(40%)时，该文所提方法可纠正98.6%的标签噪声，并训练网络达到98.7%的分类精度。即使标签噪声比例很大(80%)时，该文方法仍可纠正87.8%的标签噪声，并训练网络达到82.3%的分类精度。
-
关键词:
- 合成孔径雷达 /
- 标签噪声 /
- 标签噪声纠正 /
- 标签噪声不确定性建模 /
- 模糊聚类算法
Abstract: The success of deep supervised learning in Synthetic Aperture Radar (SAR) Automatic Target Recognition (ATR) relies on a large number of labeled samples. However, label noise often exists in large-scale datasets, which highly influence network training. This study proposes loss curve fitting-based label noise uncertainty modeling and a noise uncertainty-based correction method. The loss curve is a discriminative feature to model label noise uncertainty using an unsupervised fuzzy clustering algorithm. Then, according to this uncertainty, the sample set is divided into different subsets: the noisy-label set, clean-label set, and fuzzy-label set, which are further used in training loss with different weights to correct label noise. Experiments on the Moving and Stationary Target Acquisition and Recognition (MSTAR) dataset prove that our method can deal with varying ratios of label noise during network training and correct label noise effectively. When the training dataset contains a small ratio of label noise (40%), the proposed method corrects 98.6% of these labels and trains the network with 98.7% classification accuracy. Even when the proportion of label noise is large (80%), the proposed method corrects 87.8% of label noise and trains the network with 82.3% classification accuracy. -
图 1 混合正确和噪声标签样本训练分类网络的损失曲线(以含80%标签噪声数据集训练ResNet18网络300次获得)
Figure 1. Loss curves of the classification network trained by mixed-noisy-and-clean labels (obtained by training ResNet18 with 80% noisy labels after 300 epochs)
图 2 混合正确和噪声标签样本训练分类网络的损失曲线(以含80%标签噪声数据集训练ResNet18网络300次获得)和聚类中心
Figure 2. Loss curves of the classification network trained by mixed-noisy-and-clean labels (obtained by training ResNet18 with 80% noisy labels after 300 epochs) and clustering centers for clean and noisy labels
图 4 本文方法训练分类网络的损失曲线
Figure 4. Loss curves of clean and noisy samples for our proposed method
表 1 标签噪声数据集训练分类网络模型精度(%)
Table 1. Classification accuracy of the models trained with noisy labels and clean labels (%)
训练网络模型 分类精度 20%的正确标签 92.13 混合20%的正确标签 & 80%的噪声标签 27.46 100%的正确标签 98.30 
下载: 导出CSV
1 含噪标签数据集训练分类网络
1. Train a classification network with noisy labels
输入：X：训练集中的图像样本。 ${Y_{\mathrm{n}}}$：训练集中的样本标签(包括噪声标签)。 $ f\left( { \cdot ;\theta } \right) $：一个分类网络(本文中为CNN)。 输出：CNN训练权重$ {\theta ^{{T_2}}} $ 步骤1：混有噪声和正确标签数据集$(X,{Y_{\mathrm{n}}})$训练网络${T_1}$次 获得$ f\left( { \cdot ;{\theta ^{{T_1}}}} \right) $和$\left\{ {{{\boldsymbol{l}}}_i^{{T_1}}} \right\}_{i = 1}^N$。 步骤2：标签噪声不确定性建模 初始化c； for i in $ \left[1,T_c\right] $ iterations: do 根据式(2)计算${\boldsymbol{c}}(k)$ 根据式(3)计算${\mu _i}(k)$ end for 获得${{\boldsymbol{c}}^ * }(k)$和$ \mu _i^ * (k) $ 步骤3：基于噪声不确定度的数据划分 获得噪声样本集$ {D_{\mathrm{n}}} $、正确样本集$ {D_{\mathrm{c}}} $、模糊样本集$ {D_{\mathrm{f}}} $ $ {D_{\text{n}}} = \left\{ {({{\boldsymbol{x}}_i},{{\boldsymbol{y}}_i})|\mu _i^ * (2) > {\tau _1}} \right\}_{i = 1}^N $ $ {D_{\mathrm{c}}} = \left\{ {({{\boldsymbol{x}}_i},{{\boldsymbol{y}}_i})|\mu _i^ * (2) < {\tau _2}} \right\}_{i = 1}^N $ $ {D_{\mathrm{f}}} = \left\{ {({{\boldsymbol{x}}_i},{{\boldsymbol{y}}_i})|{\tau _2} \le \mu _i^ * (2) \le {\tau _1}} \right\}_{i = 1}^N $ 通过mixup数据增强获得$ {D_{{\text{aug}}}} $ 根据式(5)计算${{\boldsymbol{x}}_{{\mathrm{mix}}}}$ 根据式(6)计算${{\boldsymbol{y}}_{{\mathrm{mix}}}}$ $ {D_{{\text{aug}}}} = \left\{ {\left( {{{\boldsymbol{x}}_{{\text{mix}}}},{{\boldsymbol{y}}_{{\text{mix}}}}} \right)} \right\} $ $ {D_{\mathrm{m}}} = {D_{\text{c}}} \cup {D_{\mathrm{f}}} \cup {D_{{\mathrm{aug}}}} $ 步骤4：使用${D_{\mathrm{m}}}$分组加权纠正训练网络${T_2}$次
下载: 导出CSV
表 2 MSTAR数据集中训练和测试数据集中的目标数量
Table 2. Number of targets in the training and testing datasets of the MSTAR dataset
地面目标图像 训练数据集 测试数据集 总数据集 2S1 299 274 573 BMP2 233 195 428 BRDM2 298 274 572 BTR60 256 195 451 BTR70 233 196 429 D7 299 274 573 T62 299 273 572 T72 232 196 428 ZIL131 299 274 573 ZSU234 299 274 573
下载: 导出CSV
表 3 不同比例标签噪声下的纠正精度(%)
Table 3. The correction accuracy with different noise ratio (%)
算法 40 (36.4) 60 (54.0) 80 (72.5) BMM-based 98.7 84.8 61.1 LNMC 97.9 92.2 78.1 本文方法 98.6 97.2 87.8 注：由于制作标签噪声时一些样本标签可能被随机重新标注为正确标签，实际噪声比例略低于设置比例，括号内为实验中真实标签噪声比例。加粗项表示最优结果。
下载: 导出CSV
表 4 不同比例标签噪声下的网络分类精度(%)
Table 4. The classification accuracy with different noise ratio (%)
下载: 导出CSV
表 5 噪声比80%下$ {{\boldsymbol{\tau}} _1},{\boldsymbol{{\tau}} _2} $不同取值时的网络分类精度
Table 5. The classification accuracy with different $ {{\boldsymbol{\tau}} _1},{{\boldsymbol{\tau}} _2} $ values under 80% noise ratio
$ {\tau _1} $ $ {\tau _2} $ 分类精度(%) 0.7 0.1 80.8 0.8 0.1 80.9 0.9 0.1 80.9 0.7 0.2 82.7 0.8 0.2 82.3 0.9 0.2 82.5 0.7 0.3 82.2 0.8 0.3 82.3 0.9 0.3 82.3
下载: 导出CSV
表 6 噪声比40%下$ {{\boldsymbol{\tau}} _1},{{\boldsymbol{\tau}} _2} $不同取值时的网络分类精度
Table 6. The classification accuracy with different $ {{\boldsymbol{\tau}} _1},{{\boldsymbol{\tau}} _2} $ values under 40% noise ratio
$ {\tau _1} $ $ {\tau _2} $ 分类精度(%) 0.7 0.1 96.4 0.8 0.1 96.8 0.9 0.1 96.6 0.7 0.2 97.6 0.8 0.2 98.7 0.9 0.2 97.5 0.7 0.3 97.6 0.8 0.3 97.6 0.9 0.3 97.4
下载: 导出CSV
表 7 Mixup方法消融实验(%)
Table 7. Ablation study on mixup method (%)
是否使用mixup 40 (36.4) 60 (54.0) 80 (72.5) 否 94.7 90.3 73.2 是 98.7 94.9 82.3 注：由于制作标签噪声时一些样本标签可能被随机重新标注为正确标签，实际噪声比例略低于设置比例，括号内为实验中真实标签噪声比例。
下载: 导出CSV
-
[1] CUI Zongyong, TANG Cui, CAO Zongjie, et al. SAR unlabeled target recognition based on updating CNN with assistant decision[J]. IEEE Geoscience and Remote Sensing Letters, 2018, 15(10): 1585–1589. doi: 10.1109/LGRS.2018.2851600. [2] PEI Jifang, HUANG Yulin, HUO Weibo, et al. SAR automatic target recognition based on multiview deep learning framework[J]. IEEE Transactions on Geoscience and Remote Sensing, 2018, 56(4): 2196–2210. doi: 10.1109/TGRS.2017.2776357. [3] WANG Chen, SHI Jun, ZHOU Yuanyuan, et al. Semisupervised learning-based SAR ATR via self-consistent augmentation[J]. IEEE Transactions on Geoscience and Remote Sensing, 2021, 59(6): 4862–4873. doi: 10.1109/TGRS.2020.3013968. [4] BAI Xueru, XUE Ruihang, WANG Li, et al. Sequence SAR image classification based on bidirectional convolution-recurrent network[J]. IEEE Transactions on Geoscience and Remote Sensing, 2019, 57(11): 9223–9235. doi: 10.1109/TGRS.2019.2925636. [5] AMRANI M, JIANG Feng, XU Yunzhong, et al. SAR-oriented visual saliency model and directed acyclic graph support vector metric based target classification[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2018, 11(10): 3794–3810. doi: 10.1109/JSTARS.2018.2866684. [6] ZHOU Yuanyuan, SHI Jun, WANG Chen, et al. SAR ground moving target refocusing by combining mRe³ network and TVβ-LSTM[J]. IEEE Transactions on Geoscience and Remote Sensing, 2022, 60: 5200814. doi: 10.1109/TGRS.2020.3033656. [7] WANG Chen, SHI Jun, YANG Xiaqing, et al. Geospatial object detection via deconvolutional region proposal network[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2019, 12(8): 3014–3027. doi: 10.1109/JSTARS.2019.2919382. [8] HE Kaiming, ZHANG Xiangyu, REN Shaoqing, et al. Deep residual learning for image recognition[C]. The 2016 IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, USA, 2016: 770–778. doi: 10.1109/CVPR.2016.90. [9] ARAZO E, ORTEGO D, ALBERT P, et al. Unsupervised label noise modeling and loss correction[C]. The 36th International Conference on Machine Learning, Long Beach, USA, 2019: 312–321. [10] ZHANG Chiyuan, BENGIO S, HARDT M, et al. Understanding deep learning (still) requires rethinking generalization[J]. Communications of the ACM, 2021, 64(3): 107–115. doi: 10.1145/3446776. [11] SONG H, KIM M, PARK D, et al. Learning from noisy labels with deep neural networks: A survey[J]. IEEE Transactions on Neural Networks and Learning Systems, 2023, 34(11): 8135–8153. doi: 10.1109/TNNLS.2022.3152527. [12] VEIT A, ALLDRIN N, CHECHIK G, et al. Learning from noisy large-scale datasets with minimal supervision[C]. The 2017 IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, USA, 2017: 839–847. doi: 10.1109/CVPR.2017.696. [13] VAHDAT A. Toward robustness against label noise in training deep discriminative neural networks[C]. The 31st International Conference on Neural Information Processing Systems, Long Beach, USA, 2017: 5601–5610. [14] REED S, LEE H, ANGUELOV D, et al. Training deep neural networks on noisy labels with bootstrapping[C]. The 3rd International Conference on Learning Representations, San Diego, USA, 2015. [15] LEE K H, HE Xiaodong, ZHANG Lei, et al. CleanNet: Transfer learning for scalable image classifier training with label noise[C]. The 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Salt Lake City, USA, 2018: 5447–5456. doi: 10.1109/CVPR.2018.00571. [16] ZHANG Zhilu and SABUNCU M R. Generalized cross entropy loss for training deep neural networks with noisy labels[C]. The 32nd International Conference on Neural Information Processing Systems, Montréal, Canada, 2018: 8792–8802. [17] KANG Jian, FERNANDEZ-BELTRAN R, DUAN Puhong, et al. Robust normalized softmax loss for deep metric learning-based characterization of remote sensing images with label noise[J]. IEEE Transactions on Geoscience and Remote Sensing, 2021, 59(10): 8798–8811. doi: 10.1109/TGRS.2020.3042607. [18] SRIVASTAVA N, HINTON G, KRIZHEVSKY A, et al. Dropout: A simple way to prevent neural networks from overfitting[J]. The Journal of Machine Learning Research, 2014, 15(1): 1929–1958. [19] GOODFELLOW I J, SHLENS J, and SZEGEDY C. Explaining and harnessing adversarial examples[C]. The 3rd International Conference on Learning Representations, San Diego, USA, 2015. [20] ZHANG Hongyi, CISSÉ M, DAUPHIN Y N, et al. Mixup: Beyond empirical risk minimization[C]. The 6th International Conference on Learning Representations, Vancouver, Canada, 2018. [21] PEREYRA G, TUCKER G, CHOROWSKI J, et al. Regularizing neural networks by penalizing confident output distributions[C]. The 5th International Conference on Learning Representations, Toulon, France, 2017. [22] SZEGEDY C, VANHOUCKE V, IOFFE S, et al. Rethinking the inception architecture for computer vision[C]. The 2016 IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, USA, 2016: 2818–2826. doi: 10.1109/CVPR.2016.308. [23] HUA Yuansheng, LOBRY S, MOU Lichao, et al. Learning multi-label aerial image classification under label noise: A regularization approach using word embeddings[C]. The 2020 IEEE International Geoscience and Remote Sensing Symposium, Waikoloa, USA, 2020: 525–528. doi: 10.1109/IGARSS39084.2020.9324069. [24] SHENG Mengmeng, SUN Zeren, CAI Zhenhuang, et al. Adaptive integration of partial label learning and negative learning for enhanced noisy label learning[C]. The 38th AAAI Conference on Artificial Intelligence, Vancouver, Canada, 2024. doi: 10.1609/aaai.v38i5.28284. [25] ALBERT P, ORTEGO D, ARAZO E, et al. Addressing out-of-distribution label noise in webly-labelled data[C]. The 2022 IEEE/CVF Winter Conference on Applications of Computer Vision, Waikoloa, USA, 2022: 392–401. doi: 10.1109/WACV51458.2022.00245. [26] ZHANG Dongyu, HU Ruofan, and RUNDENSTEINER E A. CoLafier: Collaborative noisy label purifier with local intrinsic dimensionality guidance[C]. The 2024 SIAM International Conference on Data Mining, Houston, USA, 2024: 82–90. [27] NGUYEN D T, MUMMADI C K, NGO T P N, et al. SELF: Learning to filter noisy labels with self-ensembling[C]. The 8th International Conference on Learning Representations, Addis Ababa, Ethiopia, 2020. [28] WEI Hongxin, FENG Lei, CHEN Xiangyu, et al. Combating noisy labels by agreement: A joint training method with co-regularization[C]. The 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, USA, 2020: 13726–13735. doi: 10.1109/CVPR42600.2020.01374. [29] HAN Bo, YAO Quanming, YU Xingrui, et al. Co-teaching: Robust training of deep neural networks with extremely noisy labels[C]. The 32nd International Conference on Neural Information Processing Systems, Montréal, Canada, 2018: 8536–8546. [30] PARK D, CHOI S, KIM D, et al. Robust data pruning under label noise via maximizing re-labeling accuracy[C]. The 37th International Conference on Neural Information Processing Systems, New Orleans, USA, 2024: 3257. [31] 赵娟萍, 郭炜炜, 柳彬, 等. 基于概率转移卷积神经网络的含噪标记SAR图像分类[J]. 雷达学报, 2017, 6(5): 514–523. doi: 10.12000/JR16140.ZHAO Juanping, GUO Weiwei, LIU Bin, et al. Convolutional neural network-based SAR image classification with noisy labels[J]. Journal of Radars, 2017, 6(5): 514–523. doi: 10.12000/JR16140. [32] SHANG Ronghua, LIN Junkai, JIAO Licheng, et al. SAR image segmentation using region smoothing and label correction[J]. Remote Sensing, 2020, 12(5): 803. doi: 10.3390/rs12050803. [33] HUANG Zhongling, DUMITRU C O, PAN Zongxu, et al. Classification of large-scale high-resolution SAR images with deep transfer learning[J]. IEEE Geoscience and Remote Sensing Letters, 2021, 18(1): 107–111. doi: 10.1109/LGRS.2020.2965558. [34] 滑文强, 王爽, 侯彪. 基于半监督学习的SVM-Wishart极化SAR图像分类方法[J]. 雷达学报, 2015, 4(1): 93–98. doi: 10.12000/JR14138.HUA Wenqiang, WANG Shuang, and HOU Biao. Semi-supervised learning for classification of polarimetric SAR images based on SVM-wishart[J]. Journal of Radars, 2015, 4(1): 93–98. doi: 10.12000/JR14138. [35] SUN Yuanshuang, WANG Yinghua, LIU Hongwei, et al. Gradual domain adaptation with pseudo-label denoising for SAR target recognition when using only synthetic data for training[J]. Remote Sensing, 2023, 15(3): 708. doi: 10.3390/rs15030708. [36] WANG Chen, SHI Jun, ZHOU Yuanyuan, et al. Label noise modeling and correction via loss curve fitting for SAR ATR[J]. IEEE Transactions on Geoscience and Remote Sensing, 2022, 60: 5216210. doi: 10.1109/TGRS.2021.3121397. [37] KEYDEL E R, LEE S W, and MOORE J T. MSTAR extended operating conditions: A tutorial[C]. The SPIE 2757, Algorithms for Synthetic Aperture Radar Imagery III, Orlando, USA, 1996: 228–242. doi: 10.1117/12.242059. [38] SUTSKEVER I, MARTENS J, DAHL G, et al. On the importance of initialization and momentum in deep learning[C]. The 30th International Conference on Machine Learning, Atlanta, USA, 2013: 1139–1147. [39] PASZKE A, GROSS S, MASSA F, et al. PyTorch: An imperative style, high-performance deep learning library[C]. The 33rd Conference on Neural Information Processing Systems, Vancouver, Canada, 2019: 8026–8037. -
图(5) / 表(8)
计量
- 文章访问数: 298
- HTML全文浏览量: 117
- PDF下载量: 93
- 被引次数: 0
