-
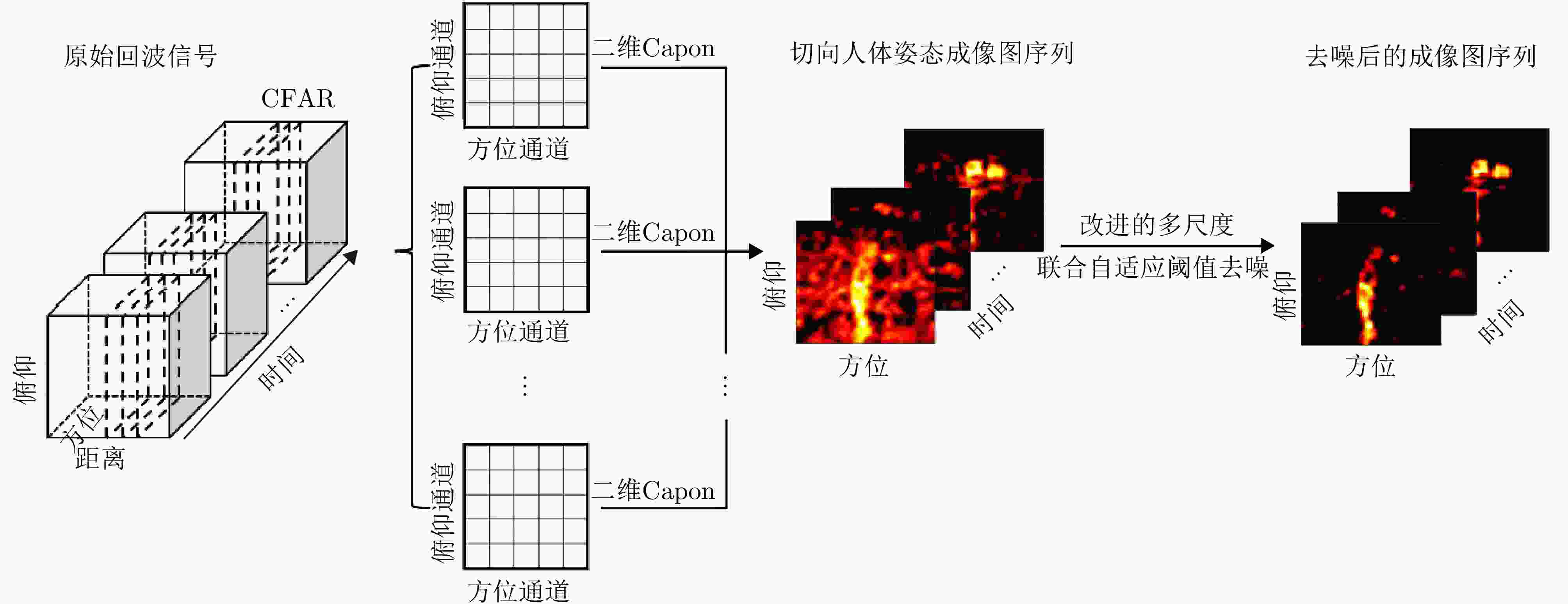
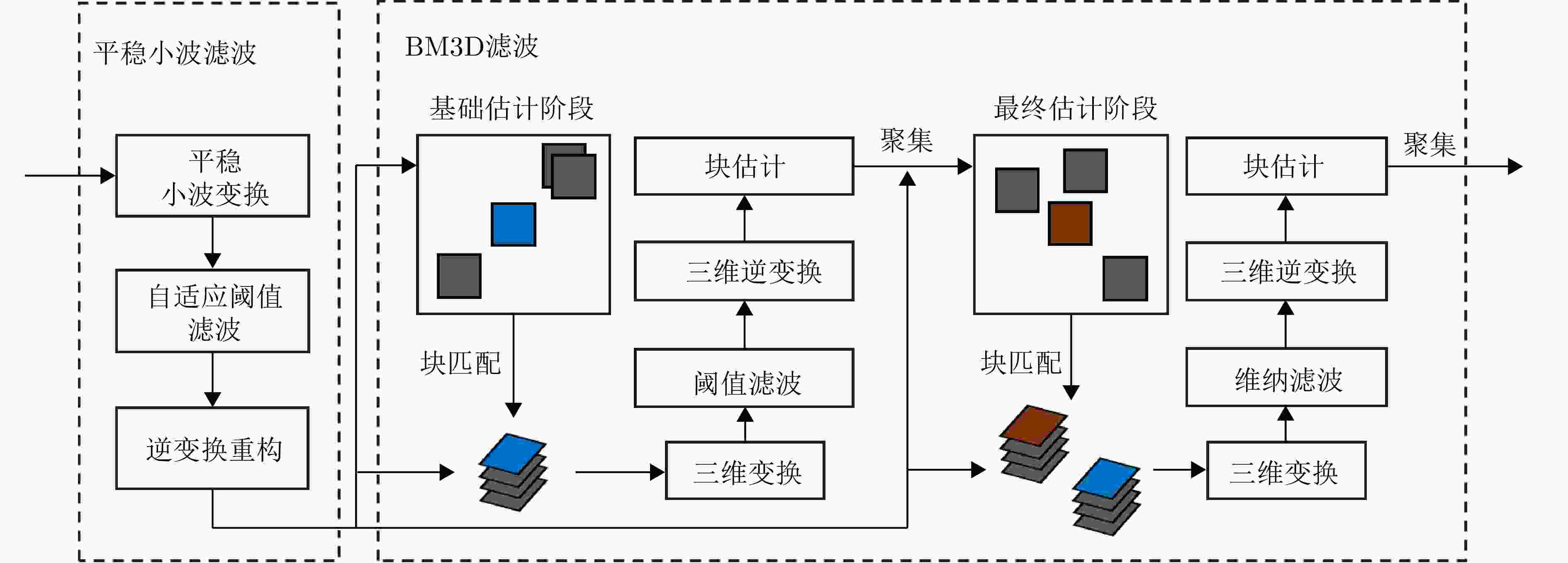
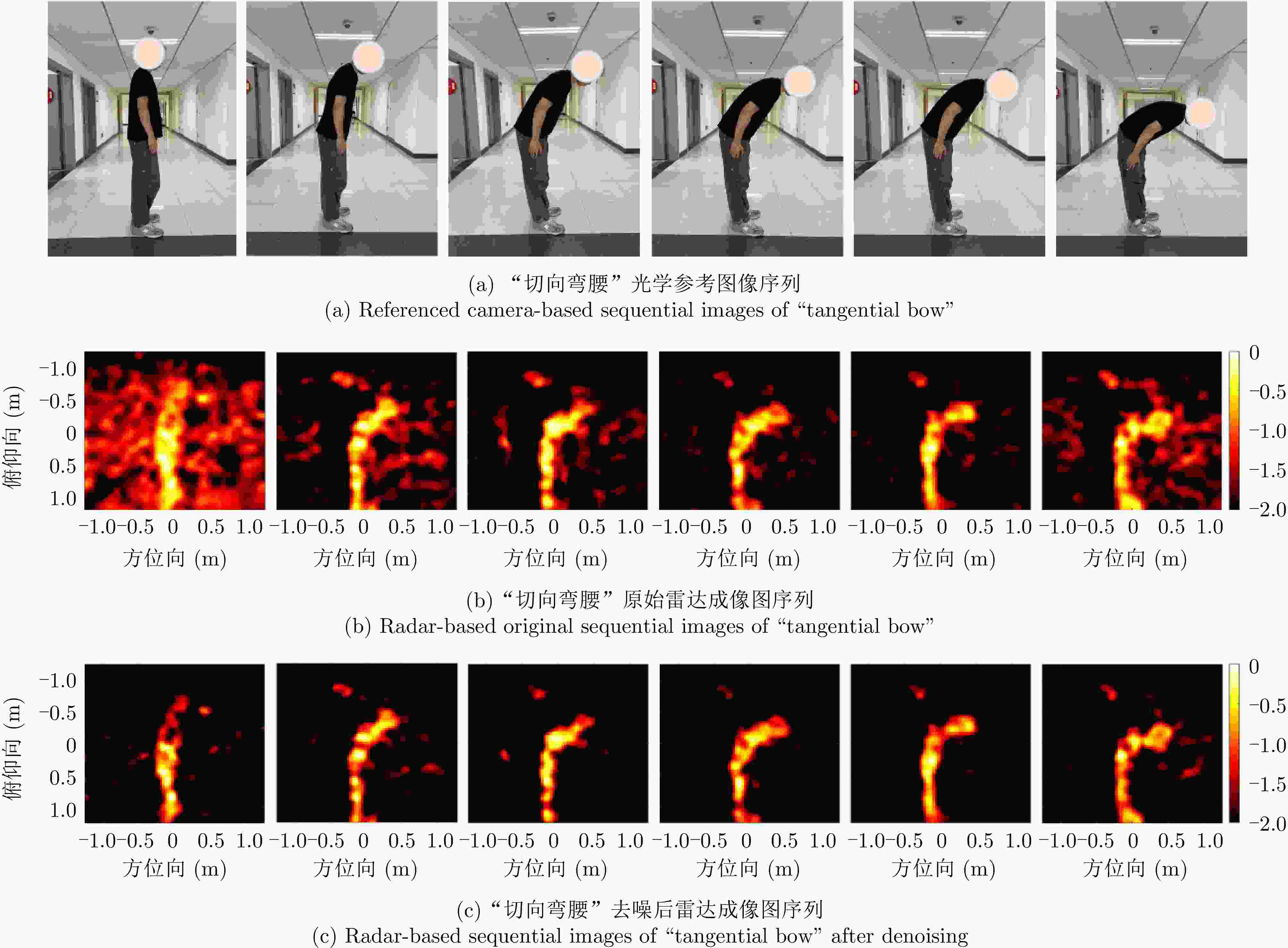
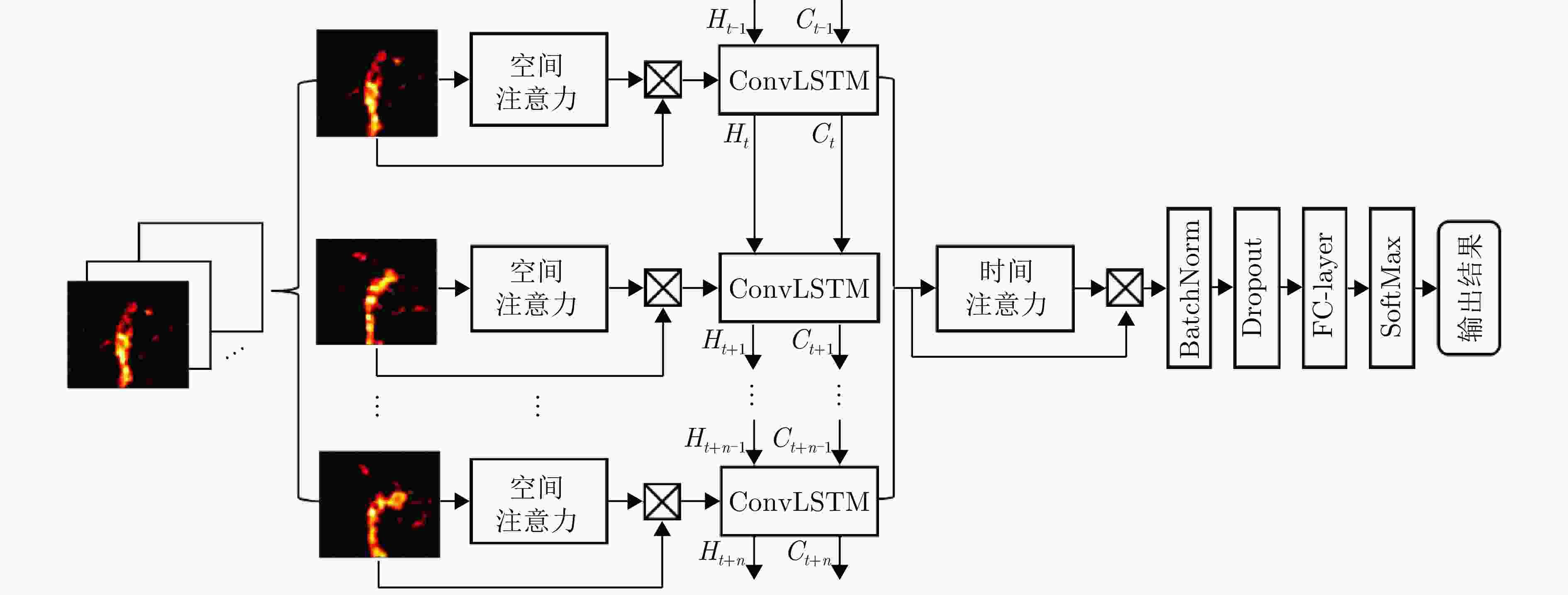
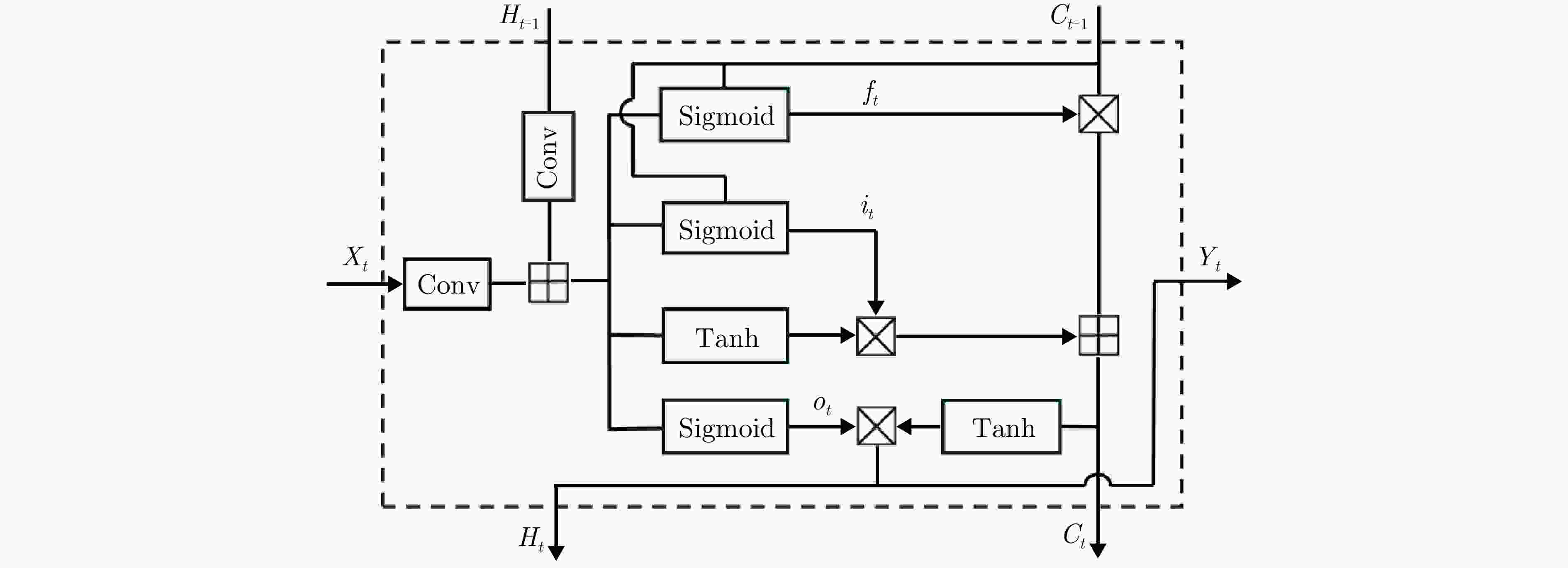
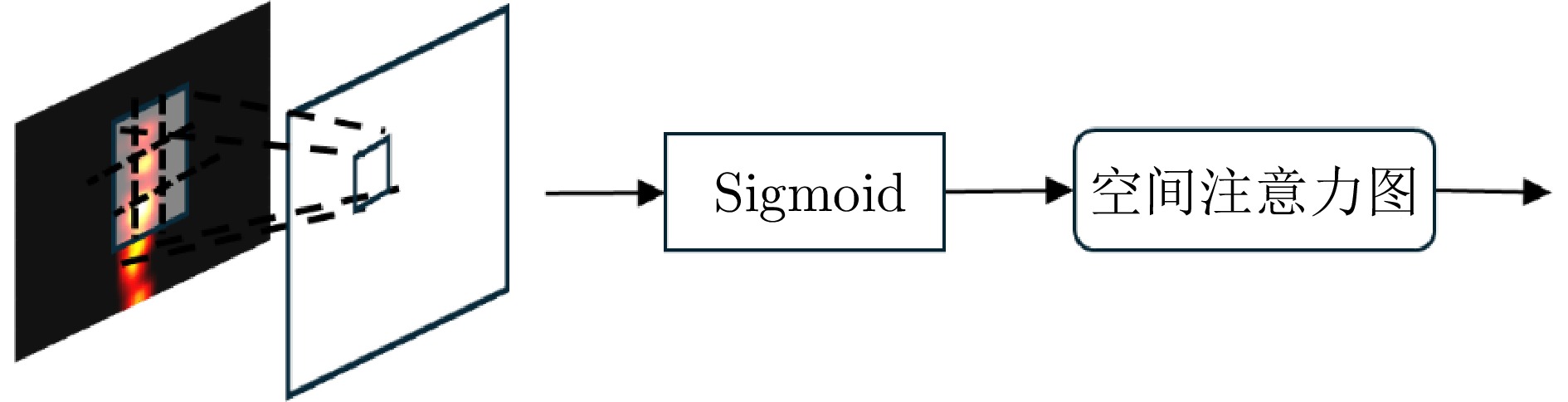
摘要: 现有的基于雷达传感器的人体动作识别研究主要聚焦于相对雷达径向运动产生的微多普勒特征。当面对非径向,特别是静态姿势或者运动方向与雷达波束中心垂直的切向动作(切向人体姿态)时,传统基于微多普勒的方法无法对径向运动微弱的切向人体姿态进行有效表征,导致识别性能大幅下降。为了解决这一问题,该文提出了一种基于多发多收(MIMO)雷达成像图序列的切向人体姿态识别方法,以高质量成像图序列的形式来表征切向姿态的人体轮廓结构及其动态变化,通过提取图像内的空间特征和图序列间的时序特征,实现对切向人体姿态的准确识别。首先,通过恒虚警检测算法(CFAR)定位人体目标所在距离门,接着,利用慢时滑窗将目标动作划分为帧序列,对每帧数据用傅里叶变换和二维Capon算法估计出切向姿态的距离、俯仰角度和方位角度,得到切向姿态的成像图,将各帧成像图按照时序串联起来,构成切向人体姿态成像图序列;然后,提出了一种改进的多域联合自适应阈值去噪算法,抑制环境杂波,增强人体轮廓和结构特征,改善成像质量;最后,采用了一种基于空时注意力模块的卷积长短期记忆网络模型(ST-ConvLSTM),利用ConvLSTM单元来学习切向人体姿态成像图序列中的多维特征,并结合空时注意力模块来强调成像图内的空间特征和图序列间的时序特征。对比实验的分析结果表明,相比于传统方法,该文所提出的方法在8种典型的切向人体姿态的识别中取得了96.9%的准确率,验证了该方法在切向人体姿态识别上的可行性和优越性。Abstract: Recent research on radar-based human activity recognition has typically focused on activities that move toward or away from radar in radial directions. Conventional Doppler-based methods can barely describe the true characteristics of nonradial activities, especially static postures or tangential activities, resulting in a considerable decline in recognition performance. To address this issue, a method for recognizing tangential human postures based on sequential images of a Multiple-Input Multiple-Output (MIMO) radar system is proposed. A time sequence of high-quality images is achieved to describe the structure of the human body and corresponding dynamic changes, where spatial and temporal features are extracted to enhance the recognition performance. First, a Constant False Alarm Rate (CFAR) algorithm is applied to locate the human target. A sliding window along the slow time axis is then utilized to divide the received signal into sequential frames. Next, a fast Fourier transform and the 2D Capon algorithm are performed on each frame to estimate range, pitch angle, and azimuth angle information, which are fused to create a tangential posture image. They are connected to form a time sequence of tangential posture images. To improve image quality, a modified joint multidomain adaptive threshold-based denoising algorithm is applied to improve the image quality by suppressing noises and enhancing human body outline and structure. Finally, a Spatio-Temporal-Convolution Long Short Term Memory (ST-ConvLSTM) network is designed to process the sequential images. In particular, the ConvLSTM cell is used to extract continuous image features by combining convolution operation with the LSTM cell. Moreover, spatial and temporal attention modules are utilized to emphasize intraframe and interframe focus for improving recognition performance. Extensive experiments show that our proposed method can achieve an accuracy rate of 96.9% in classifying eight typical tangential human postures, demonstrating its feasibility and superiority in tangential human posture recognition.
-
Key words:
- MIMO radar /
- Tangential human posture recognition /
- Sequential images /
- Image denoising /
- Deep learning
-
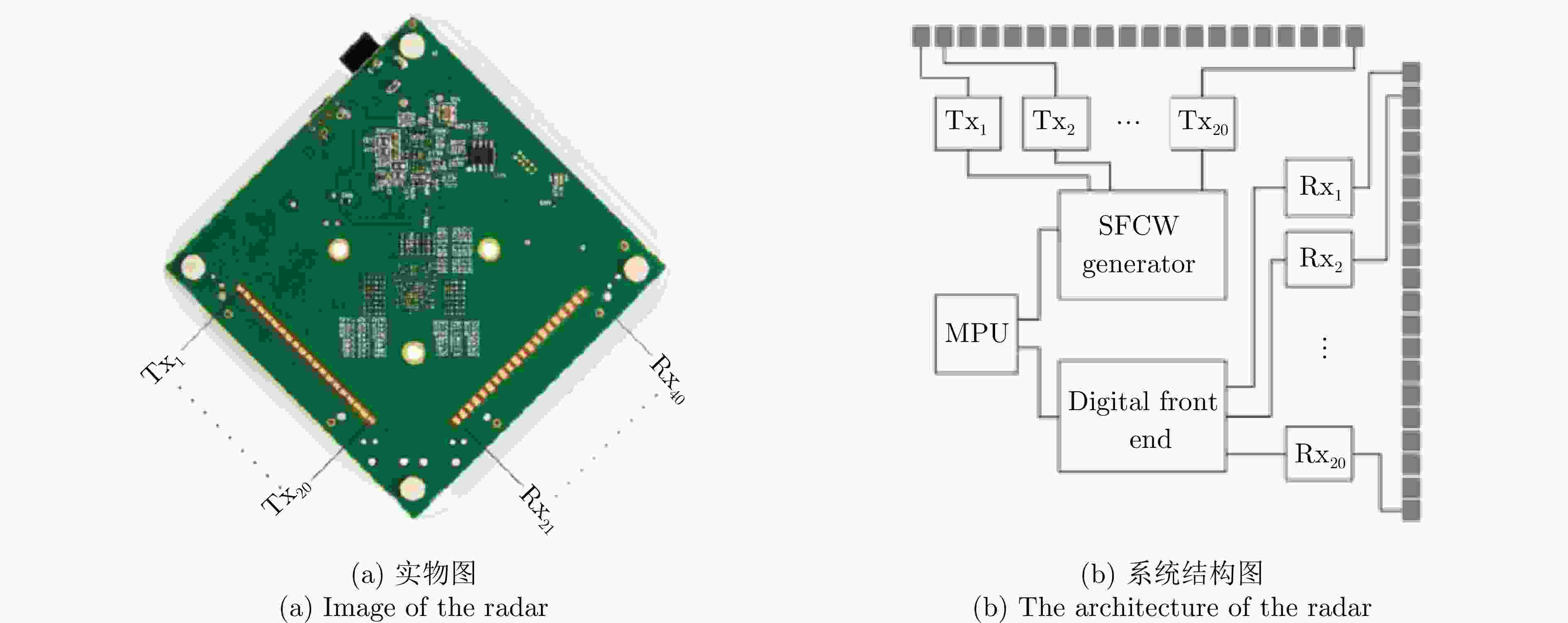
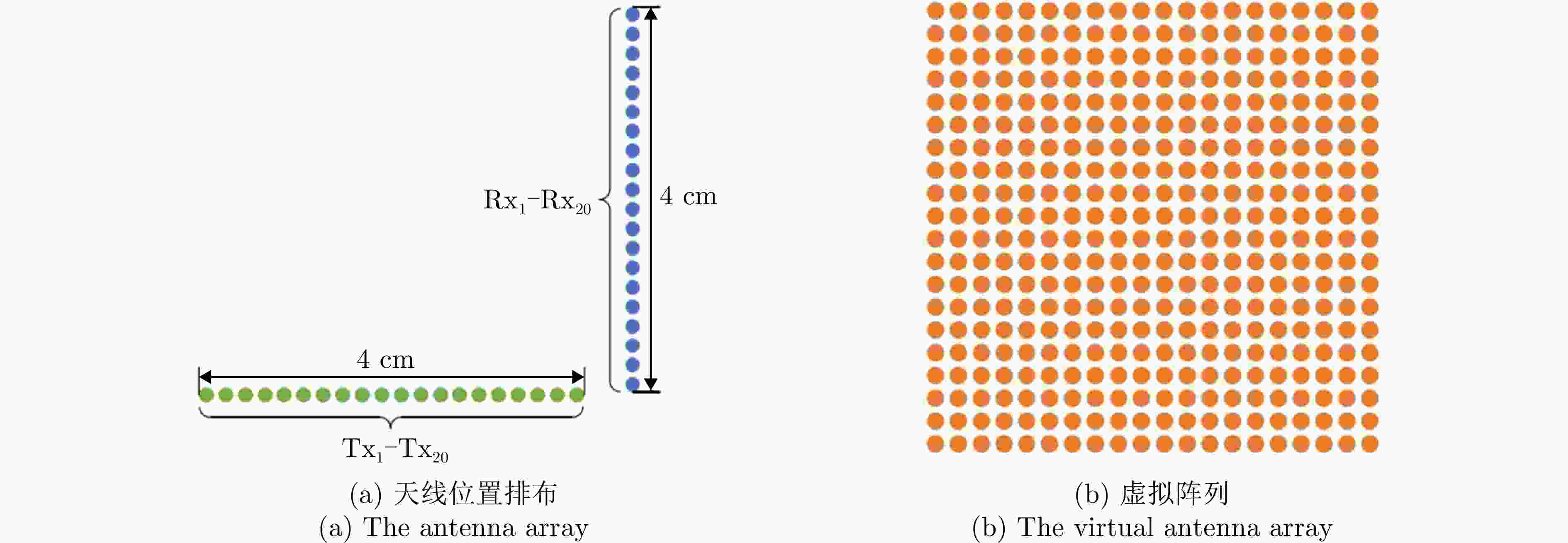
表 1 IMAGEVK-74雷达配置参数
Table 1. IMAGEVK-74 radar configuration parameters
参数 数值 起始频率 62 GHz 终止频率 66 GHz 中频带宽 100 MHz 频率步进 40 MHz 发射功率 –10 dBm 帧率 20 Hz 阵列数 20Tx, 20Rx 频率采样数 64 距离分辨率 3.75 cm 角度分辨率 6.7° 表 2 切向人体姿态识别方法分类结果汇总
Table 2. Results of tangential human postures recognition methods
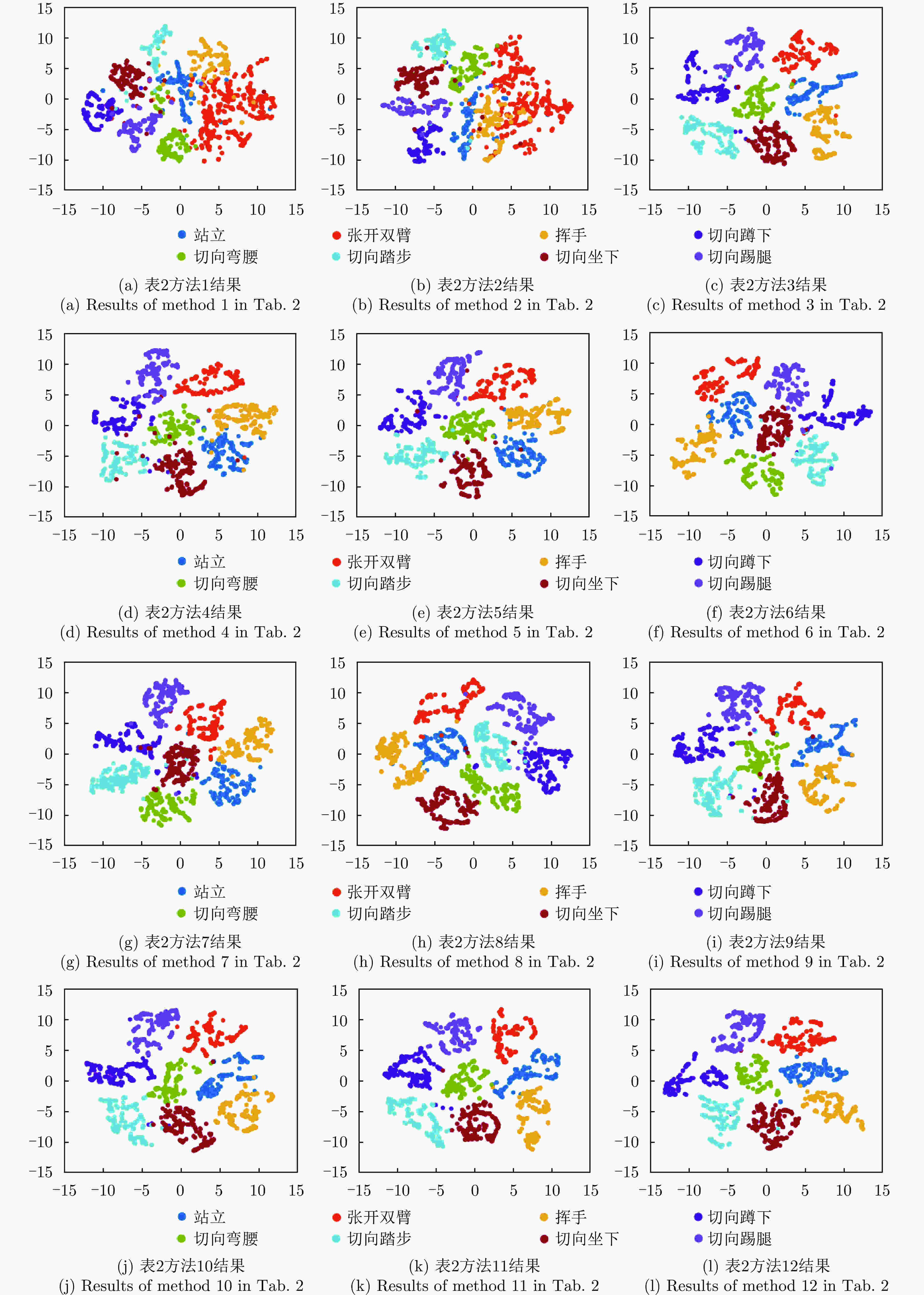
序号 输入特征 去噪算法 去噪耗时(s) 模型 模型耗时(ms) 模型尺寸(kB) 准确率(%) 方法1 时间-距离图 N/A N/A CNN[40] 2.60 2602 72.7 方法2 时间-多普勒图 N/A N/A CNN[40] 2.60 2602 70.3 方法3 成像图序列 N/A N/A ST-ConvLSTM 1.93 151 91.4 方法4 成像图序列 MTI 0.13 ST-ConvLSTM 1.93 151 89.8 方法5 成像图序列 SWT 0.03 ST-ConvLSTM 1.93 151 92.1 方法6 成像图序列 BM3D 4.40 ST-ConvLSTM 1.93 151 93.0 方法7 成像图序列 Proposed 4.61 3DCNN[41] 2.38 3806 90.6 方法8 成像图序列 Proposed 4.61 CNN-LSTM[42] 0.92 41299 91.4 方法9 成像图序列 Proposed 4.61 ConvLSTM 1.29 148 93.8 方法10 成像图序列 Proposed 4.61 S-ConvLSTM 1.62 150 94.5 方法11 成像图序列 Proposed 4.61 T-ConvLSTM 1.35 148 95.3 方法12 成像图序列 Proposed 4.61 ST-ConvLSTM
(Proposed)1.93 151 96.9 表 3 面对个体差异基于留一法的所提算法鲁棒性结果
Table 3. Robustness performance in individual diversity study
志愿者 准确率(留一法) 1 93.8% 2 91.3% 3 95.0% 4 97.5% 5 96.2% 6 93.8% 7 90.0% 8 92.5% -
[1] 金添, 宋永坤, 戴永鹏, 等. UWB-HA4D-1.0: 超宽带雷达人体动作四维成像数据集[J]. 雷达学报, 2022, 11(1): 27–39. doi: 10.12000/JR22008.JIN Tian, SONG Yongkun, DAI Yongpeng, et al. UWB-HA4D-1.0: An ultra-wideband radar human activity 4D imaging dataset[J]. Journal of Radars, 2022, 11(1): 27–39. doi: 10.12000/JR22008. [2] LE KERNEC J, FIORANELLI F, DING Chuanwei, et al. Radar signal processing for sensing in assisted living: The challenges associated with real-time implementation of emerging algorithms[J]. IEEE Signal Processing Magazine, 2019, 36(4): 29–41. doi: 10.1109/MSP.2019.2903715. [3] QI Fugui, LV Hao, WANG Jianqi, et al. Quantitative evaluation of channel micro-Doppler capacity for MIMO UWB radar human activity signals based on time-frequency signatures[J]. IEEE Transactions on Geoscience and Remote Sensing, 2020, 58(9): 6138–6151. doi: 10.1109/TGRS.2020.2974749. [4] TANG Longzhen, GUO Shisheng, JIAN Qiang, et al. Through-wall human activity recognition with complex-valued range-time-Doppler feature and region-vectorization ConvGRU[J]. IEEE Transactions on Geoscience and Remote Sensing, 2023, 61: 5111014. doi: 10.1109/TGRS.2023.3329561. [5] LI Zhi, JIN Tian, LI Lianlin, et al. Spatiotemporal processing for remote sensing of trapped victims using 4-D imaging radar[J]. IEEE Transactions on Geoscience and Remote Sensing, 2023, 61: 5103412. doi: 10.1109/TGRS.2023.3266039. [6] YANG Shufan, LE KERNEC J, ROMAIN O, et al. The human activity radar challenge: Benchmarking based on the ‘radar signatures of human activities’ dataset from Glasgow university[J]. IEEE Journal of Biomedical and Health Informatics, 2023, 27(4): 1813–1824. doi: 10.1109/JBHI.2023.3240895. [7] BAI Xueru, HUI Ye, WANG Li, et al. Radar-based human gait recognition using dual-channel deep convolutional neural network[J]. IEEE Transactions on Geoscience and Remote Sensing, 2019, 57(12): 9767–9778. doi: 10.1109/TGRS.2019.2929096. [8] LI Changzhi, PENG Zhengyu, HUANG T Y, et al. A review on recent progress of portable short-range noncontact microwave radar systems[J]. IEEE Transactions on Microwave Theory and Techniques, 2017, 65(5): 1692–1706. doi: 10.1109/TMTT.2017.2650911. [9] KIM Y and LING Hao. Human activity classification based on micro-Doppler signatures using a support vector machine[J]. IEEE Transactions on Geoscience and Remote Sensing, 2009, 47(5): 1328–1337. doi: 10.1109/TGRS.2009.2012849. [10] DING Chuanwei, HONG Hong, ZOU Yu, et al. Continuous human motion recognition with a dynamic range-Doppler trajectory method based on FMCW radar[J]. IEEE Transactions on Geoscience and Remote Sensing, 2019, 57(9): 6821–6831. doi: 10.1109/TGRS.2019.2908758. [11] EROL B and AMIN M G. Radar data cube processing for human activity recognition using multisubspace learning[J]. IEEE Transactions on Aerospace and Electronic Systems, 2019, 55(6): 3617–3628. doi: 10.1109/TAES.2019.2910980. [12] DING Chuanwei, ZHANG Li, CHEN Haoyu, et al. Sparsity-based human activity recognition with pointnet using a portable FMCW radar[J]. IEEE Internet of Things Journal, 2023, 10(11): 10024–10037. doi: 10.1109/JIOT.2023.3235808. [13] LI Xinyu, HE Yuan, FIORANELLI F, et al. Semisupervised human activity recognition with radar micro-Doppler signatures[J]. IEEE Transactions on Geoscience and Remote Sensing, 2022, 60: 5103112. doi: 10.1109/TGRS.2021.3090106. [14] KIM W Y and SEO D H. Radar-based human activity recognition combining range-time-Doppler maps and range-distributed-convolutional neural networks[J]. IEEE Transactions on Geoscience and Remote Sensing, 2022, 60: 1002311. doi: 10.1109/TGRS.2022.3162833. [15] QIAO Xingshuai, AMIN M G, SHAN Tao, et al. Human activity classification based on micro-Doppler signatures separation[J]. IEEE Transactions on Geoscience and Remote Sensing, 2022, 60: 5105014. doi: 10.1109/TGRS.2021.3105124. [16] LUO Fei, BODANESE E, KHAN S, et al. Spectro-temporal modeling for human activity recognition using a radar sensor network[J]. IEEE Transactions on Geoscience and Remote Sensing, 2023, 61: 5103913. doi: 10.1109/TGRS.2023.3270365. [17] DING Chuanwei, CHAE R, WANG Jing, et al. Inattentive driving behavior detection based on portable FMCW radar[J]. IEEE Transactions on Microwave Theory and Techniques, 2019, 67(10): 4031–4041. doi: 10.1109/TMTT.2019.2934413. [18] WANG Bo, ZHANG Hao, and GUO Yongxin. Radar-based soft fall detection using pattern contour vector[J]. IEEE Internet of Things Journal, 2023, 10(3): 2519–2527. doi: 10.1109/JIOT.2022.3213693. [19] 元志安, 周笑宇, 刘心溥, 等. 基于RDSNet的毫米波雷达人体跌倒检测方法[J]. 雷达学报, 2021, 10(4): 656–664. doi: 10.12000/JR21015.YUAN Zhi’an, ZHOU Xiaoyu, LIU Xinpu, et al. Human fall detection method using millimeter-wave radar based on RDSNet[J]. Journal of Radars, 2021, 10(4): 656–664. doi: 10.12000/JR21015. [20] TAHMOUSH D and SILVIOUS J. Radar micro-Doppler for long range front-view gait recognition[C]. 3rd IEEE International Conference on Biometrics: Theory, Applications, and Systems (BTAS), Washington, USA, 2009: 1–6. doi: 10.1109/BTAS.2009.5339049. [21] ALNUJAIM I, RAM S S, OH D, et al. Synthesis of micro-Doppler signatures of human activities from different aspect angles using generative adversarial networks[J]. IEEE Access, 2021, 9: 46422–46429. doi: 10.1109/ACCESS.2021.3068075. [22] QI Fugui, LI Zhao, MA Yangyang, et al. Generalization of channel micro-Doppler capacity evaluation for improved finer-grained human activity classification using MIMO UWB radar[J]. IEEE Transactions on Microwave Theory and Techniques, 2021, 69(11): 4748–4761. doi: 10.1109/TMTT.2021.3076055. [23] FIORANELLI F, PATEL J, GÜRBÜZ S Z, et al. Multistatic human micro-Doppler classification with degraded/jammed radar data[C]. 2019 IEEE Radar Conference (RadarConf), Boston, USA, 2019: 1–6. doi: 10.1109/RADAR.2019.8835618. [24] THIEL M and SARABANDI K. Ultrawideband multi-static scattering analysis of human movement within buildings for the purpose of stand-off detection and localization[J]. IEEE Transactions on Antennas and Propagation, 2011, 59(4): 1261–1268. doi: 10.1109/TAP.2011.2109349. [25] FIORANELLI F, RITCHIE M, and GRIFFITHS H. Aspect angle dependence and multistatic data fusion for micro-Doppler classification of armed/unarmed personnel[J]. IET Radar, Sonar & Navigation, 2015, 9(9): 1231–1239. doi: 10.1049/iet-rsn.2015.0058. [26] FAIRCHILD D P and NARAYANAN R M. Multistatic micro-Doppler radar for determining target orientation and activity classification[J]. IEEE Transactions on Aerospace and Electronic Systems, 2016, 52(1): 512–521. doi: 10.1109/TAES.2015.130595. [27] FIORANELLI F, RITCHIE M, GÜRBÜZ S Z, et al. Feature diversity for optimized human micro-Doppler classification using multistatic radar[J]. IEEE Transactions on Aerospace and Electronic Systems, 2017, 53(2): 640–654. doi: 10.1109/TAES.2017.2651678. [28] QIAO Xingshuai, LI Gang, SHAN Tao, et al. Human activity classification based on moving orientation determining using multistatic micro-Doppler radar signals[J]. IEEE Transactions on Geoscience and Remote Sensing, 2022, 60: 5104415. doi: 10.1109/TGRS.2021.3100482. [29] YU J T, YEN Li, and TSENG P H. mmWave radar-based hand gesture recognition using range-angle image[C]. 2020 IEEE 91st Vehicular Technology Conference (VTC2020-Spring), Antwerp, Belgium, 2020: 1–5. doi: 10.1109/VTC2020-Spring48590.2020.9128573. [30] ZHAO Yubin, YAROVOY A, and FIORANELLI F. Angle-insensitive human motion and posture recognition based on 4D imaging radar and deep learning classifiers[J]. IEEE Sensors Journal, 2022, 22(12): 12173–12182. doi: 10.1109/JSEN.2022.3175618. [31] YANG Yang, HOU Chunping, LANG Yue, et al. Omnidirectional motion classification with monostatic radar system using micro-Doppler signatures[J]. IEEE Transactions on Geoscience and Remote Sensing, 2020, 58(5): 3574–3587. doi: 10.1109/TGRS.2019.2958178. [32] YANG Yang, ZHANG Yutong, SONG Chunying, et al. Omnidirectional spectrogram generation for radar-based omnidirectional human activity recognition[J]. IEEE Transactions on Geoscience and Remote Sensing, 2023, 61: 5105513. doi: 10.1109/TGRS.2023.3278409. [33] YANG Yang, LI Junhan, LI Beichen, et al. Few-shot omnidirectional human motion recognition using monostatic radar system[J]. IEEE Transactions on Instrumentation and Measurement, 2023, 72: 2531414. doi: 10.1109/TIM.2023.3328079. [34] 张哲熙. 基于BM3D的图像去噪算法研究[D]. [硕士论文], 西安电子科技大学, 2017.ZHANG Zhexi. Research on image denoising algorithm based on BM3D[D]. [Master dissertation], Xidian University, 2017. [35] DABOV K, FOI A, KATKOVNIK V, et al. Image denoising with block-matching and 3D filtering[C]. Image Processing: Algorithms and Systems, Neural Networks, and Machine Learning, San Jose, USA, 2006: 606414. doi: 10.1117/12.643267. [36] WANG Xinheng, ISTEPANIAN R S H, and SONG Yonghua. Microarray image enhancement by denoising using stationary wavelet transform[J]. IEEE Transactions on Nanobioscience, 2003, 2(4): 184–189. doi: 10.1109/TNB.2003.816225. [37] 王安义, 战金龙, 卢建军. 一种新的二维Capon算法的研究[J]. 西安科技学院学报, 2003, 23(4): 437–440. doi: 10.3969/j.issn.1672-9315.2003.04.023.WANG Anyi, ZHAN Jinlong, and LU Jianjun. A new 2-D Capon algorithm[J]. Journal of Xi’an University of Science and Technology, 2003, 23(4): 437–440. doi: 10.3969/j.issn.1672-9315.2003.04.023. [38] RAHMAN S A and ADJEROH D A. Deep learning using convolutional LSTM estimates biological age from physical activity[J]. Scientific Reports, 2019, 9(1): 11425. doi: 10.1038/s41598-019-46850-0. [39] SUDHAKARAN S and LANZ O. Convolutional long short-term memory networks for recognizing first person interactions[C]. The IEEE International Conference on Computer Vision Workshops (ICCVW), Venice, Italy, 2017: 2339–2346. doi: 10.1109/ICCVW.2017.276. [40] KIM Y and MOON T. Human detection and activity classification based on micro-Doppler signatures using deep convolutional neural networks[J]. IEEE Geoscience and Remote Sensing Letters, 2016, 13(1): 8–12. doi: 10.1109/LGRS.2015.2491329. [41] LI Wenxuan, ZHANG Dongheng, LI Yadong, et al. Real-time fall detection using mmWave radar[C]. IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Singapore, 2022: 16–20. doi: 10.1109/ICASSP43922.2022.9747153. [42] KIM Y, ALNUJAIM I, and OH D. Human activity classification based on point clouds measured by millimeter wave MIMO radar with deep recurrent neural networks[J]. IEEE Sensors Journal, 2021, 21(12): 13522–13529. doi: 10.1109/JSEN.2021.3068388. -



 作者中心
作者中心 专家审稿
专家审稿 责编办公
责编办公 编辑办公
编辑办公

 下载:
下载: