作者中心
专家审稿
责编办公
编辑办公
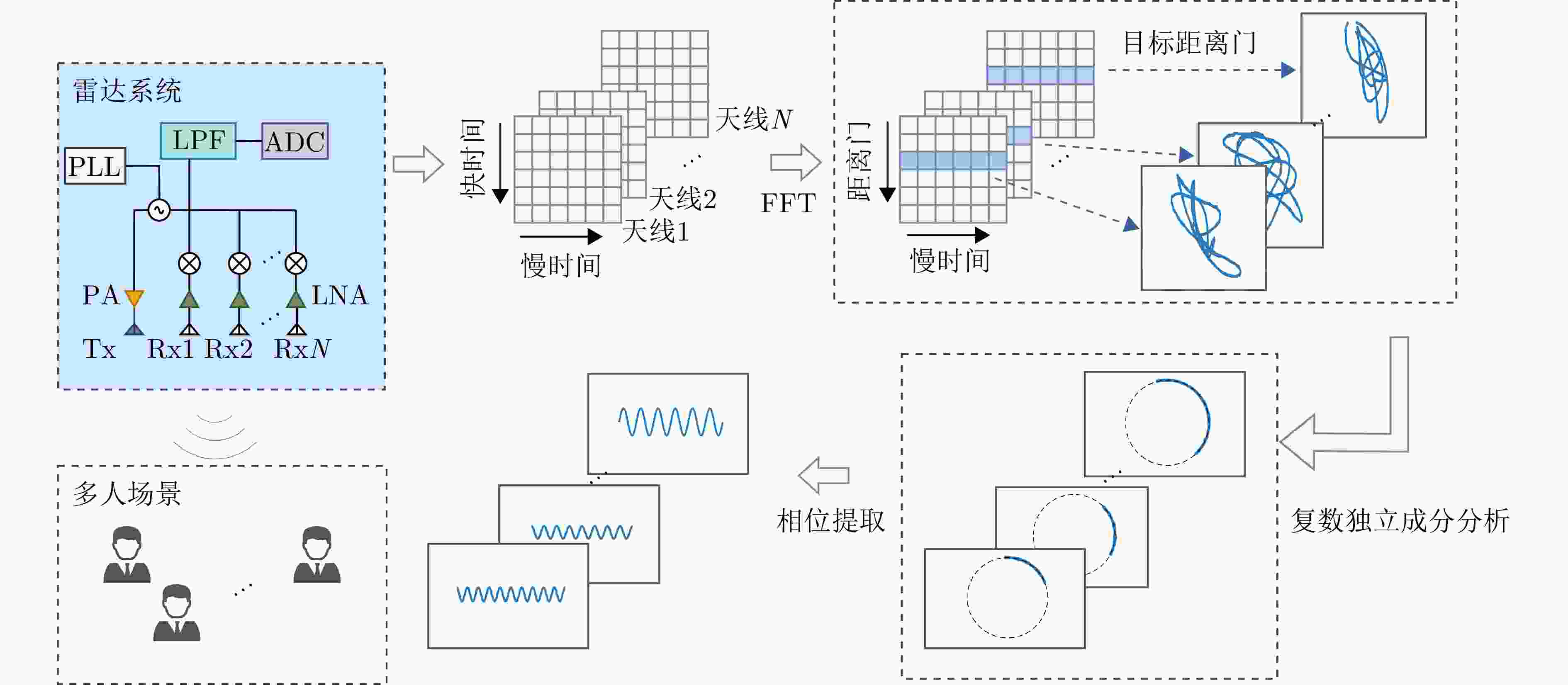
Noncontact Multiperson Respiratory Detection Method Based on Blind Source Separation
-
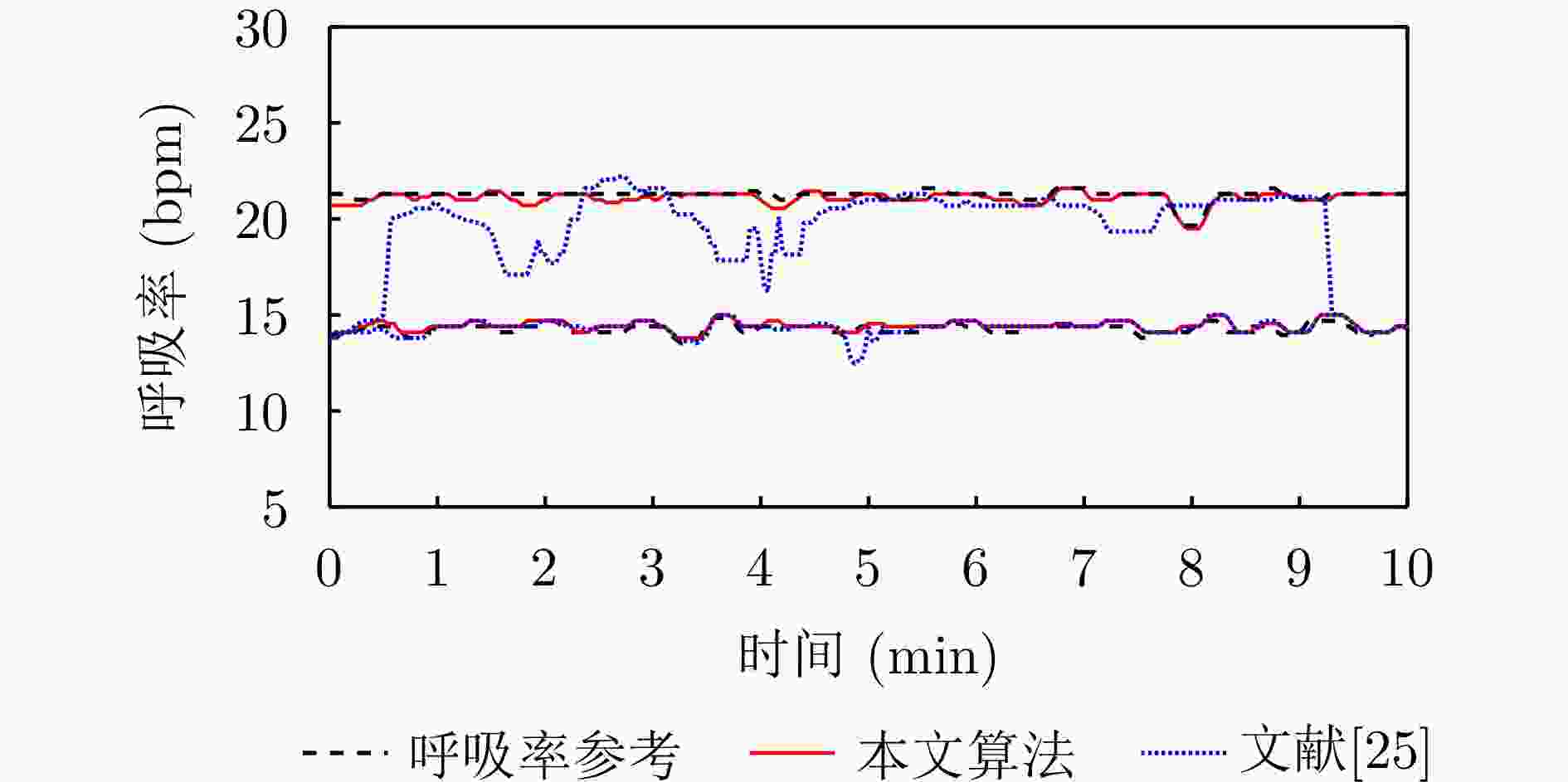
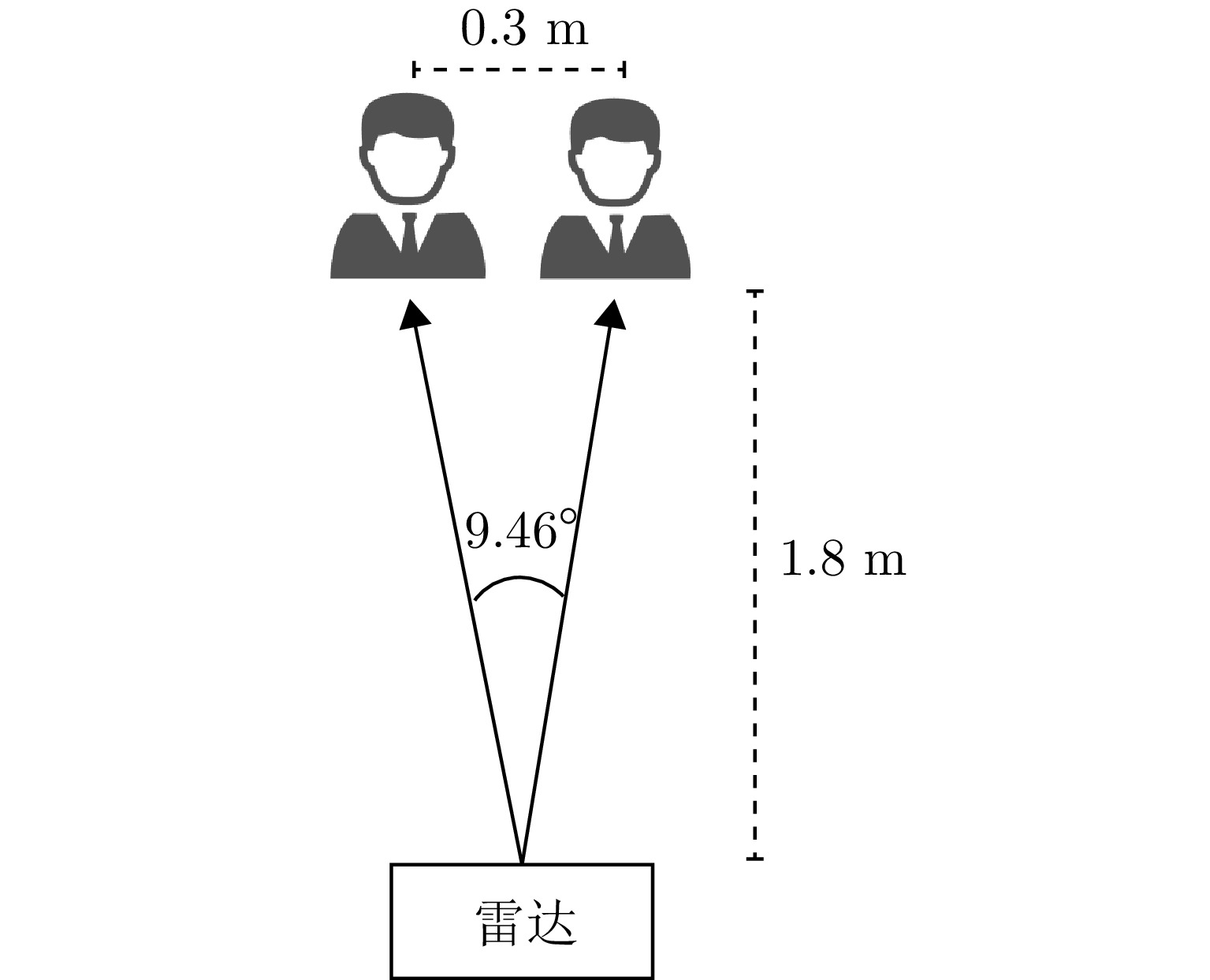
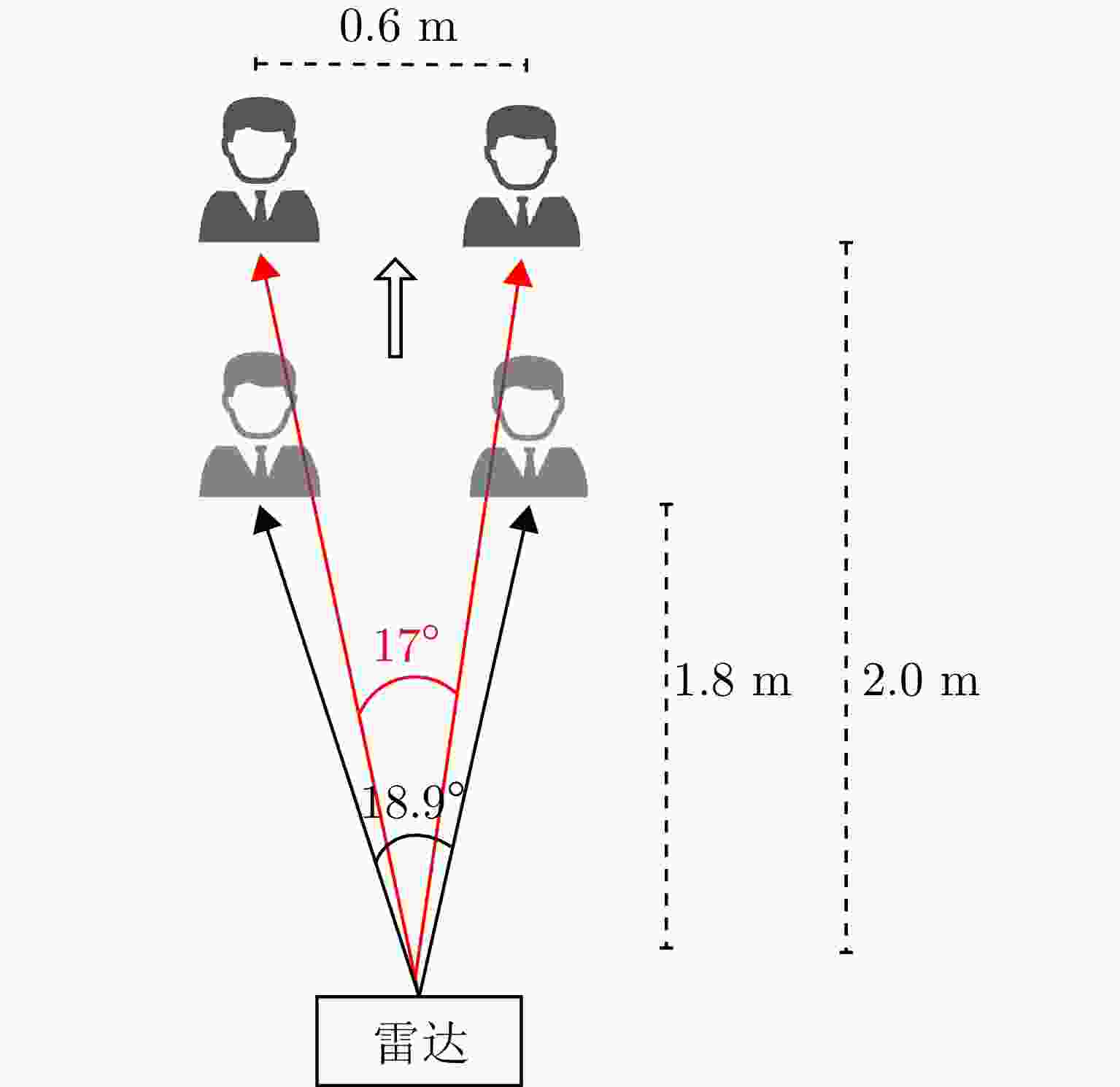
摘要: 近年来，人们越来越关注多人环境下的呼吸监测，以及如何同时监测多人的健康状态。在多人呼吸检测的算法中，盲源分离算法因其无需先验信息并且对硬件性能依赖性较小而备受研究者关注。然而，在多人呼吸监测场景中，目前的盲源分离算法通常将相位信号作为源信号进行分离，该文引入FMCW雷达下距离维信号和相位信号的对比，推导出相位信号作为源信号存在近似误差，并通过仿真验证距离维信号作为源信号时分离效果更好。另外，该文提出了基于非圆复数独立成分分析的多人呼吸信号分离算法，分析了不同呼吸信号参数对分离效果的影响，仿真和实测实验表明，所提出的方法适用于天线个数不小于目标个数时多人呼吸信号的检测，并且在目标角度差为9.46°时，也能够准确分离呼吸信号。Abstract: In recent years, there has been an increasing interest in respiratory monitoring in multiperson environments and simultaneous monitoring of the health status of multiple people. Among the algorithms developed for multiperson respiratory detection, blind source separation algorithms have attracted the attention of researchers because they do not require prior information and are less dependent on hardware performance. However, in the context of multiperson respiratory monitoring, the current blind source separation algorithm usually separates phase signals as the source signal. This article compares the distance dimension and phase signals under Frequency-modulated continuous-wave radar, calculates the approximate error associated with using the phase signal as the source signal, and verifies the separation effect through simulations. The distance dimension signal is better to use as the source signal. In addition, this article proposes a multiperson respiratory signal separation algorithm based on noncircular complex independent component analysis and analyzes the impact of different respiratory signal parameters on the separation effect. Simulation and experimental measurements show that the proposed method is suitable for detecting multiperson respiratory signals under controlled conditions and can accurately separate respiratory signals when the angle of the two targets to the radar is 9.46°.
-
图 2 多人呼吸分离的总体原理图
Figure 2. Overall schematic diagram for multiperson respiration detection
图 3 两天线两目标复数盲源分离效果图
Figure 3. Effect diagram of complex blind source separation with two antennas
图 4 呼吸信号及呼吸参考信号对比
Figure 4. Comparison of the respiratory signals and respiratory reference signals
图 5 基于相位信号恢复的呼吸信号及呼吸参考信号对比
Figure 5. Comparison of respiratory signal and respiratory reference signal based on phase signal recovery
图 6 3天线3目标恢复的呼吸信号及呼吸参考信号对比
Figure 6. Comparison of the respiratory signals and respiratory reference signals recovered from three antennas and three subjects
图 7 不同信噪比下信号重构的误差
Figure 7. Error of signal reconstruction under different signal-to-noise ratios
图 8 不同呼吸参数下的波形重构误差
Figure 8. Error of signal reconstruction under different respiratory parameters
图 11 1 m处双人正对雷达时分离出的呼吸波形以及参考波形
Figure 11. Respiratory waveforms and reference waveforms separated at 1 m when two individuals face the radar directly
图 12 1 m处双人正对雷达时分离前后的星座图
Figure 12. Constellation diagrams before and after separation when two individuals face the radar directly at 1 m
图 13 1 m处双人侧对雷达时分离出的呼吸波形以及参考波形
Figure 13. Respiratory waveforms and reference waveforms separated at 1 m when two individuals face the radar sideways
图 14 1 m处双人背对雷达时分离出的呼吸波形以及参考波形
Figure 14. Respiratory waveforms and reference waveforms separated at 1 m when two individuals face away from the radar
图 15 呼吸异常时雷达分离出的呼吸波形以及参考波形
Figure 15. Respiratory waveforms and reference waveforms separated by radar during abnormal respiration
图 16 10 min内雷达得到的两个测试者的呼吸率以及参考呼吸率
Figure 16. The respiratory rates of two testers obtained by radar within 10 minutes, along with the reference respiratory rate
图 17 两人距离雷达1.8 m场景示意图
Figure 17. Illustration of two people at a distance of 1.8 m from the radar
图 18 两人距离雷达1.8 m时分离出两人的雷达呼吸信号以及呼吸参考信号
Figure 18. Radar respiratory signals of two persons separated when the distance to the radar is 1.8 m, and the reference respiratory signal
图 19 两人呼吸频率一致时分离出两人的雷达呼吸信号以及呼吸参考信号
Figure 19. Radar respiratory signals of two persons separated when their respiratory frequencies are consistent, and the reference respiratory signal
图 20 两人距离雷达1.8 m和2 m场景示意图
Figure 20. Illustration of two people at a distance of 1.8 m and 2.0 m from the radar
图 21 1.8 m处两个目标的呼吸波形及角度
Figure 21. Respiratory waveforms and angles of two subjects at 1.8 m
图 22 2 m处两个目标的呼吸波形及角度
Figure 22. Respiratory waveforms and angles of two subjects at 2 m
1 多人呼吸分离算法流程
1. Steps of complex multiperson blind source separation algorithm
输入：N个天线的距离维信号X 输出：分离后的N个目标的距离维信号 初始化：初始化解混矩阵${{\boldsymbol{W}}^{\text{H}}} = \left[ {{{\boldsymbol{w}}_1} \;{{\boldsymbol{w}}_2}\; \cdots\; {{\boldsymbol{w}}_N}} \right] = {\boldsymbol{I}}$ 1 通过式(18)对观测数据X进行白化，得到Z 2 令$k = 1$ 3 使用式(25)对$ {{\boldsymbol{w}}_i} $进行更新，直到满足收敛条件 4 $k = k + 1$，使用步骤3完成下一个列向量的估计 5 完成所有分量分离，并使用式(26)进行正交变换 6 得到混合矩阵的估计$ \tilde {\boldsymbol{A}} = {{\boldsymbol{V}}^{ - 1}}{\boldsymbol{W}} $，以及源信号的估计
$ {\boldsymbol{Y}} = {{\boldsymbol{W}}^{\text{H}}}{\boldsymbol{Z}} $7 按照式(28)和式(29)去除相位模糊 
下载: 导出CSV
表 1 仿真实验参数
Table 1. Simulation experiment parameters for two antennas and two targets
参数 数值 载频 24 GHz 天线阵元个数 2 天线间距 $\lambda /2$
下载: 导出CSV
表 2 不同目标个数、不同天线数量时峭度和
Table 2. Sum of kurtosis for different number of targets, different number of antennas
天线个数 1个目标 2个目标 3个目标 1 1.00 1.50 1.75 2 1.00 2.35 2.77 3 1.00 2.35 3.48
下载: 导出CSV
表 3 FMCW雷达硬件参数设置
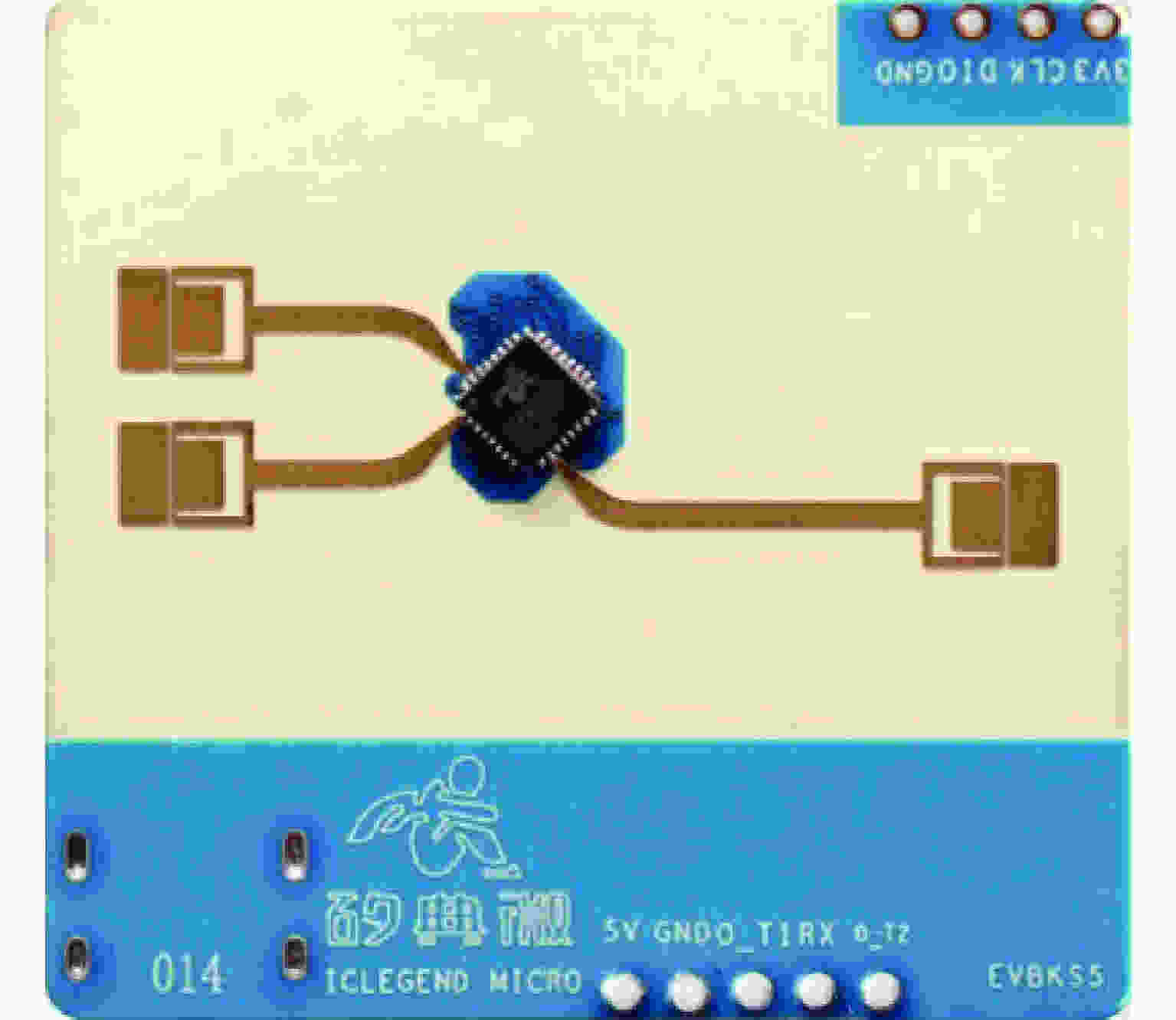
Table 3. Hardware parameters setting for FMCW radar
参数 数值 起始频率 24 GHz 带宽 1 GHz Chirp采样点个数 1024 ADC采样速率 2.5 MHz Chirp重复周期 10 ms
下载: 导出CSV
-
[1] CROSSLEY G H, BOYLE A, VITENSE H, et al. The CONNECT (Clinical Evaluation of Remote Notification to Reduce Time to Clinical Decision) trial: The value of wireless remote monitoring with automatic clinician alerts[J]. Journal of the American College of Cardiology, 2011, 57(10): 1181–1189. doi: 10.1016/j.jacc.2010.12.012. [2] NANGALIA V, PRYTHERCH D R, and SMITH G B. Health technology assessment review: Remote monitoring of vital signs-current status and future challenges[J]. Critical Care, 2010, 14(5): 233. doi: 10.1186/cc9208. [3] FIORANELLI F, LE KERNEC J, and SHAH S A. Radar for health care: Recognizing human activities and monitoring vital signs[J]. IEEE Potentials, 2019, 38(4): 16–23. doi: 10.1109/MPOT.2019.2906977. [4] DONG Shuqin, WEN Li, YE Yangtao, et al. A review on recent advancements of biomedical radar for clinical applications[J]. IEEE Open Journal of Engineering in Medicine and Biology, 2024, 5: 707–724. doi: 10.1109/OJEMB.2024.3401105. [5] ISHRAK M S, CAI Fulin, ISLAM S M M, et al. Doppler radar remote sensing of respiratory function[J]. Frontiers in Physiology, 2023, 14: 1130478. doi: 10.3389/fphys.2023.1130478. [6] ANTOLINOS E, GARCÍA-RIAL F, HERNÁNDEZ C, et al. Cardiopulmonary activity monitoring using millimeter wave radars[J]. Remote Sensing, 2020, 12(14): 2265. doi: 10.3390/rs12142265. [7] ADIB F, MAO Hongzi, KABELAC Z, et al. Smart homes that monitor breathing and heart rate[C]. The 33rd Annual ACM Conference on Human Factors in Computing Systems, Seoul, Republic of Korea, 2015: 837–846. doi: 10.1145/2702123.2702200. [8] ZHAO Heng, HONG Hong, MIAO Dongyu, et al. A noncontact breathing disorder recognition system using 2.4-GHz digital-IF Doppler radar[J]. IEEE Journal of Biomedical and Health Informatics, 2019, 23(1): 208–217. doi: 10.1109/JBHI.2018.2817258. [9] PARK B K, BORIC-LUBECKE O, and LUBECKE V M. Arctangent demodulation with DC offset compensation in quadrature Doppler radar receiver systems[J]. IEEE Transactions on Microwave Theory and Techniques, 2007, 55(5): 1073–1079. doi: 10.1109/TMTT.2007.895653. [10] XIAO Yanming, LIN J, BORIC-LUBECKE O, et al. A Ka-band low power Doppler radar system for remote detection of cardiopulmonary motion[C]. 2005 IEEE Engineering in Medicine and Biology 27th Annual Conference, Shanghai, China, 2006: 7151–7154. doi: 10.1109/IEMBS.2005.1616156. [11] LIN Jenshan, LUBECKE V M, BORIC-LUBECKE O, et al. A review on recent advances in Doppler radar sensors for noncontact healthcare monitoring[J]. IEEE Transactions on Microwave Theory and Techniques, 2013, 61(5): 2046–2060. doi: 10.1109/TMTT.2013.2256924. [12] PATERNIANI G, SGRECCIA D, DAVOLI A, et al. Radar-based monitoring of vital signs: A tutorial overview[J]. Proceedings of the IEEE, 2023, 111(3): 277–317. doi: 10.1109/JPROC.2023.3244362. [13] BORIC-LUBEKE O and LUBECKE V M. Wireless house calls: Using communications technology for health care and monitoring[J]. IEEE Microwave Magazine, 2002, 3(3): 43–48. doi: 10.1109/MMW.2002.1028361. [14] DONG Shuqin, WEN Li, LI Yuchen, et al. Remote respiratory variables tracking with biomedical radar-based IoT system during sleep[J]. IEEE Internet of Things Journal, 2024, 11(11): 19937–19948. doi: 10.1109/JIOT.2024.3367932. [15] GUAN Lei, WU Tong, YANG Xiaodong, et al. Multiperson respiratory monitoring using single-channel continuous-wave radar with time modulated array[J]. IEEE Transactions on Instrumentation and Measurement, 2023, 72: 4008111. doi: 10.1109/TIM.2023.3287258. [16] WANG Shuxuan, HAN Chong, GUO Jian, et al. MM-FGRM: Fine-grained respiratory monitoring using MIMO millimeter wave radar[J]. IEEE Transactions on Instrumentation and Measurement, 2024, 73: 4000913. doi: 10.1109/TIM.2023.3334353. [17] PHAN T, KILIC O, NAHAR S, et al. Accuracy investigation of SFCW radar in human vital signs detection for subject's relative position[C]. 2017 IEEE International Symposium on Antennas and Propagation & USNC/URSI National Radio Science Meeting, San Diego, USA, 2017: 577–578. doi: 10.1109/APUSNCURSINRSM.2017.8072331. [18] MERCURI M, LIU Yaohong, SHEELAVANT S, et al. Digital linear discrete FMCW radar for healthcare applications[C]. 2019 IEEE MTT-S International Microwave Symposium (IMS), Boston, USA, 2019: 144–147. doi: 10.1109/MWSYM.2019.8701012. [19] YAN Jiaming, HONG Hong, ZHAO Heng, et al. Through-wall multiple targets vital signs tracking based on VMD algorithm[J]. Sensors, 2016, 16(8): 1293. doi: 10.3390/s16081293. [20] EDER Y and ELDAR Y C. Sparsity-based multi-person non-contact vital signs monitoring via FMCW radar[J]. IEEE Journal of Biomedical and Health Informatics, 2023, 27(6): 2806–2817. doi: 10.1109/JBHI.2023.3255740. [21] XIONG Junjun, HONG Hong, ZHANG Hongqiang, et al. Multitarget respiration detection with adaptive digital beamforming technique based on SIMO radar[J]. IEEE Transactions on Microwave Theory and Techniques, 2020, 68(11): 4814–4824. doi: 10.1109/TMTT.2020.3020082. [22] KODA T, SAKAMOTO T, OKUMURA S, et al. Noncontact respiratory measurement for multiple people at arbitrary locations using array radar and respiratory-space clustering[J]. IEEE Access, 2021, 9: 106895–106906. doi: 10.1109/ACCESS.2021.3099821. [23] SAKAMOTO T and YAMASHITA K. Noncontact measurement of autonomic nervous system activities based on heart rate variability using ultra-wideband array radar[J]. IEEE Journal of Electromagnetics, RF and Microwaves in Medicine and Biology, 2020, 4(3): 208–215. doi: 10.1109/JERM.2019.2948827. [24] ISLAM S M M, YAVARI E, RAHMAN A, et al. Separation of respiratory signatures for multiple subjects using independent component analysis with the JADE algorithm[C]. 2018 40th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Honolulu, USA, 2018: 1234–1237. doi: 10.1109/EMBC.2018.8512583. [25] ISLAM S M M, BORIC-LUBECKE O, and LUBEKCE V M. Concurrent respiration monitoring of multiple subjects by phase-comparison monopulse radar using independent component analysis (ICA) with JADE algorithm and direction of arrival (DOA)[J]. IEEE Access, 2020, 8: 73558–73569. doi: 10.1109/ACCESS.2020.2988038. [26] ZHANG Li, LIU Yuan, HONG Hong, et al. Noncontact multi-target respiration sensing using SIMO radar with UBSS method[J]. IEEE Microwave and Wireless Components Letters, 2022, 32(3): 210–213. doi: 10.1109/LMWC.2021.3138767. [27] LIU Jingtao, LI Yuchen, LI Changzhi, et al. Accurate measurement of human vital signs with linear FMCW radars under proximity stationary clutters[J]. IEEE Transactions on Biomedical Circuits and Systems, 2021, 15(6): 1393–1404. doi: 10.1109/TBCAS.2021.3123830. [28] ZAKRZEWSKI M, RAITTINEN H, and VANHALA J. Comparison of center estimation algorithms for heart and respiration monitoring with microwave Doppler radar[J]. IEEE Sensors Journal, 2012, 12(3): 627–634. doi: 10.1109/JSEN.2011.2119299. [29] PICINBONO B. On circularity[J]. IEEE Transactions on Signal Processing, 1994, 42(12): 3473–3482. doi: 10.1109/78.340781. [30] YUE Shichao, HE Hao, WANG Hao, et al. Extracting multi-person respiration from entangled RF signals[J]. Proceedings of the ACM on Interactive, Mobile, Wearable and Ubiquitous Technologies, 2018, 2(2): 86. doi: 10.1145/3214289. [31] ERIKSSON J and KOIVUNEN V. Complex-valued ICA using second order statistics[C]. The 2004 14th IEEE Signal Processing Society Workshop Machine Learning for Signal Processing, 2004, Sao Luis, Brazil, 2004: 183–192. doi: 10.1109/MLSP.2004.1422973. [32] ERIKSSON J and KOIVUNEN V. Complex random vectors and ICA models: Identifiability, uniqueness, and separability[J]. IEEE Transactions on Information Theory, 2006, 52(3): 1017–1029. doi: 10.1109/TIT.2005.864440. [33] BRANDWOOD D H. A complex gradient operator and its application in adaptive array theory[J]. IEE Proceedings F (Communications, Radar and Signal Processing), 1983, 130(1): 11–16. doi: 10.1049/ip-f-1.1983.0003. [34] CARDOSO J F and SOULOUMIAC A. Blind beamforming for non-Gaussian signals[C]. IEE Proceedings F (Radar and Signal Processing), 1993, 140(6): 362–370. doi: 10.1049/ip-f-2.1993.0054. [35] NOVEY M and ADALI T. Complex fixed-point ICA algorithm for separation of QAM sources using Gaussian mixture model[C]. 2007 IEEE International Conference on Acoustics, Speech and Signal Processing-ICASSP'07, Honolulu, USA, 2007: II-445–II-448. doi: 10.1109/ICASSP.2007.366268. [36] NOVEY M and ADALI T. On extending the complex FastICA algorithm to noncircular sources[J]. IEEE Transactions on Signal Processing, 2008, 56(5): 2148–2154. doi: 10.1109/TSP.2007.911278. [37] RODRIGUEZ P A, CALHOUN V D, and ADALI T. De-noising, phase ambiguity correction and visualization techniques for complex-valued ICA of group fMRI data[J]. Pattern Recognition, 2012, 45(6): 2050–2063. doi: 10.1016/j.patcog.2011.04.033. -
计量
- 文章访问数: 216
- HTML全文浏览量: 71
- PDF下载量: 56
- 被引次数: 0
