作者中心
专家审稿
责编办公
编辑办公
-
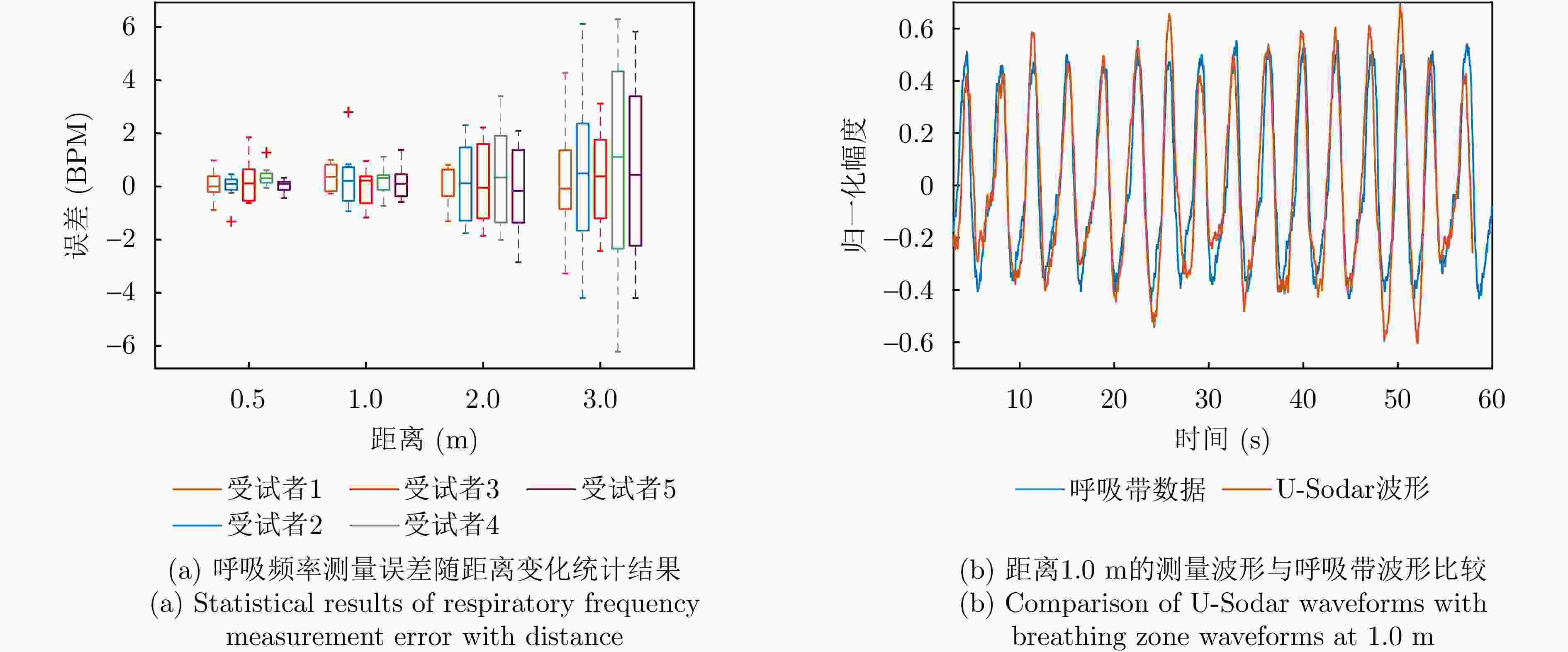
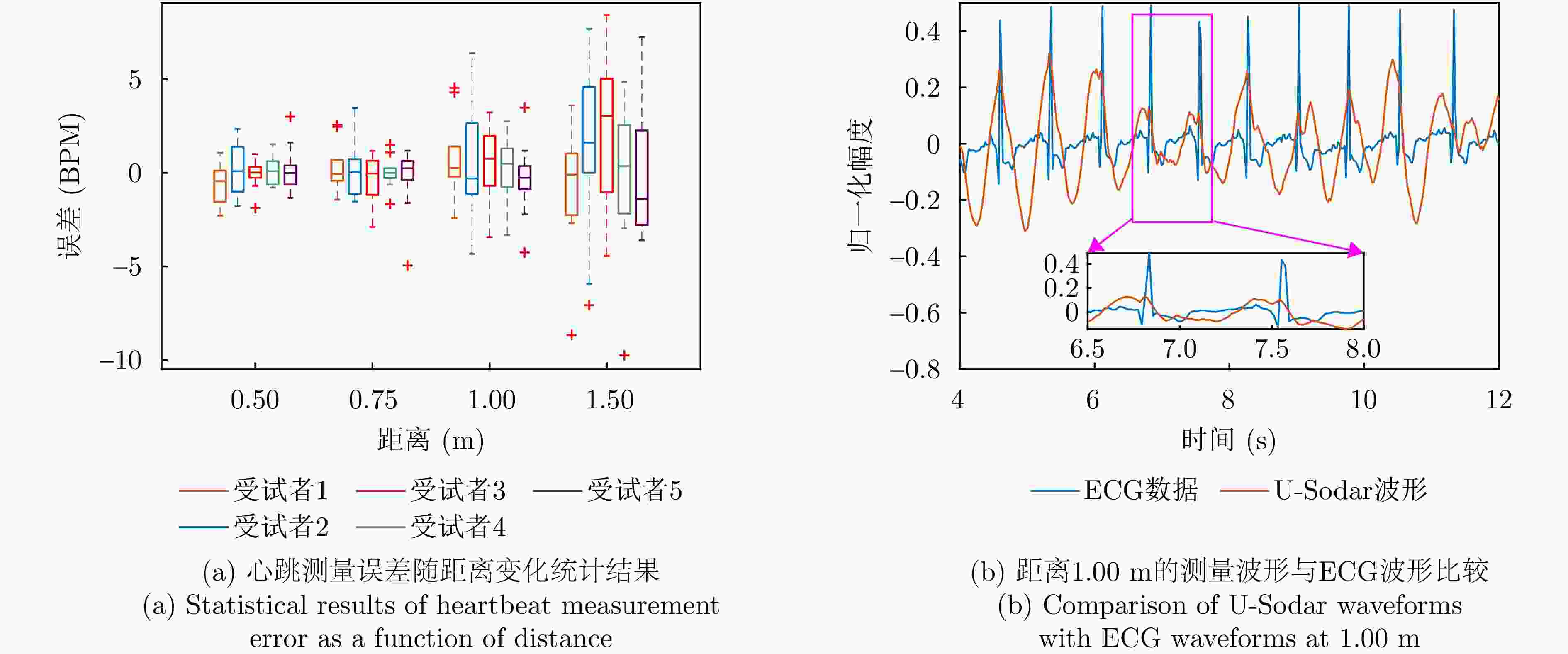
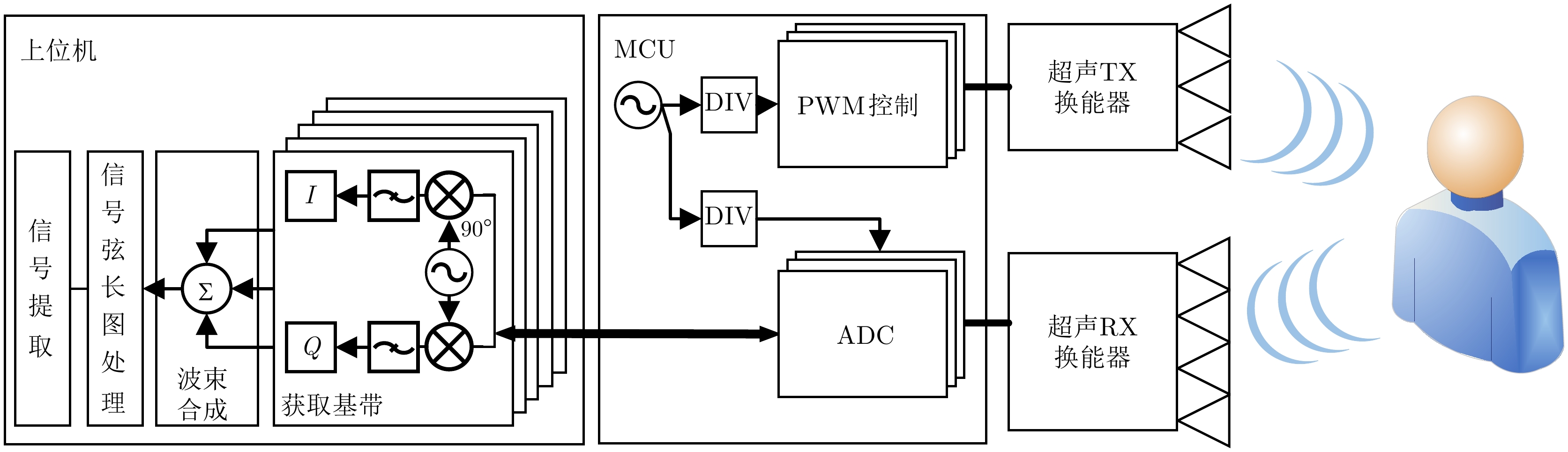
摘要: 全球老龄化趋势日益加剧，健康生活理念深入人心，居民对居家健康监测的需求也随之而来。为了减少健康监测对日常活动的影响，非接触式监测系统的需求量激增。然而，目前主流的检测方法存在隐私信任度低、电磁兼容性差和制造成本高等问题。对此，该文提出一种基于超声波雷达的非接触式生命体征信号测量系统——U-Sodar，包括一套基于3发4收MIMO架构的硬件和一套信号处理算法。其中U-Sodar本振采用分频技术，相位噪声低，检测精度高；接收机采用前端直接采样技术，在简化结构的同时有效减少外部噪声；发射采用可调PWM直接驱动，可发射多种超声波形，具备软件定义超声波系统特性。U-Sodar的信号处理算法采用信号弦长的图处理技术，利用图片滤波后重构的方法可在5 dB信噪比下实现信号相位的准确恢复。试验测试了U-Sodar系统的抗干扰性能与穿透性能，证明了超声穿透是依赖材料孔隙而非跨介质振动传导。并推导了给定信噪比与正确解调概率下的最小可测量位移。实际生命体征信号测量实验中，U-Sodar可分别在3.0 m和1.5 m距离内实现呼吸率和心率的准确测量，在1.0 m内可测得心跳波形。实验结果证明了U-Sodar超声波雷达在非接触式生命体征检测应用中的可行性及发展潜力。Abstract: Amidst the global aging trend and a growing emphasis on healthy living, there is an increased demand for unobtrusive home health monitoring systems. However, the current mainstream detection methods in this regard suffer from low privacy trust, poor electromagnetic compatibility, and high manufacturing costs. To address these challenges, this paper introduces a noncontact vital signal collection device using Ultrasonic radar (U-Sodar), including a set of hardware based on a three-transmitter four-receiver Multiple Input Multiple Output (MIMO) architecture and a set of signal processing algorithms. The U-Sodar local oscillator uses frequency division technology with low phase noise and high detection accuracy; the receiver employs front-end direct sampling technology to simplify the involved structure and effectively reduce external noise, and the transmitter uses an adjustable PWM direct drive to emit various ultrasonic waveforms, possessing software-defined ultrasonic system characteristics. The signal processing algorithm of U-Sodar adopts the graph processing technique of signal chord length and realizes accurate recovery of signal phase under 5 dB Signal-to-Noise Ratio (SNR) using picture filtering and then reconstruction. Experimental tests on the U-Sodar system demonstrated its anti-interference and penetration capabilities, proving that ultrasonic penetration relies on material porosity rather than intermedium vibration conduction. The minimum measurable displacement for a given SNR with correct demodulation probability is also derived. The results of actual human vital sign signal measurement experiments indicate that U-Sodar can accurately measure respiration and heartbeat at 3.0 m and 1.5 m, respectively, and the heartbeat waveforms can be measured within 1.0 m. Overall, the experimental results demonstrate the feasibility and application potential of U-Sodar in noncontact vital sign detection.
-
Key words:
- Non-contact detection /
- Vital signals detection /
- CW radar /
- Ultrasound /
- U-Sodar
-
1. 引言
海用雷达在对海上目标探测过程中易受海杂波影响，高海况、复杂气象条件下尤为严重。开展海杂波特性、海杂波抑制、海上目标检测跟踪与识别方法研究[1-5]，需要多种条件下的海杂波和海上目标回波实测数据，海军航空大学海上目标探测课题组于2019年提出一项“雷达对海探测数据共享计划”[6]，旨在利用X波段固态全相参雷达等多型雷达开展对海探测试验，获取不同海况、分辨率、擦地角条件下海杂波数据和海上目标回波数据，并同步获取海洋气象水文数据、目标位置与轨迹的真实数据，形成信息全记录的雷达试验数据集。
2020年度主要开展了3个方面的多次试验，包括目标雷达散射截面积(Radar Cross-Section, RCS)定标数据采集试验、不同海况海杂波与目标探测数据采集试验、海上机动目标检测跟踪数据采集试验。下面针对每个方面的试验进行介绍，并给出典型数据示例。
2. 目标RCS定标数据采集试验
目标RCS定标数据采集试验，主要是在海上投放定标体(不锈钢球，RCS为0.25 m2)，使其漂浮于海面以上，用船只拖拽定标体沿雷达径向慢速往返运动，在沿途部分位置点静止(漂浮)，雷达工作模式固定不变，采集试验全程的雷达与配合传感器数据。
如图1所示，试验期间，雷达架设地点为烟台养马岛试验点[6]，架高约为30 m。如图2所示，渔船用尼龙绳拖拽不锈钢球沿图1中所示的航线慢速运动。不锈钢球放置在4个泡沫塑料浮子上，使其完全浮于海面以上，如图2(d)所示，渔船与不锈钢球沿雷达径向的间距为100 m以上，且二者在方位上也错开一定的角度。渔船在设定海上航线的部分位置点(见图1所示航线中的黄色圆点)处静止(漂浮)，此时调整了雷达天线转速，采集多种转速条件下的雷达数据。试验期间海面状态如图2(f)所示，对应的气象水文数据如图3所示，红色原点与试验时段相对应，每15 min更新一次，综合判断海况等级为1级。
图 1 试验点及定标体运动轨迹示意图Figure 1. Experimental site and schematic diagram of calibration body’s trajectory
图 3 浪(有效波高、浪向、周期、浪速)和风(风向、风速)要素信息(红色标点对应试验时段)Figure 3. Wave (effective wave height, direction, period, speed) and wind (direction, speed) information (The red punctuation marks correspond to the experimental period)X波段试验雷达具体参数请见文献[6]，此处不再赘述。试验期间，定标体在较近距离时雷达工作于3 nm量程，脉冲重复频率(Pulsed Repetitive Frequency, PRF)为3 kHz；定标体在较远距离时雷达工作于6 nm量程，PRF为1.6 kHz。整个试验过程中，雷达主要工作于2 r/min的扫描速度，在目标静止(漂浮)时天线转速有所调整。雷达工作模式调整与采集雷达数据对应的情况，在与数据配套的数据记录表中有详细对照说明。由于雷达转速较慢，单次扫描周期的数据量大，这里仅给出了目标所在扇区的回波数据，示例数据如图4所示。
试验过程中，还同步获取了渔船的自动定位系统(Automatic Identification System, AIS)数据(MMSI: 413659899，见表1)，以及雷达视野内其他非合作船只目标的AIS数据。由于试验中所使用AIS设备自身原因，数据更新率为每次2～6 min，因此，AIS给出的位置信息与雷达给出的位置信息并不严格同步，在数据使用中可通过插值实现时空信息同步。
表 1 配试船只目标AIS数据示例Table 1. The sample AIS data of the experimental boat东经(°) 北纬(°) 时间 121.60965 37.47404 2020-07-08 09:10:00 121.61134 37.47551 2020-07-08 09:38:00 121.61275 37.476685 2020-07-08 09:40:00 121.61628 37.479015 2020-07-08 09:42:00 ··· ··· ··· 121.62507 37.48345 2020-07-08 13:50:00 121.62124 37.480255 2020-07-08 13:56:00 121.61803 37.4774 2020-07-08 13:58:00 3. 海杂波与目标探测数据采集试验
海杂波与目标探测数据采集试验，主要是采集不同海况等级条件下的海杂波数据、海上船只目标数据。此试验以天线凝视观测模式为主，采集不同方位下的雷达回波数据。
试验期间，雷达架设地点为烟台第1海水浴场试验点，如图5所示，架高约为80 m，在不同海况等级等环境下，调整雷达天线凝视的方位，凝视海面锚泊船只或航道浮标，采集几秒至几分钟时长不等的雷达凝视模式数据。采集数据时雷达工作量程为3 nm, 6 nm，对应的PRF分别为3.0 kHz, 1.6 kHz。
采集数据列表如表2所示。前7组数据均为天线凝视模式数据，由于采集数据期间，风速较大，雷达天线凝视方位随风有轻微偏移，具体偏移情况从雷达数据头中的“方位”信息位中可以得到；第8组数据为天线扫描模式数据，其中方位143°～274°范围内为发射屏蔽区，此区域内雷达发射静默。此外，扫描模式数据还有配套的AIS数据，但由于试验时海况等级较高，所有船只均回港避风，因此无运动目标，仅有锚泊的船只和航道浮标两类目标。
表 2 海杂波与目标回波数据列表Table 2. List of sea clutter and target echo data序号 数据类型 海况等级(级) 凝视方位(°) 脉冲个数 描述信息 1 海杂波 3～4 1.53 >104 4.84 km处有一个航道浮标 2 海杂波 3～4 42.18 >104 纯海杂波 3 海杂波 3～4 48.36 >104 近程为纯海杂波，6 km后有岛屿回波 4 海杂波+目标 3～4 17.36 >104 2.778 km和4.115 km处有2个漂浮目标(船+航道浮标) 5 海杂波+目标 3～4 8.01 >104 2.81 km和4.16 km处有2个漂浮强目标(2艘锚泊船只)，5.5 km后为岛屿回波 6 海杂波+目标 2 9.58 >104 小快艇，回波较强，距离8.15 km进入雷达视野而后离开，存在同频异步干扰 7 海杂波+目标 2 58.31 >104 3.86 km和7.15 km处有2个目标(船+岛屿) 8 海杂波+目标 3～4 扇区：257～360
0～1269个扫描周期 24 r/min扫描模式数据，有配套AIS数据 典型的海杂波数据、海杂波+目标数据如图6(a)—图6(d)所示，限于篇幅，这里仅给出两组实测数据的时域原始回波与多普勒谱。
4. 海上机动目标检测跟踪数据采集试验
海上机动目标检测跟踪数据采集试验，主要是利用小型快艇作为配试目标，沿预定航线运动，并在某些特定位置点进行机动，雷达工作于扫描模式，采集试验全程的雷达与配合传感器数据。
试验期间，雷达架设地点为烟台第1海水浴场试验点，架高约为80 m，如图5所示。雷达工作于6 nm量程、24 r/min的扫描模式，PRF为1.6 kHz。试验时间为14:32—15:18，共采集1186个连续扫描周期数据，雷达工作模式调整与采集雷达数据对应的情况，在与数据配套的数据记录表中有详细说明。典型试验数据示例如图7所示，试验期间风和浪要素数据如图8所示，有效波高为1 m左右，综合判断海况等级为3级。
图 8 浪(有效波高、浪向、周期、浪速)和风(风向、风速)要素信息(红色标点对应试验时段)Figure 8. Wave (effective wave height, direction, period, speed) and wind (direction, speed) information (The red punctuation marks correspond to the experimental period)配试目标为约10 m长小型快艇，如图9所示，沿预定航线行驶，示意图如图10所示，受海上航道来往船只影响，小快艇的实际航线与预定航线有偏差。快艇上安装了AIS设备，具体位置信息可查阅AIS数据(MMSI: 413659899)，如表3所示。此外，试验时还同步记录了雷达视野内非合作目标的AIS信息，可用作参考。
表 3 配试船只目标AIS数据示例Table 3. The sample AIS data for experimental boat东经(°) 北纬(°) 时间 121.4206 37.551258 2020-07-22 14:32:00 121.421776 37.553226 2020-07-22 14:34:00 121.4288 37.561104 2020-07-22 14:40:00 121.43016 37.559105 2020-07-22 14:42:00 ··· ··· ··· 121.43651 37.553654 2020-07-22 15:14:00 121.43177 37.54867 2020-07-22 15:16:00 121.4288 37.547638 2020-07-22 15:18:00 5. 总结
“雷达对海探测数据共享计划”2020年度完成了雷达目标RCS定标数据采集试验、不同海况海杂波与目标探测数据采集试验、海上机动目标检测跟踪数据采集试验3个方面的多次试验，获取了不同海况、目标以及雷达工作模式下的海杂波与目标回波数据，并同步获取了风和浪要素数据、目标AIS数据、可见光/红外数据等配合传感器数据。同时在试验过程中也发现了一些问题，例如目标AIS信息更新率过慢，导致将目标AIS数据作为真值数据使用时，与雷达数据存在严重的数据时空不匹配；可见光/红外设备数据在恶劣天气下获取图像不清晰或难以获取远距离目标图像；现有雷达在高海况、恶劣天气下天线凝视方位不稳定等问题，后续还需不断解决。
附录
X波段雷达对海探测实测数据的公开共享将依托雷达学报官方网站进行，试验数据于每次试验后上传至“数据/雷达对海探测数据”页面中(如附图1所示)，具体网址为http://radars.ie.ac.cn/web/data/getData?dataType=DatasetofRadarDetectingSea，数据将根据对海探测试验进度定期更新。
2020年度对海探测实测数据量巨大，因此截取具有代表性的试验段数据分3期发布，数据发布信息表如附表1所示。
第1期主要发布海杂波与目标凝视模式探测数据，分为两组，包括纯海杂波数据、海杂波+目标回波数据，数据量约17 GB；第2期主要发布雷达目标RCS定标试验数据，提供下载的数据为截取的配试船拖不锈钢球向雷达运动阶段的数据，数据量大于20 GB；第3期主要发布海上机动目标检测跟踪试验数据，提供下载的数据是截取的配试快艇沿图10所示航线中右上方第1个圆运动的数据，数据量不低于40 GB。
1 2020年度数据发布信息表1. Annual data release information table of 2020发布期号 试验日期 海况等级(级) 数据量(GB) 雷达天线
工作模式发射脉冲
模式目标位置
信息记录气象水文
数据1 2021.01.04～
2021.01.062～4 >10 凝视、扫描 模式2 有距离方位记录 有 2 2020.07.08 1～2 >20 扫描(2 r/min为主) 模式2 有船只AIS数据 有 3 2020.07.22 3 >40 扫描(24 r/min为主) 模式2 有船只AIS数据+5个航道浮标距离方位记录 有 注：① 所有雷达数据均为脉压后的I/Q复数据；② 发射脉冲模式2，对应每个重复周期雷达相继发射1个单载频脉冲和1个LFM脉冲；③ AIS数据更新周期较长，约2 min更新一次，与雷达目标数据率不匹配；④ 数据格式与2019年度第1期数据格式相同[6]。 -
图 1 基于U-Sodar的人体生命体征信号测量示意图
Figure 1. Overview of U-Sodar vital signal monitoring system
图 3 回波信号基带组成的星座图示意图
Figure 3. Constellation diagram depicting the baseband composition of the echo signal
图 4 含噪信号在相位解调中的解调误差示意图
Figure 4. Schematic of demodulation error in phase demodulation of noise-containing signals
图 5 给定信噪比与解调正确概率下的最小可测量相差图
Figure 5. The minimum measurable phase difference for a given SNR and probability of correct demodulation
图 8 U-Sodar方向图测试场景布置
Figure 8. Arrangement of the test scene for U-Sodar directional diagram testing
图 15 各通道测量静止墙面信号矢量图
Figure 15. Measurement of stationary wall signal vector diagram for each channel
图 20 不同信噪比信号处理结果对比
Figure 20. Comparison of signal processing results with different signal-to-noise ratios
图 21 不同体动幅度模拟结果对比
Figure 21. Comparison of simulation results for different body movement distances
图 22 基于U-Sodar的生命体征测量实验场景示意图
Figure 22. Schematic of the experimental setup for measuring vital signs with U-Sodar
表 1 各类型非接触测量方案比较
Table 1. Comparing various types of non-contact measurement schemes
比较内容 可见光/红外光 微波雷达 声学信号 U-Sodar 隐私保护 – • – • 毫米级位移测量 – • – • 信号来向区分 • • – • 抗电磁干扰 • – • • 无电磁辐射 • – • • 穿透能力 – • • • 环境适应能力 – • – – 目前设备体积 • • • – 设备成本 – – • • 注：•为优秀，–为较差。 
下载: 导出CSV
表 2 U-Sodar系统的关键芯片型号
Table 2. U-Sodar system key chip models
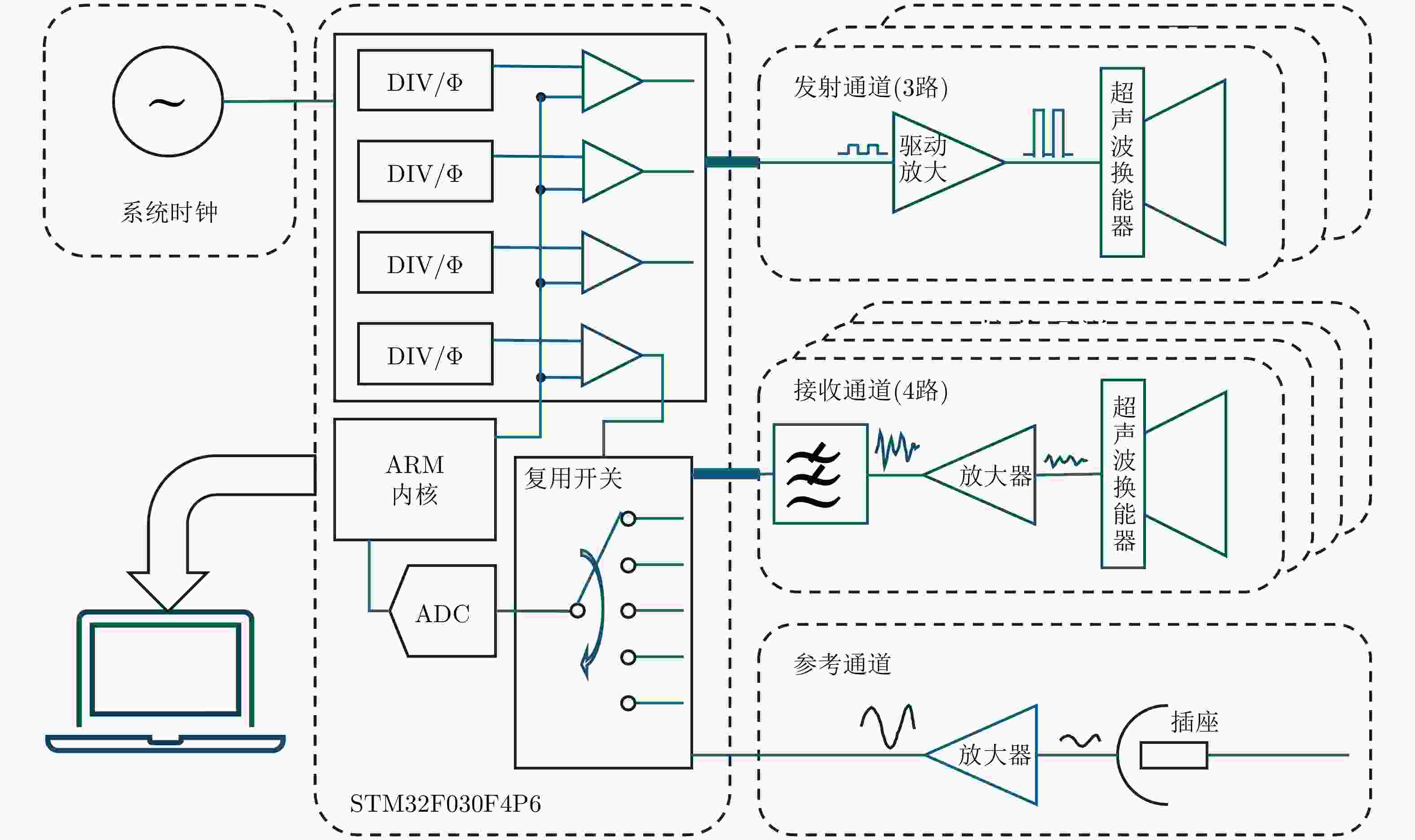
芯片功能 芯片型号 主控芯片 STM32F030F4P6 发射驱动芯片 SRV8837 接收放大器芯片 MS8051 LDO电源芯片 RT9193 逻辑门芯片 SN74LVC1G02DCKR USB串口转换芯片 CH340N 收发换能器探头 TCT40-16
下载: 导出CSV
表 3 受试者信息
Table 3. Volunteer information
受试者编号 性别 年龄 身高(cm) 体重(kg) BMI (kg/m2) 标识色 1 男 26 173 60.0 20.0 棕 2 男 24 180 78.5 24.2 蓝 3 男 23 178 71.0 22.4 红 4 女 24 166 63.0 22.9 绿 5 女 22 155 46.0 19.1 紫 注：根据中国BMI标准：≤18.4为偏瘦、18.5～23.9为正常、24.0～27.9为过重、≥28为肥胖。
下载: 导出CSV
-
[1] United Nations. Ageing[EB/OL]. https://www.un.org/en/global-issues/ageing, 2024. [2] 民政部, 全国老龄办. 2022年度国家老龄事业发展公报[EB/OL]. https://www.gov.cn/lianbo/bumen/202312/P020231214405906944856.pdf, 2023.Ministry of Civil Affairs of China, National Office for Aging of China. 2022 national report on the development of aging services[EB/OL] https://www.gov.cn/lianbo/bumen/202312/P020231214405906944856.pdf, 2023. [3] PIRZADA P, WILDE A, and HARRIS-BIRTILL D. Remote photoplethysmography for heart rate and blood oxygenation measurement: A review[J]. IEEE Sensors Journal, 2024, 24(15): 23436–23453. doi: 10.1109/JSEN.2024.3405414. [4] WANG Wenjin, DEN BRINKER A C, STUIJK S, et al. Algorithmic principles of remote PPG[J]. IEEE Transactions on Biomedical Engineering, 2017, 64(7): 1479–1491. doi: 10.1109/TBME.2016.2609282. [5] KOBAYASHI L, CHUCK C C, KIM C K, et al. Comparison of video photoplethysmography, video motion analysis, and passive infrared thermography against traditional contact methods for acquiring vital signs in emergency department populations[C]. 2023 IEEE 14th Annual Ubiquitous Computing, Electronics & Mobile Communication Conference, New York, USA, 2023: 134–141. doi: 10.1109/UEMCON59035.2023.10316088. [6] PEREIRA C B, YU Xinchi, BLAZEK V, et al. Robust remote monitoring of breathing function by using infrared thermography[C]. 2015 37th Annual International Conference of the IEEE Engineering in Medicine and Biology Society, Milan, Italy, 2015: 4250–4253. doi: 10.1109/EMBC.2015.7319333. [7] 方震, 简璞, 张浩, 等. 基于FMCW雷达的非接触式医疗健康监测技术综述[J]. 雷达学报, 2022, 11(3): 499–516. doi: 10.12000/JR22019.FANG Zhen, JIAN Pu, ZHANG Hao, et al. Review of noncontact medical and health monitoring technologies based on FMCW radar[J]. Journal of Radars, 2022, 11(3): 499–516. doi: 10.12000/JR22019. [8] XIONG Junjun, HONG Hong, XIAO Lei, et al. Vital signs detection with difference beamforming and orthogonal projection filter based on SIMO-FMCW radar[J]. IEEE Transactions on Microwave Theory and Techniques, 2023, 71(1): 83–92. doi: 10.1109/TMTT.2022.3181129. [9] MA Yuanren, ZHAO Heng, ZHUANG Zhongxu, et al. Sleep-disordered breathing detection based on radar-pulse oximeter sensor fusion[C]. 2023 Asia-Pacific Microwave Conference, Taipei, China, 2023: 260–262. doi: 10.1109/APMC57107.2023.10439668. [10] SUN Li, BAI Ge, LUO Changhao, et al. A large-scale movement path fitting based phase compensation algorithm for FMCW radar vital sign detection[C]. 2024 IEEE Topical Conference on Wireless Sensors and Sensor Networks, San Antonio, USA, 2024: 37–40. doi: 10.1109/WiSNeT59910.2024.10438585. [11] 工业和信息化部. 中华人民共和国无线电频率划分规定[EB/OL]. https://www.gov.cn/zhengce/zhengceku/2018-12/31/content_5439640.htm, 2023.Ministry of Industry and Information Technology of China. Provisions on the allocation of radio frequencies of the People’s Republic of China[EB/OL]. https://www.gov.cn/zhengce/zhengceku/2018-12/31/content_5439640.htm, 2023. [12] 国际电信联盟. ITU-R SM.2093-4[EB/OL]. https://www.itu.int/dms_pub/itu-r/opb/rep/R-REP-SM.2093-4-2021-PDF-C.pdf, 2021.ITU. ITU-R SM.2093-4[EB/OL]. https://www.itu.int/dms_pub/itu-r/opb/rep/R-REP-SM.2093-4-2021-PDF-C.pdf, 2021. [13] 国家药品监督管理局. YY 9706.102-2021 医用电气设备 第1-2部分: 基本安全和基本性能的通用要求 并列标准: 电磁兼容 要求和试验[S]. 北京: 中国标准出版社, 2021.National Medical Products Administration. YY 9706.102-2021 Medical electrical equipment—Part 1-2: General requirements for basic safety and essential performance—collateral standard: Electromagnetic compatibility—requirements and tests[S]. Beijing: Standards Press of China, 2021. [14] Micradar. Healthy care radar[EB/OL]. https://en.micradar.cn/, 2024. [15] NAM Y, REYES B A, and CHON K H. Estimation of respiratory rates using the built-in microphone of a smartphone or headset[J]. IEEE Journal of Biomedical and Health Informatics, 2016, 20(6): 1493–1501. doi: 10.1109/JBHI.2015.2480838. [16] FUJITA Y, WATANABE K, KOBAYASHI K, et al. Development of system for unrestrained measurement of vital signs in the bathroom[C]. SICE Annual Conference 2011, Tokyo, Japan, 2011: 2322–2325. [17] DAFNA E, HALEVI M, BEN OR D, et al. Estimation of macro sleep stages from whole night audio analysis[C]. Annu Int Conf IEEE Eng Med Biol Soc 2016, Florida, USA, 2016: 2847–2850. doi: 10.1109/EMBC.2016.7591323. [18] WANG Zhi, ZHANG Fusang, LI Siheng, et al. Exploiting passive beamforming of smart speakers to monitor human heartbeat in real time[C]. 2021 IEEE Global Communications Conference, Madrid, Spain, 2021: 1–6. doi: 10.1109/GLOBECOM46510.2021.9685922. [19] 王军强. 噪声敏感建筑隔声与声舒适性要求[J]. 声学技术, 2023, 42(1): 57–61. doi: 10.16300/j.cnki.1000-3630.2023.01.010.WANG Junqiang. Requirements for sound insulation and sound comfort of noise-sensitive buildings[J]. Technical Acoustics, 2023, 42(1): 57–61. doi: 10.16300/j.cnki.1000-3630.2023.01.010. [20] 国家环境保护总部. GB 22337-2008 社会生活环境噪声排放标准[S]. 北京: 中国环境科学出版社, 2008.National Environmental Protection Headquarters. GB 22337-2008 Emission standard for community noise[S]. Beijing: China Environmental Press, 2008. [21] AL-NAJI A, AL-ASKERY A J, GHARGHAN S K, et al. A system for monitoring breathing activity using an ultrasonic radar detection with low power consumption[J]. Journal of Sensor and Actuator Networks, 2019, 8(2): 32. doi: 10.3390/jsan8020032. [22] AMBROSANIO M, FRANCESCHINI S, GRASSINI G, et al. A multi-channel ultrasound system for non-contact heart rate monitoring[J]. IEEE Sensors Journal, 2020, 20(4): 2064–2074. doi: 10.1109/JSEN.2019.2949435. [23] WANG Yili. Vital signs estimation scheme based on autocorrelation and variational mode decomposition using ultra-wide band radar[C]. 2023 8th International Conference on Intelligent Computing and Signal Processing, Xi’an, China, 2023: 350–354. doi: 10.1109/ICSP58490.2023.10248772. [24] MA Shaopeng, XUE Wei, CHEN Kehui, et al. Radar vital signs detection method based on variational mode decomposition and wavelet transform[C]. 2021 China Automation Congress, Beijing, China, 2021: 7469–7474. doi: 10.1109/CAC53003.2021.9728129. [25] XIA Ziliang, WANG Xinhuai, WEI Hongbo, et al. Detection of vital signs based on variational mode decomposition using FMCW radar[C]. 2021 International Conference on Microwave and Millimeter Wave Technology, Nanjing, China, 2021: 1–3. doi: 10.1109/ICMMT52847.2021.9617967. [26] YANG Xuan, WANG Ziying, ZHANG Li, et al. A novel arc-chord approximation demodulation based on green’s theorem[C]. 2023 IEEE MTT-S International Wireless Symposium, Qingdao, China, 2023: 1–3. doi: 10.1109/IWS58240.2023.10222839. [27] LV Qinyi, CAO Congqi, and ZHOU Deyun. Wireless vital-sign detection based on improved arc-chord approximation demodulation[C]. 2022 IEEE MTT-S International Microwave Biomedical Conference, Suzhou, China, 2022: 57–59. doi: 10.1109/IMBioC52515.2022.9790242. [28] LV Qinyi, MIN Lingtong, CAO Congqi, et al. Time-domain Doppler biomotion detections immune to unavoidable DC offsets[J]. IEEE Transactions on Instrumentation and Measurement, 2021, 70: 8505010. doi: 10.1109/TIM.2021.3125096. [29] ZHANG Li, FU Changhong, ZHUANG Zhongxu, et al. Kalman filter and cross-multiply algorithm with adaptive DC offset removal[J]. IEEE Transactions on Instrumentation and Measurement, 2022, 71: 4002710. doi: 10.1109/TIM.2022.3147317. [30] CAO Zhiyuan, ZHANG Chengcheng, JIN Zirui, et al. A DC offset cancellation circuit using digital assistance technique and self-calibrating comparator for RF transceiver[C]. 2023 IEEE 15th International Conference on ASIC, Nanjing, China, 2023: 1–4. doi: 10.1109/ASICON58565.2023.10396145. [31] HAZRA S, FUSCO A, KIPRIT G N, et al. Robust radar-based vital sensing with adaptive sinc filtering and random body motion rejections[J]. IEEE Sensors Letters, 2023, 7(5): 7001604. doi: 10.1109/LSENS.2023.3266237. [32] TARIQ A and GHAFOURI-SHIRAZ H. Vital signs detection using Doppler radar and continuous wavelet transform[C]. 5th European Conference on Antennas and Propagation, Rome, Italy, 2011: 285–288. [33] ZHANGI T, VALERIO G, SARRAZIN J, et al. Wavelet-based analysis of 60 GHz Doppler radar for non-stationary vital sign monitoring[C]. 2017 11th European Conference on Antennas and Propagation, Paris, France, 2017: 1876–1877. doi: 10.23919/EuCAP.2017.7928689. [34] FU Yangye, SUN Lijuan, GUO Jian, et al. EEMD-MICA based heart rate extraction algorithm for radar signals[C]. 2023 35th Chinese Control and Decision Conference, Yichang, China, 2023: 1649–1655. doi: 10.1109/CCDC58219.2023.10327001. [35] INDU S, GUPTA A, KAW A, et al. Life detection system using continuous wave Doppler radar and blind source separation[C]. 2017 Devices for Integrated Circuit, Kalyani, India, 2017: 711–715. doi: 10.1109/DEVIC.2017.8074043. [36] LIU Heng, WANG Yong, ZHOU Mu, et al. Millimeter-wave radar vital signs detection based on modified independent component analysis[C]. 2023 IEEE 11th Asia-Pacific Conference on Antennas and Propagation, Guangzhou, China, 2023: 1–2. doi: 10.1109/APCAP59480.2023.10470254. [37] CHOWDHURY J H, SHIHAB M, PRAMANIK S K, et al. Separation of heartbeat waveforms of simultaneous two-subjects using independent component analysis and empirical mode decomposition[J]. IEEE Microwave and Wireless Technology Letters, 2024, 34(8): 1059–1062. doi: 10.1109/LMWT.2024.3420253. [38] HUANG C Y, FANG Guanwei, CHUANG H R, et al. Clutter-resistant vital sign detection using amplitude-based demodulation by EEMD-PCA-correlation algorithm for FMCW radar systems[C]. 2019 49th European Microwave Conference, Paris, France, 2019: 928–931. doi: 10.23919/EuMC.2019.8910730. [39] YU Xiaogang, LI Changzhi, and LIN J. Noise analysis for noncontact vital sign detectors[C]. 2010 IEEE 11th Annual Wireless and Microwave Technology Conference, Melbourne, USA, 2010: 1–4. doi: 10.1109/WAMICON.2010.5461889. [40] MARZO A, CORKETT T, and DRINKWATER B W. Ultraino: An open phased-array system for narrowband airborne ultrasound transmission[J]. IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, 2018, 65(1): 102–111. doi: 10.1109/TUFFC.2017.2769399. [41] MÄKINEN Y, AZZARI L, and FOI A. Collaborative filtering of correlated noise: Exact transform-domain variance for improved shrinkage and patch matching[J]. IEEE Transactions on Image Processing, 2020, 29: 8339–8354. doi: 10.1109/TIP.2020.3014721. [42] WANG Jingyu, WANG Xiang, ZHU Zhongbo, et al. 1-D microwave imaging of human cardiac motion: An ab-initio investigation[J]. IEEE Transactions on Microwave Theory and Techniques, 2013, 61(5): 2101–2107. doi: 10.1109/TMTT.2013.2252186. [43] YANG Xiufang, JIAO Zhen, and YANG Yankang. Researchon linear demodulation method of Doppler radar vital signal[C]. 2022 IEEE International Conference on Electrical Engineering, Big Data and Algorithms, Changchun, China, 2022: 1381–1385. doi: 10.1109/EEBDA53927.2022.9744892. [44] WANG Jingyu, WANG Xiang, CHEN Lei, et al. Noncontact distance and amplitude-independent vibration measurement based on an extended DACM algorithm[J]. IEEE Transactions on Instrumentation and Measurement, 2014, 63(1): 145–153. doi: 10.1109/TIM.2013.2277530. 期刊类型引用(35)
1. 方蕊，彭章友. 基于广播电视卫星的双基海杂波建模与实测数据分析. 工业控制计算机. 2025(01): 58-59+62 . 
百度学术2. 薛健，孙孟玲，潘美艳. 基于支持向量回归和分位数的雷达K分布海杂波形状参数估计方法. 电子与信息学报. 2024(04): 1399-1407 . 百度学术3. 田华飞，魏广芬，简涛，周战，罗沅. 子空间干扰加高斯杂波背景下基于GLRT的斜对称方向检测器设计. 海军航空大学学报. 2024(02): 224-234 . 百度学术4. 杨诗曼，王中训，李珊，韩孟孟，刘宁波. 海上目标雷达与AIS航迹时空匹配方法. 海军航空大学学报. 2024(02): 199-204+274 . 百度学术5. 田凯祥，李保珠，王中训，刘宁波. 低海况下多姿态海上目标特征分析. 雷达科学与技术. 2024(02): 126-134 . 百度学术6. 连静，杨勇，谢晓霞，王雪松. 大掠射角对海雷达导引头实测回波特性分析. 系统工程与电子技术. 2024(05): 1535-1543 . 百度学术7. 汪翔，汪育苗，陈星宇，臧传飞，崔国龙. 基于深度学习的多特征融合海面目标检测方法. 雷达学报. 2024(03): 554-564 . 
本站查看8. 黄胜彬，潘大鹏，陈涛. 基于多维特征融合的海面目标检测. 舰船电子对抗. 2024(03): 84-91 . 百度学术9. 田凯祥，于恒力，王中训，刘宁波，韩孟孟. 基于雷达目标特征可分性的一维特征选择方法. 海军航空大学学报. 2024(04): 453-460+500 . 百度学术10. 韩喆璇，于恒力，王中训，刘宁波，孙艳丽. 基于相对多普勒峰高特征的OS-CFAR改进方法. 海军航空大学学报. 2024(04): 475-484 . 百度学术11. 陈胜垚，胡晨康，程智勇，席峰，刘中. 基于残差单元与注意力门的非对称编解码海杂波抑制网络. 电子学报. 2024(08): 2628-2640 . 百度学术12. 关键，姜星宇，刘宁波，丁昊，黄勇. 海杂波背景下的双极化最大特征值目标检测. 系统工程与电子技术. 2024(11): 3715-3725 . 百度学术13. 陈铎，范一飞，粟嘉，郭子薰，陶明亮. 基于广义逆高斯纹理结构的目标检测算法. 系统工程与电子技术. 2024(12): 4018-4025 . 百度学术14. ZANG Chuanfei，WANG Yumiao，WANG Xiang，XU Congan，CUI Guolong. Sea clutter suppression via cuttable encoder-decoderaugmentation network. Journal of Systems Engineering and Electronics. 2024(06): 1428-1440 . 必应学术15. 陈佳音，郭山红，朱海锐，盛卫星，韩玉兵. 基于多特征融合的海面目标智能检测算法. 现代雷达. 2024(12): 24-30 . 百度学术16. 张俊玲，董玫，陈伯孝. 基于可调Q因子小波变换的海杂波抑制算法. 系统工程与电子技术. 2023(02): 343-351 . 百度学术17. 陈鹏，许震，曹振新，王宗新. 基于图特征学习的海杂波抑制算法. 兵工学报. 2023(02): 534-544 . 百度学术18. 黄瀚仪，胡仕友，郭胜龙，李珊君，舒勤. 基于稀疏分解的海面微动目标识别. 系统工程与电子技术. 2023(04): 1016-1023 . 百度学术19. 张梦雨，王中训，李飞，刘宁波，董云龙. CNN海况等级分类方法的性能. 烟台大学学报(自然科学与工程版). 2023(02): 196-203 . 百度学术20. 关键，刘宁波，王国庆，丁昊，董云龙，黄勇，田凯祥，张梦雨. 雷达对海探测试验与目标特性数据获取——海上目标双极化多海况散射特性数据集. 雷达学报. 2023(02): 456-469 . 本站查看21. 许述文，焦银萍，白晓惠，蒋俊正. 基于频域多通道图特征感知的海面小目标检测. 电子与信息学报. 2023(05): 1567-1574 . 百度学术22. 关键，伍僖杰，丁昊，刘宁波，黄勇，曹政，魏嘉彧. 基于三维凹包学习算法的海面小目标检测方法. 电子与信息学报. 2023(05): 1602-1610 . 百度学术23. 邓稼麒，李正周，党楚佳，陈文豪，秦天奇. 基于海面场景感知的雷达目标检测方法. 中国电子科学研究院学报. 2023(02): 129-137 . 百度学术24. 董云龙，张兆祥，刘宁波，黄勇，丁昊，张梦雨. 雷达回波三特征联合海况分类方法. 雷达科学与技术. 2023(02): 189-198 . 百度学术25. 马全鑫，杜晓林，董军，李建波，田团伟. 基于几何方法的结构化协方差矩阵估计. 雷达科学与技术. 2023(02): 143-150 . 百度学术26. 刘言，刘宁波，黄勇，王中训. 利用相位特征筛选参考单元的改进CFAR方法. 烟台大学学报(自然科学与工程版). 2023(03): 371-378 . 百度学术27. 田凯祥，于晓涵，王中训，刘宁波. 基于实测数据的海杂波与海面小目标特征分析. 海军航空大学学报. 2023(04): 313-322 . 百度学术28. 董云龙，张兆祥，刘宁波，黄勇，丁昊. 海杂波多普勒谱Hurst指数特性分析及目标检测. 雷达科学与技术. 2023(04): 355-363+374 . 百度学术29. 杨政，程永强，吴昊，黎湘，王宏强. 基于正交投影的子带信息几何雷达弱小目标检测方法. 雷达学报. 2023(04): 776-792 . 本站查看30. 杨金龙，成勇，刘佳. 基于多核相关滤波X波段雷达多目标跟踪算法. 信息与控制. 2023(05): 561-573 . 百度学术31. 杜延磊，杨晓峰，汪胜，殷君君，杨会章，杨健. 海面雷达散射及其杂波幅度统计特性的空间遍历性数值仿真研究. 系统工程与电子技术. 2023(12): 3806-3818 . 百度学术32. 马红光，郭金库，姜勤波，刘志强. 一种基于自适应滤波的海杂波背景下多目标检测方法. 现代信息科技. 2022(04): 72-76 . 百度学术33. 董云龙，刘洋，刘宁波，丁昊，关键. 基于雷达方程修正的目标探测距离评估方法. 信号处理. 2022(10): 2102-2113 . 百度学术34. 杜延磊，高帆，刘涛，杨健. 基于数值仿真的X波段极化SAR海杂波统计建模与特性分析. 系统工程与电子技术. 2021(10): 2742-2755 . 百度学术35. 刘用功，尹勇. 目标船感知技术综述. 广州航海学院学报. 2021(04): 1-4+30 . 百度学术其他类型引用(41)
-
下载:
百度学术
计量
- 文章访问数: 499
- HTML全文浏览量: 112
- PDF下载量: 192
- 被引次数: 76
