有限视距多传感器集群目标可扩展跟踪方法

张栩琪; 周彬; 刘海琪; 廖骥; 刘永旭; 杨光

doi:10.12000/JR24054

有限视距多传感器集群目标可扩展跟踪方法

DOI: 10.12000/JR24054

张栩琪^1, ,,
周彬¹,
刘海琪²,
廖骥¹,
刘永旭¹,
杨光¹

1.
电子信息控制重点实验室成都 610036
2.
四川大学数学学院成都 610065

基金项目: 国家部委基金

详细信息

作者简介:
张栩琪，博士，工程师，主要研究方向为目标跟踪、信息融合、信号和信息处理等

周　彬，硕士，研究员，主要研究方向为电子对抗总体技术、信号和信息处理等

刘海琪，博士，博士后，主要研究方向为目标跟踪、数据关联和优化方法等

廖　骥，硕士，高级工程师，主要研究方向为信号探测、无源定位等

刘永旭，博士，高级工程师，主要研究方向为卫星电子载荷总体技术、信号和信息处理等

杨　光，硕士，高级工程师，主要研究方向为电子对抗总体技术、信号和信息处理等

通讯作者:
张栩琪 502671142@qq.com

责任主编：易伟 Corresponding Editor: YI Wei
中图分类号: TN957
计量
- 文章访问数: 290
- HTML全文浏览量: 195
- PDF下载量: 52
- 被引次数: 0
出版历程
- 收稿日期: 2024-03-29
- 修回日期: 2024-05-25
- 网络出版日期: 2024-06-27
- 刊出日期: 2024-12-28

A Scalable Method for Group Target Tracking Using Multisensor with Limited Field of Views

1.
Science and Technology on Electronic Information Control Laboratory, Chengdu 610036, China
2.
School of Mathematics, Sichuan University, Chengdu 610065, China

Funds: The National Ministries Foundation

More Information

Corresponding author: ZHANG Xuqi, 502671142@qq.com

摘要

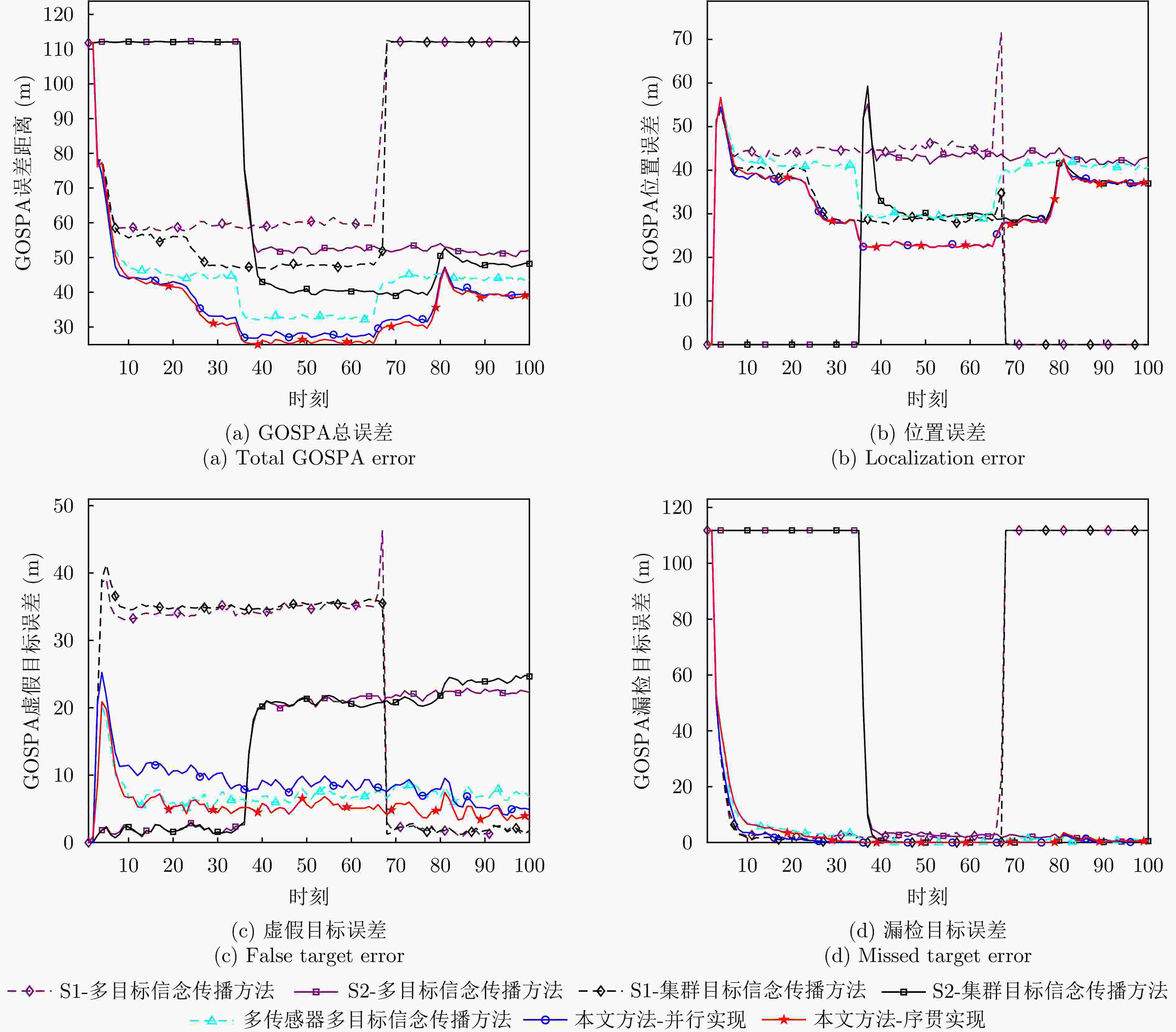
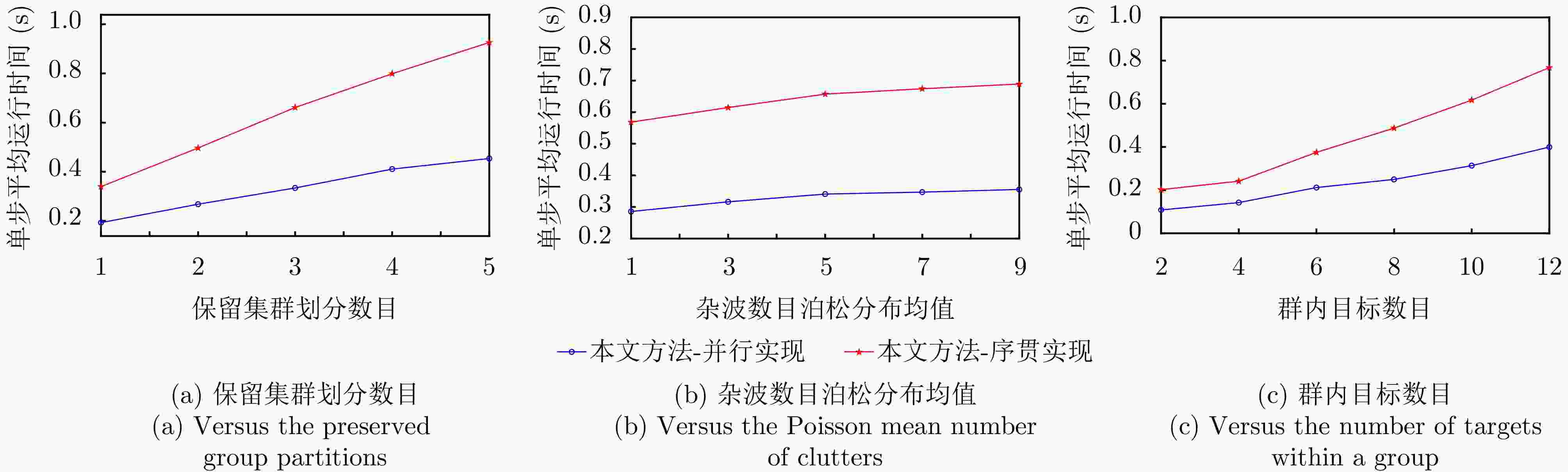
摘要: 在实际应用中，单传感器的视距、计算资源通常是有限的，多传感器网络的发展和应用为解决具有挑战性的目标跟踪问题提供了更多的可能性。相比于多目标跟踪，集群目标跟踪由于群内目标距离近、协同运动、数目多以及集群分裂合并等因素，会面临更具挑战性的数据关联和计算上的问题，而这些问题在多传感器融合系统中会进一步复杂化。针对有限视距情形下的多传感器集群目标跟踪问题，该文提出了一种可扩展的多传感器集群目标信念传播跟踪方法。该方法在贝叶斯框架下考虑集群结构的不确定性，构建多传感器集群目标联合后验概率密度分解和相应的因子图，以及通过在设计的因子图上运行信念传播算法高效求解数据关联问题。此外，该方法具有计算处理可扩展性，其计算复杂度与传感器数目、集群划分数目和观测数目呈线性关系，与目标数目呈二次关系。最后，仿真实验对比了不同方法关于GOSPA和OSPA⁽²⁾的性能，结果表明所提方法能够无缝跟踪集群目标和非群目标、充分利用多传感器信息互补优势、提升跟踪精度。
- 多传感器融合 /
- 有限视距 /
- 集群目标跟踪 /
- 可扩展性 /
- 信念传播
Abstract: In practical applications, the field of view and computation resources of an individual sensor are limited, and the development and application of multisensor networks provide more possibilities for solving challenging target tracking problems. Compared with multitarget tracking, group target tracking encounters more challenging data association and computation problems due to factors such as the proximity of targets within groups, coordinated motions, a large number of involved targets, and group splitting and merging, which will be further complicated in the multisensor fusion systems. For group target trackingunder sensors with limited field of view, we propose a scalable multisensor group target tracking method via belief propagation. Within the Bayesian framework, the method considers the uncertainty of the group structure, constructs the decomposition of the joint posterior probability density of the multisensor group targets and corresponding factor graph, and efficiently solves the data association problem by running belief propagation on the devised factor graph. Furthermore, the method has excellent scalability and low computational complexity, scaling linearly only on the numbers of sensors, preserved group partitions, and sensor measurements, and scaling quadratically on the number of targets. Finally, simulation experiments compare the performance of different methods on GOSPA and OSPA⁽²⁾, which verify that the proposed method can seamlessly track grouped and ungrouped targets, fully utilize the complementary information among sensors, and improve tracking accuracy.
- Multisensor fusion /
- Limited field of view /
- Group target tracking /
- Scalability /
- Belief propagation

HTML全文

图 1 集群划分变量示意

Figure 1. Examples of the group partition variable

下载: 全尺寸图片幻灯片

图 2 式(13)在k时刻采用多传感器序贯的因子图描述

Figure 2. The factor graph description of the Eq. (13) in a sensor-sequential processing manner, shown for the time k

下载: 全尺寸图片幻灯片

图 3 式(13)在k时刻采用多传感器并行的因子图描述

Figure 3. The factor graph description of the Eq. (13) in a sensor-parallel processing manner, shown for the time k

下载: 全尺寸图片幻灯片

图 4 有限视距多传感器集群目标信念传播跟踪方法结构图

Figure 4. The flowchart of the proposed group target belief propagation tracking method using multisensor with limited field of views

下载: 全尺寸图片幻灯片

图 5 目标轨迹、传感器位置和视距范围(场景1)

Figure 5. Ground truths, sensor locations, and corresponding field of views (scenario 1)

下载: 全尺寸图片幻灯片

图 6 不同方法的GOSPA误差对比结果(场景1)

Figure 6. The comparison results of GOSPA error for different methods (scenario 1)

下载: 全尺寸图片幻灯片

图 7 不同方法的OSPA⁽²⁾误差对比结果 (场景1)

Figure 7. The comparison results of OSPA⁽²⁾ error for different methods (scenario 1)

下载: 全尺寸图片幻灯片

图 8 不同参数设置下本文方法单步平均运行时间的变化情况

Figure 8. The average runtimes per time step of the proposed method under different settings of parameters

下载: 全尺寸图片幻灯片

图 9 场景2：目标轨迹、传感器位置和视距范围

Figure 9. Scenario 2: Ground truths, sensor locations, and corresponding field of views

下载: 全尺寸图片幻灯片

图 10 不同方法的GOSPA误差对比结果(场景2)

Figure 10. The comparison results of GOSPA error for different methods (scenario 2)

下载: 全尺寸图片幻灯片

图 11 不同方法的OSPA⁽²⁾误差对比结果(场景2)

Figure 11. The comparison results of OSPA⁽²⁾ error for different methods (scenario 2)

下载: 全尺寸图片幻灯片

图 12 目标轨迹、传感器位置和视距范围(场景3)

Figure 12. Ground truths, sensor locations, and corresponding field of views (scenario 3)

下载: 全尺寸图片幻灯片

图 13 不同传感器数目、不同方法的对比结果

Figure 13. The comparison results of different methods and different numbers of sensors

下载: 全尺寸图片幻灯片

1 M-best集群目标多传感器序贯信念传播跟踪算法

1. M-best multisensor group target belief propagation tracking method

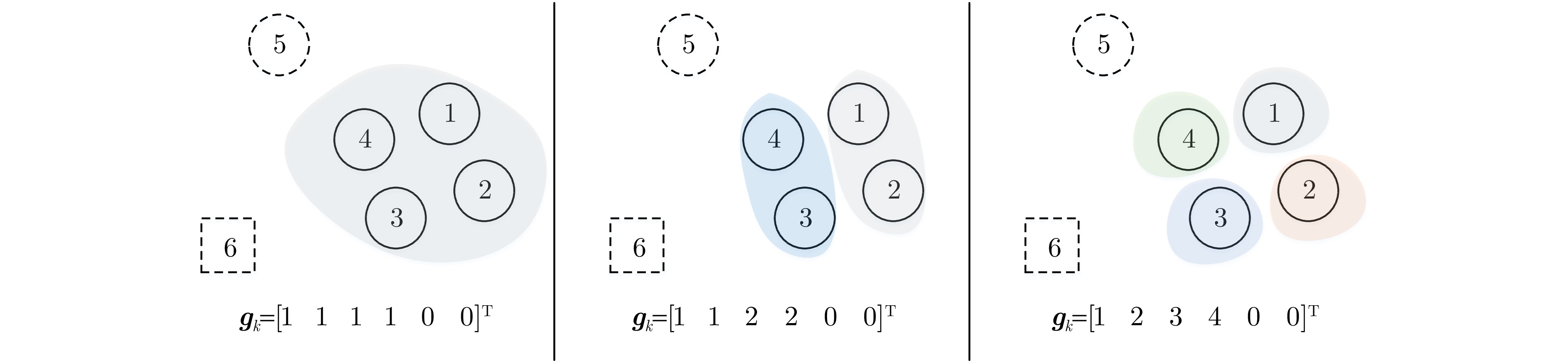
输入：$k - 1$时刻的融合信念密度$ \tilde p({{\boldsymbol{y}}_{k - 1}}) $；多传感器在k时刻接收到的观测信息${{\boldsymbol{z}}_{k,s}},s \in \{ 1,2, \cdots ,S\} $；
输出：k时刻的融合信念密度$\tilde p({{\boldsymbol{y}}_k})$和目标状态估计；
1: 根据式(14)计算${\alpha _k}({\underline {\boldsymbol{g}} _k}),{\underline {\boldsymbol{g}} _k} \in {\underline{ \mathcal{G}} _k}$，保留前M个最有可能的集群划分并重新归一化${\alpha _k}({\underline {\boldsymbol{g}} _k})$，以及根据式(15)计算${\stackrel \smile {\alpha } _k}({\underline {\boldsymbol{x}} _k},{\underline {\boldsymbol{r}} _k})$和初始化融　合信念密度${\tilde p_0}({{\boldsymbol{x}}_{k,0}},{{\boldsymbol{r}}_{k,0}}): = {\stackrel \smile {\alpha } _k}({\underline {\boldsymbol{x}} _k},{\underline {\boldsymbol{r}} _k})$；
2: 对于每一个$s \in \{ 1,2, \cdots ,S\} $，执行下述步骤：
2.1: 根据融合信念密度${\tilde p_{s - 1}}({{\boldsymbol{x}}_{k,s - 1}},{{\boldsymbol{r}}_{k,s - 1}})$和式(17)、式(18)进行观测评估，分别计算$\beta (a_{k,s}^{(i)})$和$\xi (b_{k,s}^{(m)})$；
2.2: 根据式(19)、式(20)执行迭代数据关联，以及根据式(22)、式(23)分别计算$\kappa (a_{k,s}^{(i)})$和$\iota (b_{k,s}^{(m)})$；
2.3: 根据式(24)、式(25)进行观测更新，分别计算$\gamma _{k,s}^{(i)}({\underline {\boldsymbol{x}}} _{k,s}^{(i)},{\underline{\boldsymbol{r}}} _{k,s}^{(i)})$和$\varsigma _{k,s}^{(m)}({\boldsymbol{\bar x}}_{k,s}^{(m)},\bar r_{k,s}^{(m)})$；
2.4: 根据式(26)、式(27)计算获得传感器s关联更新步的融合信念密度${\tilde p_s}({{\boldsymbol{x}}_{k,s}},{{\boldsymbol{r}}_{k,s}})$；
3: S个传感器处理结束后，获得k时刻的信念密度$\tilde p({{\boldsymbol{y}}_k}): = {\tilde p_S}({{\boldsymbol{x}}_{k,S}},{{\boldsymbol{r}}_{k,S}})$，并根据3.2.3节内容执行航迹确认、航迹删除和计算状态估计。

下载: 导出CSV

表 1 目标的存活时刻区间

Table 1. The lifespan (time step) of the targets

目标编号	存活时刻区间	目标编号	存活时刻区间
1	[1, 50]	9	[31, 80]
2, 3, 4	[11, 60]	10, 11	[41, 90]
5, 6	[21, 60]	12	[51, 100]
7, 8	[31, 70]	13, 14, 15	[66, 100]

下载: 导出CSV

参考文献(40)

[1]	BAR-SHALOM Y, WILLETT P K, and TIAN Xin. Tracking and Data Fusion: A Handbook of Algorithms[M]. Storrs: YBS Publishing, 2011.
[2]	BLACKMAN S and POPOLI R. Design and Analysis of Modern Tracking Systems[M]. Boston: Artech House, 1999.
[3]	李继广, 陈欣, 董彦非, 等. 基于协同滤波轨迹预测的机动目标RTPN拦截制导律[J]. 北京航空航天大学学报, 2024, 50(1): 86–96. doi: 10.13700/j.bh.1001-5965.2022.0211. LI Jiguang, CHEN Xin, DONG Yanfei, et al. RTPN interception guidance law for maneuvering target based on collaborative filtering trajectory prediction[J]. Journal of Beijing University of Aeronautics and Astronautics, 2024, 50(1): 86–96. doi: 10.13700/j.bh.1001-5965.2022.0211.
[4]	曾雅俊, 王俊, 魏少明, 等. 分布式多传感器多目标跟踪方法综述[J]. 雷达学报, 2023, 12(1): 197–213. doi: 10.12000/JR22111. ZENG Yajun, WANG Jun, WEI Shaoming, et al. Review of the method for distributed multi-sensor multi-target tracking[J]. Journal of Radars, 2023, 12(1): 197–213. doi: 10.12000/JR22111.
[5]	孟琭, 杨旭. 目标跟踪算法综述[J]. 自动化学报, 2019, 45(7): 1244–1260. doi: 10.16383/j.aas.c180277. MENG Lu and YANG Xu. A survey of object tracking algorithms[J]. Acta Automatica Sinica, 2019, 45(7): 1244–1260. doi: 10.16383/j.aas.c180277.
[6]	HOSEINNEZHAD R, VO B N, VO B T, et al. Visual tracking of numerous targets via multi-Bernoulli filtering of image data[J]. Pattern Recognition, 2012, 45(10): 3625–3635. doi: 10.1016/j.patcog.2012.04.004.
[7]	VO B N, MALLICK M, BAR-SHALOM Y, et al. Multitarget tracking[J]. Wiley Encyclopedia of Electrical and Electronics Engineering, 2015. doi: 10.1002/047134608X.W8275.
[8]	SINGER R A and STEIN J J. An optimal tracking filter for processing sensor data of imprecisely determined origin in surveillance systems[C]. 1971 IEEE Conference on Decision and Control, Miami Beach, USA, 1971: 171–175. doi: 10.1109/CDC.1971.270971.
[9]	REID D. An algorithm for tracking multiple targets[J]. IEEE Transactions on Automatic Control, 1979, 24(6): 843–854. doi: 10.1109/TAC.1979.1102177.
[10]	MAHLER R P S. Statistical Multisource-Multitarget Information Fusion[M]. Boston: Artech House, 2007.
[11]	WILLIAMS J L and LAU R A. Convergence of loopy belief propagation for data association[C]. The Sixth International Conference on Intelligent Sensors, Sensor Networks and Information Processing, Brisbane, Australia, 2010: 175–180. doi: 10.1109/ISSNIP.2010.5706750.
[12]	MEYER F, KROPFREITER T, WILLIAMS J L, et al. Message passing algorithms for scalable multitarget tracking[J]. Proceedings of the IEEE, 2018, 106(2): 221–259. doi: 10.1109/JPROC.2018.2789427.
[13]	GAGLIONE D, BRACA P, SOLDI G, et al. Fusion of sensor measurements and target-provided information in multitarget tracking[J]. IEEE Transactions on Signal Processing, 2022, 70: 322–336. doi: 10.1109/TSP.2021.3132232.
[14]	LAN Hua, MA Jirong, WANG Zengfu, et al. A message passing approach for multiple maneuvering target tracking[J]. Signal Processing, 2020, 174: 107621. doi: 10.1016/j.sigpro.2020.107621.
[15]	SUN Mengwei, DAVIES M E, PROUDLER I K, et al. Adaptive kernel Kalman filter based belief propagation algorithm for maneuvering multi-target tracking[J]. IEEE Signal Processing Letters, 2022, 29: 1452–1456. doi: 10.1109/LSP.2022.3184534.
[16]	SHARMA P, SAUCAN A A, BUCCI D J, et al. Decentralized Gaussian filters for cooperative self-localization and multi-target tracking[J]. IEEE Transactions on Signal Processing, 2019, 67(22): 5896–5911. doi: 10.1109/TSP.2019.2946017.
[17]	CORMACK D and HOPGOOD J R. Message passing and hierarchical models for simultaneous tracking and registration[J]. IEEE Transactions on Aerospace and Electronic Systems, 2021, 57(3): 1524–1537. doi: 10.1109/TAES.2020.3046090.
[18]	KROPFREITER T, MEYER F, and HLAWATSCH F. A fast labeled multi-Bernoulli filter using belief propagation[J]. IEEE Transactions on Aerospace and Electronic Systems, 2020, 56(3): 2478–2488. doi: 10.1109/TAES.2019.2941104.
[19]	LIANG Mingchao and MEYER F. Neural enhanced belief propagation for multiobject tracking[J]. IEEE Transactions on Signal Processing, 2024, 72: 15–30. doi: 10.1109/TSP.2023.3314275.
[20]	LAU R A and WILLIAMS J L. Tracking a coordinated group using expectation maximisation[C]. The Eighth IEEE International Conference on Intelligent Sensors, Sensor Networks and Information Processing, Melbourne, Australia, 2013: 282–287. doi: 10.1109/ISSNIP.2013.6529803.
[21]	ZHANG Xuqi, MENG Fanqin, LIU Haiqi, et al. Seamless tracking of group targets and ungrouped targets using belief propagation[EB/OL]. https://arxiv.org/abs/2208.12035, 2022.
[22]	GADALETA S, POORE A B, ROBERTS S, et al. Multiple hypothesis clustering and multiple frame assignment tracking[C]. SPIE 5428, Signal and Data Processing of Small Targets, Orlando, USA, 2004: 294–307. doi: 10.1117/12.542213.
[23]	ZHANG Xuqi, LIU Haiqi, MENG Fanqin, et al. Group target tracking via jointly optimizing group partition and association[J]. Automatica, 2023, 153: 111013. doi: 10.1016/J.AUTOMATICA.2023.111013.
[24]	MIHAYLOVA L, CARMI A Y, SEPTIER F, et al. Overview of Bayesian sequential Monte Carlo methods for group and extended object tracking[J]. Digital Signal Processing, 2014, 25: 1–16. doi: 10.1016/j.dsp.2013.11.006.
[25]	POORE A B. Multidimensional assignment formulation of data association problems arising from multitarget and multisensor tracking[J]. Computational Optimization and Applications, 1994, 3(1): 27–57. doi: 10.1007/BF01299390.
[26]	GNING A, MIHAYLOVA L, MASKELL S, et al. Group object structure and state estimation with evolving networks and Monte Carlo methods[J]. IEEE Transactions on Signal Processing, 2011, 59(4): 1383–1396. doi: 10.1109/TSP.2010.2103062.
[27]	LU Zhejun, HU Weidong, LIU Yongxiang, et al. Seamless group target tracking using random finite sets[J]. Signal Processing, 2020, 176: 107683. doi: 10.1016/j.sigpro.2020.107683.
[28]	PANG S K, LI J, and GODSILL S J. Detection and tracking of coordinated groups[J]. IEEE Transactions on Aerospace and Electronic Systems, 2011, 47(1): 472–502. doi: 10.1109/TAES.2011.5705687.
[29]	LI Qing and GODSILL S. A new leader-follower model for Bayesian tracking[C]. The 23rd IEEE International Conference on Information Fusion (FUSION), Rustenburg, South Africa, 2020: 1–7. doi: 10.23919/FUSION45008.2020.9190329.
[30]	易伟, 袁野, 刘光宏, 等. 多雷达协同探测技术研究进展: 认知跟踪与资源调度算法[J]. 雷达学报, 2023, 12(3): 471–499. doi: 10.12000/JR23036. YI Wei, YUAN Ye, LIU Guanghong, et al. Recent advances in multi-radar collaborative surveillance: Cognitive tracking and resource scheduling algorithms[J]. Journal of Radars, 2023, 12(3): 471–499. doi: 10.12000/JR23036.
[31]	齐崇英, 贺峰, 陈超. 多雷达组网与协同探测关键技术研究[J]. 指挥控制与仿真, 2023, 45(6): 42–46. doi: 10.3969/j.issn.1673-3819.2023.06.007. QI Chongying, HE Feng, and CHEN Chao. Research on key technology of multi-radar network and cooperative detection[J]. Command Control & Simulation, 2023, 45(6): 42–46. doi: 10.3969/j.issn.1673-3819.2023.06.007.
[32]	李劲东. 中国高分辨率对地观测卫星遥感技术进展[J]. 前瞻科技, 2022, 1(1): 112–125. doi: 10.3981/j.issn.2097-0781.2022.01.010. LI Jindong. Advances in high-resolution earth observation satellite remote sensing technologies in China[J]. Science and Technology Foresight, 2022, 1(1): 112–125. doi: 10.3981/j.issn.2097-0781.2022.01.010.
[33]	PAO L Y and TRAILOVIC L. The optimal order of processing sensor information in sequential multisensor fusion algorithms[J]. IEEE Transactions on Automatic Control, 2000, 45(8): 1532–1536. doi: 10.1109/9.871766.
[34]	WANG Yang, JING Zhongliang, HU Shiqiang, et al. On the sensor order in sequential integrated probability data association filter[J]. Science China Information Sciences, 2012, 55(3): 491–500. doi: 10.1007/s11432-011-4542-y.
[35]	LIU Long, JI Hongbing, and FAN Zhenhua. Improved Iterated-corrector PHD with Gaussian mixture implementation[J]. Signal Processing, 2015, 114: 89–99. doi: 10.1016/j.sigpro.2015.01.007.
[36]	MALLICK M, KRISHNAMURTHY V, and VO B N. Integrated Tracking, Classification, and Sensor Management: Theory and Applications[M]. Piscataway: Wiley, 2013: 9–11.
[37]	RISTIC B and ARULAMPALAM S. Bernoulli particle filter with observer control for bearings-only tracking in clutter[J]. IEEE Transactions on Aerospace and Electronic Systems, 2012, 48(3): 2405–2415. doi: 10.1109/TAES.2012.6237599.
[38]	RAHMATHULLAH A S, GARCÍA-FERNÁNDEZ Á F, and SVENSSON L. Generalized optimal sub-pattern assignment metric[C]. The 20th International Conference on Information Fusion (Fusion), Xi’an, China, 2017: 1–8. doi: 10.23919/ICIF.2017.8009645.
[39]	BEARD M, VO B T, and VO B N. OSPA⁽²⁾: Using the OSPA metric to evaluate multi-target tracking performance[C]. 2017 International Conference on Control, Automation and Information Sciences (ICCAIS), Chiang Mai, Thailand, 2017: 86–91. doi: 10.1109/ICCAIS.2017.8217598.
[40]	ARULAMPALAM M S, MASKELL S, GORDON N, et al. A tutorial on particle filters for online nonlinear/non-Gaussian Bayesian tracking[J]. IEEE Transactions on Signal Processing, 2002, 50(2): 174–188. doi: 10.1109/78.978374.