考虑综合性能最优的非短视快速天基雷达多目标跟踪资源调度算法

王增福; 杨广宇; 金术玲

doi:10.12000/JR23162

考虑综合性能最优的非短视快速天基雷达多目标跟踪资源调度算法

doi: 10.12000/JR23162

1.
西北工业大学自动化学院西安 710072
2.
中国电子科技集团公司第三十八研究所合肥 230088

基金项目: 国家自然科学基金(U21B2008)

详细信息

作者简介:
王增福，博士，副教授，主要研究方向为信息融合、传感器管理、路径规划等

杨广宇，硕士生，主要研究方向为天基雷达资源调度

金术玲，博士，高级工程师，主要研究方向为雷达总体设计等

通讯作者:
王增福 wangzengfu@nwpu.edu.cn

责任主编：严俊坤 Corresponding Editor: YAN Junkun
中图分类号: TN95
计量
- 文章访问数: 381
- HTML全文浏览量: 222
- PDF下载量: 78
- 被引次数: 0
出版历程
- 收稿日期: 2023-09-07
- 修回日期: 2023-11-18
- 网络出版日期: 2023-12-20
- 刊出日期: 2024-02-28

A Non-myopic and Fast Resource Scheduling Algorithm for Multi-target Tracking of Space-based Radar Considering Optimal Integrated Performance

1.
School of Automation, Northwestern Polytechnical University, Xi’an 710072, China
2.
The 38th Research Institute of China Electronics Technology Group Corporation, Hefei 230088, China

Funds: The National Natural Science Foundation of China (U21B2008)

More Information

Corresponding author: WANG Zengfu, wangzengfu@nwpu.edu.cn

摘要

摘要: 合理有效的资源调度是天基雷达效能得以充分发挥的关键。针对天基雷达多目标跟踪资源调度问题，建立了综合考虑目标威胁度、跟踪精度与低截获概率(LPI)的代价函数；考虑目标的不确定、天基平台约束以及长远期期望代价，建立了多约束下的基于部分可观测的马尔可夫决策过程(POMDP)的资源调度模型；采用拉格朗日松弛法将多约束下的多目标跟踪资源调度问题转换分解为多个无约束的子问题；针对连续状态空间、连续动作空间及连续观测空间引起的维数灾难问题，采用基于蒙特卡罗树搜索(MCTS)的在线POMDP算法—POMCPOW算法进行求解，最终提出了一种综合多指标性能的非短视快速天基雷达多目标跟踪资源调度算法。仿真表明，与已有调度算法相比，所提算法资源分配更合理，系统性能更优。
- 天基雷达 /
- 资源调度 /
- 多目标跟踪 /
- 部分可观测的马尔可夫决策过程 /
- 蒙特卡罗树搜索(MCTS)
Abstract: Appropriate and effective resource scheduling is the key to achieving the best performance for a space-based radar. Considering the resource scheduling problem of multi-target tracking in a space-based radar system, we establish a cost function that considers target threat, tracking accuracy, and Low Probability of Interception (LPI). Considering target uncertainty and constraints of the space-based platform and long-term expected cost, we establish a resource scheduling model based on the Partially Observable Markov Decision Process (POMDP) with multiple constraints. To transform and decompose the resource scheduling problem of multi-target tracking with multiple constraints into multiple unconstrained sub-problems, we use the Lagrangian relaxation method. To deal with the curse of dimensionality caused by the continuous state space, continuous action space and continuous observation space, we use the online POMDP algorithm based on the Monte Carlo Tree Search (MCTS) and partially observable Monte Carlo planning with observation widening algorithm. Finally, a non-myopic and fast resource scheduling algorithm with comprehensive performance indices for multi-target tracking in a space-based radar system is proposed. Simulation results show that the proposed algorithm, when compared with the existing scheduling algorithms, allocates resources more appropriately and shows better performance.
- Space-based radar /
- Resource scheduling /
- Multi-target tracking /
- Partially observable Markov decision process /
- Monte Carlo Tree Search (MCTS)

HTML全文

图 1 基于LR-POMCPOW的天基雷达多目标跟踪资源调度方法框图

Figure 1. Schematic diagram of the proposed LR-POMCPOW for resource scheduling of space-based radar multi-target tracking

下载: 全尺寸图片幻灯片

图 2 蒙特卡罗树搜索算法的过程

Figure 2. The process of the MCTS algorithm

下载: 全尺寸图片幻灯片

图 3 威胁度对雷达资源分配影响分析STK仿真图示

Figure 3. STK-based demonstration for impact of distinct target threat levels on radar resource allocation

下载: 全尺寸图片幻灯片

图 4 目标威胁度结果

Figure 4. Target threat level results

下载: 全尺寸图片幻灯片

图 5 各目标的预算比($\tau/T $)分配结果

Figure 5. Budget ratio ($\tau/T $) allocation results for each target

下载: 全尺寸图片幻灯片

图 6 相对距离对雷达资源分配影响分析STK仿真图示

Figure 6. STK-based demonstration for impact of distinct relative distances on radar resource allocation

下载: 全尺寸图片幻灯片

图 7 目标径向距离

Figure 7. The slant range of targets

下载: 全尺寸图片幻灯片

图 8 相对距离影响下预算比($\tau / T $)分配结果

Figure 8. Budget ratio ($\tau / T $) allocation results influenced by relative distance

下载: 全尺寸图片幻灯片

图 9 多目标跟踪的STK仿真图示

Figure 9. STK-based demonstration for multi-target tracking

下载: 全尺寸图片幻灯片

图 10 目标跟踪轨迹

Figure 10. Target tracking trajectory

下载: 全尺寸图片幻灯片

图 11 多目标跟踪下各目标的预算比($ \tau / T $)分配结果

Figure 11. Budget ratio ($ \tau / T$) allocation results of each target under multi-target tracking

下载: 全尺寸图片幻灯片

图 12 各目标分配平均辐射功率

Figure 12. The average radiation power allocated to each target

下载: 全尺寸图片幻灯片

图 13 目标1跟踪位置RMSE

Figure 13. RMSE on position of target1

下载: 全尺寸图片幻灯片

图 14 目标1跟踪速度RMSE

Figure 14. RMSE on speed of target1

下载: 全尺寸图片幻灯片

图 15 总平均辐射功率对比

Figure 15. Comparison of total average radiation power

下载: 全尺寸图片幻灯片

图 16 总预算比对比

Figure 16. Comparison of the total budget ratio ($ \tau / T $)

下载: 全尺寸图片幻灯片

图 17 各算法期望累积多目标总折扣代价对比

Figure 17. Comparison of the expected cumulative multi-target discount cost

下载: 全尺寸图片幻灯片

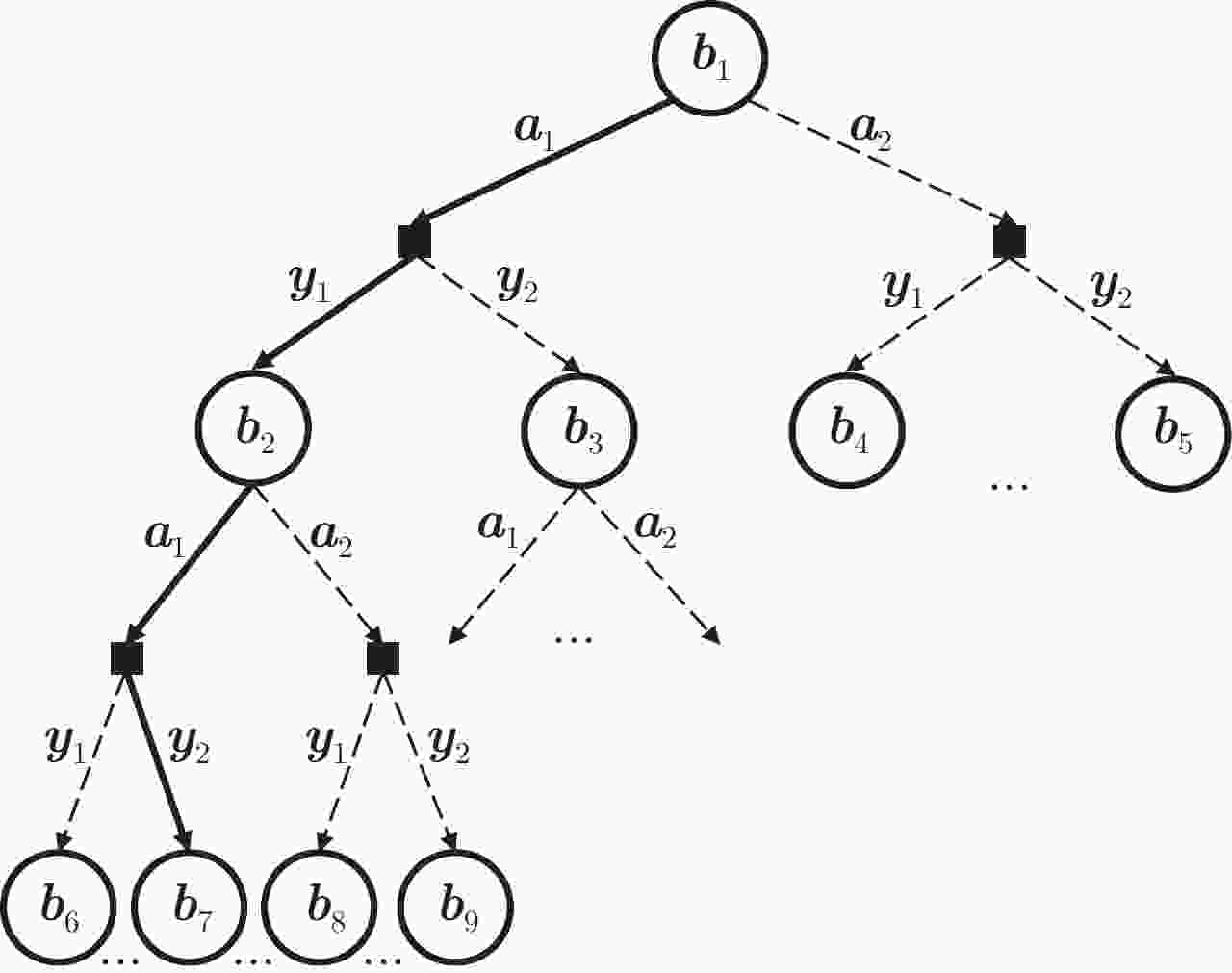
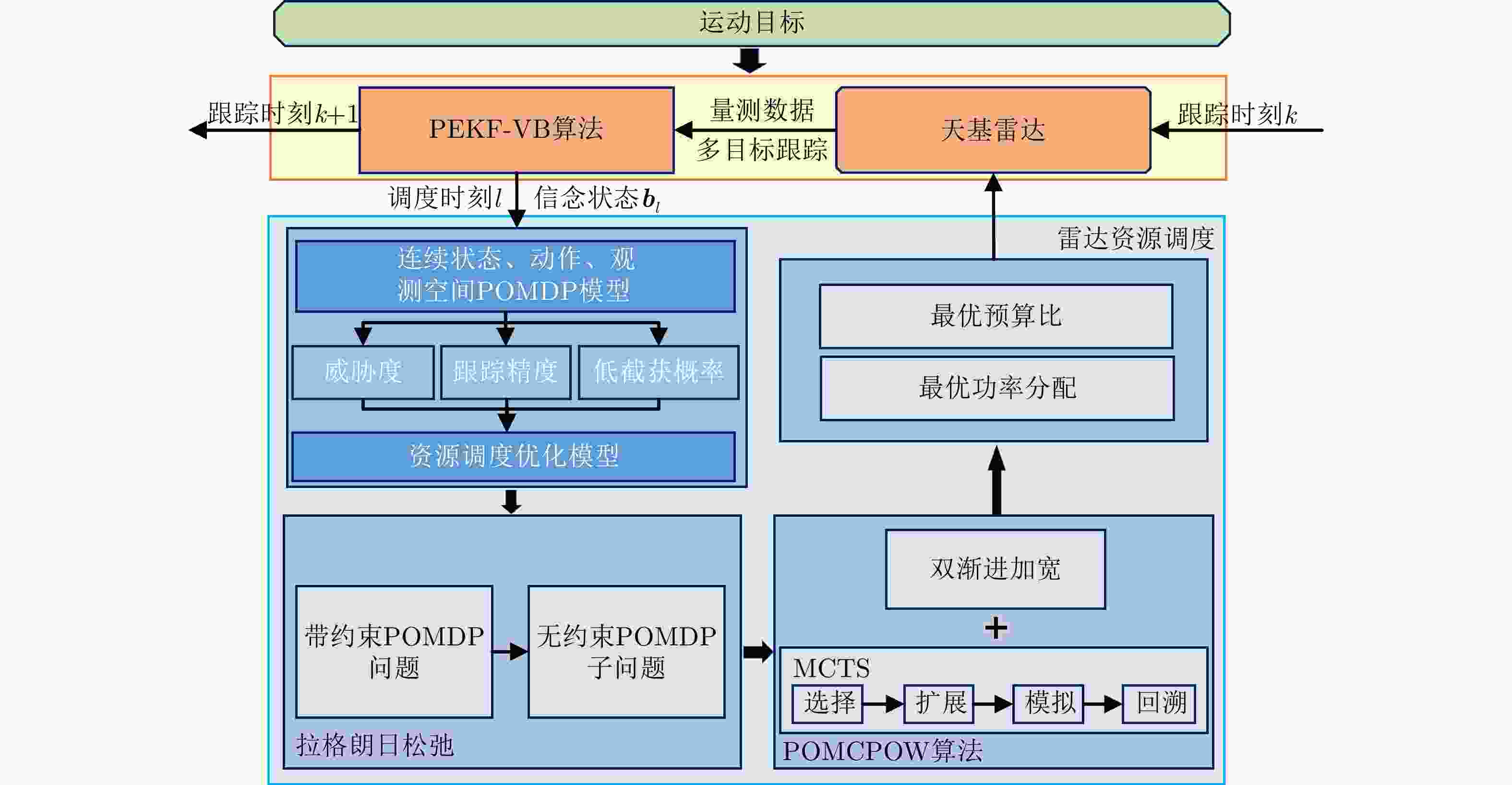
1 POMCPOW算法

1. POMCPOW algorithm

Input：信念状态b₁，搜索深度d，拉格朗日算子向量${\boldsymbol{\varLambda}}^e $，模拟　次数$\varGamma $，动作空间${\mathcal{A}} $
Output：最优策略${\boldsymbol{\pi}}^e $
1: for l=1:${\mathcal{L}} $ do
2: 　for n=1:$\varGamma $ do
3: 　　x$\leftarrow $从b_l中采样
4: 　　SIMULATE(x,$\hbar $,${\boldsymbol{\lambda}}_l^e $,d)
5: 　end for
6: 　${\boldsymbol{a}}_l^e \leftarrow \mathop {\arg \min }\limits_{{\boldsymbol{a}}_l} {\mathcal{Q}}({\boldsymbol{b}}_l,{\boldsymbol{a}}_l)$
7: 　预测u步得到下一调度时刻的信念状态b_l+1
8: end for
9: return ${\boldsymbol{\pi}}^e=[{\boldsymbol{a}}_1^e\;{\boldsymbol{a}}_2^e\;\cdots\;{\boldsymbol{a}}_{\mathcal{L}}^e] $
10: procedure SIMULATE (${\boldsymbol{x}},\hbar,{\boldsymbol{\lambda}},d $)
11: if d=0 then
12: return 0
13: end if
14: if $\|{\mathcal{C}}(\hbar)\| \le \delta_{\boldsymbol{a}} N(\hbar)^{\alpha_{\boldsymbol{a}}}$ then
15: ${\boldsymbol{a}} \leftarrow $ NEXTACTION$(\hbar) $
16: ${\mathcal{C}}(\hbar) \leftarrow {\mathcal{C}}(\hbar) \cup \{{\boldsymbol{a}}\}$
17: end if 　18: ${\boldsymbol{a}}\leftarrow \mathop {\arg \min }\limits_{{\boldsymbol{a}}\in{\mathcal{C}}(\hbar) } {\mathcal{Q}}(\hbar {\boldsymbol{a}}) -\mu \sqrt{\dfrac{\log N(\hbar )}{N(\hbar {\boldsymbol{a}})}}$
19: ${\boldsymbol{x}}',{\boldsymbol{y}},\;C \leftarrow {\mathcal{G}}({\boldsymbol{x}},{\boldsymbol{a}},{\boldsymbol{\lambda}})$
20: if $\|{\mathcal{C}}(\hbar {\boldsymbol{a}})\|\le\delta_{\boldsymbol{y}} N(\hbar {\boldsymbol{a}})^{\alpha_{\boldsymbol{y}}} $ then
21: M$(\hbar {\boldsymbol{ay}}) \leftarrow M( \hbar {\boldsymbol{ay}})$+1
22: else 　23: 选择${\boldsymbol{y}}\in {\mathcal{C}}(\hbar {\boldsymbol{a}}){\mathrm{w.p}}.\dfrac{M(\hbar {\boldsymbol{ay}})}{\displaystyle\sum\nolimits_{\boldsymbol{y}} M(\hbar {\boldsymbol{ay}})}$
24: end if
25: 增加${\boldsymbol{x}}' $至$ X(\hbar {\boldsymbol{ay}}) $
26: 增加${\mathrm{Pr}}({\boldsymbol{y}}\|{\boldsymbol{x}}',{\boldsymbol{a}}) $至$W(\hbar {\boldsymbol{ay}}) $
27: if ${\boldsymbol{y}}\notin {\mathcal{C}}(\hbar {\boldsymbol{a}}) $ then
28: ${\mathcal{C}}(\hbar {\boldsymbol{a}}) \leftarrow {\mathcal{C}}(\hbar {\boldsymbol{a}}) \cup \{{\boldsymbol{y}}\}$
29: $C_{\mathrm{total}} \leftarrow {\mathrm{ROLLOUT}} ({\boldsymbol{x}},\hbar,{\boldsymbol{\lambda}},d)$
30: else 　31: 选择${\boldsymbol{x}}'\in X(\hbar {\boldsymbol{ay}}) {\mathrm{w.p.}}\dfrac{W(\hbar {\boldsymbol{ay}}[i])}{\displaystyle\sum\nolimits_{j=1}^mW(\hbar {\boldsymbol{ay}})[j]}$
32: $C \leftarrow \varLambda ({\boldsymbol{x}},{\boldsymbol{a}}) $
33: $C_{\mathrm{total}} \leftarrow C +\gamma{\mathrm{SIMULATE}}({\boldsymbol{x}},\hbar {\boldsymbol{ay}}, {\boldsymbol{\lambda}}, d-1)$
34: end if
35: $N (\hbar) \leftarrow N (\hbar)+1 $
36: $N (\hbar {\boldsymbol{a}}) \leftarrow N (\hbar {\boldsymbol{a}})+1 $ 　37: ${\mathcal{Q}} (\hbar {\boldsymbol{a}}) \leftarrow {\mathcal{Q}} (\hbar {\boldsymbol{a}})+ \dfrac{C_{\mathrm{total}}-{\mathcal{Q}}(\hbar {\boldsymbol{a}})}{N(\hbar {\boldsymbol{a}}) }$
38: end procedure

下载: 导出CSV

2 Rollout算法

2. Rollout algorithm

1: procedure ROLLOUT$({\boldsymbol{x}},\hbar,{\boldsymbol{\lambda}},d) $
2: 　if d=0 then
3: 　　return 0
4: 　end if
5: 　${\boldsymbol{a}} \leftarrow{\boldsymbol{\pi}}_{\mathrm{rollout}} (\hbar,\cdot)$
6: 　${\boldsymbol{x}}',{\boldsymbol{y}},C \leftarrow {\mathcal{G}}({\boldsymbol{x}},{\boldsymbol{a}},{\boldsymbol{\lambda}})$
7: 　return $C+\gamma {\mathrm{ROLLOUT}}({\boldsymbol{x}}', \hbar {\boldsymbol{ay}},{\boldsymbol{\lambda}}, d-1) $
8: end procedure

下载: 导出CSV

3 基于LR-POMCPOW的天基雷达多目标跟踪资源调度算法

3. LR-POMCPOW-based resource scheduling algorithm for multi-target tracking of space-based radar

Input: 动作空间${\mathcal{A}} $，初始信念状态B₁，最大迭代次数e_m，初始迭代步长$\gamma_{\mathrm{LR}} $，模拟次数$\varGamma $，搜索深度d
Output：最优策略${\boldsymbol{\pi}}^* $，最优累积多目标总代价值V^*(B₁)
1：调度次数$\kappa=1 $
2：while $\kappa\le K $ do
3：　迭代次数e=0，拉格朗日乘子向量初始值设定为${\boldsymbol{\varLambda}}^0=[{\boldsymbol{\lambda}}_1^0\; {\boldsymbol{\lambda}}_2^0\;\cdots\;{\boldsymbol{\lambda}}_{\mathcal{L}}^0] ^{\mathrm{T}}$
4：　while e ≤e_m do
5：　　for i=1:${\mathcal{I}} $ do
6：　　　给定信念状态${\boldsymbol{b}}_{i,\kappa} $，搜索深度d，拉格朗日算子向量${\boldsymbol{\varLambda}}^e $，模拟次数$ \varGamma$，动作空间${\mathcal{A}} $，转至算法1进行求解，得到目标i的最优策略　　　　　 ${\boldsymbol{\pi}}^e_i=[{\boldsymbol{a}}_{i,1}^e\;{\boldsymbol{a}}_{i,2}^e\;\cdots\; {\boldsymbol{a}}_{i,{\mathcal{L}}}^e] $
7：　　end for
8：　　分别计算次梯度$\varsigma_{1,l}=\displaystyle\sum\nolimits_{i=1}^{\mathcal{I}} p_{{\mathrm{av}},i,l}-E/ \mathfrak{U}$, $\varsigma_{2,l} =\displaystyle\sum\nolimits_{i=1}^{\mathcal{I}} \tau_{i,l}/T-\eta ,\forall l,1\le l \le {\mathcal{L}}$
9：　　对于$\forall l,1\le l \le {\mathcal{L}} $，$\varsigma_{1,l} $, $\varsigma_{2,l} $等于0或小于给定误差阈值$\varepsilon $，则迭代结束，并保存对应的策略$\bar{\boldsymbol{\pi}} =[{\boldsymbol{\pi}}_1^\;{\boldsymbol{\pi}}_2^\;\cdots\; {\boldsymbol{\pi}}_{\mathcal{I}} ^*]^{\mathrm{T}}$，转至步骤13
10：　更新拉格朗日乘子向量${\boldsymbol{\varLambda}} ^e$，令$\lambda_{1,l}^{e+1}=\max\{ 0, \lambda_{1,l}^e + \gamma_{\mathrm{LR}}\cdot \varsigma_{1,l} \} $, $ \lambda_{2,l}^{e+1}= \max\{ 0, \lambda_{2,l}^e + \gamma_{\mathrm{LR}}\cdot \varsigma_{2,l} \}, \forall l, 1\le l \le {\mathcal{L}}$
11：　令e=e+1，返回至步骤4
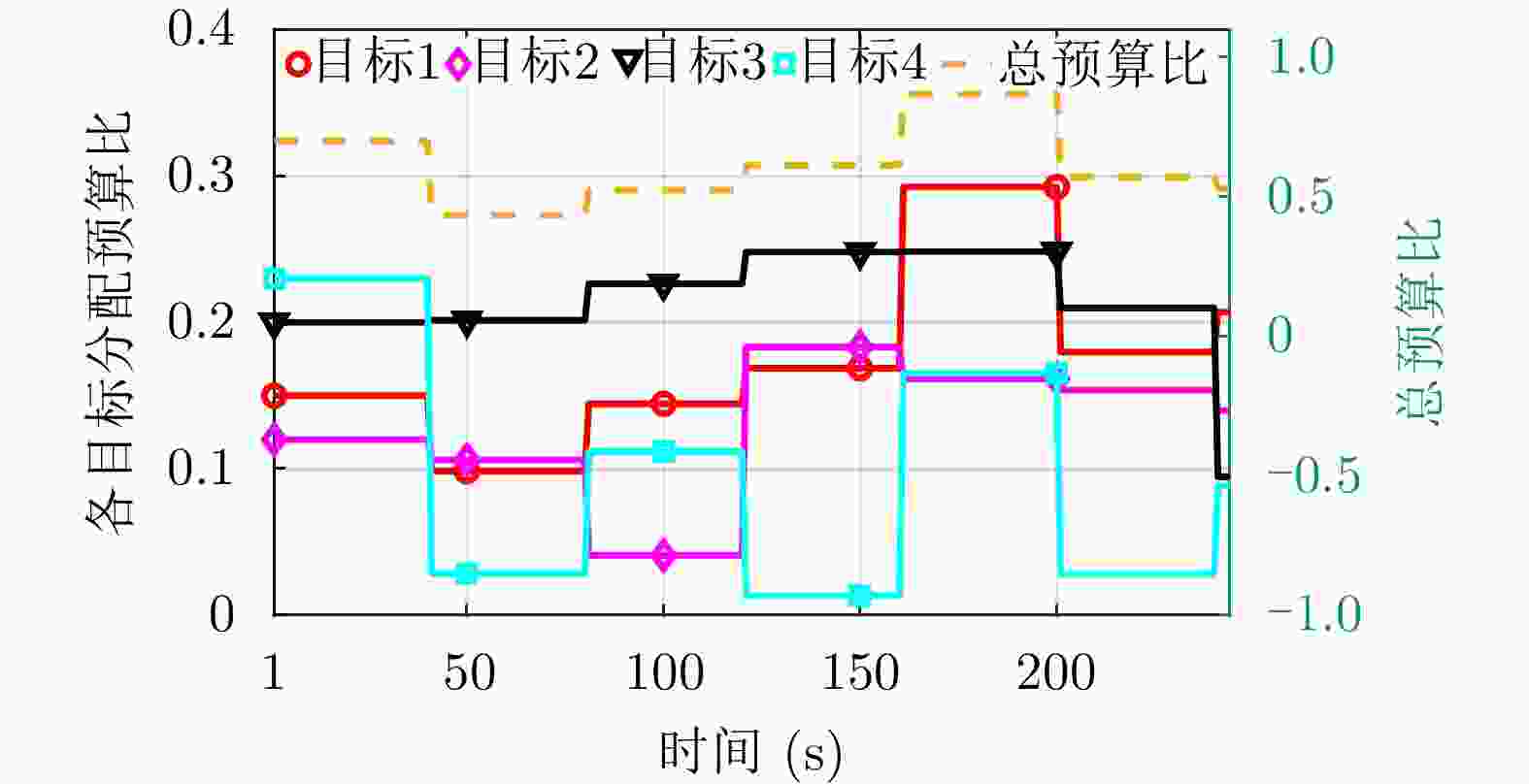
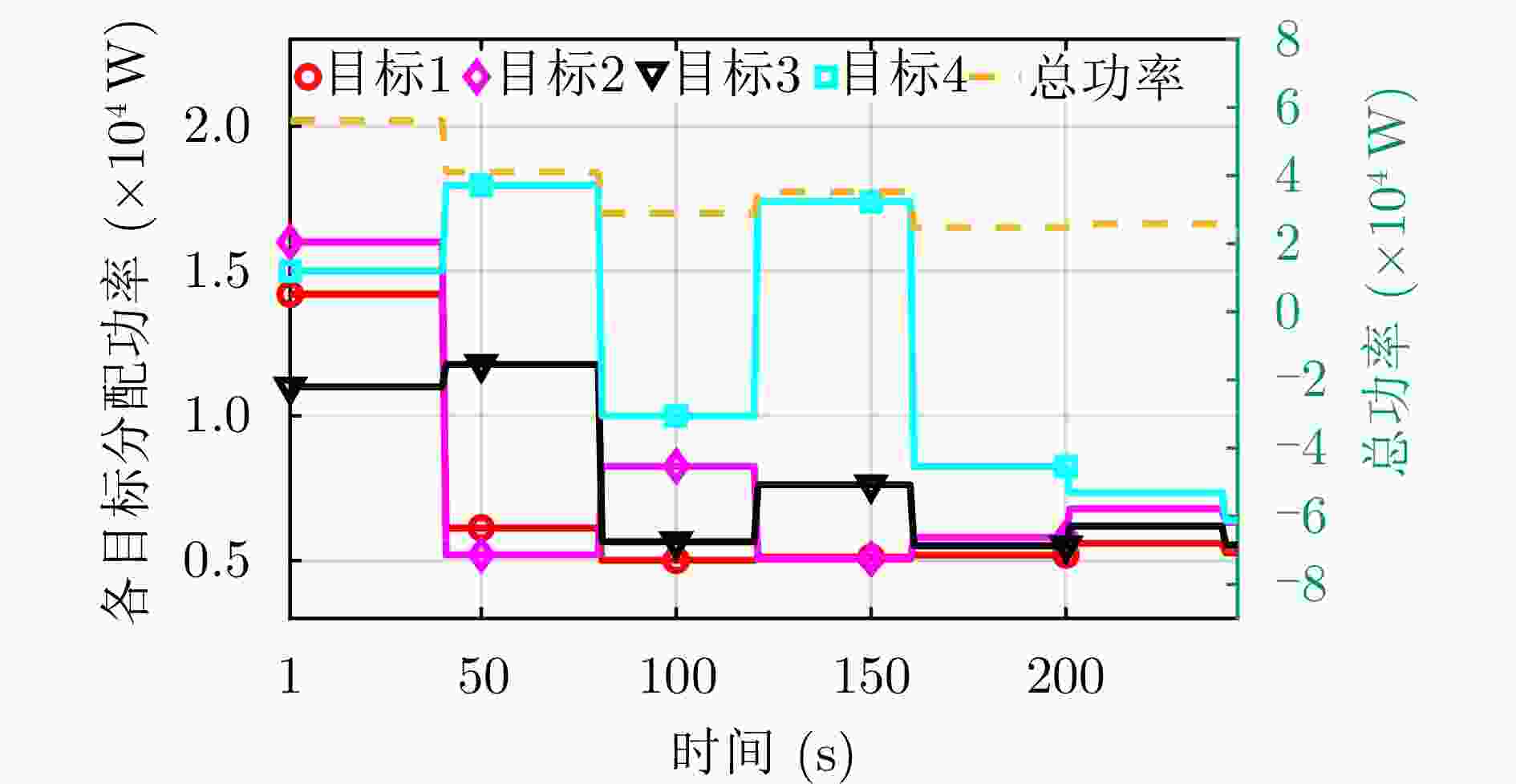
12： end while 　13：选取本次调度各目标策略的首个动作，构成动作向量$\bar {\boldsymbol{\pi}}_\kappa=[{\boldsymbol{a}}_{1,1}^\;{\boldsymbol{a}}_{2,1}^\;\cdots\;{\boldsymbol{a}}_{{\mathcal{I}},1}^*] ^{\mathrm{T}}$
14：当$\kappa $大于K时结束迭代，利用PEKF-VB算法执行完剩余更新步，并转至步骤20
15： for i=1:${\mathcal{I}} $ do
16：　利用PEKF-VB算法执行u步更新，得到信念状态${\boldsymbol{b}}_{i,\kappa+1} $
17： end for
18：令$\kappa=\kappa+1 $
19：end while
20：根据最优策略$\bar{\boldsymbol{\pi}}^=[\bar {\boldsymbol{\pi}}_1\;\bar {\boldsymbol{\pi}}_2\;\cdots\; \bar {\boldsymbol{\pi}}_K] $计算式(17)的最优累积多目标总代价值V^(B₁)

下载: 导出CSV

表 1 仿真基本参数设置

Table 1. Basic parameter settings of simulation

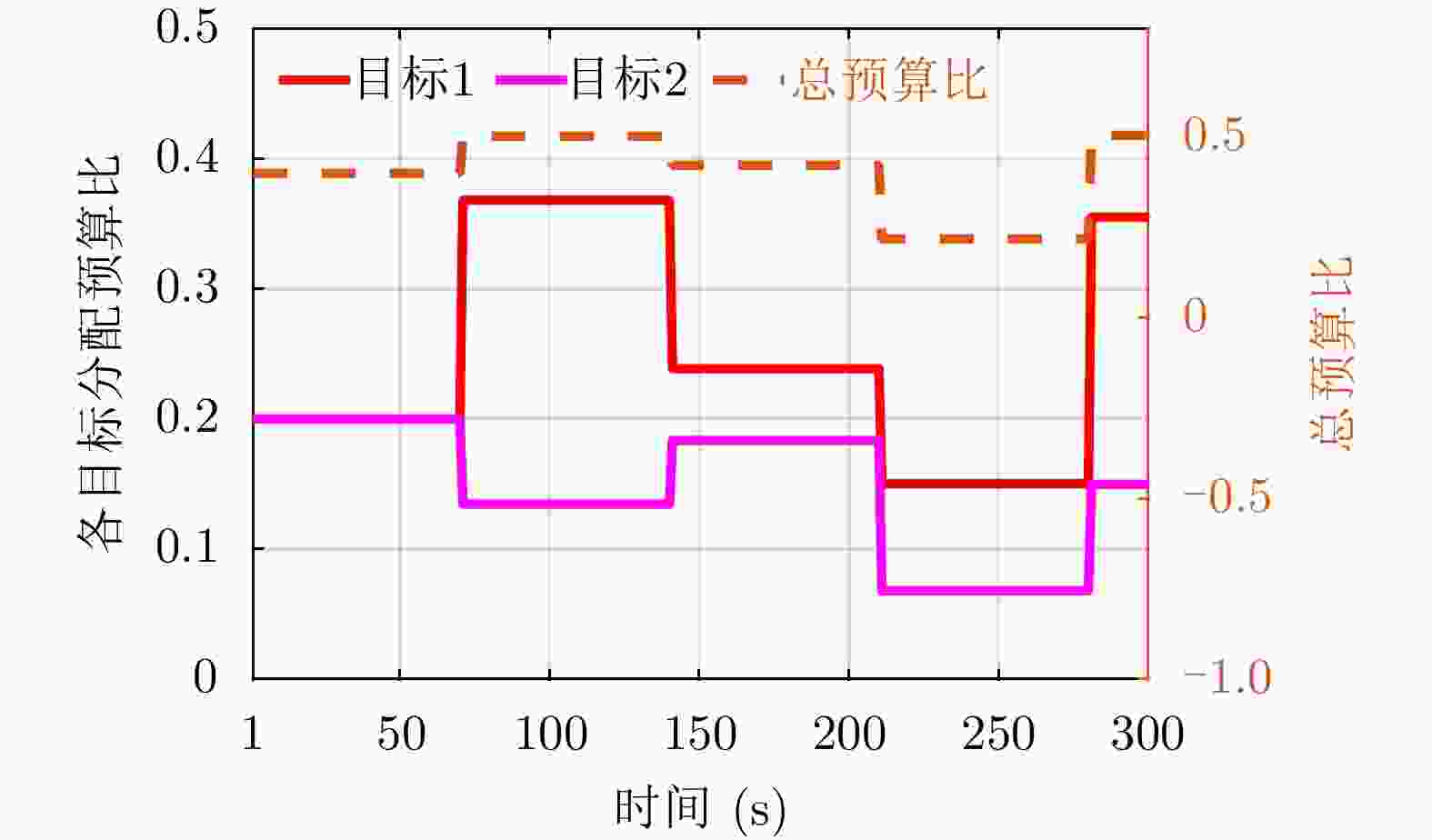
参数	数值
搜索深度d	6
模拟次数$\varGamma $	600
状态粒子数N_particles	600
折扣因子$\gamma $	1
脉冲宽度$\nu $	1 μs
第l次调度时初始拉格朗日算子${{\lambda}}_l^0 $	[50, 50]
LR最大迭代次数e_m	50
LR初始迭代步长$\gamma_{\mathrm{LR}} $	20
LR误差阈值$\varepsilon $	0.01
最大时间预算比$\eta $	0.5
轨道6根数¹	[7400 km, 0, 0.61 rad, 0 rad, 0 rad, 0.84 rad]
格林尼治恒星时角(GHA)	4.98 rad
窗口起始时间t_start (UTCG)	4 May 2023 04:14:43.000
窗口结束时间t_end (UTCG)	4 May 2023 04:19:42.000
¹轨道高度指圆形轨道下的半长袖，即地心与天基雷达卫星之间的距离。

下载: 导出CSV

表 2 场景1初始时刻目标相关参数

Table 2. Parameters related to target initialization of scenario 1

区域内目标	初始位置(km)	初始速度(km/s)	$\sigma \;({\mathrm{m}}^2) $	r (km)	$\tau\;({\mathrm{s}}) $	p_av (W)
参考目标	—	—	11	1250.00	0.20	1×10⁴
目标1	[–3563.04,4533.712,2741.618]	[0.008,0.109,–0.168]	14	1570.05	0.20	1×10⁴
目标2	[–3728.76,4427.435,2695.038]	[–0.123,–0.126,0.037]	15	1572.54	0.20	1×10⁴
我方飞机	[–3560.39,4547.62,2722.091]	[–0.164,–0.110,–0.031]	—	—	—	—

下载: 导出CSV

表 3 场景2初始时刻目标相关参数

Table 3. Parameters related to target initialization of scenario 2

区域内目标	初始位置(km)	初始速度(km/s)	$\sigma \;({\mathrm{m}}^2) $	r (km)	$\tau\;({\mathrm{s}}) $	p_av (W)
参考目标	—	—	11	900.00	0.20	1×10⁴
目标1	[–3579.26,4512.89,2754.72]	[0.139,0.115,–0.008]	10	750.44	0.25	1×10⁴
目标2	[–3596.33,4574.503,2628.813]	[–0.055,0.051,–0.164]	15	1413.93	0.25	1×10⁴

下载: 导出CSV

表 4 场景3初始时刻目标相关参数

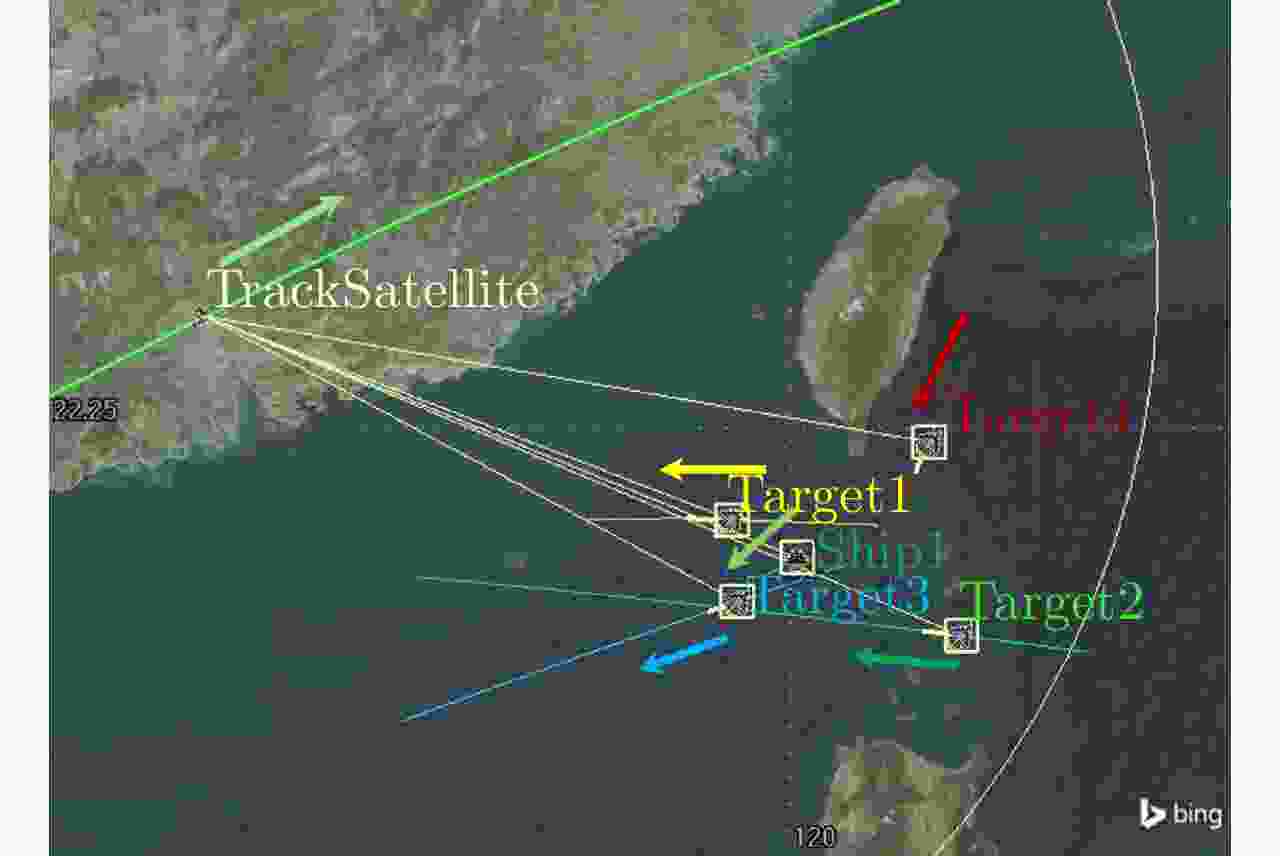
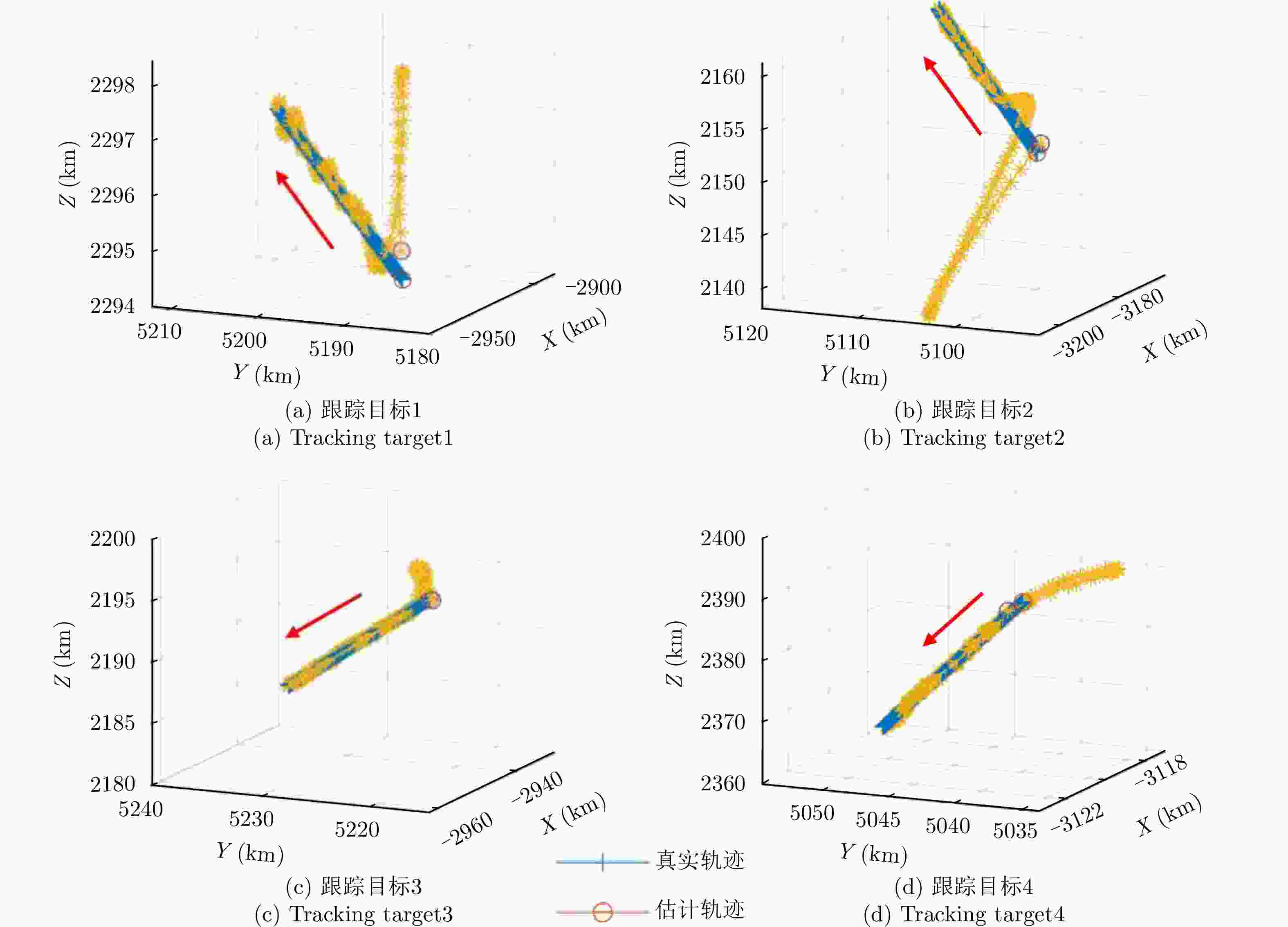
Table 4. Parameters related to target initialization of scenario 3

区域内目标	初始位置(km)	初始速度(km/s)	$\sigma\;({\mathrm{m}}^2) $	r (km)	$\tau\;({\mathrm{s}}) $	p_av (W)
参考目标	—	—	11	1300.00	0.20	1.00×10⁴
目标1	[–2924.49,5193.69,2294.53]	[0.201,0.111,0.008]	10	1325.83	0.15	1.42×10⁴
目标2	[–3192.74,5100.13,2155.14]	[0.173,0.098,0.025]	15	1559.51	0.12	1.60×10⁴
目标3	[–2947.68,5222.76,2197.083]	[0.137,0.102,–0.057]	15	1353.37	0.20	1.10×10⁴
目标4	[–3109.56,5044.01,2392.48]	[0.028,0.081,–0.135]	12	1480.35	0.23	1.50×10⁴
我方舰船	[–2992.27,5162.81,2244.70]	[0.010,0.009,–0.007]	—	—	—	—

下载: 导出CSV

表 5 各算法超参数

Table 5. Algorithm hyperparameters

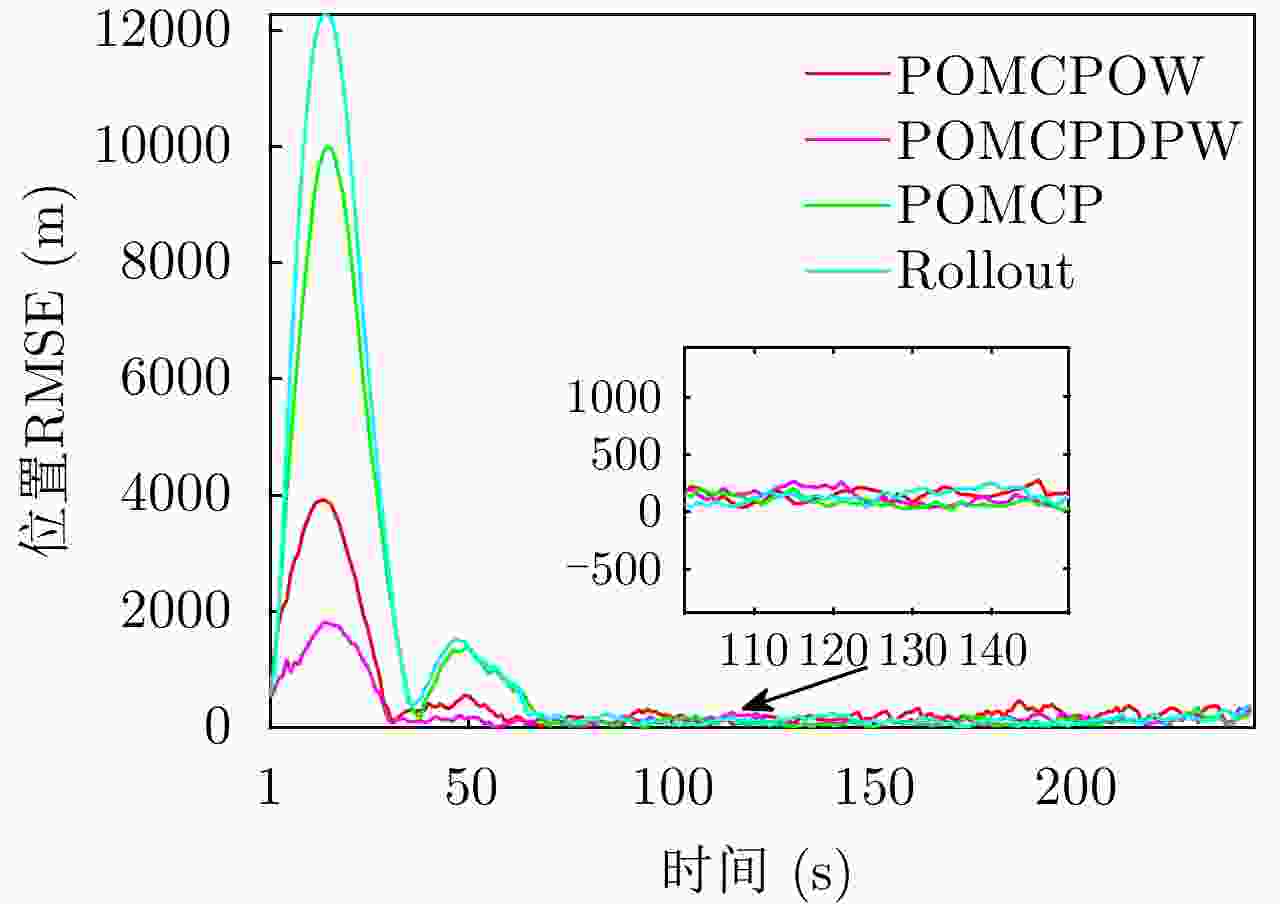
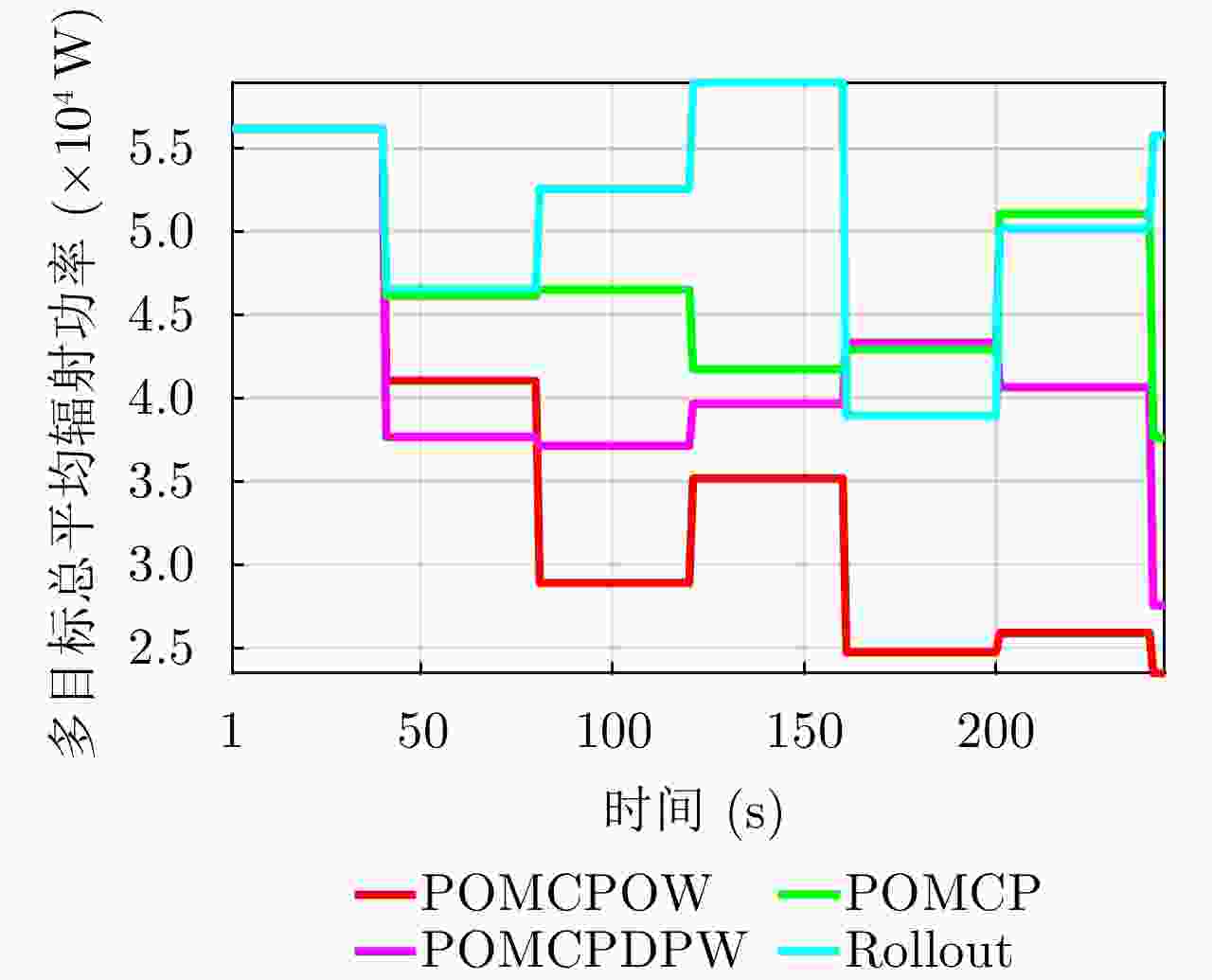
比较的算法	$\mu $	$\delta_{\boldsymbol{a}} $	$\alpha_{\boldsymbol{a}} $	$\delta_{\boldsymbol{y}} $	$\alpha_{\boldsymbol{y}} $	M_r
POMCPOW	100	35	1/100	8	1/120	—
POMCPDPW	30	3	1/30	5	1/55	—
POMCP	70	—	—	—	—	—
Rollout	—	—	—	—	—	30

下载: 导出CSV

参考文献(37)

[1]	XIE Mingchi, YI Wei, KIRUBARAJAN T, et al. Joint node selection and power allocation strategy for multitarget tracking in decentralized radar networks[J]. IEEE Transactions on Signal Processing, 2018, 66(3): 729–743. doi: 10.1109/TSP.2017.2777394
[2]	DAI Jinhui, YAN Junkun, WANG Penghui, et al. Optimal resource allocation for multiple target tracking in phased array radar network[C]. 2019 International Conference on Control, Automation and Information Sciences (ICCAIS), Chengdu, China, 2019: 1–4.
[3]	SUN Jun, LU Xiujuan, YUAN Ye, et al. Resource allocation for multi-target tracking in multi-static radar systems with imperfect detection performance[C]. 2020 IEEE Radar Conference (RadarConf20), Florence, Italy, 2020: 1–6.
[4]	ZHANG Haowei, LIU Weijian, ZONG Binfeng, et al. An efficient power allocation strategy for maneuvering target tracking in cognitive MIMO radar[J]. IEEE Transactions on Signal Processing, 2021, 69: 1591–1602. doi: 10.1109/TSP.2020.3047227
[5]	LU Xiujuan, YI Wei, and KONG Lingjiang. Joint online route planning and resource optimization for multitarget tracking in airborne radar systems[J]. IEEE Systems Journal, 2022, 16(3): 4198–4209. doi: 10.1109/JSYST.2021.3116020
[6]	SHI Chenguang, ZHOU Jianjiang, and WANG Fei. Adaptive resource management algorithm for target tracking in radar network based on low probability of intercept[J]. Multidimensional Systems and Signal Processing, 2018, 29(4): 1203–1226. doi: 10.1007/s11045-017-0494-8
[7]	SHI Chenguang, WANG Yijie, SALOUS S, et al. Joint transmit resource management and waveform selection strategy for target tracking in distributed phased array radar network[J]. IEEE Transactions on Aerospace and Electronic Systems, 2022, 58(4): 2762–2778. doi: 10.1109/TAES.2021.3138869
[8]	CHHETRI A S, MORRELL D, and PAPANDREOU-SUPPAPPOLA A. Energy efficient target tracking in a sensor network using non-myopic sensor scheduling[C]. 2005 7th International Conference on Information Fusion, Philadelphia, USA, 2005: 558–565.
[9]	HERO A O and COCHRAN D. Sensor management: Past, present, and future[J]. IEEE Sensors Journal, 2011, 11(12): 3064–3075. doi: 10.1109/JSEN.2011.2167964
[10]	FERRI G, MUNAFÒ A, GOLDHAHN R, et al. A non-myopic, receding horizon control strategy for an AUV to track an underwater target in a bistatic sonar scenario[C]. 53rd IEEE Conference on Decision and Control, Los Angeles, USA, 2014: 5352–5358.
[11]	JI Shihao, PARR R, and CARIN L. Nonmyopic multiaspect sensing with partially observable Markov decision processes[J]. IEEE Transactions on Signal Processing, 2007, 55(6): 2720–2730. doi: 10.1109/TSP.2007.893747
[12]	KRISHNAMURTHY V and DJONIN D V. Optimal threshold policies for multivariate POMDPs in radar resource management[J]. IEEE Transactions on Signal Processing, 2009, 57(10): 3954–3969. doi: 10.1109/TSP.2009.2022915
[13]	JIANG Xiaofeng, ZHOU Feng, JIAN Yang, et al. An optimal POMDP-based anti-jamming policy for cognitive radar[C]. 2017 13th IEEE Conference on Automation Science and Engineering (CASE), Xi’an, China, 2017: 938–943.
[14]	SHAN Ganlin, XU Gongguo, and QIAO Chenglin. A non-myopic scheduling method of radar sensors for maneuvering target tracking and radiation control[J]. Defence Technology, 2020, 16(1): 242–250. doi: 10.1016/j.dt.2019.10.001
[15]	SCHÖPE M I, DRIESSEN H, and YAROVOY A. A constrained POMDP formulation and algorithmic solution for radar resource management in multi-target tracking[J]. ISIF Journal of Advances in Information Fusion, 2021, 16(1): 31–47.
[16]	HAWKINS J T. A Langrangian decomposition approach to weakly coupled dynamic optimization problems and its applications[D]. [Ph.D. dissertation], Massachusetts Institute of Technology, 2003.
[17]	CASTANON D A. Approximate dynamic programming for sensor management[C]. The 36th IEEE Conference on Decision and Control, San Diego, USA, 1997: 1202–1207.
[18]	LI Yuan, ZHU Huayong, and SHEN Lincheng. The Lagrangian relaxation based resources allocation methods for air-to-ground operations under uncertainty circumstances[C]. 2009 Chinese Control and Decision Conference, Guilin, China, 2009: 5609–5614.
[19]	KURNIAWATI H, HSU D, and LEE W S. SARSOP: Efficient Point-based POMDP Planning by Approximating Optimally Reachable Belief Spaces[M]. BROCK O, TRINKLE J, and RAMOS F. Robotics: Science and Systems. Cambridge: MIT Press, 2009: 1–8.
[20]	PINEAU J, GORDON G, and THRUN S. Point-based value iteration: An anytime algorithm for POMDPs[C]. The 18th International Joint Conference on Artificial Intelligence, Acapulco, Mexico, 2003: 1025–1030.
[21]	SPAAN M T J and VLASSIS N. Perseus: Randomized point-based value iteration for POMDPs[J]. Journal of Artificial Intelligence Research, 2005, 24: 195–220. doi: 10.1613/jair.1659
[22]	SMITH T and SIMMONS R. Heuristic search value iteration for POMDPs[C]. The 20th Conference on Uncertainty in Artificial Intelligence, Banff, Canada, 2004: 520–527.
[23]	ROSS S, PINEAU J, PAQUET S, et al. Online planning algorithms for POMDPs[J]. Journal of Artificial Intelligence Research, 2008, 32: 663–704. doi: 10.1613/jair.2567
[24]	SILVER D and VENESS J. Monte-Carlo planning in large POMDPs[C]. The 23rd International Conference on Neural Information Processing Systems, Vancouver, British, 2010: 2164–2172.
[25]	YE Nan, SOMANI A, HSU D, et al. DESPOT: Online POMDP planning with regularization[J]. Journal of Artificial Intelligence Research, 2017, 58: 231–266. doi: 10.1613/jair.5328
[26]	KURNIAWATI H and YADAV V. An online POMDP Solver for Uncertainty Planning in Dynamic Environment[M]. INABA M and CORKE P. Robotics Research: The 16th International Symposium ISRR. Cham, Switzerland: Springer, 2016: 611–629.
[27]	SUNBERG Z and KOCHENDERFER M. Online algorithms for POMDPs with continuous state, action, and observation spaces[C]. The Thirty-Third International Conference on Automated Planning and Scheduling, Delft, The Netherlands, 2018: 259–263.
[28]	KERSHAW D J and EVANS R J. Optimal waveform selection for tracking systems[J]. IEEE Transactions on Information Theory, 1994, 40(5): 1536–1550. doi: 10.1109/18.333866
[29]	SIRA S P, PAPANDREOU-SUPPAPPOLA A, and MORRELL D. Dynamic configuration of time-varying waveforms for agile sensing and tracking in clutter[J]. IEEE Transactions on Signal Processing, 2007, 55(7): 3207–3217. doi: 10.1109/TSP.2007.894418
[30]	LI Xi, CHENG Ting, SU Yang, et al. Joint time-space resource allocation and waveform selection for the collocated MIMO radar in multiple targets tracking[J]. Signal Processing, 2020, 176: 107650. doi: 10.1016/j.sigpro.2020.107650
[31]	KOCH W. Adaptive parameter control for phased-array tracking[C]. SPIE 3809, Signal and Data Processing of Small Targets 1999, Denver, USA, 1999: 444–455.
[32]	KATSILIERIS F, DRIESSEN H, and YAROVOY A. Threat-based sensor management for target tracking[J]. IEEE Transactions on Aerospace and Electronic Systems, 2015, 51(4): 2772–2785. doi: 10.1109/TAES.2015.140052
[33]	HU Yumei, WANG Xuezhi, LAN Hua, et al. An iterative nonlinear filter using variational Bayesian optimization[J]. Sensors, 2018, 18(12): 4222. doi: 10.3390/s18124222
[34]	何子述, 程子扬, 李军, 等. 集中式MIMO雷达研究综述[J]. 雷达学报, 2022, 11(5): 805–829. doi: 10.12000/JR22128 HE Zishu, CHENG Ziyang, LI Jun, et al. A survey of collocated MIMO radar[J]. Journal of Radars, 2022, 11(5): 805–829. doi: 10.12000/JR22128
[35]	LIM M H, TOMLIN C J, and SUNBERG Z N. Sparse tree search optimality guarantees in POMDPs with continuous observation spaces[C]. Twenty-Ninth International Joint Conference on Artificial Intelligence, Yokohama, Japan, 2020: 1–16.
[36]	JI Shihao, PARR R, LI Hui, et al. Point-based policy iteration[C]. The Twenty-Second National Conference on Artificial Intelligence, Vancouver, British, 2007: 1243–1249.
[37]	SCHÖPE M I, DRIESSEN H, and YAROVOY A. Multi-task sensor resource balancing using Lagrangian relaxation and policy rollout[C]. 2020 IEEE 23rd International Conference on Information Fusion (FUSION), Rustenburg, South Africa, 2020: 1–8.