作者中心
专家审稿
责编办公
编辑办公
Sea-detecting Radar Experiment and Target Feature Data Acquisition for Dual Polarization Multistate Scattering Dataset of Marine Targets（in English）
-
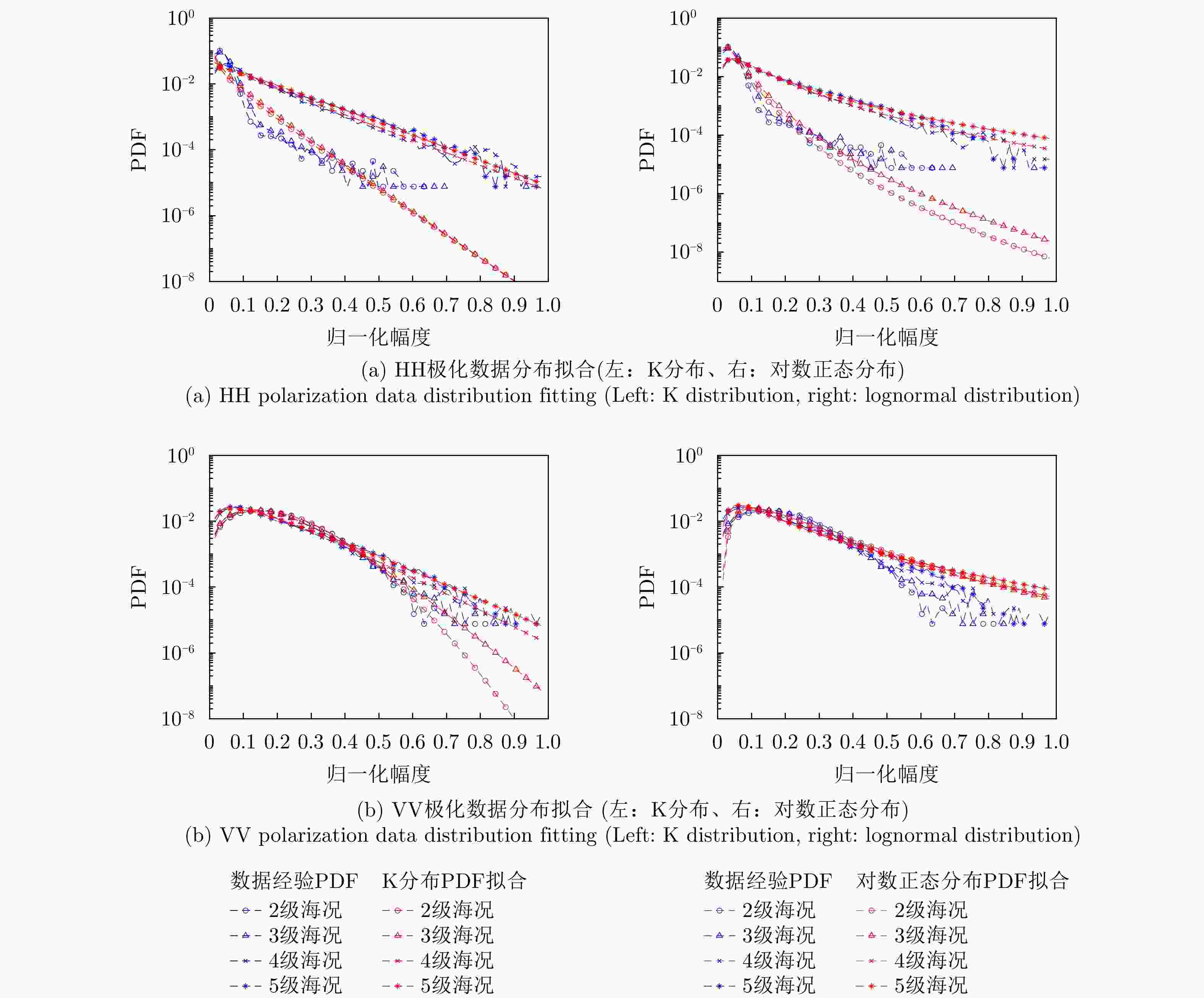
摘要: 海上目标检测识别受制于海上目标及海杂波环境特性，基于实测数据认知海上目标的本质特征有利于推进目标检测识别技术进步。针对海上目标散射特性数据不足的问题，升级“雷达对海探测数据共享计划(SDRDSP)”，扩展雷达目标观测的物理维度、提升雷达及辅助数据采集能力，获取不同极化、海况下的海上目标及环境数据，构建海上目标双极化多海况散射特性数据集，并分析其统计分布特性、时间与空间相关性和多普勒谱特性，为数据使用提供支持。后续将推进海上目标类型与数量的持续积累，为海上目标检测识别性能提升和智能化发展提供数据支持。Abstract: Marine target detection and recognition depend on the characteristics of marine targets and sea clutter. Therefore, understanding the essential features of marine targets based on the measured data is crucial for advancing target detection and recognition technology. To address the issue of insufficient data on the scattering characteristics of marine targets, the Sea-Detecting Radar Data-Sharing Program (SDRDSP) was upgraded to obtain data on marine targets and their environment under different polarizations and sea states. This upgrade expanded the physical dimension of radar target observation and improved radar and auxiliary data acquisition capabilities. Furthermore, a dual-polarized multistate scattering characteristic dataset of marine targets was constructed, and the statistical distribution characteristics, time and space correlation, and Doppler spectrum were analyzed, supporting the data usage. In the future, the types and quantities of maritime targets will continue to accumulate, providing data support for improving marine target detection and recognition performance and intelligence.
-
Key words:
- Radar experiment /
- Sea target detection /
- Sea clutter /
- Target detection and recognition
-
1. Introduction
Synthetic Aperture Radar (SAR), unlike traditional optical observation methods, has all-day and all-weather surveillance capability, making it widely used in fields such as land and resource surveying and natural disaster monitoring[1]. Traditional SAR imaging, on the other hand, can only obtain an azimuth-range two-Dimensional (2-D) image and cannot accurately reflect the three-Dimensional (3-D) scattering characteristics of the target, which limits the SAR image’s further application. TomoSAR (Synthetic Aperture Radar Tomography) is an extension of SAR imaging technology. It extends the synthetic aperture principle in the elevation direction, allowing it to obtain azimuth-range-elevation information from multiple 2-D complex-valued images and thus achieve 3-D imaging[2]. Reigber et al.[3,4] presented the first airborne TomoSAR imaging results in 1999, achieving 3-D imaging of forest regions using spectral estimation methods. Fornaro and Serafino[5] carried out the spaceborne experiment of TomoSAR imaging in 2006, using long-term baseline data, and confirmed the feasibility and effectiveness of applying spectral estimation technology to elevation reconstruction. Reale et al.[6] demonstrated in 2011 that high-resolution data combined with advanced interference-processing techniques could effectively reconstruct the 3-D structure of buildings. Shahzad and Zhu[7] proposed a new building facade reconstruction method in 2013. It obtains the 3-D point cloud of the Bellagio Hotel in Las Vegas, confirming the TomoSAR point cloud’s superiority in building a dynamic city model. Wang et al.[8] proposed an iterative reweighted alternating direction multiplier method for fast TomoSAR imaging in 2017. Wang and Zhu[9] proposed a TomoSAR imaging method based on kernel principal component analysis in 2018, which uses minimal cost to separate multiple scatterers distributed along the elevation direction in the same azimuth-range resolution cell. Qin et al.[10] introduced a machine learning-based building target recognition and extraction algorithm in 2019 to address the problems of low elevation resolution, layover, and low efficiency of building target feature extraction in TomoSAR. It increased the efficiency of feature extraction of observation targets and validated the method’s effectiveness using airborne array 3-D SAR data. D-TomoSAR (Differential Synthetic Aperture Radar Tomography) is a TomoSAR extension. It is possible to achieve azimuth-range-elevation-time four-Dimensional (4-D) imaging by using multi-baseline observation data. It not only solved the problem of high dislocation and ambiguity in TomoSAR, but it also obtained highly accurate target deformation information. Lombardini first proposed the D-TomoSAR concept in 2003[11]. Fornaro et al.[12] demonstrated in 2007 that D-TomoSAR could be regarded as an effective alternative to traditional permanent scatterer monitoring techniques, allowing effective monitoring of large-scale scene deformation. Fornaro et al.[13] proposed and applied a technique for separable relevant time series of interfering scatterers to D-TomoSAR in Rome in 2008. It demonstrated that this technique could be used to monitor the deformation of urban complex scenes. Zhu et al.[14] achieved D-TomoSAR imaging of Las Vegas using TerraSAR-X data in 2009, resulting in an urban 4-D map. Fornaro et al.[15] used ERS data for D-TomoSAR imaging of Rome’s Grotta Perfetta area in 2010, demonstrating that the D-TomoSAR method can effectively distinguish different scatterers in the same resolution cell, overcome the limitations of differential interference, and thus improve the monitoring capacity of urban infrastructure deformation. Zhu and Bamler[16] proposed a “time-distorted” method and implemented D-TomoSAR imaging of urban areas based on TerraSAR-X data in 2011, effectively obtaining the linear and seasonal deformation velocity of urban buildings. Siddique et al.[17] used 50 TerraSAR-X images in 2015 to combine the D-TomoSAR method and permanent scatterer interference technology to obtain spatial-temporal inversion results of high-rise buildings. Wang and Liu[18] proposed a generalized D-TomoSAR imaging system model and a quasi-maximum likelihood-based algorithm that inversed multiple deformation velocities, including linear and seasonal deformation velocities, in 2020. At the moment, TomoSAR and D-TomoSAR imaging technologies have shown great application potential in 3-D reconstruction and long-term deformation monitoring of urban buildings and infrastructures.
Compressive Sensing (CS) is an important sparse signal processing technology that can achieve high-quality recovery for sparse signals from fewer samples[19-21]. The observed scene’s elevation distribution must be sparse for CS-Tomo-SAR to work. Because urban areas are mostly made up of man-made structures, their elevation distributions satisfy the sparsity condition. As a result, CS has a promising application in 3-D and 4-D urban imaging. Initially, the elevation resolution of TomoSAR is far lower than the azimuth or range direction due to the orbit limitation of modern meter-resolution spaceborne SAR systems. As a result, there is an urgent need for a super-resolution algorithm to solve this problem. Zhu and Bamler[22] introduced a TomoSAR imaging method based on CS theory in 2010. It is discovered that, when compared to traditional spectral estimation methods, the proposed algorithm can achieve super-resolving elevation distribution reconstruction. In 2012, Zhu and Bamler[23] applied the proposed SL1MMER algorithm to Terra-SAR-X spaceborne data processing and obtained a high-resolution 3-D image of the Bellagio Hotel in Las Vegas, validating the SL1MMER algorithm’s super-resolution capability. Weiss et al.[24] proposed an adaptive CS algorithm for Tomo-SAR in 2015, which accurately identifies two scatterer positions in the same resolution cell. In 2017, Li et al.[25] investigated the SPICE-based TomoSAR imaging method and used 8 Terra-SAR-X strip map images to create a high-precision 3-D reconstruction of a building in Genhe, Inner Mongolia. Zhu and Bamler[26] applied the CS technique to D-TomoSAR imaging and demonstrated its superiority over conventional spectral estimation methods on multi-scatterer separation in elevation direction in 2010. It is also mentioned that CS can automatically determine the number of scatterers, making it ideal for 3-D and 4-D imaging of spaceborne SAR systems. In 2010, Zhu and Bamler[27] used the SL1MMER algorithm to obtain D-TomoSAR imaging results of the Las Vegas Convention Center, validating the advantages and capabilities of CS in 4-D imaging. Leng et al.[28] (2014) demonstrated the elevation reconstruction and deformation monitoring results of Barcelona by applying the least absolute shrinkage and selection operator CS algorithm to building regions.
The Gaofen-3 (GF-3) satellite is China’s first C-band multi-polarization 1-meter resolution SAR satellite. On August 10, 2016, it was launched by a CZ-4C carrier rocket[29]. The “China High-resolution Earth Observation Project” includes only one civil microwave remote sensing imaging satellite, the GF-3. It has high-resolution, wider swath, multi-imaging mode, and long-period operation capabilities and can perform all-day and all-weather global ocean and land monitoring[30]. The GF-3 is now successfully used in high-precision surveying and mapping, natural disaster monitoring, and other fields[31,32]. However, because high-dimensional imaging capability was not considered during system design, the collected GF-3 SAR images have Spatio-Temporal de-coherence, which poses some challenges for their future applications to InSAR, D-InSAR, TomoSAR, and D-TomoSAR. Yu et al.[33] used the GF-3 data data to conduct interferometric experiments in the areas surrounding Dengfeng city in Henan Province, China, in 2019. They verified the interference capability of the GF-3 and demonstrated that it could be used to extract surface deformation information by comparing experimental results with the Sentinel-1 satellite. Huang et al.[34] successfully extracted and obtained the digital elevation model of the surveillance region using interferometric experiments based on the GF-3 data in July 2021.
In this paper, we used seven complex-valued SAR images of the GF-3 to perform TomoSAR and D-TomoSAR imaging experiments with CS technology, resulting in high-resolution 3-D and 4-D images of the buildings surrounding Yanqi Lake in Beijing, China. Based on a Chinese satellite, we achieved high-quality 3-D reconstruction and high-precision deformation monitoring, which provides technical support for subsequent interference series applications and multi-dimensional high-resolution imaging of the GF-3.
The remainder of this paper is structured as follows. Section 2 provides a brief overview of the TomoSAR and D-TomoSAR imaging models, as well as the CS solution for the first two models. The GF-3 dataset, which is used in this paper, is introduced in Section 3. Section 4 performs TomoSAR and D-TomoSAR imaging experiments on simulated data to demonstrate the effectiveness of CS in high-resolution 3-D imaging and high-precision deformation monitoring. In Section 5, we performed TomoSAR and D-TomoSAR imaging studies of the buildings around Yanqi Lake in Beijing, using seven complex-valued SAR images of the GF-3, and obtained 3-D and 4-D images of representative buildings and large-scale areas. Section 6 contains the conclusions.
2. Imaging Model
2.1 TomoSAR imaging model
TomoSAR performs aperture synthesis along the elevation direction using multiple registered 2-D complex-valued SAR images of the same area, obtaining the target’s 3-D scattering information[3,4,35,36]. Fig. 1 depicts the imaging geometry of TomoSAR. Let N denote the number of data acquisition baselines and
${b_n}\left( {n = 1,2,\cdots,N} \right)$ denote the elevation aperture. The focused complex-valued measurement at the$ {n_{{\text{th}}}} $ SAR image can be expressed for a given azimuth-range pixel as
Figure 1. TomoSAR imaging geometrygn=∫Δsγ(s)exp(−j2πξns)ds (1) where
$ {\xi _n} = - 2{b_n}/\left( {\lambda r} \right) $ denotes the elevation frequency,$ \lambda $ denotes the wavelength, r denotes the slant range,$ \gamma \left( s \right) $ denotes the complex reflection function along the elevation direction s, and$ \Delta s $ denotes the elevation span. After discretizing the complex reflectivity function$ \gamma \left( s \right) $ along the elevation direction s, the imaging model in Eq. (1) can be approximated asgN×1=RN×L⋅γL×1 (2) where L denotes the number of points along the elevation direction,
${\boldsymbol{g}} = {\left[ {{g_1},{g_2},\cdots,{g_N}} \right]^{\rm{T}}}$ denotes the measurement vector,${\boldsymbol{R}} = \exp \left( { - {\rm{j}}2\pi {\xi _n}{s_l}} \right)$ denotes the observation matrix constructed based on the TomoSAR imaging geometry, and${\boldsymbol{\gamma}} = \left[ \gamma \left( {{s_1}} \right), \gamma \left( {{s_2}} \right),\cdots,\gamma \left( {{s_L}} \right) \right]^{\rm{T}}$ denotes the discrete complex reflection function along$ {s_l}\left( {l = 1,2,\cdots,L} \right) $ . From Eq. (2), the TomoSAR imaging model can be considered an irregular sampling-based discrete Fourier transform of$ \gamma \left( s \right) $ . A SAR measurement can thus be thought of as a spectral parameter of the target complex reflection function along the elevation direction. For the non-parametric spectral analysis problem, the theoretical elevation resolution$ {\rho _s} $ is determined by the elevation aperture$ \Delta b $ . In the case of dense sampling in the elevation,$ {\rho _s} $ can be calculated byρs=λr2Δb (3) 2.2 D-TomoSAR imaging model
When compared to TomoSAR, D-TomoSAR adds another time dimension. It combines two apertures into elevation and deformation velocity directions to achieve joint resolution, yielding a 4-D image of the observed target[11]. For N complex-valued images, when the elevation aperture position is
$ {b_n} $ and time baseline is$ {t_n} $ , the focused measurement of the$ {n_{{\text{th}}}} $ acquisition can be expressed asgn=∫Δsγ(s)exp(−j2πξns)exp(−j2πηnV(s))ds (4) where
${\eta _n} = - 2\pi {t_n}/\lambda$ denotes the temporal frequency and$ V\left( s \right) $ denotes the deformation velocity. The model in Eq. (4) also can be written asgn=∫Δs∫Δvγ(s)δ(v−V(s))⋅exp(−j2π(ξns+ηnv))dvds (5) where
$ \Delta v $ denotes the deformation velocity span of the observed target and$ \delta \left( \cdot \right) $ denotes the spectral distribution induced by the deformation. Let$ {a_\gamma }\left( {s,v} \right) = \gamma \left( s \right)\delta \left( {v - V\left( s \right)} \right) $ , then we can rewrite Eq. (5) as:gn=∫Δs∫Δva(s,v)exp(−j2π(ξns+ηnv))dvds (6) The above model can be considered a 2-D Fourier transform of
$ a\left( {s,v} \right) $ on the elevation-deformation plane. Thus, its projection in the vertical direction is$ \gamma \left( s \right) $ [37]. After discretizing s and v in Eq. (6), the D-TomoSAR imaging model can be expressed asgN×1=RN×LQ⋅γLQ×1 (7) where
${\boldsymbol{g}} = {\left[ {{g_1},{g_2},\cdots,{g_N}} \right]^{\rm{T}}}$ denotes the measurement vector,${\boldsymbol{R}} = \exp \left( { - {\rm{j}}2\pi \left( {{\xi _n}{s_l} + {\eta _n}{v_q}} \right)} \right)$ is the D-TomoSAR observation matrix,${s_l}\left( {n = 1,2,\cdots,L} \right)$ denotes the discrete elevation distribution,${v_q}\left( {q = 1,2,\cdots,Q} \right)$ denotes the discrete distribution in the deformation direction, and$ \gamma $ consists of a discretized$ a\left( {s,v} \right) $ . Then the deformation resolution$ {\rho _v} $ can be calculated with the time aperture size of$ \Delta {\text{t}} $ byρv=λ2Δt (8) 2.3 CS reconstruction
The observed target in the city region is primarily man-made architecture, with a sparse elevation distribution, i.e., finite scatterers in each azimuth-range resolution cell. Thus, for the models in Eqs. (2) and (7), when the measurement matrix R satisfies the Restricted Isometry Property (RIP) condition, we can achieve CS-based TomoSAR and D-TomoSAR imaging by solving the following equation:
ˆγ=argminγ{‖g−Rγ‖22+β‖γ‖1} (9) where
$ \beta $ denotes the regularization parameters, determined by the noise level and the number of samples. The CS algorithm quickly recovers high-quality signals from acquired samples[38,39]. This paper employs the CS algorithm for TomoSAR and D-TomoSAR imaging due to its benefits.3. Introduction to the GF-3 Dataset
The GF-3 dataset used in this paper is made up of seven complex-valued images, the parameters of which are listed in Tab. 1. The elevation aperture size of the seven images in this dataset is 1417 m. The time baseline spans 464 d, from June 2018 to September 2019. Fig. 2 depicts the spatial-temporal baseline distribution and the specific parameters are listed in Tab. 2. The SAR image acquired on March 1, 2019, serves as the master image in this paper, with the remaining six serving as slave images. By the way, the slave images’ spatial-temporal baseline position is calculated relative to the master image. The simulations in Section 4 of this paper will be run using the parameters listed in Tab. 1. Section 5 will carry out experiments using the GF-3 datasets.
Table 1. Parameters of the GF-3 datasetParameter Value Parameter Value Spatial baseline span 1417.4 m Number of scenes 7 Temporal baseline span 464 d Azimuth resolution 0.3626 m Slant range 1052747 m Range resolution 0.765692 m Wavelength 0.056 m Elevation resolution 20.6174 m Incident angle 47.2330015° Information resolution 21.8 mm/year | Show Table
DownLoad:
CSV
Figure 2. Spatio-temporal baseline distribution of the GF-3 datasetTable 2. Spatio-temporal baseline parameters of the GF-3datasetNumber Time of acquisition Spatial baseline (m) Temporal baseline (d) 1 2018.06.13 –459.108 –261 2 2019.01.31 –628.551 –29 3 2019.03.01 0 0 4 2019.03.30 –724.517 29 5 2019.07.24 692.863 145 6 2019.08.22 –38.211 174 7 2019.09.20 –510.491 203 | Show TableDownLoad:
CSV
4. Simulations
We set two scatterers in the elevation direction using the experimental parameters listed in Tab. 1, generated seven scenes of simulated data, and added noise with SNR = 20 dB. TomoSAR and D-TomoSAR imaging use conventional spectral estimation methods and the CS algorithm, respectively[40]. This section will present the simulation results of three spectral estimation algorithms, namely BeamForming (BF)[41], Adaptive beamforming (Capon)[42], and MUltiple SIgnal Classification (MUSIC)[43,44], which will be compared to the results of CS to demonstrate the advantages of the CS algorithm in TomoSAR and D-TomoSAR imaging. The TomoSAR imaging results of two scattering points in the elevation directions are shown in Fig. 3. The elevation position distribution is represented by the x-coordinate, and the scattering point’s amplitude value is represented by the y-coordinate. The distances between the two scatterers were set to 11 m and 50 m, respectively. When the distance is less than 11 m, the three spectral estimation methods are unable to accurately separate the two scatterers, resulting in a failed reconstruction. At the same time, the CS algorithm is still capable of effectively distinguishing two scatterers to achieve elevation super-resolution imaging. When the distance is 50 m, the reconstruction result of the BF algorithm has significant and irregular sidelobes. Based on the results, the reconstruction images of the Capon and MUSIC algorithms have lower sidelobes than BF, which improves the quality of the elevation reconstruction. When compared to the other three spectral estimation algorithms, CS can effectively suppress sidelobes and noise while also improving elevation resolution. The TomoSAR imaging results for a pixel with three scatterers in the elevation direction are shown in Fig. 4. The distance between three scatterers is 20 m, which is comparable to the imaging results obtained with two scatterers. As can be seen, the CS algorithm works well for multiple scatterer separation.
Figure 3. TomoSAR reconstructed reflectivity profiles of two scattering points along the elevation direction (left image: the distance between two scatterers is 11 m; right image: the distance between two scatters is 50 m)
Figure 4. TomoSAR reconstructed reflectivity profiles of three scattering points along the elevation direction (the distance between three scatterers is 20 m)Following that, several D-TomoSAR simulations were run. It is also assumed that the azimuth-range resolution cell contains two scatterers, located at –10 m and 10 m, respectively, and that the distance between them is less than the elevation resolution. The deformation velocities are set to 4 mm/year and –7 mm/year. We obtained the corresponding simulated data and added an additive noise with SNR = 20 dB based on the parameters in Tab. 1. Fig. 5 depicts the D-TomoSAR simulation results of various algorithms. The x-coordinate represents the target elevation position, and the y-coordinate represents the scatterer’s linear deformation variable. According to Fig. 5, three spectral estimation methods could not distinguish the two scatterers in the elevation direction due to algorithm limitations, particularly the BF algorithm, which is difficult to break through the theoretical resolution. The CS algorithm can accurately distinguish two scatterers separated by 20 m, which is consistent with the above results and further validates CS’s super-resolution ability in 3-D imaging. According to Tab. 1, the theoretical resolution of deformation is about 21.8 mm/year. While only the CS algorithm is capable of accurately estimating deformation rates of 4 mm/year and –7 mm/year, it confirms its superiority over spectral estimation techniques in deformation monitoring.
Figure 5. D-TomoSAR simulation results (elevation position of two scatterers are –10 m and 10 m; deformation velocity of two scatterers are 4 mm/year and –7 mm/year, respectively)5. Results of the GF-3 Dataset
5.1 Representative building inversion
We present the TomoSAR and D-TomoSAR reconstruction results based on the GF-3 dataset in this section. The Haihuayundu Eco-agriculture Ltd and the Yanqi Lake International Convention and Exhibition Center in Beijing were chosen as two representative buildings in the observation scene for TomoSAR and D-TomoSAR imaging. The optical image of the Haihuayundu Eco-agriculture Ltd is shown in Fig. 6(a), and the area framed by the red dashed line is the target of interest. The 2-D SAR image of the Haihuayundu Eco-agriculture Ltd is shown in Fig. 6(b). The height information of five buildings in the area is obtained by TomoSAR reconstruction, as shown in Fig. 7(a). The heights of the five individual buildings are all 35 m, which is consistent with the actual height, as shown in Fig. 7(a). It demonstrated the efficacy of the CS-TomoSAR imaging technology and demonstrated that it could be used for high-precision 3-D imaging of the GF-3 dataset. The reconstruction result of D-TomoSAR based on the CS algorithm is shown in Fig.7(b). The five buildings have different deformations, which may be related to the seasonal thermal expansion and contraction of building materials. It should be monitored daily to avoid the risks associated with it. A 3-D point cloud of the Haihuayundu Eco-agriculture Ltd, which more accurately reflects the 3-D scattering structure of the buildings, is shown in Fig. 8 to provide a visual representation of the interested area.
Figure 6. The Haihuayundu Eco-agriculture Ltd
Figure 7. Elevation and deformation velocity maps of the Haihuayundu Eco-agriculture Ltd
Figure 8. 3-D point cloud of the Haihuayundu Eco-agriculture LtdThe optical and SAR images of the Yanqi Lake International Convention and Exhibition Center, with an actual height of about 30 m, are shown in Fig. 9. The CS-TomoSAR imaging result is shown in Fig. 10(a), and its 3-D point cloud image is shown in Fig. 11. The reconstructed image clearly reflects the 3-D structure of the building, and the height of the reconstructed building corresponds to the actual information. It also demonstrates that we can perform high-precision 3-D reconstruction of complex buildings using the GF-3 SAR data. The D-TomoSAR result of the Yanqi Lake International Convention and Exhibition Center based on CS technology is shown in Fig. 10(b). According to Fig. 10(b), the building’s deformation velocity ranges between 10 mm/year and –10 mm/year. The linear deformation rate of the left and right halves of the building is opposite, indicating that the ground beneath the building may be changing between uplift and collapse, which should be monitored more closely.
Figure 9. Beijing Yanqi Lake International Convention and Exhibition Center
Figure 10. Elevation and deformation velocity maps of Beijing Yanqi Lake International Convention and Exhibition Center
Figure 11. 3-D point cloud of Beijing Yanqi Lake International Convention and Exhibition Center5.2 3-D and 4-D imaging of large-scale scene
The TomoSAR and D-TomoSAR imaging results of a large-scale scene from the GF-3 dataset are shown in this section. The optical and SAR images of Dingxiumeiquan Town are shown in Fig. 12. The TomoSAR imaging results based on CS are shown in Fig. 13(a). The heights of the buildings in the area are all between 15 and 20 m. Because the actual buildings have 4 to 6 floors, the results are consistent. The D-TomoSAR imaging results are shown in Fig. 13(b). It demonstrates that building deformation in the lower left and upper right areas of Dingxiumeiquan Town is approximately –10 mm/year, most likely due to construction in these areas causing ground subsidence. The deformation rate in the center of Dingxiumeiquan Town is approximately 5 mm/year and is relatively stable. These experiments demonstrate that by utilizing the GF-3 dataset, we were able to achieve the high-quality 3-D reconstruction of large-scale scenes as well as high-precision deformation monitoring, thereby confirming the GF-3 satellite’s application potential in urban sensing and monitoring.
Figure 12. The Dingxiumeiquan Town
Figure 13. Elevation and deformation velocity maps of the Dingxiumeiquan Town6. Conclusions
In this paper, we conduct TomoSAR and D-TomoSAR imaging research using a GF-3 SAR complex-valued image dataset, obtain 3-D and 4-D images of two representative buildings in Beijing’s Yanqi Lake area, and show 3-D and 4-D SAR images of a large-scale area. These studies validate the potential of the Chinese GF-3 satellite for TomoSAR and D-TomoSAR imaging applications, as well as provide technical support for the GF-3’s subsequent expansion into interference series applications.
In the future, our team will continue relevant research and collect the GF-3 data from multiple areas and scenes. We will also investigate new high-resolution TomoSAR and D-TomoSAR imaging algorithms to realize large-scale 3-D and 4-D reconstruction of urban complex scenes, as well as further investigate GF-3’s enormous potential in interferometric series applications.
-
图 3 HD-LD-CJ-22型雷达数据采集设备与显控软件
Figure 3. HD-LD-CJ-22 radar data acquisition and control software
图 6 试验海域气象水文数据(NC数据)
Figure 6. Meteorological and hydrological data of the test sea area (NC data)
图 9 海杂波单元幅度分布拟合结果
Figure 9. Amplitude distribution fitting results of sea clutter bins
S1 雷达对海探测数据2022年第1期——海上目标散射特性数据集
S1. Sea-detecting radar data 2022 phase 1－－Sea target scattering feature dataset
表 1 已共享的雷达对海探测数据
Table 1. Shared sea-detecting radar data
年期 雷达波段 极化方式 数据简介 2019年第1期 X HH 3组数据，主要为扫描和凝视观测模式下的海杂波数据，目标为海面非合作目标。 2020年第1期 X HH 2组数据，主要为凝视观测模式下的海杂波数据、海杂波+目标数据，目标为锚泊船只和航道浮标。 2020年第2期 X HH 2组数据，为海面机动目标跟踪试验数据，目标为海面合作目标(小型快艇)。 2020年第3期 X HH 1组数据，为雷达目标RCS定标试验数据，目标为RCS为0.25 m2不锈钢球，由渔船拖动或漂浮。 2021年第1期 X HH 5组数据，为云雨气象条件下的雷达不同转速扫描试验数据，海面无合作目标。 
下载: 导出CSV
表 2 X波段试验雷达参数
Table 2. Parameters of X-band experimental radars
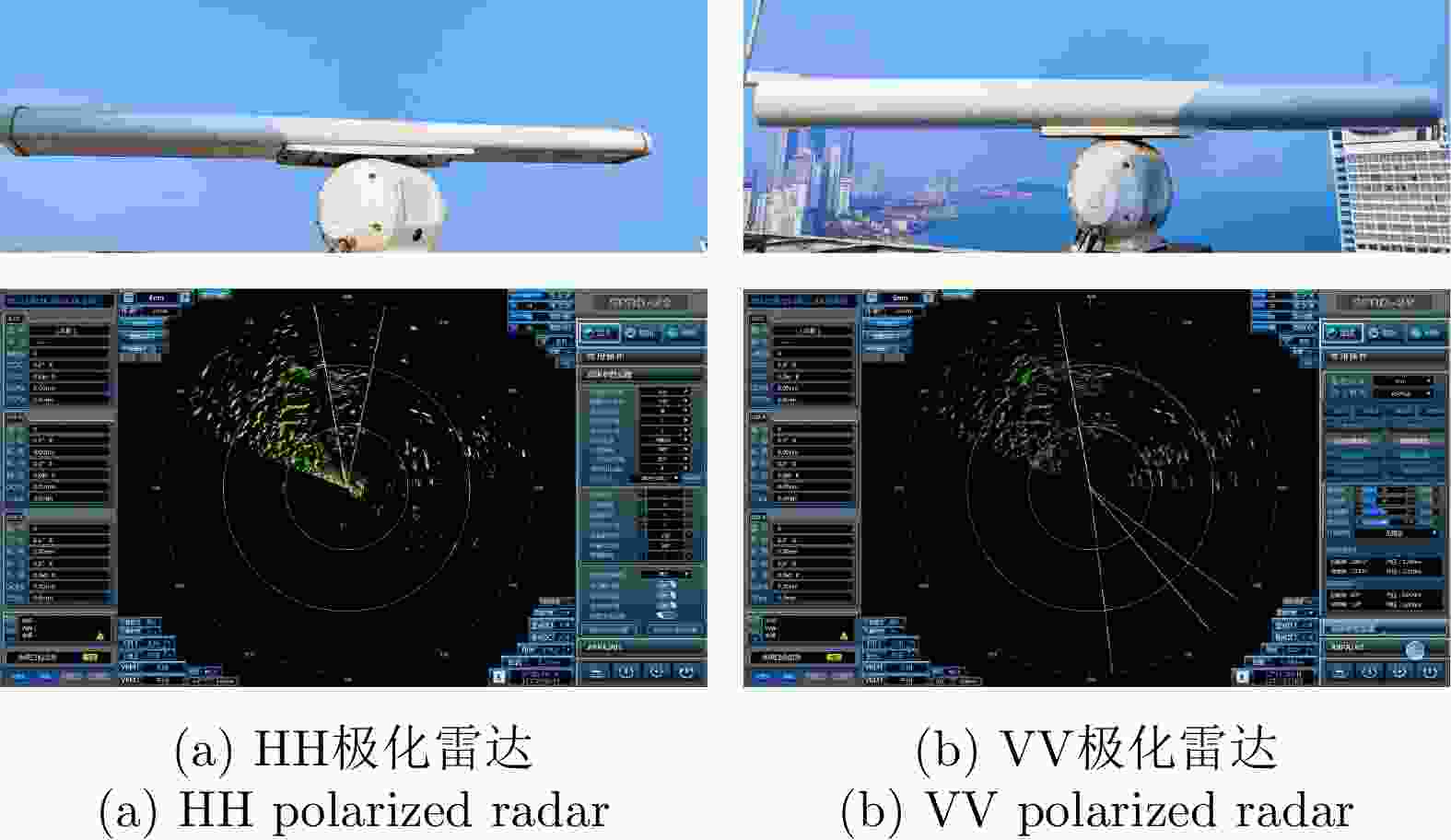
雷达技术指标 HH极化 VV极化 工作频段 X X 工作频率范围 9.3～9.5 GHz 9.3～9.5 GHz 量程 1/16～96 n mile 1/16～96 n mile 扫描带宽 25 MHz (T2, T3) 25 MHz (T2, T3) 距离分辨率 6 m 6 m 脉冲重复频率(kHz) 1.6, 2.0, 3.0, 5.0, 10.0 1.6, 2.0, 3.0, 5.0, 10.0 发射波形 T1：单频
T2：LFM
T3：LFMT1：单频
T2：LFM
T3：LFM脉冲宽度 T1：0.15 μs
T2：8 μs
T3：25 μsT1：0.15 μs
T2：8 μs
T3：25 μs发射峰值功率 100 W 100 W 天线转速(r/min) 2, 6, 12, 24, 48 2, 6, 12, 24, 48 天线长度 2.0 m 2.5 m 天线工作模式 圆扫、扇扫、
固定指向圆扫、扇扫、
固定指向天线极化方式 HH VV 天线水平波束宽度 1.2° 1.1° 天线垂直波束宽度 22° 23°
下载: 导出CSV
表 3 海上目标散射特性数据集概况表
Table 3. Summary table of sea target scattering characteristics dataset
序号 海况
等级数据
组数雷达天线
工作模式工作
量程发射脉冲模式 目标
种类气象水文数据 擦地角
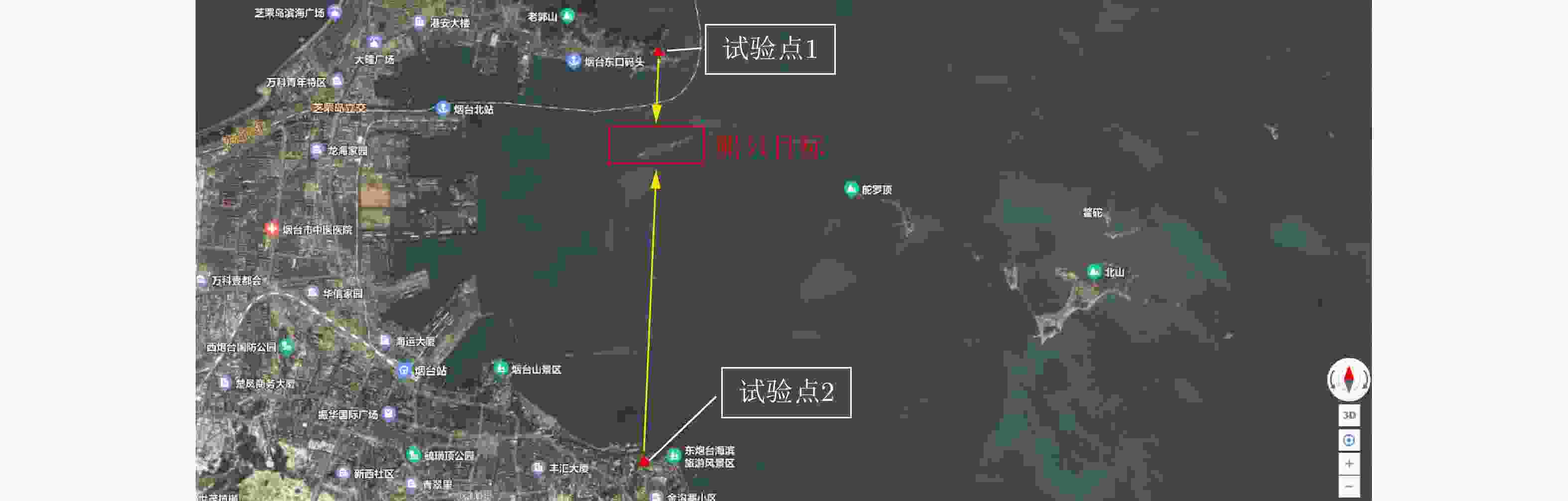
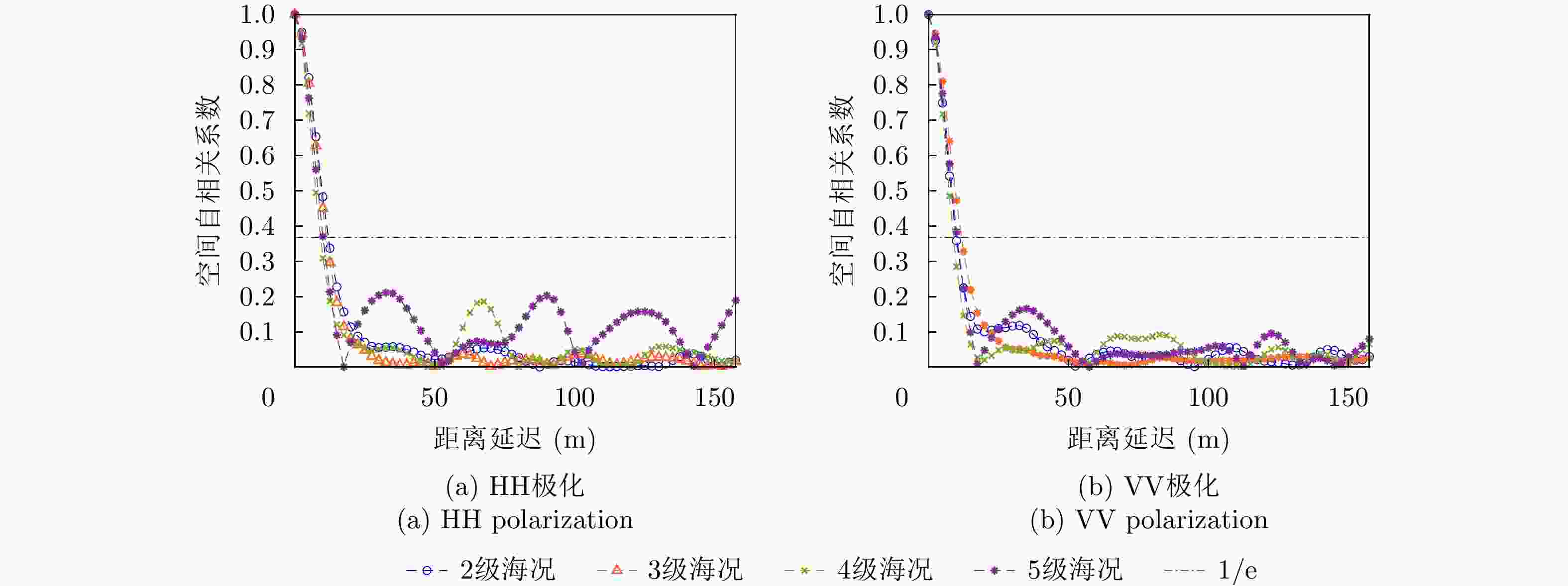
(°)1 2级 10组 凝视 6 n mile T1+T2 航道浮标 有 0.68～1.09 2 3级 54组 凝视 6 n mile T1+T2 航道浮标 有 0.68～1.09 3 4级 48组 凝视 6 n mile T1+T2 航道浮标 有 0.68～1.09 4 5级 30组 凝视 6 n mile T1+T2 航道浮标 有 0.68～1.09 注：① 每天气象水文数据形成一个nc格式文件，提供风速/风向/浪高/浪向/浪周期信息；
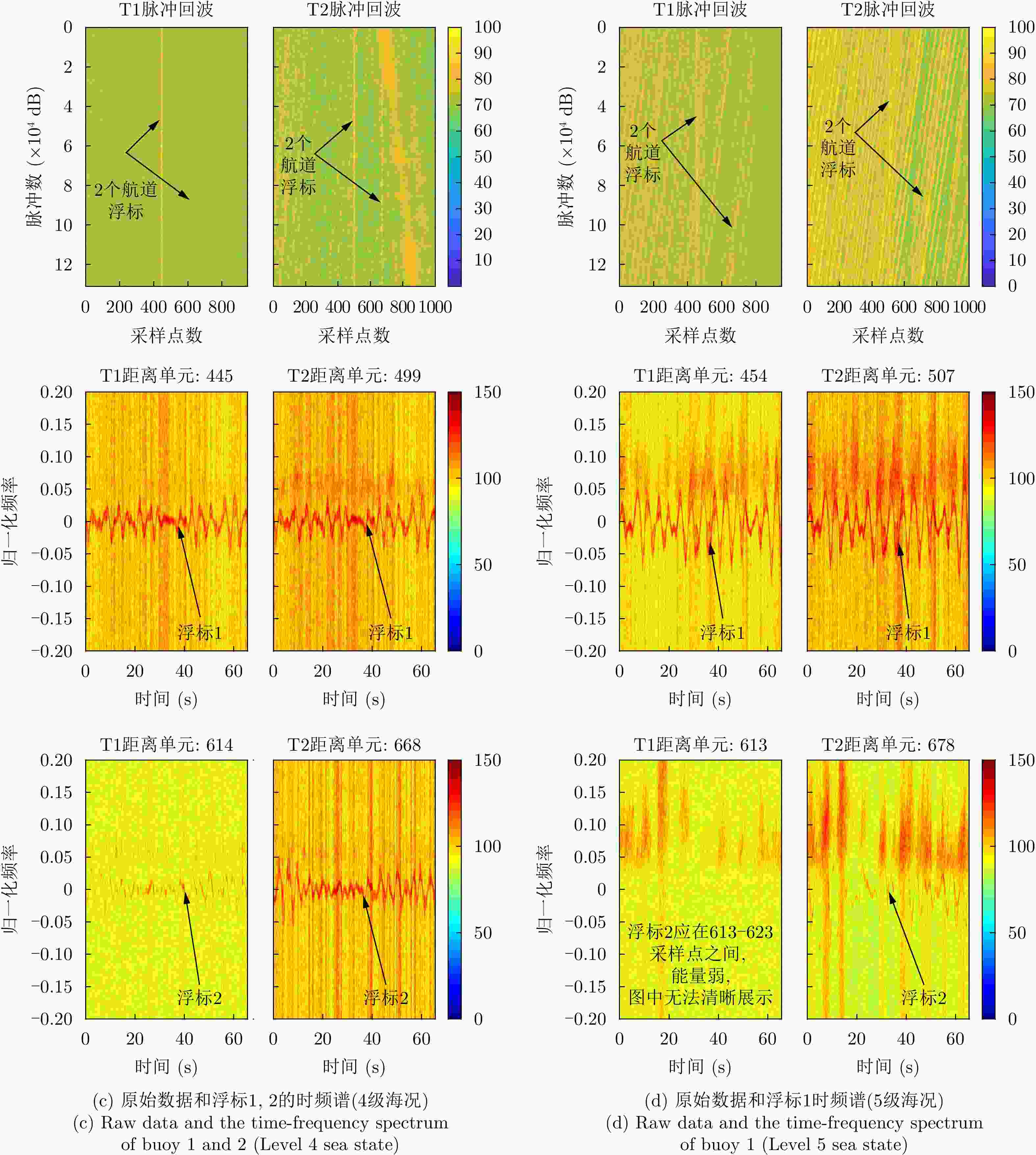
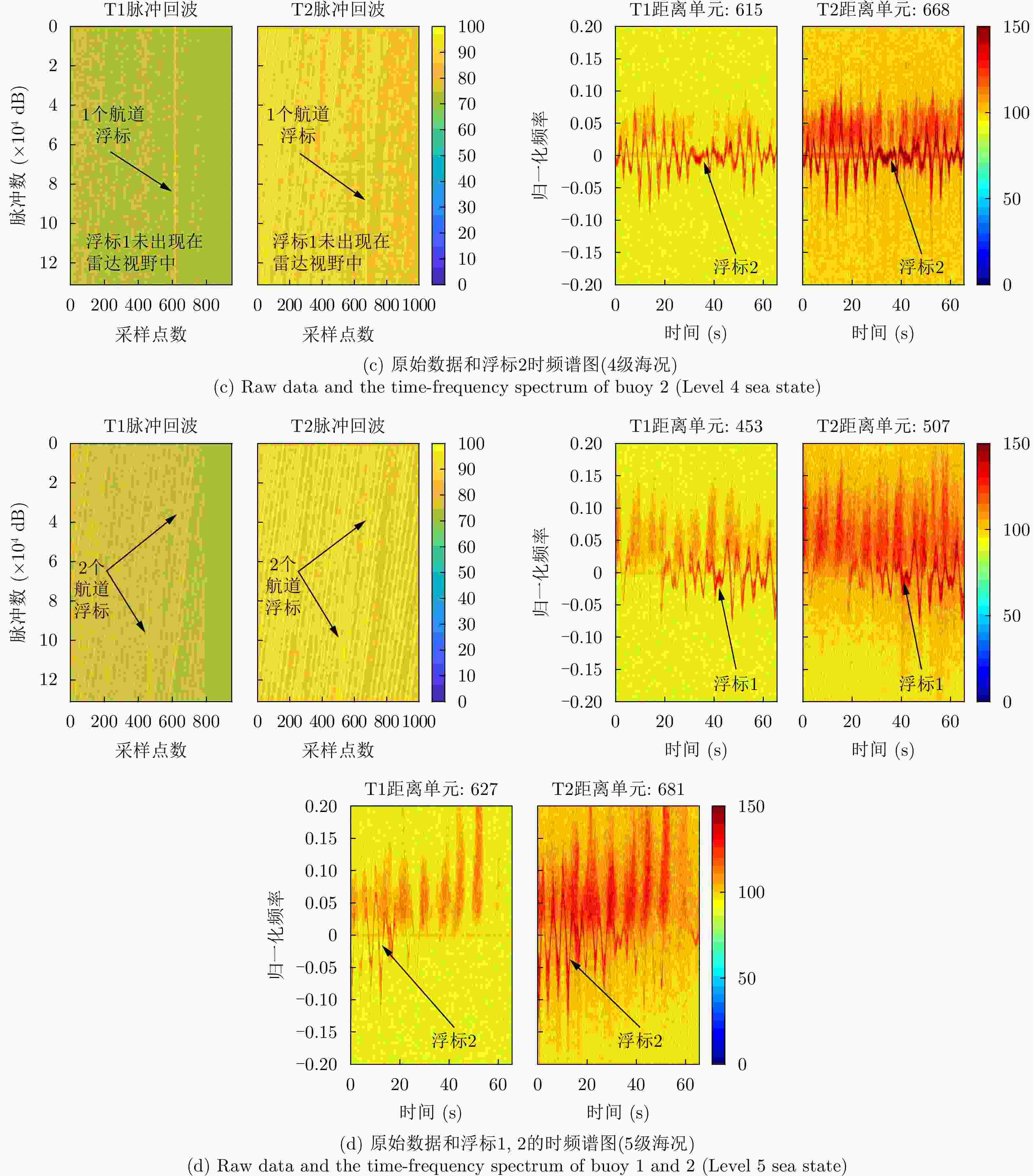
② 凝视模式下每组数据包含的脉冲数均为217个；
③ 发射脉冲模式T1+T2，对应图2中的模式2；
④ 雷达垂直波束保持不变，擦地角范围是通过雷达架高和数据对应的径向距离范围折算得到的。
下载: 导出CSV
表 4 2－5级海况HH与VV极化雷达示例数据
Table 4. Sample data of HH and VV polarized radars in level 2－5 sea states
数据名 包含
脉冲数PRF
(kHz)T1
采样点数T2
采样点数T1, T2采样起始
距离(km)采样间隔(m) 目标 浪高
(m)浪向 海况
等级20221115050027 _stare_HH217 2 950 1000 4.2525 2.5 浮标1, 2 0.4 西 2级 20221115050036 _stare_VV217 2 950 1000 4.2525 2.5 浮标1, 2 0.4 西 2级 20221114190046 _stare_HH217 2 950 1000 4.2525 2.5 浮标1, 2 0.7 西西北 3级 20221114190055 _stare_VV217 2 950 1000 4.2525 2.5 浮标1, 2 0.7 西西北 3级 20221113210051 _stare_HH217 2 950 1000 4.2525 2.5 浮标1, 2 1.3 北东北 4级 20221113210023 _stare_VV217 2 950 1000 4.2525 2.5 浮标2 1.3 北东北 4级 20221113040027 _stare_HH217 2 950 1000 4.2525 2.5 浮标1, 2 2.6 北 5级 20221113040009 _stare_VV217 2 950 1000 4.2525 2.5 浮标1, 2 2.6 北 5级
下载: 导出CSV
表 1 Shared sea-detecting radar data
Year, issue Radar band Polarization mode Data description 2019, Issue 1 X HH 3 datasets: Primarily sea clutter data collected in scanning and staring observation modes with noncooperative surface targets. 2020, Issue 1 X HH 2 datasets: Sea clutter data and combined sea clutter + target data collected in staring observation mode with anchored vessels and channel buoys as targets. 2020, Issue 2 X HH 2 datasets: Test data for tracking maneuvering surface targets collected using cooperative targets (small speedboats). 2020, Issue 3 X HH 1 dataset: Radar target RCS calibration test data collected using a 0.25 m 2 stainless steel sphere as the target, either towed by a fishing boat or left floating. 2021, Issue 1 X HH 5 datasets: Radar scanning test data under cloudy and rainy meteorological conditions without cooperative surface targets.
下载: 导出CSV
表 2 Parameters of X-band experimental radars
Radar specifications HH polarization VV polarization Operating band X X Operating frequency range (GHz) 9.3–9.5 9.3–9.5 Range (n miles) 1/16–96 1/16–96 Scanning bandwidth (MHz) 25 (T2, T3) 25 (T2, T3) Range resolution (m) 6 6 Pulse repetition frequency (kHz) 1.6, 2.0, 3.0, 5.0, 10.0 1.6, 2.0, 3.0, 5.0, 10.0 Transmit waveform T1：Single frequency
T2：LFM
T3：LFMT1：Single frequency
T2：LFM
T3：LFMPulse width (μs) T1：0.15
T2：8
T3：25T1：0.15
T2：8
T3：25Peak transmit power (W) 100 100 Antenna rotation speed (rpm) 2, 6, 12, 24, 48 2, 6, 12, 24, 48 Antenna length (m) 2.0 2.5 Antenna operating modes Circular, Sector, Fixed Direction Circular, Sector, Fixed Direction Antenna polarization HH VV Antenna horizontal beamwidth (°) 1.2 1.1 Antenna vertical beamwidth (°) 22 23
下载: 导出CSV
表 3 Summary of the datasets of sea target scattering characteristics
No. Marine state level Number of datasets Radar antenna mode Operating range Transmit pulse mode Target type Meteorological and hydrological data Clutter grazing angle (°) 1 Level 2 10 Staring 6 n miles T1+T2 Channel buoy Yes 0.68～1.09 2 Level 3 54 Staring 6 n miles T1+T2 Channel buoy Yes 0.68～1.09 3 Level 4 48 Staring 6 n miles T1+T2 Channel buoy Yes 0.68～1.09 4 Level 5 30 Staring 6 n miles T1+T2 Channel buoy Yes 0.68～1.09 Notes:① Meteorological and hydrological data for each day are stored in a .nc format file, providing information on wind speed, wind direction, wave height, wave direction, and wave period.
② Each dataset in staring mode contains 2 17 pulses.
③ The transmit pulse mode T1 + T2 corresponds to mode 2 in Fig. 2.
④ The radar’s vertical beamwidth remains constant, and the grazing angle range is calculated based on the radar’s installation height and the corresponding radial distance range of the data.
下载: 导出CSV
表 4 Sample data of HH and VV polarized radars in levels 2–5 sea state
Data name Pulse
countPRF
(kHz)T1
sampling
pointsT2
sampling
pointsT1, T2
sampling start
distance (km)Sampling
interval (m)Target Wave
height (m)Wave
directionMarine
state level20221115050027
_stare_HH2 17 2 950 1000 4.2525 2.5 Buoys 1, 2 0.4 West Level 2 20221115050036
_stare_VV2 17 2 950 1000 4.2525 2.5 Buoys 1, 2 0.4 West Level 2 20221114190046
_stare_HH2 17 2 950 1000 4.2525 2.5 Buoys 1, 2 0.7 West-northwest Level 3 20221114190055
_stare_VV2 17 2 950 1000 4.2525 2.5 Buoys 1, 2 0.7 West-northwest Level 3 20221113210051
_stare_HH2 17 2 950 1000 4.2525 2.5 Buoys 1, 2 1.3 North-northeast Level 4 20221113210023
_stare_VV2 17 2 950 1000 4.2525 2.5 Buoy 2 1.3 North-northeast Level 4 20221113040027
_stare_HH2 17 2 950 1000 4.2525 2.5 Buoys 1, 2 2.6 North Level 5 20221113040009
_stare_VV2 17 2 950 1000 4.2525 2.5 Buoys 1, 2 2.6 North Level 5
下载: 导出CSV
-
[1] 关键. 雷达海上目标特性综述[J]. 雷达学报, 2020, 9(4): 674–683. doi: 10.12000/JR20114.GUAN Jian. Summary of marine radar target characteristics[J]. Journal of Radars, 2020, 9(4): 674–683. doi: 10.12000/JR20114. [2] 丁昊, 刘宁波, 董云龙, 等. 雷达海杂波测量试验回顾与展望[J]. 雷达学报, 2019, 8(3): 281–302. doi: 10.12000/JR19006.DING Hao, LIU Ningbo, DONG Yunlong, et al. Overview and prospects of radar sea clutter measurement experiments[J]. Journal of Radars, 2019, 8(3): 281–302. doi: 10.12000/JR19006. [3] 陈小龙, 黄勇, 关键, 等. MIMO雷达微弱目标长时积累技术综述[J]. 信号处理, 2020, 36(12): 1947–1964. doi: 10.16798/j.issn.1003-0530.2020.12.001.CHEN Xiaolong, HUANG Yong, GUAN Jian, et al. Review of long-time integration techniques for weak targets using MIMO radar[J]. Journal of Signal Processing, 2020, 36(12): 1947–1964. doi: 10.16798/j.issn.1003-0530.2020.12.001. [4] 许述文, 白晓惠, 郭子薰, 等. 海杂波背景下雷达目标特征检测方法的现状与展望[J]. 雷达学报, 2020, 9(4): 684–714. doi: 10.12000/JR20084.XU Shuwen, BAI Xiaohui, GUO Zixun, et al. Status and prospects of feature-based detection methods for floating targets on the sea surface[J]. Journal of Radars, 2020, 9(4): 684–714. doi: 10.12000/JR20084. [5] 贺丰收, 何友, 刘准钆, 等. 卷积神经网络在雷达自动目标识别中的研究进展[J]. 电子与信息学报, 2020, 42(1): 119–131. doi: 10.11999/JEIT180899.HE Fengshou, HE You, LIU Zhunga, et al. Research and development on applications of convolutional neural networks of radar automatic target recognition[J]. Journal of Electronics &Information Technology, 2020, 42(1): 119–131. doi: 10.11999/JEIT180899. [6] 刘宁波, 董云龙, 王国庆, 等. X波段雷达对海探测试验与数据获取[J]. 雷达学报, 2019, 8(5): 656–667. doi: 10.12000/JR19089.LIU Ningbo, DONG Yunlong, WANG Guoqing, et al. Sea-detecting X-band radar and data acquisition program[J]. Journal of Radars, 2019, 8(5): 656–667. doi: 10.12000/JR19089. [7] 刘宁波, 丁昊, 黄勇, 等. X波段雷达对海探测试验与数据获取年度进展[J]. 雷达学报, 2021, 10(1): 173–182. doi: 10.12000/JR21011.LIU Ningbo, DING Hao, HUANG Yong, et al. Annual progress of the sea-detecting X-band radar and data acquisition program[J]. Journal of Radars, 2021, 10(1): 173–182. doi: 10.12000/JR21011. [8] DROSOPOULOS A. Description of the OHGR database[R]. Technical Note 94–14, 1994. [9] DE WIND H J, CILLIERS J C, and HERSELMAN P L. DataWare: Sea clutter and small boat radar reflectivity databases [Best of the Web][J]. IEEE Signal Processing Magazine, 2010, 27(2): 145–148. doi: 10.1109/msp.2009.935415. 期刊类型引用(4)
1. Xiaolan Qiu，Zekun Jiao，Zhe Zhang，Qiancheng Yan，Chibiao Ding. Advances and prospects in SAR microwave vision three-dimensional imaging. National Science Open. 2024(05): 53-83 . 
必应学术2. 任子帅，张照，高雨欣，郭睿. 基于自适应高程约束的TomoSAR三维成像. 雷达学报. 2023(05): 1056-1068 . 
本站查看3. 郭华东，吴文瑾，张珂，李新武. 新型SAR对地环境观测. 测绘学报. 2022(06): 862-872 . 百度学术4. 林赟，张琳，韦立登，张汉卿，冯珊珊，王彦平，洪文. 无先验模型复杂结构设施SAR全方位三维成像方法研究. 雷达学报. 2022(05): 909-919 . 本站查看其他类型引用(13)
-
DownLoad:
必应学术
计量
- 文章访问数: 3096
- HTML全文浏览量: 1145
- PDF下载量: 604
- 被引次数: 17
