作者中心
专家审稿
责编办公
编辑办公
A Novel Joint Radar-communication Waveform Design Method Based on Distributed Aperture
-
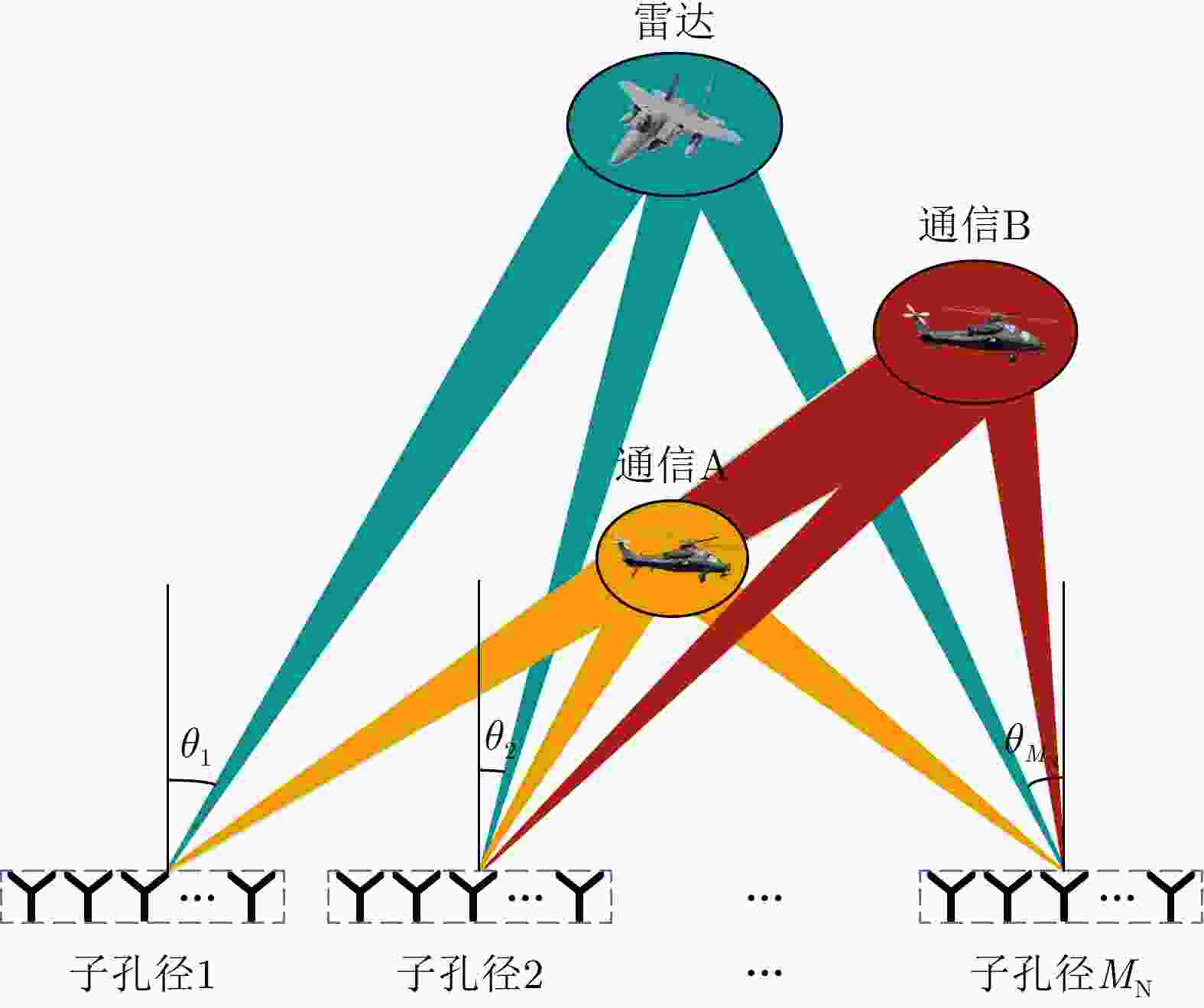
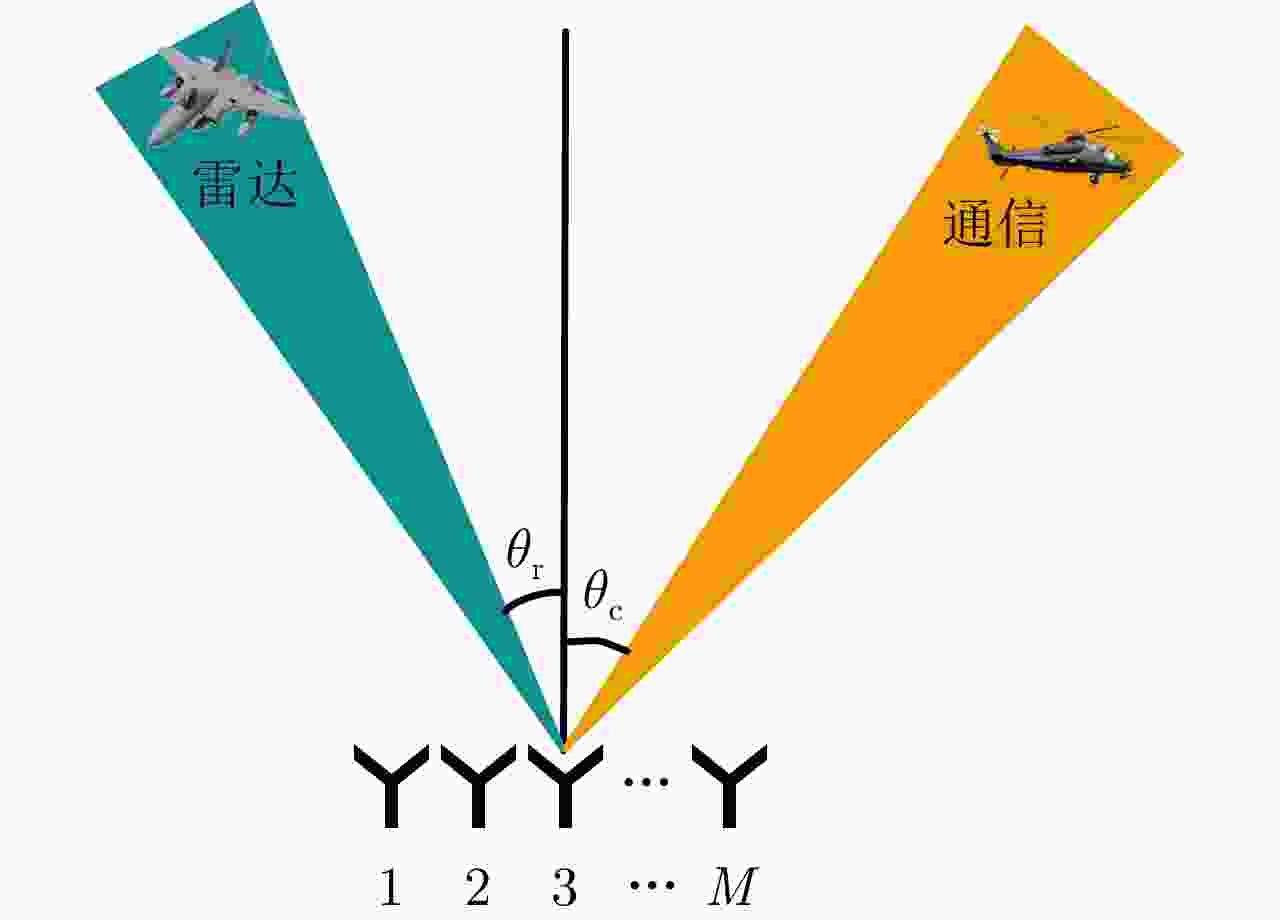
摘要: 雷达通信一体化波形设计是近年来的研究热点。基于紧凑式阵列的一体化波形支持多方向目标探测和多用户通信，但面对主瓣内同方向不同距离的干扰和窃听行为时，存在抗主瓣干扰能力差、通信信息泄露等问题。因此，该文提出了一种基于分布式孔径的雷达通信一体化波形设计方法以操控波形在三维空间的分布。首先，根据近场信号传播模型建立波形合成约束，在指定位置合成所需的雷达和通信波形。然后，对各个子孔径增加恒模约束，构建以最小化发射功率为准则的一体化波形优化模型。由于模型的非凸性，采用交替投影算法进行迭代求解。仿真结果表明，该文所提方法在雷达目标和通信目标位置同时合成了期望波形，实现了三维空间波形操控。Abstract: Joint radar-communication waveform design has been the focus of intensive research in recent years. The integrated waveform based on a collocated antenna can simultaneously detect targets and communicate with multiple users in different directions. However, integrated waveforms possess poor anti-jamming properties and lack secure communication abilities, which limits their capacity to address the jamming and eavesdropping behaviors that generate at various ranges in the same beam direction. In this study, a novel joint radar-communication waveform design method based on a distributed aperture is proposed to control waveform distributions in the three-dimensional space. First, the waveform synthesis constraint is established to synthesize the desired radar and communication waveforms in designated directions. Second, the constant modulus constraint is added to each sub-aperture, following which an integrated waveform optimization model is established based on the minimum transmission power. Finally, the alternating projection algorithm is used to iteratively solve the nonconvex optimization problem. Simulation results demonstrate that the proposed method synthesizes desired waveforms at target positions and realizes three-dimensional spatial waveform manipulation.
-
图 2 基于紧凑式阵列的一体化波形空间能量和波形分布示意图
Figure 2. Space energy and waveform distribution of the integrated waveform based on collocated antenna
图 4 分布式孔径与波胞的几何关系
Figure 4. Geometric relationship between distributed aperture and wave cell
图 8 场景1中雷达合成波形的空间分布情况
Figure 8. Spatial distribution of radar synthetic waveform in the first scenario
图 9 场景1中雷达目标周围合成波形的时域表现
Figure 9. Time domain representation of synthetic waveforms around radar target in the first scenario
图 10 场景1中通信合成波形的空间分布情况
Figure 10. Spatial distribution of communication synthetic waveform in the first scenario
图 11 场景1中通信目标周围合成波形表现
Figure 11. Performance of synthetic waveforms around communication user in the first scenario
图 14 场景2中雷达合成波形的空间分布情况
Figure 14. Spatial distribution of radar synthetic waveforms in the second scenario
图 15 场景2中雷达目标周围合成波形的时域表现
Figure 15. Time domain representation of synthetic waveforms around radar target in the second scenario
图 16 场景2中通信合成波形的空间分布情况
Figure 16. Spatial distribution of radar synthetic waveform in the second scenario
图 17 场景2中通信目标周围合成波形表现
Figure 17. Performance of synthetic waveforms around communication user in the second scenario
图 20 场景3中雷达合成波形的空间分布情况
Figure 20. Spatial distribution of radar synthetic waveforms in the third scenario
图 21 场景3中雷达目标周围合成波形的时域表现
Figure 21. Time domain representation of synthetic waveforms around radar target in the third scenario
图 22 场景3中通信合成波形的空间分布情况
Figure 22. Spatial distribution of radar synthetic waveform in the third scenario
图 23 场景3中通信目标周围合成波形表现
Figure 23. Performance of synthetic waveforms around communication user in the third scenario
1 基于“波胞形成”的一体化波形优化模型求解算法流程
1. Integrated waveform optimization model solving algorithm based on “wave cell”
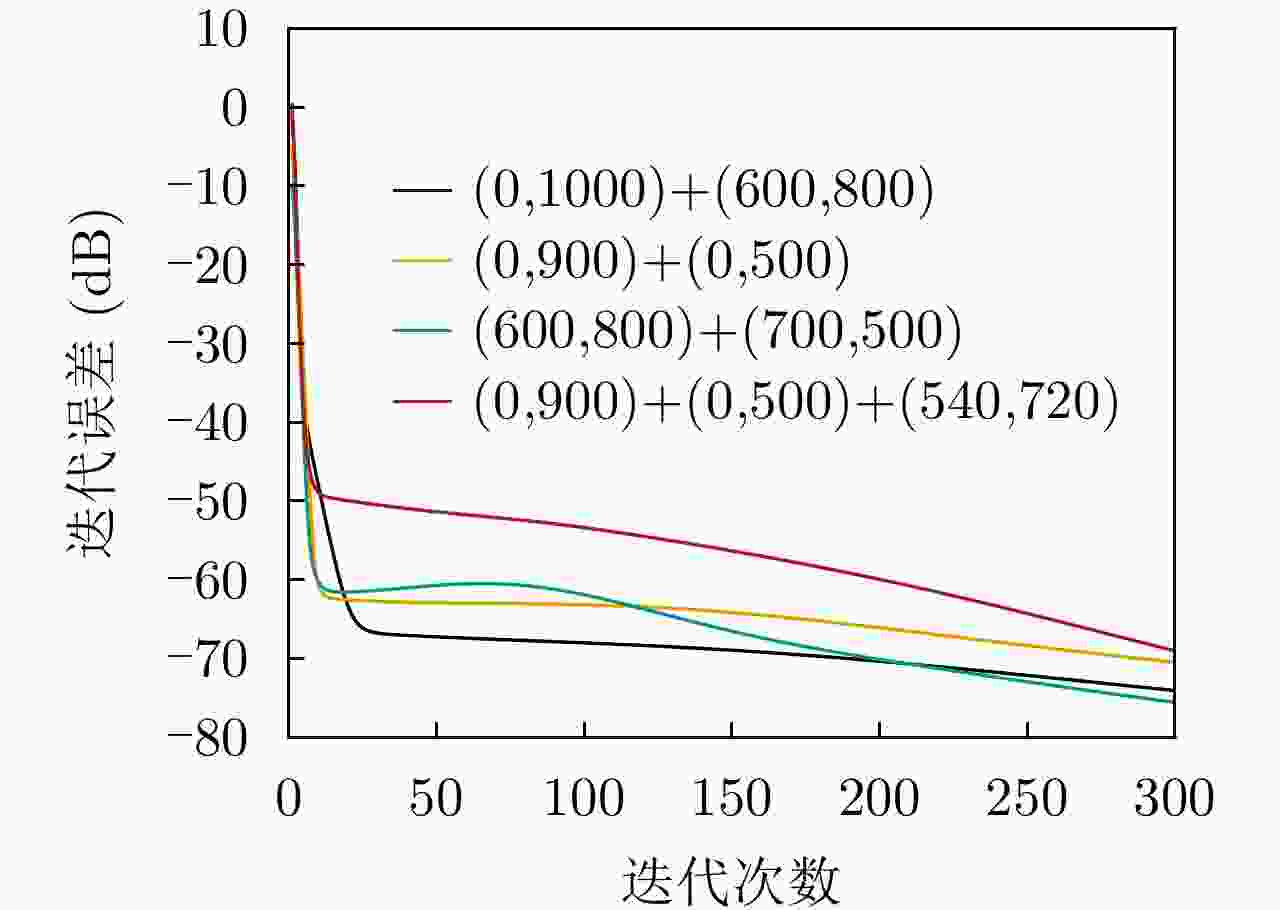
1. 输入：A, S, I, $ {\boldsymbol{\varepsilon }}$ 2. 初始化：计算${{\boldsymbol{X}}^{\left( 0 \right)}}$(根据式(12)) 3. for $i = 1,2, \cdots ,I$执行 4. 计算$ {{\boldsymbol{\tilde X}}^{\left( i \right)}} $(根据式(18)) 5. for $ {m_{\text{N}}} = 1,2, \cdots ,{M_{\text{N}}} $ 6. 计算$ {\sigma _{{m_{\text{N}}}}} $(根据式(21)) 7. 计算${ {\boldsymbol{X} }^{\left( i \right)} }\left( {\left( { {m_{\text{N} } } - 1} \right){M_{\text{M} } } + 1:{m_{\text{N} } }{M_{\text{M} } },}: \right)$(根据
式(22))8. end for(当$ {m_{\text{N}}} = {M_{\text{N}}} $时) 9. 计算迭代误差$ \Delta {\boldsymbol{X}} = {{{{{\left\| {{{\boldsymbol{X}}^{\left( i \right)}} - {{\boldsymbol{X}}^{\left( {i - 1} \right)}}} \right\|}_{\text{F}}}} \mathord{\left/ {\vphantom {{{{\left\| {{{\boldsymbol{X}}^{\left( i \right)}} - {{\boldsymbol{X}}^{\left( {i - 1} \right)}}} \right\|}_{\text{F}}}} {\left\| {{{\boldsymbol{X}}^{\left( {i - 1} \right)}}} \right\|}}} \right. } {\left\| {{{\boldsymbol{X}}^{\left( {i - 1} \right)}}} \right\|}}_{\text{F}}} $ 10. end for(当$\Delta {\boldsymbol{X} } \le {{\varepsilon} }$或$i = I$时) 11. 输出：${{\boldsymbol{X}}^{\left( i \right)}}$ 
下载: 导出CSV
表 1 仿真参数
Table 1. Simulation parameters
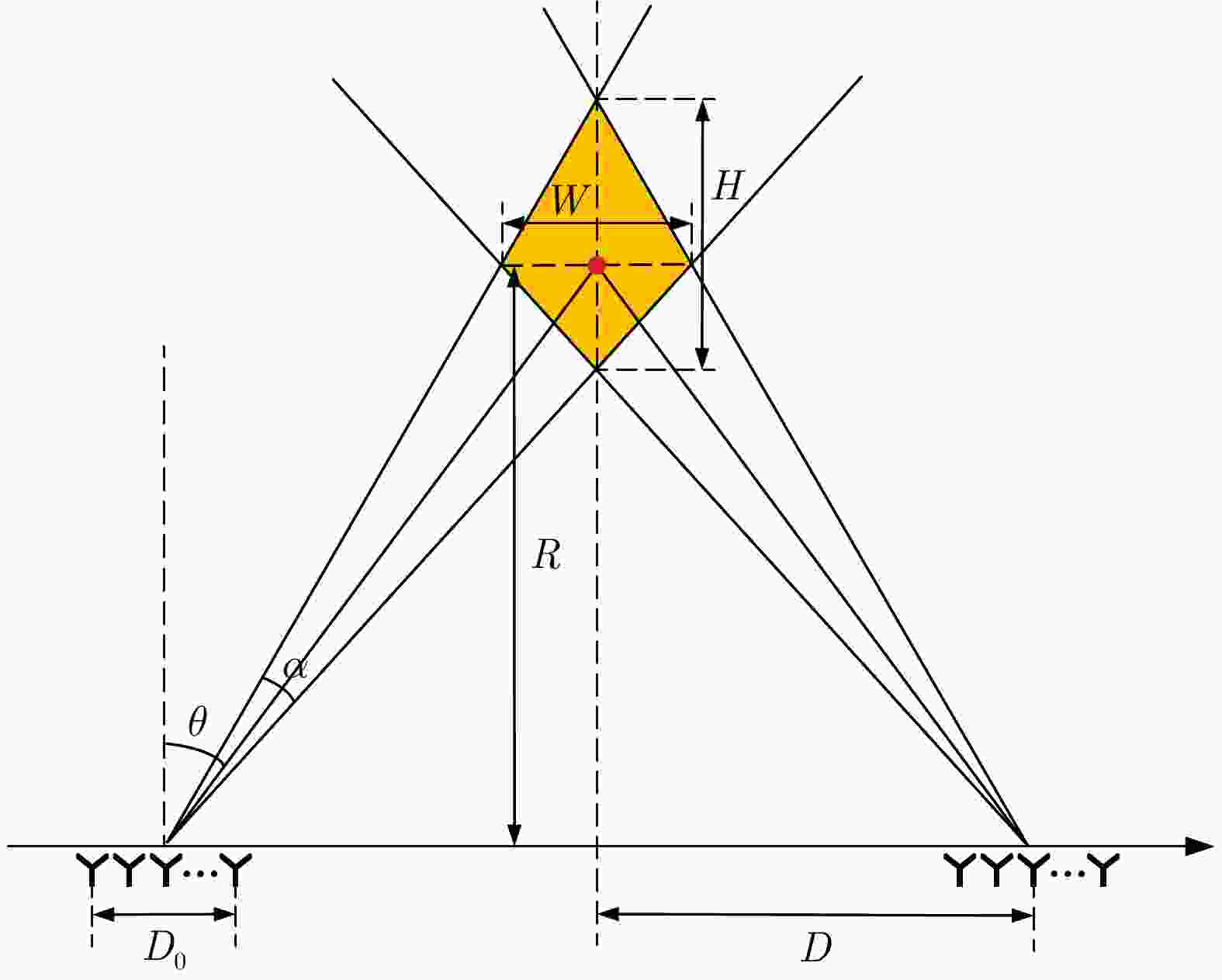
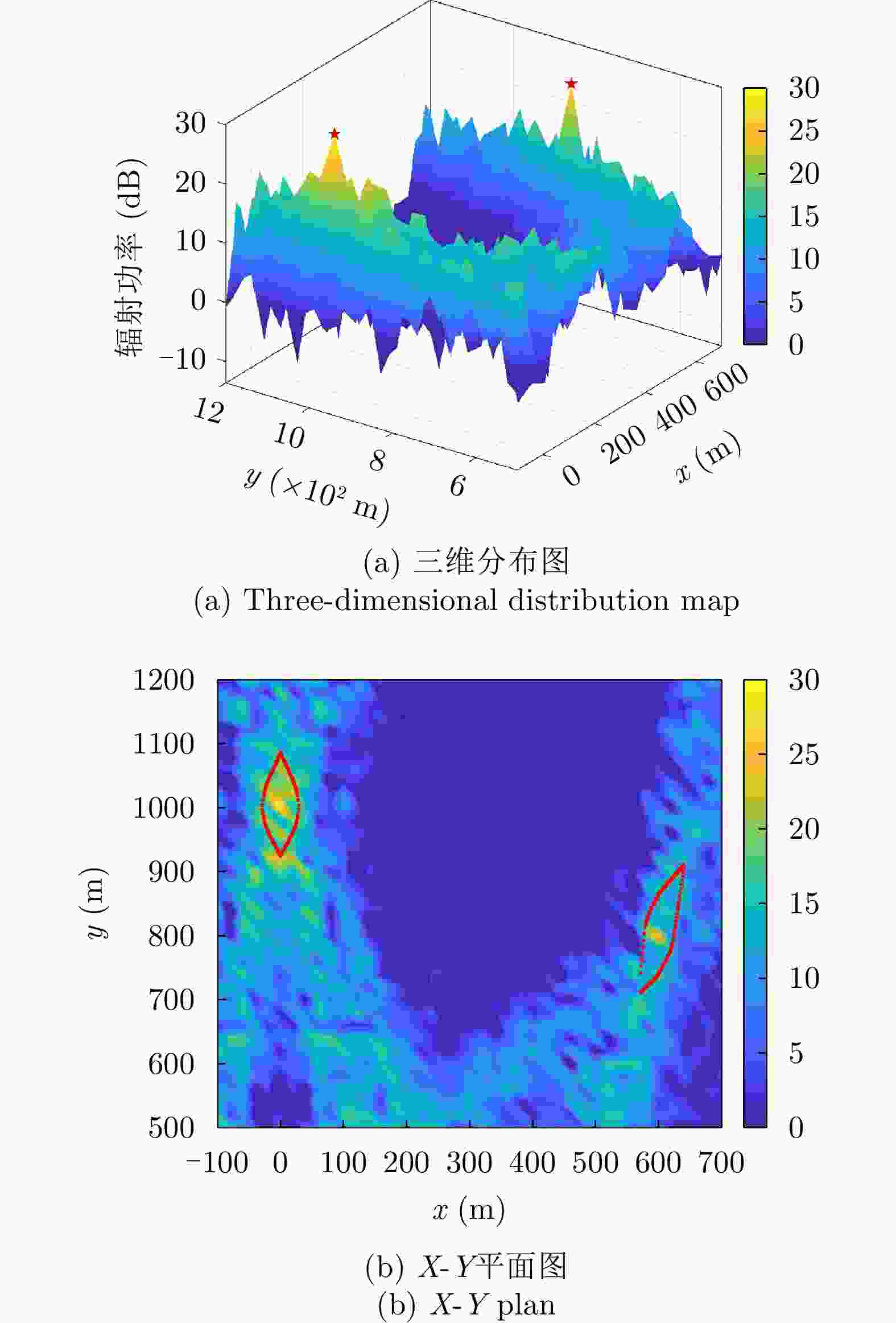
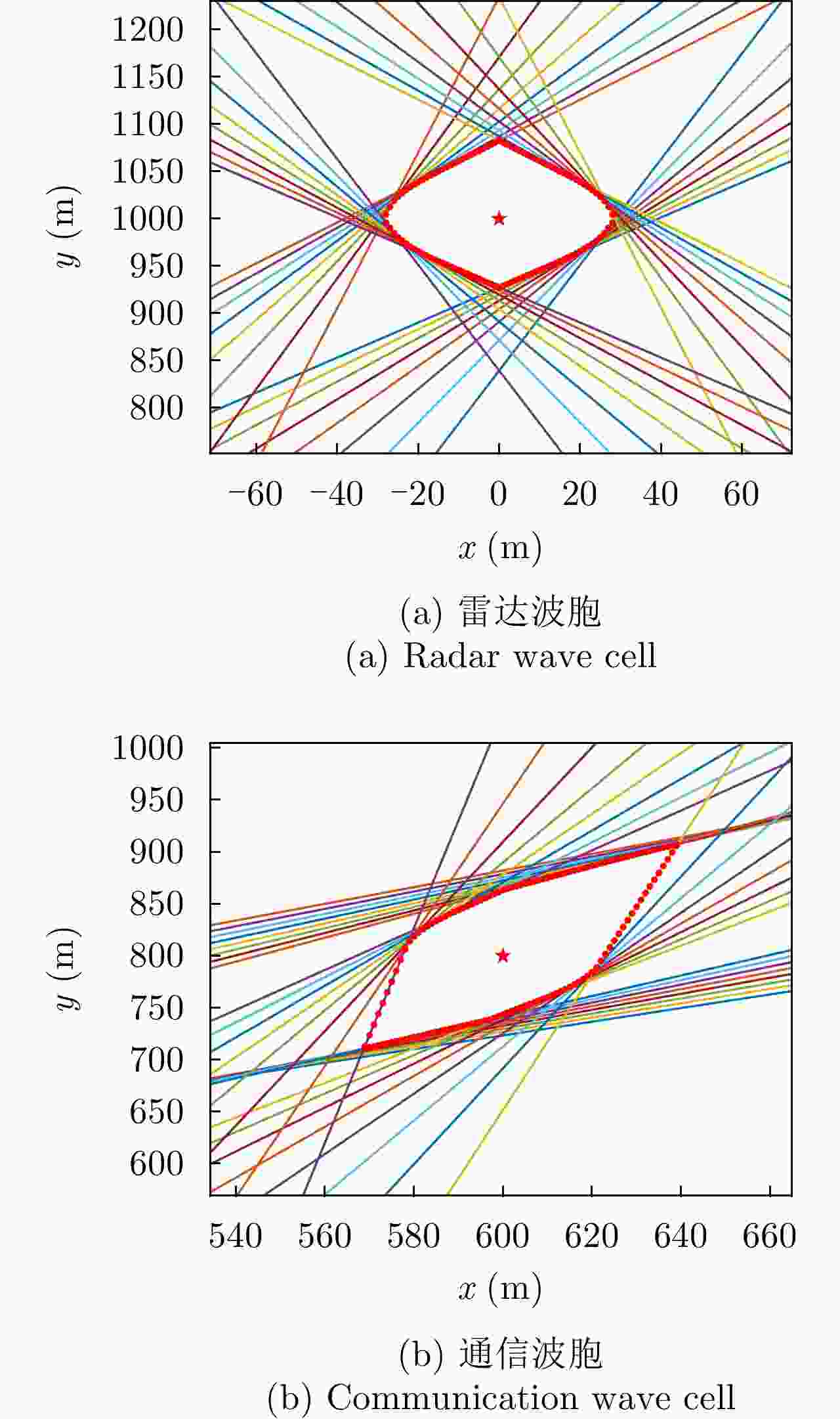
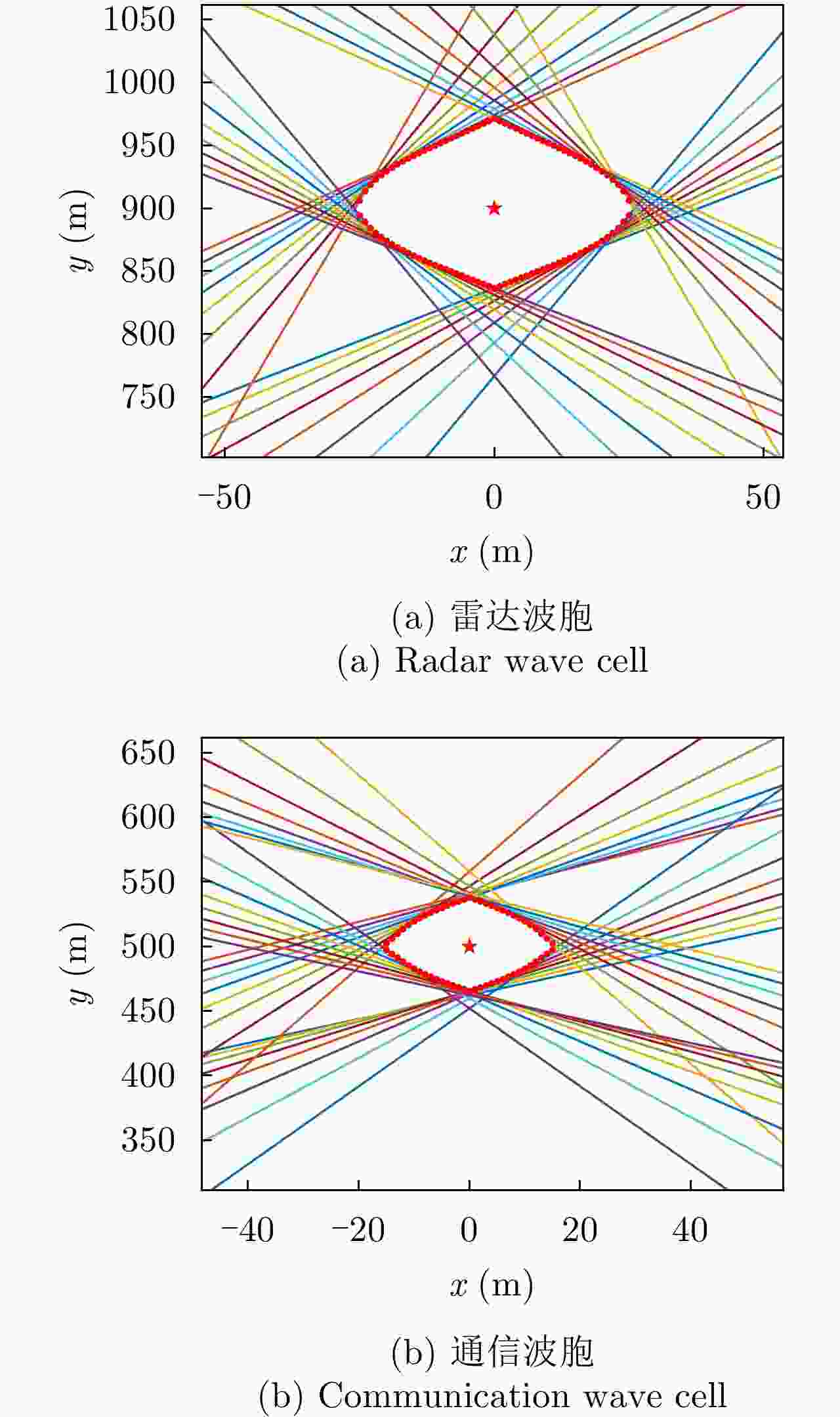
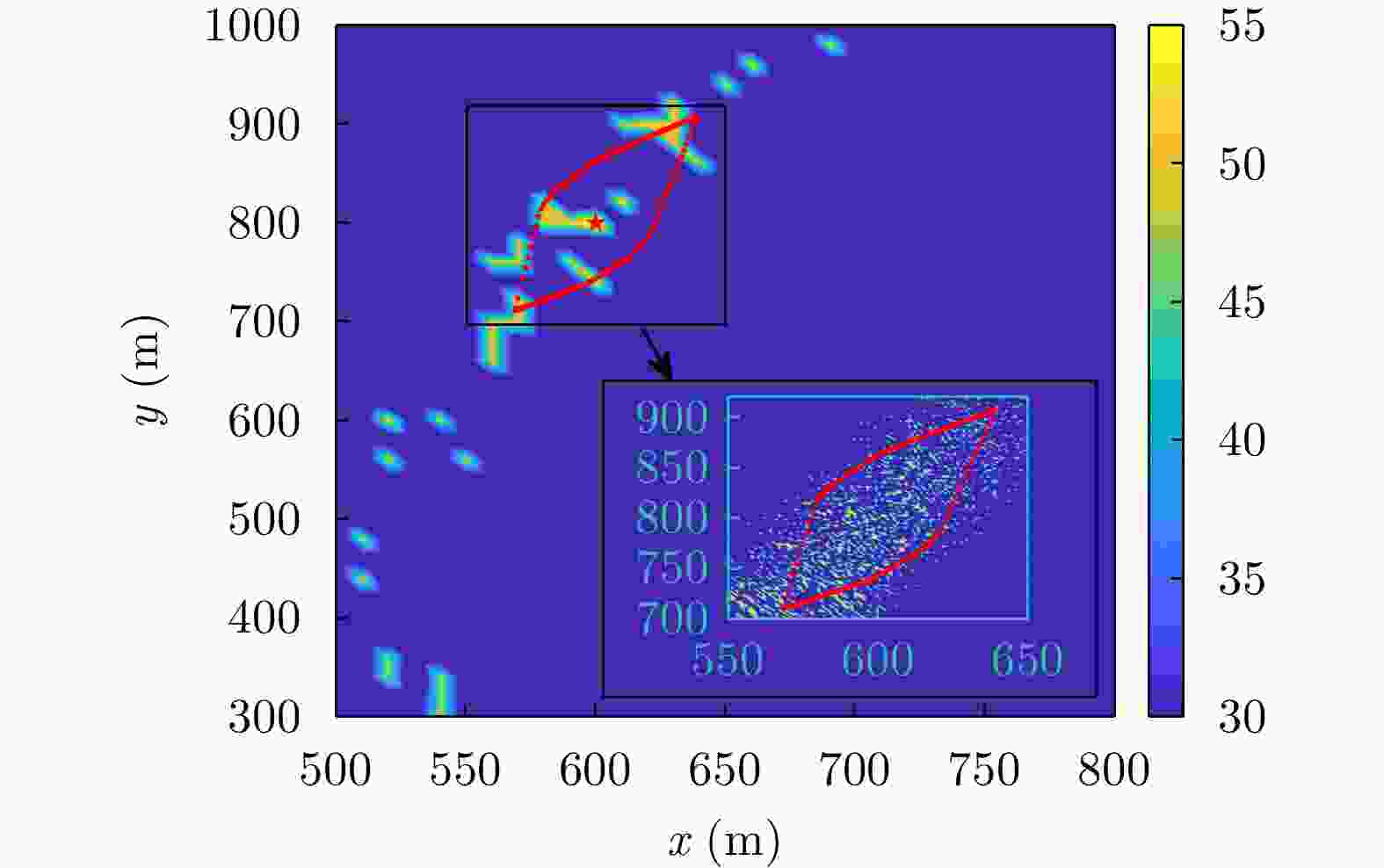
参数名称 参数符号 数值 分布式孔径总阵元个数 M 512 子孔径个数 ${M_{\text{N}}}$ 16 子孔径内阵元个数 ${M_{\text{M}}}$ 32 子孔径内阵元间距(m) d 0.05 子孔径间距(m) ${D_d}$ 50 采样点数 N 1024 波形载频(GHz) ${f_0}$ 3 波形时宽(μs) T 2.048 雷达波形带宽(MHz) B 300 符号个数 ${N_{{\text{sym}}}}$ 64 期望波形间功率差(dB) $ \Delta {P_{{\text{rc}}}} $ 3 最大迭代次数 I 300
下载: 导出CSV
表 2 场景1中波胞尺寸分析
Table 2. Wave cell size analysis in the first scenario
类别 理论值(m) 测量值(m) 误差(%) 宽度 高度 宽度 高度 宽度 高度 雷达波胞 59.098 160.380 59.068 160.380 0.05 0 通信波胞 46.835 123.191 46.797 123.136 0.08 0.04
下载: 导出CSV
表 3 场景1中空间合成波形雷达性能表现
Table 3. Radar performance of spatial synthetic waveform in the first scenario
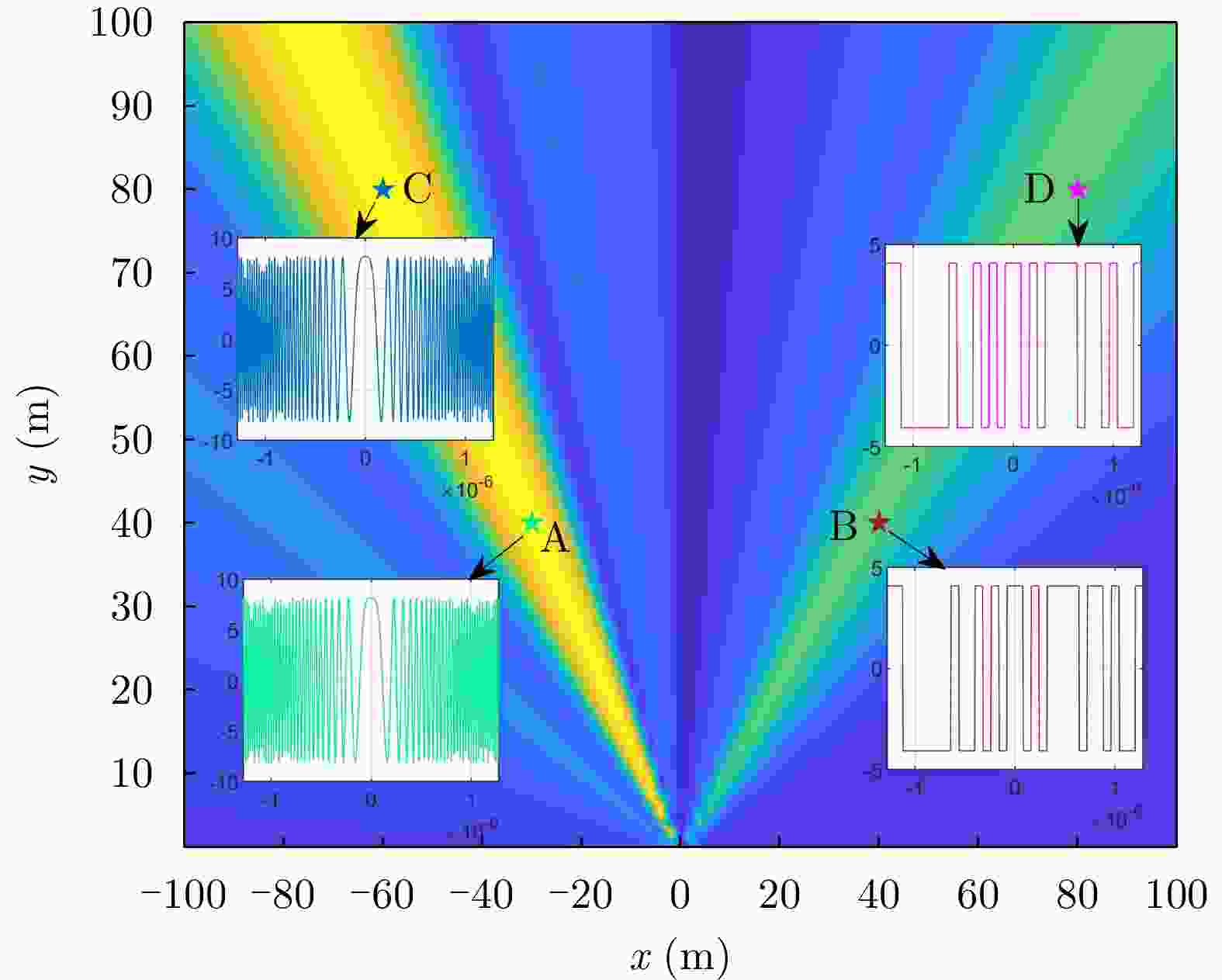
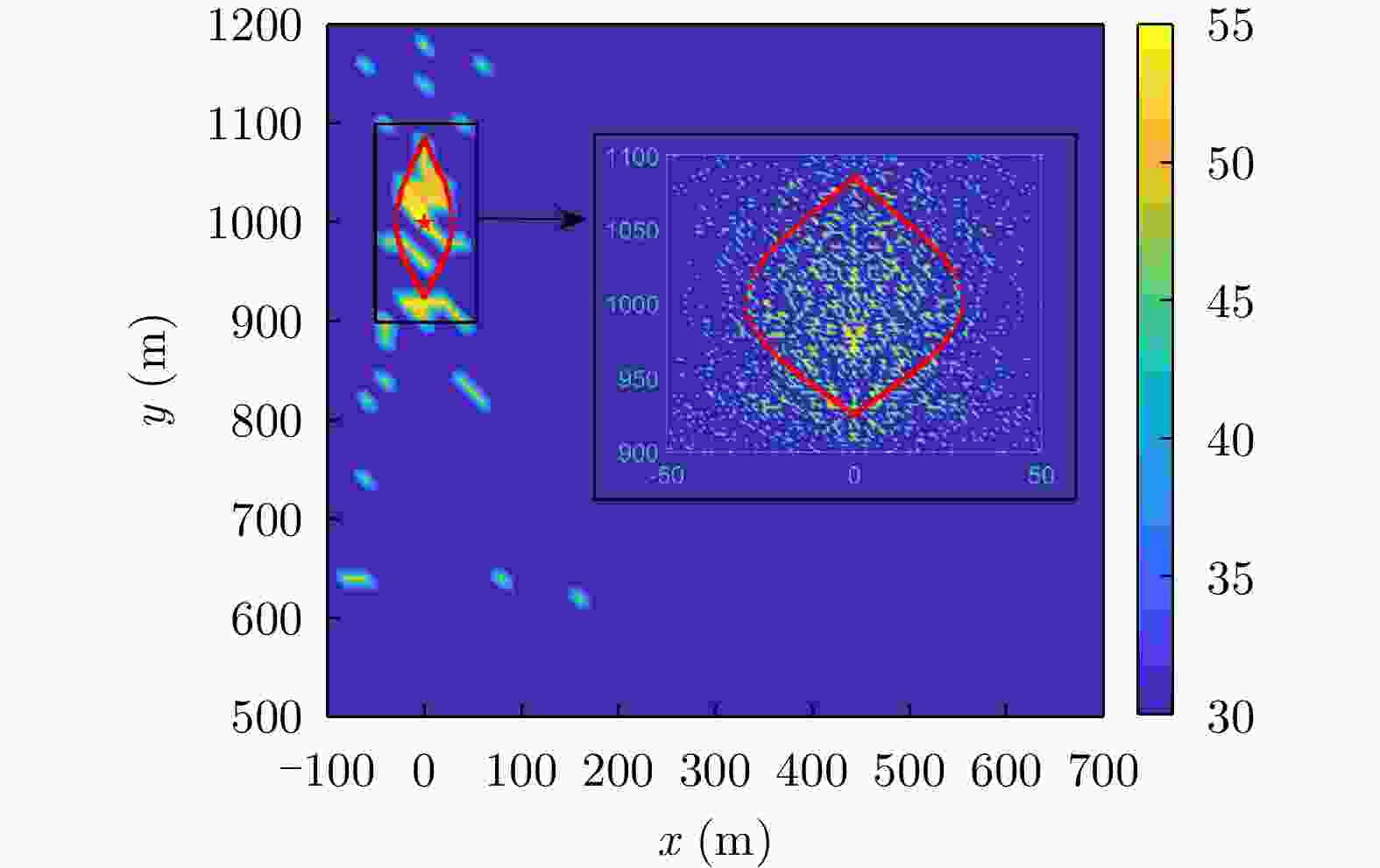
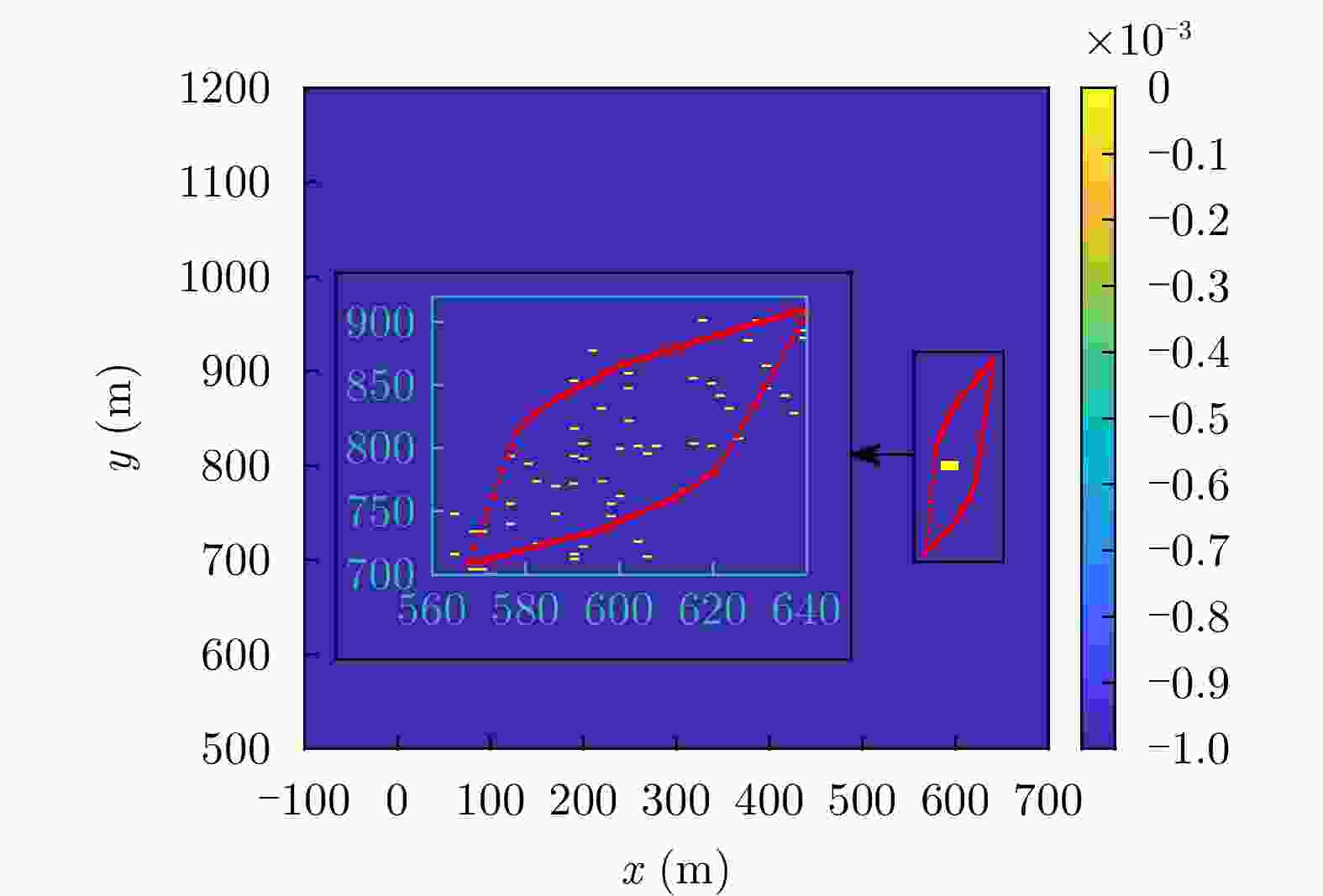
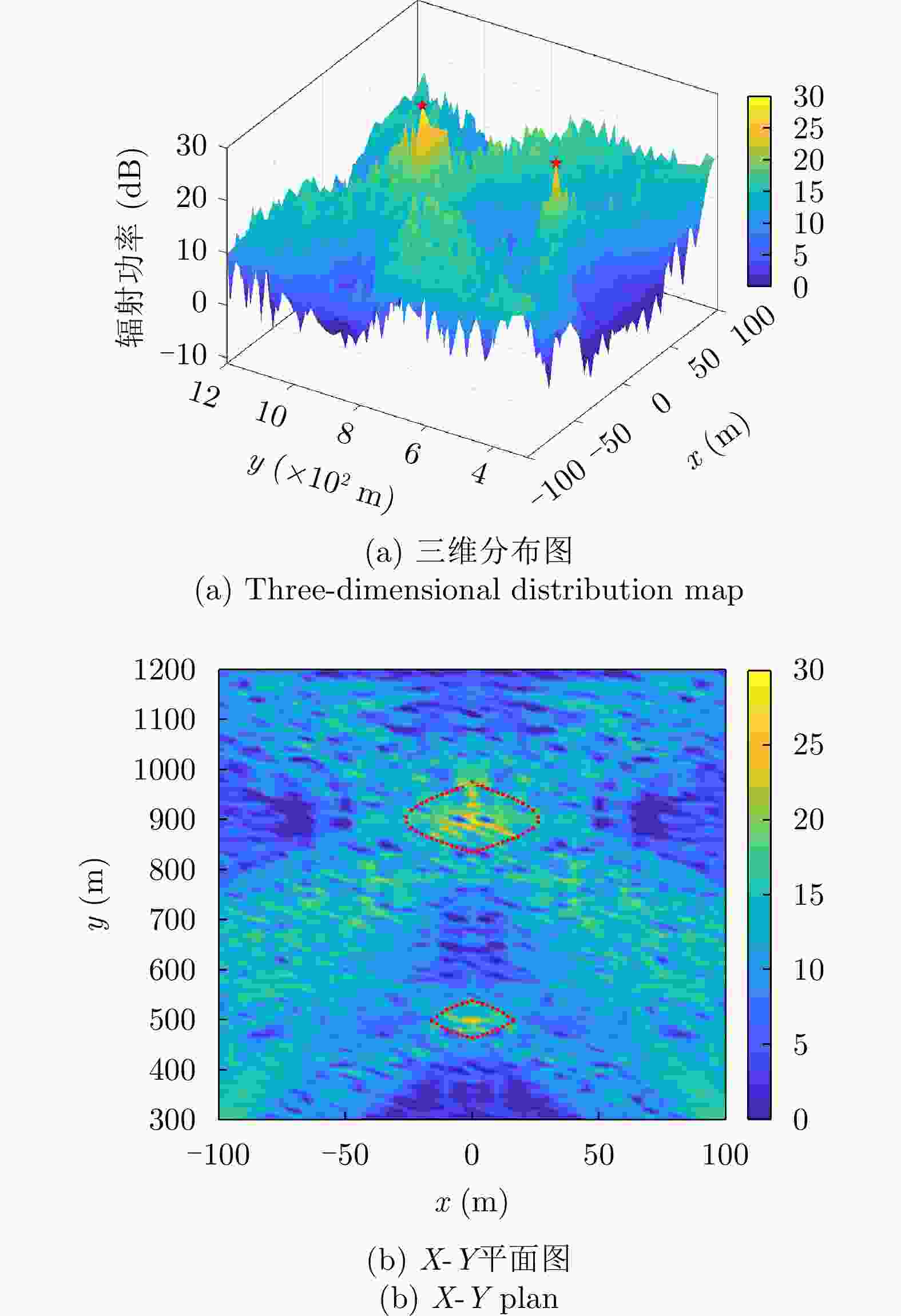
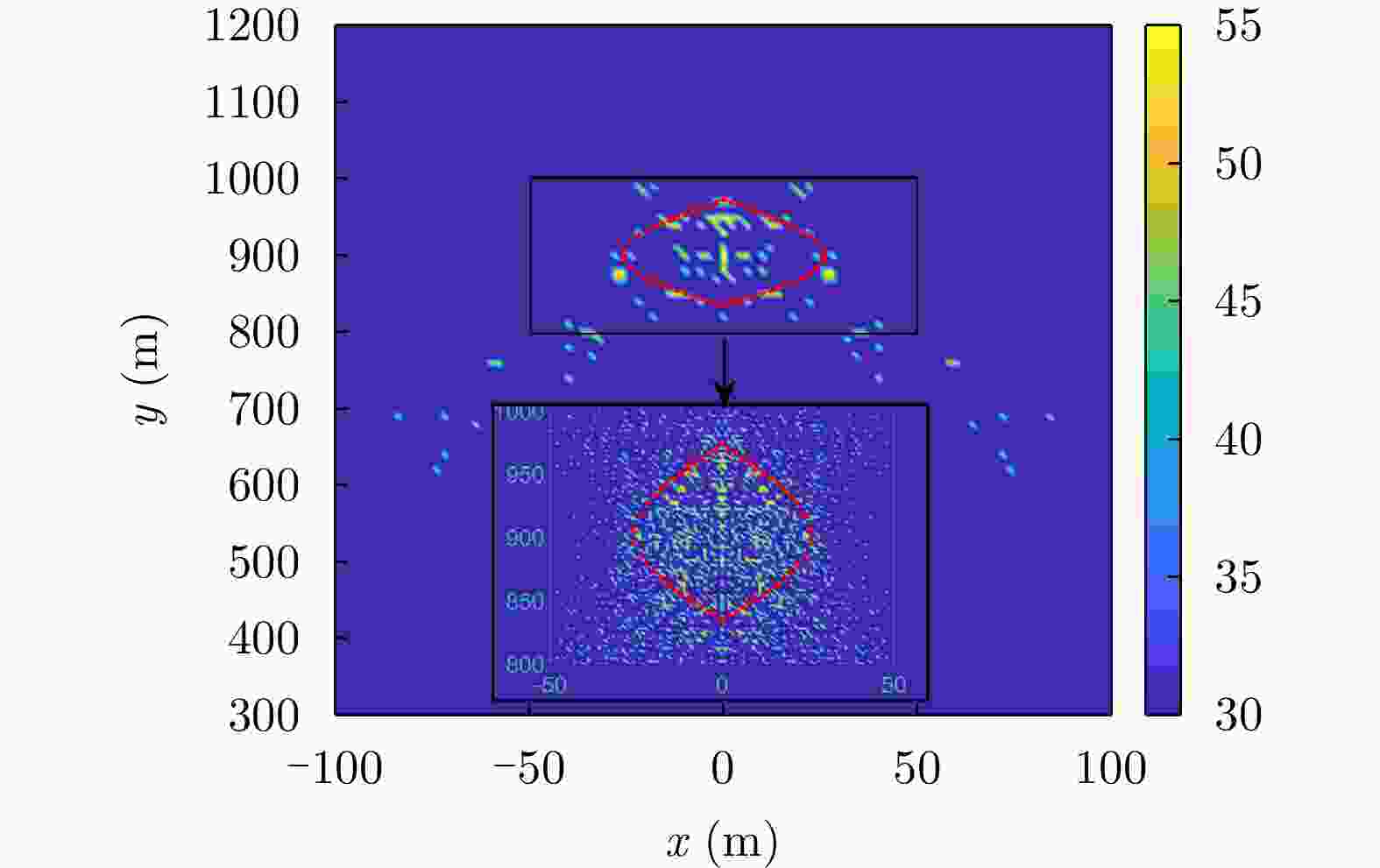
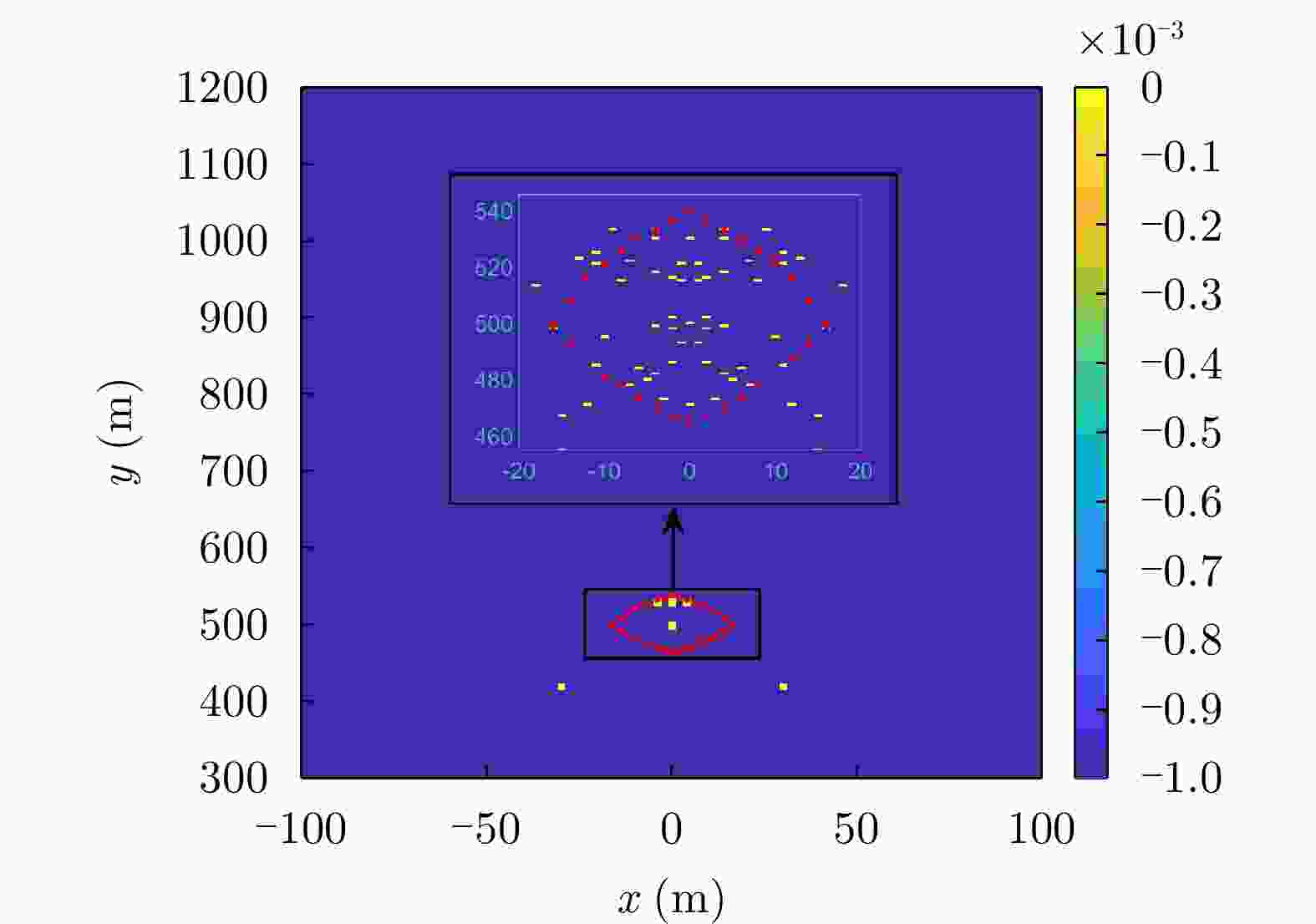
空间坐标(m) 是否位于雷达波胞内 脉压峰值(dB) 峰值旁瓣比(dB) 积分旁瓣比(dB) (0,1000) 是 60.21 –13.30 –9.73 (0,970) 是 53.94 –13.30 –9.72 (–26,940) 否 18.38 –13.22 –3.39
下载: 导出CSV
表 4 场景2中波胞尺寸分析
Table 4. Wave cell size analysis in the second scenario
类别 理论值(m) 测量值(m) 误差(%) 宽度 高度 宽度 高度 宽度 高度 雷达波胞 53.597 139.095 53.570 139.097 0.05 0.001 通信波胞 32.495 74.472 32.500 74.470 0.02 0.003
下载: 导出CSV
表 5 场景2中空间合成波形雷达性能表现
Table 5. Radar performance of spatial synthetic waveform in the second scenario
空间坐标(m) 是否位于
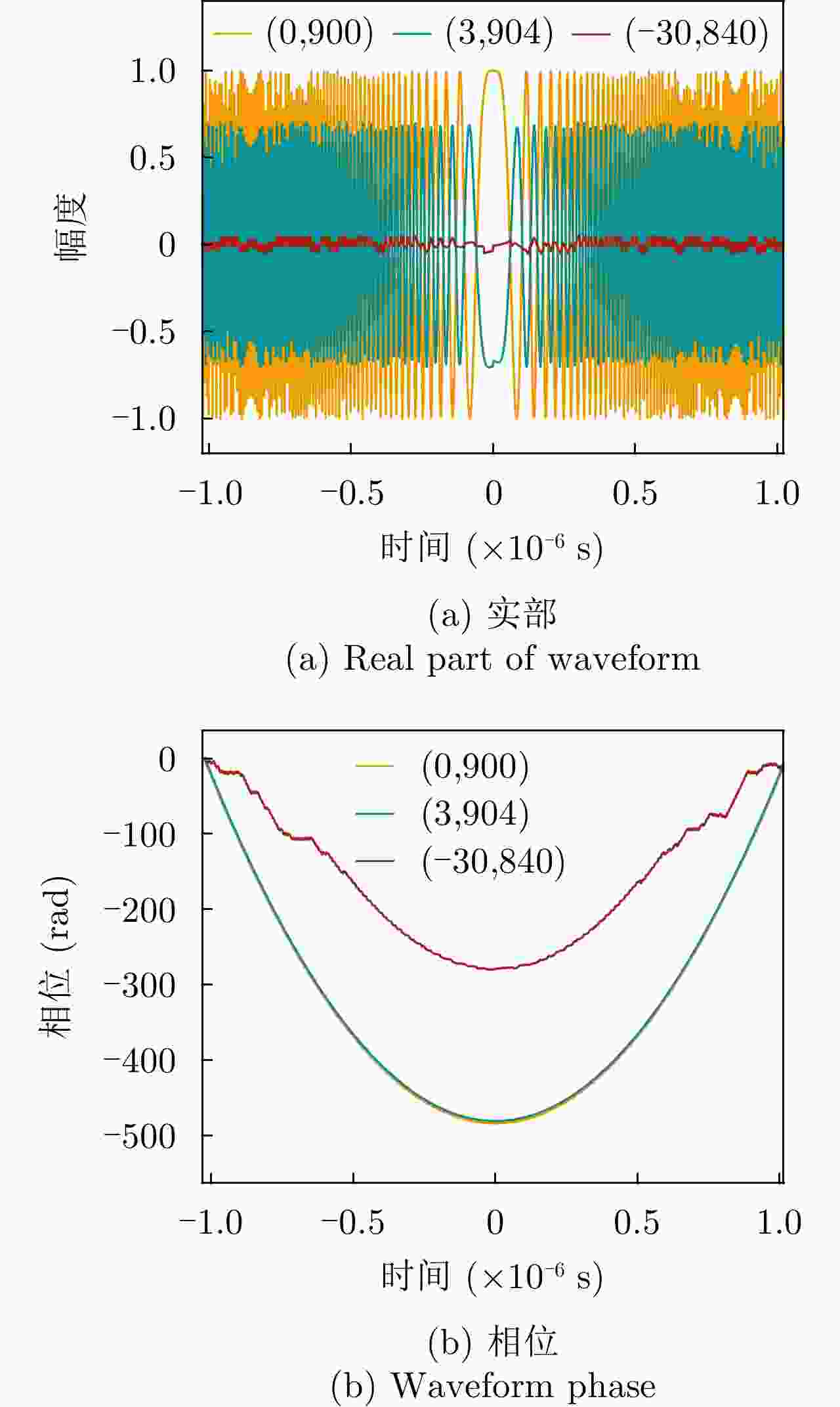
雷达波胞内脉压峰值(dB) 峰值旁瓣比(dB) 积分旁瓣比(dB) (0,900) 是 60.21 –13.30 –9.73 (3,904) 是 56.87 –13.30 –9.72 (–30,840) 否 27.82 –12.02 0.15
下载: 导出CSV
表 6 场景3中波胞尺寸分析
Table 6. Wave cell size analysis in the third scenario
类别 理论值(m) 测量值(m) 误差(%) 宽度 高度 宽度 高度 宽度 高度 雷达波胞 45.355 119.372 45.354 119.372 0.002 0 通信波胞 36.607 72.135 34.607 72.134 0 0.001
下载: 导出CSV
表 7 场景3中空间合成波形雷达性能表现
Table 7. Radar performance of spatial synthetic waveform in the third scenario
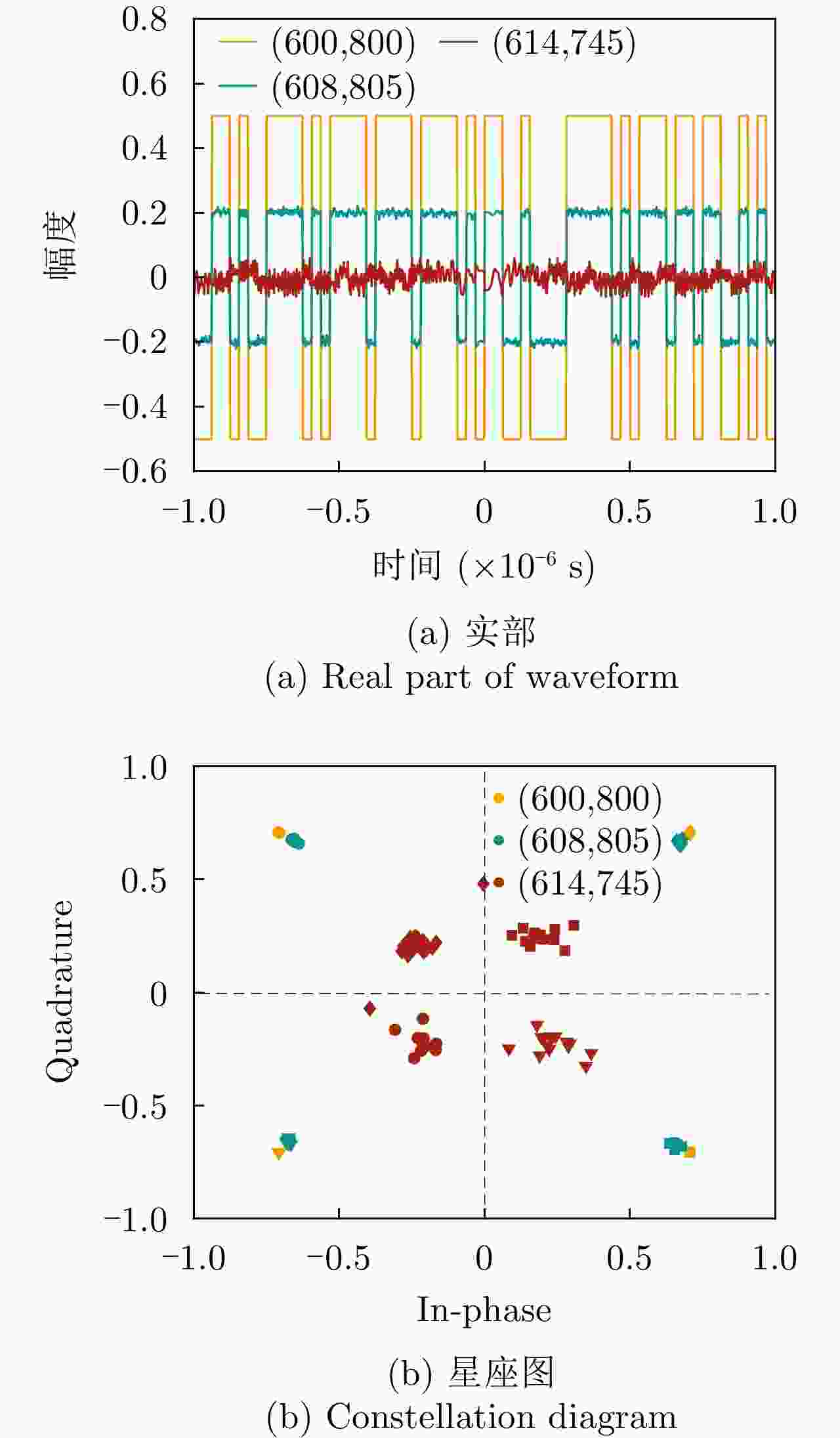
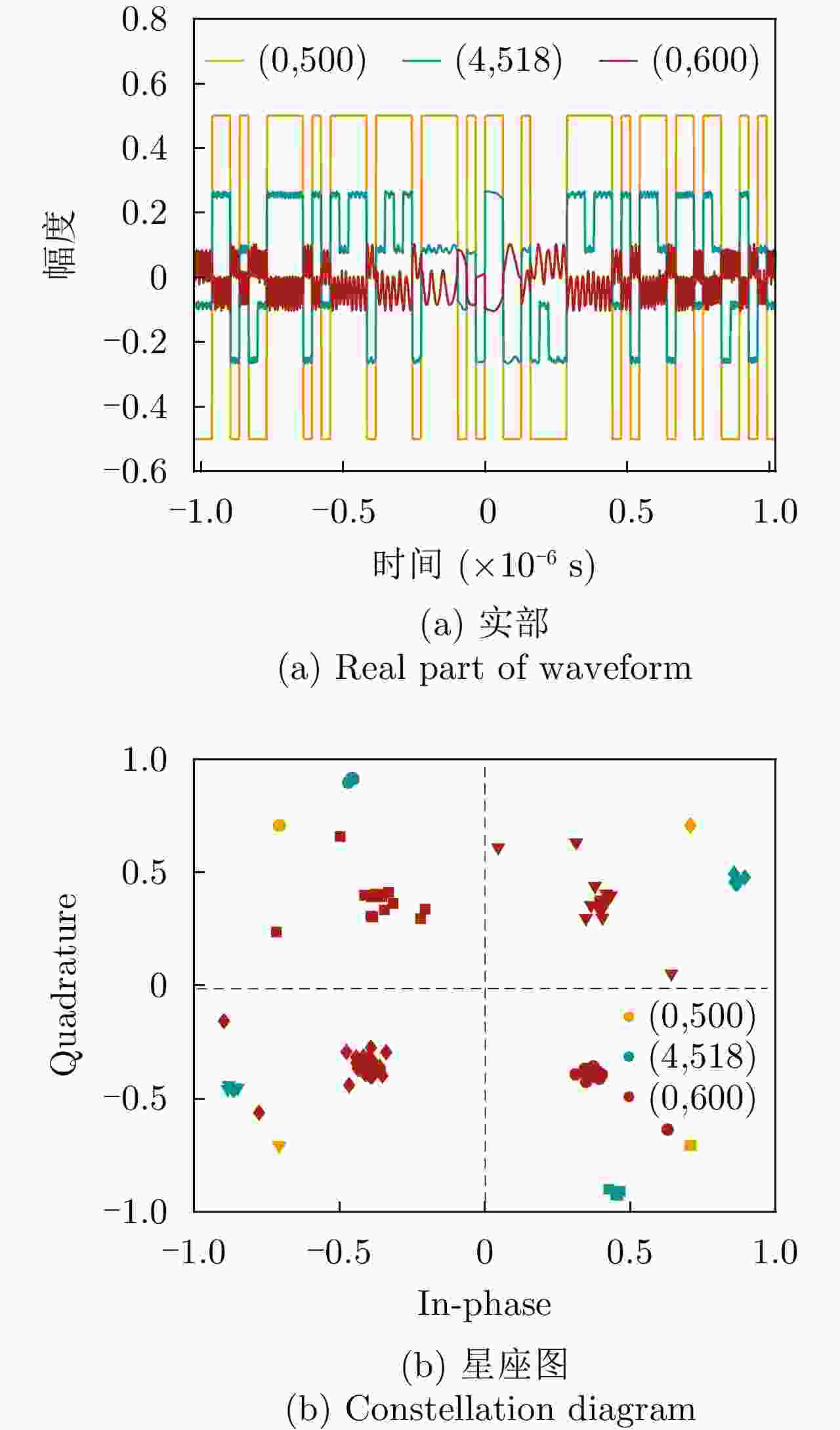
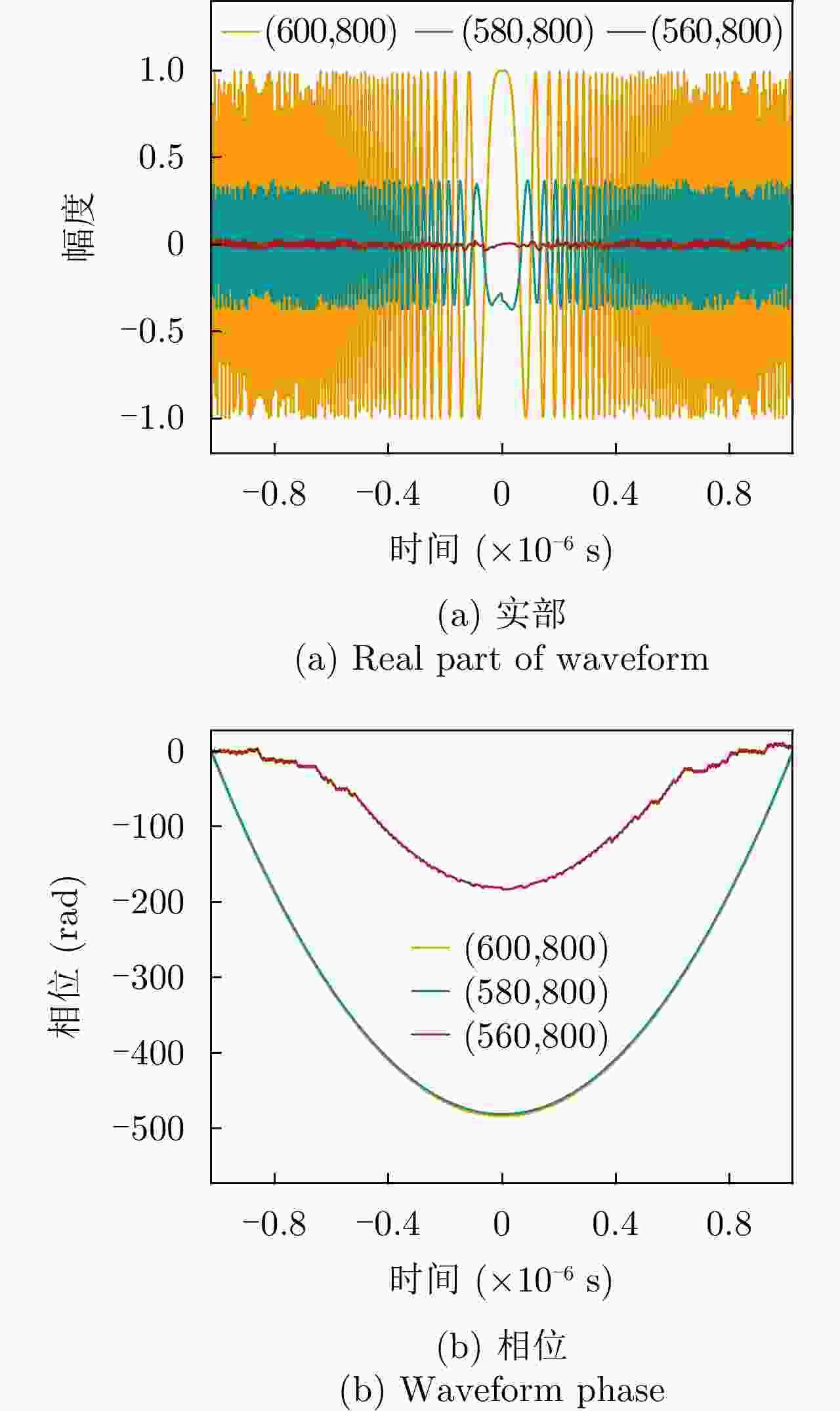
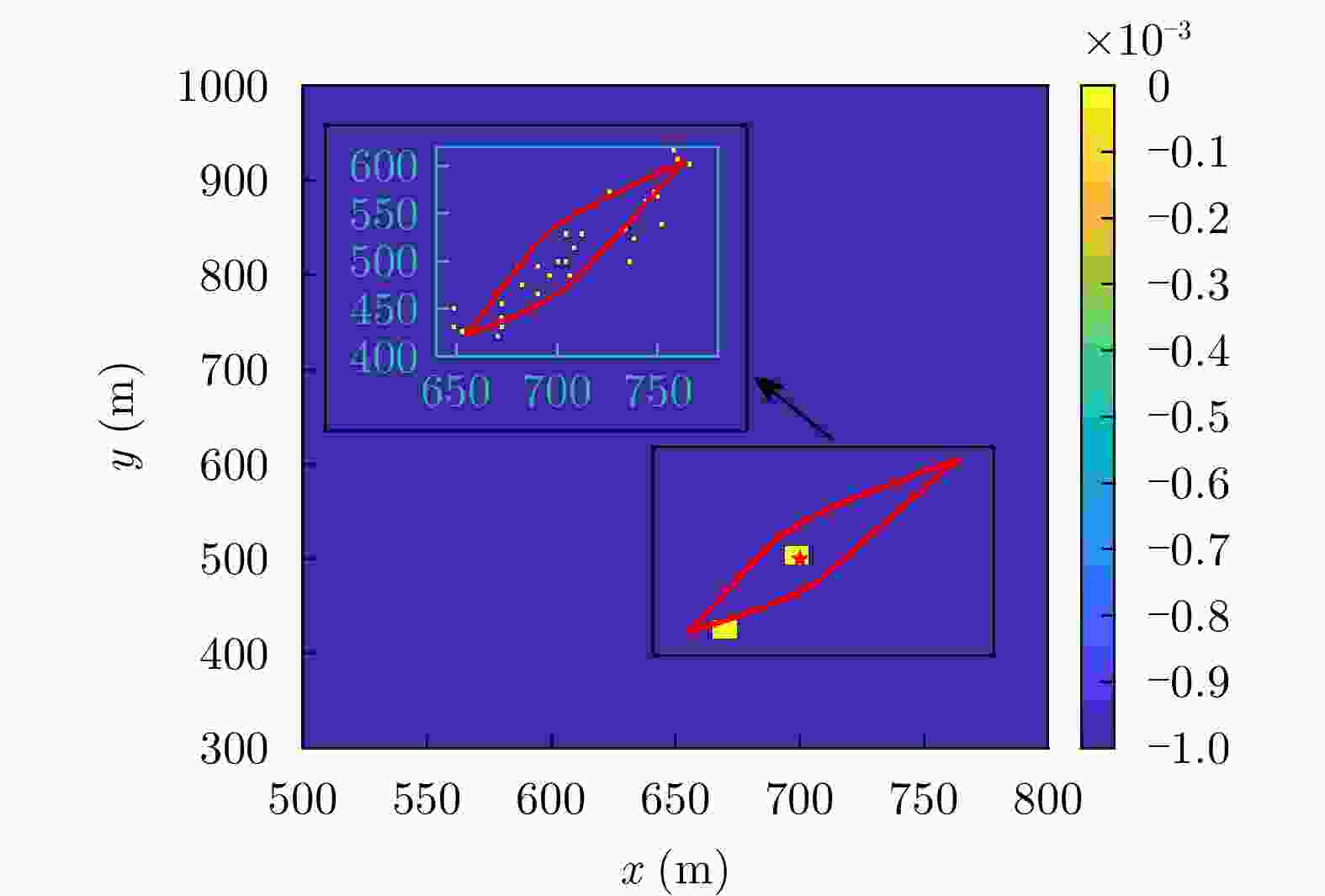
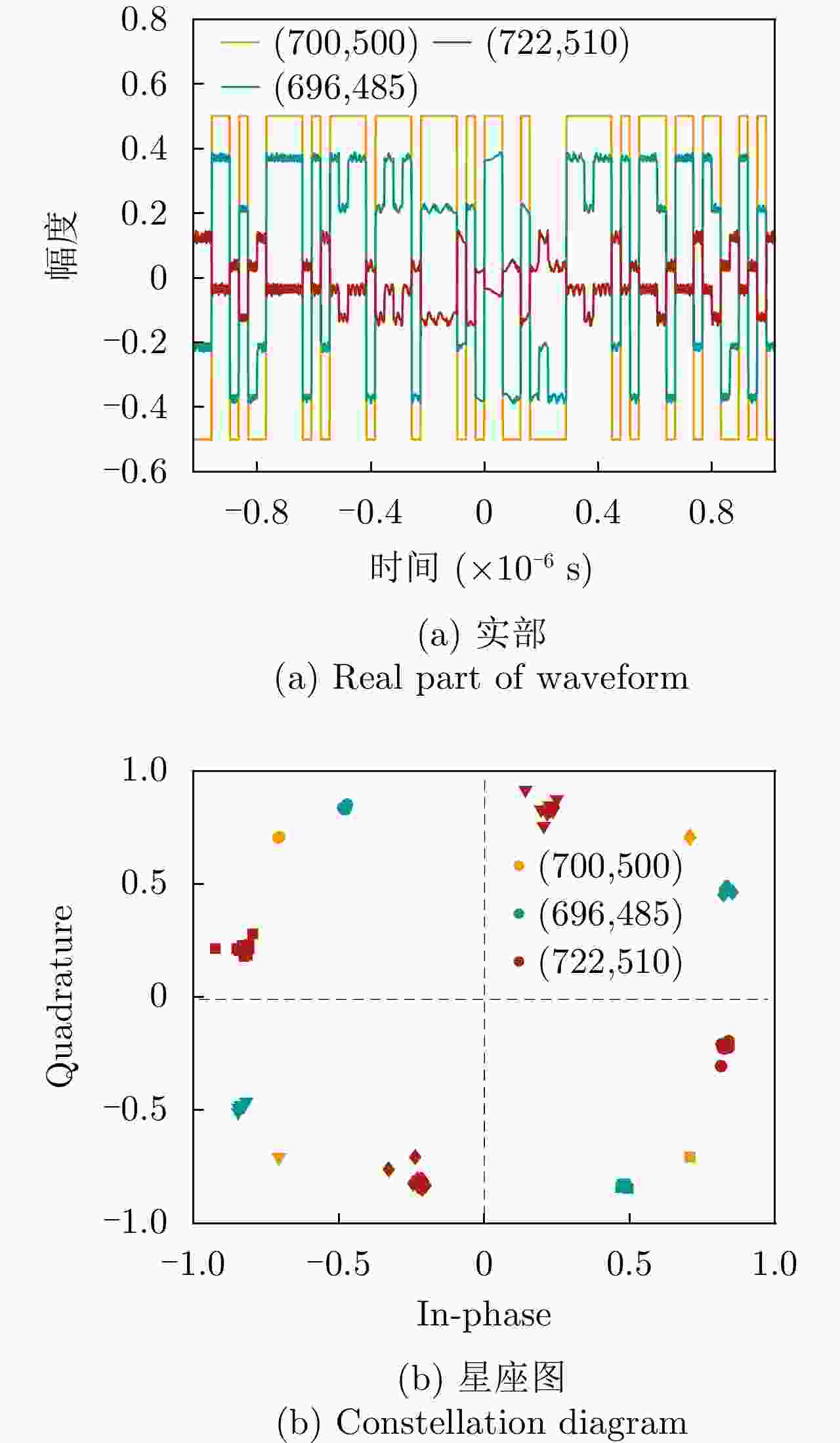
空间坐标(m) 是否位于雷达波胞内 脉压峰值(dB) 峰值旁瓣比(dB) 积分旁瓣比(dB) $\left( {600,800} \right)$ 是 60.21 –13.30 –9.73 $\left( {580,800} \right)$ 是 44.59 –13.30 –9.67 $\left( {560,800} \right)$ 否 22.96 –12.87 0.16
下载: 导出CSV
-
[1] MA Dingyou, SHLEZINGER N, HUANG Tianyao, et al. FRaC: FMCW-based joint radar-communications system via index modulation[J]. IEEE Journal of Selected Topics in Signal Processing, 2021, 15(6): 1348–1364. doi: 10.1109/JSTSP.2021.3118219 [2] ZHOU Zimu, WU Chenshu, YANG Zheng, et al. Sensorless sensing with WiFi[J]. Tsinghua Science and Technology, 2015, 20(1): 1–6. doi: 10.1109/TST.2015.7040509 [3] 梁兴东, 李焱磊, 刘云龙, 等. 一体化信号处理与先进处理架构展望[J]. 信号处理, 2022, 38(11): 2221–2233. doi: 10.16798/j.issn.1003-0530.2022.11.001LIANG Xingdong, LI Yanlei, LIU Yunlong, et al. Prospect of integrated signal processing and advanced processing architecture[J]. Journal of Signal Processing, 2022, 38(11): 2221–2233. doi: 10.16798/j.issn.1003-0530.2022.11.001 [4] ZHANG J A, RAHMAN L, WU Kai, et al. Enabling joint communication and radar sensing in mobile networks—A survey[J]. IEEE Communications Surveys & Tutorials, 2022, 24(1): 306–345. doi: 10.1109/COMST.2021.3122519 [5] LIYANAARACHCHI S D, RIIHONEN T, BARNETO C B, et al. Optimized waveforms for 5G-6G communication with sensing: Theory, simulations and experiments[J]. IEEE Transactions on Wireless Communications, 2021, 20(12): 8301–8315. doi: 10.1109/TWC.2021.3091806 [6] JACYNA G M, FELL B, and MCLEMORE D. A high-level overview of fundamental limits studies for the DARPA SSPARC program[C]. 2016 IEEE Radar Conference, Philadelphia, USA, 2016: 1–6. [7] 刘永军, 廖桂生, 李海川, 等. 电磁空间分布式一体化波形设计与信息获取[J]. 中国科学基金, 2021, 35(5): 701–707. doi: 10.16262/j.cnki.1000-8217.2021.05.005LIU Yongjun, LIAO Guisheng, LI Haichuan, et al. Distributed integrated waveform design and information acquisition in electromagnetic space[J]. Bulletin of National Natural Science Foundation of China, 2021, 35(5): 701–707. doi: 10.16262/j.cnki.1000-8217.2021.05.005 [8] 刘凡, 袁伟杰, 原进宏, 等. 雷达通信频谱共享及一体化: 综述与展望[J]. 雷达学报, 2021, 10(3): 467–484. doi: 10.12000/JR20113LIU Fan, YUAN Weijie, YUAN Jinhong, et al. Radar-communication spectrum sharing and integration: Overview and prospect[J]. Journal of Radars, 2021, 10(3): 467–484. doi: 10.12000/JR20113 [9] 马丁友, 刘祥, 黄天耀, 等. 雷达通信一体化: 共用波形设计和性能边界[J]. 雷达学报, 2022, 11(2): 198–212. doi: 10.12000/JR21146MA Dingyou, LIU Xiang, HUANG Tianyao, et al. Joint radar and communications: Shared waveform designs and performance bounds[J]. Journal of Radars, 2022, 11(2): 198–212. doi: 10.12000/JR21146 [10] HASSANIEN A, AMIN M G, ZHANG Y D, et al. Phase-modulation based dual-function radar-communications[J]. IET Radar, Sonar & Navigation, 2016, 10(8): 1411–1421. doi: 10.1049/iet-rsn.2015.0484 [11] HASSANIEN A, HIMED B, and RIGLING B D. A dual-function MIMO radar-communications system using frequency-hopping waveforms[C]. 2017 IEEE Radar Conference, Seattle, USA, 2017: 1721–1725. [12] LIU Yongjun, LIAO Guisheng, YANG Zhiwei, et al. Joint range and angle estimation for an integrated system combining MIMO radar with OFDM communication[J]. Multidimensional Systems and Signal Processing, 2019, 30(2): 661–687. doi: 10.1007/s11045-018-0576-2 [13] LIU Yongjun, LIAO Guisheng, CHEN Yufeng, et al. Super-resolution range and velocity estimations with OFDM integrated radar and communications waveform[J]. IEEE Transactions on Vehicular Technology, 2020, 69(10): 11659–11672. doi: 10.1109/TVT.2020.3016470 [14] WANG Jie, LIANG Xingdong, CHEN Longyong, et al. First demonstration of airborne MIMO SAR system for multimodal operation[J]. IEEE Transactions on Geoscience and Remote Sensing, 2022, 60: 5204113. doi: 10.1109/TGRS.2021.3066478 [15] 杨婧, 余显祥, 沙明辉, 等. MIMO系统探通一体化信号矩阵设计方法[J]. 雷达学报, 2023, 12(2): 262–274. doi: 10.12000/JR22087YANG Jing, YU Xianxiang, SHA Minghui, et al. Dual function radar and communication signal matrix design method for MIMO system[J]. Journal of Radars, 2023, 12(2): 262–274. doi: 10.12000/JR22087 [16] HASSANIEN A, AMIN M G, ZHANG Y D, et al. Dual-function radar-communications: Information embedding using sidelobe control and waveform diversity[J]. IEEE Transactions on Signal Processing, 2016, 64(8): 2168–2181. doi: 10.1109/TSP.2015.2505667 [17] JI Shilong, CHEN Hui, HU Quan, et al. A dual-function radar-communication system using FDA[C]. 2018 IEEE Radar Conference, Oklahoma City, USA, 2018: 224–229. [18] NUSENU S Y, SHAO Huaizong, PAN Ye, et al. Dual-function radar-communication system design via sidelobe manipulation based on FDA butler matrix[J]. IEEE Antennas and Wireless Propagation Letters, 2019, 18(3): 452–456. doi: 10.1109/LAWP.2019.2894015 [19] LIU Fan, ZHOU Longfei, MASOUROS C, et al. Toward dual-functional radar-communication systems: Optimal waveform design[J]. IEEE Transactions on Signal Processing, 2018, 66(16): 4264–4279. doi: 10.1109/TSP.2018.2847648 [20] LIU Fan, MASOUROS C, and GRIFFITHS H. Dual-functional radar-communication waveform design under constant-modulus and orthogonality constraints[C]. 2019 Sensor Signal Processing for Defence Conference, Brighton, UK, 2019: 1–5. [21] LIU Fan, MASOUROS C, RATNARAJAH T, et al. On range sidelobe reduction for dual-functional radar-communication waveforms[J]. IEEE Wireless Communications Letters, 2020, 9(9): 1572–1576. doi: 10.1109/LWC.2020.2997959 [22] MCCORMICK P M, BLUNT S D, and METCALF J G. Simultaneous radar and communications emissions from a common aperture, Part I: Theory[C]. 2017 IEEE Radar Conference, Seattle, USA, 2017: 1685–1690. [23] MCCORMICK P M, RAVENSCROFT B, BLUNT S D, et al. Simultaneous radar and communication emissions from a common aperture, Part II: Experimentation[C]. 2017 IEEE Radar Conference, Seattle, USA, 2017: 1697–1702. [24] JIANG Mengchao, LIAO Guisheng, YANG Zhiwei, et al. Integrated waveform design for an integrated radar and communication system with a uniform linear array[C]. 2020 IEEE 11th Sensor Array and Multichannel Signal Processing Workshop, Hangzhou, China, 2020: 1–5. [25] JIANG Mengchao, LIAO Guisheng, YANG Zhiwei, et al. Integrated radar and communication waveform design based on a shared array[J]. Signal Processing, 2021, 182: 107956. doi: 10.1016/j.sigpro.2020.107956 [26] 王文钦, 张顺生. 频控阵雷达技术研究进展综述[J]. 雷达学报, 2022, 11(5): 830–849. doi: 10.12000/JR22141WANG Wenqin and ZHANG Shunsheng. Recent advances in frequency diverse array radar techniques[J]. Journal of Radars, 2022, 11(5): 830–849. doi: 10.12000/JR22141 [27] 兰岚, 廖桂生, 许京伟, 等. 基于频率分集阵列的多功能一体化波形设计与信号处理方法[J]. 雷达学报, 2022, 11(5): 850–870. doi: 10.12000/JR22163LAN Lan, LIAO Guisheng, XU Jingwei, et al. Waveform design and signal processing method of a multifunctional integrated system based on a frequency diverse array[J]. Journal of Radars, 2022, 11(5): 850–870. doi: 10.12000/JR22163 [28] 刘泉华, 张凯翔, 梁振楠, 等. 地基分布式相参雷达技术研究综述[J]. 信号处理, 2022, 38(12): 2443–2459. doi: 10.16798/j.issn.1003-0530.2022.12.001LIU Quanhua, ZHANG Kaixiang, LIANG Zhennan, et al. Research overview of ground-based distributed coherent aperture radar[J]. Journal of Signal Processing, 2022, 38(12): 2443–2459. doi: 10.16798/j.issn.1003-0530.2022.12.001 [29] BALLANCE W P and MILLER T W. Impact of mainlobe interference angular extent on adaptive beamforming[C]. 1991 Conference Record of the Twenty-Fifth Asilomar Conference on Signals, Systems & Computers, Pacific Grove, USA, 1991: 989–993. [30] 陈炜宇, 骆俊杉, 王方刚, 等. 无线隐蔽通信容量限与实现技术综述[J]. 通信学报, 2022, 43(8): 203–218. doi: 10.11959/j.issn.1000−436x.2022153CHEN Weiyu, LUO Junshan, WANG Fanggang, et al. Survey of capacity limits and implementation techniques in wireless covert communication[J]. Journal on Communications, 2022, 43(8): 203–218. doi: 10.11959/j.issn.1000−436x.2022153 [31] 宋庆大, 高进涛, 荣辉. 关于分布式雷达组网的技术研究[J]. 科技创新导报, 2009(6): 17–18. doi: 10.3969/j.issn.1674-098X.2009.06.013SONG Qingda, GAO Jintao, and RONG Hui. Research on distributed radar networking technology[J]. Science and Technology Innovation Herald, 2009(6): 17–18. doi: 10.3969/j.issn.1674-098X.2009.06.013 [32] 鲁耀兵, 高红卫, 周宝亮. 分布式孔径相参合成雷达技术[J]. 雷达学报, 2017, 6(1): 55–64. doi: 10.12000/JR17014LU Yaobing, GAO Hongwei, and ZHOU Baoliang. Distributed aperture coherence-synthetic radar technology[J]. Journal of Radars, 2017, 6(1): 55–64. doi: 10.12000/JR17014 [33] GRATHWOHL A, STELZIG M, KANZ J, et al. Taking a look beneath the surface: Multicopter UAV-based ground-penetrating imaging radars[J]. IEEE Microwave Magazine, 2022, 23(10): 32–46. doi: 10.1109/MMM.2022.3188126 [34] NANZER J A, MGHABGHAB S R, ELLISON S M, et al. Distributed phased arrays: Challenges and recent advances[J]. IEEE Transactions on Microwave Theory and Techniques, 2021, 69(11): 4893–4907. doi: 10.1109/TMTT.2021.3092401 [35] LI Jian and STOICA P. MIMO radar with colocated antennas[J]. IEEE Signal Processing Magazine, 2007, 24(5): 106–114. doi: 10.1109/MSP.2007.904812 [36] FISHLER E, HAIMOVICH A, BLUM R S, et al. Spatial diversity in radars—Models and detection performance[J]. IEEE Transactions on Signal Processing, 2006, 54(3): 823–838. doi: 10.1109/TSP.2005.862813 [37] 杨善元, 杨燕译. 波[M]. 北京: 地震出版社, 1988: 4–15.YANG Shanyuan, YANG Yan, translation. Waveform[M]. Beijing: Seismological Press, 1988: 4–15. [38] 张嘉焱, 舒挺, 袁成卫. 高功率微波空间功率合成的初步研究[J]. 强激光与粒子束, 2007, 19(6): 915–918.ZHANG Jiayan, SHU Ting, and YUAN Chengwei. Primary study on spatial powers combining of parallel and intersectant beams of high power microwave[J]. High Power Laser and Particle Beams, 2007, 19(6): 915–918. [39] BAUSCHKE H H, COMBETTES P L, and LUKE D R. Phase retrieval, error reduction algorithm, and Fienup variants: A view from convex optimization[J]. Journal of The Optical Society of America A, 2002, 19(7): 1334–1345. doi: 10.1364/JOSAA.19.001334 -
计量
- 文章访问数: 1268
- HTML全文浏览量: 560
- PDF下载量: 241
- 被引次数: 0
