作者中心
专家审稿
责编办公
编辑办公
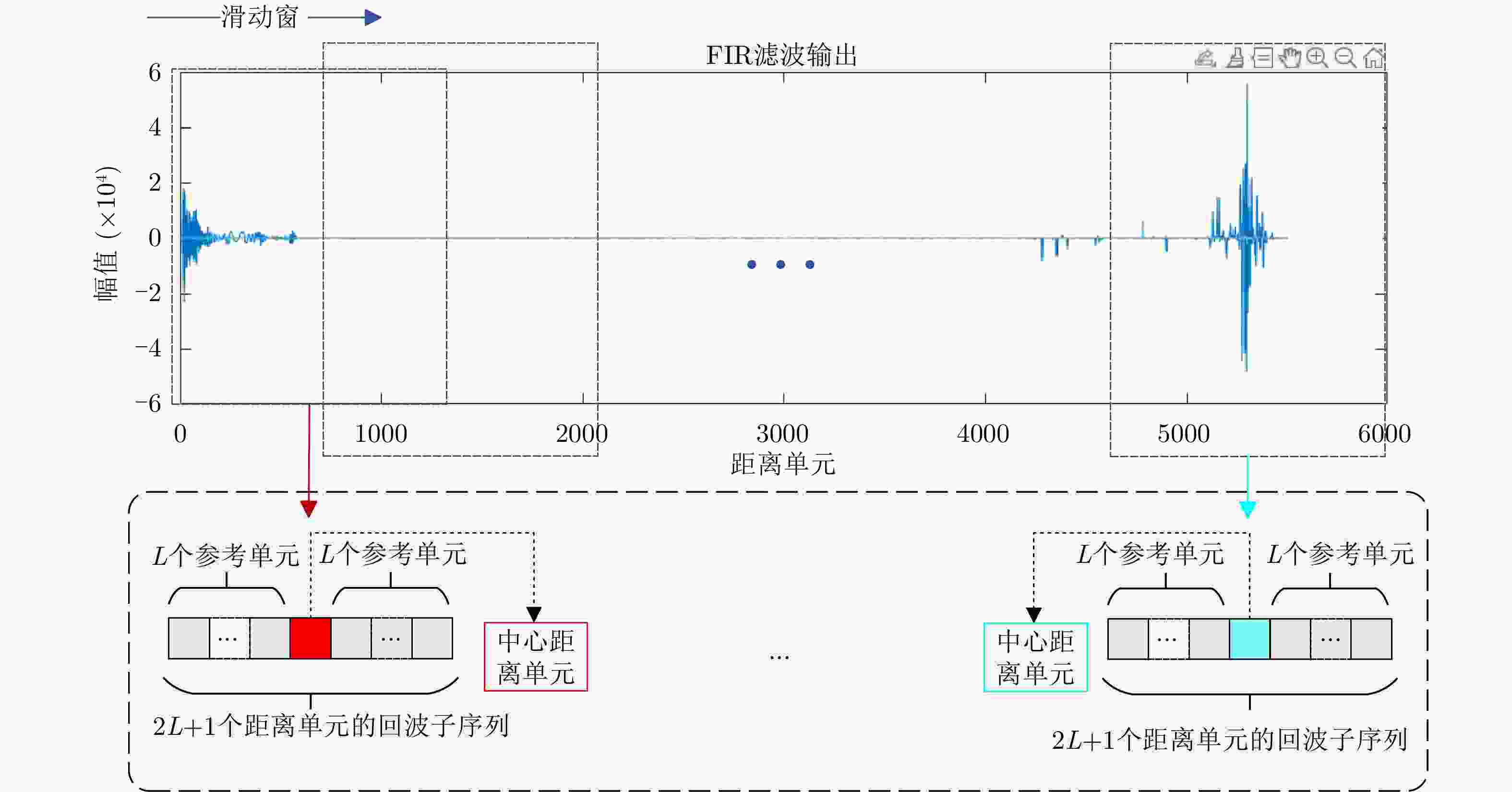
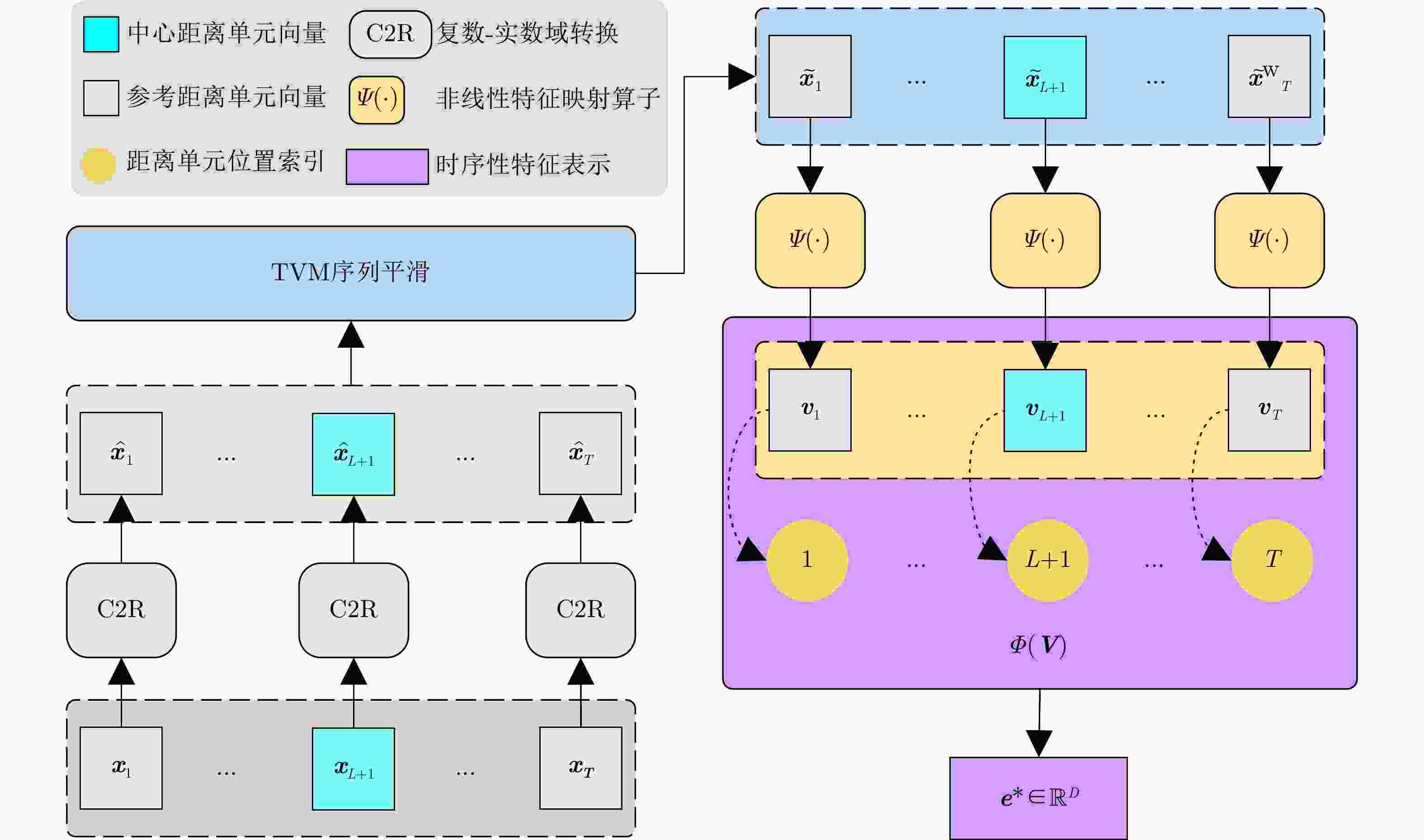
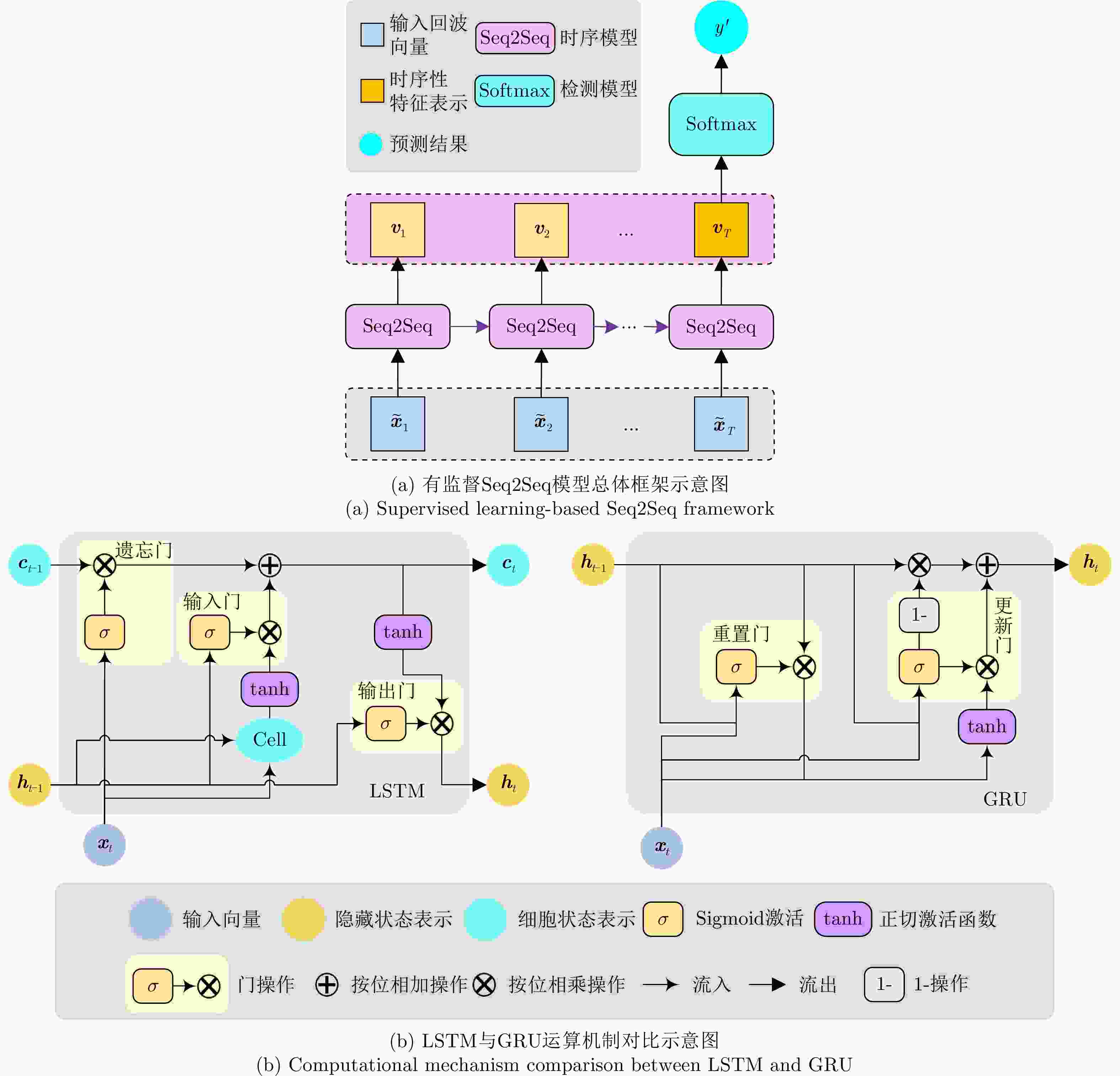
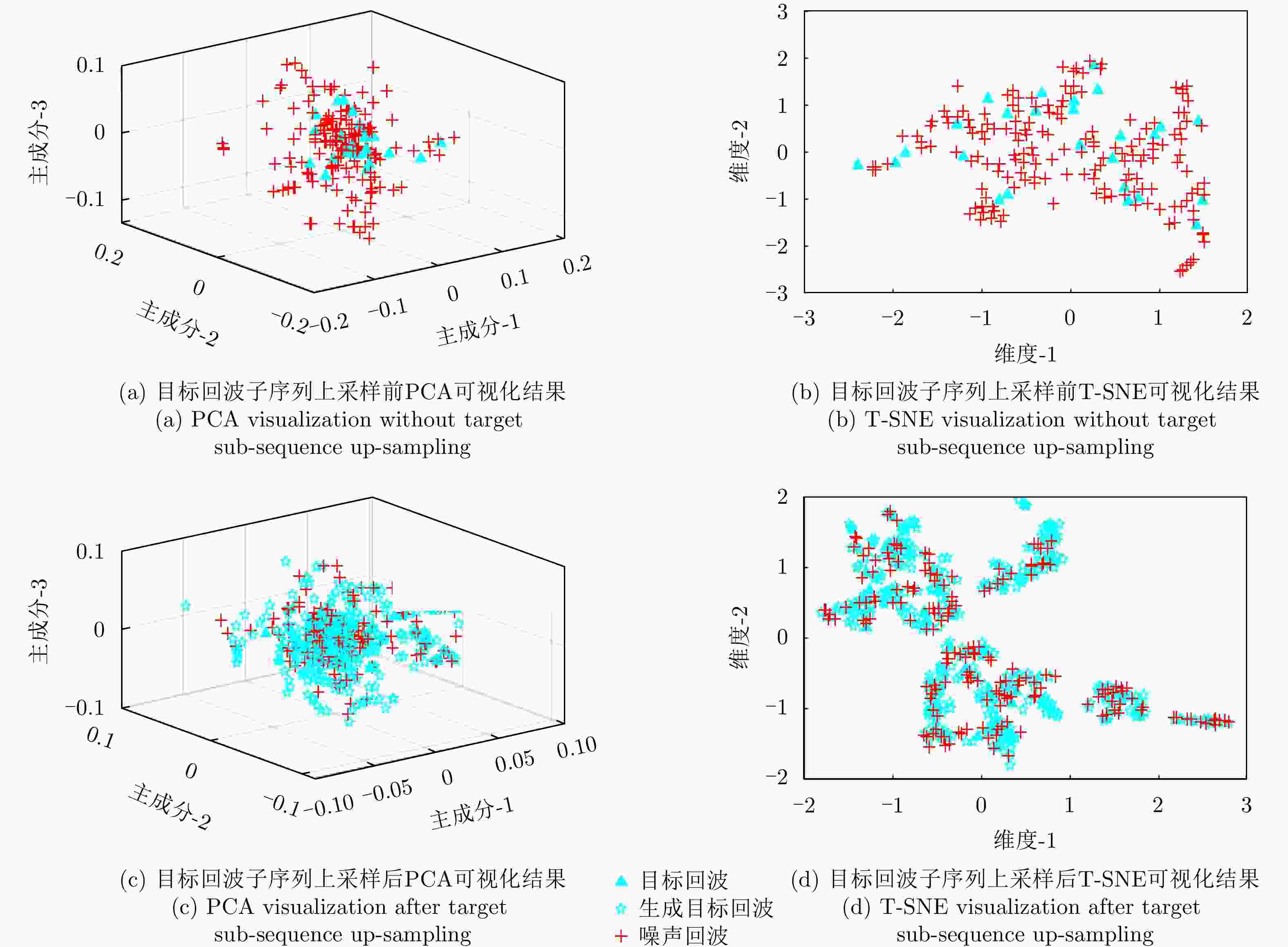
Capturing Temporal-dependence in Radar Echo for Spatial-temporal Sparse Target Detection
-
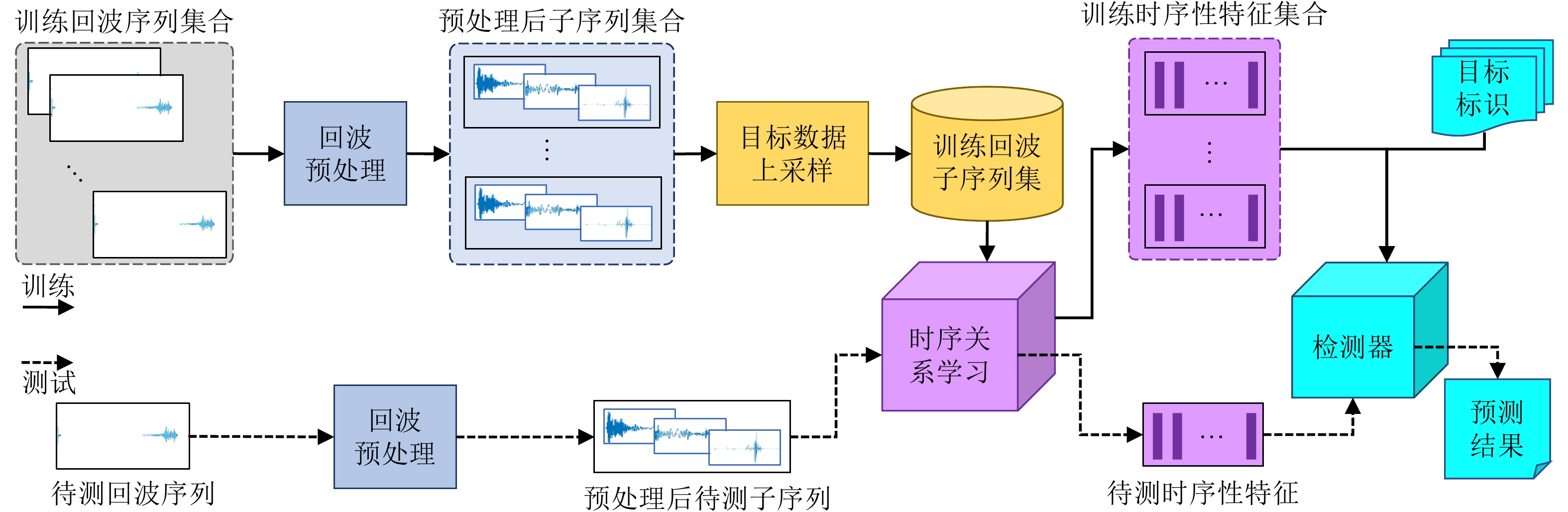
摘要: 该文基于低慢小目标探测的地面预警雷达实测回波数据，系统性地提出了一种数据驱动式的目标检测方法框架，解决了两个关键问题：(1)针对当前数据驱动式的目标检测方法未能充分利用特征表示学习来发挥优势的问题，提出了回波时序依赖关系的表示学习方法，并给出无监督和有监督学习的两种实现方式；(2)低慢小目标在雷达探测范围中呈现稀疏性，目标-杂波数目的极度不均衡致使网络判决面严重向杂波倾斜。因此，该文提出利用异常值检测方法中的样本均衡思想，有效缓解了检测模型的判决偏移问题。最后基于实测数据对所提方法框架的各组成部分进行了消融实验，实验结果充分验证了回波时序性特征表示学习和样本均衡策略的有效性。在实测序贯验证条件下，两种检测方法均取得了优于多种CFAR方法的综合检测性能。Abstract: Existing data-driven object detection methods use the Constant False Alarm Rate (CFAR) principle to achieve more robust detection performance using supervised learning. This study systematically proposes a data-driven target detection framework based on the measured echo data from the ground early warning radar for low-altitude slow dim target detection. This framework addresses two key problems in this field: (1) aiming at the problem that current data-driven object detection methods fail to make full use of feature representation learning to exert its advantages, a representation learning method of echo temporal dependency is proposed, and two implementations, including unsupervised- and supervised-learning are given; (2) Low-altitude slow dim targets show extreme sparsity in the radar detection range, such unevenness of target-clutter sample scale causes the trained model to seriously tilt to the clutter samples, resulting in the decision deviation. Therefore, we further propose incorporating the data balancing policy of abnormal detection into the framework. Finally, ablation experiments are performed on the measured X-band echo data for each component in the proposed framework. Experimental results completely validate the effectiveness of our echo temporal representation learning and balancing policy. Additionally, under real sequential validation, our proposed method achieves comprehensive detection performance that is superior to multiple CFAR methods.
-
图 1 回波时序关系依赖的时空域稀疏条件下雷达目标检测框架
Figure 1. Radar echo temporal relation learning-based spatial-temporal sparse target detection
图 4 EchoDarwin无监督回波时序性特征表示学习示意图
Figure 4. The diagram of EchoDarwin for unsupervised temporal feature learning of radar echo
图 5 基于有监督Seq2Seq模型的雷达回波时序性特征表示学习方法示意图
Figure 5. The illustration of supervised Seq2Seq-based radar echo temporal feature learning method
图 6 目标-杂波样本规模均衡化处理示意图
Figure 6. The illustration of target-clutter sample scale balance
图 7 目标样本均衡化处理前后数据分布可视化对比
Figure 7. The target sample scale visualization of target-clutter sample scale balancing
图 8 回波时序关系依赖的雷达目标检测框架训练流程示意图
Figure 8. The illustration of training process for echo temporal relation-based radar target detection framework
图 9 不同目标样本均衡化处理程度对检测性能的影响
Figure 9. The target sample scale visualization of target-clutter sample scale balancing
图 10 实测序贯验证条件下与多种CFAR方法的检测结果对比示例图(一次扫描周期)
Figure 10. Example of detection results comparison with CFARs under sequential validation of real-measured data (in one radar scanning cycle)
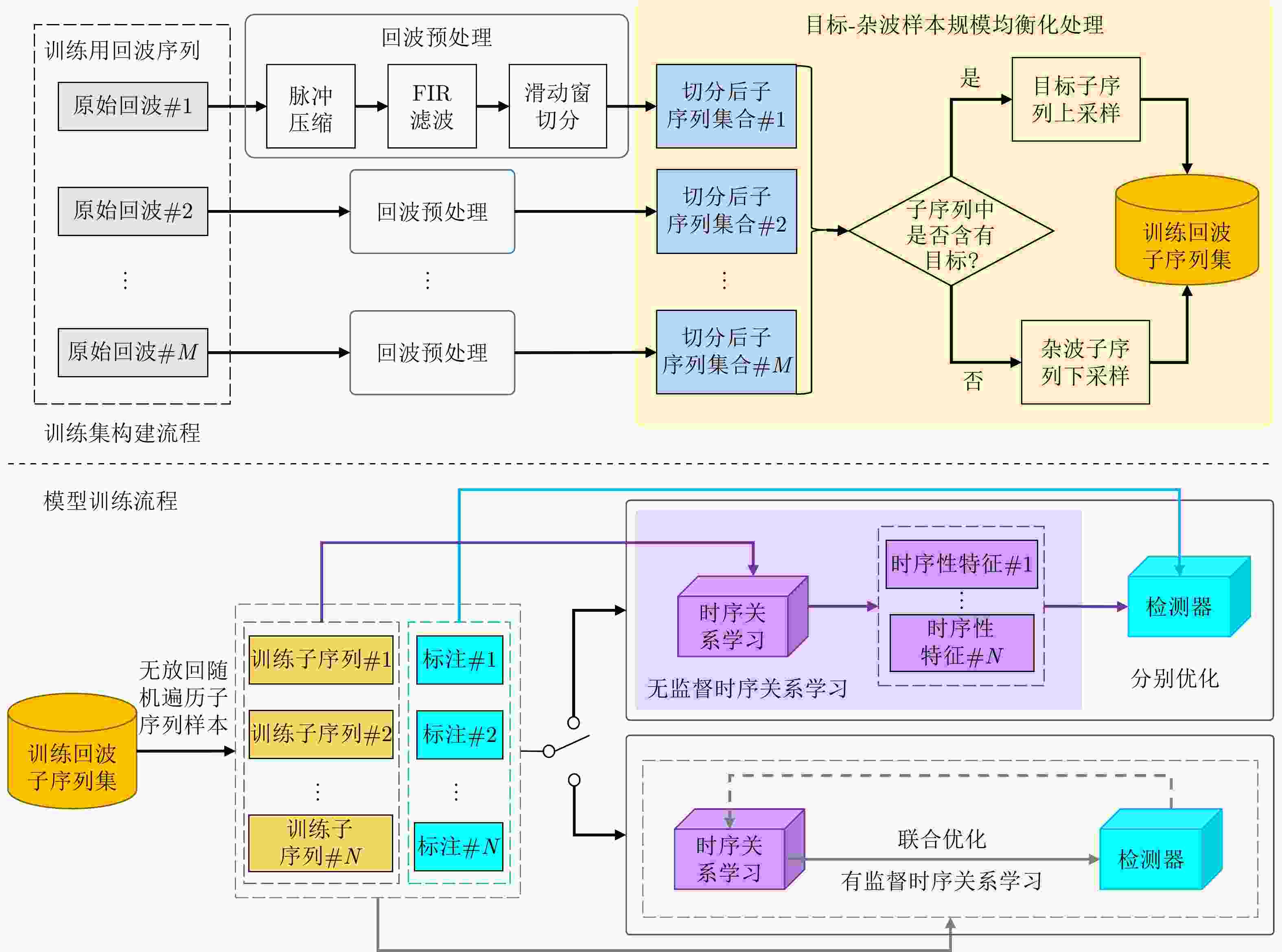
表 1 目标-杂波样本规模均衡化处理算法
Table 1. Target-Clutter sample scale balancing algorithm
输入: • 目标样本集合：$ {\varOmega _{{\text{tgt}}}} = \left\{ {{{\boldsymbol{X}}_1},{{\boldsymbol{X}}_2},\; \cdots ,\;{{\boldsymbol{X}}_M}} \right\},\;{{\boldsymbol{X}}_i} \in {{\mathbb{C}}^{T \times P}},\;i = 1,2,\; \cdots ,\;M $； • 生成比例值：${\rm{SyncRatio}} = N \times 100\%$； • 生成所需近邻个数：k； • 定义生成样本集合：$ \varOmega _{{\text{sync}}}^\dagger = \{ \} $； 1. 初始化： 1.1 逐样本行优先reshape：${\varOmega }_{\text{tgt} }\to {\varOmega }_{\text{tgt} }^{\text{vec} }=\left\{ {{\boldsymbol{X}}}_{1}^{\text{vec} },{{\boldsymbol{X}}}_{2}^{\text{vec} },\cdots,{{\boldsymbol{X}}}_{M}^{\text{vec} }\right\},\;{{\boldsymbol{X}}}_{i}^{\text{vec} }\in {\mathbb{C} }^{TP}$； 1.2 样本生成序号：$ r = 1 $； 2. While $r \le \left\lfloor {{\rm{SyncRatio}}/100 \times M} \right\rfloor$ do (其中，$ \left\lfloor \cdot \right\rfloor $为向下取整) 2.1 有放回地从$ \varOmega _{{\text{tgt}}}^{{\text{vec}}} $随机采样一个$ {\boldsymbol{X}}_s^{{\text{vec}}} $，其中$s = \left\lfloor {M \times {{\rm{rand}}} (1)} \right\rfloor + 1$； 2.2 计算$ {\boldsymbol{X}}_s^{{\text{vec}}} $的k个近邻$ \varOmega _{{\text{nn}}}^{(s)} = \left\{ {{\boldsymbol{X}}_1^{(s)},{\boldsymbol{X}}_2^{(s)},\; \cdots ,\;{\boldsymbol{X}}_k^{(s)}} \right\} $； 2.3 从$ \varOmega _{{\text{nn}}}^{(s)} $随机选取一个近邻$ {\boldsymbol{X}}_n^{(s)} $，其中$n = \left\lfloor {k \times {{\rm{rand}}} (1)} \right\rfloor + 1$； 2.4 生成新的目标样本向量：${\boldsymbol{X} }{_r^{ {\text{vec} }' } } = {\boldsymbol{X} }_s^{ {\text{vec} } } + \gamma \odot ({\boldsymbol{X} }_s^{ {\text{vec} } } - {\boldsymbol{X} }_n^{(s)})$, $\gamma = {{\rm{rand}}} (1)$ (16)
(其中，$ \odot $为按元素位置，${{\rm{rand}}} (1)$表示随机从0~1之间采样一个值)；2.5 目标样本向量切片还原：${\boldsymbol{X} }{_r^{ {\text{vec} }' } } \to { {\boldsymbol{X} }'_r} \in { {\mathbb{C} }^{T \times P} }$； 2.6 将新样本放入生成集合：$ \varOmega _{{\text{sync}}}^\dagger = $$\varOmega _{ {\text{sync} } }^\dagger \cup \left\{ { { {\boldsymbol{X} }'_r} } \right\}$； 2.7 判断r是否满足终止条件。 3. 合并目标样本集合和生成后的目标样本集合：$ \varOmega _{{\text{tgt}}}^\dagger {\text{ = }}{\varOmega _{{\text{tgt}}}} \cup $$ \varOmega _{{\text{sync}}}^\dagger $； 4. End. 输出：平衡后目标样本集合$ \varOmega _{{\text{tgt}}}^\dagger $。 
下载: 导出CSV
表 2 雷达回波时序关系学习网络结构及训练配置
Table 2. Network structure and training configuration of radar echo temporal relationship learning
网络名称 输入序列维度 时序编码层描述23 输出层描述24 Bi-LSTM 21×12 {Bi-lstm_128}×2 FC(128, 2) + Softmax Bi-GRU 21×12 {Bi-GRU_128}×2 FC(128, 2) + Softmax MLP-LSTM 21×12 FC(12, 32)+FC(32, 32)+LeakyReLU+Bi-lstm_128 FC(128, 2) + Softmax ConvLSTM 21×1×1×12 (Conv_1×1_32)+BN+LeakyReLU+ Bi-lstm_128 FC(128, 2) + Softmax 优化算法：Adam[38]；初始学习率：0.01；批大小：32；最大迭代次数：100
下载: 导出CSV
表 3 EchoDarwin+SVM消融实验结果
Table 3. Ablation experiment results of EchoDarwin
TVM NFM 评价指标 正确率(%) 虚警率(%) 检测精度(%) 目标召回率(%) F值 × × 74.8 9.8 84.0 57.7 0.684 × Chi-2 80.7 17.7 80.0 78.8 0.794 × PosNeg 84.1 11.8 85.8 79.6 0.826 √ × 75.2 9.1 85.0 57.7 0.687 √ Chi-2 80.0 20.2 78.0 80.3 0.791 √ PosNeg 84.8 13.0 84.9 82.4 0.837 注：表3—表5中加粗数据代表性能表现最优。
下载: 导出CSV
表 4 EchoDarwin与其他非学习序列表示的性能对比结果
Table 4. Performance comparison between EchoDarwin and other representations of non-learning sequence
方法 特征维度 评价指标 正确率(%) 虚警率(%) 检测精度(%) 目标召回率(%) F值 Temp. Avg-Pooling 24 82.4 14.4 83.1 78.8 0.809 Temp. Max-Pooling 24 80.7 15.7 81.4 76.6 0.789 Temp. Concatenation 24×21 82.4 11.8 85.2 75.9 0.803 EchoDarwin 24 84.8 13.0 84.9 82.4 0.837
下载: 导出CSV
表 5 无监督与有监督式回波表示学习方法检测性能对比
Table 5. Comparison of detection performance between unsupervised and supervised echo representation learning methods
方法 模型 特征维度 正确率(%) 虚警率(%) 检测精度(%) 目标召回率(%) F值 无监督 EchoDarwin+SVM 24 84.8 13.0 84.9 82.4 0.837 Bi-EchoDarwin+SVM 48 85.9 12.4 86.0 84.0 0.849 有监督 LSTM 128 91.4 13.1 87.8 94.9 0.912 Bi-LSTM 128 96.6 6.6 93.7 99.3 0.964 GRU 128 95.2 5.8 94.2 95.6 0.949 Bi-GRU 128 96.6 4.4 95.7 97.1 0.964 MLP-LSTM 128 94.8 8.8 91.8 97.8 0.947 ConvLSTM 128 93.8 8.0 92.2 94.9 0.935
下载: 导出CSV
表 6 不同目标样本生成比例下Bi-EchoDarwin的检测性能结果
Table 6. Detection performance of Bi-EchoDarwin under different target sample generation ratio
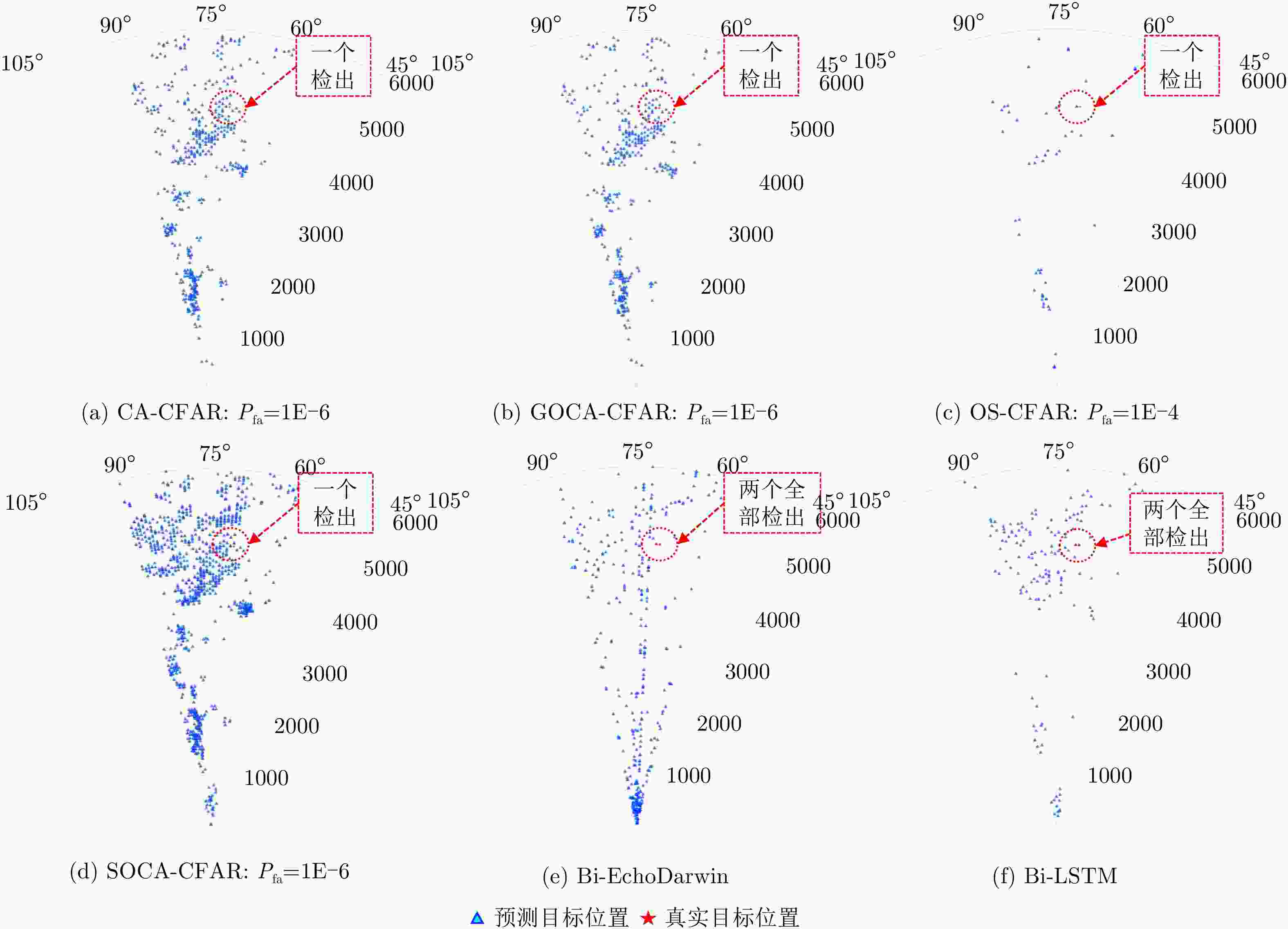
目标样本生成比例(SyncRatio)(%) 正确率(%) 虚警率(%) 检测精度(%) 目标召回率(%) F值 #训练/#测试 0 93.3 0 100 8.3 0.154 338/165 200 85.8 7.8 64.7 59.5 0.620 389/190 400 82.8 6.5 77.8 56.5 0.654 440/215 600 80.8 4.6 87.3 55.2 0.676 491/240 800 86.4 6.5 89.6 76.8 0.827 542/265 1000 85.9 13.0 84.9 84.0 0.849 593/310
下载: 导出CSV
表 7 所提方法与多种CFAR方法在RSPD下的检出结果统计情况
Table 7. Statistical analysis of detection results of the proposed method and multiple CFAR methods under RSPD
检测方法 RSPD 3个扫描周期的平均检出情况(共计6个目标) 3个扫描周期的恒虚警概率值(${P_{{\rm{fa}}} }$) 正确率(%) 目标检出情况(检出/实际) 虚警率(%) CA-CFAR 99.77 3/6 0.23 {1E–6, 1E–6, 1E–7} GOCA-CFAR 99.85 3/6 0.15 {1E–6, 1E–7, 1E–7} OS-CFAR 99.77 2/6 0.23 {1E–4, 1E–3, 1E–3} SOCA-CFAR 99.29 3/6 0.71 {1E–6, 1E–7, 1E–7} Bi-EchoDarwin 99.61 5/6 0.39 – Bi-LSTM 99.92% 6/6 0.08% –
下载: 导出CSV
-
[1] BIJELIC M, GRUBER T, and RITTER W. A benchmark for lidar sensors in fog: Is detection breaking down?[C]. 2018 IEEE Intelligent Vehicles Symposium (IV), Changshu, China, 2018: 760–767. [2] MADANI Sohrab, GUAN Jayden, AHMED Waleed, et al. Radatron: Accurate Detection Using Multi-resolution Cascaded MIMO Radar, ECCV 2022, 160–178. [3] 王俊, 郑彤, 雷鹏, 等. 深度学习在雷达中的研究综述[J]. 雷达学报, 2018, 7(4): 395–411. doi: 10.12000/JR18040WANG Jun, ZHENG Tong, LEI Peng, et al. Study on deep learning in radar[J]. Journal of Radars, 2018, 7(4): 395–411. doi: 10.12000/JR18040 [4] ROHLING H. Radar CFAR thresholding in clutter and multiple target situations[J]. IEEE Transactions on Aerospace and Electronic Systems, 1983, AES-19(4): 608–621. doi: 10.1109/TAES.1983.309350 [5] KELLY E J. An adaptive detection algorithm[J]. IEEE Transactions on Aerospace and Electronic Systems, 1986, AES-22(2): 115–127. doi: 10.1109/TAES.1986.310745 [6] ROBEY F C, FUHRMANN D R, KELLY E J, et al. A CFAR adaptive matched filter detector[J]. IEEE Transactions on Aerospace and Electronic Systems, 1992, 28(1): 208–216. doi: 10.1109/7.135446 [7] COLUCCIA A and RICCI G. Radar detection in K-distributed clutter plus thermal noise based on KNN methods[C]. 2019 IEEE Radar Conference (RadarConf), Boston, USA, 2019: 1–5, [8] COLUCCIA A, FASCISTA A, and RICCI G. A KNN-based radar detector for coherent targets in non-Gaussian noise[J]. IEEE Signal Processing Letters, 2021, 28: 778–782. doi: 10.1109/LSP.2021.3071972 [9] BRODESKI D, BILIK I, and GIRYES R. Deep radar detector[C]. 2019 IEEE Radar Conference (RadarConf), Boston, USA, 2019: 1–6, [10] BALL J E. Low signal-to-noise ratio radar target detection using Linear Support Vector Machines (L-SVM)[C]. 2014 IEEE Radar Conference, Cincinnati, USA, 2014: 1291–1294. [11] WANG Jingang and LI Songbin. Maritime radar target detection in sea clutter based on CNN with dual-perspective attention[J]. IEEE Geoscience and Remote Sensing Letters, 2023, 20: 3500405. doi: 10.1109/LGRS.2022.3230443 [12] QU Qizhe, WANG Yongliang, LIU Weijian, et al. A false alarm controllable detection method based on CNN for sea-surface small targets[J]. IEEE Geoscience and Remote Sensing Letters, 2022, 19: 4025705. doi: 10.1109/LGRS.2022.3190865 [13] WANG Yizhou, JIANG Zhongyu, LI Yudong, et al. RODNet: A real-time radar object detection network cross-supervised by camera-radar fused object 3D localization[J]. IEEE Journal of Selected Topics in Signal Processing, 2021, 15(4): 954–967. doi: 10.1109/JSTSP.2021.3058895 [14] GAO Xiangyu, XING Guanbin, ROY S, et al. RAMP-CNN: A novel neural network for enhanced automotive radar object recognition[J]. IEEE Sensors Journal, 2021, 21(4): 5119–5132. doi: 10.1109/JSEN.2020.3036047 [15] KAUL P, DE MARTINI D, GADD M, et al. RSS-Net: Weakly-supervised multi-class semantic segmentation with FMCW radar[C]. 2020 IEEE Intelligent Vehicles Symposium (IV), Las Vegas, USA, 2020: 431–436. [16] OUAKNINE A, NEWSON A, PÉREZ P, et al. Multi-view radar semantic segmentation[C]. 2021 IEEE/CVF International Conference on Computer Vision (ICCV), Montreal, Canada, 2021: 15651–15660. [17] WANG Li, TANG Jun, and LIAO Qingmin. A study on radar target detection based on deep neural networks[J]. IEEE Sensors Letters, 2019, 3(3): 7000504. doi: 10.1109/LSENS.2019.2896072 [18] LORAN T, DA SILVA A B C, JOSHI S K, et al. Ship detection based on faster R-CNN using range-compressed airborne radar data[J]. IEEE Geoscience and Remote Sensing Letters, 2023, 20: 3500205. doi: 10.1109/LGRS.2022.3229141 [19] OUAKNINE A, NEWSON A, REBUT J, et al. CARRADA dataset: Camera and automotive radar with range- angle- Doppler annotations[C]. 25th International Conference on Pattern Recognition, Milan, Italy, 2021: 5068–5075. [20] HUANG Zhongling, PAN Zongxu, and LEI Bin. What, where, and how to transfer in SAR target recognition based on deep CNNs[J]. IEEE Transactions on Geoscience and Remote Sensing, 2020, 58(4): 2324–2336. doi: 10.1109/tgrs.2019.2947634 [21] JITHESH V, SAGAYARAJ M J, and SRINIVASA K G. LSTM recurrent neural networks for high resolution range profile based radar target classification[C]. 2017 3rd International Conference on Computational Intelligence & Communication Technology (CICT), Ghaziabad, India, 2017: 1–6. [22] 丁鹭飞, 耿富录, 陈建春. 雷达原理[M]. 4版. 北京: 电子工业出版社, 2009: 169–170.DING Lufei, GENG Fulu, and CHEN Jianchun. Principles of Radar[M]. 4th ed. Beijing: Publishing House of Electronics Industry, 2009: 169–170. [23] MAHAFZA B R. MATLAB Simulations for Radar Systems Design[M]. New York, USA: Chapman and Hall, 2003: 19. [24] MARHON S A, CAMERON C J F, and KREMER S C. Recurrent Neural Networks[M]. BIANCHINI M, MAGGINI M, and JAIN L C. Handbook on Neural Information Processing. Berlin: Springer, 2013: 29–65. [25] GRAVES A. Generating sequences with recurrent neural networks[EB/OL]. https://arxiv.org/abs/1308.0850, 2013. [26] HOCHREITER S and SCHMIDHUBER J. Long short-term memory[J]. Neural Computation, 1997, 9(8): 1735–1780. doi: 10.1162/neco.1997.9.8.1735 [27] ZHANG Liwen, HAN Jiqing, and DENG Shiwen. Unsupervised temporal feature learning based on sparse coding embedded BoAW for acoustic event recognition[C]. The 19th Annual Conference of the International Speech Communication Association, Hyderabad, India, 2018: 3284–3288. [28] DRUCKER H, BURGES C J C, KAUFMAN L, et al. Support vector regression machines[C]. The 9th International Conference on Neural Information Processing Systems, Denver, Colorado, 1996: 155–161. [29] LIN C J, WENG R C, and KEERTHI S S. Trust region newton method for large-scale logistic regression[J]. Journal of Machine Learning Research, 2008, 9: 627–650. [30] VEDALDI A and ZISSERMAN A. Efficient additive kernels via explicit feature maps[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2012, 34(3): 480–492. doi: 10.1109/TPAMI.2011.153 [31] ARANDJELOVIĆ R and ZISSERMAN A. Three things everyone should know to improve object retrieval[C]. 2012 IEEE Conference on Computer Vision and Pattern Recognition, Providence, USA, 2012: 2911–2918. [32] CHO K, VAN MERRIENBOER B, GULCEHRE C, et al. Learning phrase representations using RNN encoder-decoder for statistical machine translation[C]. The 2014 Conference on Empirical Methods in Natural Language Processing, Doha, Qatar, 2014: 1724–1734. [33] CHAWLA N V, BOWYER K W, HALL L O, et al. SMOTE: Synthetic minority over-sampling technique[J]. Journal of Artificial Intelligence Research, 2002, 16: 321–357. doi: 10.1613/jair.953 [34] ZHANG Hongyi, CISSÉ M, DAUPHIN Y N, et al. mixup: Beyond empirical risk minimization[C]. 6th International Conference on Learning Representations, Vancouver, Canada, 2018. [35] VAPNIK V N. Statistical Learning Theory[M]. New York: Wiley, 1998. [36] GRAVES A and SCHMIDHUBER J. Framewise phoneme classification with bidirectional LSTM networks[C]. 2005 IEEE International Joint Conference on Neural Networks, Montreal, Canada, 2005: 2047–2052. [37] ZHANG Xiaohu, ZOU Yuexian, and SHI Wei. Dilated convolution neural network with LeakyReLU for environmental sound classification[C]. 2017 22nd International Conference on Digital Signal Processing (DSP), London, UK, 2017: 1–5. [38] DIEDERIK P and KINGMA J B. Adam: A method for stochastic optimization[C]. 3rd International Conference on Learning Representations, San Diego, USA, 2015. -
计量
- 文章访问数: 1337
- HTML全文浏览量: 634
- PDF下载量: 253
- 被引次数: 0
