无先验模型复杂结构设施SAR全方位三维成像方法研究

林赟; 张琳; 韦立登; 张汉卿; 冯珊珊; 王彦平; 洪文

doi:10.12000/JR22148

无先验模型复杂结构设施SAR全方位三维成像方法研究

doi: 10.12000/JR22148

林赟¹,
张琳¹,
韦立登²,
张汉卿^{3, 4},
冯珊珊^{3, 4},
王彦平¹,
洪文^{3, 4, ,}

1.
北方工业大学信息学院雷达监测技术实验室北京 100144
2.
北京无线电测量研究所北京 100854
3.
中国科学院空天信息创新研究院北京 100094
4.
中国科学院空间信息处理与应用系统技术重点实验室北京 100190

基金项目: 国家自然科学基金(61860206013, 62131001)，快速扶持项目(80913010302)，北京市教育委员会创新团队建设计划(IDHT20190501)

详细信息

作者简介:
林　赟，博士，副研究员，硕士生导师，主要研究方向为多角度SAR三维成像技术

韦立登，博士，研究员，研究方向为机载SAR成像与InSAR处理技术

洪　文，博士，研究员，博士生导师，研究方向为合成孔径雷达(SAR)成像新概念新体制、多维度SAR成像机理与方法

通讯作者:
洪文 whong@mail.ie.ac.cn

责任主编：张晓玲 Corresponding Editor: ZHANG Xiaoling
中图分类号: TN959
计量
- 文章访问数: 1108
- HTML全文浏览量: 614
- PDF下载量: 159
- 被引次数: 0
出版历程
- 收稿日期: 2022-07-14
- 修回日期: 2022-08-04
- 网络出版日期: 2022-08-22
- 刊出日期: 2022-10-28

Research on Full-aspect Three-dimensional SAR Imaging Method for Complex Structural Facilities without Prior Model

LIN Yun¹,
ZHANG Lin¹,
WEI Lideng²,
ZHANG Hanqing^{3, 4},
FENG Shanshan^{3, 4},
WANG Yanping¹,
HONG Wen^{3, 4
, ,}

1.
Radar Monitoring Technology Laboratory, School of Information, North China University of Technology, Beijing 100144, China
2.
Beijing Institute of Radio Measurement, Beijing 100854, China
3.
Aerospace Information Research Institute, Chinese Academy of Sciences, Beijing 100094, China
4.
Key Laboratory of Technology in Geo-Spatial Information Processing and Application System, Chinese Academy of Sciences, Beijing 100190, China

Funds: The National Natural Science Foundation of China (61860206013, 62131001), Rapid Support Project (80913010302), Innovation Team Building Support Program of Beijing Municipal Education Commission (IDHT20190501)

More Information

Corresponding author: HONG Wen, whong@mail.ie.ac.cn

摘要

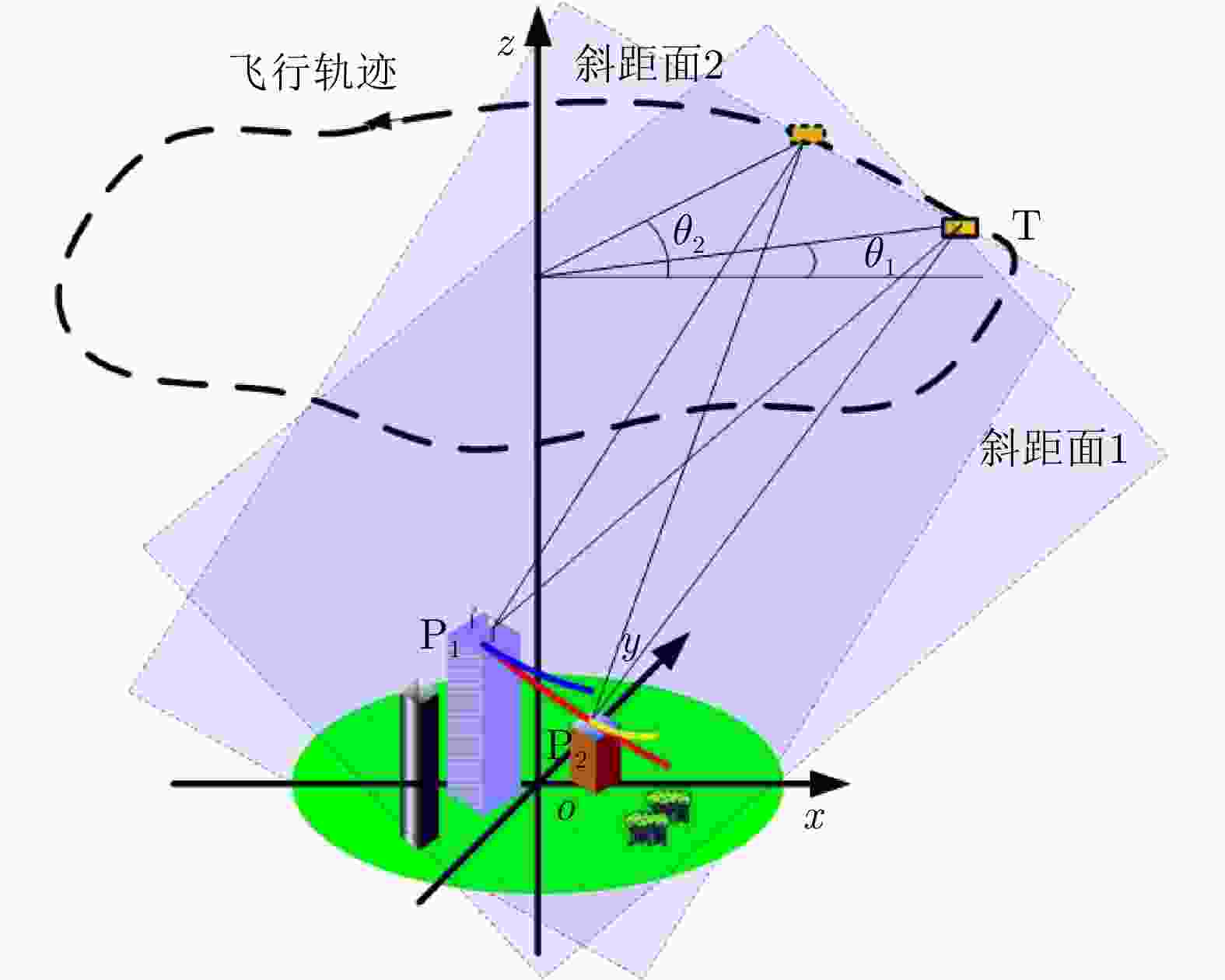
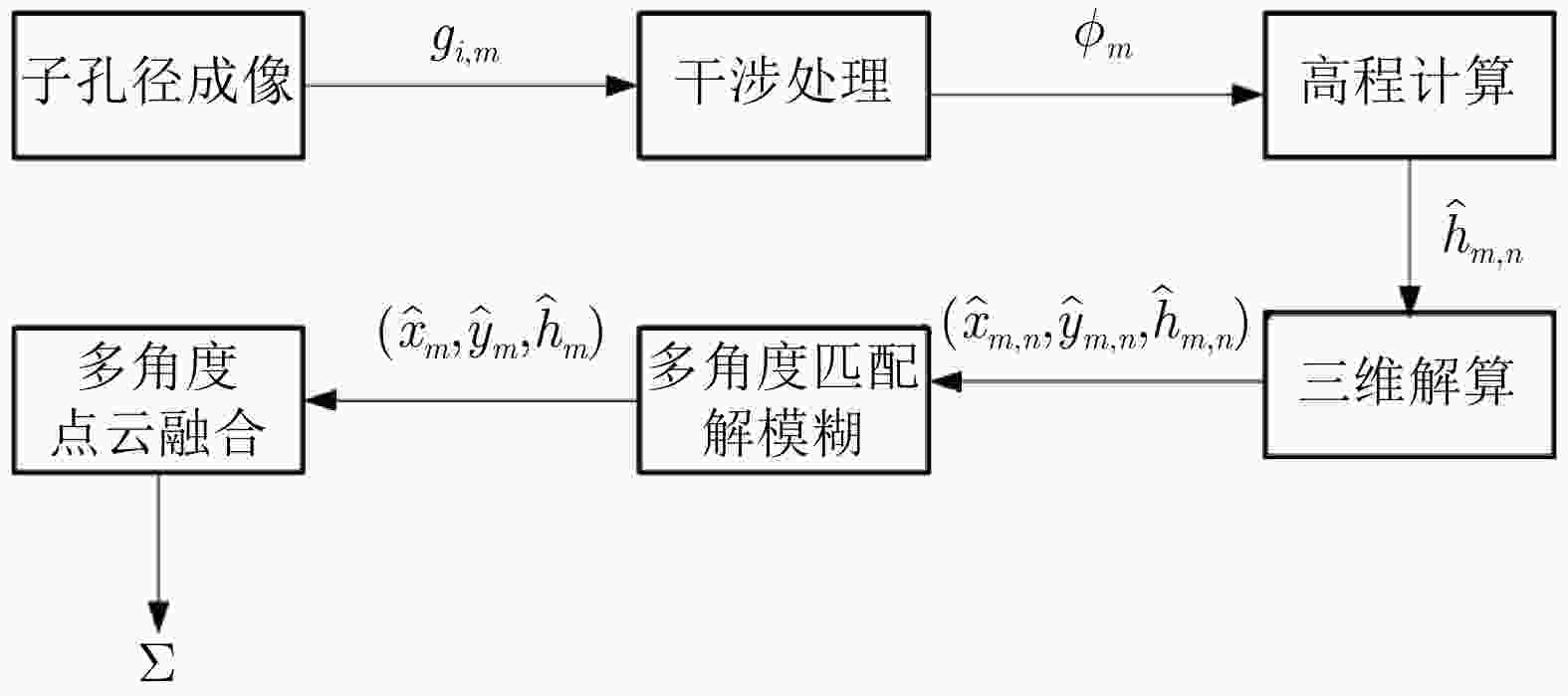
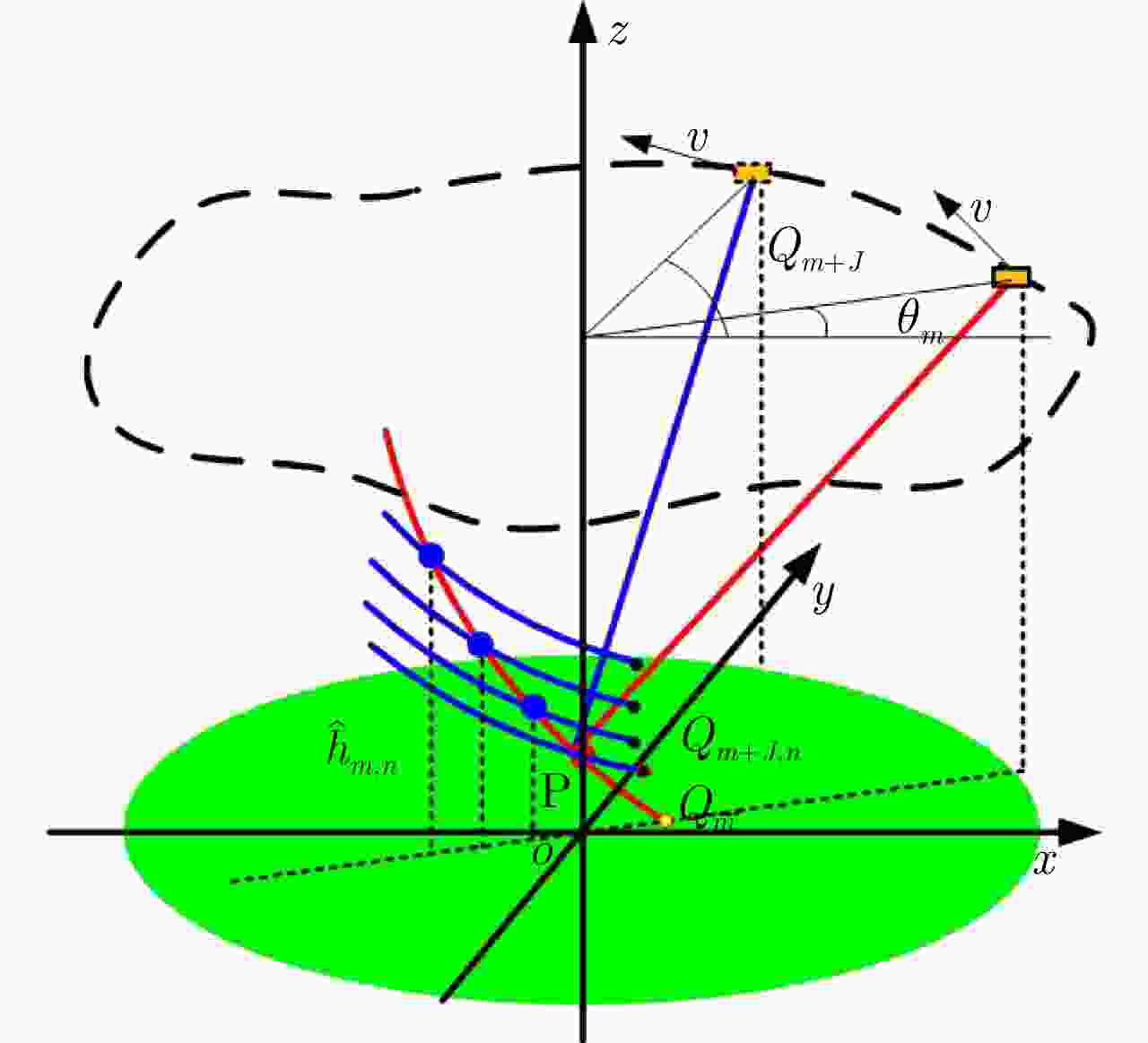
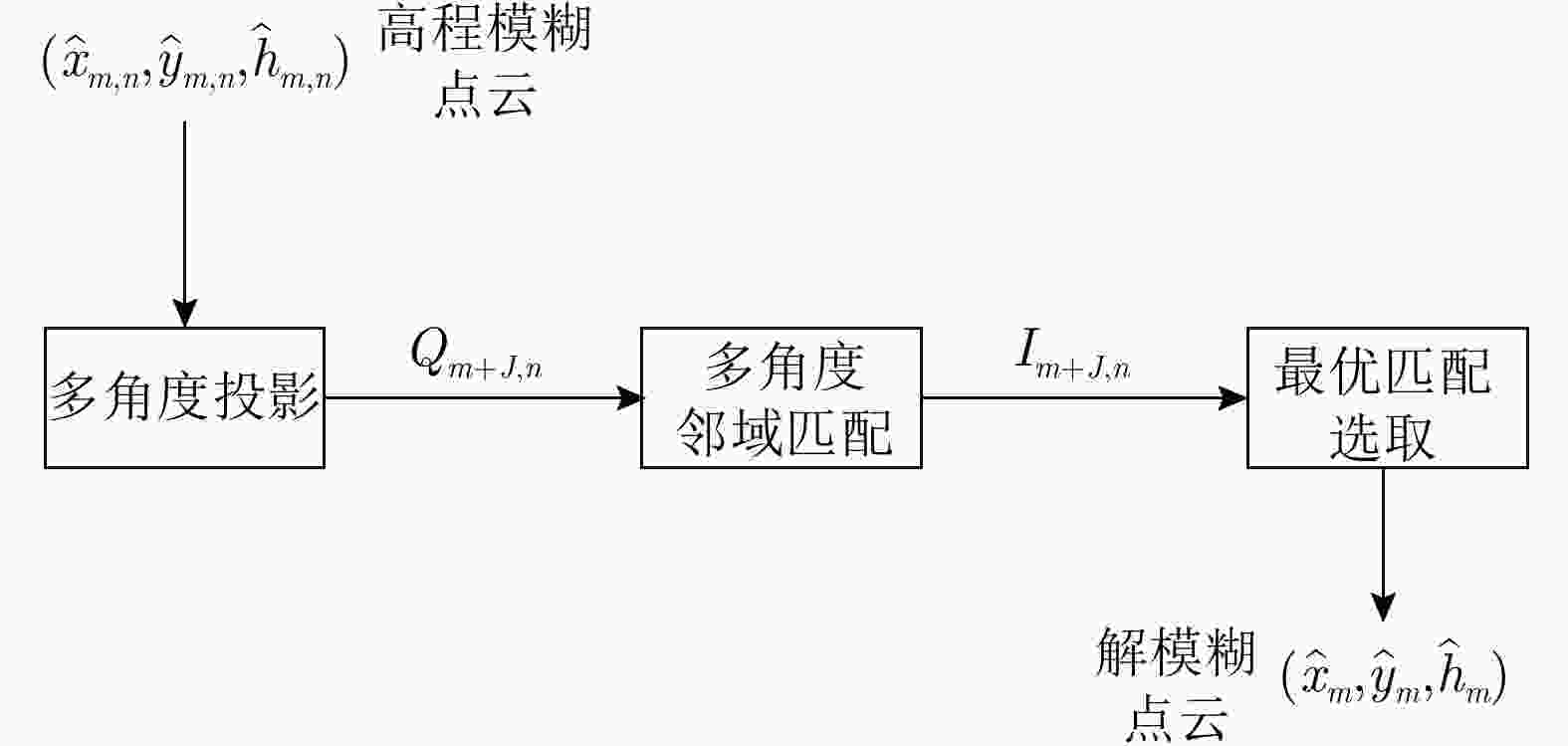
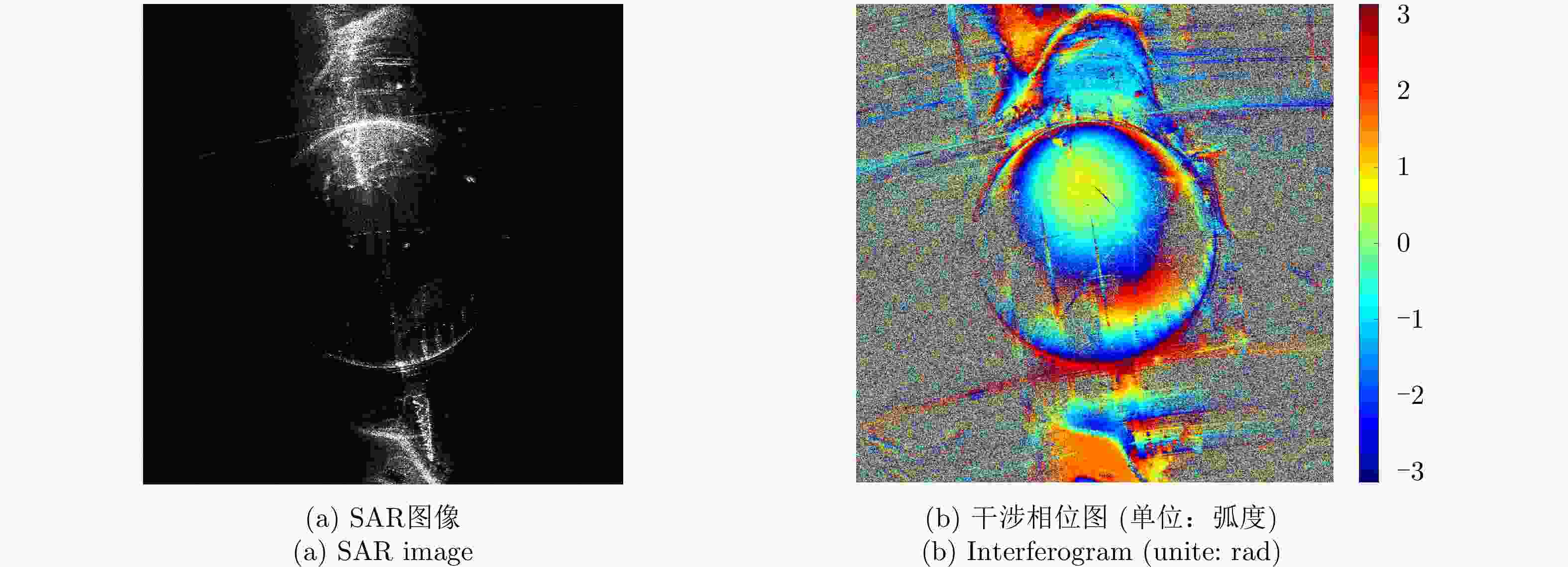
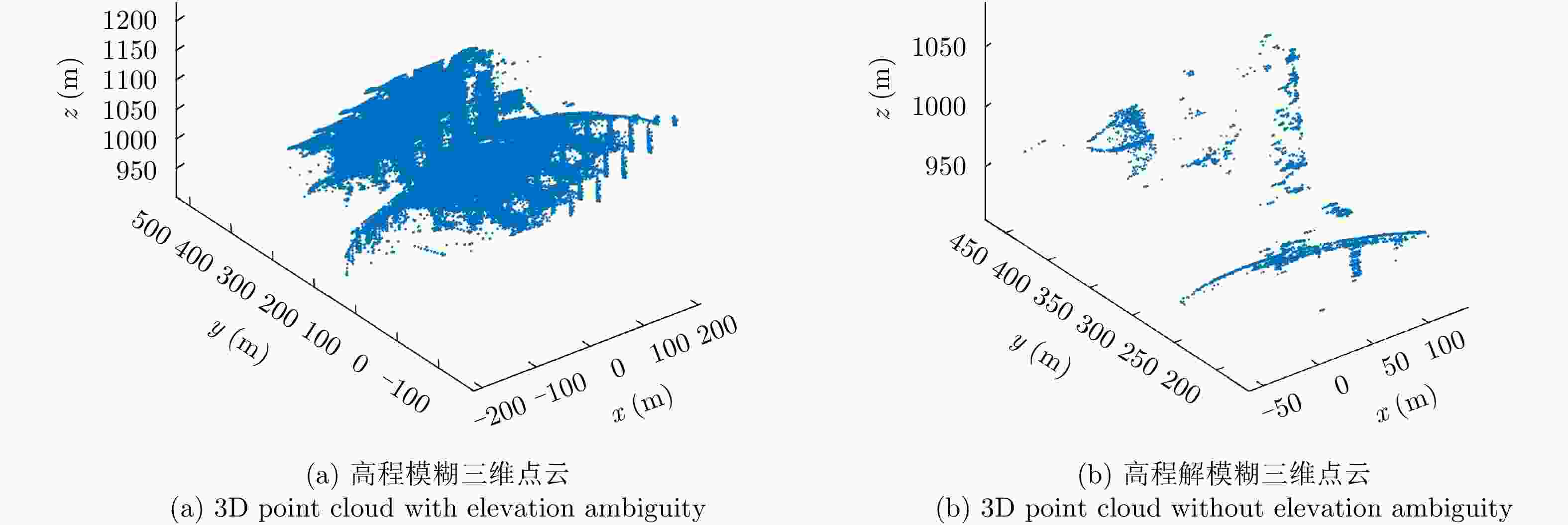
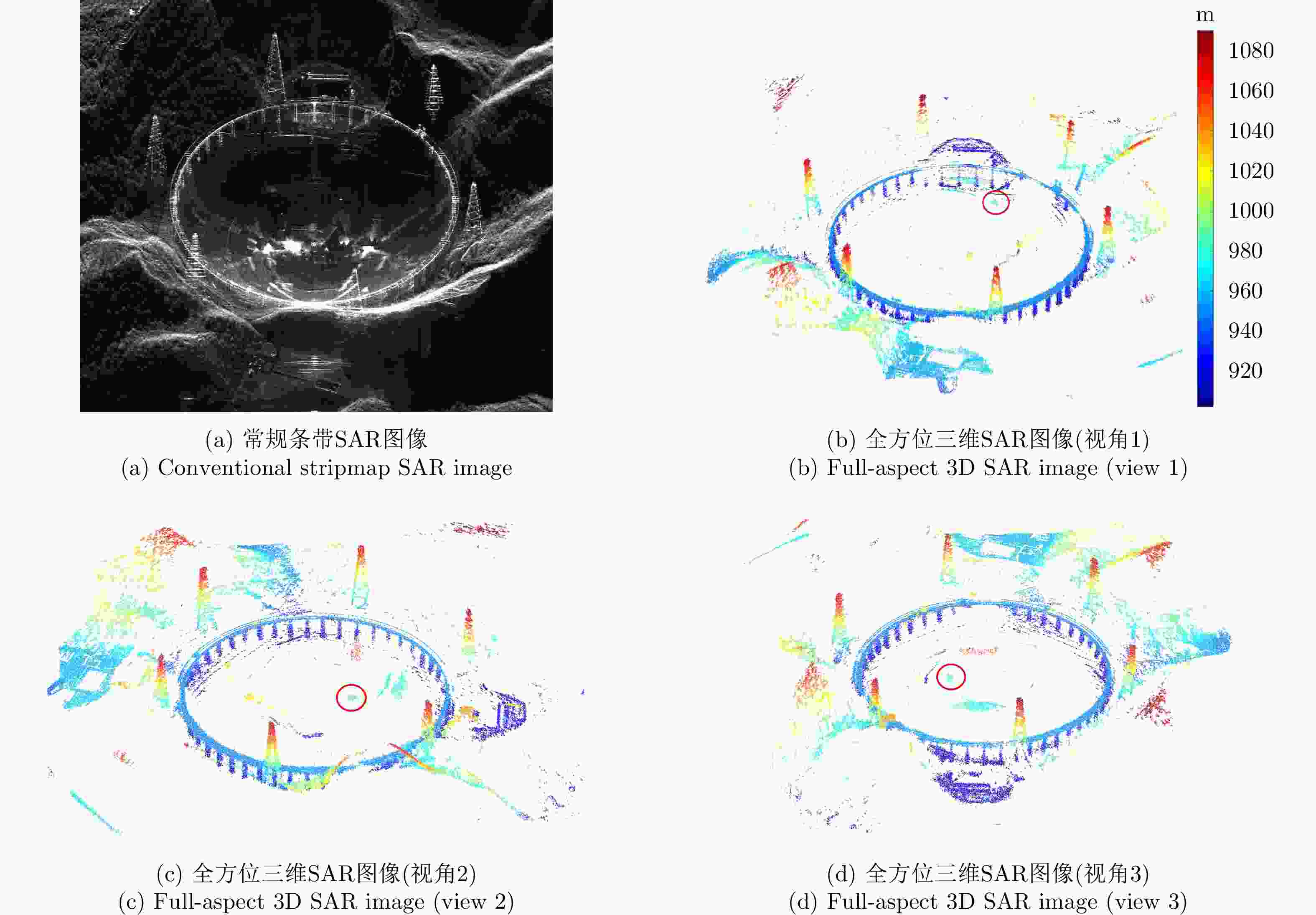
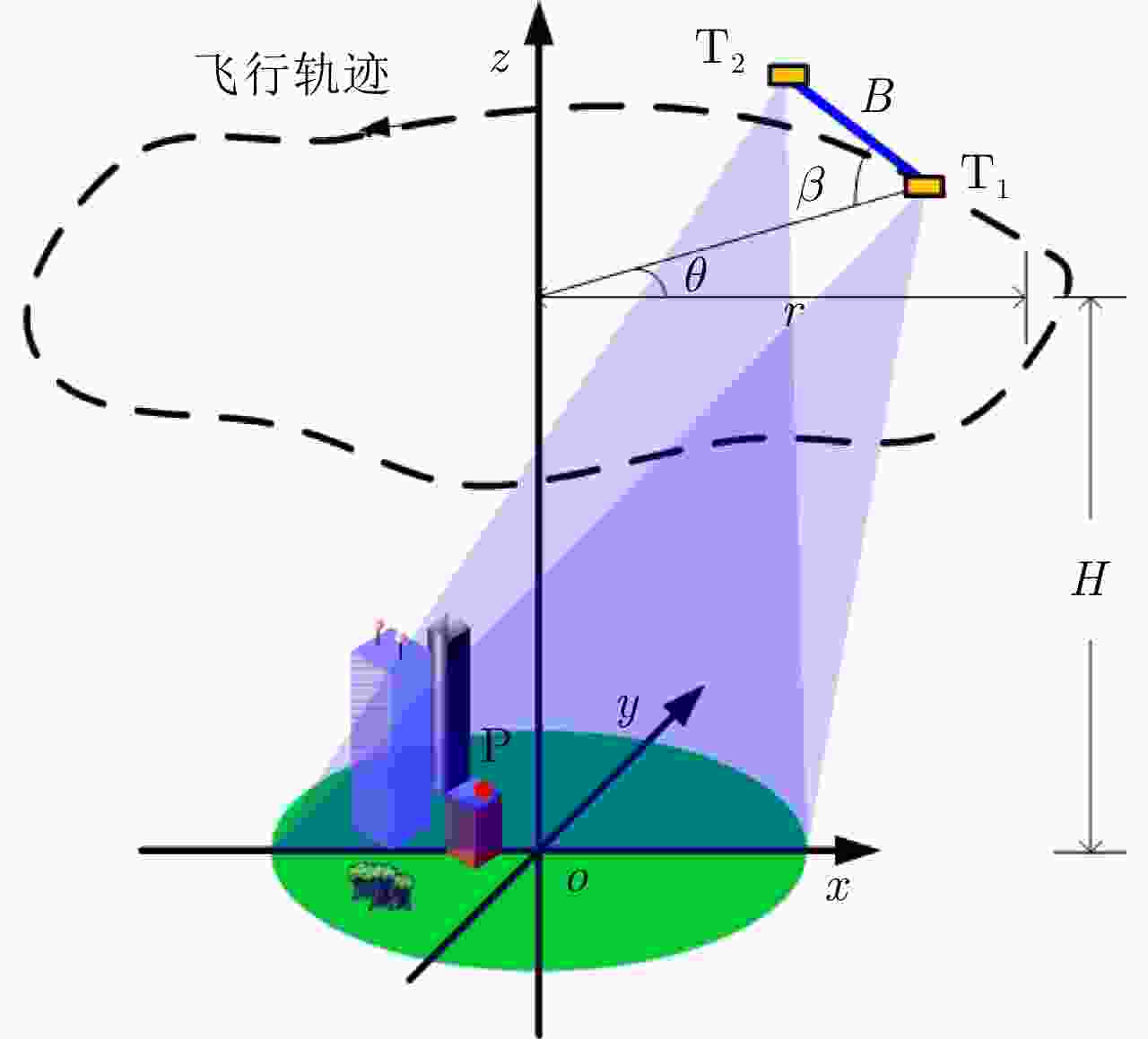
摘要: 复杂结构设施的SAR三维成像是SAR成像领域的热点和难点问题。现有SAR三维成像依赖于高程方向的多通道或多次飞行，对雷达系统或数据获取的要求较高。该文提出无先验模型复杂结构设施三维成像方法，仅需一次飞行即可获得先验信息未知区域全场景全方位三维图像。该方法充分利用圆迹SAR的全方位观测、解叠掩和解高程模糊优势，无需目标预先建模和三维成像网格构建，适用于大面积区域复杂结构设施的精细三维成像，在雷达三维成像实用化技术方面取得了重要进展。通过该方法首次获得FAST射电望远镜的雷达全方位三维图像，验证了理论与方法的正确性与有效性。
- SAR三维成像 /
- 多角度SAR /
- 全方位SAR /
- 圆迹SAR /
- 干涉SAR
Abstract: SAR three-Dimensional (3D) imaging of complex structural facilities is an important and challenging issue in SAR imaging. The existing 3D SAR imaging relies on multiple channels or flights in the elevation direction, exerting high demands on the radar system or data acquisition. This paper proposes a 3D imaging method for complex structural facilities without a prior model, and the full-aspect 3D image of the entire scene in the region with unknown prior information can be obtained solely using a single flight. This method completely utilizes the full-aspect observation as well as the layover and elevation ambiguity resolving capabilities of circular SAR without requiring target pre-modeling and 3D imaging grid construction. Moreover, the method is suitable for fine 3D imaging complex structural facilities in large areas. Significant progress has been made in the practical technology of radar 3D imaging. The full-aspect 3D radar images of the FAST radio telescope are obtained for the first time with the proposed method, thus verifying the correctness and effectiveness of our theory and method.
- 3D SAR imaging /
- Multi-aspect SAR /
- Full-aspect SAR /
- Circular SAR /
- InSAR

HTML全文

图 1 干涉圆迹SAR观测几何

Figure 1. InCSAR imaging geometry

下载: 全尺寸图片幻灯片

图 2 圆迹SAR解叠掩能力示意图

Figure 2. Layover resolving capability of circular SAR

下载: 全尺寸图片幻灯片

图 3 无先验模型SAR全方位三维成像方法流程图

Figure 3. Flow chart of full-aspect 3D SAR imaging method without prior model

下载: 全尺寸图片幻灯片

图 4 干涉圆迹SAR瞬时观测几何

Figure 4. Instantaneous geometry of InCAR

下载: 全尺寸图片幻灯片

图 5 多角度解模糊示意图

Figure 5. Diagram of multi-aspect ambiguity resolving

下载: 全尺寸图片幻灯片

图 6 多角度匹配解模糊流程

Figure 6. Flow chart of multi-aspect ambiguity resolving

下载: 全尺寸图片幻灯片

图 7 机载实验飞行轨迹与观测目标

Figure 7. Flight trajectory and the observed object

下载: 全尺寸图片幻灯片

图 8 某子孔径SAR图像与干涉相位图

Figure 8. SAR image and interferogram of certain subapture

下载: 全尺寸图片幻灯片

图 9 某子孔径三维点云

Figure 9. 3D point cloud of certain subapture

下载: 全尺寸图片幻灯片

图 10 常规条带SAR图像与全方位三维SAR图像对比

Figure 10. Comparison between conventional stripmap SAR image and full-aspect 3D SAR image

下载: 全尺寸图片幻灯片

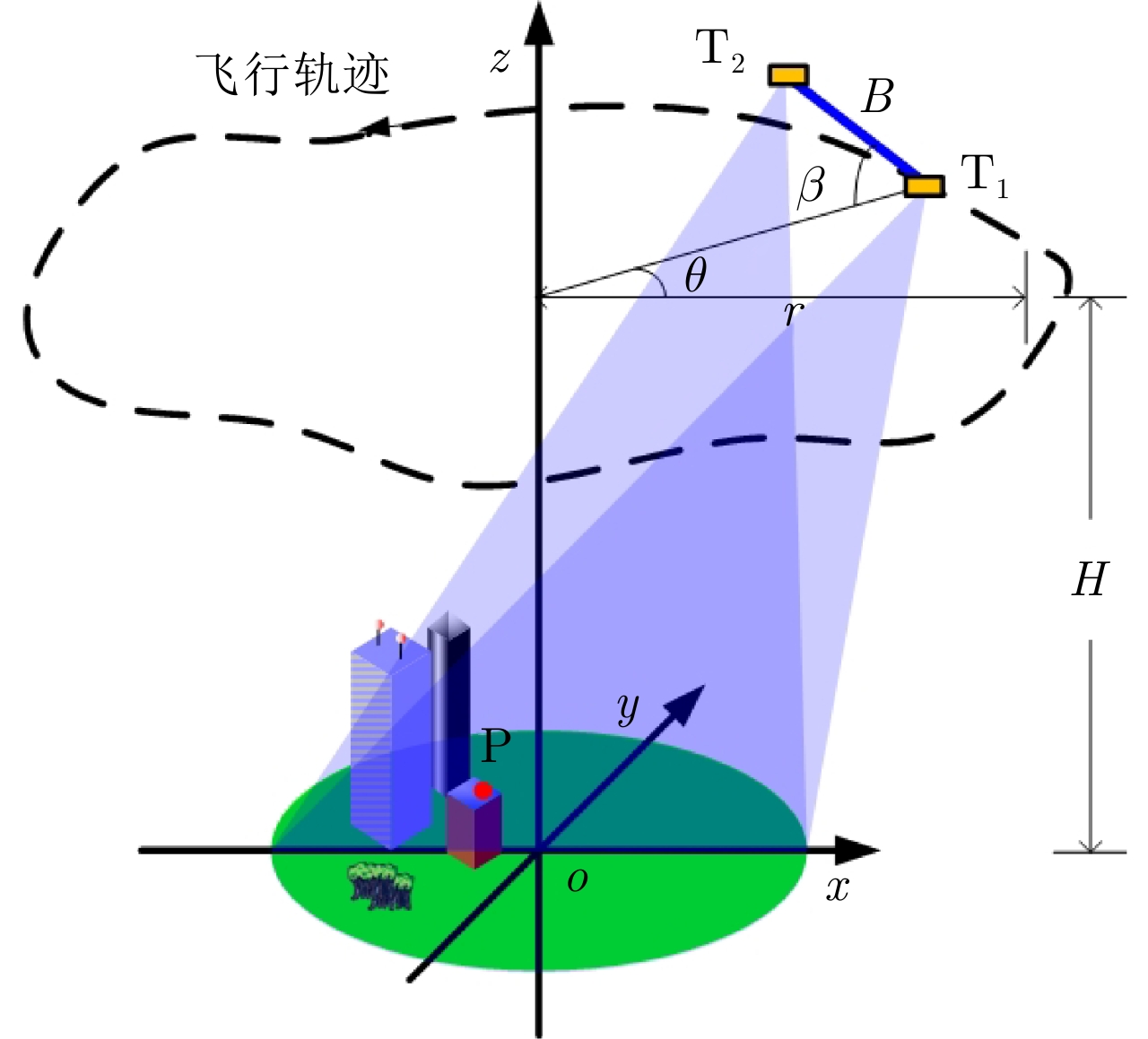
表 1 Ka波段机载干涉圆迹SAR实验参数

Table 1. Parameters of Ka-band airborne InCSAR experiment

参数数值参数数值

中心频率 35 GHz 带宽 900 MHz
基线长度 0.156 m 基线倾角 45°
飞行高度 4000 m 飞行半径 3000 m
场景海拔 940 m

下载: 导出CSV

参考文献(39)

[1]	洪文. 圆迹SAR成像技术研究进展[J]. 雷达学报, 2012, 1(2): 124–135. doi: 10.3724/SP.J.1300.2012.20046 HONG Wen. Progress in circular SAR imaging technique[J]. Journal of Radars, 2012, 1(2): 124–135. doi: 10.3724/SP.J.1300.2012.20046
[2]	LIN Yun, HONG Wen, TAN Weixian, et al. Airborne circular SAR imaging: Results at P-band[C]. 2012 IEEE International Geoscience and Remote Sensing Symposium, Munich, Germany, 2012: 5594–5597.
[3]	安道祥, 陈乐平, 冯东, 等. 机载圆周SAR成像技术研究[J]. 雷达学报, 2020, 9(2): 221–242. doi: 10.12000/JR20026 AN Daoxiang, CHEN Leping, FENG Dong, et al. Study of the airborne circular synthetic aperture radar imaging technology[J]. Journal of Radars, 2020, 9(2): 221–242. doi: 10.12000/JR20026
[4]	朱岱寅, 张营, 俞翔, 等. 微型合成孔径雷达成像信号处理技术[J]. 雷达学报, 2019, 8(6): 793–803. doi: 10.12000/JR19094 ZHU Daiyin, ZHANG Ying, YU Xiang, et al. Imaging signal processing technology for miniature synthetic aperture radar[J]. Journal of Radars, 2019, 8(6): 793–803. doi: 10.12000/JR19094
[5]	洪文, 王彦平, 林赟, 等. 新体制SAR三维成像技术研究进展[J]. 雷达学报, 2018, 7(6): 633–654. doi: 10.12000/JR18109 HONG Wen, WANG Yanping, LIN Yun, et al. Research progress on three-dimensional SAR imaging techniques[J]. Journal of Radars, 2018, 7(6): 633–654. doi: 10.12000/JR18109
[6]	LIN Yun, HONG Wen, LI Yang, et al. Study on fine feature description of multi-aspect SAR observations[C]. 2016 IEEE International Geoscience and Remote Sensing Symposium, Beijing, China, 2016: 5682–5685.
[7]	毕辉, 金双, 王潇, 等. 基于高分三号SAR数据的城市建筑高分辨率高维成像[J]. 雷达学报, 2022, 11(1): 40–51. doi: 10.12000/JR21113 BI Hui, JIN Shuang, WANG Xiao, et al. High-resolution high-dimensional imaging of urban building based on GaoFen-3 SAR data[J]. Journal of Radars, 2022, 11(1): 40–51. doi: 10.12000/JR21113
[8]	赵曜, 许俊聪, 全相印, 等. 基于稀疏和低秩结构的层析SAR成像方法[J]. 雷达学报, 2022, 11(1): 52–61. doi: 10.12000/JR21210 ZHAO Yao, XU Juncong, QUAN Xiangyin, et al. Tomographic SAR imaging method based on sparse and low-rank structures[J]. Journal of Radars, 2022, 11(1): 52–61. doi: 10.12000/JR21210
[9]	ERTIN E, AUSTIN C D, SHARMA S, et al. GOTCHA experience report: Three-dimensional SAR imaging with complete circular apertures[C]. SPIE 6568, Algorithms for Synthetic Aperture Radar Imagery XIV, Orlando, United States, 2007: 9–20.
[10]	BAO Qian, LIN Yun, HONG Wen, et al. Holographic SAR tomography image reconstruction by combination of adaptive imaging and sparse Bayesian inference[J]. IEEE Geoscience and Remote Sensing Letters, 2017, 14(8): 1248–1252. doi: 10.1109/LGRS.2017.2704601
[11]	DONG Feng, AN Daoxiang, CHEN Leping, et al. Holographic SAR tomography 3-D reconstruction based on iterative adaptive approach and generalized likelihood ratio test[J]. IEEE Transactions on Geoscience and Remote Sensing, 2021, 59(1): 305–315. doi: 10.1109/TGRS.2020.2994201
[12]	AUSTIN C D, ERTIN E, and MOSES R L. Sparse signal methods for 3-D radar imaging[J]. IEEE Journal of Selected Topics in Signal Processing, 2011, 5(3): 408–423. doi: 10.1109/JSTSP.2010.2090128
[13]	ERTIN E, MOSES R L, and POTTER L C. Interferometric methods for three-dimensional target reconstruction with multipass circular SAR[J]. IET Radar, Sonar & Navigation, 2010, 4(3): 464–473. doi: 10.1049/iet-rsn.2009.0048
[14]	PONCE O, PRATS-IRAOLA P, SCHEIBER R, et al. First airborne demonstration of holographic SAR tomography with fully polarimetric multicircular acquisitions at L-band[J]. IEEE Transactions on Geoscience and Remote Sensing, 2016, 54(10): 6170–6196. doi: 10.1109/TGRS.2016.2582959
[15]	PONCE O, PRATS P, SCHEIBER R, et al. Polarimetric 3-D imaging with airborne holographic SAR tomography over glaciers[C]. 2015 IEEE International Geoscience and Remote Sensing Symposium, Milan, Italy, 2015: 5280–5283.
[16]	PONCE O, JOERG H, SCHEIBER R, et al. First study on holographic SAR tomography over agricultural crops at C-/X-band[C]. 2016 IEEE International Geoscience and Remote Sensing Symposium, Beijing, China, 2016: 7403–7406.
[17]	仇晓兰, 焦泽坤, 杨振礼, 等. 微波视觉三维SAR关键技术及实验系统初步进展[J]. 雷达学报, 2022, 11(1): 1–19. doi: 10.12000/JR22027 QIU Xiaolan, JIAO Zekun, YANG Zhenli, et al. Key technology and preliminary progress of microwave vision 3D SAR experimental system[J]. Journal of Radars, 2022, 11(1): 1–19. doi: 10.12000/JR22027
[18]	刘燕, 谭维贤, 林赟, 等. 基于圆迹SAR的建筑物轮廓信息提取[J]. 电子与信息学报, 2015, 37(4): 946–952. doi: 10.11999/JEIT140717 LIU Yan, TAN Weixian, LIN Yun, et al. An approach of the outlines extraction of building footprints from the circular SAR data[J]. Journal of Electronics &Information Technology, 2015, 37(4): 946–952. doi: 10.11999/JEIT140717
[19]	YU Lingjuan, LIN Yun, LI Yang, et al. Height profile estimation of power lines based on two-dimensional CSAR imagery[J]. IEEE Geoscience and Remote Sensing Letters, 2016, 13(3): 339–343. doi: 10.1109/LGRS.2015.2512285
[20]	ZHANG Ying, ZHU Daiyin, and KONG Yingying. 3-D structure-from-motion retrieval based on circular videosar sequences[C]. 2019 IEEE International Geoscience and Remote Sensing Symposium, Yokohama, Japan, 2019: 134–137.
[21]	CHEN Leping, AN Daoxiang, HUANG Xiaotao, et al. A 3D reconstruction strategy of vehicle outline based on single-pass single-polarization CSAR data[J]. IEEE Transactions on Image Processing, 2017, 26(11): 5545–5554. doi: 10.1109/TIP.2017.2738566
[22]	ZHOU Chaowei, ZHOU Yejian, SUO Zhiyong, et al. Voxel area sculpturing-based 3D scene reconstruction from single-pass CSAR data[J]. Electronics Letters, 2020, 56(11): 566–567. doi: 10.1049/el.2020.0263
[23]	ZHAO Yue, LIN Yun, HONG Wen, et al. Adaptive imaging of anisotropic target based on circular-SAR[J]. Electronics Letters, 2016, 52(16): 1406–1408. doi: 10.1049/el.2016.1764
[24]	赵月, 林赟, 王彦平, 等. 基于圆迹SAR的目标方位散射特征提取研究[J]. 信号处理, 2017, 33(4): 613–617. doi: 10.16798/j.issn.1003-0530.2017.04.024 ZHAO Yue, LIN Yun, WANG Yanping, et al. Target feature extraction on azimuth angles based on circular SAR[J]. Journal of Signal Processing, 2017, 33(4): 613–617. doi: 10.16798/j.issn.1003-0530.2017.04.024
[25]	TENG Fei, HONG Wen, and LIN Yun. Aspect entropy extraction using circular SAR data and scattering anisotropy analysis[J]. Sensors, 2019, 19(2): 346. doi: 10.3390/s19020346
[26]	TENG Fei, LIN Yun, WANG Yanping, et al. An anisotropic scattering analysis method based on the statistical properties of multi-angular SAR images[J]. Remote Sensing, 2020, 12(13): 2152. doi: 10.3390/rs12132152
[27]	LI Yang, YIN Qiang, LIN Yun, et al. Anisotropy scattering detection from multiaspect signatures of circular polarimetric SAR[J]. IEEE Geoscience and Remote Sensing Letters, 2018, 15(10): 1575–1579. doi: 10.1109/LGRS.2018.2850859
[28]	XUE Feiteng, LIN Yun, HONG Wen, et al. An improved H/α unsupervised classification method for circular PolSAR images[J]. IEEE Access, 2018, 6: 34296–34306. doi: 10.1109/ACCESS.2018.2838329
[29]	XU Feng, LI Yongchen, and JIN Yaqiu. Polarimetric-anisotropic decomposition and anisotropic entropies of high-resolution SAR images[J]. IEEE Transactions on Geoscience and Remote Sensing, 2016, 54(9): 5467–5482. doi: 10.1109/TGRS.2016.2565693
[30]	杨彦辉, 林赟, 洪文. 利用星载SAR单轨多角度地距图像提取高程信息[J]. 测绘科学, 2019, 44(7): 96–104. doi: 10.16251/j.cnki.1009-2307.2019.07.015 YANG Yanhui, LIN Yun, and HONG Wen. Elevation extraction from multi-angle and ground-range images in single orbit based on spaceborne SAR[J]. Science of Surveying and Mapping, 2019, 44(7): 96–104. doi: 10.16251/j.cnki.1009-2307.2019.07.015
[31]	FENG Shanshan, LIN Yun, WANG Yanping, et al. DEM generation with a scale factor using multi-aspect SAR imagery applying radargrammetry[J]. Remote Sensing, 2020, 12(3): 556. doi: 10.3390/rs12030556
[32]	ZHANG Hanqing, LIN Yun, FENG Shanshan, et al. 3-D target reconstruction using C-band circular SAR imagery based on background constraints[C]. 2021 IEEE International Geoscience and Remote Sensing Symposium, Brussels, Belgium, 2021: 2923–2926.
[33]	FENG Shanshan, LIN Yun, WANG Yanping, et al. 3D point cloud reconstruction using inversely mapping and voting from single pass CSAR images[J]. Remote Sensing, 2021, 13(17): 3534. doi: 10.3390/rs13173534
[34]	LIN Yun, HONG Wen, TAN Weixian, et al. Interferometric circular SAR method for three-dimensional imaging[J]. IEEE Geoscience and Remote Sensing Letters, 2011, 8(6): 1026–1030. doi: 10.1109/LGRS.2011.2150732
[35]	LIN Yun, BAO Qian, HOU Liying, et al. Full-aspect 3D target reconstruction of interferometric circular SAR[C]. SPIE 10004, Image and Signal Processing for Remote Sensing XXII, Edinburgh, UK, 2016: 424–432.
[36]	侯丽英, 林赟, 洪文. 干涉圆迹SAR的目标三维重建方法研究[J]. 雷达学报, 2016, 5(5): 538–547. doi: 10.12000/JR16009 HOU Liying, LIN Yun, and HONG Wen. Three-dimensional reconstruction method study based on interferometric circular SAR[J]. Journal of Radars, 2016, 5(5): 538–547. doi: 10.12000/JR16009
[37]	刘燕, 林赟, 谭维贤, 等. 基于圆迹干涉SAR的DEM提取[J]. 电子与信息学报, 2015, 37(6): 1463–1469. doi: 10.11999/JEIT141022 LIU Yan, LIN Yun, TAN Weixian, et al. DEM extraction based on interferometric circular SAR[J]. Journal of Electronics &Information Technology, 2015, 37(6): 1463–1469. doi: 10.11999/JEIT141022
[38]	LIU Jiayin, QIU Xiaolan, and HONG Wen. Automated ortho-rectified SAR image of GF-3 satellite using reverse-range-Doppler method[C]. 2016 IEEE International Geoscience and Remote Sensing Symposium, Beijing, China, 2016: 4445–4448.
[39]	YOO J C and HAN T H. Fast normalized cross-correlation[J]. Circuits, Systems and Signal Processing, 2009, 28(6): 819–843. doi: 10.1007/s00034-009-9130-7