作者中心
专家审稿
责编办公
编辑办公
-
摘要: 由于多输入多输出(MIMO)系统具有波形、空间分集和多路复用等优势，MIMO探通一体化(DFRC)系统通过共享软硬件资源以同时实现目标探测和保密通信功能受到了极大关注。该文针对基于预编码矩阵调制的MIMO探通一体化系统，提出了基于交替方向乘子(ADMM)的一体化信号矩阵设计方法。通过用户和窃听用户参考密码本约束下最大化方向图峰值主瓣旁瓣电平比(PMSR)，保证了探测方向图性能的同时防止通信信息被窃听。针对预编码矩阵通信解调问题，提出了基于交替方向惩罚(ADPM)的排序学习优化解调方法，提升了一体化波形信息解调效率。数值仿真验证了所提设计方法实现探通一体化的有效性，与已有算法相比可实现多用户通信和更高的PMSR。Abstract: Due to several advantages of the Multi-Input Multi-Output (MIMO) system in terms of waveform, space diversity, and multiplexing, the MIMO Dual Function Radar and Communication (DFRC) system, which is responsible for target detection and securing the communication by sharing the software and hardware resources, has attracted great attention. This paper addresses the MIMO DFRC system based on permutation matrix modulation and proposes a DFRC signal matrix design method based on the Alternation Direction Method of Multipliers (ADMM). By maximizing the Peak Mainlobe to Sidelobe level Ratio (PMSR) of the beampattern with the constraints of the reference codebook for both users and eavesdroppers, the system guarantees excellent detection performance along with protecting the communication information from interception. Aiming at the communication demodulation of the permutation matrix, a permutation learning demodulation method based on the Alternating Direction Penalty Method (ADPM) is proposed to improve the demodulation efficiency of the co-use waveform. Numerical simulations verify the effectiveness of the proposed methods to achieve dual function, capable of realizing multiuser communication and deriving higher PMSR compared with the existing counterparts.
-
图 1 基于预编码矩阵调制的MIMO探通一体化系统框架示意图
Figure 1. The framework diagram of the MIMO DFRC system based on permutation matrix modulation
图 2 假设
$\theta _1^{{\text{com}}} = - {60^\circ }$ 时发射方向图Figure 2. The transmit beampattern with
$\theta _1^{{\text{com}}} = - {60^\circ }$ 
图 6
${\boldsymbol{s}}\left( {{{65}^\circ }} \right)$ 与${\boldsymbol{s}}\left( { - {{60}^\circ }} \right)$ 元素分布Figure 6. The element distributions of
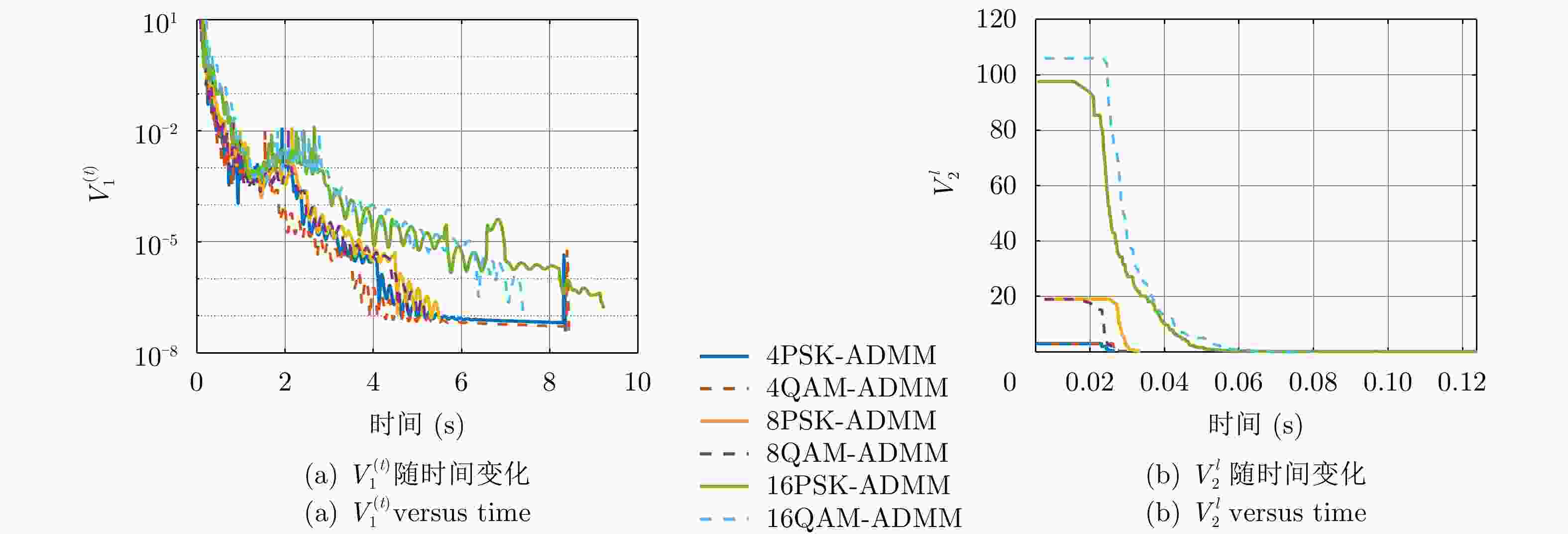
${\boldsymbol{s}}\left( {{{65}^\circ }} \right)$ and${\boldsymbol{s}}\left( { - {{60}^\circ }} \right)$ 算法1 基于ADMM的一体化信号矩阵设计方法 Alg. 1 DFRC waveform matrix design method based on ADMM 输入：$\left\{ {\boldsymbol{y} }_{i}^{(0)}\right\},{ {\epsilon} }^{(0)},\left\{ {\boldsymbol{z} }_{s}^{(0)}\right\},{ {\eta} }^{(0)},\left\{ {\boldsymbol{x} }_{c}^{(0)}\right\},\left\{ {\boldsymbol{v} }_{h}^{(0)}\right\},\left\{ {\boldsymbol{\mu} }_{i}^{(0)}\right\},\left\{ {\boldsymbol{\iota} }_{s}^{(0)}\right\},\left\{ {\boldsymbol{\xi} }_{c}^{(0)}\right\},\left\{ { {\boldsymbol{\lambda} } }_{h}^{(0)}\right\},{\boldsymbol{n} }^{\left(0\right)},{\boldsymbol{\zeta} }^{\left(0\right)},{\boldsymbol{\rho} },\varDelta ,{\delta }_{1}$； 输出：MIMO一体化系统加权向量$ {{\boldsymbol{\boldsymbol{w}}}^ \star } $； 步骤1. $ t = 0 $； 步骤2. 通过求解以下问题更新$ {\boldsymbol{w}}^{\left(t\text{+}1\right)},\left\{{\boldsymbol{y}}_{i}^{\left(t\text{+}1\right)}\right\},{{\epsilon}}^{\left(t\text{+}1\right)},\left\{{\boldsymbol{z}}_{s}^{\left(t\text{+}1\right)}\right\},{{\eta}}^{\left(t\text{+}1\right)},\left\{{\boldsymbol{x}}_{c}^{\left(t\text{+}1\right)}\right\},\left\{{\boldsymbol{v}}_{h}^{\left(t\text{+}1\right)}\right\}, $$ {{\boldsymbol{\boldsymbol{n}}}^{\left( {t{\text{ + }}1} \right)}} $： ${\boldsymbol{w} }^{(t+1)}:=\mathrm{arg}\;\underset{\boldsymbol{w} }{\mathrm{min} }\;{L}_{ { {\boldsymbol \rho} } }\left({\boldsymbol{w}},\left\{ {\boldsymbol{y} }_{i}^{(t)}\right\},{ {\epsilon} }^{(t)},\left\{ {\boldsymbol{z} }_{s}^{(t)}\right\},{ {\eta} }^{(t)},\left\{ {\boldsymbol{x} }_{c}^{(t)}\right\},\left\{ {\boldsymbol{v} }_{h}^{(t)}\right\},\left\{ {\boldsymbol{\mu} }_{i}^{(t)}\right\},\left\{ {\boldsymbol{\iota} }_{s}^{(t)}\right\},\left\{ {\boldsymbol{\xi} }_{c}^{(t)}\right\},{ {\boldsymbol{\lambda} } }_{h}^{(t)},{\boldsymbol{n} }^{\left(t\right)},{\boldsymbol{\zeta} }^{\left(t\right)}\right)$ (22) $\begin{aligned}& \left\{ {\boldsymbol{y} }_{i}^{(t+1)},{ {\epsilon} }^{(t+1)}\right\}:=\mathrm{arg}\;\underset{ {\boldsymbol{y} }_{i},\epsilon}{\mathrm{min} }\;{L}_{ { {\boldsymbol \rho} } }\left({\boldsymbol{w} }^{(t+1)},\left\{ {\boldsymbol{y} }_{i}\right\},\epsilon,\left\{ {\boldsymbol{z} }_{s}^{(t)}\right\},{ {\eta} }^{(t)}, \left\{ {\boldsymbol{x} }_{c}^{(t)}\right\},\left\{ {\boldsymbol{v} }_{h}^{(t)}\right\},\left\{ {\boldsymbol{\mu} }_{i}^{(t)}\right\},\left\{ {\boldsymbol{\iota} }_{s}^{(t)}\right\},\left\{ {\boldsymbol{\xi} }_{c}^{(t)}\right\},{ {\boldsymbol{\lambda} } }_{h}^{(t)},{\boldsymbol{n} }^{\left(t\right)},{\boldsymbol{\zeta} }^{\left(t\right)}\right)\text{ }\\ & \quad\text{s}\text{.t}\text{. }{\Vert {\boldsymbol{y} }_{i}\Vert }^{2}\ge \epsilon,i=1,2,\cdots ,I; \qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\quad\;\, (23)\end{aligned}$ $\begin{array}{l}\left\{ {\boldsymbol{z} }_{s}^{(t+1)},{ {\eta} }^{(t+1)}\right\}:=\mathrm{arg}\;\underset{ {\boldsymbol{z} }_{s},\eta }{\mathrm{min} }\;{L}_{ { {\boldsymbol \rho} } }\left({\boldsymbol{w} }^{(t+1)},\left\{ {\boldsymbol{y} }_{i}^{(t+1)}\right\},{ {\epsilon} }^{(t+1)},\left\{ {\boldsymbol{z} }_{s}\right\}, \eta ,\left\{ {\boldsymbol{x} }_{c}^{(t)}\right\},\left\{ {\boldsymbol{v} }_{h}^{(t)}\right\},\left\{ {\boldsymbol{\mu} }_{i}^{(t)}\right\},\left\{ {\boldsymbol{\iota} }_{s}^{(t)}\right\},\left\{ {\boldsymbol{\xi} }_{c}^{(t)}\right\},{ {\boldsymbol{\lambda} } }_{h}^{(t)},{\boldsymbol{n} }^{\left(t\right)},{\boldsymbol{\zeta} }^{\left(t\right)}\right)\text{ }\\ \quad\text{s}\text{.t}\text{. }{\Vert {\boldsymbol{z} }_{s}\Vert }^{2}\le \eta ,s=1,2,\cdots ,S; \qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\;\;\, (24)\end{array}$ $\begin{array}{l}\left\{ {\boldsymbol{x} }_{c}^{(t+1)},{b}_{c}^{(t+1)}\right\}:=\mathrm{arg}\underset{ {\boldsymbol{x} }_{c},{b}_{c} }{\mathrm{min} }{L}_{ { {\boldsymbol \rho} } }\left({\boldsymbol{w} }^{(t+1)},\left\{ {\boldsymbol{y} }_{i}^{(t+1)}\right\},{ {\epsilon} }^{(t+1)},\left\{ {\boldsymbol{z} }_{s}^{(t+1)}\right\}, { {\eta} }^{(t+1)},\left\{ {\boldsymbol{x} }_{c}\right\},\left\{ {\boldsymbol{v} }_{h}^{(t)}\right\},\left\{ {\boldsymbol{\mu} }_{i}^{(t)}\right\},\left\{ {\boldsymbol{\iota} }_{s}^{(t)}\right\},\left\{ {\boldsymbol{\xi} }_{c}^{(t)}\right\},{ {\boldsymbol{\lambda} } }_{h}^{(t)},{\boldsymbol{n} }^{\left(t\right)},{\boldsymbol{\zeta} }^{\left(t\right)}\right)\text{ }\\ \quad\text{s}\text{.t}\text{. }{\boldsymbol{x} }_{c}={b}_{c}{\overline{{\boldsymbol{a}}} }_{1},{l}_{c}\le {b}_{c}\le {u}_{c},c=1,2,\cdots ,C; \qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\, (25)\end{array}$ $\begin{aligned}& \left\{ {\boldsymbol{v} }_{h}^{(t+1)},{r}_{h}^{(t+1)} \right\} :=\mathrm{arg}\underset{ {\boldsymbol{v} }_{h},{r}_{h} }{\mathrm{min} }\;{L}_{ { {\boldsymbol \rho} } }\left({\boldsymbol{w} }^{(t+1)},\left\{ {\boldsymbol{y} }_{i}^{(t+1)}\right\},{ {\epsilon} }^{(t+1)},\left\{ {\boldsymbol{z} }_{s}^{(t+1)} \right\}, { {\eta} }^{(t+1)},\left\{ {\boldsymbol{x} }_{c}^{(t+1)} \right\},\left\{ {\boldsymbol{v} }_{h}\right\},\left\{ {\boldsymbol{\mu} }_{i}^{(t)}\right\},\left\{ {\boldsymbol{\iota} }_{s}^{(t)}\right\},\left\{ {\boldsymbol{\xi} }_{c}^{(t)} \right\},{ {\boldsymbol{\lambda} } }_{h}^{(t)},{\boldsymbol{n} }^{\left(t\right)},{\boldsymbol{\zeta} }^{\left(t\right)}\right)\\ & \quad\text{s}\text{.t}\text{. }{\boldsymbol{v} }_{h}={r}_{h} { {\textit{1}}}_{K},h=1,2,\cdots ,E \qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\;\, (26)\end{aligned}$ $\begin{aligned}& {\boldsymbol{n} }^{\left(t\text{+}1\right)}:=\mathrm{arg}\;\underset{\boldsymbol{n} }{\mathrm{min} }\;{L}_{ { {\boldsymbol \rho} } }\left({\boldsymbol{w} }^{(t+1)},\left\{ {\boldsymbol{y} }_{i}^{(t+1)}\right\},{ {\epsilon} }^{(t+1)},\left\{ {\boldsymbol{z} }_{s}^{(t+1)}\right\}, { {\eta} }^{(t+1)},\left\{ {\boldsymbol{x} }_{c}^{(t+1)}\right\},\left\{ {\boldsymbol{v} }_{h}^{(t+1)}\right\},\left\{ {\boldsymbol{\mu} }_{i}^{(t)}\right\},\left\{ {\boldsymbol{\iota} }_{s}^{(t)}\right\},\left\{ {\boldsymbol{\xi} }_{c}^{(t)}\right\},{ {\boldsymbol{\lambda} } }_{h}^{(t)},{\boldsymbol{n} },{\boldsymbol{\zeta} }^{\left(t\right)}\right)\\& \quad\text{s}\text{.t}\text{. }{\Vert {\boldsymbol{n} }\Vert }^{2}=\varDelta \qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad \quad\;\, (27)\end{aligned}$ 步骤3. 通过下列公式更新$\left\{ {{\boldsymbol{\boldsymbol{\mu}}}_i^{(t + 1)}} \right\},\left\{ {{\boldsymbol{\boldsymbol{\iota}}}_s^{(t + 1)}} \right\},\left\{ {{\boldsymbol{\boldsymbol{\xi}}}_c^{(t + 1)}} \right\},\left\{ {{\boldsymbol{\lambda }}_h^{(t + 1)}} \right\},{{\boldsymbol{\boldsymbol{\zeta}}}^{\left( {t{\text{ + }}1} \right)}}$： $ {\boldsymbol{\boldsymbol{\mu}}}_i^{(t + 1)}: = {\boldsymbol{\boldsymbol{\mu}}}_i^{(t)} + {\boldsymbol{\boldsymbol{y}}}_i^{(t + 1)} - {{\boldsymbol{A}}^{\text{H}}}\left( {{\theta _i}} \right){{\boldsymbol{\boldsymbol{w}}}^{(t + 1)}} $ (28) $ {\boldsymbol{\boldsymbol{\iota}}}_s^{(t + 1)}: = {\boldsymbol{\boldsymbol{\iota}}}_s^{(t)} + {\boldsymbol{\boldsymbol{z}}}_s^{(t + 1)} - {{\boldsymbol{A}}^{\text{H}}}\left( {{\vartheta _s}} \right){{\boldsymbol{\boldsymbol{w}}}^{(t + 1)}} $ (29) $ {\boldsymbol{\boldsymbol{\xi}}}_c^{(t + 1)}: = {\boldsymbol{\boldsymbol{\xi}}}_c^{(t)} + {\boldsymbol{\boldsymbol{x}}}_c^{(t + 1)} - {{\boldsymbol{A}}^{\text{H}}}\left( {\theta _c^{{\text{com }}}} \right){{\boldsymbol{\boldsymbol{w}}}^{(t + 1)}} $ (30) $ {\boldsymbol{\lambda }}_h^{(t + 1)}: = {\boldsymbol{\lambda }}_h^{(t)} + {\boldsymbol{\boldsymbol{v}}}_h^{(t + 1)} - {{\boldsymbol{A}}^{\text{H}}}\left( {\theta _h^{{\text{eav }}}} \right){{\boldsymbol{\boldsymbol{w}}}^{(t + 1)}} $ (31) ${{\boldsymbol{\boldsymbol{\zeta}}}^{\left( {t{\text{ + }}1} \right)}} = {{\boldsymbol{\boldsymbol{\zeta}}}^{\left( t \right)}} + {{\boldsymbol{\boldsymbol{n}}}^{(t + 1)}} - {{\boldsymbol{\boldsymbol{w}}}^{(t + 1)}}$ (32) 步骤4. 如果原始可行性容差$V_1^{(t + 1)} = \displaystyle\sum\limits_{i = 1}^I {{{\left\| {{\boldsymbol{\boldsymbol{y}}}_i^{(t + 1)} - {{\boldsymbol{A}}^{\text{H}}}\left( {{\theta _i}} \right){{\boldsymbol{\boldsymbol{w}}}^{(t + 1)}}} \right\|}^2}} + $$\displaystyle\sum\limits_{s = 1}^S {{{\left\| {{\boldsymbol{\boldsymbol{z}}}_s^{(t + 1)} - {{\boldsymbol{A}}^{\text{H}}}\left( {{\vartheta _s}} \right){{\boldsymbol{\boldsymbol{w}}}^{(t + 1)}}} \right\|}^2}} + $$\displaystyle\sum\limits_{c = 1}^C { { {\left\| { {\boldsymbol{\boldsymbol{x} } }_c^{(t + 1)} - { {\boldsymbol{A} }^{\text{H} } }\left( {\theta _c^{ {\text{com } } } } \right){ {\boldsymbol{\boldsymbol{w} } }^{(t + 1)} } } \right\|}^2} }$
$+\displaystyle\sum\limits_{h = 1}^E { { {\left\| { {\boldsymbol{\boldsymbol{v} } }_h^{(t + 1)} - { {\boldsymbol{A} }^{\text{H} } }\left( {\theta _h^{ {\text{eav } } } } \right){ {\boldsymbol{\boldsymbol{w} } }^{(t + 1)} } } \right\|}^2} }$$+ {\left\| { { {\boldsymbol{\boldsymbol{n} } }^{(t + 1)} } - { {\boldsymbol{\boldsymbol{w} } }^{(t + 1)} } } \right\|^2} \le {\delta _1}$，则输出${{\boldsymbol{\boldsymbol{w}}}^ \star } = {{\boldsymbol{\boldsymbol{w}}}^{\left( {t + 1} \right)}}$；否则$t: = t + 1$，回到步骤2。
下载: 导出CSV
算法2 基于ADPM的排序学习优化解调方法 Alg. 2 The permutation learning demodulation method
based on ADPM输入：${{\boldsymbol{p}}^0},{\boldsymbol{u}}_1^0,{\boldsymbol{u}}_2^0,{\boldsymbol{\kappa }}_1^0,{\boldsymbol{\kappa }}_2^0,{\rho ^0},{\boldsymbol{g}},{\boldsymbol{B}},{\boldsymbol{C}},{\delta _2},{\delta _3}$； 输出：问题(56)的最优解$ {{\boldsymbol{p}}^ \star } $； 步骤1. $ l = 0 $； 步骤2. 通过求解以下问题更新${{\boldsymbol{p}}^{l{\text{ + }}1}},{\boldsymbol{u}}_1^{l{\text{ + }}1},{\boldsymbol{u}}_2^{l{\text{ + }}1}$：
$\begin{aligned} { {\boldsymbol{p} }^{l + 1} }: =& \arg \mathop {\min }\limits_{\boldsymbol{p} } {\mathcal{L}_{ {\rho ^l} } }\left( { {\boldsymbol{p} },{\boldsymbol{u} }_1^l,{\boldsymbol{u} }_2^l,{\boldsymbol{\kappa } }_1^l,{\boldsymbol{\kappa } }_2^l} \right){\text{ } } \\& {\text{s} }{\text{.t} }{\text{. } }{p_i} \in \{ 0,1\} ,i = 1,2, \cdots ,{K^2} \qquad\qquad\qquad\qquad\; (60)\end{aligned}$$\begin{aligned} {\boldsymbol{u} }_1^{l + 1}: =& \arg \mathop {\min }\limits_{ {\boldsymbol{u} }_1^{} } {\mathcal{L}_{ {\rho ^l} } }\left( { { {\boldsymbol{p} }^{l + 1} },{\boldsymbol{u} }_1^{},{\boldsymbol{u} }_2^l,{\boldsymbol{\kappa } }_1^l,{\boldsymbol{\kappa } }_2^l} \right){\text{ } } \\ & {\text{s} }{\text{.t} }{\text{. } }{\boldsymbol{B} }{ {\boldsymbol{u} }_1} = { { { {\textit{1} } } }_K} \qquad\qquad\qquad\qquad\qquad\qquad\qquad\quad\;\, (61)\end{aligned}$ $\begin{aligned} {\boldsymbol{u} }_2^{l + 1}: =& \arg \mathop {\min }\limits_{ { {\boldsymbol{u} }_2} } {\mathcal{L}_{ {\rho ^l} } }\left( { { {\boldsymbol{p} }^{l + 1} },{\boldsymbol{u} }_1^{l + 1},{\boldsymbol{u} }_2^{},{\boldsymbol{\kappa } }_1^l,{\boldsymbol{\kappa } }_2^l} \right){\text{ } } \\ & {\text{s} }{\text{.t} }{\text{. } }{\boldsymbol{C} }{ {\boldsymbol{u} }_2} = { { { {\textit{1} } } }_K} \qquad\qquad\quad\qquad\qquad\qquad\qquad\quad\; (62)\end{aligned}$ 步骤3. 通过下列公式更新${\boldsymbol{\kappa }}_1^{l + 1},{\boldsymbol{\kappa }}_2^{l + 1},{\rho ^{l + 1}}$： ${\rho }^{l+1}=\left\{\begin{aligned}& {\delta }_{2}{\rho }^{l},\text{ }\Vert {p}^{l+1}-{p}^{l}\Vert =0 \\ & {\rho }^{l},\text{ }其他\text{ } \end{aligned}\right.$ (63) $ {\boldsymbol{\kappa }}_1^{l + 1}: = {\boldsymbol{\kappa }}_1^l + {\rho ^{l + 1}}\left( {{\boldsymbol{u}}_1^{l + 1} - {{\boldsymbol{p}}^{l + 1}}} \right) $ (64) $ {\boldsymbol{\kappa }}_2^{l + 1}: = {\boldsymbol{\kappa }}_2^l + {\rho ^{l + 1}}\left( {{\boldsymbol{u}}_2^{l + 1} - {{\boldsymbol{p}}^{l + 1}}} \right) $ (65) 4. 如果原始可行性容差
${V}_2^{l + 1} = {\left\| { {\boldsymbol{u} }_1^{l + 1} - { {\boldsymbol{p} }^{l + 1} } } \right\|^2} + {\left\| { {\boldsymbol{u} }_2^{l + 1} - { {\boldsymbol{p} }^{l + 1} } } \right\|^2} \le {\delta _3}$，则输出
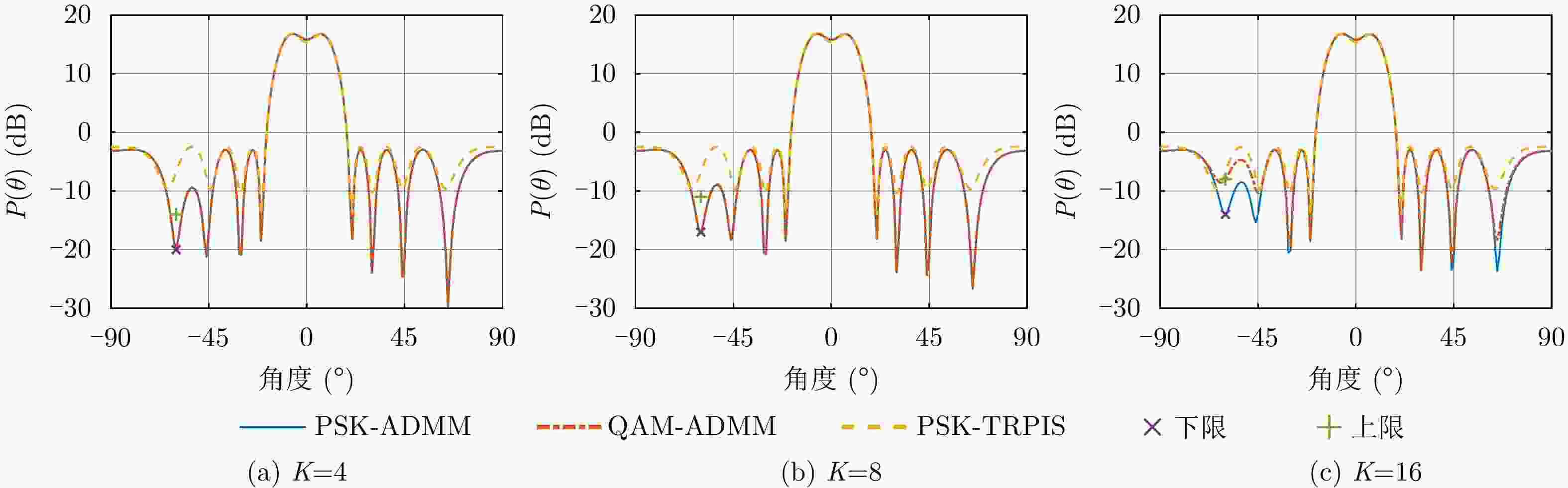
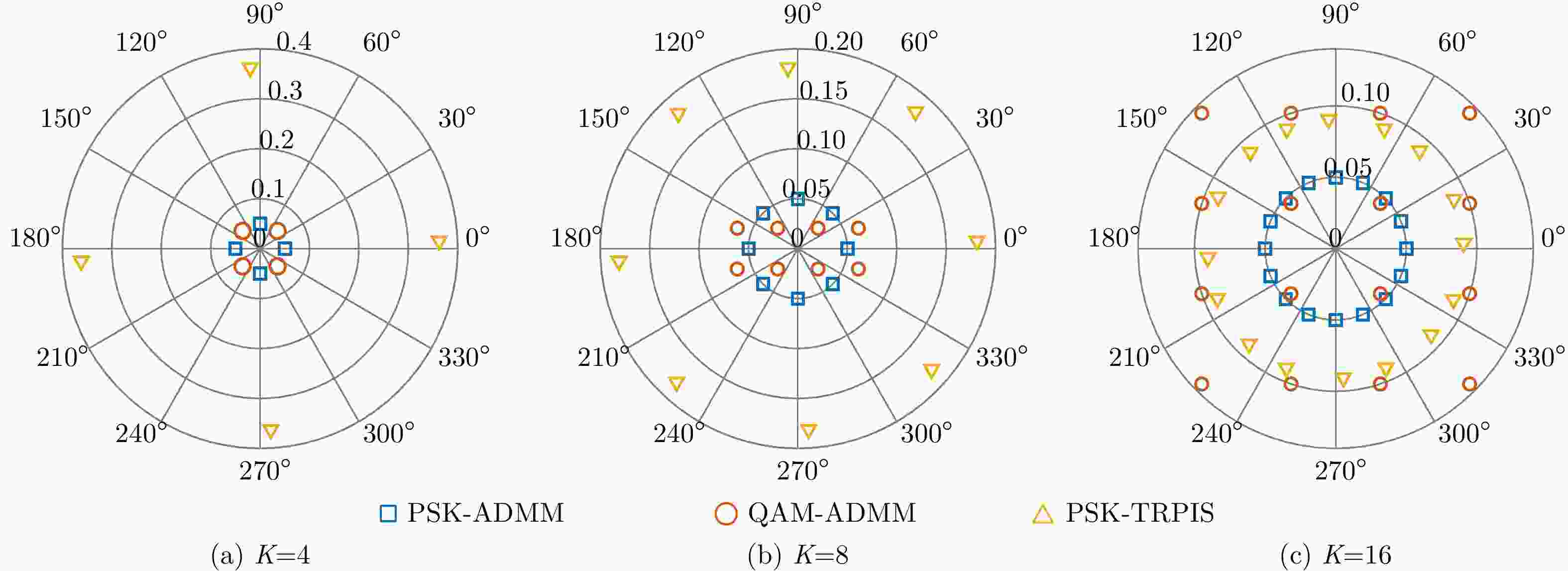
$ {{\boldsymbol{p}}^ \star } = {{\boldsymbol{p}}^{l + 1}} $；否则$ l: = l + 1 $，回到步骤2。
下载: 导出CSV
表 1 不同算法所得PMSR
Table 1. PMSR derived by different methods
数值 PSK-ADMM QAM-ADMM PSK-TRPIS $K = 4$ 18.7693 18.7715 17.8392 $K = 8$ 18.7693 18.7735 $K = 16$ 18.7535 18.8135
下载: 导出CSV
表 2 不同算法所需时间
Table 2. Computing time required by different methods
数值 PSK-ADMM QAM-ADMM PSK-TRPIS $K = 4$ 8.354 8.434 8.276 $K = 8$ 5.502 5.182 8.281 $K = 16$ 9.221 7.398 8.282
下载: 导出CSV
-
[1] 刘凡, 袁伟杰, 原进宏, 等. 雷达通信频谱共享及一体化: 综述与展望[J]. 雷达学报, 2021, 10(3): 467–484. doi: 10.12000/JR20113LIU Fan, YUAN Weijie, YUAN Jinhong, et al. Radar-communication spectrum sharing and integration: Overview and prospect[J]. Journal of Radars, 2021, 10(3): 467–484. doi: 10.12000/JR20113 [2] ZHENG Le, LOPS M, ELDAR Y C, et al. Radar and communication coexistence: An overview: A review of recent methods[J]. IEEE Signal Processing Magazine, 2019, 36(5): 85–99. doi: 10.1109/MSP.2019.2907329 [3] KHAWAR A, ABDELHADI A, and CLANCY C T. On the impact of time-varying interference-channel on the spatial approach of spectrum sharing between S-band radar and communication system[C]. IEEE Military Communications Conference, Baltimore, USA, 2014: 807–812. [4] 马丁友, 刘祥, 黄天耀, 等. 雷达通信一体化: 共用波形设计和性能边界[J]. 雷达学报, 2022, 11(2): 198–212. doi: 10.12000/JR21146MA Dingyou, LIU Xiang, HUANG Tianyao, et al. Joint radar and communications: Shared waveform designs and performance bounds[J]. Journal of Radars, 2022, 11(2): 198–212. doi: 10.12000/JR21146 [5] LIU Fan, ZHOU Longfei, MASOUROS C, et al. Toward dual-functional radar-communication systems: Optimal waveform design[J]. IEEE Transactions on Signal Processing, 2018, 66(16): 4264–4279. doi: 10.1109/TSP.2018.2847648 [6] 刘凡. MIMO雷达与多用户MIMO通信频谱共享关键技术研究[D]. [博士论文], 北京理工大学, 2018.LIU Fan. Research on the spectrum sharing of MIMO radar and MU-MIMO communications[D]. [Ph. D. dissertation], Beijing Institute of Technology, 2018. [7] HASSANIEN A, AMIN M G, ZHANG Y D, et al. Signaling strategies for dual-function radar communications: An overview[J]. IEEE Aerospace and Electronic Systems Magazine, 2016, 31(10): 36–45. doi: 10.1109/MAES.2016.150225 [8] 崔国龙, 余显祥, 杨婧, 等. 认知雷达波形优化设计方法综述[J]. 雷达学报, 2019, 8(5): 537–557. doi: 10.12000/JR19072CUI Guolong, YU Xianxiang, YANG Jing, et al. An overview of waveform optimization methods for cognitive radar[J]. Journal of Radars, 2019, 8(5): 537–557. doi: 10.12000/JR19072 [9] LIU Yongjun, LIAO Guisheng, and YANG Zhiwei. Robust OFDM integrated radar and communications waveform design based on information theory[J]. Signal Processing, 2019, 162: 317–329. doi: 10.1016/j.sigpro.2019.05.001 [10] WANG Xiangrong, HASSANIEN A, and AMIN M G. Dual-function MIMO radar communications system design via sparse array optimization[J]. IEEE Transactions on Aerospace and Electronic Systems, 2019, 55(3): 1213–1226. doi: 10.1109/TAES.2018.2866038 [11] HASSANIEN A, HIMED B, and RIGLING B D. A dual-function MIMO radar-communications system using frequency-hopping waveforms[C]. IEEE Radar Conference, Seattle, USA, 2017: 1721–1725. [12] WANG Xiangrong and HASSANIEN A. Phase modulated communications embedded in correlated FH-MIMO radar waveforms[C]. IEEE Radar Conference, Florence, Italy, 2020: 1–6. [13] WANG Xiangrong, XU Jing, HASSANIEN A, et al. Joint communications with FH-MIMO radar systems: An extended signaling strategy[C]. IEEE International Conference on Acoustics, Speech and Signal Processing, Toronto, Canada, 2021: 8253–8257. [14] MA Dingyou, SHLEZINGER N, HUANG Tianyao, et al. FRaC: FMCW-based joint radar-communications system via index modulation[J]. IEEE Journal of Selected Topics in Signal Processing, 2021, 15(6): 1348–1364. doi: 10.1109/JSTSP.2021.3118219 [15] 刘永军, 廖桂生, 杨志伟, 等. 一种超分辨OFDM雷达通信一体化设计方法[J]. 电子与信息学报, 2016, 38(2): 425–433. doi: 10.11999/JEIT150320LIU Yongjun, LIAO Guisheng, YANG Zhiwei, et al. A super-resolution design method for integration of OFDM radar and communication[J]. Journal of Electronics &Information Technology, 2016, 38(2): 425–433. doi: 10.11999/JEIT150320 [16] LIU Yongjun, LIAO Guisheng, CHEN Yufeng, et al. Super-resolution range and velocity estimations with OFDM integrated radar and communications waveform[J]. IEEE Transactions on Vehicular Technology, 2020, 69(10): 11659–11672. doi: 10.1109/TVT.2020.3016470 [17] HASSANIEN A, AMIN M G, ZHANG Y D, et al. Non-coherent PSK-based dual-function radar-communication systems[C]. IEEE Radar Conference, Philadelphia, USA, 2016: 1–6. [18] HASSANIEN A, HIMED B, and AMIN M G. Transmit/receive beamforming design for joint radar and communication systems[C]. IEEE Radar Conference, Oklahoma City, USA, 2018: 1481–1486. [19] HASSANIEN A, ABOUTANIOS E, AMIN M G, et al. A dual-function MIMO radar-communication system via waveform permutation[J]. Digital Signal Processing, 2018, 83: 118–128. doi: 10.1016/j.dsp.2018.08.010 [20] LIU Fan, MASOUROS C, LI Ang, et al. MU-MIMO communications with MIMO radar: From co-existence to joint transmission[J]. IEEE Transactions on Wireless Communications, 2018, 17(4): 2755–2770. doi: 10.1109/TWC.2018.2803045 [21] YU Xianxiang, YAO Xue, YANG Jing, et al. Integrated waveform design for MIMO radar and communication via spatio-spectral modulation[J]. IEEE Transactions on Signal Processing, 2022, 70: 2293–2305. doi: 10.1109/TSP.2022.3170687 [22] WU Wenhua, CAO Yunhe, WANG Shenghua, et al. MIMO waveform design combined with constellation mapping for the integrated system of radar and communication[J]. Signal Processing, 2020, 170: 107443. doi: 10.1016/j.sigpro.2019.107443 [23] FAN Wen, LIANG Junli, CHEN Zihao, et al. Spectrally compatible aperiodic sequence set design with low cross- and auto-correlation PSL[J]. Signal Processing, 2021, 183: 107960. doi: 10.1016/J.SIGPRO.2020.107960 [24] FAN Wen, LIANG Junli, and LI Jian. Constant modulus MIMO radar waveform design with minimum peak sidelobe transmit beampattern[J]. IEEE Transactions on Signal Processing, 2018, 66(16): 4207–4222. doi: 10.1109/TSP.2018.2847636 [25] LIANG Junli, FAN Xuhui, SO H C, et al. Array beampattern synthesis without specifying lobe level masks[J]. IEEE Transactions on Antennas and Propagation, 2020, 68(6): 4526–4539. doi: 10.1109/TAP.2020.2972331 [26] HASSANIEN A, VOROBYOV S A, and KHABBAZIBASMENJ A. Transmit radiation pattern invariance in MIMO radar with application to DOA estimation[J]. IEEE Signal Processing Letters, 2015, 22(10): 1609–1613. doi: 10.1109/LSP.2015.2417220 [27] YU Xianxiang, CUI Guolong, YANG Jing, et al. Wideband MIMO radar waveform design[J]. IEEE Transactions on Signal Processing, 2019, 67(13): 3487–3501. doi: 10.1109/TSP.2019.2916732 [28] 余显祥. 基于约束优化理论的MIMO雷达波形设计算法研究[D]. [博士论文], 电子科技大学, 2020.YU Xianxiang. Research on MIMO radar waveform design algorithms based on constrained optimization theory[D]. [Ph. D. dissertation], University of Electronic Science and Technology of China, 2020. [29] LIU Fan, MASOUROS C, LI Ang, et al. Robust MIMO beamforming for cellular and radar coexistence[J]. IEEE Wireless Communications Letters, 2017, 6(3): 374–377. doi: 10.1109/LWC.2017.2693985 [30] BERGIN J and GUERCI J R. MIMO Radar: Theory and Application[M]. Fitchburg: Artech House, 2018: 45–49. -
图(9) / 表(4)
计量
- 文章访问数: 1769
- HTML全文浏览量: 824
- PDF下载量: 318
- 被引次数: 0
