极化干涉SAR面向城区不同处理模式的误差影响分析

吕泽鑫; 仇晓兰; 张柘; 丁赤飚

doi:10.12000/JR22059

极化干涉SAR面向城区不同处理模式的误差影响分析

DOI: 10.12000/JR22059

吕泽鑫^{1, 4, 5},
仇晓兰^{1, 2, 3, 4, ,},
张柘^{2, 3},
丁赤飚^{1, 4, 5}

1.
中国科学院空间信息处理与应用系统技术重点实验室北京 100190
2.
苏州市空天大数据智能应用技术重点实验室苏州 215124
3.
苏州空天信息研究院苏州 215124
4.
中国科学院空天信息创新研究院北京 100190
5.
中国科学院大学电子电气与通信工程学院北京 100049

基金项目: 国家自然科学基金(61991421, 62022082)

详细信息

作者简介:
吕泽鑫(1994-)，男，中国科学院空天信息创新研究院在读博士生。研究方向为无人机极化干涉SAR误差分析、干涉SAR高程反演、极化干涉SAR在城区中的应用

仇晓兰(1982–)，女，中国科学院空天信息创新研究院研究员，博士生导师，IEEE高级会员、IEEE地球科学与遥感快报副主编、雷达学报青年编委。主要研究方向为SAR成像处理、SAR图像理解

张　柘(1988–)，男，博士，中国科学院空天信息创新研究院、苏州空天信息研究院研究员，博士生导师。研究方向为稀疏信号处理与合成孔径雷达成像

丁赤飚(1969–)，男，研究员，博士生导师，中国科学院院士，先后主持多项国家863重点项目和国家级遥感卫星地面系统工程建设等项目，曾获国家科技进步一等奖、二等奖，国家发明二等奖等奖励。研究方向为合成孔径雷达、遥感信息处理和应用系统等

通讯作者:
仇晓兰 xlqiu@mail.ie.ac.cn

责任主编：陈尔学 Corresponding Editor: CHEN Erxue
中图分类号: TN959.3
计量
- 文章访问数: 1064
- HTML全文浏览量: 391
- PDF下载量: 106
- 被引次数: 0
出版历程
- 收稿日期: 2022-04-02
- 修回日期: 2022-05-28
- 网络出版日期: 2022-06-27
- 刊出日期: 2022-08-28

Error Analysis of Polarimetric Interferometric SAR under Different Processing Modes in Urban Areas

LYU Zexin^{1, 4, 5},
QIU Xiaolan^{1, 2, 3, 4
, ,},
ZHANG Zhe^{2, 3},
DING Chibiao^{1, 4, 5}

1.
Key Laboratory of Technology in Geo-Spatial Information Processing and Application Systems, Chinese Academy of Sciences, Beijing 100190, China
2.
Key Laboratory of Intelligent Aerospace Big data Application Technology, Suzhou 215124, China
3.
Suzhou Aerospace Information Research Institute, Suzhou 215124, China
4.
Aerospace Information Research Institute, Chinese Academy of Sciences, Beijing 100190, China
5.
School of Electronic, Electrical and Communication Engineering, University of Chinese Academy of Sciences, Beijing 100049, China

Funds: The National Natural Science Foundation of China (61991421, 62022082)

More Information

Corresponding author: QIU Xiaolan, xlqiu@mail.ie.ac.cn

摘要

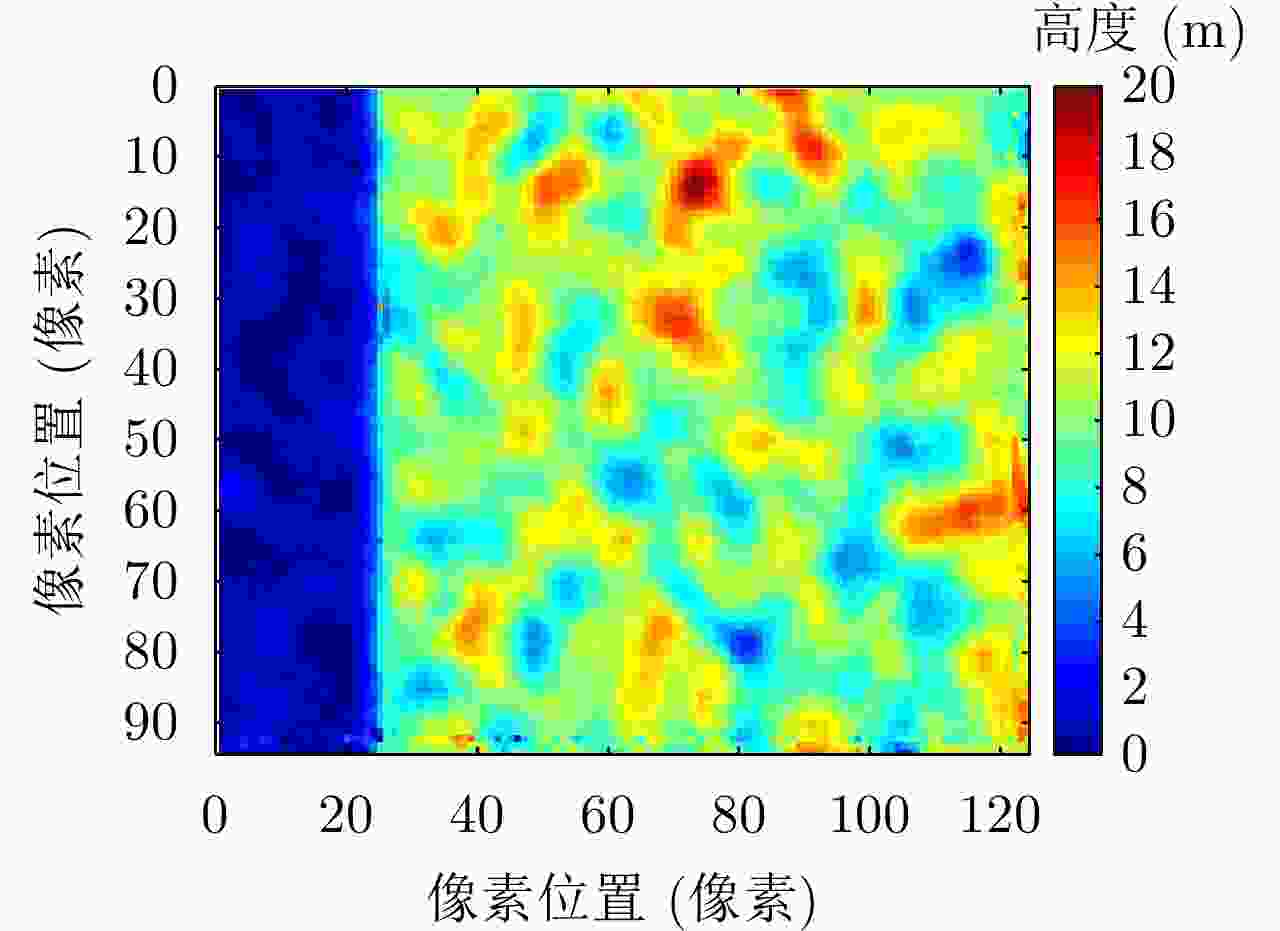
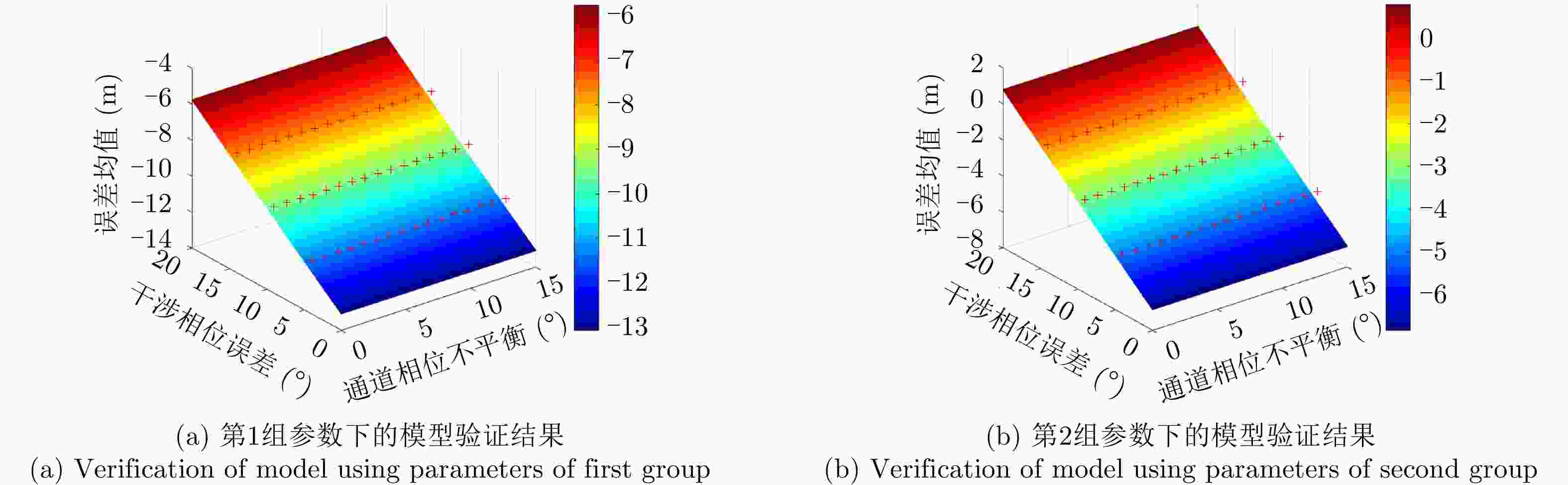
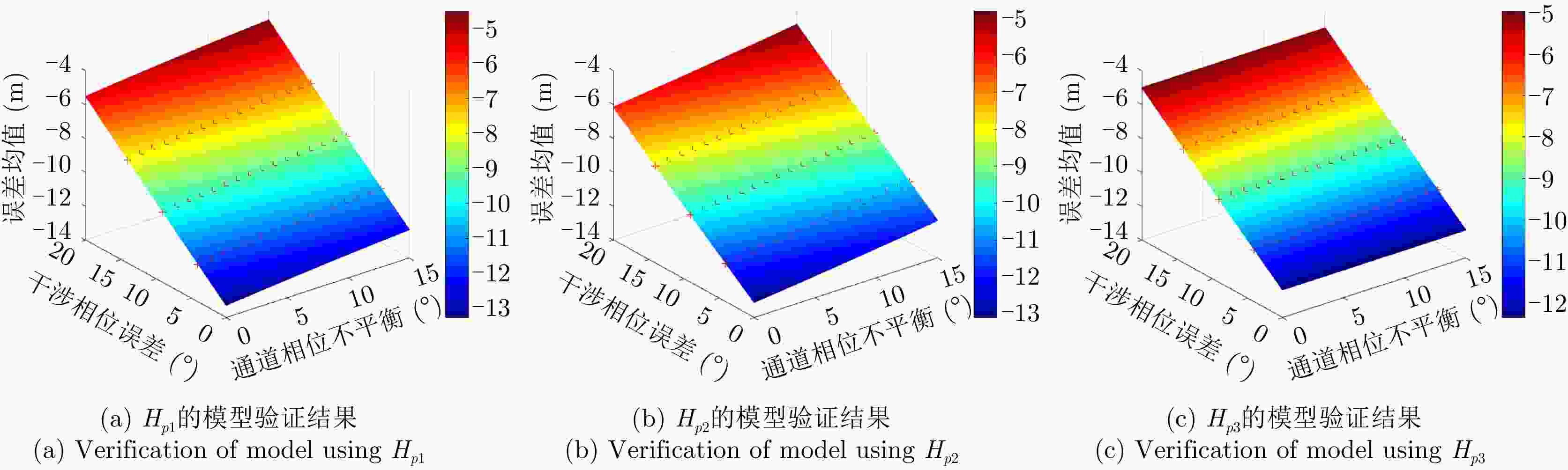
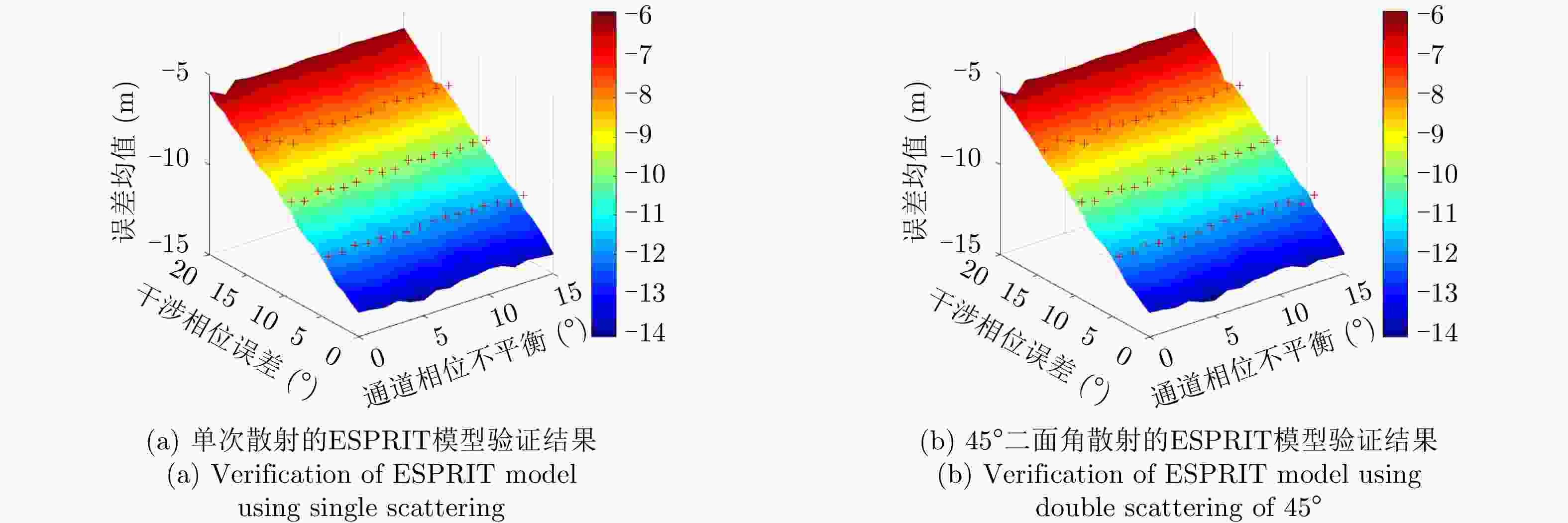
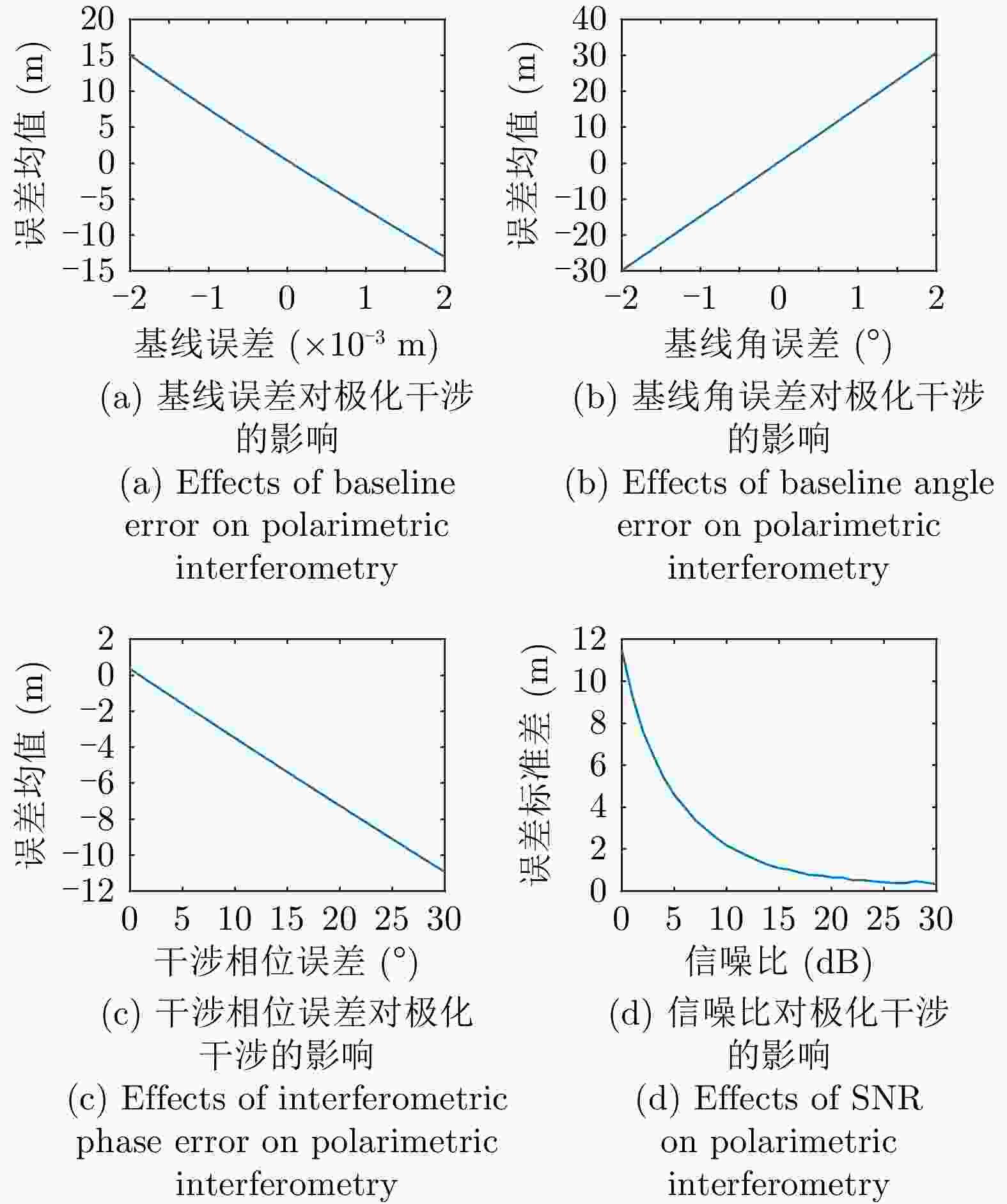
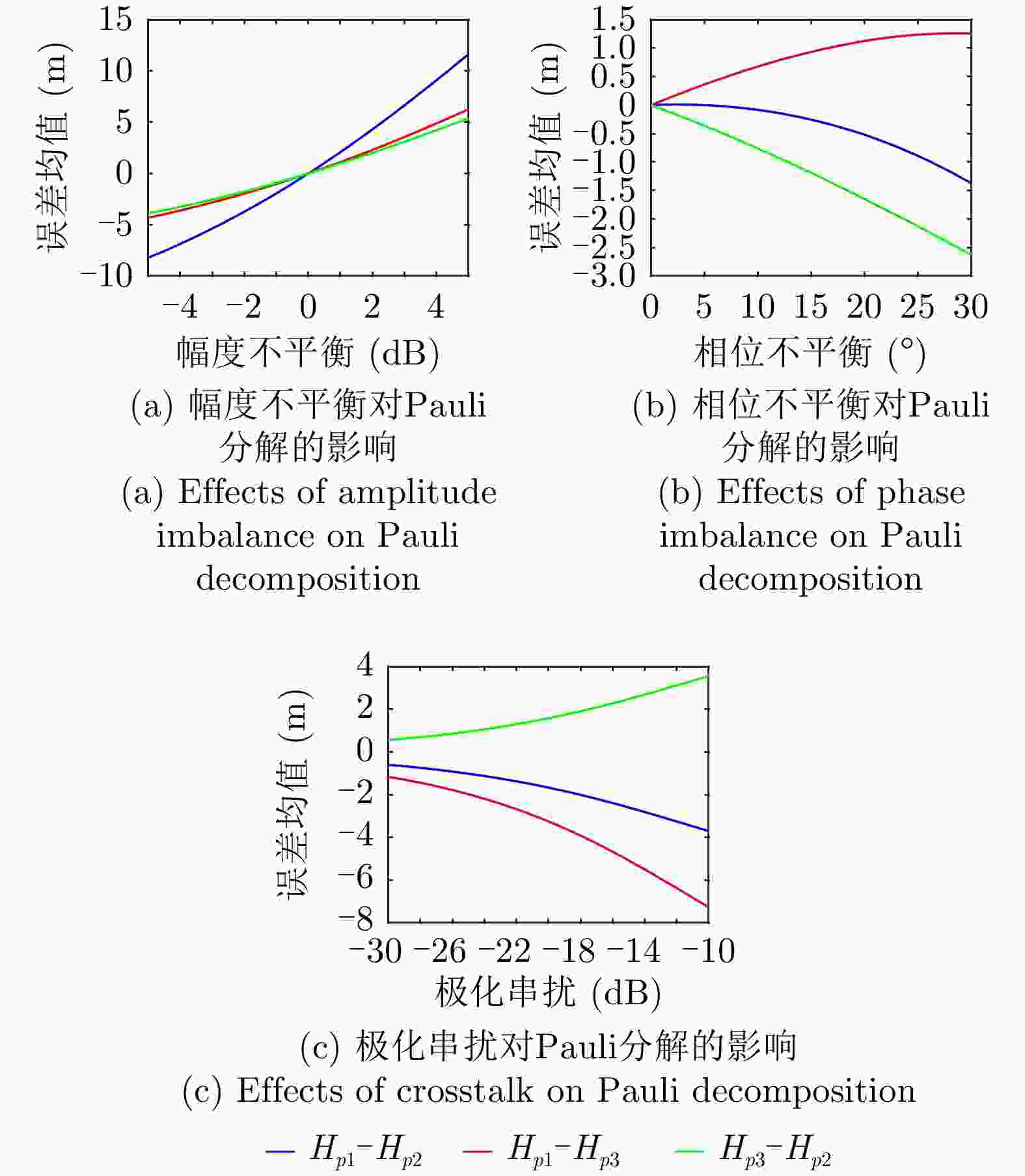
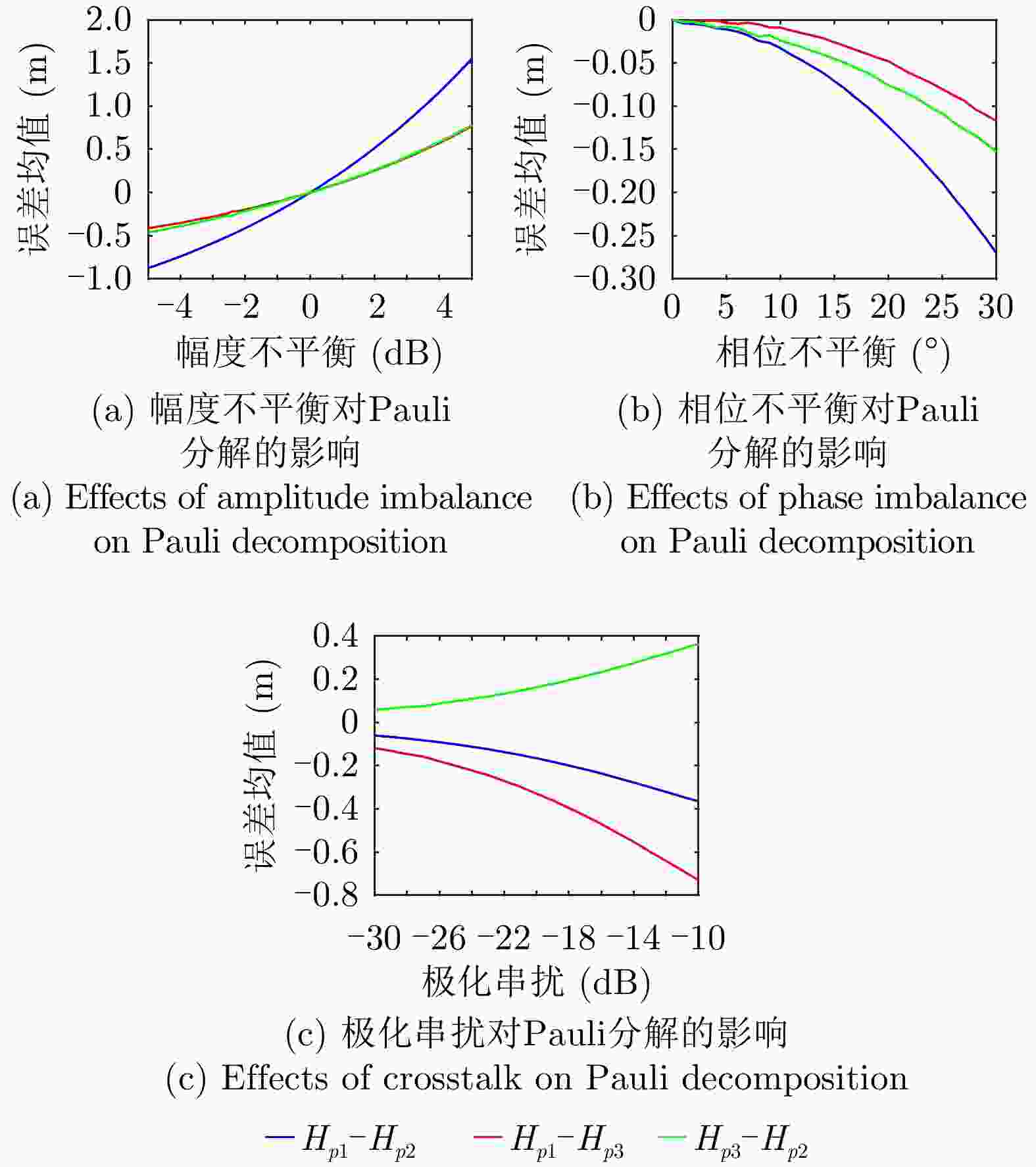
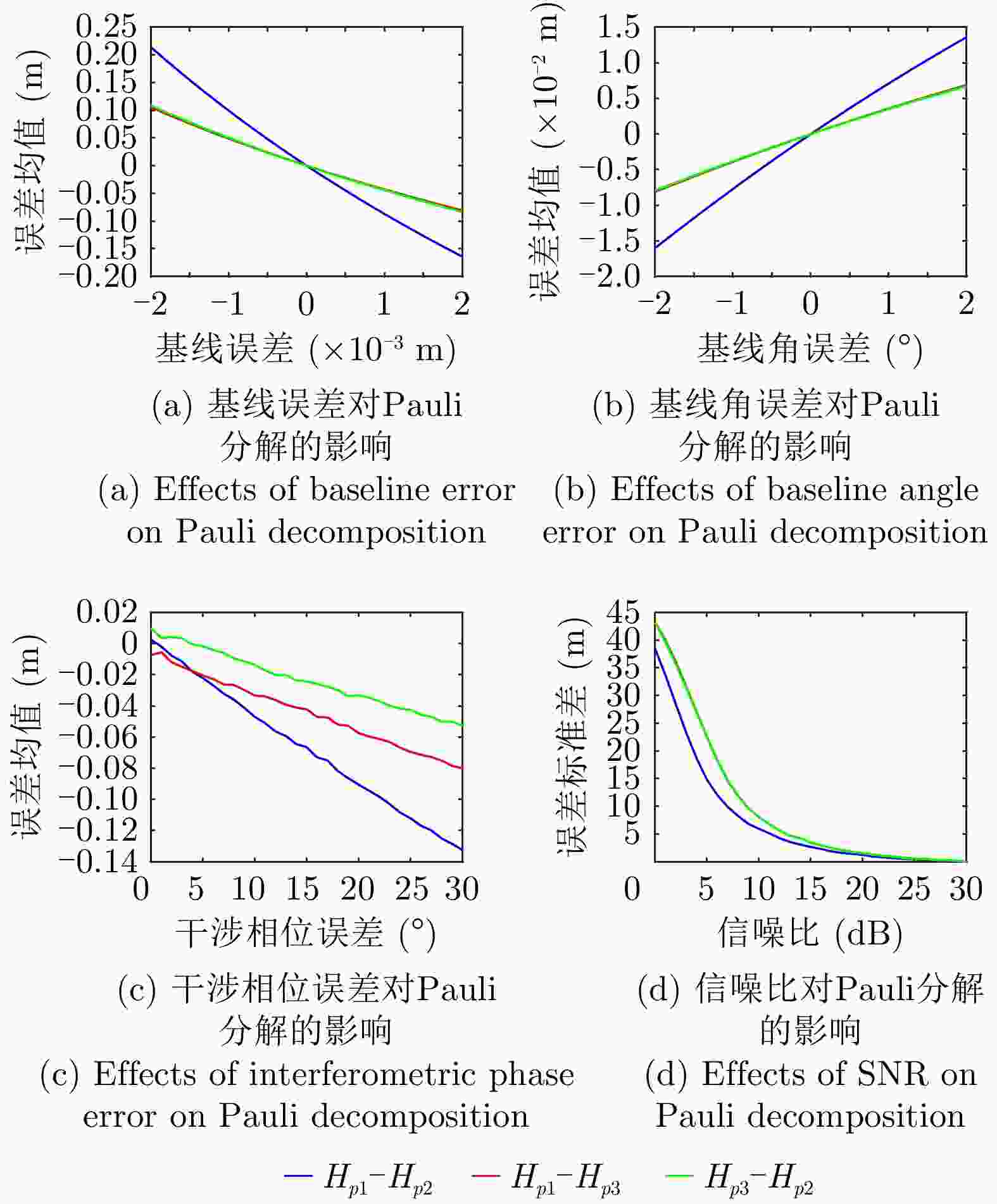
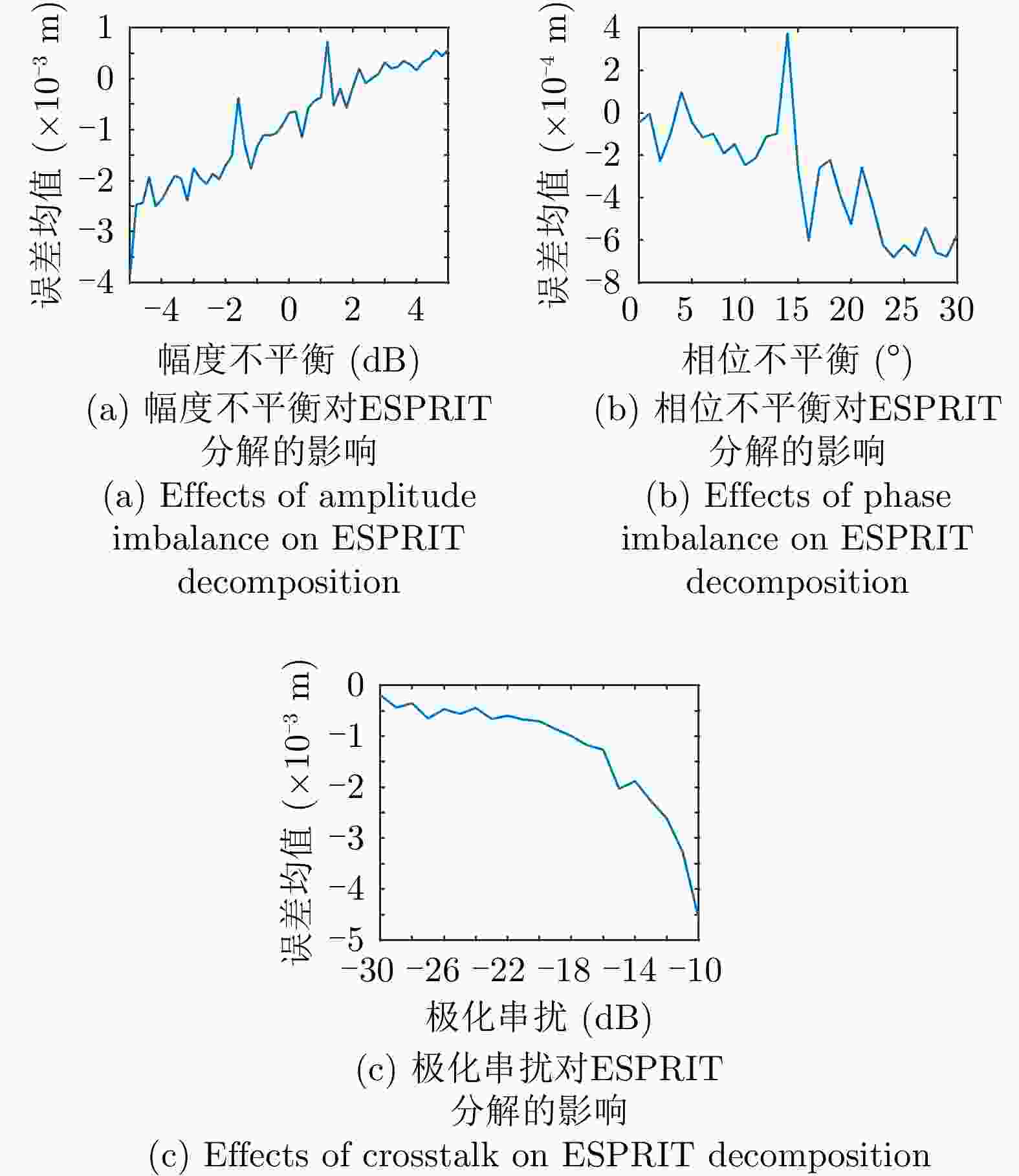
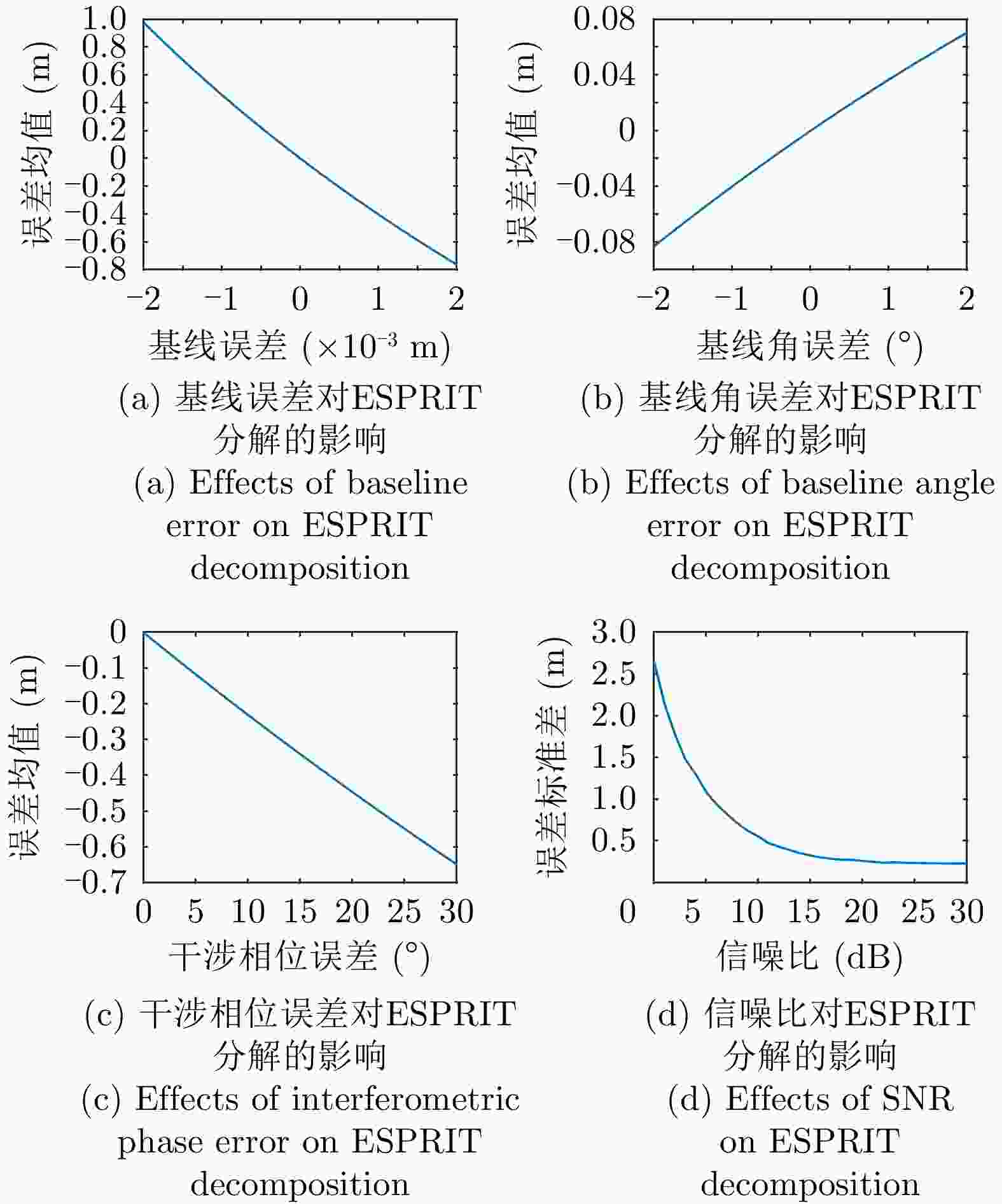
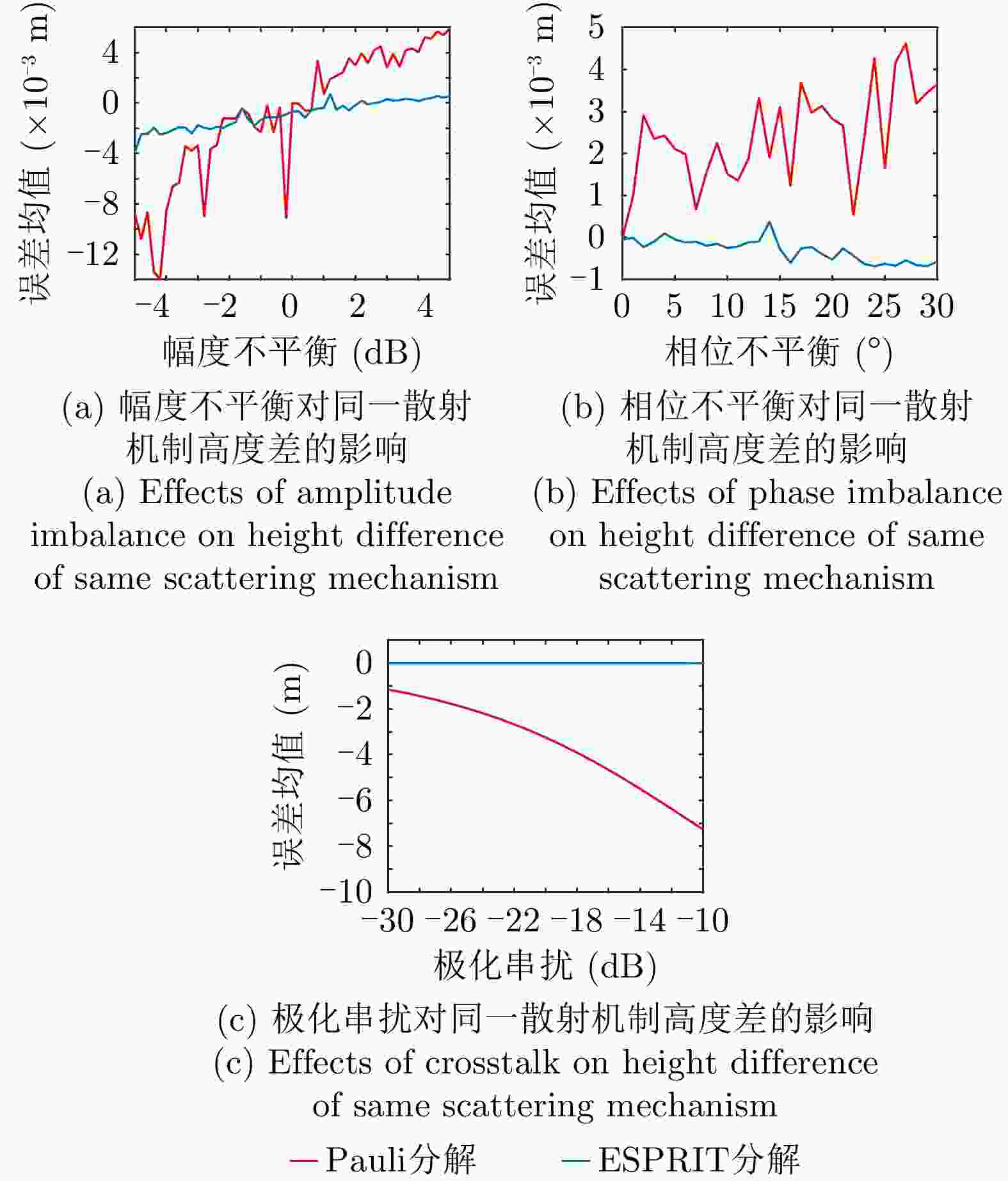
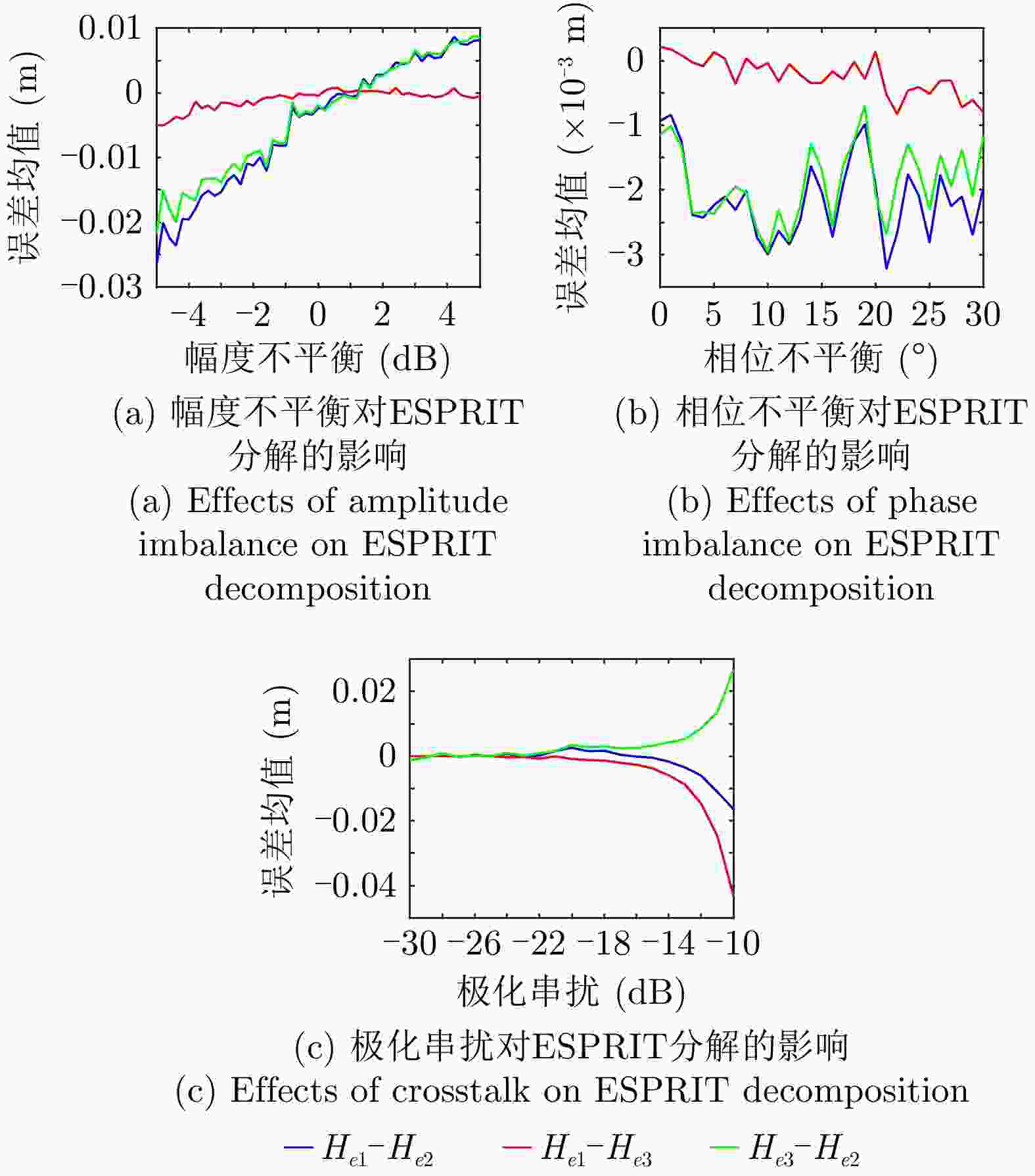
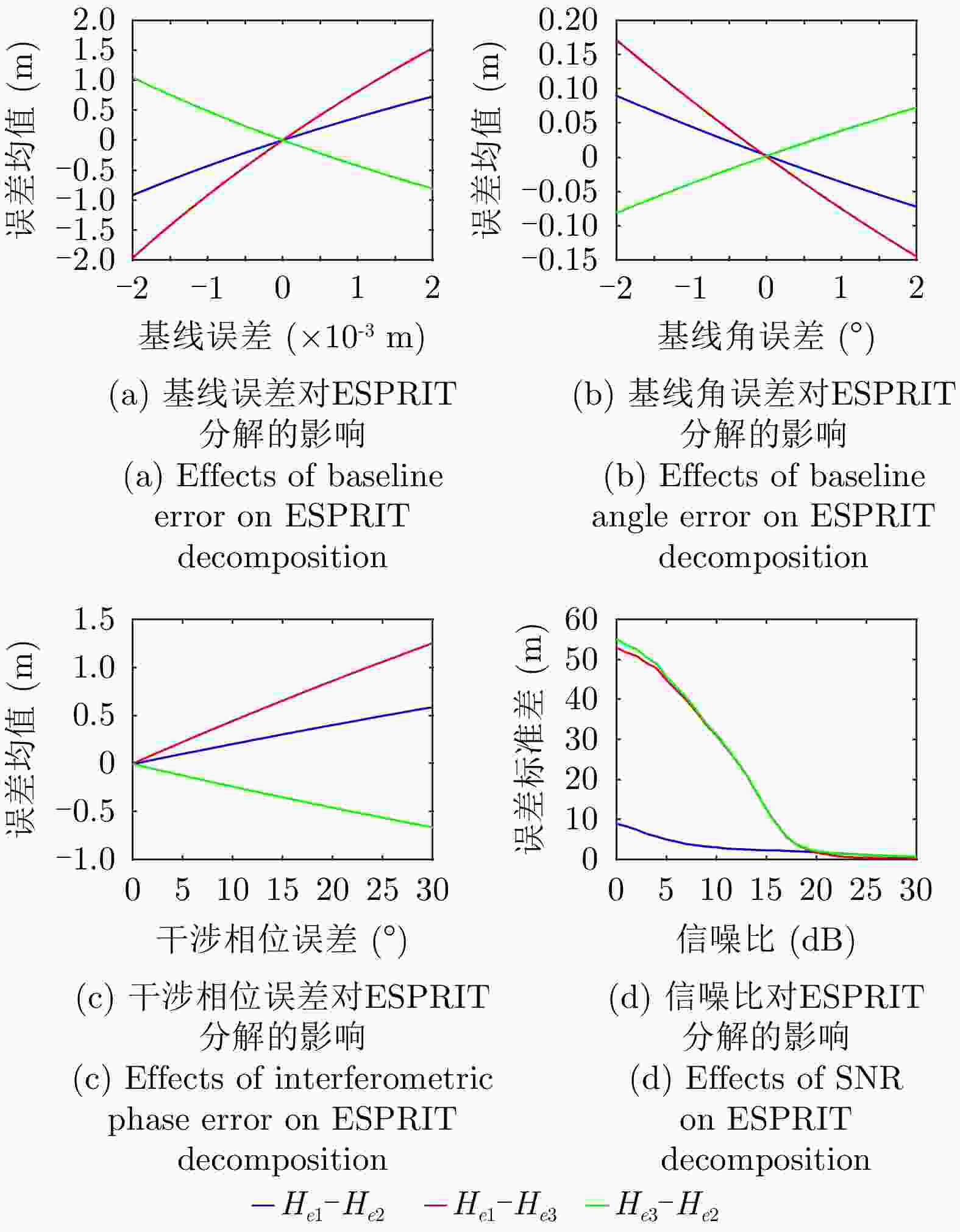
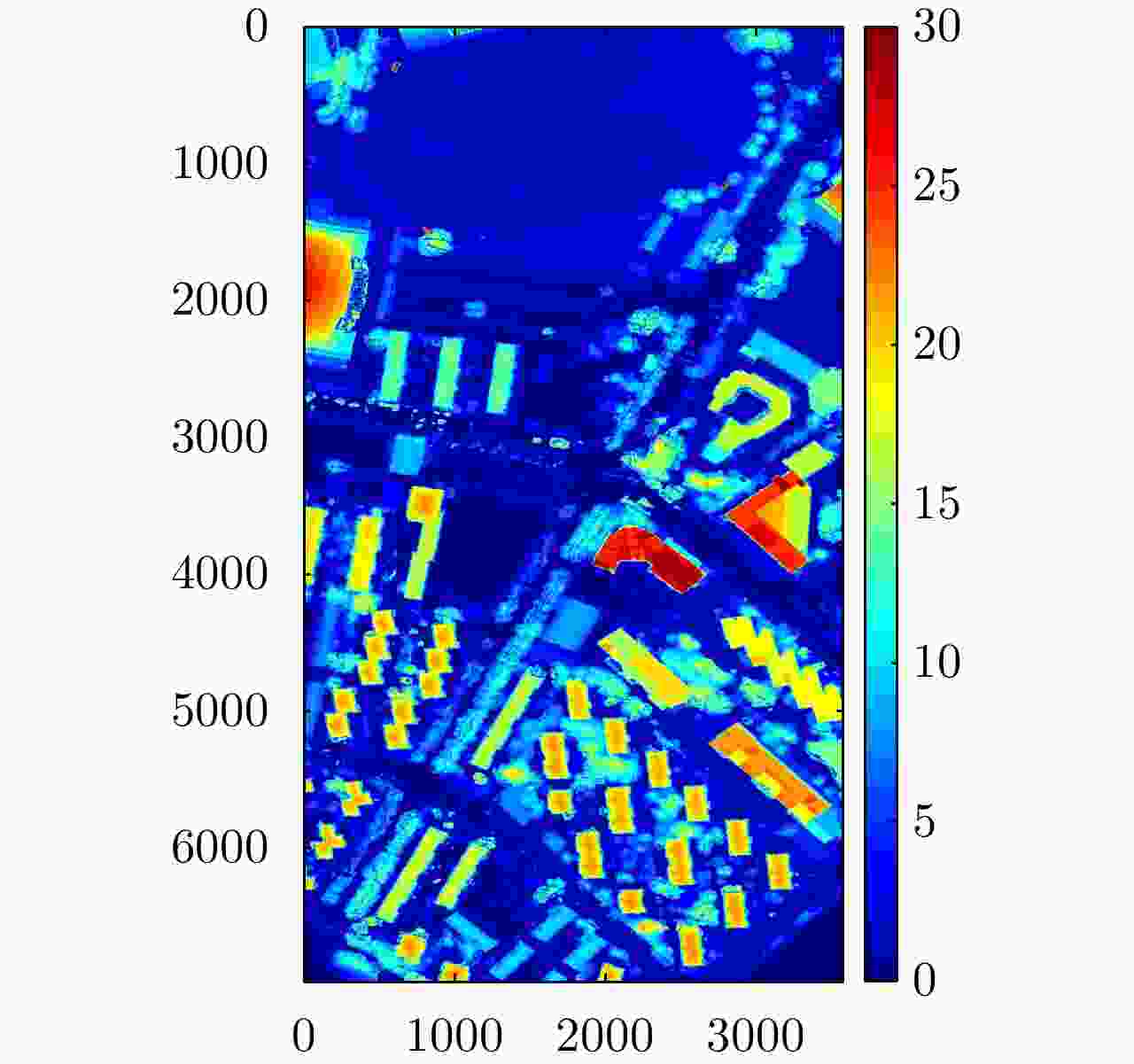
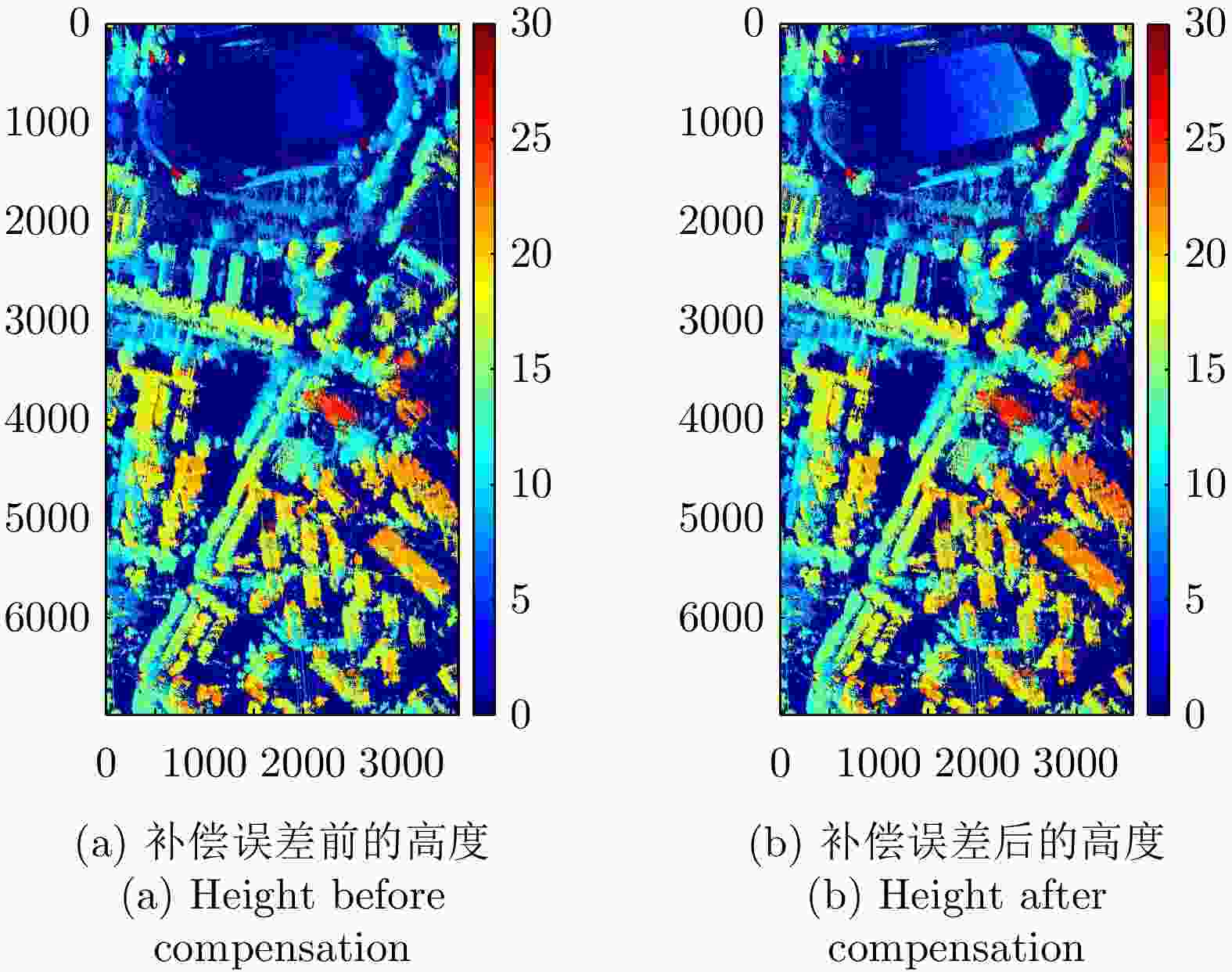
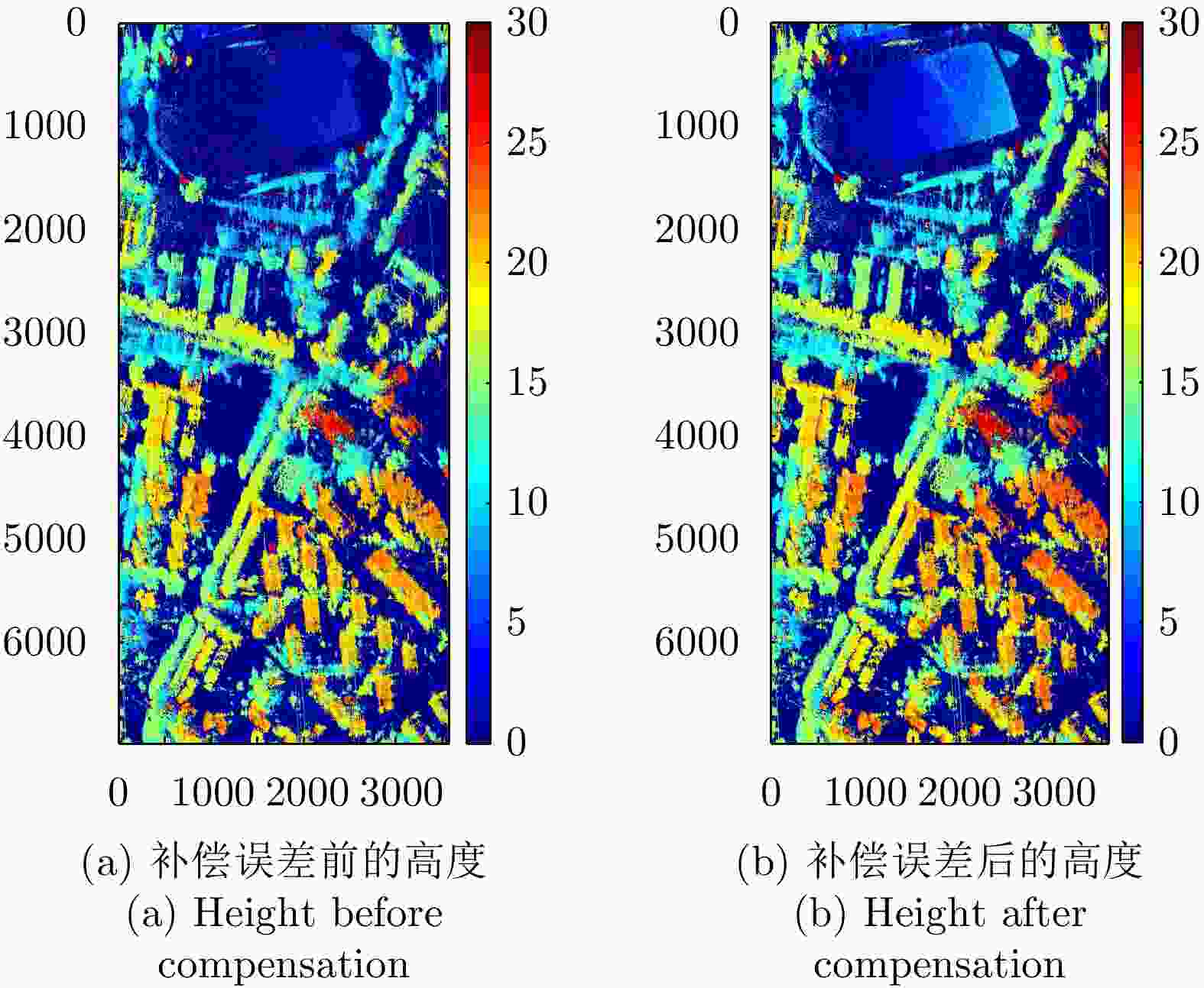
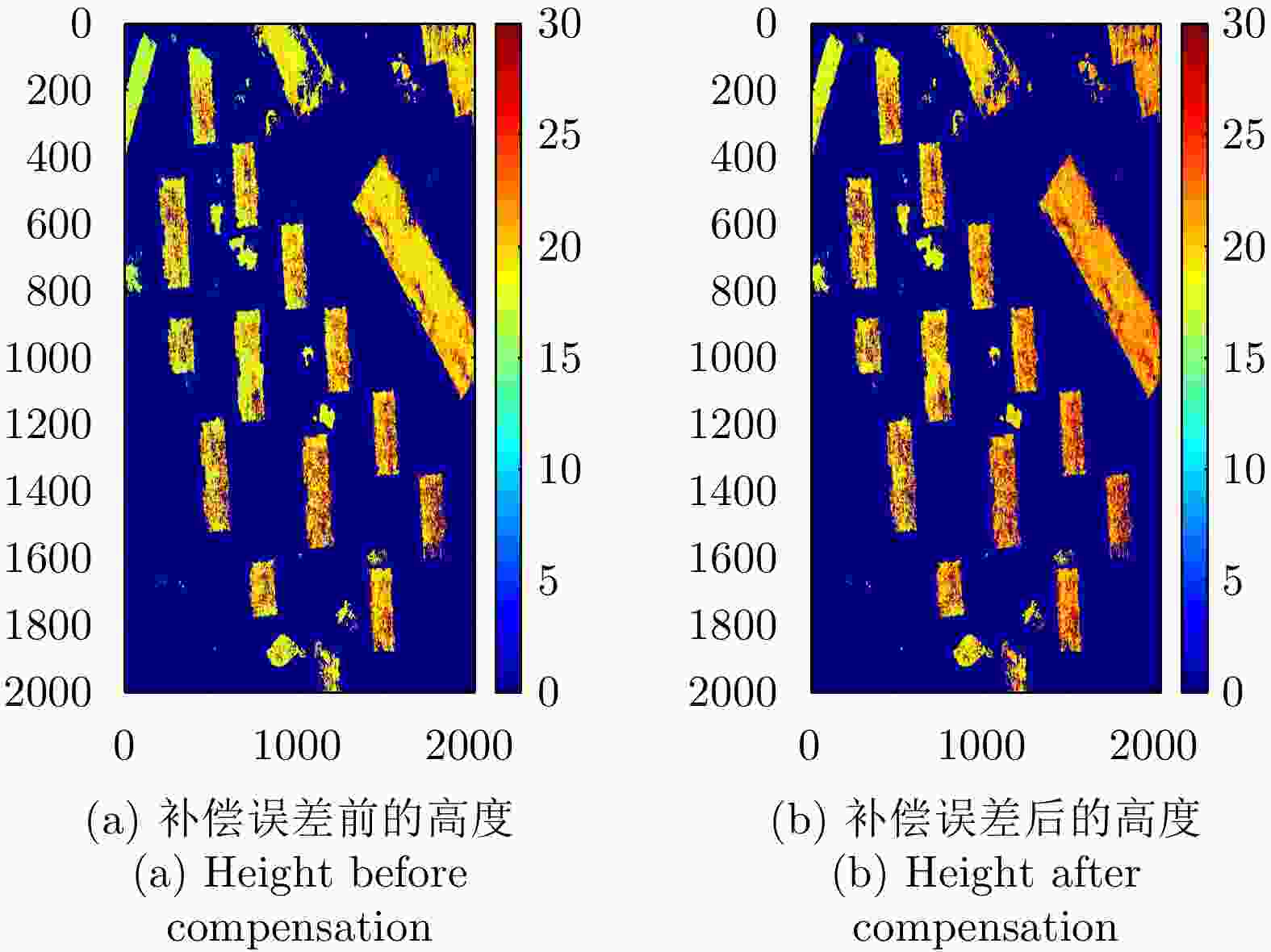
摘要: 极化干涉合成孔径雷达(PolInSAR)在城区等复杂场景下的应用受到了越来越多的关注。面向城区的极化干涉SAR处理主要包括基于极化最优相干的干涉测高、基于极化分解的干涉测高、联立极化干涉观测方程直接求解不同散射机制高度这3种模式。现有研究对各类误差在极化干涉SAR不同处理模式下的综合影响分析尚很欠缺。该文在构建极化干涉SAR误差模型的基础上，提出了联立极化观测方程下散射机制的求解方法，推导了极化失真和干涉误差在极化干涉SAR不同处理模式下的综合影响模型，并通过仿真验证了模型的正确性，同时给出了3种处理模式补偿误差后的高度反演结果，补偿误差后通过极化最优相干得到建筑区域高度的均方根误差(RMSE)为2.77 m。在此基础上，通过仿真给出了极化干涉SAR不同处理模型下的误差影响曲线，比较了不同处理模型受误差影响的程度，并给出了合理解释，研究结果为极化干涉SAR系统设计、处理方法选择及数据应用提供了参考。
- 极化干涉合成孔径雷达 /
- 误差分析 /
- 极化最优相干 /
- Pauli分解 /
- ESPRIT分解
Abstract: Polarimetric Interferometric Synthetic Aperture Radar (PolInSAR) simultaneously has interferometric height measurement and full-polarized detection capabilities, which can better reflect the structural properties of feature targets. Therefore, its potential for application in complex scenarios, such as urban areas, has attracted increasing attention. In urban areas, the processing mainly includes three modes: using interferometry to extract height based on polarimetric optimal coherence, using interferometry based on polarized decomposition, and associating polarimetric interferometric observation equations to retrieve the heights of different scattering mechanisms. The analysis of error factors and effects on Interferometric SAR (InSAR) and polarized SAR is almost complete, but the analysis of error effects under different processing modes of PolInSAR is insufficient. Based on the PolInSAR error model, our paper proposes a method for solving the scattering mechanism under the simultaneous polarization observation equation. Moreover, we derive the model including each error under different processing modes in PolInSAR from the aspect of polarized errors, interferometric errors, and the Signal-to-Noise Ratio (SNR). Furthermore, the model is verified through simulations, and we provide height inversion results through three processing modes after compensating for polarized errors and interferometric errors. After the error compensation, we obtain a Root Mean Squared Error (RMSE) in building areas of 2.77 m through polarimetric optimal coherence. Finally, the simulations provide the error impact curves under different processing modes of PolInSAR and compare the degree of different processing methods affected by errors, which provides a reasonable explanation for the design of the PolInSAR system, selection of processing methods, and data application.
- Polarimetric Interferometric SAR (PolInSAR) /
- Error analysis /
- Polarimetric optimal coherence /
- Pauli decomposition /
- ESPRIT decomposition

HTML全文

图 1 干涉SAR观测几何示意图

Figure 1. The schematic diagram of InSAR

下载: 全尺寸图片幻灯片

图 2 仿真图像

Figure 2. Simulation image

下载: 全尺寸图片幻灯片

图 3 极化干涉误差模型的验证

Figure 3. Verification of PolInSAR error model

下载: 全尺寸图片幻灯片

图 4 Pauli分解下的极化干涉误差模型验证(单一高度)

Figure 4. Verification of error model under Pauli decomposition (Single height)

下载: 全尺寸图片幻灯片

图 5 Pauli分解下的极化干涉误差模型验证(高度差)

Figure 5. Verification of error model under Pauli decomposition (Height difference)

下载: 全尺寸图片幻灯片

图 6 结合ESPRIT的极化相干误差模型验证(单一高度)

Figure 6. Verification of error model of PolInSAR combined with ESPRIT (Single Height)

下载: 全尺寸图片幻灯片

图 7 结合ESPRIT的极化相干误差模型验证

Figure 7. Verification of error model of PolInSAR combined with ESPRIT

下载: 全尺寸图片幻灯片

图 8 极化串扰对ESPRIT分解得到的高度的影响

Figure 8. Effects of crosstalk on height obtained by ESPRIT decomposition

下载: 全尺寸图片幻灯片

图 9 两天线极化失真一致时，极化失真对ESPRIT误差模型的影响

Figure 9. Effects of polarization distortion on ESPRIT error model when distortion is equal on two antennas

下载: 全尺寸图片幻灯片

图 10 极化失真对极化干涉高度反演的影响

Figure 10. Effects of polarization distortion on height obtained by PolInSAR

下载: 全尺寸图片幻灯片

图 11 干涉误差对极化干涉高度反演的影响

Figure 11. Effects of interferometric error on height obtained by PolInSAR

下载: 全尺寸图片幻灯片

图 12 极化失真对Pauli分解下高度反演结果的影响

Figure 12. Effects of polarization distortion on height obtained by Pauli decomposition

下载: 全尺寸图片幻灯片

图 13 干涉误差对Pauli分解下高度反演结果的影响

Figure 13. Effects of interferometric error on height obtained by PolInSAR

下载: 全尺寸图片幻灯片

图 14 极化失真对Pauli分解的影响

Figure 14. Effects of polarization distortion on Pauli decomposition

下载: 全尺寸图片幻灯片

图 15 干涉误差与信噪比对Pauli分解的影响

Figure 15. Effects of interferometric error on Pauli decomposition

下载: 全尺寸图片幻灯片

图 16 极化失真对ESPRIT分解的影响

Figure 16. Effects of polarization distortion on ESPRIT

下载: 全尺寸图片幻灯片

图 17 干涉误差对ESPRIT分解的影响

Figure 17. Effects of interferometric error on ESPRIT

下载: 全尺寸图片幻灯片

图 18 极化失真对散射机制高度差的影响

Figure 18. Effects of polarization distortion on height difference of scattering mechanisms

下载: 全尺寸图片幻灯片

图 19 干涉误差对散射机制高度差的影响

Figure 19. Effects of interferometric error on height difference of scattering mechanisms

下载: 全尺寸图片幻灯片

图 20 3类机制混合的极化误差对ESPRIT分解的影响

Figure 20. Effects of polarization distortion on ESPRIT mixed by 3 mechanisms

下载: 全尺寸图片幻灯片

图 21 3类机制混合的干涉误差对ESPRIT分解的影响

Figure 21. Effects of interferometric error on ESPRIT mixed by 3 mechanisms

下载: 全尺寸图片幻灯片

图 22 无人机载极化干涉SAR系统

Figure 22. UAV-borne PolInSAR system

下载: 全尺寸图片幻灯片

图 23 无人机载极化干涉SAR系统成像区域

Figure 23. Imaging area of UAV-borne system

下载: 全尺寸图片幻灯片

图 24 真实高度

Figure 24. Real height

下载: 全尺寸图片幻灯片

图 25 极化最优相干反演的高度图

Figure 25. Height retrieved by polarimetric optimal coherence

下载: 全尺寸图片幻灯片

图 26 单次散射反演的高度图

Figure 26. Height retrieved by single scattering

下载: 全尺寸图片幻灯片

图 27 ESPRIT反演的高度图

Figure 27. Height retrieved by ESPRIT

下载: 全尺寸图片幻灯片

表 1 系统仿真参数

Table 1. Simulation parameters of system

参数	数值
中心频率	15.2 GHz
飞行高度	205 m
斜距	889 m
基线	0.6 m
基线角	–1°

下载: 导出CSV

表 2 ESPRIT方法得到散射机制的结果

Table 2. Scattering mechanisms obtained by ESPRIT

极化方式	主图像	辅图像	含串扰的主图像	含串扰的辅图像
单次散射	–0.89 +0.11i	–0.85 –0.25	–0.54 +0.03i	–0.45 –0.33i
0°二次散射	0.02 –0.01i	0.02 –0.01i	0.02 +0.01i	0.02 +0.01i
45°二次散射	1	1	1	1

下载: 导出CSV

表 3 ESPRIT方法得到的干涉相位

Table 3. Interferometric phase obtained by ESPRIT

极化方式	理想(°)	含串扰(°)
单次散射	58.90	58.41
45°二次散射	84.87	84.24

下载: 导出CSV

表 4 Pauli分解得到散射机制的结果

Table 4. Scattering mechanisms obtained by Pauli decomposition

极化方式	主图像	辅图像	含串扰的主图像	含串扰的辅图像
单次散射	0.10	0.29	0.09+0.04i	0.28+0.04i
0°二次散射	0.002	0.001i	–0.001i	0.003
45°二次散射	1	1	1	1

下载: 导出CSV

表 5 –20 dB串扰误差下两种分解的干涉相位误差

Table 5. Interferometric phase error of two decompositions under –20 dB crosstalk

极化方式	ESPRIT (°)	Pauli (°)
单次散射	0.49	15.69
45°二次散射	0.63	–0.45

下载: 导出CSV

参考文献(22)

[1]	CLOUDE S R and PAPATHANASSIOU K P. Polarimetric SAR interferometry[J]. IEEE Transactions on Geoscience and Remote Sensing, 1998, 36(5): 1551–1565. doi: 10.1109/36.718859
[2]	TREUHAFT R N and CLOUDE S R. The structure of oriented vegetation from polarimetric interferometry[J]. IEEE Transactions on Geoscience and Remote Sensing, 1999, 37(5): 2620–2624. doi: 10.1109/36.789657
[3]	CLOUDE S R and PAPATHANASSIOU K P. Three-stage inversion process for Polarimetric SAR interferometry[J]. IEE Proceedings-Radar, Sonar and Navigation, 2003, 150(3): 125–134. doi: 10.1049/ip-rsn:20030449
[4]	PAPATHANASSIOU K P and CLOUDE S R. Single-baseline Polarimetric SAR interferometry[J]. IEEE Transactions on Geoscience and Remote Sensing, 2001, 39(11): 2352–2363. doi: 10.1109/36.964971
[5]	GARESTIER F, DUBOIS-FERNANDEZ P, DUPUIS X, et al. PolInSAR analysis of X-band data over vegetated and urban areas[J]. IEEE Transactions on Geoscience and Remote Sensing, 2006, 44(2): 356–364. doi: 10.1109/TGRS.2005.862525
[6]	王萍, 汪长城, 彭星, 等. 基于PolInSAR三分量分解的建筑物高度向信息提取方法[J]. 测绘工程, 2014, 23(6): 16–20, 26. doi: 10.3969/j.issn.1006-7949.2014.06.004 WANG Ping, WANG Changcheng, PENG Xing, et al. Building height information extraction method based on three-component decomposition for PolInSAR data[J]. Engineering of Surveying and Mapping, 2014, 23(6): 16–20, 26. doi: 10.3969/j.issn.1006-7949.2014.06.004
[7]	GUILLASO S, FERRO-FAMIL L, REIGBER A, et al. Analysis of built-up areas from Polarimetric interferometric SAR images[C]. 2003 IEEE International Geoscience and Remote Sensing Symposium, Toulouse, France, 2003: 1727–1729.
[8]	COLIN E, TITIN-SCHNAIDER C, and TABBARA W. An interferometric coherence optimization method in radar polarimetry for high-resolution imagery[J]. IEEE Transactions on Geoscience and Remote Sensing, 2006, 44(1): 167–175. doi: 10.1109/TGRS.2005.859357
[9]	COLIN-KOENIGUER E and TROUVÉ N. Performance of building height estimation using high-resolution PolInSAR images[J]. IEEE Transactions on Geoscience and Remote Sensing, 2014, 52(9): 5870–5879. doi: 10.1109/TGRS.2013.2293605
[10]	CLOUDE S R. Calibration requirements for forest parameter estimation using POLinSAR[C]. CEOS Working Group on Calibration/Validation SAR Workshop, London, UK, 2002: 151–158.
[11]	张林涛, 洪峻, 明峰. PolInSAR极化误差对最优相干相位的影响研究[J]. 电子与信息学报, 2011, 33(2): 412–417. doi: 10.3724/SP.J.1146.2010.00331 ZHANG Lintao, HONG Jun, and MING Feng. Study on the impact of Polarimetric error on optimal coherence phase of PolInSAR[J]. Journal of Electronics &Information Technology, 2011, 33(2): 412–417. doi: 10.3724/SP.J.1146.2010.00331
[12]	许丽颖. 极化干涉合成孔径雷达系统与信息处理技术研究[D]. [博士论文], 中国科学院电子学研究所, 2014: 127–136. XU Liying. Study on system and information processing of Polarimetric SAR interferometry[D]. [Ph. D. dissertation], Institute of Electronics, Chinese Academy of Sciences, 2014: 127–136.
[13]	孙翔. 极化干涉合成孔径雷达地物参数估计与系统设计方法研究[D]. [博士论文], 中国科学院电子学研究所, 2018: 110–113. SUN Xiang. On approach of estimating ground feature parameters and system design of Polarimetric SAR interferometry[D]. [Ph. D. dissertation], Institute of Electronics, Chinese Academy of Sciences, 2018: 110–113.
[14]	SUN Zhongchang, GUO Huadong, LI Xinwu, et al. Error analysis of DEM derived from airborne single-pass interferometric SAR data[C]. 2011 IEEE International Geoscience and Remote Sensing Symposium, Vancouver, Canada, 2011: 3405–3408.
[15]	ZHAO Shuyuan, GU Defeng, YI Bin, et al. Error analysis for the baseline estimation and calibration of distributed InSAR satellites[C]. 2016 IEEE International Geoscience and Remote Sensing Symposium, Beijing, China, 2016: 4179–4182.
[16]	生强强. InSAR DEM精度分析与定量评估方法[D]. [硕士论文], 西安电子科技大学, 2018. SHENG Qiangqiang. InSAR DEM accuracy analysis and quantitative evaluation[D]. [Master dissertation], Xidian University, 2018.
[17]	方东生, 吕孝雷, 李缘廷, 等. 运动补偿对机载SAR重轨干涉成像的影响分析[J]. 雷达科学与技术, 2016, 14(4): 355–363. doi: 10.3969/j.issn.1672-2337.2016.04.003 FANG Dongsheng, LV Xiaolei, LI Yuanting, et al. Effect of motion compensation on airborne repeat pass InSAR imaging[J]. Radar Science and Technology, 2016, 14(4): 355–363. doi: 10.3969/j.issn.1672-2337.2016.04.003
[18]	WANG Huiqiang, ZHU Jianjun, FU Haiqiang, et al. Modeling and robust estimation for the residual motion error in airborne SAR interferometry[J]. IEEE Geoscience and Remote Sensing Letters, 2019, 16(1): 65–69. doi: 10.1109/LGRS.2018.2867868
[19]	孙晗伟, 曾涛, 杨健, 等. SAR残余相位误差对森林高度反演影响的全链路模拟与分析[J]. 武汉大学学报: 信息科学版, 2015, 40(2): 153–158. doi: 10.13203/j.whugis20130052 SUN Hanwei, ZENG Tao, YANG Jian, et al. Simulation and analysis of SAR residual phase error on forest height inversion[J]. Geomatics and Information Science of Wuhan University, 2015, 40(2): 153–158. doi: 10.13203/j.whugis20130052
[20]	LV Zexin, LI Fangfang, QIU xiaolan, et al. Effects of motion compensation residual error and polarization distortion on UAV-borne PolInSAR[J]. Remote Sensing, 2021, 13(4): 618. doi: 10.3390/rs13040618
[21]	ROY R and KAILATH T. ESPRIT-estimation of signal parameters via rotational invariance techniques[J]. IEEE Transactions on Acoustics, Speech, and Signal Processing, 1989, 37(7): 984–995. doi: 10.1109/29.32276
[22]	LV Zexin, QIU Xiaolan, CHENG Yao, et al. Multi-rotor UAV-borne PolInSAR data processing and preliminary analysis of height inversion in urban area[J]. Remote Sensing, 2022, 14(9): 2161. doi: 10.3390/rs14092161