作者中心
专家审稿
责编办公
编辑办公
A Geometry Constrained Moving Least Squares-based High-precision 3D Reconstruction Method of Mountains from TomoSAR Point Clouds
-
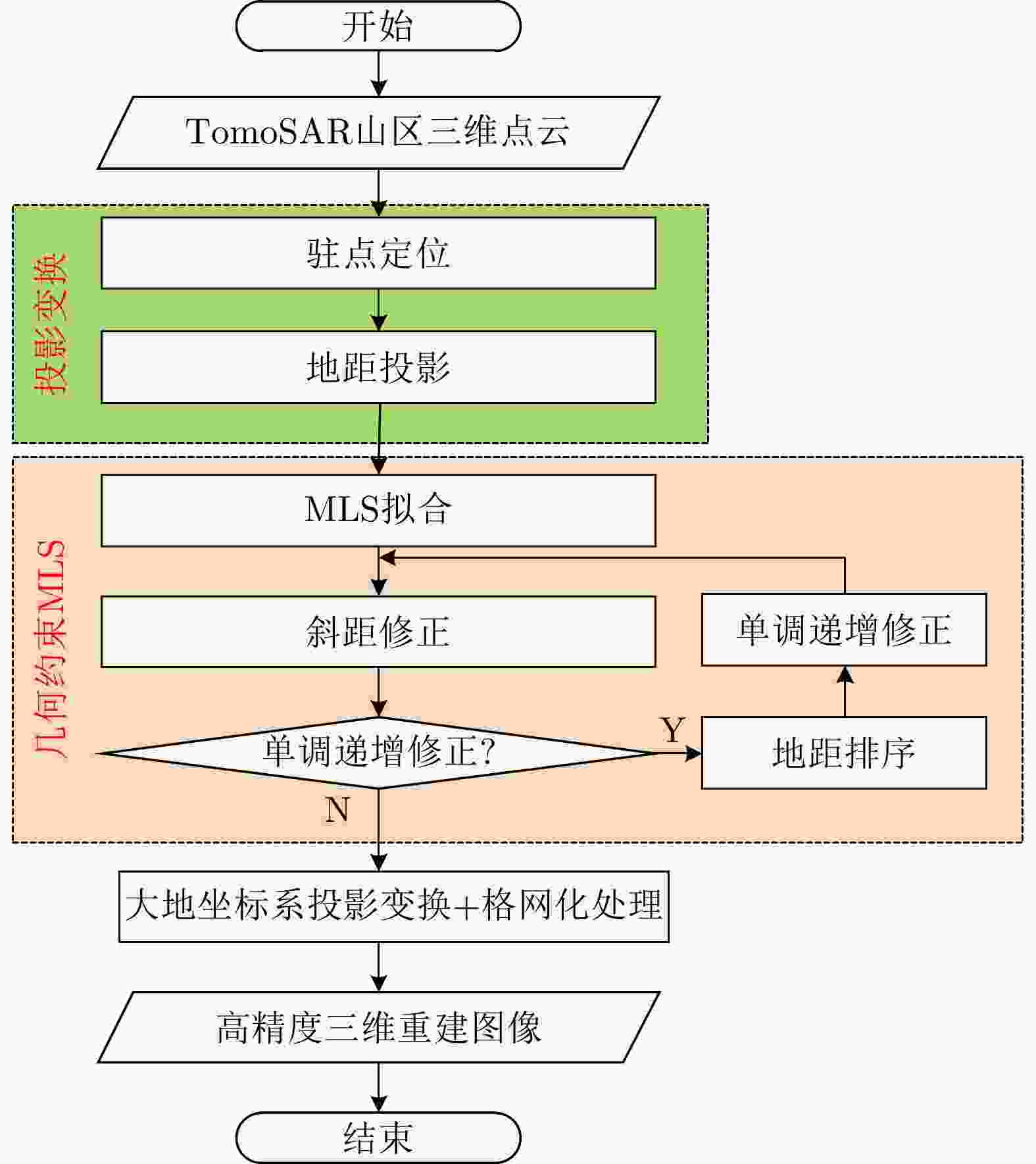
摘要: 层析合成孔径雷达(TomoSAR)是一种先进的山区三维重建技术手段。然而，TomoSAR点云存在着较强烈的高程向定位误差，给高精度的山区三维重建带来了挑战。针对这个问题，该文提出了一种基于几何约束移动最小二乘(MLS)的高精度TomoSAR山区点云三维重建方法。该方法不仅具有传统MLS基于局部子空间思想进行复杂曲面结构拟合的优势，还可以充分地利用TomoSAR点云高程随地距单调递增的特点进行重建误差修正。首先，将点云投影到新的方位-地距-高程坐标系。然后，使用所提的基于迭代求解的几何约束MLS进行高程向定位误差修正。最后，通过投影变换得到山区三维重建结果。仿真和实测的机载阵列TomoSAR山区数据以及AW3D30 DSM数据和1:10000 DEM数据，验证了该文方法的有效性，同时表明了机载阵列TomoSAR用于山区高精度三维重建等应用的可行性和优越性。
-
关键词:
- 三维重建 /
- 层析合成孔径雷达 /
- 点云 /
- 山区 /
- 几何约束移动最小二乘
Abstract: Tomographic Synthetic Aperture Radar (TomoSAR) is an advanced technology for three-dimensional (3D) mountain reconstruction. However, the TomoSAR mountain point clouds have a significant location error in the elevation direction, making high-precision 3D reconstruction of mountains difficult. A geometry constrained Moving Least Squares (MLS)-based high-precision 3D reconstruction method is addressed in this issue. This method not only has the benefits of the traditional MLS in that it uses the local subspace principle for fitting complex surface structures but also fully uses the TomoSAR point cloud characteristic of monotonically increasing elevation with ground distance for reconstruction error correction. The point clouds are first projected onto a new azimuth-ground-elevation domain. Subsequently, the suggested iterative solution-based geometry constrained MLS performs location error correction in the elevation direction. Finally, the projection transformation is used to generate 3D reconstruction results of mountains. The simulation and measurement of airborne array TomoSAR mountain data, AW3D30 DSM data, and 1:10,000 DEM data validate the effectiveness of the proposed method and demonstrate the feasibility and superiority of airborne array TomoSAR for applications such as high-precision 3D mountain reconstruction. -
图 1 TomoSAR山区观测几何示意图(y和z分别表示地距向和高度向，r和s分别表示斜距向和高程向)
Figure 1. Diagram of TomoSAR mountain observation geometry (y and z indicate the ground direction and the height direction, respectively, r and s indicate the range direction and the elevation direction, respectively)
图 3 斜距-高程平面S形山区叠掩地形结构图
Figure 3. The S shaped layover mountainous terrain on the range-elevation plane
图 4 两种典型地形驻点定位示意
Figure 4. Diagram of two typical terrain for stagnation point positioning
图 7 基于数据1的不同方法的精度对比曲线
Figure 7. The precision comparison curves of different methods based on data 1
图 8 本文方法对于切片5的主要中间结果
Figure 8. The main intermediate results of the proposed method for slice 5
图 9 观测场景的SAR图像(颜色图表示归一化后的散射强度)
Figure 9. SAR image of the observation scene (the color map indicates the normalized scattering intensity)
图 12 三维重建图像(颜色图表示归一化后的散射强度)
Figure 12. The three-dimensional reconstruction image (the color map indicates the normalized scattering intensity)
表 1 几何约束MLS求解算法
Table 1. The solution algorithm of the geometry constrained MLS
输入：投影变换点云${\rm{P} } = \left\{ { {p_i}\left( { {a_i},{y_i},{h_i} } \right)|{a_i} \in \left( { {A_1},{A_2}, \cdots ,{A_J} } \right),i = 1,2, \cdots ,{N_{{\rm{total}}} } } \right\}$，斜距r，以及MLS参数和单调递增修正参数${\rm{pwin}}$,
${\rm{Te}}$和${\rm{dh}}$。1：步骤1 执行MLS，输出点云${\rm{P} }' = \left\{ { {p_i}\left( { {a_i},{y_i},h_i'} \right)|{a_i} \in \left( { {A_1},{A_2}, \cdots ,{A_J} } \right),i = 1,2, \cdots ,{N_{{\rm{total}}} } } \right\}$; 2：步骤2 斜距修正：考虑到MLS拟合结果可能存在斜距误差，该步会使用原始斜距r对其修正，得点云
${\rm{P}}' = \left\{ { {p_i}\left( { {a_i},{r_i},h_i'} \right)|{a_i} \in \left( { {A_1},{A_2}, \cdots ,{A_J} } \right),i = 1,2, \cdots ,{N_{{\rm{total}}} } } \right\}$；3：步骤3 单调递增判断： 4： (i) 更新点云${\rm{P}}'$的地距：$y_i' = {r_i}\sin{\theta _i}$，其中$ {\theta _i} $可由式(3)求得； 5： (ii) 计算稀疏高程$h_i' \pm {\rm{dh}}$在子空间${\rm{pwin}}$内的权函数${\boldsymbol{v}} = \left\{ { {v_i}|i = 1,2, \cdots ,{N_{ {\rm{total} } } } } \right\}$； 6： (iii) 如果存在$ {v_i} = 1 $，进入步骤4，反之，输出结果。 7：步骤4 单调递增修正： 8： (i) 逐方位向循环${\rm{P}}_j' = \left\{ { {p_i}\left( { {a_i},y_i',h_i'} \right)|{a_i} \in \left( { {A_1},{A_2}, \cdots ,{A_J} } \right),i = 1,2, \cdots ,{N_j} } \right\}$ 9： * 更新地距，得到点${p_i}\left( { {a_i},y_i'',h_i'} \right)$，其中$y'' = {\rm{sort}}\left( {y'} \right)$ 10： * 初始化：${\rm{Is}}\_{\rm{ite}} = 0,{\rm{de}} = 1,n = 1$ 11： * 逐点修正： 12： ${\rm{while}}\;\;\;n < {N_j}$ 13： 计算稀疏高程$h_i' \pm {\rm{dh}}$在子空间${\rm{pwin}}$内的权函数$ {v_n} $ 14： ${\rm{if}}\;\;{v_n}\;\;{\rm{and}}\;\;{\rm{de}} > {\rm{Te}}$ 15： 对该点执行MLS，得到${p_i}\left( { {a_i},y_i'',h_i'' } \right)$ 16： 更新${\rm{de}} = \left| {h_i{''} - h_i'} \right|$ 17： else 18： 更新$ n = n + 1 $ 19： ${\rm{if}}\;\;{\rm{de}} < {\rm{Te}}$ 20： 提前终止该点修正，即${\rm{Is}}\_{\rm{ite}} = 1$ 21： ${\rm{if}}\;\;n = {N_j}\;\;{\rm{and}}\;\;{\rm{Is}}\_{\rm{ite}} = 1$ 22： 开始新的一轮修正，即$ n = 1 $, ${\rm{Is}}\_{\rm{ite}} = 0$ 23： (ii) 输出${\rm{P} }'' = \left\{ { {p_i}\left( { {a_i},y_i'',h_i'' } \right)|{a_i} \in \left( { {A_1},{A_2}, \cdots ,{A_J} } \right),i = 1,2, \cdots ,{N_{ {\rm{total} } } } } \right\}$ 24： (iii) 更新${\rm{P}}' = {\rm{P}}''$，返回步骤2 输出：点云${\rm{P}}' = \left\{ { {p_i}\left( { {a_i},{r_i},h_i'} \right)|{a_i} \in \left( { {A_1},{A_2}, \cdots ,{A_J} } \right),i = 1,2, \cdots ,{N_{{\rm{total}}} } } \right\}$ 
下载: 导出CSV
表 2 仿真结果精度(m)
Table 2. Precision of the simulated results (m)
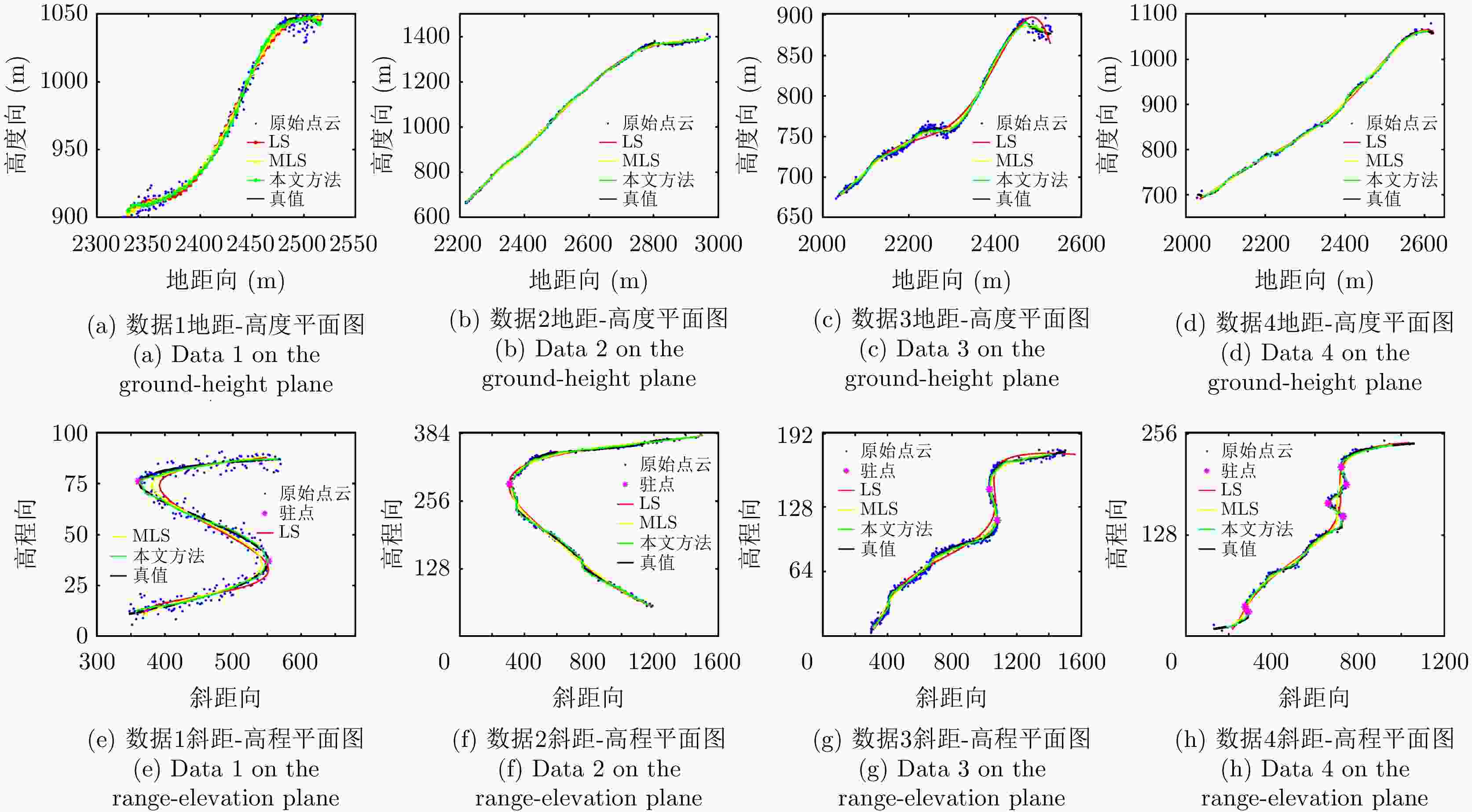
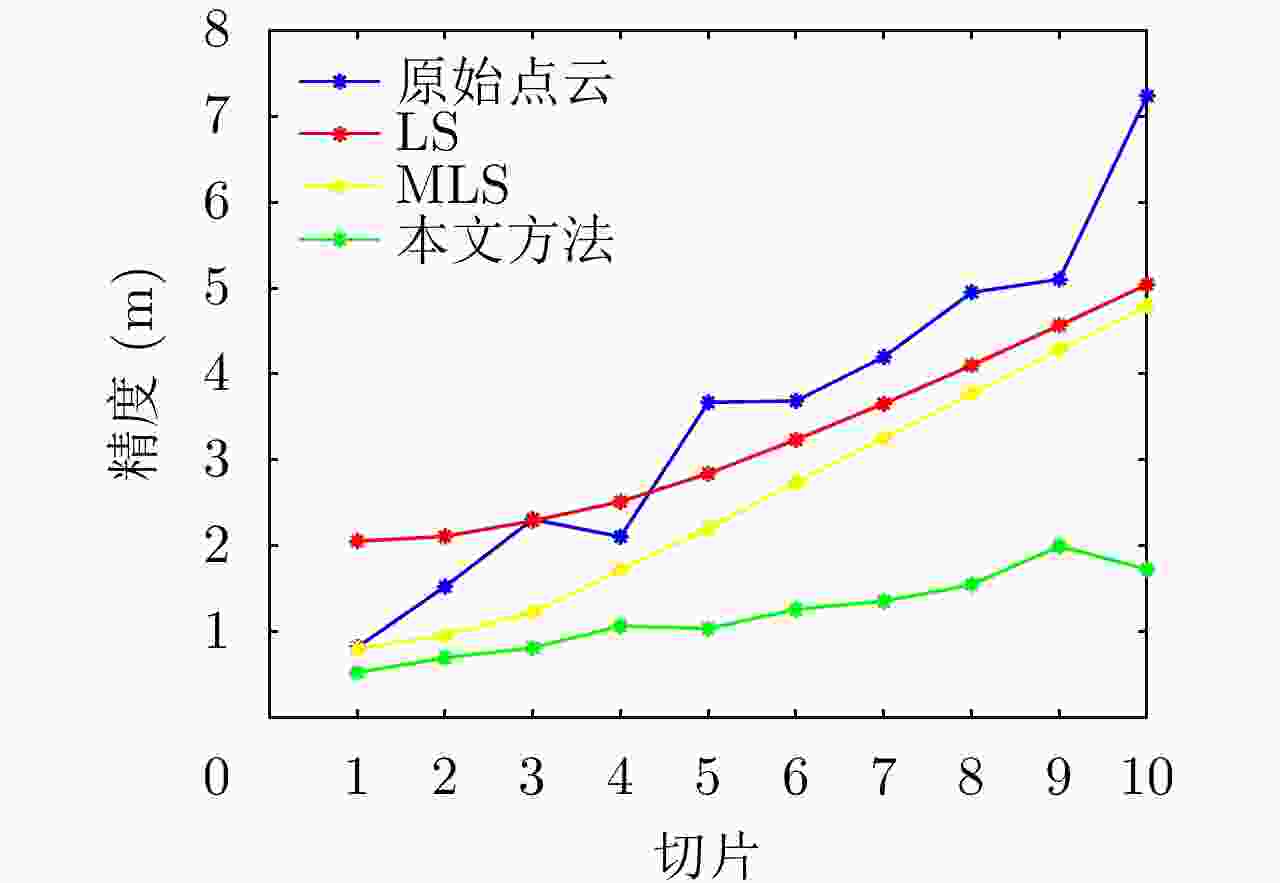
数据 原始点云 LS MLS 本文方法 数据1 3.67 2.84 2.20 1.04 数据2 3.11 4.71 4.46 2.36 数据3 2.50 4.15 2.18 0.90 数据4 2.74 3.79 2.95 1.10
下载: 导出CSV
表 3 主要实验参数
Table 3. Main experimental parameters
参数 数值 频段 X 飞行高度 3.5 km 带宽 500 MHz 基线长度 2.0 m 基线间隔 0.2 m 基线水平夹角 0° 中心下视角 35°
下载: 导出CSV
-
[1] KÖNINGER A and BARTEL S. 3D-GIS for urban purposes[J]. Geoinformatica, 1998, 2(1): 79–103. doi: 10.1023/A:1009797106866 [2] WANG Yuanyuan and ZHU Xiaoxiang. Automatic feature-based geometric fusion of Multiview TomoSAR point clouds in urban area[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2015, 8(3): 953–965. doi: 10.1109/JSTARS.2014.2361430 [3] MINH D H T, LE TOAN T, ROCCA F, et al. SAR tomography for the retrieval of forest biomass and height: Cross-validation at two tropical forest sites in French Guiana[J]. Remote Sensing of Environment, 2016, 175: 138–147. doi: 10.1016/j.rse.2015.12.037 [4] EL IDRISSI ESSEBTEY S, VILLARD L, BORDERIES P, et al. Long-term trends of P-band temporal decorrelation over a tropical dense forest-experimental results for the BIOMASS mission[J]. IEEE Transactions on Geoscience and Remote Sensing, 2022, 60: 5102415. doi: 10.1109/TGRS.2021.3082395 [5] LI Mofan, XIANG Yin, CHEN Xinliang, et al. Altitude ambiguity suppression method based on dual-frequency interfering and multi-frequency averaging for sparse baseline TomoSAR[J]. Electronics Letters, 2019, 55(22): 1194–1196. doi: 10.1049/el.2019.2198 [6] GUO Jiao, LI Zhenfang, and BAO Zheng. Using multibaseline InSAR to recover layovered terrain considering wideband array problem[J]. IEEE Geoscience and Remote Sensing Letters, 2008, 5(4): 583–587. doi: 10.1109/LGRS.2008.2000623 [7] ZHU Xiaoxiang and SHAHZAD M. Facade reconstruction using Multiview spaceborne TomoSAR point clouds[J]. IEEE Transactions on Geoscience and Remote Sensing, 2014, 52(6): 3541–3552. doi: 10.1109/TGRS.2013.2273619 [8] ZHANG Fubo, LIANG Xingdong, WU Yirong, et al. 3D surface reconstruction of layover areas in continuous terrain for multi-baseline SAR interferometry using a curve model[J]. International Journal of Remote Sensing, 2015, 36(8): 2093–2112. doi: 10.1080/01431161.2015.1030042 [9] 张福博. 阵列干涉SAR三维重建信号处理技术研究[D]. [博士论文], 中国科学院大学, 2015.ZHANG Fubo. Research on signal processing of 3-D reconstruction in linear array synthetic aperture radar interferometry[D]. [Ph. D. dissertation], University of Chinese Academy of Sciences, 2015. [10] LI Xiaowan, ZHANG Fubo, LI Yanlei, et al. An elevation ambiguity resolution method based on segmentation and reorganization of TomoSAR point cloud in 3D mountain reconstruction[J]. Remote Sensing, 2021, 13(24): 5118. doi: 10.3390/rs13245118 [11] FISCHLER M A and BOLLES R C. Random sample consensus: A paradigm for model fitting with applications to image analysis and automated cartography[J]. Communications of the ACM, 1981, 24(6): 381–395. doi: 10.1145/358669.358692 [12] D’HONDT O, GUILLASO S, and HELLWICH O. Geometric primitive extraction for 3D reconstruction of urban areas from tomographic SAR data[C]. Joint Urban Remote Sensing Event 2013, Sao Paulo, Brazil, 2013: 206–209. [13] SHAHZAD M and ZHU Xiaoxiang. Robust reconstruction of building facades for large areas using spaceborne TomoSAR point clouds[J]. IEEE Transactions on Geoscience and Remote Sensing, 2015, 53(2): 752–769. doi: 10.1109/TGRS.2014.2327391 [14] SHAHZAD M and ZHU Xiaoxiang. Reconstructing 2-D/3-D building shapes from Spaceborne tomographic synthetic aperture radar data[J]. The International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences, 2014, XL-3: 313–320. doi: 10.5194/isprsarchives-XL-3-313-2014 [15] ZHOU Siyan, LI Yanlei, ZHANG Fubo, et al. Automatic regularization of TomoSAR point clouds for buildings using neural networks[J]. Sensors, 2019, 19(17): 3748. doi: 10.3390/s19173748 [16] AVRON H, SHARF A, GREIF C, et al. ℓ1-sparse reconstruction of sharp point set surfaces[J]. ACM Transactions on Graphics, 2010, 29(5): 135. doi: 10.1145/1857907.1857911 [17] FU Yan and ZHAI Jinlei. Research on scattered points cloud denoising algorithm[C]. 2015 IEEE International Conference on Signal Processing, Communications and Computing (ICSPCC), Ningbo, China, 2015: 1–5. [18] GU Xiaoying, LIU Yongshan, and WU Qiong. A filtering algorithm for scattered point cloud based on curvature features classification[J]. Journal of Information and Computational Science, 2015, 12(2): 525–532. doi: 10.12733/jics20105244 [19] DIGNE J and DE FRANCHIS C. The bilateral filter for point clouds[J]. Image Processing on Line, 2017, 7: 278–287. doi: 10.5201/ipol.2017.179 [20] ZENG Jin, CHEUNG G, NG M, et al. 3D point cloud denoising using graph Laplacian regularization of a low dimensional manifold model[J]. IEEE Transactions on Image Processing, 2020, 29: 3474–3489. doi: 10.1109/TIP.2019.2961429 [21] GERNHARDT S, ADAM N, EINEDER M, et al. Potential of very high resolution SAR for persistent scatterer interferometry in urban areas[J]. Annals of GIS, 2010, 16(2): 103–111. doi: 10.1080/19475683.2010.492126 [22] NEALEN A. An as-short-as-possible introduction to the least squares, weighted least squares and moving least squares methods for scattered data approximation and interpolation[R/OL]. http://www.nealen.com/projects, 2004. [23] LEVIN D. The approximation power of moving least-squares[J]. Mathematics of Computation, 1998, 67(224): 1517–1531. doi: 10.1090/S0025-5718-98-00974-0 [24] JIAO Zekun, DING Chibiao, QIU Xiaolan, et al. Urban 3D imaging using airborne TomoSAR: Contextual information-based approach in the statistical way[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2020, 170: 127–141. doi: 10.1016/j.isprsjprs.2020.10.013 [25] BUDILLON A, EVANGELISTA A, and SCHIRINZI G. Three-dimensional SAR focusing from multipass signals using compressive sampling[J]. IEEE Transactions on Geoscience and Remote Sensing, 2011, 49(1): 488–499. doi: 10.1109/TGRS.2010.2054099 [26] 孙婷. 基于移动最小二乘近似权函数的选取及其应用[D]. [硕士论文], 苏州大学, 2010.SUN Ting. Selection and application of weight function based on MLS[D]. [Master dissertation], Soochow University, 2010. [27] 曾清红, 卢德唐. 基于移动最小二乘法的曲线曲面拟合[J]. 工程图学学报, 2004, 25(1): 84–89. doi: 10.3969/j.issn.1003-0158.2004.01.017ZENG Qinghong and LU Detang. Curve and surface fitting based on moving least-squares methods[J]. Journal of Engineering Graphics, 2004, 25(1): 84–89. doi: 10.3969/j.issn.1003-0158.2004.01.017 [28] AUER S. 3D synthetic aperture radar simulation for interpreting complex urban reflection scenarios[D]. [Ph. D. dissertation], Technische Universität München, 2011. [29] 生强强. InSAR DEM精度分析与定量评估方法[D]. [硕士论文], 西安电子科技大学, 2018.SHENG Qiangqiang. InSAR DEM accuracy analysis and quantitative evaluation[D]. [Master dissertation], Xidian University, 2018. [30] TAKAKU J, TADONO T, DOUTSU M, et al. Updates of ‘AW3D30’ Alos global digital surface model with other open access datasets[J]. The International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences, 2020, XLIII-B4-2020: 183–189. doi: 10.5194/isprs-archives-XLIII-B4-2020-183-2020 -
图(12) / 表(3)
计量
- 文章访问数: 1449
- HTML全文浏览量: 682
- PDF下载量: 141
- 被引次数: 0
