作者中心
专家审稿
责编办公
编辑办公
Joint Design of Doppler-tolerant Complementary Sequences and Receiving Filters Against Interrupted Sampling Repeater Jamming
-
摘要: 作为一种典型的相干干扰，间歇采样转发干扰利用欠采样原理，能够在雷达接收机产生多个高逼真假目标，使雷达对真实目标的检测失效。针对这一问题，该文提出了一种基于多普勒容忍的多脉冲互补序列和接收滤波器联合设计的抗间歇采样转发干扰方法。首先，考虑设计序列的多普勒容限，以最小化发射序列和接收滤波器模糊函数旁瓣能量以及干扰信号和接收滤波器模糊函数能量为优化指标，同时考虑了发射波形的恒模约束以及非匹配滤波体制的信噪比损失约束等。然后，提出了基于优化最小化方法的交替迭代优化算法解决所提出的非凸优化问题。最后，仿真实验表明，相比于传统方法，该文方法设计的收发序列具有更好的脉压旁瓣性能和抗间歇采样转发干扰性能，能够显著提升雷达在干扰场景下对运动目标的检测能力。Abstract: As a typical coherent jamming method, Interrupted Sampling Repeater Jamming (ISRJ) can generate multiple false targets with high fidelity at the radar receiver using under-sampling, which causes real targets detection to become invalid. To solve this problem, an anti-ISRJ method based on the joint design of Doppler-tolerant complementary sequences and receiving filters is proposed in this paper. First, by considering the Doppler tolerance of sequences, the sum of the energy of the ambiguity function of transmitted sequences and receiving filters and energy of the ambiguity function of ISRJ signals and receiving filters is chosen as the objective function. Meanwhile, the constant modulus constraint on sequences and signal-to-noise ratio constraint are considered. Then, an alternately iterative algorithm based on the Majorization-Minimization (MM) method is proposed to solve the non-convex optimization problem. Finally, numerical results are presented as a way to compare with conventional methods, and the sequences and receiving filters designed by the proposed method show better pulse compression correlation and anti-ISRJ performance. These procedures can substantially improve the radar detection ability to move targets in the jamming scene.
-
图 2 设计序列的模糊函数性能
Figure 2. Ambiguity functions of designed sequences by the proposed method
图 4 不同信干比和信噪比条件下下本文方法脉压输出干扰峰值
Figure 4. The jamming peak of the pulse compression output of the proposed method with different SJRs and SNRs
图 5 不同干扰参数下ISRJ信号脉压输出峰值
Figure 5. The peak of the pulse compression output of the ISRJ signals under different jamming parameters
表 1 抗ISRJ的多普勒容忍互补序列和接收滤波器集联合设计流程
Table 1. Joint design of Doppler tolerant complementary sequences and receiving filters for anti-ISRJ
1：令$i = 0$，利用随机相位序列初始化${{\boldsymbol{x}}^{\left( 0 \right)} }$和${{\boldsymbol{h}}^{\left( 0 \right)} }$ 2：重复 3：对于固定的${{\boldsymbol{x}}^{\left( i \right)} }$，根据式(23)和式(24)计算矩阵${\boldsymbol{P}}_{}^{\left( i \right)}$和矢量${{\boldsymbol{p}}^{\left( i \right)} }$ 4：利用SQUAREM加速框架和式(26)更新计算${{\boldsymbol{h}}^{\left( {i + 1} \right)} }$ 5：对于固定的${{\boldsymbol{h}}^{\left( {i + 1} \right)} }$，根据式(31)和式(32)计算矩阵${{\boldsymbol{Q}}^{\left( {i + 1} \right)} }$和
矢量${{\boldsymbol{q}}^{\left( {i + 1} \right)} }$6：利用SQUAREM加速框架和式(34)更新计算${{\boldsymbol{x}}^{\left( {i + 1} \right)} }$ 7：令$i = i + 1$ 8：直到满足收敛准则。输出${{\boldsymbol{x}}^{\left( i \right)} }$和${{\boldsymbol{h}}^{\left( i \right)} }$ 
下载: 导出CSV
表 2 互补序列和接收滤波器模糊函数旁瓣峰值和实际信噪比损失(dB)
Table 2. Peak sidelobe levels and actual SNR losses of the ambiguity functions of complementary sequences and receiving filters (dB)
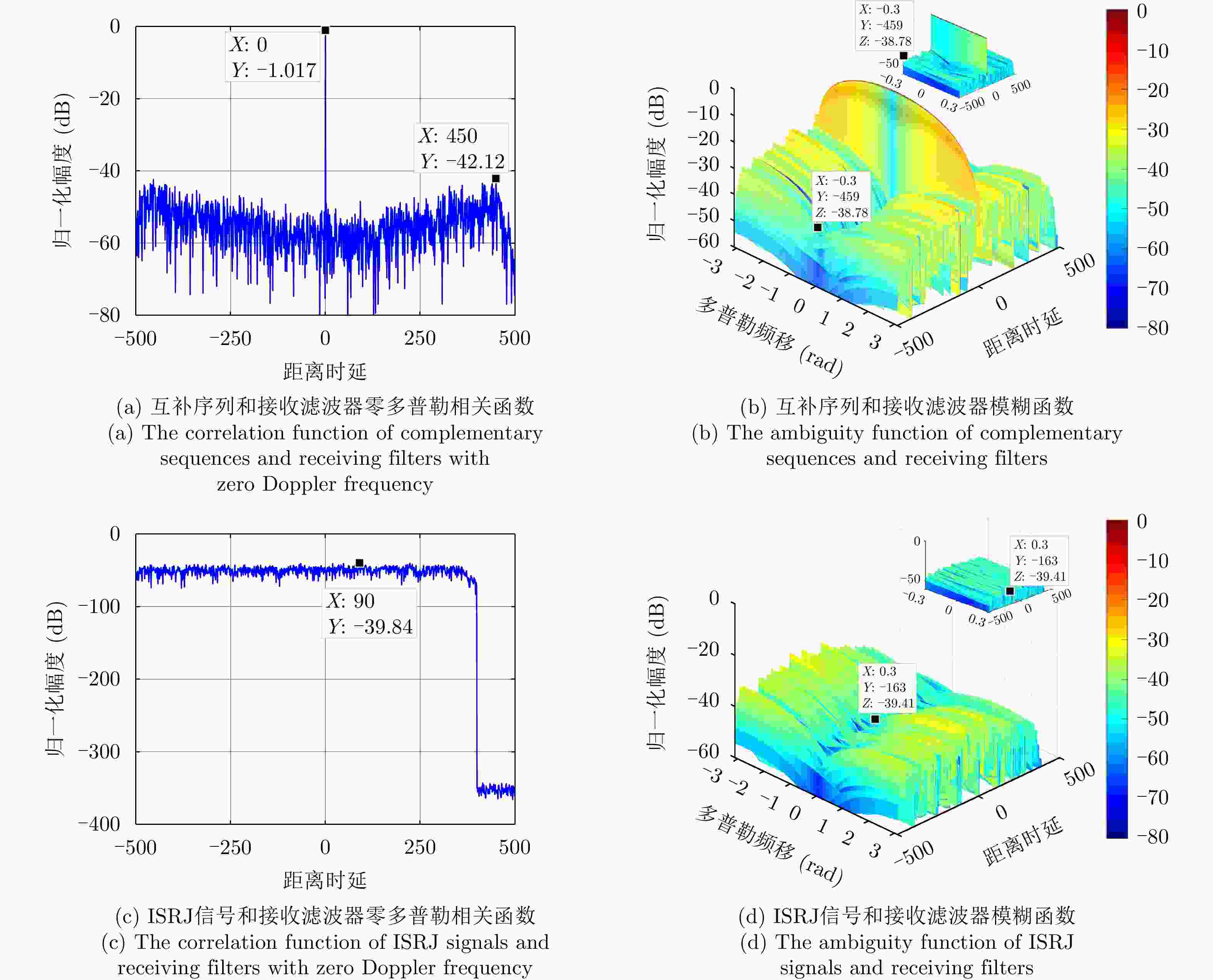
信噪比损失约束 脉冲数 K = 2 K = 4 K = 6 $\mu = 1.0{\text{ dB}}$ $ - 38.78\left( {1.017} \right)$ $ - 46.26\left( {1.007} \right)$ $ - 53.52\left( {1.007} \right)$ $\mu = 1.5{\text{ dB}}$ $ - 39.28\left( {1.512} \right)$ $ - 51.95\left( {1.503} \right)$ $ - 56.71\left( {1.501} \right)$ $\mu = 2.0{\text{ dB}}$ $ - 39.61\left( {2.016} \right)$ $ - 52.71\left( {2.003} \right)$ $ - 62.83\left( {2.001} \right)$
下载: 导出CSV
表 3 ISRJ信号和接收滤波器模糊函数峰值(dB)
Table 3. Peak levels of the ambiguity functions of ISRJ signals and receiving filters (dB)
信噪比损失约束 脉冲数 K = 2 K = 4 K = 6 $\mu = 1.0{\text{ dB}}$ $ - 39.41$ $ - 48.93$ $ - 53.51$ $\mu = 1.5{\text{ dB}}$ $ - 39.55$ $ - 51.64$ $ - 56.39$ $\mu = 2.0{\text{ dB}}$ $ - 40.01$ $ - 52.16$ $ - 60.82$
下载: 导出CSV
表 4 干扰场景仿真参数
Table 4. Simulation parameters of the jamming scene
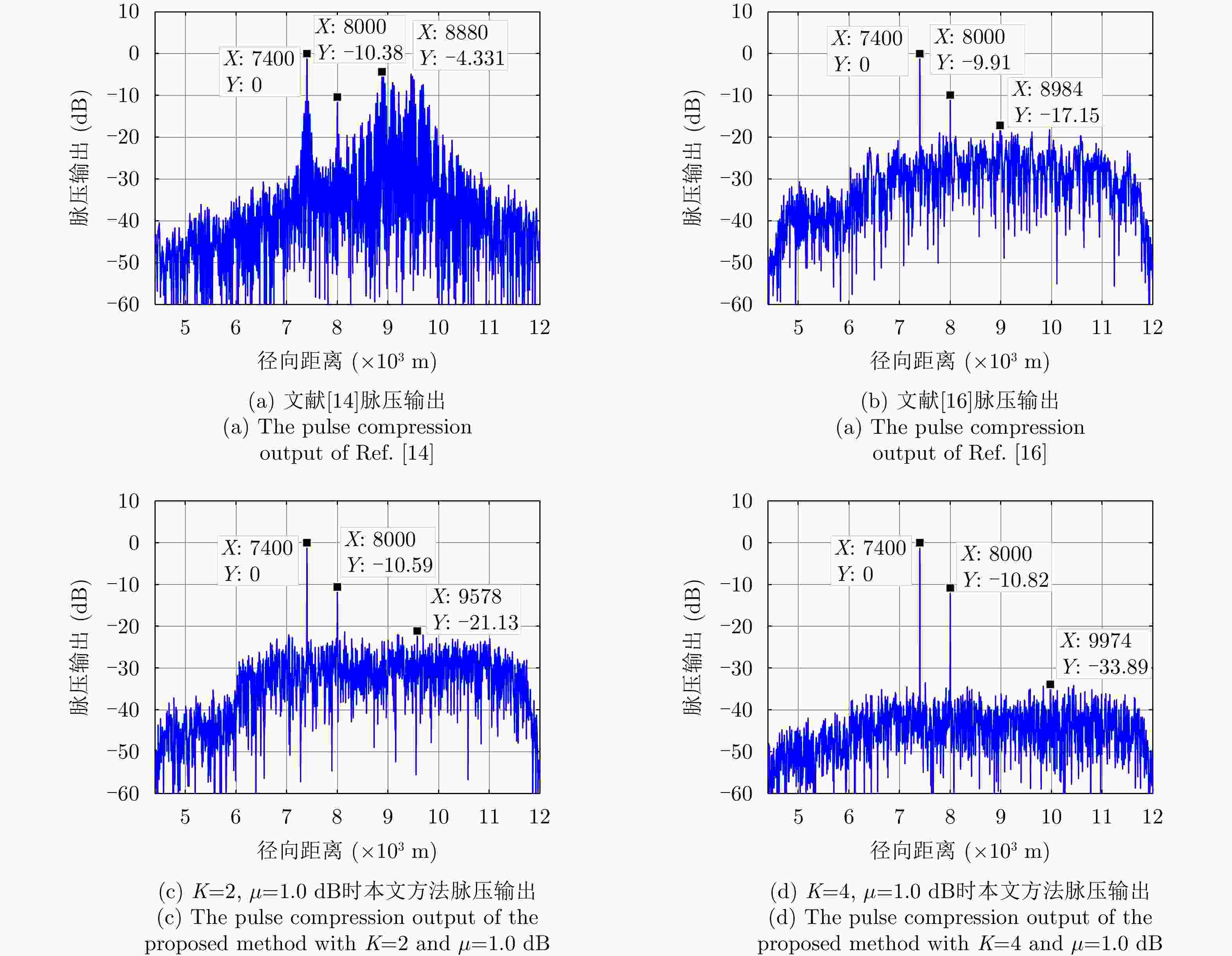
参数 数值 雷达载频 ${f_0} = 2{\text{ GHz}}$ 脉冲重复频率 ${\text{PRF} } = 5{\text{ kHz} }$ 目标距离 ${d_1} = 7400{\text{ m}},{d_2} = 8000{\text{ m}}$ 目标速度 ${v_1} = 30{\text{ } }{ {\text{m} }/ {\rm{s}}},{v_2} = 40{\text{ } }{ {\text{m} } / {\rm{s}}}$ 目标雷达散射截面积 ${\text{RCS}}_1^2{\text{ = }}0{\text{ dB}},{\text{RCS}}_2^2{\text{ = }} - 10{\text{ dB }}$ ISRJ干扰机距离 ${\bar d_1} = 9000{\text{ m}},{\bar d_2} = 9500{\text{ m}}$ ISRJ干扰机速度 ${\bar v_1} = 0{\text{ } }{ {\text{m} } /{\rm{s}}},{\bar v_2} = 0{\text{ } }{ {\text{m} }/{\rm{s}}}$ ISRJ干扰机时延 0.5 μs 信干比 $- 15{\text{ dB} }$ 信噪比 $15{\text{ dB} }$
下载: 导出CSV
-
[1] FENG Dejun, XU Letao, PAN Xiaoyi, et al. Jamming wideband radar using interrupted-sampling repeater[J]. IEEE Transactions on Aerospace and Electronic Systems, 2017, 53(3): 1341–1354. doi: 10.1109/TAES.2017.2670958 [2] LIU Yongcai, WANG Wei, PAN Xiaoyi, et al. Inverse omega-K algorithm for the electromagnetic deception of synthetic aperture radar[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2016, 9(7): 3037–3049. doi: 10.1109/JSTARS.2016.2543961 [3] 刘忠. 基于DRFM的线性调频脉冲压缩雷达干扰新技术[D]. [博士论文], 国防科学技术大学, 2006: 1–5.LIU Zhong. Jamming technique for countering LFM pulse compression radar based on digital radio frequency memory[D]. [Ph. D. dissertation], National University of Defense Technology, 2006: 1–5. [4] 李永祯, 黄大通, 邢世其, 等. 合成孔径雷达干扰技术研究综述[J]. 雷达学报, 2020, 9(5): 753–764. doi: 10.12000/JR20087LI Yongzhen, HUANG Datong, XING Shiqi, et al. A review of synthetic aperture radar jamming technique[J]. Journal of Radars, 2020, 9(5): 753–764. doi: 10.12000/JR20087 [5] 王雪松, 刘建成, 张文明, 等. 间歇采样转发干扰的数学原理[J]. 中国科学 E辑:信息科学, 2006, 36(8): 891–901. doi: 10.3969/j.issn.1674-7259.2006.08.007WANG Xuesong, LIU Jiancheng, ZHANG Wenming, et al. Mathematic principles of interrupted-sampling repeater jamming (ISRJ)[J]. Science in China Series E:Information Sciences, 2006, 36(8): 891–901. doi: 10.3969/j.issn.1674-7259.2006.08.007 [6] 周阳, 毕大平, 沈爱国, 等. 基于运动调制的SAR-GMTI间歇采样遮蔽干扰方法[J]. 雷达学报, 2017, 6(4): 359–367. doi: 10.12000/JR16075ZHOU Yang, BI Daping, SHEN Aiguo, et al. Intermittent sampling repeater shading jamming method based on motion modulation for SAR-GMTI[J]. Journal of Radars, 2017, 6(4): 359–367. doi: 10.12000/JR16075 [7] BERGER S D. Digital radio frequency memory linear range gate stealer spectrum[J]. IEEE Transactions on Aerospace and Electronic Systems, 2003, 39(2): 725–735. doi: 10.1109/TAES.2003.1207279 [8] OLIVIER K, CILLIERS J M, and DU PLESSIS M. Design and performance of wideband DRFM for radar test and evaluation[J]. Electronics Letters, 2011, 47(14): 824–825. doi: 10.1049/el.2011.0362 [9] XIONG Wei, ZHANG Gong, and LIU Wenbo. Efficient filter design against interrupted sampling repeater jamming for wideband radar[J]. EURASIP Journal on Advances in Signal Processing, 2017, 2017: 9. doi: 10.1186/s13634-017-0446-3 [10] 周超, 刘泉华, 胡程. 间歇采样转发式干扰的时频域辨识与抑制[J]. 雷达学报, 2019, 8(1): 100–106. doi: 10.12000/JR18080ZHOU Chao, LIU Quanhua, and HU Cheng. Time-frequency analysis techniques for recognition and suppression of interrupted sampling repeater jamming[J]. Journal of Radars, 2019, 8(1): 100–106. doi: 10.12000/JR18080 [11] 张建中, 穆贺强, 文树梁, 等. 基于脉内步进LFM波形的抗间歇采样转发干扰方法[J]. 系统工程与电子技术, 2019, 41(5): 1013–1020. doi: 10.3969/j.issn.1001-506X.2019.05.12ZHANG Jianzhong, MU Heqiang, WEN Shuliang, et al. Anti interrupted-sampling repeater jamming method based on stepped LFM waveform[J]. Systems Engineering and Electronics, 2019, 41(5): 1013–1020. doi: 10.3969/j.issn.1001-506X.2019.05.12 [12] 周畅, 汤子跃, 余方利, 等. 基于脉内正交的抗间歇采样转发干扰方法[J]. 系统工程与电子技术, 2017, 39(2): 269–276. doi: 10.3969/j.issn.1001-506X.2017.02.06ZHOU Chang, TANG Ziyue, YU Fangli, et al. Anti intermittent sampling repeater jamming method based on intrapulse orthogonality[J]. Systems Engineering and Electronics, 2017, 39(2): 269–276. doi: 10.3969/j.issn.1001-506X.2017.02.06 [13] GONG Shixian, WEI Xizhang, and LI Xiang. ECCM scheme against interrupted sampling repeater jammer based on time-frequency analysis[J]. Journal of Systems Engineering and Electronics, 2014, 25(6): 996–1003. doi: 10.1109/JSEE.2014.00114 [14] ZHOU Chao, LIU Quanhua, and CHEN Xinliang. Parameter estimation and suppression for DRFM-based interrupted sampling repeater jammer[J]. IET Radar, Sonar & Navigation, 2018, 12(1): 56–63. doi: 10.1049/iet-rsn.2017.0114 [15] ZHOU Kai, LI Dexin, SU Yi, et al. Joint design of transmit waveform and mismatch filter in the presence of interrupted sampling repeater jamming[J]. IEEE Signal Processing Letters, 2020, 27: 1610–1614. doi: 10.1109/LSP.2020.3021667 [16] ZHOU Kai, LI Dexin, QUAN Sinong, et al. SAR waveform and mismatched filter design for countering interrupted-sampling repeater jamming[J]. IEEE Transactions on Geoscience and Remote Sensing, 2022, 60: 5214514. doi: 10.1109/TGRS.2021.3107328 [17] 王福来, 庞晨, 黄大通, 等. 一种同时全极化雷达发射波形和接收滤波器联合设计的抗间歇采样转发干扰方法[J]. 中国科学: 信息科学, in press.WANG Fulai, PANG Chen, HUANG Datong, et al. An anti-jamming method against interrupted sampling repeater jamming based on designing transmitted waveforms and receiving filters for simultaneous polarimetric radar[J]. Scientia Sinica Informationis, in press. [18] WANG Fulai, PANG Chen, WU Hao, et al. Designing constant modulus complete complementary sequence with high Doppler tolerance for simultaneous polarimetric radar[J]. IEEE Signal Processing Letters, 2019, 26(12): 1837–1841. doi: 10.1109/LSP.2019.2949686 [19] WANG Fulai, PANG Chen, ZHOU Jian, et al. Design of complete complementary sequences for ambiguity functions optimization with a PAR constraint[J]. IEEE Geoscience and Remote Sensing Letters, 2022, 19: 3505705. doi: 10.1109/LGRS.2021.3071249 [20] SONG Junxiao, BABU P, and PALOMAR D P. Sequence design to minimize the weighted integrated and peak sidelobe levels[J]. IEEE Transactions on Signal Processing, 2016, 64(8): 2051–2064. doi: 10.1109/TSP.2015.2510982 [21] ZHENG Hao, JIU Bo, and LIU Hongwei. Waveform design based ECCM scheme against interrupted sampling repeater jamming for wideband MIMO radar in multiple targets scenario[J]. IEEE Sensors Journal, 2022, 22(2): 1652–1669. doi: 10.1109/JSEN.2021.3131491 [22] ZHAO Licheng, SONG Junxiao, BABU P, et al. A unified framework for low autocorrelation sequence design via majorization–minimization[J]. IEEE Transactions on Signal Processing, 2017, 65(2): 438–453. doi: 10.1109/TSP.2016.2620113 [23] VARADHAN R and ROLAND C. Simple and globally convergent methods for accelerating the convergence of any EM algorithm[J]. Scandinavian Journal of Statistics, 2008, 35(2): 335–353. doi: 10.1111/j.1467-9469.2007.00585.x -
图(5) / 表(4)
计量
- 文章访问数: 1852
- HTML全文浏览量: 540
- PDF下载量: 238
- 被引次数: 0
