一种快速抗间歇采样转发干扰波形和滤波器联合设计算法

周凯; 何峰; 粟毅

doi:10.12000/JR22015

一种快速抗间歇采样转发干扰波形和滤波器联合设计算法

DOI: 10.12000/JR22015

国防科技大学电子科学学院长沙 410073

基金项目: 国家自然科学基金(61771478, 61901501, 62001488)

详细信息

作者简介:
周　凯(1993–)，男，湖南岳阳人，现为国防科技大学电子科学学院博士研究生，研究方向为雷达波形设计、雷达电子抗干扰技术和合成孔径雷达成像

何　峰(1976–)，男，湖北孝感人，博士，现为国防科技大学电子科学学院研究员，研究方向为合成孔径雷达成像、雷达多维波形编码设计

粟　毅(1961–)，男，山东泰安人，博士，现为国防科技大学电子科学学院教授，博士生导师，研究方向为新体制雷达系统、雷达信号处理

通讯作者:
何峰 hefeng@nudt.edu.cn

粟毅 yi.su@yeah.net

责任主编：崔国龙 Corresponding Editor: CUI Guolong
中图分类号: TN972
计量
- 文章访问数: 1478
- HTML全文浏览量: 639
- PDF下载量: 288
- 被引次数: 10
出版历程
- 收稿日期: 2022-01-16
- 修回日期: 2022-03-17
- 网络出版日期: 2022-04-06
- 刊出日期: 2022-04-28

Fast Algorithm for Joint Waveform and Filter Design against Interrupted Sampling Repeater Jamming

College of Electronic Science, National University of Defense Technology, Changsha 410073, China

Funds: The National Natural Science Foundation of China (61771478, 61901501, 62001488)

More Information

Corresponding author: HE Feng, hefeng@nudt.edu.cn; SU Yi, yi.su@yeah.net

摘要

摘要: 该文研究了一种快速的抗间歇采样转发干扰波形和滤波器联合设计方法。基于罚函数和帕累托最优化原理给出了联合设计模型的优化数学模型。推导优化波形和滤波器过程中矩阵迹的解析表达式，有效降低了算法的计算复杂度。提出了一种基于平方迭代加速方法，解决了主分量最小化方法目标函数近似造成的算法收敛速度降低问题，进一步加快了算法运行速度。仿真结果表明，该文所提出的算法比传统方法具有更快的运行速度。同时，当干扰目标和真实目标在距离上不可分时，该文方法仍能够有效抑制间歇采样转发干扰。
- 波形设计 /
- 滤波器设计 /
- 间歇采样转发干扰 /
- 主分量最小化 /
- 平方迭代加速方法
Abstract: To suppress interrupted sampling jamming, a joint waveform and filter design method was proposed in this study. A fast algorithm was also suggested to design sequences with large code lengths. The joint design problem was formulated on the basis of the penalty function and Pareto optimization method. By deriving the theoretical solution of the trace of matrices in each iteration, the computation order of the proposed algorithm was decreased significantly compared to that of the conventional algorithm. Moreover, an accelerated scheme based on the squared iterative method, which further improves the running speed of the algorithm, was proposed. Simulation results demonstrate that the proposed algorithm runs faster than traditional algorithms. Moreover, the designed waveform and filter can be applied to suppress interrupted sampling repeater jamming when the false targets are inseparable from the true targets in time-frequency domains.
- Waveform design /
- Filter design /
- Interrupted Sampling Repeater Jamming (ISRJ) /
- Majorization minimization /
- Squared iterative method

HTML全文

图 1 非匹配滤波性能随着权值的变化曲线

Figure 1. Curves of mismatch output performance versus Pareto weights

下载: 全尺寸图片幻灯片

图 2 波形实部幅度图

Figure 2. The amplitude of the real part of waveform

下载: 全尺寸图片幻灯片

图 3 波形和干扰信号非匹配滤波输出(N=512)

Figure 3. Mismatch output of the waveform and jamming signal (N=512)

下载: 全尺寸图片幻灯片

图 4 积分旁瓣比和积分能量比随峰值增益损耗变化

Figure 4. Integrated sidelobe levels and integrated levels versus loss of processing gain

下载: 全尺寸图片幻灯片

图 5 运行时间对比图

Figure 5. Comparison of running time

下载: 全尺寸图片幻灯片

图 6 不同波形长度下的运行时间图

Figure 6. Running time versus different code length

下载: 全尺寸图片幻灯片

图 7 波形和干扰信号非匹配滤波输出(N=800)

Figure 7. Mismatch output of waveform and jamming signal (N=800)

下载: 全尺寸图片幻灯片

图 8 抗间歇采样转发干扰评估

Figure 8. Evaluation of interrupted sampling repeater jamming suppression

下载: 全尺寸图片幻灯片

图 9 干扰机位置对抗干扰性能的影响

Figure 9. Jamming suppression performance versus location of jammer

下载: 全尺寸图片幻灯片

图 10 干扰峰值随着重复周期和占空比的估计误差变化图

Figure 10. Jamming peak versus the relative error of pulse repetition period and duty ratio

下载: 全尺寸图片幻灯片

表 1 快速抗间歇采样转发干扰波形和滤波器联合设计算法

Table 1. Fast algorithm for joint waveform and filter design against interrupted sampling repeater jamming

输入：波形和滤波器长度N
1：用随机相位编码序列初始化 ${{\boldsymbol{x}}^{\left( 0 \right)}}$ 和 ${{\boldsymbol{h}}^{\left( 0 \right)}}$ ；
2：重复
3：　 ${{\boldsymbol{h}}_1} = F\left( {{{\boldsymbol{h}}^{\left( l \right)}},{{\boldsymbol{x}}^{\left( l \right)}}} \right)$
4：　 ${{\boldsymbol{h}}_2} = F\left( {{{\boldsymbol{h}}_1},{{\boldsymbol{x}}^{\left( l \right)}}} \right)$
5：　 ${{\boldsymbol{r}}_1} = {{\boldsymbol{h}}_1} - {{\boldsymbol{h}}^{\left( l \right)}}$
6：　 ${{\boldsymbol{v}}_1} = {{\boldsymbol{h}}_2} - {{\boldsymbol{h}}_1} - {{\boldsymbol{r}}_1}$
7：　 ${\alpha _1} = - {{{{\left\\| {{{\boldsymbol{r}}_1}} \right\\|}_2}} \mathord{\left/ {\vphantom {{{{\left\\| {{{\boldsymbol{r}}_1}} \right\\|}_2}} {{{\left\\| {{{\boldsymbol{v}}_1}} \right\\|}_2}}}} \right. } {{{\left\\| {{{\boldsymbol{v}}_1}} \right\\|}_2}}}$
8：　 ${{\boldsymbol{h}}^{\left( {l + 1} \right)}} = F\left( {{{\boldsymbol{h}}^{\left( l \right)}} - 2{\alpha _1}{{\boldsymbol{r}}_1} + \alpha _1^2{{\boldsymbol{v}}_1},{{\boldsymbol{x}}^{\left( l \right)}}} \right)$
9：　若 $f\left( {{{\boldsymbol{x}}^{\left( l \right)}},{{\boldsymbol{h}}^{\left( {l + 1} \right)}}} \right) > f\left( {{{\boldsymbol{x}}^{\left( l \right)}},{{\boldsymbol{h}}^{\left( l \right)}}} \right)$ ，循环
10：　　 ${\alpha _1} \leftarrow {{\left( {{\alpha _1} - 1} \right)} \mathord{\left/ {\vphantom {{\left( {{\alpha _1} - 1} \right)} 2}} \right. } 2}$
11：　　 ${{\boldsymbol{h}}^{\left( {l + 1} \right)}} = F\left( {{{\boldsymbol{h}}^{\left( l \right)}} - 2\alpha {{\boldsymbol{r}}_1} + {\alpha ^2}{{\boldsymbol{v}}_1},{{\boldsymbol{x}}^{\left( l \right)}}} \right)$
12：　结束
13：　 ${{\boldsymbol{x}}_1} = G\left( {{{\boldsymbol{h}}^{\left( {l + 1} \right)}},{{\boldsymbol{x}}^{\left( l \right)}}} \right)$
14：　 ${{\boldsymbol{x}}_2} = G\left( {{{\boldsymbol{h}}^{\left( {l + 1} \right)}},{{\boldsymbol{x}}_1}} \right)$
15：　 ${{\boldsymbol{r}}_2} = {{\boldsymbol{x}}_1} - {{\boldsymbol{x}}^{\left( l \right)}}$
16：　 ${{\boldsymbol{v}}_2} = {{\boldsymbol{x}}_2} - {{\boldsymbol{x}}_1} - {{\boldsymbol{r}}_1}$
17：　 ${\alpha _2} = - {{{{\left\\| {{{\boldsymbol{r}}_2}} \right\\|}_2}} \mathord{\left/ {\vphantom {{{{\left\\| {{{\boldsymbol{r}}_2}} \right\\|}_2}} {{{\left\\| {{{\boldsymbol{v}}_2}} \right\\|}_2}}}} \right. } {{{\left\\| {{{\boldsymbol{v}}_2}} \right\\|}_2}}}$
18：　 ${{\boldsymbol{x}}^{\left( {l + 1} \right)}} = G\left( {{{\boldsymbol{h}}^{\left( {l + 1} \right)}},{{\boldsymbol{x}}^{\left( l \right)}} - 2{\alpha _2}{{\boldsymbol{r}}_2} + \alpha _2^2{{\boldsymbol{v}}_2}} \right)$
19：　若 $f\left( {{{{\boldsymbol{\tilde x}}}^{\left( l \right)}},{{\boldsymbol{h}}^{\left( {l + 1} \right)}}} \right) > f\left( {{{\boldsymbol{x}}^{\left( l \right)}},{{\boldsymbol{h}}^{\left( {l + 1} \right)}}} \right)$ ，循环
20: 　　 ${\alpha _2} \leftarrow {{\left( {{\alpha _2} - 1} \right)} \mathord{\left/ {\vphantom {{\left( {{\alpha _2} - 1} \right)} 2}} \right. } 2}$
21：　　 ${{\boldsymbol{x}}^{\left( {l + 1} \right)}} = G\left( {{{\boldsymbol{h}}^{\left( {l + 1} \right)}},{{\boldsymbol{x}}^{\left( l \right)}} - 2{\alpha _2}{{\boldsymbol{r}}_2} + \alpha _2^2{{\boldsymbol{v}}_2}} \right)$
22：　结束
23：　 $l \leftarrow l + 1$
24：直至收敛
输出：波形和滤波器。

下载: 导出CSV

表 2 算法性能对比

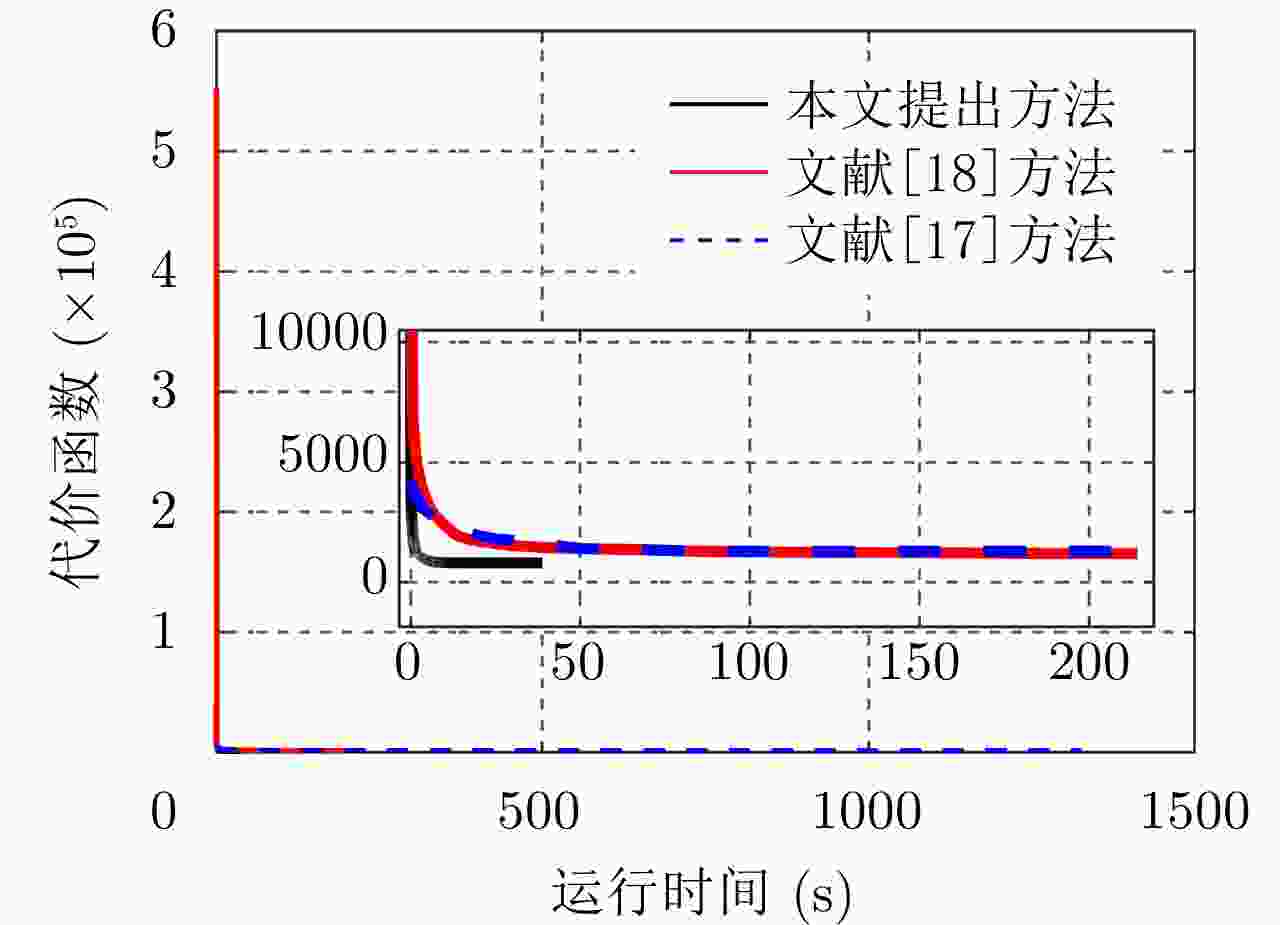
Table 2. Performance comparison of tested algorithms

方法	LPG (dB)	ISLR (dB)	ILs (dB)	干扰峰值(dB)	Running time (s)
文献[17]	–1.73	–10.71	–10.77	–30	1329.51
文献[18]	–1.71	–11.16	–11.34	–28.75	214.32
本文方法	–1.71	–11.17	–11.70	–29.73	38.80

下载: 导出CSV

表 3 仿真参数

Table 3. Simulation parameters

参数	数值
时宽(μs)	40
带宽(MHz)	20
采样重复周期(μs)	10
采样信号时宽(μs)	2.5
雷达位置(m)	(0,0,0)
干扰机位置(m)	(0,2000,0)
目标位置(m)	(0,3000,0)
干扰机时延(μs)	2

下载: 导出CSV

表 4 两组波形和非匹配滤波器性能对比

Table 4. The mismatch output performance of designed waveform via tested algorithms

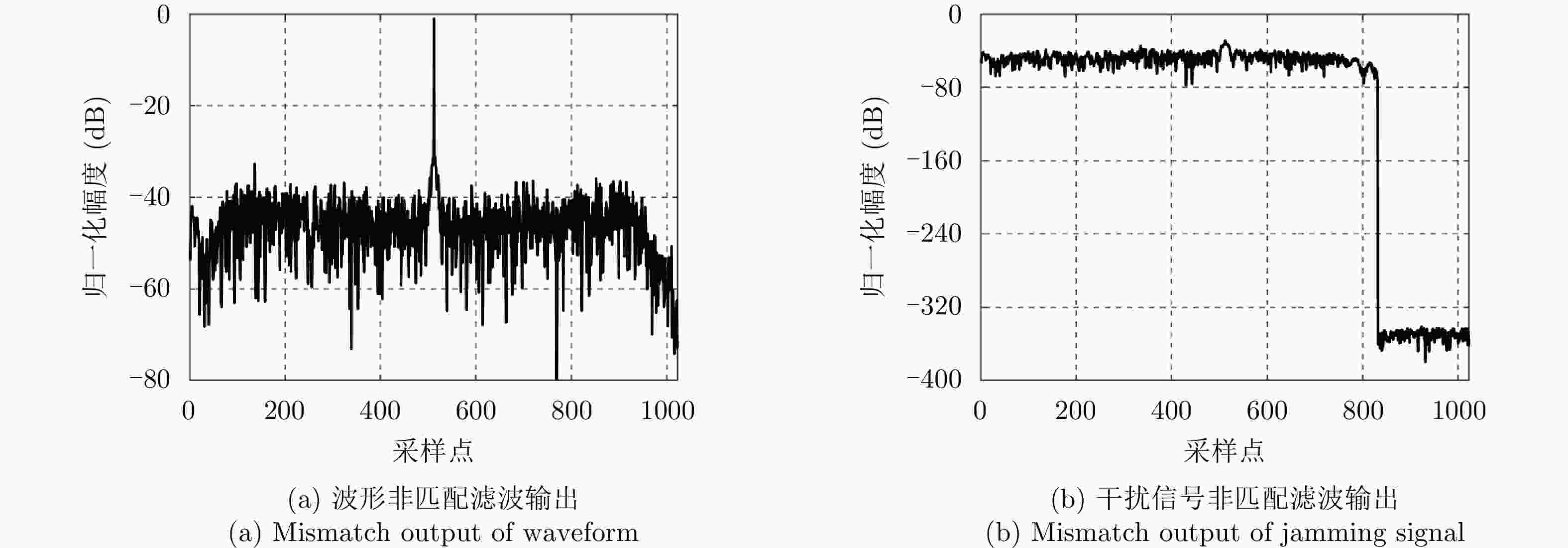
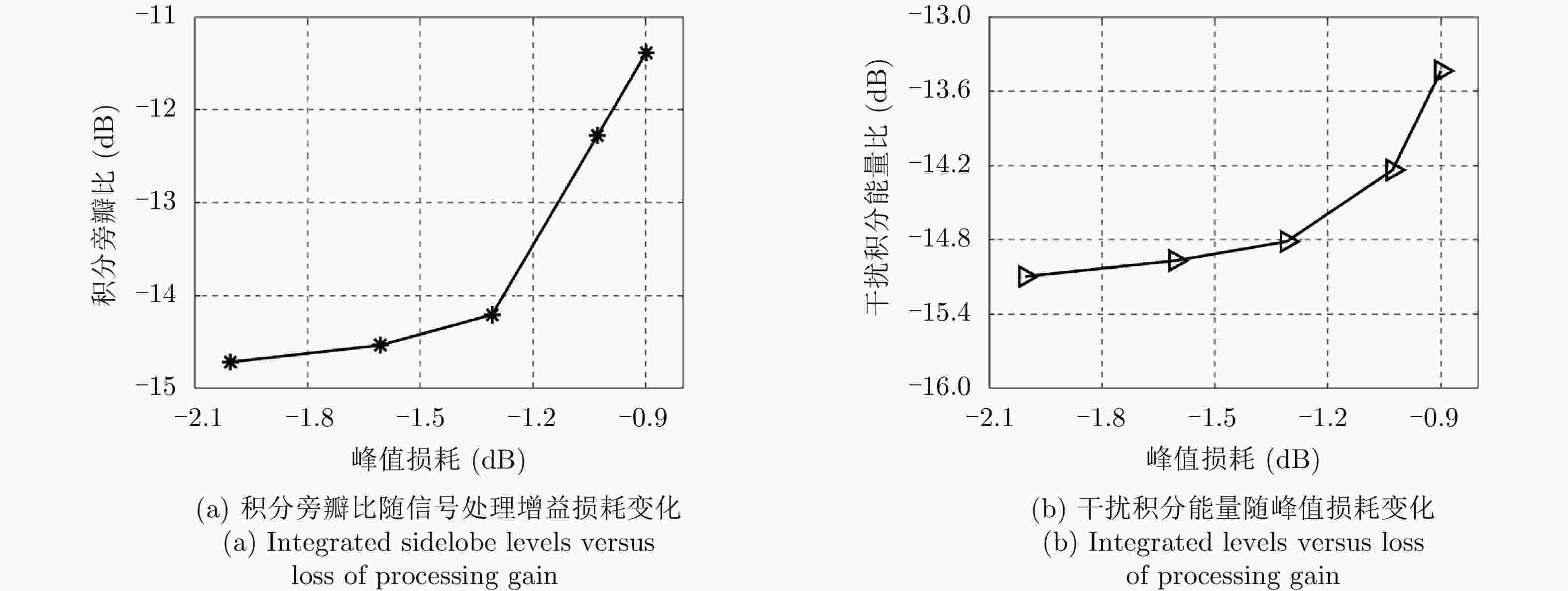
方法	LPG (dB)	ISLR (dB)	ILs (dB)	Peak interference (dB)
文献[17]	–1.61	–11.73	–14.29	–30.00
本文方法	–1.61	–12.60	–14.52	–29.99

下载: 导出CSV

表 5 抗干扰性能对比

Table 5. Performance comparison of jamming suppression

方法	信号处理损耗(dB)	干扰峰值(dB)
文献[13]	0	–0.19
文献[10]	0	–14.96
文献[17]	–1.40	–9.16
本文方法	–1.11	–10.55

下载: 导出CSV

参考文献(29)

[1]	HEAGNEY C P. Digital radio frequency memory synthetic instrument enhancing US navy automated test equipment mission[J]. IEEE Instrumentation & Measurement Magazine, 2018, 21(4): 41–63. doi: 10.1109/MIM.2018.8423745
[2]	SOUMEKH M. SAR-ECCM using phase-perturbed LFM chirp signals and DRFM repeat jammer penalization[J]. IEEE Transactions on Aerospace and Electronic Systems, 2006, 42(1): 191–205. doi: 10.1109/TAES.2006.1603414
[3]	李永祯, 黄大通, 邢世其, 等. 合成孔径雷达干扰技术研究综述[J]. 雷达学报, 2020, 9(5): 753–764. doi: 10.12000/JR20087 LI Yongzhen, HUANG Datong, XING Shiqi, et al. A review of synthetic aperture radar jamming technique[J]. Journal of Radars, 2020, 9(5): 753–764. doi: 10.12000/JR20087
[4]	TIAN Tian, ZHOU Feng, BAI Xueru, et al. A partitioned deceptive jamming method against TOPSAR[J]. IEEE Transactions on Aerospace and Electronic Systems, 2020, 56(2): 1538–1552. doi: 10.1109/TAES.2019.2933958
[5]	WANG Xuesong, LIU Jiancheng, ZHANG Wenming, et al. Mathematic principles of interrupted-sampling repeater jamming (ISRJ)[J]. Science in China Series F:Information Sciences, 2007, 50(1): 113–123. doi: 10.1007/s11432-007-2017-y
[6]	FENG Dejun, XU Letao, PAN Xiaoyi, et al. Jamming wideband radar using interrupted-sampling repeater[J]. IEEE Transactions on Aerospace and Electronic Systems, 2017, 53(3): 1341–1354. doi: 10.1109/TAES.2017.2670958
[7]	吴晓芳, 王雪松, 卢焕章. 对SAR的间歇采样转发干扰研究[J]. 宇航学报, 2009, 30(5): 2043–2048, 2072. doi: 10.3873/j.issn.1000-1328.2009.05.050 WU Xiaofang, WANG Xuesong, and LU Huanzhang. Study of intermittent sampling repeater jamming to SAR[J]. Journal of Astronautics, 2009, 30(5): 2043–2048, 2072. doi: 10.3873/j.issn.1000-1328.2009.05.050
[8]	杨伟宏, 陈永光, 王涛. 对波形捷变SAR的间歇采样快/慢时间调制干扰[J]. 系统工程与电子技术, 2012, 34(12): 2456–2462. doi: 10.3969/j.issn.1001-506x.2012.12.09 YANG Weihong, CHEN Yongguang, and WANG Tao. Intermittent sampling jamming against waveform agile SAR modulated in fast or slow time[J]. Systems Engineering and Electronics, 2012, 34(12): 2456–2462. doi: 10.3969/j.issn.1001-506x.2012.12.09
[9]	WU Qihua, ZHAO Feng, AI Xiaofeng, et al. Two-dimensional blanket jamming against ISAR using nonperiodic ISRJ[J]. IEEE Sensors Journal, 2019, 19(11): 4031–4038. doi: 10.1109/JSEN.2019.2897363
[10]	周超, 刘泉华, 胡程. 间歇采样转发式干扰的时频域辨识与抑制[J]. 雷达学报, 2019, 8(1): 100–106. doi: 10.12000/JR18080 ZHOU Chao, LIU Quanhua, and HU Cheng. Time-frequency analysis techniques for recognition and suppression of interrupted sampling repeater jamming[J]. Journal of Radars, 2019, 8(1): 100–106. doi: 10.12000/JR18080
[11]	WU Wenzhen, ZOU Jiangwei, CHEN Jian, et al. False-target recognition against interrupted-sampling repeater jamming based on integration decomposition[J]. IEEE Transactions on Aerospace and Electronic Systems, 2021, 57(5): 2979–2991. doi: 10.1109/TAES.2021.3068443
[12]	CHEN Jian, WU Wenzhen, XU Shiyou, et al. Band pass filter design against interrupted-sampling repeater jamming based on time-frequency analysis[J]. IET Radar, Sonar & Navigation, 2019, 13(10): 1646–1654. doi: 10.1049/iet-rsn.2018.5658
[13]	ZHOU Chao, LIU Quanhua, and CHEN Xinliang. Parameter estimation and suppression for DRFM-based interrupted sampling repeater jammer[J]. IET Radar, Sonar & Navigation, 2018, 12(1): 56–63. doi: 10.1049/iet-rsn.2017.0114
[14]	周畅, 汤子跃, 朱振波, 等. 抗间歇采样转发干扰的波形设计方法[J]. 电子与信息学报, 2018, 40(9): 2198–2205. doi: 10.11999/JEIT171236 ZHOU Chang, TANG Ziyue, ZHU Zhenbo, et al. Anti-interrupted sampling repeater jamming waveform design method[J]. Journal of Electronics &Information Technology, 2018, 40(9): 2198–2205. doi: 10.11999/JEIT171236
[15]	周畅, 汤子跃, 余方利, 等. 基于脉内正交的抗间歇采样转发干扰方法[J]. 系统工程与电子技术, 2017, 39(2): 269–276. doi: 10.3969/j.issn.1001-506X.2017.02.06 ZHOU Chang, TANG Ziyue, YU Fangli, et al. Anti intermittent sampling repeater jamming method based on intrapulse orthogonality[J]. Systems Engineering and Electronics, 2017, 39(2): 269–276. doi: 10.3969/j.issn.1001-506X.2017.02.06
[16]	张建中, 穆贺强, 文树梁, 等. 基于脉内步进LFM波形的抗间歇采样转发干扰方法[J]. 系统工程与电子技术, 2019, 41(5): 1013–1020. doi: 10.3969/j.issn.1001-506X.2019.05.12 ZHANG Jianzhong, MU Heqiang, WEN Shuliang, et al. Anti interrupted-sampling repeater jamming method based on stepped LFM waveform[J]. Systems Engineering and Electronics, 2019, 41(5): 1013–1020. doi: 10.3969/j.issn.1001-506X.2019.05.12
[17]	ZHOU Kai, LI Dexin, SU Yi, et al. Joint design of transmit waveform and mismatch filter in the presence of interrupted sampling repeater jamming[J]. IEEE Signal Processing Letters, 2020, 27: 1610–1614. doi: 10.1109/LSP.2020.3021667
[18]	ZHOU Kai, LI Dexin, QUAN Sinong, et al. SAR waveform and mismatched filter design for countering interrupted-sampling repeater jamming[J]. IEEE Transactions on Geoscience and Remote Sensing, 2022, 60: 5214514. doi: 10.1109/TGRS.2021.3107328
[19]	周凯, 李德鑫, 粟毅, 等. 基于雷达发射波形和非匹配滤波联合设计的间歇采样转发干扰抑制方法[J]. 电子与信息学报, 2021, 43(7): 1939–1946. doi: 10.11999/JEIT200299 ZHOU Kai, LI Dexin, SU Yi, et al. Joint transmitted waveform and mismatched filter design against interrupted-sampling repeater jamming[J]. Journal of Electronics &Information Technology, 2021, 43(7): 1939–1946. doi: 10.11999/JEIT200299
[20]	ZHOU Kai, QUAN Sinong, LI Dexin, et al. Waveform and filter joint design method for pulse compression sidelobe reduction[J]. IEEE Transactions on Geoscience and Remote Sensing, 2022, 60: 5107615. doi: 10.1109/TGRS.2021.3131590
[21]	SONG Junxiao, BABU P, and PALOMAR D P. Optimization methods for designing sequences with low autocorrelation sidelobes[J]. IEEE Transactions on Signal Processing, 2015, 63(15): 3998–4009. doi: 10.1109/TSP.2015.2425808
[22]	SONG Junxiao, BABU P, and PALOMAR D P. Sequence set design with good correlation properties via majorization-minimization[J]. IEEE Transactions on Signal Processing, 2016, 64(11): 2866–2879. doi: 10.1109/TSP.2016.2535312
[23]	SUN Ying, BABU P, and PALOMAR D P. Majorization-minimization algorithms in signal processing, communications, and machine learning[J]. IEEE Transactions on Signal Processing, 2017, 65(3): 794–816. doi: 10.1109/TSP.2016.2601299
[24]	LIANG Junli, SO H C, LI Jian, et al. Unimodular sequence design based on alternating direction method of multipliers[J]. IEEE Transactions on Signal Processing, 2016, 64(20): 5367–5381. doi: 10.1109/TSP.2016.2597123
[25]	CHANG Huibin, ENFEDAQUE P, MARCHESINI S, et al. Blind ptychographic phase retrieval via convergent alternating direction method of multipliers[J]. SIAM Journal on Imaging Sciences, 2019, 12(1): 153–185. doi: 10.1137/18M1188446
[26]	BOLTE J, SABACH S, and TEBOULLE M. Proximal alternating linearized minimization for nonconvex and nonsmooth problems[J]. Mathematical Programming, 2014, 146(1/2): 459–494. doi: 10.1007/s10107-013-0701-9
[27]	GEIPING J and MOELLER M. Composite optimization by nonconvex majorization-minimization[J]. SIAM Journal on Imaging Sciences, 2018, 11(4): 2494–2528. doi: 10.1137/18M1171989
[28]	VARADHAN R and ROLAND C. Simple and globally convergent methods for accelerating the convergence of any EM algorithm[J]. Scandinavian Journal of Statistics, 2008, 35(2): 335–353. doi: 10.1111/j.1467-9469.2007.00585.x
[29]	ZHAO Licheng, SONG Junxiao, BABU P, et al. A unified framework for low autocorrelation sequence design via majorization-minimization[J]. IEEE Transactions on Signal Processing, 2017, 65(2): 438–453. doi: 10.1109/TSP.2016.2620113

施引文献

期刊类型引用(5)

1.	张顺生，李鑫，黄栎冰，王文钦. 距离角度失配条件下的FDA-MIMO雷达运动目标检测算法. 信号处理. 2024(01): 197-206 . 百度学术
2.	丁俊淞，张顺生，王文钦. 基于多普勒偏移补偿的非线性FDA-MIMO雷达运动目标检测算法. 信号处理. 2024(02): 272-279 . 百度学术
3.	陈雨馨，彭意群，柳润金，丁一鹏. 基于CK-Hough联合算法的人体微多普勒频率估计. 中南大学学报(自然科学版). 2024(09): 3329-3341 . 百度学术
4.	刘德顺，夏德平，陈露，马艳峰. 基于神经网络的FDA-MIMO低截获发射波形和接收波束形成联合设计. 雷达学报. 2024(06): 1239-1251 . 本站查看
5.	施兴相，廖可非. 频率分集阵列的ISAR成像技术. 国外电子测量技术. 2023(03): 8-13 . 百度学术