共形FDA-MIMO雷达降维目标参数估计研究

陈慧; 田湘; 李子豪; 姜欣睿

doi:10.12000/JR21197

Reduced-dimension Target Parameter Estimation For Conformal FDA-MIMO Radar

DOI: 10.12000/JR21197

School of Information and Communication Engineering, University of Electronic Science andTechnology of China, Chengdu 611731, China

Funds: The National Natural Science Foundation of China (61571081), Sichuan Science and Technology Program (18ZDYF2551), Fundamental Research Funds for the Central Universities (ZYGX2018J005)

More Information

Author Bio:
CHEN Hui received the Ph.D. degree in the department of electronic engineering from the University of Electronic Science and Technology of China (UESTC), Chengdu, China, in 2013. Since January 2014, she has been with the School of Information Engineering and Communication, UESTC, where she is currently an Associate Professor. From November 2011 to May 2013, she was a visiting scholar at Columbia University, NY, USA. Her research interests include array signal processing, wireless communication and artificial intelligence

TIAN Xiang was born in Sichuan, China in 1998. She received the Bachelor Degree in 2020 from Chengdu University of Information Technology. She is pursuing the Master Degree in University of Electronic Science and Technology of China. Her major interests are conformal array and frequency inverse array

LI Zihao was born in Sichuan, China in 1996. He received the Master Degree in 2021 from University of Electronic Science and Technology of China. His major interests are conformal array and frequency diverse array radar

JIANG Xinrui was born in Shanxi, China in 1996. She received the Master Degree in 2021 from University of Electronic Science and Technology of China. She specializes in signal recognition, coding recognition and signal processing

Corresponding author: CHEN Hui, huichen0929@uestc.edu.cn

摘要

摘要:
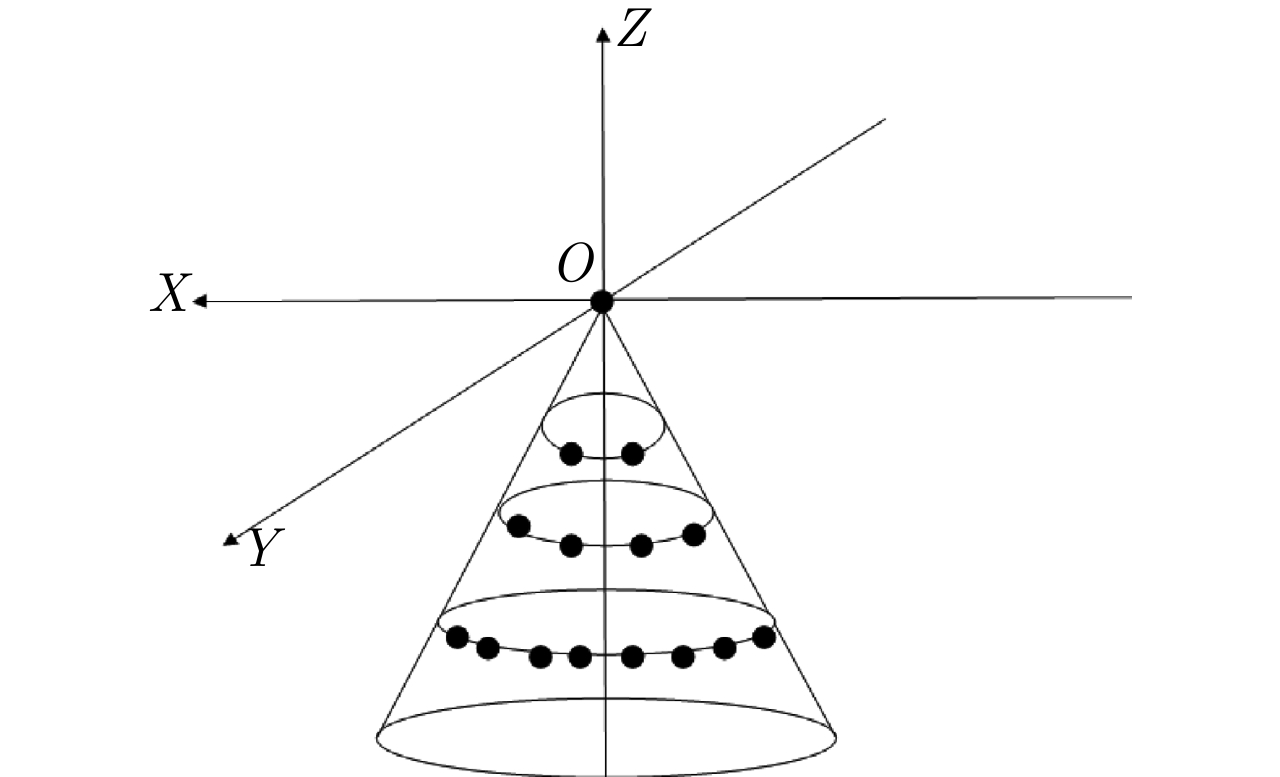
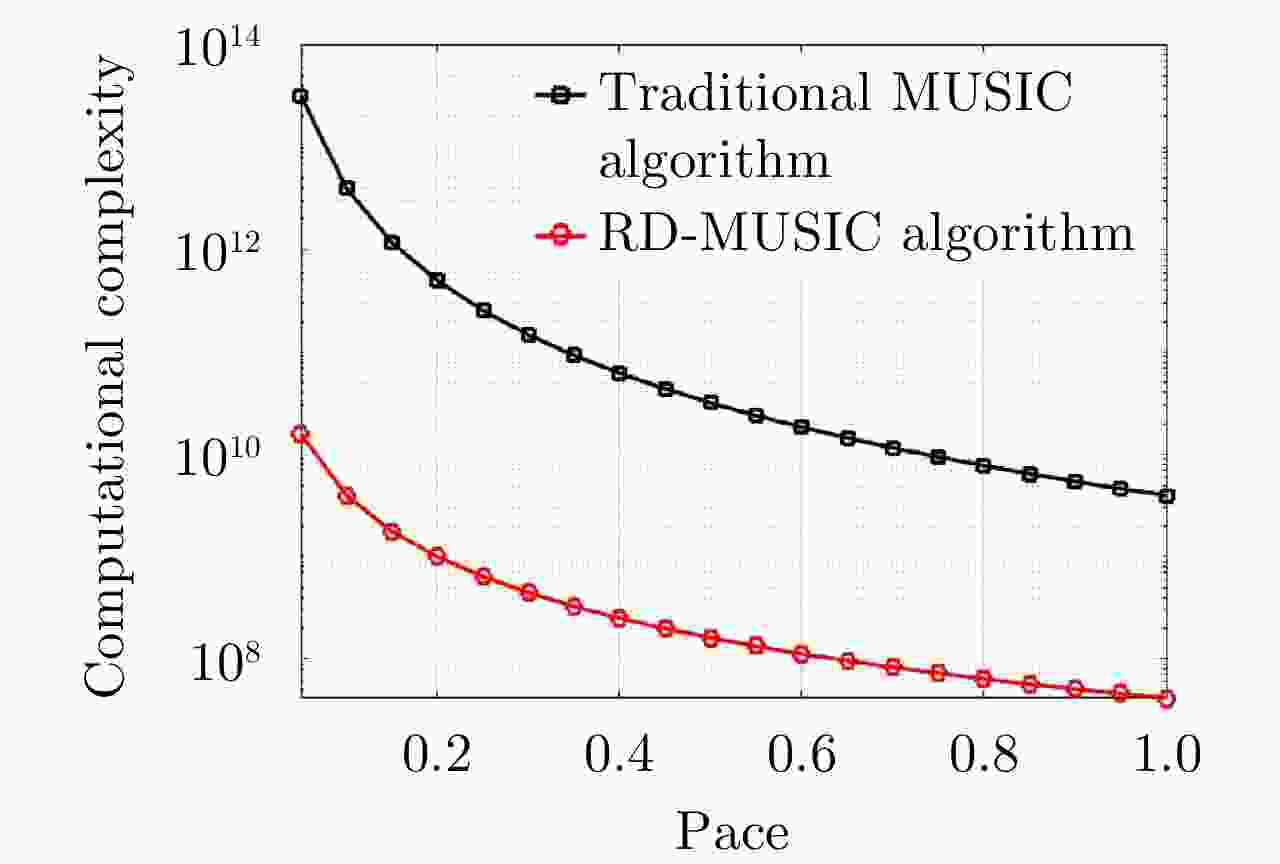
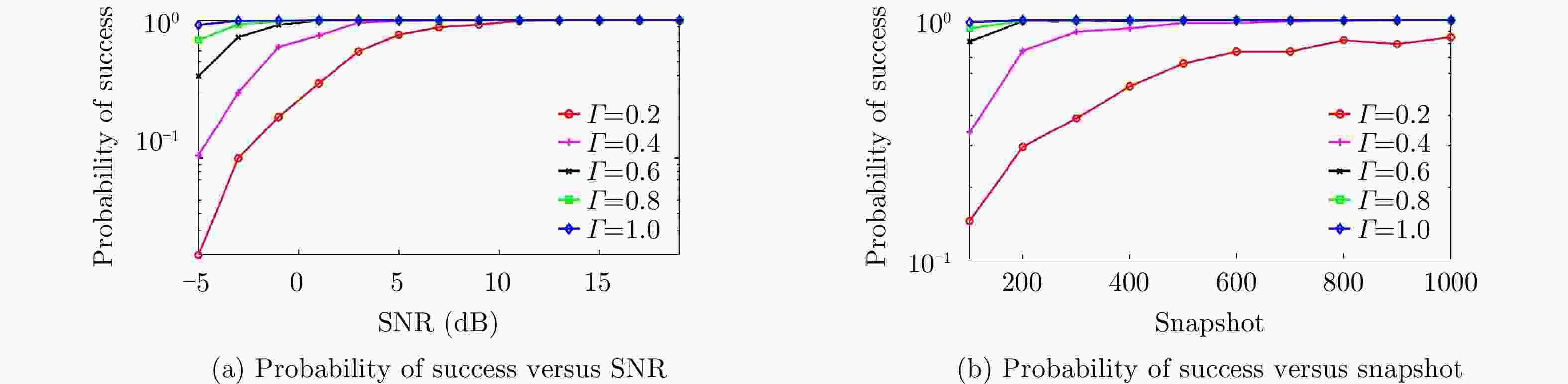
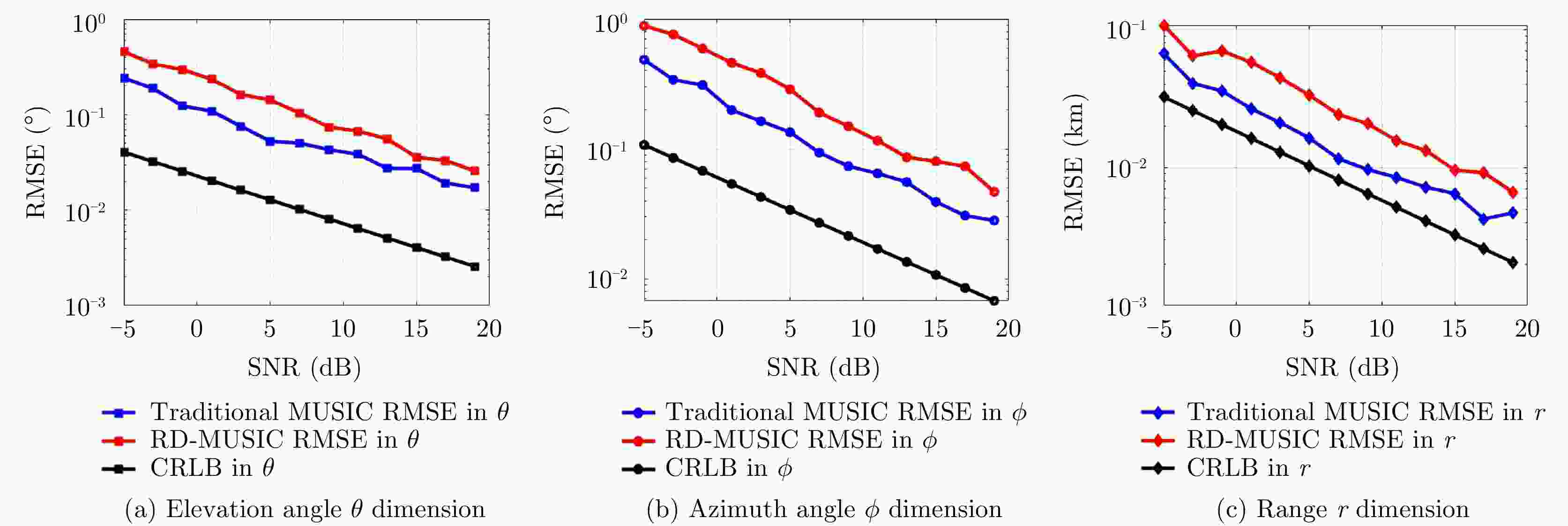
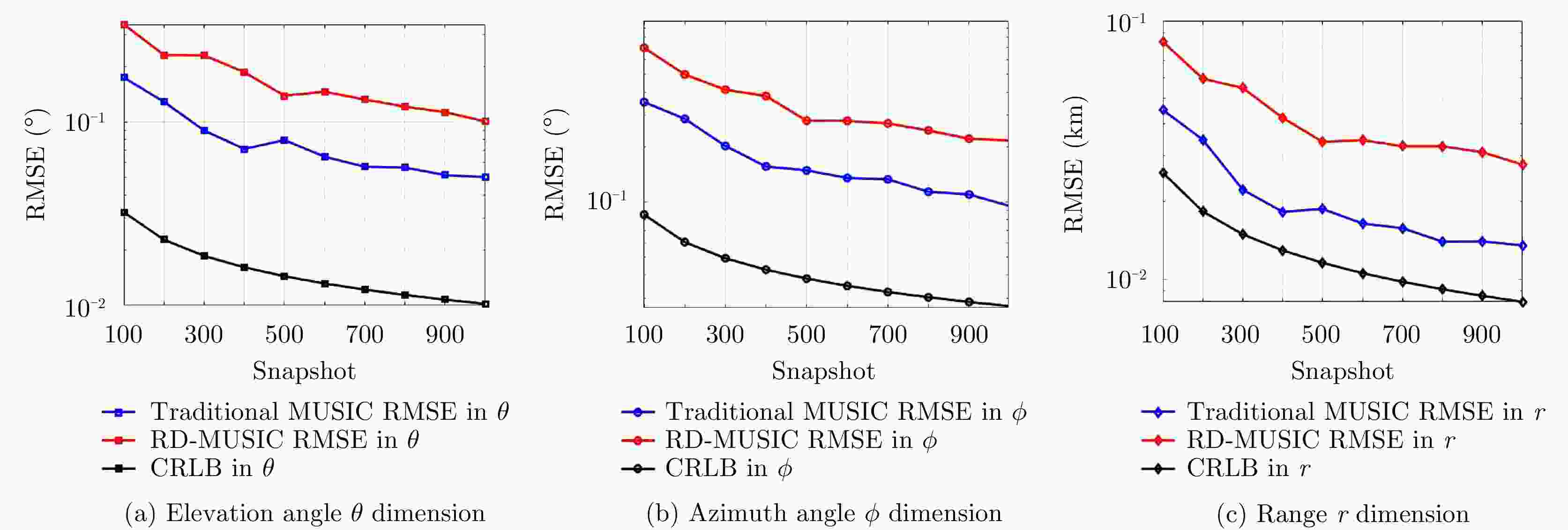
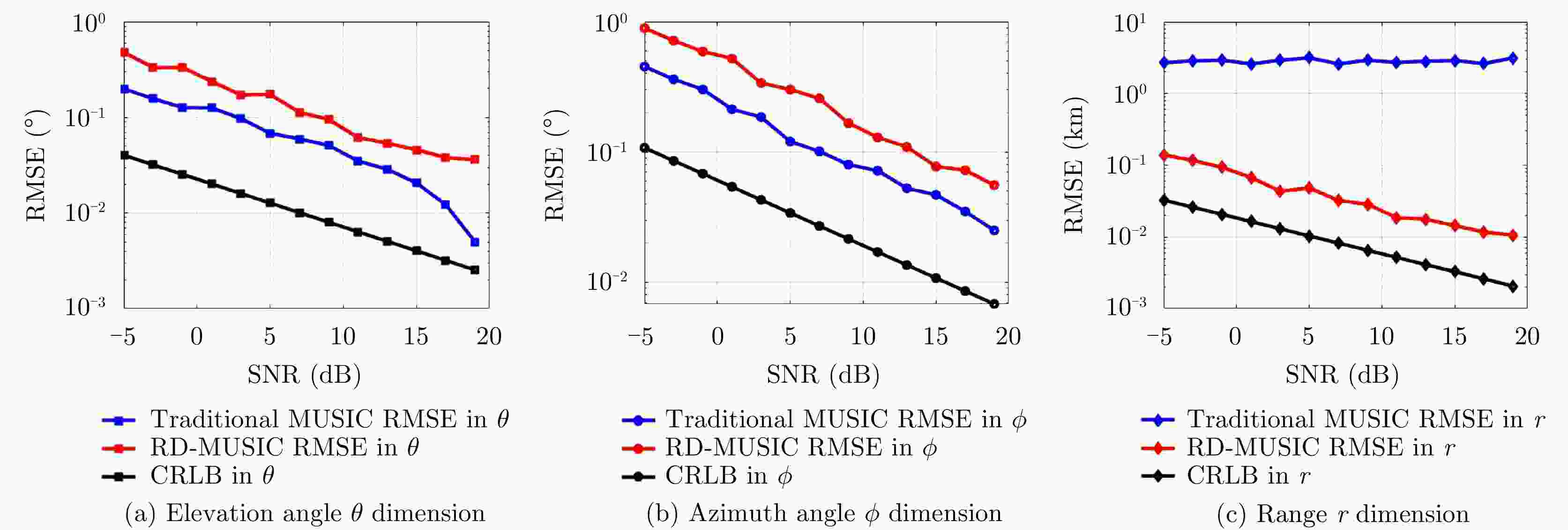
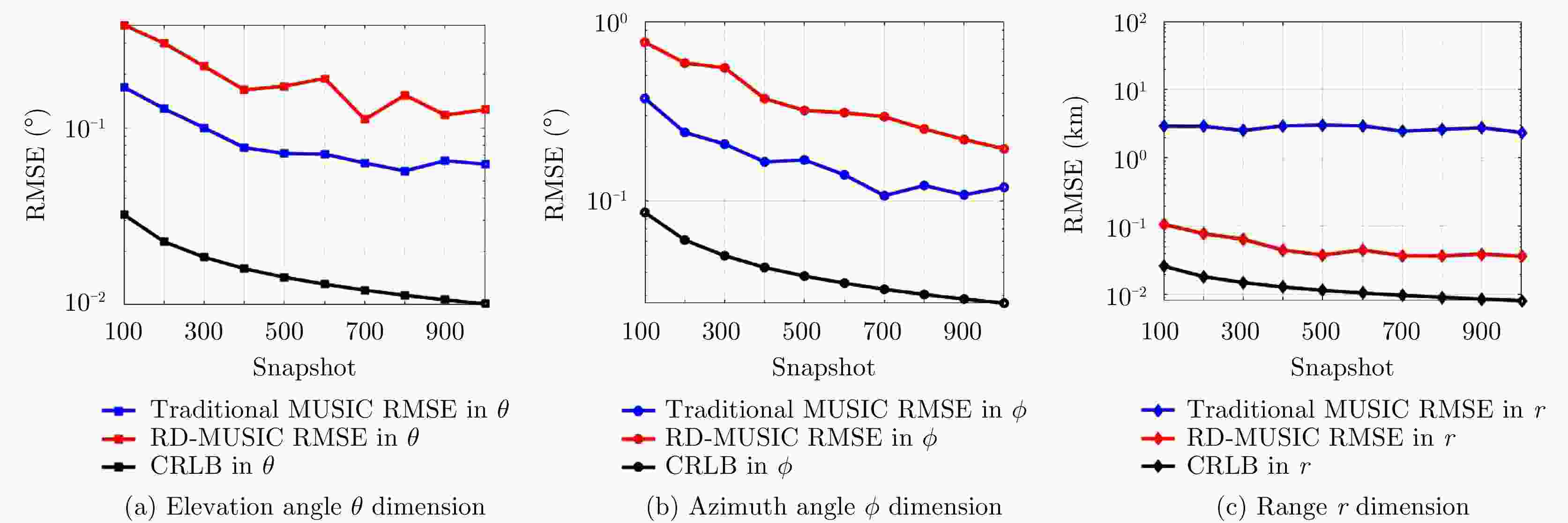
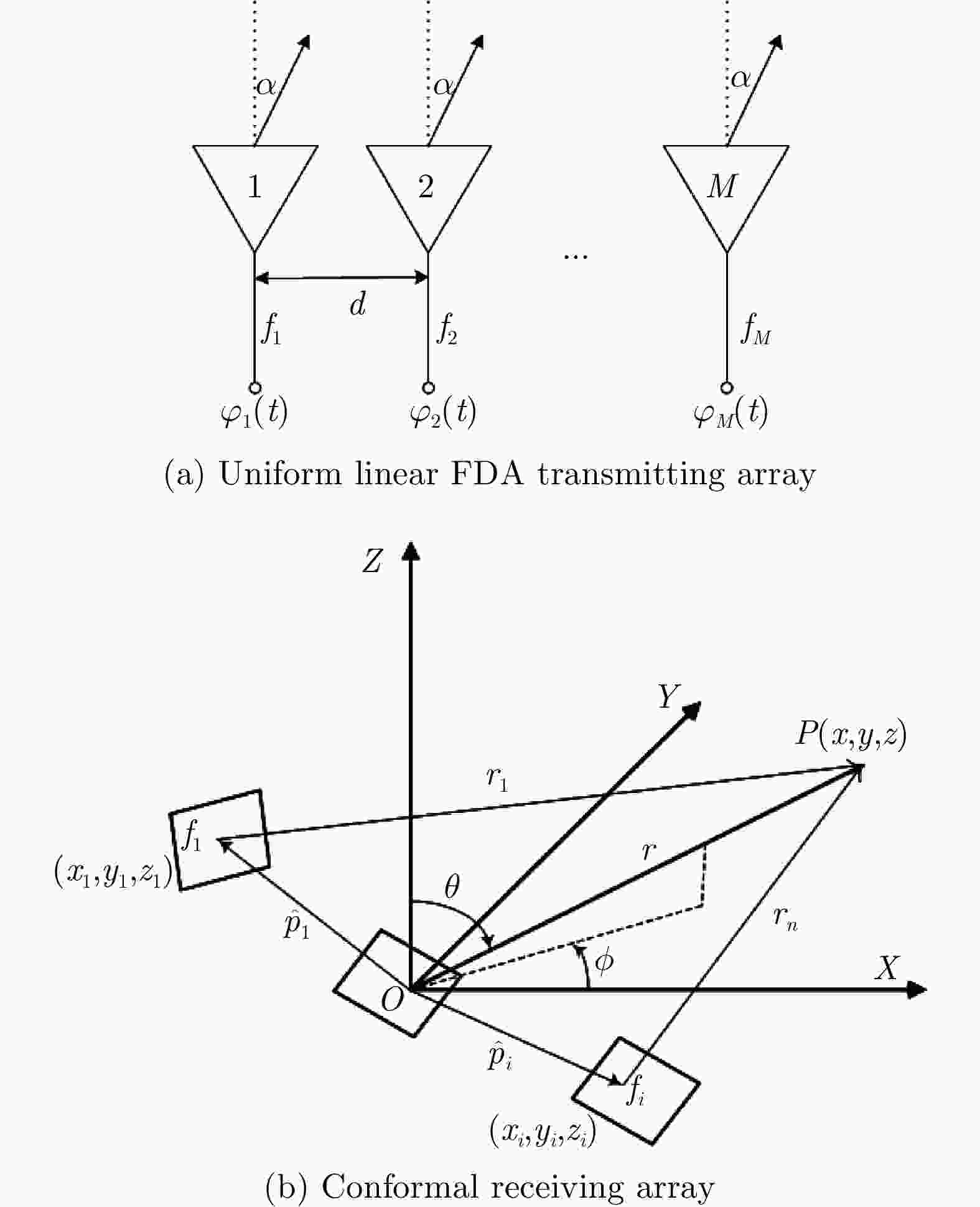
频控阵多输入多输出(FDA-MIMO)雷达是一种具有距离-角度-时间依赖性波束模式且能够提高自由度的系统。该文将可实现降低空气动力学对载体影响、附着在载体表面的共形阵列引入到FDA-MIMO雷达中。首先创建共形FDA-MIMO测量模型，推导参数估计的克拉默-拉奥下界(CRLB)。为了避免传统三维多重信号分类算法(3D-MUSIC)三维搜索，提出一种降维多信号分类(RD-MUSIC)算法实现目标参数估计。仿真结果表明，该算法与3D-MUSIC算法相比，估计精度有所下降，但计算复杂度显著降低。此外，与3D-MUSIC算法相比，该算法具有更好的多目标距离估计性能。
- 共形阵 /
- 频控阵多输入多输出 /
- 参数估计 /
- 三维多重信号分类 /
- 降维多信号分类
Abstract:
Frequency Diverse Array (FDA) Multiple-Input Multiple-Output (MIMO) radar equipped with a FDA can possess beam patterns that are dependent on range, angle, and time, and it can increase the degree of freedom. This paper introduces a conformal array attached to the surface of the carrier, the array can reduce the aerodynamic impact on the carrier and reduce the cross section of the FDA-MIMO radar. First, the conformal FDA-MIMO measurement model is formulated, and a Cramér-Rao Lower Bound (CRLB) is derived to evaluate the parameter estimation performance. To avoid the three-dimensional search of the traditional three-dimensional MUltiple SIgnal Classification (3D-MUSIC) algorithm, a Reduced-Dimension MUltiple SIgnal Classification (RD-MUSIC) algorithm is proposed for parameter estimation. The simulation results demonstrate that the proposed algorithm has a slightly lower estimation accuracy than the 3D-MUSIC algorithm but a much lower computational complexity. In addition, the proposed algorithm has better range estimation performance for multiple targets than the 3D-MUSIC algorithm.
- Conformal array /
- FDA-MIMO /
- Parameter estimation /
- 3D-MUSIC /
- RD-MUSIC

HTML全文

Figure 1. Conformal FDA-MIMO radar

下载: 全尺寸图片幻灯片

Figure 2. Conformal FDA-MIMO semi conical receiving array

下载: 全尺寸图片幻灯片

Figure 3. Comparison of computational complexity under different scan spacing

下载: 全尺寸图片幻灯片

Figure 4. The parameter estimation probability of RD-MUSIC algorithm with different thresholds

下载: 全尺寸图片幻灯片

Figure 5. The RMSE versus snapshot for single target case

下载: 全尺寸图片幻灯片

Figure 6. The RMSE versus SNR for two targets case

下载: 全尺寸图片幻灯片

Figure 7. The RMSE versus snapshot for two targets case

下载: 全尺寸图片幻灯片

Figure 8. The RMSE versus snapshot for two targets case

下载: 全尺寸图片幻灯片

参考文献(28)

[1]	ANTONIK P, WICKS M C, GRIFFITHS H D, et al. Frequency diverse array radars[C]. 2006 IEEE Conference on Radar, Verona, USA, 2006: 215–216. doi: 10.1109/RADAR.2006.1631800.
[2]	WANG Wenqin, SHAO Huaizong, and CAI Jingye. Range-angle-dependent beamforming by frequency diverse array antenna[J]. International Journal of Antennas and Propagation, 2012, 2012: 760489. doi: 10.1155/2012/760489
[3]	SAMMARTINO P F, BAKER C J, and GRIFFITHS H D. Frequency diverse MIMO techniques for radar[J]. IEEE Transactions on Aerospace and Electronic Systems, 2013, 49(1): 201–222. doi: 10.1109/TAES.2013.6404099
[4]	LI Shengyuan, ZHANG Linrang, LIU Nan, et al. Range-angle dependent detection for FDA-MIMO radar[C]. 2016 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Beijing, China, 2016: 6629–6632. doi: 10.1109/IGARSS.2016.7730731.
[5]	CHENG Jie, CHEN Hui, GUI Ronghua, et al. Persymmetric adaptive detector for FDA-MIMO radar[C]. 2020 IEEE Radar Conference (RadarConf20), Florence, Italy, 2020: 1–5. doi: 10.1109/RadarConf2043947.2020.9266641.
[6]	ZHU Yu, LIU Lei, LU Zheng, et al. Target detection performance analysis of FDA-MIMO radar[J]. IEEE Access, 2019, 7: 164276–164285. doi: 10.1109/ACCESS.2019.2943082
[7]	LAN Lan, MARINO A, AUBRY A, et al. GLRT-based adaptive target detection in FDA-MIMO radar[J]. IEEE Transactions on Aerospace and Electronic Systems, 2021, 57(1): 597–613. doi: 10.1109/TAES.2020.3028485
[8]	LAN Lan, XU Jingwei, LIAO Guisheng, et al. Suppression of mainbeam deceptive jammer with FDA-MIMO radar[J]. IEEE Transactions on Vehicular Technology, 2020, 69(10): 11584–11598. doi: 10.1109/TVT.2020.3014689
[9]	LAN Lan, ROSAMILIA M, AUBRY A, et al. Single-snapshot angle and incremental range estimation for FDA-MIMO radar[J]. IEEE Transactions on Aerospace and Electronic Systems, 2021, 57(6): 3705–3718. doi: 10.1109/TAES.2021.3083591
[10]	CHEN Hui and SHAO Huaizong. Sparse reconstruction based target localization with frequency diverse array MIMO radar[C]. 2015 IEEE China Summit and International Conference on Signal and Information Processing (ChinaSIP), Chengdu, China, 2015: 94–98. doi: 10.1109/ChinaSIP.2015.7230369.
[11]	XU Jingwei, LIAO Guisheng, ZHU Shengqi, et al. Joint range and angle estimation using MIMO radar with frequency diverse array[J]. IEEE Transactions on Signal Processing, 2015, 63(13): 3396–3410. doi: 10.1109/TSP.2015.2422680
[12]	XIONG Jie, WANG Wenqin, and GAO Kuandong. FDA-MIMO radar range-angle estimation: CRLB, MSE, and resolution analysis[J]. IEEE Transactions on Aerospace and Electronic Systems, 2018, 54(1): 284–294. doi: 10.1109/TAES.2017.2756498
[13]	CUI Can, YAN Yisheng, WANG Wenqin, et al. Resolution threshold of music algorithm for FDA-MIMO radar[C]. 2018 IEEE Radar Conference (RadarConf18), Oklahoma City, USA, 2018: 230–234. doi: 10.1109/RADAR.2018.8378562.
[14]	CHEN Xiaolong, CHEN Baoxin, XUE Yonghua, et al. Space-range-Doppler focus processing: A novel solution for moving target integration and estimation using FDA-MIMO radar[C]. 2018 International Conference on Radar (RADAR), Brisbane, Australia, 2018: 1–4. doi: 10.1109/RADAR.2018.8557297.
[15]	CUI Can, XU Jian, GUI Ronghua, et al. Search-free DOD, DOA and range estimation for bistatic FDA-MIMO radar[J]. IEEE Access, 2018, 6: 15431–15445. doi: 10.1109/ACCESS.2018.2816780
[16]	LIU Yi, YANG Hu, JIN Zusheng, et al. A multibeam cylindrically conformal slot array antenna based on a modified rotman lens[J]. IEEE Transactions on Antennas and Propagation, 2018, 66(7): 3441–3452. doi: 10.1109/TAP.2018.2829816
[17]	DOHMEN C, ODENDAAL J W, and JOUBERT J. Synthesis of conformal arrays with optimized polarization[J]. IEEE Transactions on Antennas and Propagation, 2007, 55(10): 2922–2925. doi: 10.1109/TAP.2007.905501
[18]	XIAO Shiwei, YANG Shiwen, ZHANG Hangyu, et al. Practical implementation of wideband and wide-scanning cylindrically conformal phased array[J]. IEEE Transactions on Antennas and Propagation, 2019, 67(8): 5729–5733. doi: 10.1109/TAP.2019.2922760
[19]	COSTA M, RICHTER A, and KOIVUNEN V. DoA and polarization estimation for arbitrary array configurations[J]. IEEE Transactions on Signal Processing, 2012, 60(5): 2330–2343. doi: 10.1109/TSP.2012.2187519
[20]	MOHAMMADI S, GHANI A, and SEDIGHY S H. Direction-of-arrival estimation in conformal microstrip patch array antenna[J]. IEEE Transactions on Antennas and Propagation, 2018, 66(1): 511–515. doi: 10.1109/TAP.2017.2772085
[21]	NECHAEV Y B, ALGAZINOV E K, and PESHKOV I W. Estimation of the Cramer-Rao bound for radio direction-finding on the azimuth and elevation of the cylindical antenna arrays[C]. 2018 41st International Conference on Telecommunications and Signal Processing (TSP), Athens, Greece, 2018: 1–4. doi: 10.1109/TSP.2018.8441419.
[22]	LI Wentao, CUI Can, YE Xiutiao, et al. Quasi-time-invariant 3-D focusing beampattern synthesis for conformal frequency diverse array[J]. IEEE Transactions on Antennas and Propagation, 2020, 68(4): 2684–2697. doi: 10.1109/TAP.2019.2955199
[23]	FENG Maoyuan, CUI Zhongma, YANG Yunxiu, et al. A reduced-dimension MUSIC algorithm for monostatic FDA-MIMO radar[J]. IEEE Communications Letters, 2021, 25(4): 1279–1282. doi: 10.1109/LCOMM.2020.3045440
[24]	ZHANG Xiaofei, CHEN Weiyang, ZHENG Wang, et al. Localization of near-field sources: A reduced-dimension MUSIC algorithm[J]. IEEE Communications Letters, 2018, 22(7): 1422–1425. doi: 10.1109/LCOMM.2018.2837049
[25]	BURGER H A. Use of Euler-rotation angles for generating antenna patterns[J]. IEEE Antennas and Propagation Magazine, 1995, 37(2): 56–63. doi: 10.1109/74.382344
[26]	MILLIGAN T. More applications of Euler rotation angles[J]. IEEE Antennas and Propagation Magazine, 1999, 41(4): 78–83. doi: 10.1109/74.789738
[27]	STOICA P and NEHORAI A. MUSIC, maximum likelihood and Cramer-Rao bound[C]. International Conference on Acoustics, Speech, and Signal Processing, New York, USA, 1988: 2296–2299. doi: 10.1109/ICASSP.1988.197097.
[28]	STOICA P and NEHORAI A. MUSIC, maximum likelihood and Cramer-Rao bound: Further results and comparisons[C]. International Conference on Acoustics, Speech, and Signal Processing, Glasgow, UK, 1989: 2605–2608. doi: 10.1109/ICASSP.1989.267001.