一种结合稀疏重建和匹配滤波的距离模糊抑制方法

齐萌; 黄丽佳; 仇晓兰; 张问一; 胡玉新; 初庆伟

doi:10.12000/JR21181

一种结合稀疏重建和匹配滤波的距离模糊抑制方法

doi: 10.12000/JR21181

齐萌^{1, 2, 3},
黄丽佳^{1, 2, 3, ,},
仇晓兰^{1, 2, 3},
张问一^{1, 2, 3},
胡玉新^{1, 2, 3},
初庆伟^{1, 2}

1.
中国科学院空天信息创新研究院北京 100094
2.
中国科学院空间信息处理与应用系统技术重点实验室北京 100190
3.
中国科学院大学电子电气与通信工程学院北京 100049

基金项目: 国家重点研发计划(2018YFC1407200)

详细信息

作者简介:
齐　萌(1997–)，女，山东潍坊人，中国科学院空天信息创新研究院硕士研究生，研究方向为合成孔径雷达信号处理与图像分析

黄丽佳(1984–)，女，辽宁大连人，博士，中国科学院空天信息创新研究院研究员，博士生导师，研究方向为合成孔径雷达信号处理与图像分析

仇晓兰(1982–)，女，江苏苏州人，中国科学院空天信息创新研究院研究员，博士生导师，IEEE高级会员、IEEE地球科学与遥感快报副主编、雷达学报青年编委。主要研究方向为SAR成像处理、SAR图像理解

张问一(1984–)，男，重庆人，中国科学院空天信息创新研究院副研究员，硕士生导师。主要研究方向为遥感信息处理系统体系架构，基于遥感数据的人工智能和大数据，智能遥感数据接收和处理

胡玉新(1981–)，男，内蒙古赤峰人，于中国科学院电子学研究所获博士学位，现为中国科学院空天信息创新研究院研究员，硕士生导师。主要研究方向为星载SAR信号处理，遥感卫星地面系统、空间信息处理系统体系架构

初庆伟(1987–)，男，山东烟台人，中国科学院空天信息创新研究院助理研究员，主要研究方向为遥感卫星数据接收处理相关技术

通讯作者:
黄丽佳　iecas8huanglijia@163.com

责任主编：王岩 Corresponding Editor: WANG Yan
中图分类号: TN958; TP391
计量
- 文章访问数: 942
- HTML全文浏览量: 432
- PDF下载量: 105
- 被引次数: 0
出版历程
- 收稿日期: 2021-11-17
- 修回日期: 2021-12-29
- 网络出版日期: 2022-01-28
- 刊出日期: 2022-02-28

Method of Range Ambiguity Suppression Combining Sparse Reconstruction and Matched Filtering

QI Meng^{1, 2, 3},
HUANG Lijia^{1, 2, 3
, ,},
QIU Xiaolan^{1, 2, 3},
ZHANG Wenyi^{1, 2, 3},
HU Yuxin^{1, 2, 3},
CHU Qingwei^{1, 2}

1.
Aerospace Information Research Institute, Chinese Academy of Science, Beijing 100094, China
2.
Key Laboratory of Technology in Geo-spatial Information Processing and Application System, Chinese Academy of Sciences, Beijing 100190, China
3.
School of Electronic, Electrical and Communication Engineering, University of Chinese Academy of Sciences, Beijing 100049, China

Funds: National Key R&D Program of China (2018YFC1407200)

More Information

Corresponding author: HUANG Lijia, iecas8huanglijia@163.com

摘要

摘要: 由于SAR天线旁瓣特性和脉冲工作体制，SAR图像在一定程度上受到距离模糊的影响。距离模糊抑制工作分别聚焦在SAR系统设计和SAR信号处理两个方面。前者通过天线赋形、正交编码等方式减小距离模糊能量接收，后者利用信号处理技术在回波域和图像域消除距离模糊能量。该文提出了一种结合稀疏重建和匹配滤波技术的距离模糊抑制方法。该方法对模糊区进行稀疏重建，利用模糊区图像和重建矩阵估计模糊区信号，从回波信号中将其分离得到模糊抑制后的主像信号，后续利用匹配滤波技术获得主像图像。该方法利用稀疏重建技术保证了模糊区信号估计的精度，利用匹配滤波技术保证了成像处理的效率。仿真实验表明，该方法可以有效抑制距离模糊，抑制效果可达10 dB及以上，并且对主像弱目标和细节具有很好的保持能力。
- SAR系统 /
- SAR成像 /
- 匹配滤波 /
- 稀疏重建 /
- 距离模糊抑制
Abstract: To a certain extent, SAR images are affected by range ambiguity due to antenna sidelobe characteristics and pulse operating system. The work of range ambiguity suppression focuses on SAR system design and signal processing. One type of idea tries to modify the way of transmitting and receiving to block the receiving of the ambiguous energy, such as multiple elevation beams and azimuth phase coding. The other ideas are algorithms that use signal processing technology to reduce the distance ambiguity energy in echo and image domains. This paper proposes a range ambiguity suppression method that combines sparse reconstruction and matched filtering. The method performs the sparse reconstruction of the ambiguity area, estimates the ambiguity area signal using the ambiguity area image and reconstruction matrix, separates it from the echo signal to obtain the primary image signal after range ambiguity suppression, and uses matched filtering to obtain the main area image. In this method, sparse reconstruction ensures the accuracy of fuzzy signal estimation, and matched filtering ensures the efficiency of imaging processing. Simulation results show that the proposed method can effectively suppress range ambiguity, with a suppression effect of 10 dB or higher, and it has a good ability to maintain the weak targets and the details of the main image.
- SAR system /
- SAR imaging /
- Matched filtering /
- Sparse reconstruction /
- Range ambiguity suppression

HTML全文

图 1 能量比1:1，匹配滤波的主像结果

Figure 1. Energy ratio 1:1, primary image results of matching filtering

下载: 全尺寸图片幻灯片

图 2 能量比1:1，本文方法的主像结果

Figure 2. Energy ratio 1:1, primary image results of the proposed method

下载: 全尺寸图片幻灯片

图 3 能量比100:1，匹配滤波的主像结果

Figure 3. Energy ratio 100:1, primary image results of matching filtering

下载: 全尺寸图片幻灯片

图 4 能量比100:1，本文方法的主像结果

Figure 4. Energy ratio 100:1, primary image results of the proposed method

下载: 全尺寸图片幻灯片

图 5 距离徙动差异对距离模糊抑制效果的影响

Figure 5. The effect of range migration difference on range ambiguity suppression

下载: 全尺寸图片幻灯片

图 6 主像区弱目标，匹配滤波的主像结果

Figure 6. Weak target in the main image area, primary image results of matching filtering

下载: 全尺寸图片幻灯片

图 7 主像区弱目标，经典稀疏重建的主像结果

Figure 7. Weak target in the main image area, primary image results of sparse reconstruction

下载: 全尺寸图片幻灯片

图 8 主像区弱目标，本文方法的主像结果

Figure 8. Weak target in the main image area, primary image results of the proposed method

下载: 全尺寸图片幻灯片

图 9 主像区面目标，匹配滤波的主像结果

Figure 9. Surface target in the main image area, primary image results of matching filtering

下载: 全尺寸图片幻灯片

图 10 主像区面目标，本文方法的主像结果

Figure 10. Surface target in the main image area, primary image results of the proposed method

下载: 全尺寸图片幻灯片

图 11 实际图像场景

Figure 11. Real image scene

下载: 全尺寸图片幻灯片

图 12 区域3主像、区域1模糊像，匹配滤波的主像结果

Figure 12. Primary image results of matching filtering, where region 3 is the main image, region 1 is the fuzzy image

下载: 全尺寸图片幻灯片

图 13 区域3主像、区域1模糊像，本文方法的主像结果

Figure 13. Primary image results of the proposed method, where region 3 is the main image, region 1 is the fuzzy image

下载: 全尺寸图片幻灯片

图 14 区域3主像、区域1模糊像，针对模糊区匹配滤波的成像结果

Figure 14. Fuzzy area image results of matching filtering, where region 3 is the main image, region 1 is the fuzzy image

下载: 全尺寸图片幻灯片

图 15 按照幅度大小排序后的主像(蓝色线)与模糊像(红色线)幅度曲线

Figure 15. Amplitude curves of main image (blue line) and fuzzy image (red line), sorted according to amplitude

下载: 全尺寸图片幻灯片

图 16 区域3主像、区域1模糊像，式(22)模糊像重建结果

Figure 16. Fuzzy reconstruction results using Eq. (22), where region 3 is the main image, region 1 is the fuzzy image

下载: 全尺寸图片幻灯片

图 17 区域3主像、区域1模糊像，式(18)模糊像重建结果

Figure 17. Fuzzy reconstruction results using Eq. (18), where region 3 is the main image, region 1 is the fuzzy image

下载: 全尺寸图片幻灯片

图 18 区域2主像、区域1模糊像，匹配滤波的主像结果

Figure 18. Primary image results of matching filtering, where region 2 is the main image, region 1 is the fuzzy image

下载: 全尺寸图片幻灯片

图 19 区域2主像、区域1模糊像，式(22)模糊抑制和主像结果

Figure 19. Fuzzy reconstruction results using Eq. (22), where region 2 is the main image, region 1 is the fuzzy image

下载: 全尺寸图片幻灯片

图 20 区域2主像、区域1模糊像，式(18)模糊抑制和主像结果

Figure 20. Fuzzy reconstruction results using Eq. (18), where region 2 is the main image, region 1 is the fuzzy image

下载: 全尺寸图片幻灯片

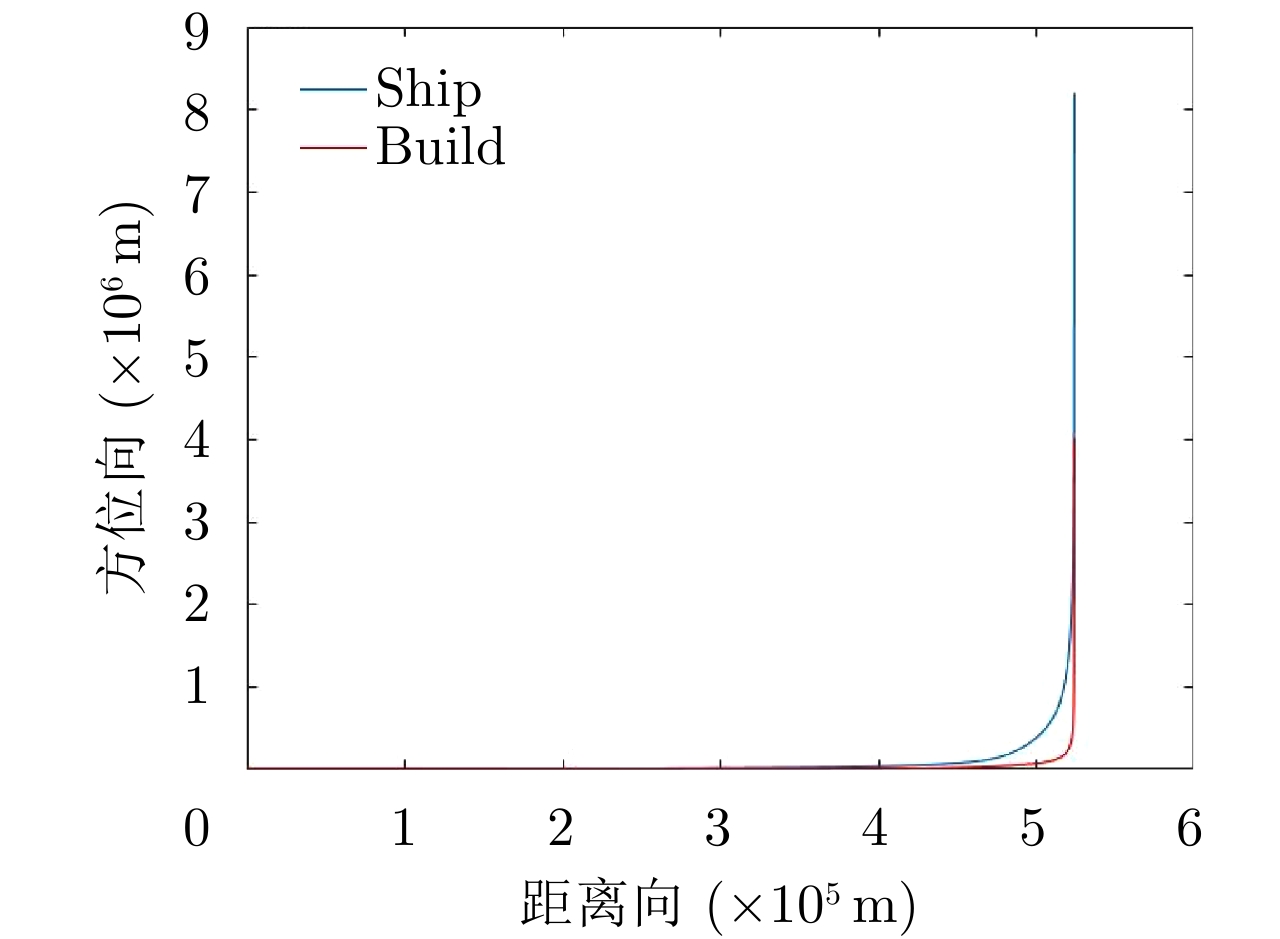
表 1 典型场景后向散射系数变化范围

Table 1. Variation range of backscattering coefficients in typical scenes

场景	最大值-平均值(dB)	最大值-最小值(dB)
山区	15.93	68.32
海面	3.08	78.01
港口	14.41	93.73
城区	17.74	96.06

下载: 导出CSV

表 2 雷达仿真参数

Table 2. Radar simulation parameters

雷达参数	数值
雷达载频(GHz)	9.6
雷达发射信号带宽(MHz)	100
脉冲重复频率(Hz)	5000
目标中心斜距(km)	600
平台飞行速度(m/s)	7000
合成孔径时间(s)	0.7
距离向名义分辨率(m)	<2.0
方位向名义分辨率(m)	<2.0

下载: 导出CSV

表 3 距离模糊抑制前后，模糊像和主像能量比

Table 3. Energy ratio before and after distance fuzzy suppression

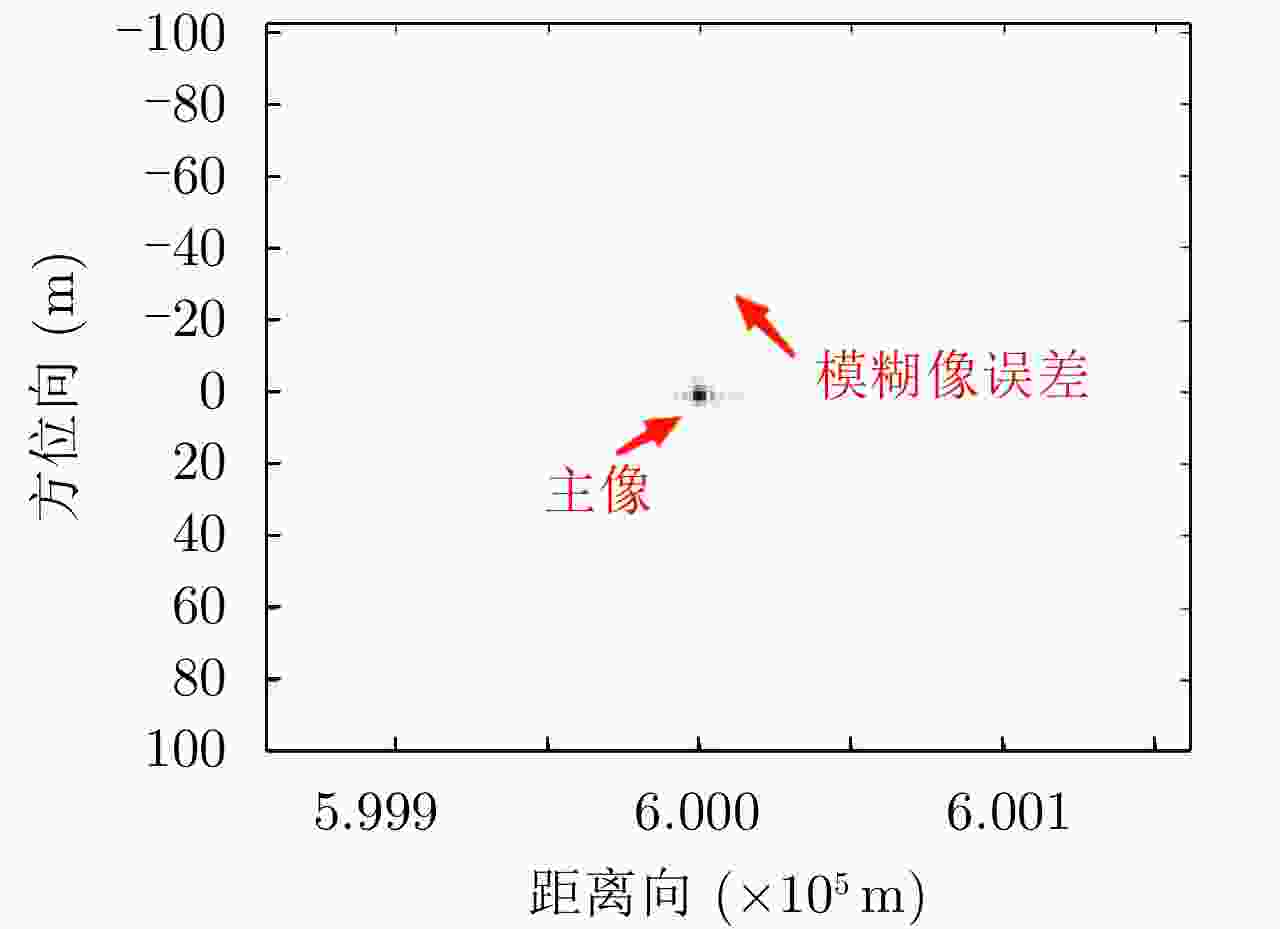
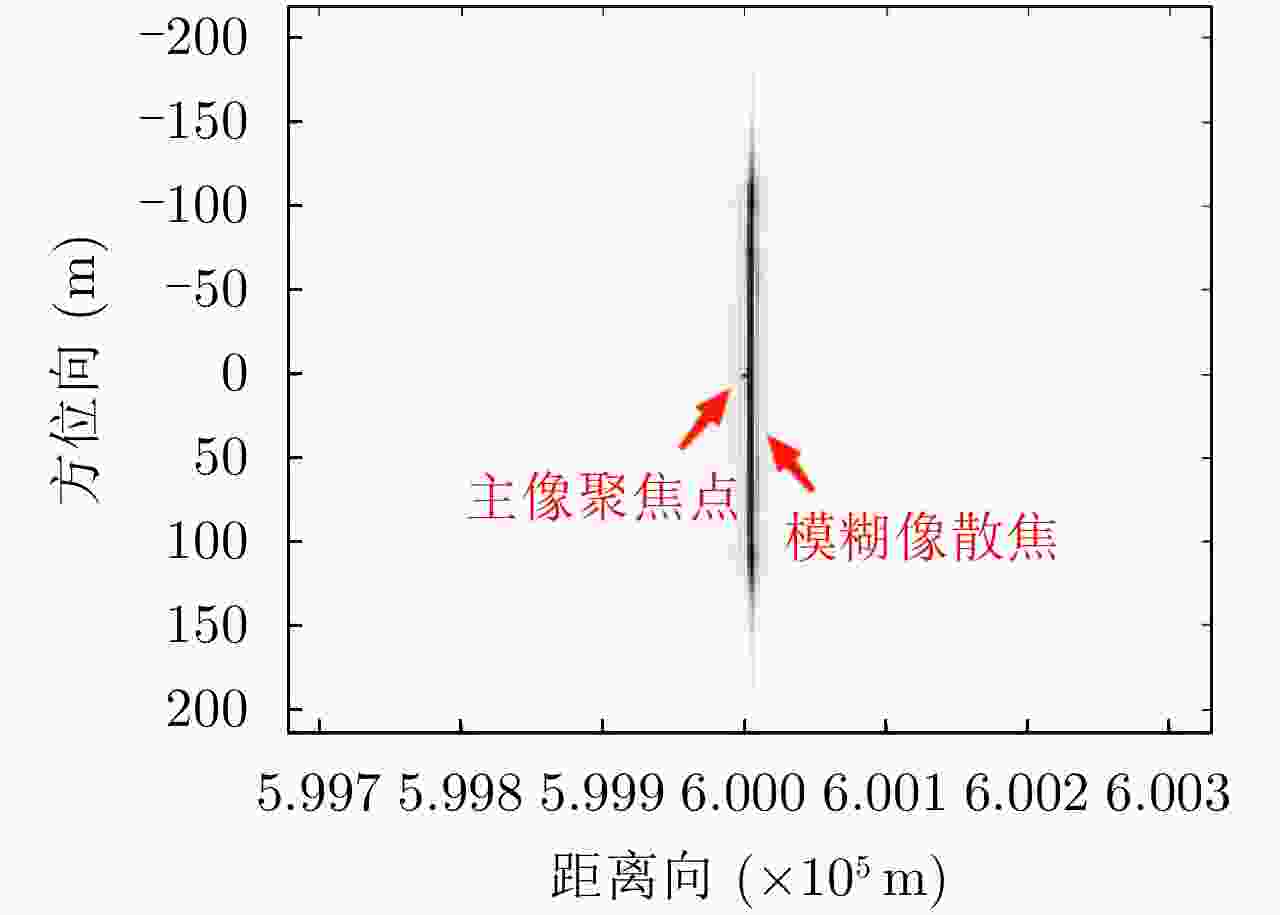
序号	方法	能量和之比(dB)	峰值能量之比(dB)
1	模糊像/主像能量1:1，匹配滤波	0.0128	–18.9953
2	模糊像/主像能量1:1，本文方法	–11.9414	–26.1393
3	模糊像/主像能量100:1，匹配滤波	19.3927	1.0088
4	模糊像/主像能量100:1，本文方法	7.9140	–6.1270
5	模糊像/主像能量1:1，加噪声匹配滤波	0.0175	–8.9656
6	模糊像/主像能量1:1，加噪声本文方法	–10.7281	–11.9066
注：5和6中，模糊像峰值能量统计受噪声影响大；能量和统计减去了噪声能量，受噪声影响较小。

下载: 导出CSV

表 4 成像前后弱目标能量对比

Table 4. Comparison of weak target energy before and after imaging

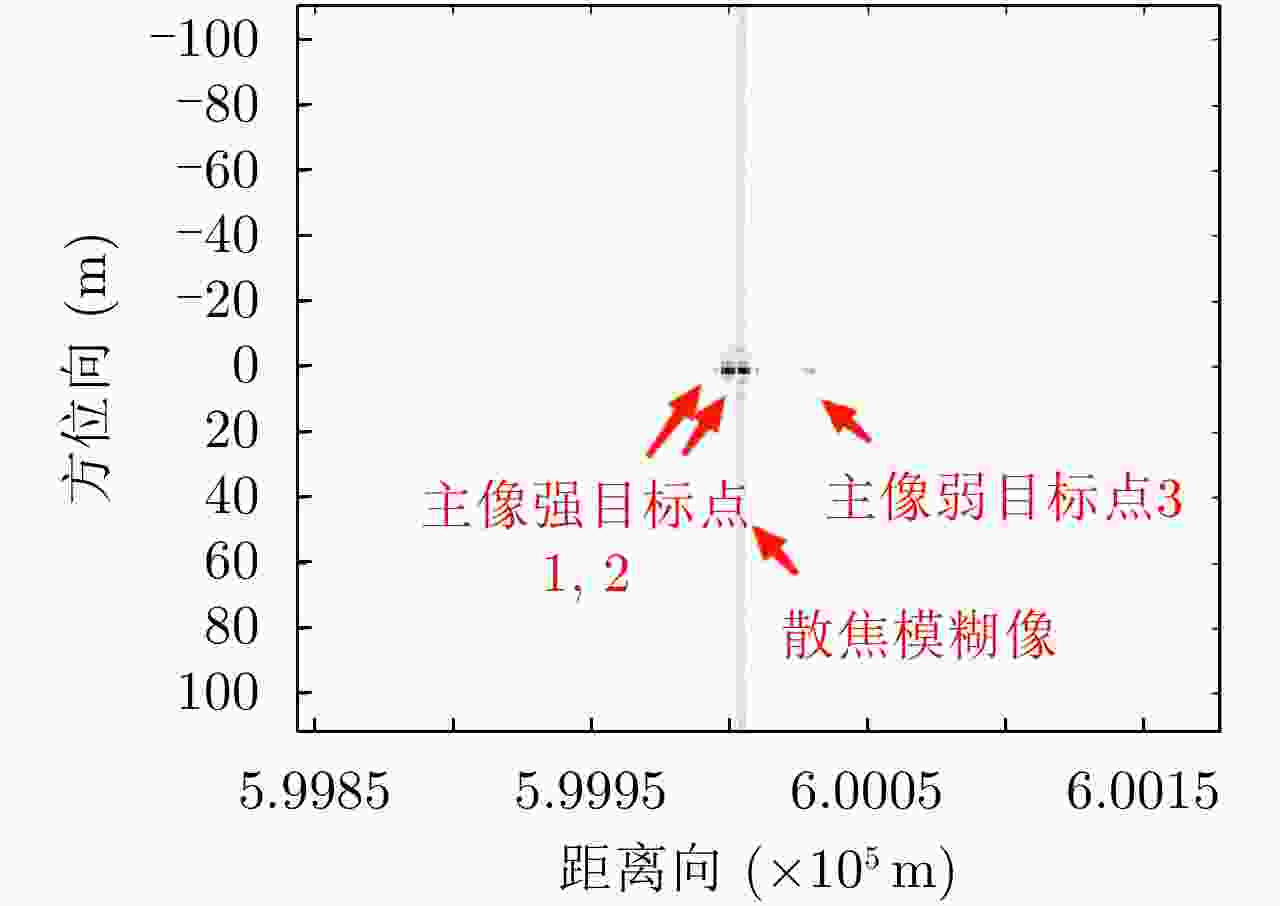
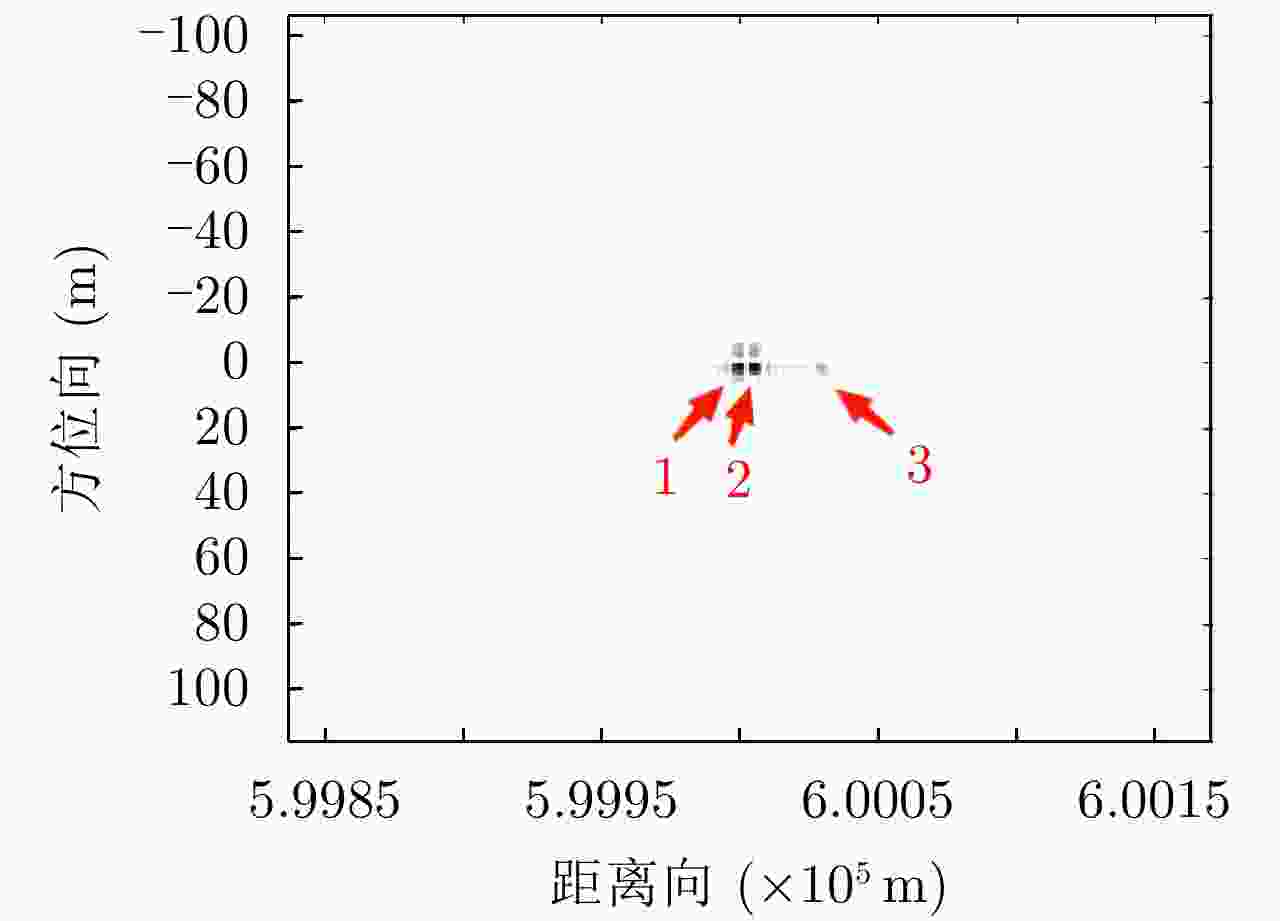
参数	数值(J)
弱目标原始能量强度	7.2703e+07
传统方法处理后弱目标能量强度	5.3230e+07
本文方法处理后弱目标能量强度	7.1773e+07

下载: 导出CSV

表 5 距离模糊抑制前后，模糊像和主像总能量比

Table 5. Total energy ratio of fuzzy image and main image before and after fuzzy suppression

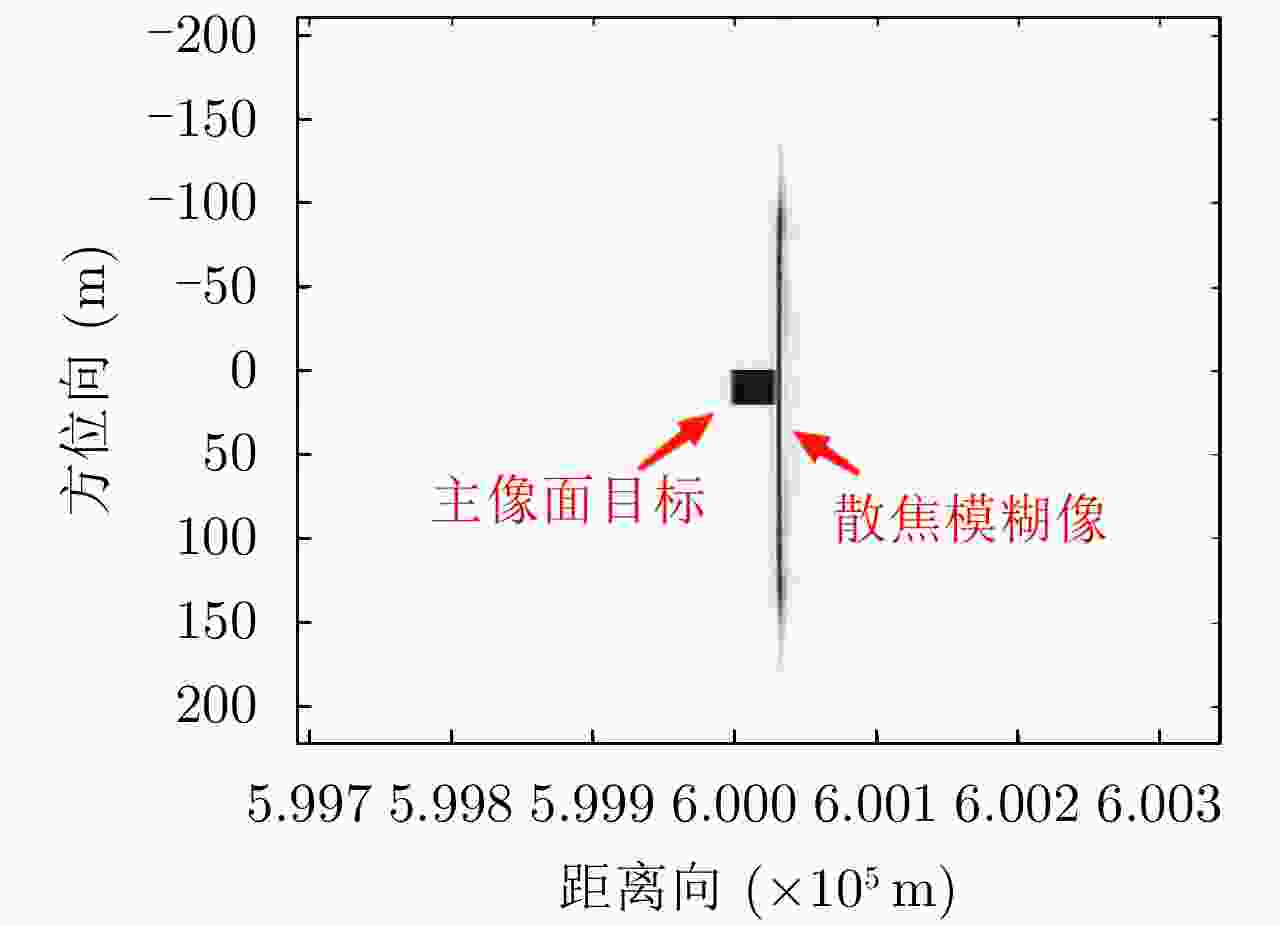
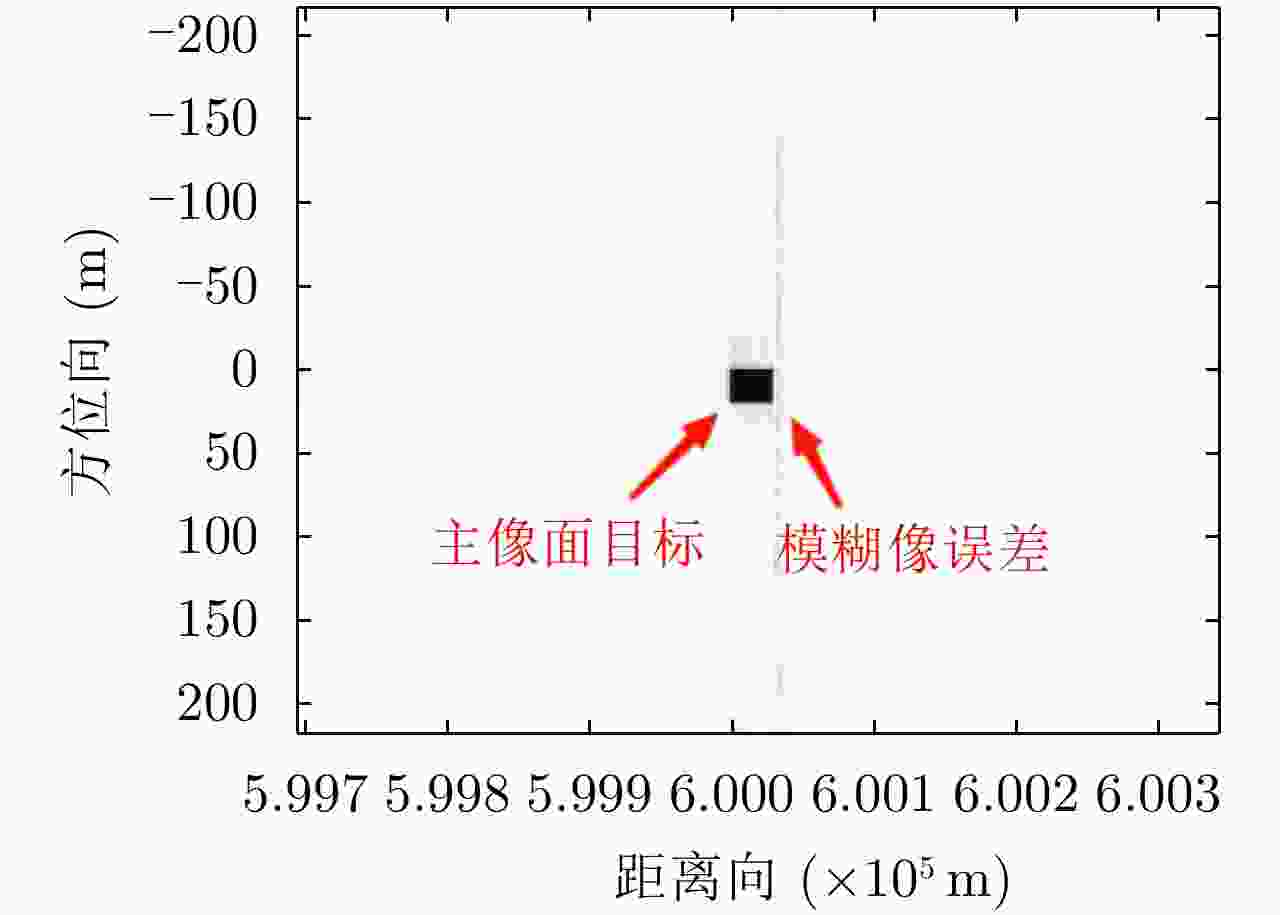
方法	能量和之比(dB)	峰值能量之比(dB)
模糊像点目标/主像面目标能量1:1，匹配滤波	–0.2622	–1.2186
模糊像点目标/主像面目标能量1:1，本文方法	–15.1669	–11.8238

下载: 导出CSV

参考文献(22)

[1]	CURLANDER J C and MCDONOUGH R N. Synthetic Aperture Radar: Systems and Signal Processing[M]. New York, USA: Wiley, 1991: 115–320.
[2]	GRIFFLTHS H D and MANCINI P. Ambiguity suppression in sars using adaptive array techniques[C]. 1991 IEEE International Symposium on Geoscience and Remote Sensing, Espoo, Finland, 1991. doi: 10.1109/IGARSS.1991.580292.
[3]	KRIEGER G, HUBER S, VILLANO M, et al. CEBRAS: Cross elevation beam range ambiguity suppression for high-resolution wide-swath and MIMO-SAR imaging[C]. 2015 IEEE International Geoscience and Remote Sensing Symposium, Milan, Italy, 2015.
[4]	MITTERMAYER J and MARTINEZ J M. Analysis of range ambiguity suppression in SAR by up and down chirp modulation for point and distributed targets[C]. 2003 IEEE International Geoscience and Remote Sensing Symposium, Toulouse, France, 2003: 4077–4079. doi: 10.1109/IGARSS.2003.1295367.
[5]	WEN Xuejiao, QIU Xiaolan, HAN Bing, et al. A range ambiguity suppression processing method for spaceborne SAR with up and down chirp modulation[J]. Sensors, 2018, 18(5): 1454. doi: 10.3390/s18051454
[6]	MO Hongbo and ZENG Zhimin. Investigation of multichannel ScanSAR with up and down chirp modulation for range ambiguity suppression[C]. 2016 IEEE International Geoscience and Remote Sensing Symposium, Beijing, China, 2016: 1130–1133. doi: 10.1109/IGARSS.2016.7729286.
[7]	LIU Mingqian, ZHANG Bingchen, XU Zhongqiu, et al. Ambiguities suppression for azimuth multichannel SAR based on L_{2, q} regularization with application to gaofen-3 ultra-fine stripmap mode[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2021, 14: 1532–1544. doi: 10.1109/JSTARS.2020.3046366
[8]	DONOHO D L. Compressed sensing[J]. IEEE Transactions on Information Theory, 2006, 52(4): 1289–1306. doi: 10.1109/TIT.2006.871582
[9]	吴一戎. 稀疏微波成像提升雷达性能[J]. 科学世界, 2019(9): 106–111. WU Yirong. Sparse microwave imaging improves radar performance[J]. Science World, 2019(9): 106–111.
[10]	肖鹏, 吴有明, 于泽, 等. 一种基于压缩感知恢复算法的SAR图像方位模糊抑制方法[J]. 雷达学报, 2016, 5(1): 35–41. doi: 10.12000/JR16004 XIAO Peng, WU Youming, YU Ze, et al. Azimuth ambiguity suppression in SAR images based on compressive sensing recovery algorithm[J]. Journal of Radars, 2016, 5(1): 35–41. doi: 10.12000/JR16004
[11]	FANG Jian, XU Zongben, JIANG Chenglong, et al. SAR range ambiguity suppression via sparse regularization[C]. 2012 IEEE International Geoscience and Remote Sensing Symposium, Munich, Germany, 2012. doi: 10.1109/IGARSS.2012.6350582.
[12]	田菁, 康利鸿, 孙希龙, 等. 稀疏微波成像技术在轨验证及应用探讨[J]. 通信学报, 2017, 38(S2): 37–42. doi: 10.11959/j.issn.1000-436x.2017263 TIAN Jing, KANG Lihong, SUN Xilong, et al. Experiment based on orbit satellite and application for sparse microwave imaging[J]. Journal on Communications, 2017, 38(S2): 37–42. doi: 10.11959/j.issn.1000-436x.2017263
[13]	毕辉, 张冰尘, 洪文, 等. 基于复图像的稀疏SAR成像方法在高分三号数据上的验证[J]. 雷达学报, 2020, 9(1): 123–130. doi: 10.12000/JR19092 BI Hui, ZHANG Bingchen, HONG Wen, et al. Verification of complex image based sparse SAR imaging method on GaoFen-3 dataset[J]. Journal of Radars, 2020, 9(1): 123–130. doi: 10.12000/JR19092
[14]	XU Zhongqiu, LIU Mingqian, ZHOU Guoru, et al. An accurate sparse SAR imaging method for enhancing region-based features via nonconvex and TV regularization[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2021, 14: 350–363. doi: 10.1109/JSTARS.2020.3034431
[15]	BI Hui, ZHANG Bingchen, ZHU Xiaoxiang, et al. L₁-regularization-based SAR imaging and CFAR detection via complex approximated message passing[J]. IEEE Transactions on Geoscience and Remote Sensing, 2017, 55(6): 3426–3440. doi: 10.1109/TGRS.2017.2671519
[16]	ÇETIN M, STOJANOVIĆ I, ÖNHON N Ö, et al. Sparsity-driven synthetic aperture radar imaging: Reconstruction, autofocusing, moving targets, and compressed sensing[J]. IEEE Signal Processing Magazine, 2014, 31(4): 27–40. doi: 10.1109/MSP.2014.2312834
[17]	胡长雨, 汪玲, 朱栋强. 结合字典学习技术的ISAR稀疏成像方法[J]. 电子与信息学报, 2019, 41(7): 1735–1742. doi: 10.11999/JEIT180747 HU Changyu, WANG Ling, and ZHU Dongqiang. Sparse ISAR imaging exploiting dictionary learning[J]. Journal of Electronics &Information Technology, 2019, 41(7): 1735–1742. doi: 10.11999/JEIT180747
[18]	LI Feng, XIN Lei, GUO Yi, et al. A framework of mixed sparse representations for remote sensing images[J]. IEEE Transactions on Geoscience and Remote Sensing, 2017, 55(2): 1210–1221. doi: 10.1109/TGRS.2016.2621123
[19]	LI Bo, LIU Falin, ZHOU Chongbin, et al. Mixed sparse representation for approximated observation-based compressed sensing radar imaging[J]. Journal of Applied Remote Sensing, 2018, 12(3): 035015. doi: 10.1117/1.JRS.12.035015
[20]	APPLEBAUM L, HOWARD S D, SEARLE S, et al. Chirp sensing codes: Deterministic compressed sensing measurements for fast recovery[J]. Applied and Computational Harmonic Analysis, 2009, 26(2): 283–290. doi: 10.1016/j.acha.2008.08.002
[21]	MALLAT S G and ZHANG Zhifeng. Matching pursuits with time-frequency dictionaries[J]. IEEE Transactions on Signal Processing, 1993, 41(12): 3397–3415. doi: 10.1109/78.258082
[22]	CANDES E J and TAO T. Decoding by linear programming[J]. IEEE Transactions on Information Theory, 2005, 51(12): 4203–4215. doi: 10.1109/TIT.2005.858979