-
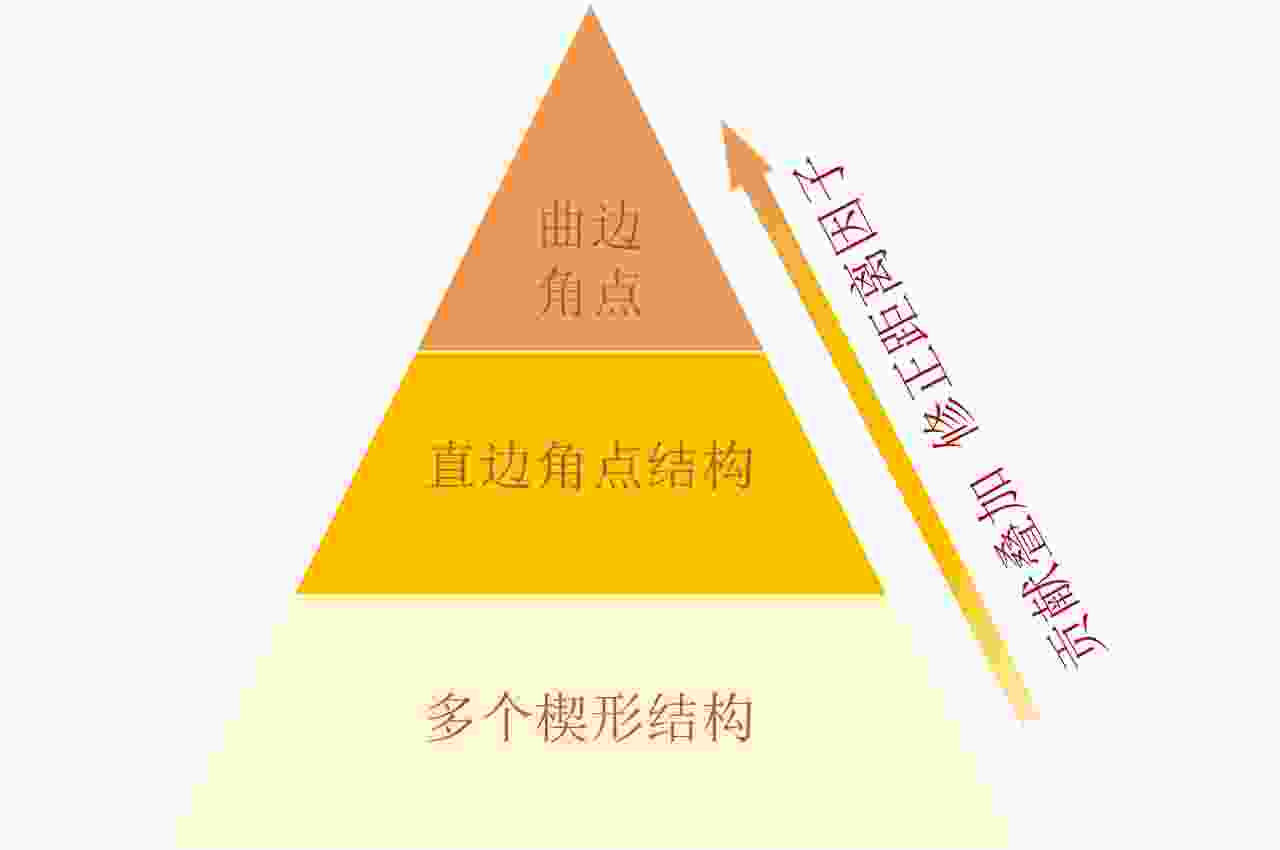
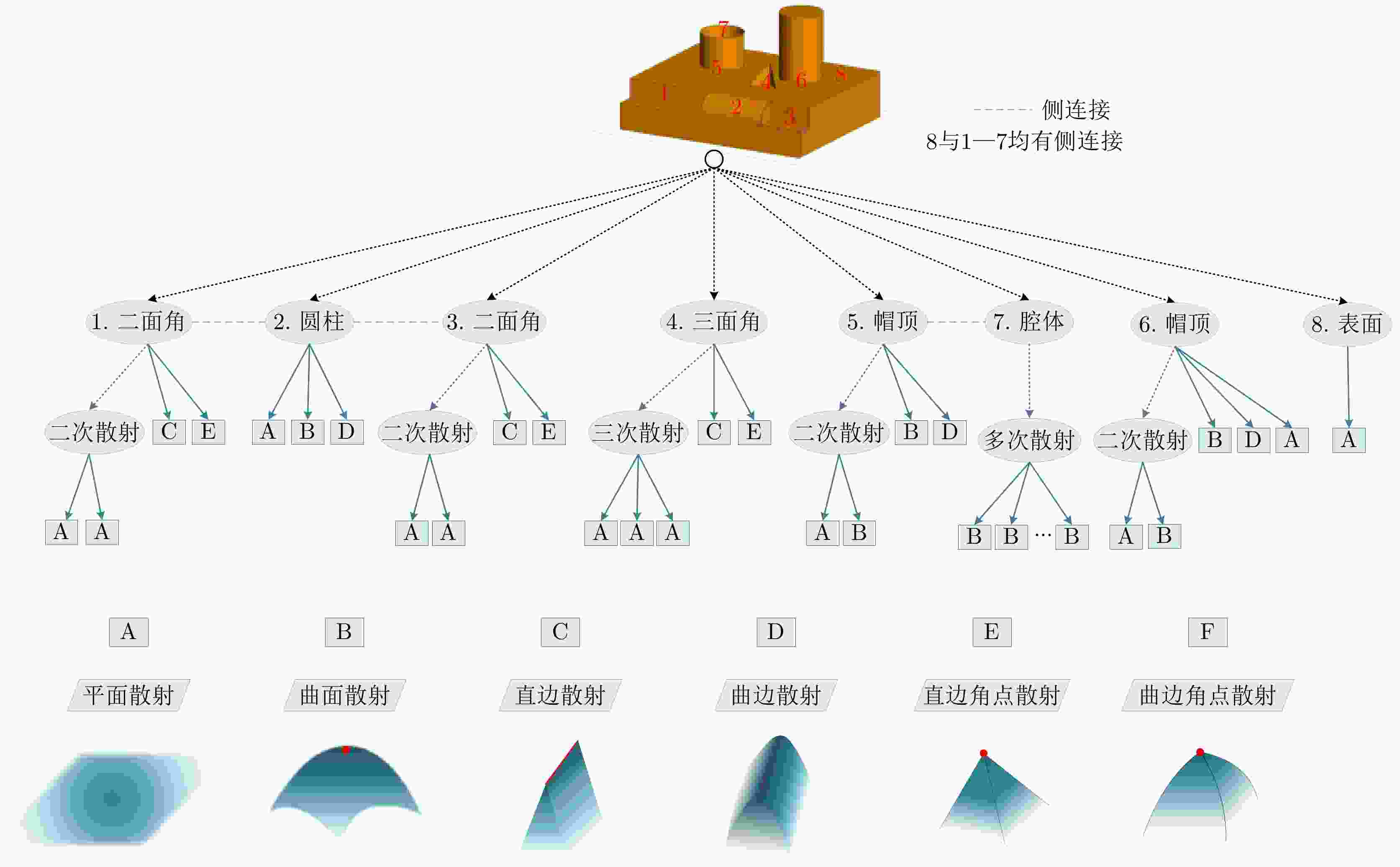
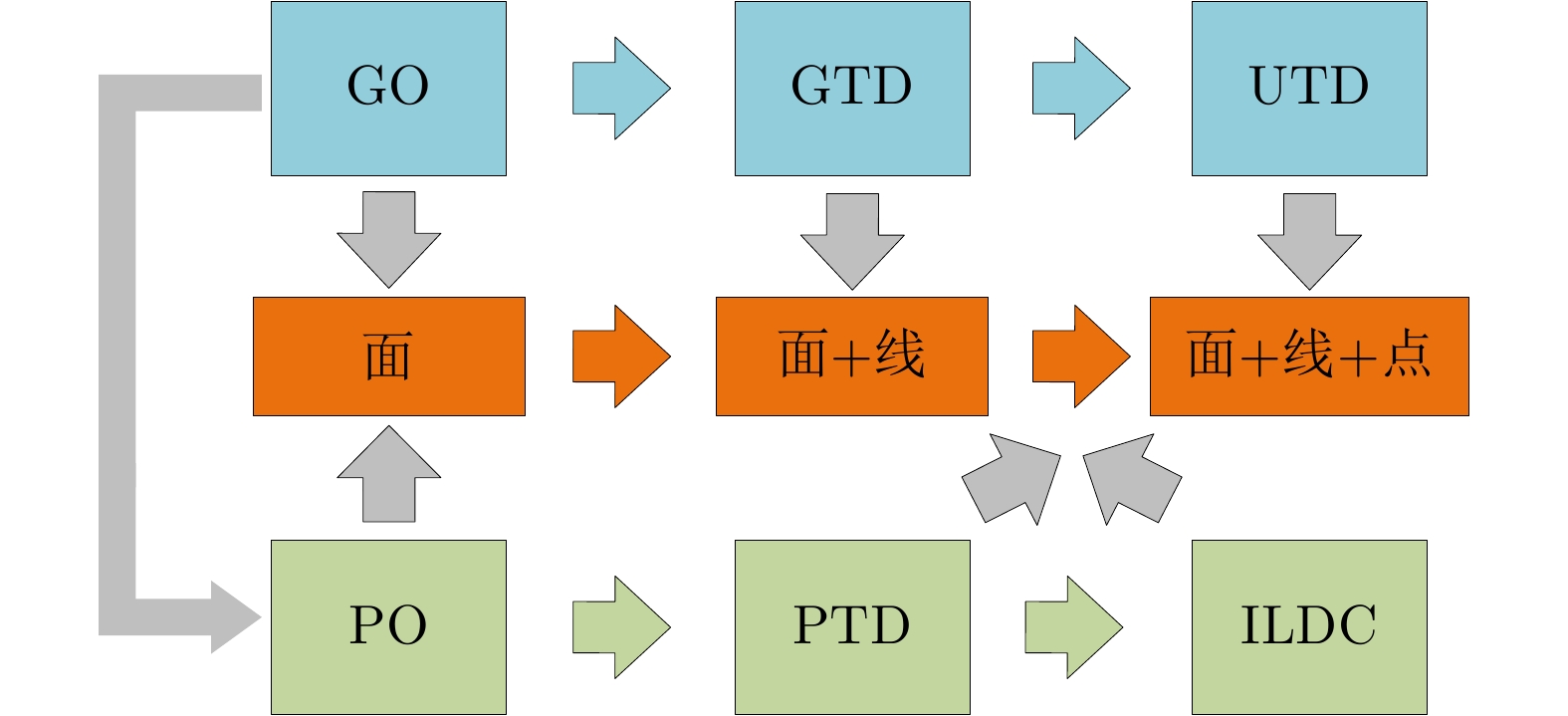
摘要: 高分辨率SAR图像中蕴含目标与环境丰富的信息,但复杂的电磁散射机制使其难以直观解译,这一直是SAR图像解译的重要研究课题。该文简单梳理了典型几何基元的高频散射建模方法,以面散射、线散射和点散射为线索简要回顾了若干高频散射机制的研究发展过程,并给出几种典型几何基元的散射机制表达式及部分仿真结果,分析了典型散射机制表征面临的难点及应用于SAR图像解译的关键科学问题,提出从几何基元出发,发展对应的散射基元,通过散射基元进行组合和相互作用以树状方式实现更完备和广泛的散射特征表征体系,最后讨论了面向SAR图像散射信息解译来构建散射机制字典的可行性。Abstract: High-resolution SAR images contain rich information about targets and their surroundings, but the complex electromagnetic scattering mechanism makes intuitive interpretation difficult, leading to an important research topic in SAR image interpretation. This paper summarizes the typical geometric primitives modeling method of high-frequency scattering, which is reviewed in detail with respect to surface, wedge, and vertex scatterings. Besides the classical expressions of these typical scattering mechanisms, some simulation results are presented. The difficulties in characterizing typical scattering mechanisms and key scientific problems applied to SAR image interpretation are analyzed. Furthermore, this paper proposes a complete and extensive scattering characteristic characterization system by combining and interacting with the scattering primitives based on the corresponding geometric primitives. Finally, the feasibility of developing a scattering mechanism dictionary for use in interpreting SAR image scattering information is discussed.
-
表 1 正六边形平板散射仿真参数表
Table 1. Scattering simulation parameters of regular hexagonal plate
参数 数值 参数 数值 频率(GHz) 1 角度间隔(°) 1 入射角(°) 0 观测距离 远场 出射角(°) –80°~80° 外切圆半径(m) 0.8485 表 2 椭球散射仿真参数表
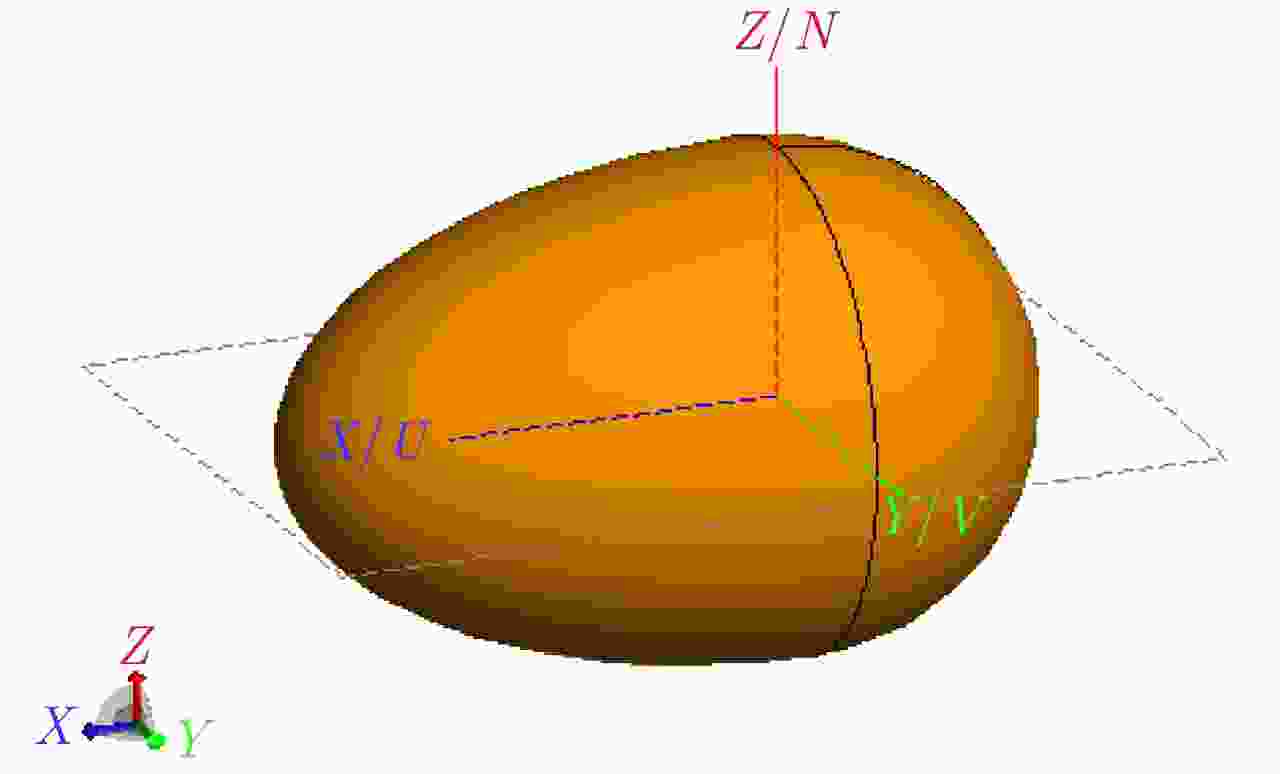
Table 2. Scattering simulation parameters of ellipsoid
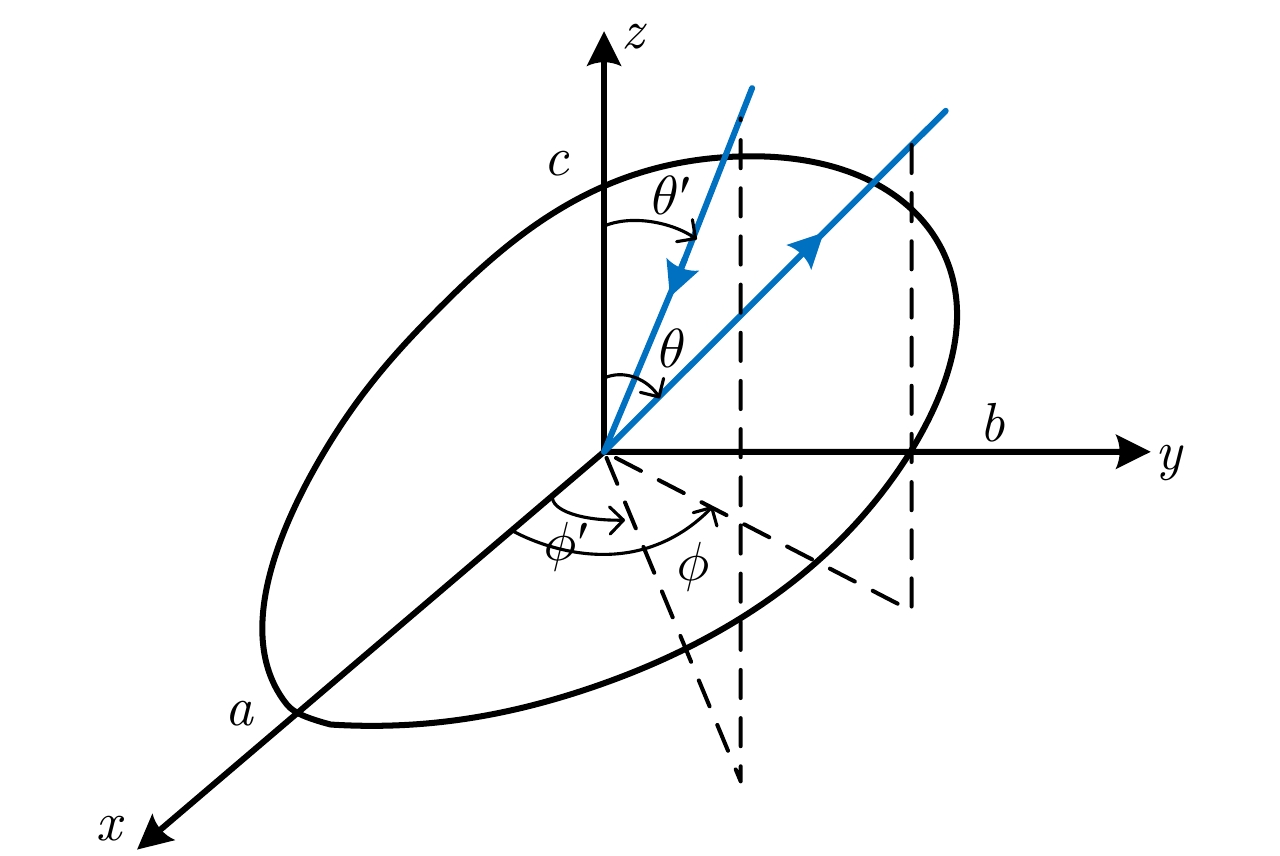
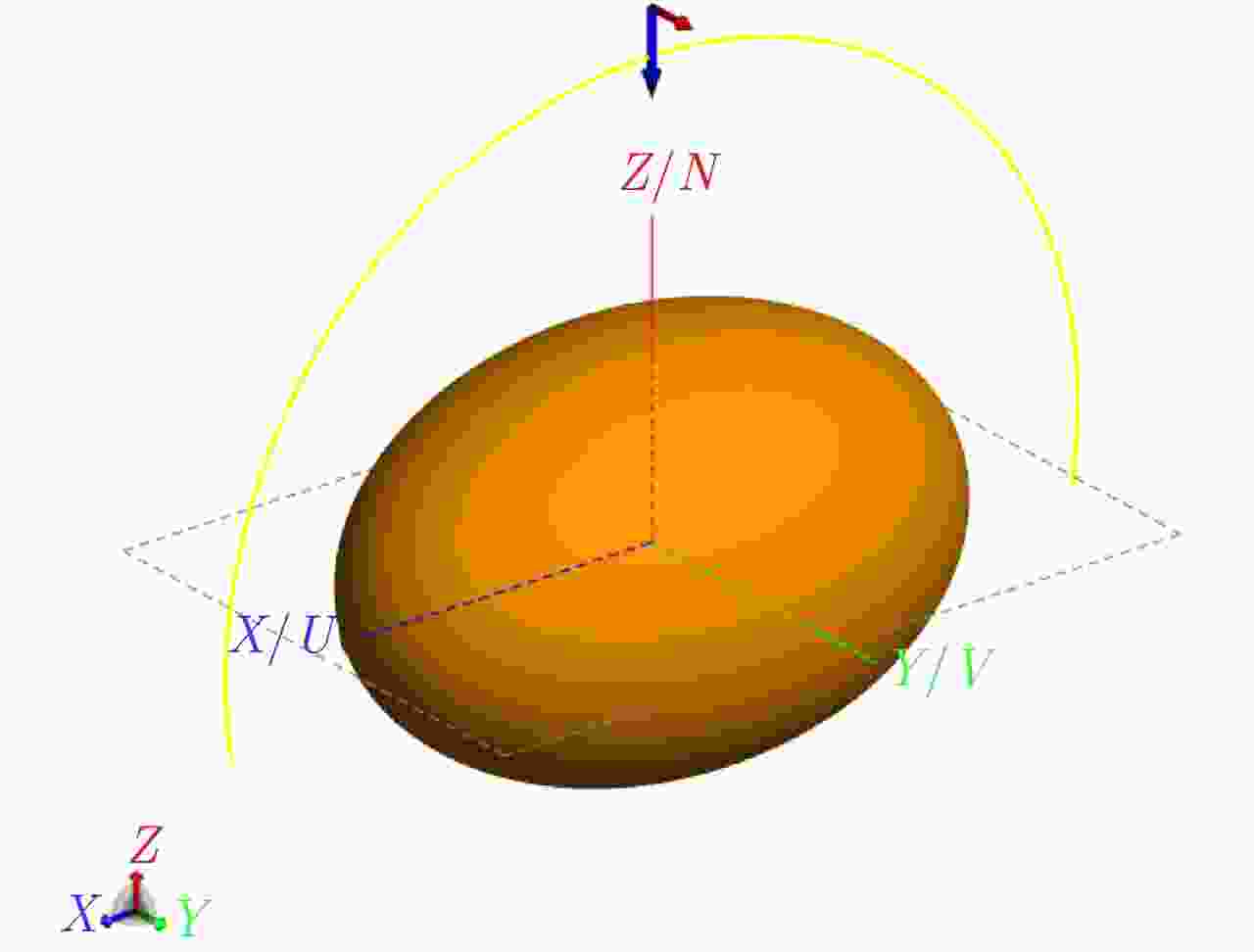
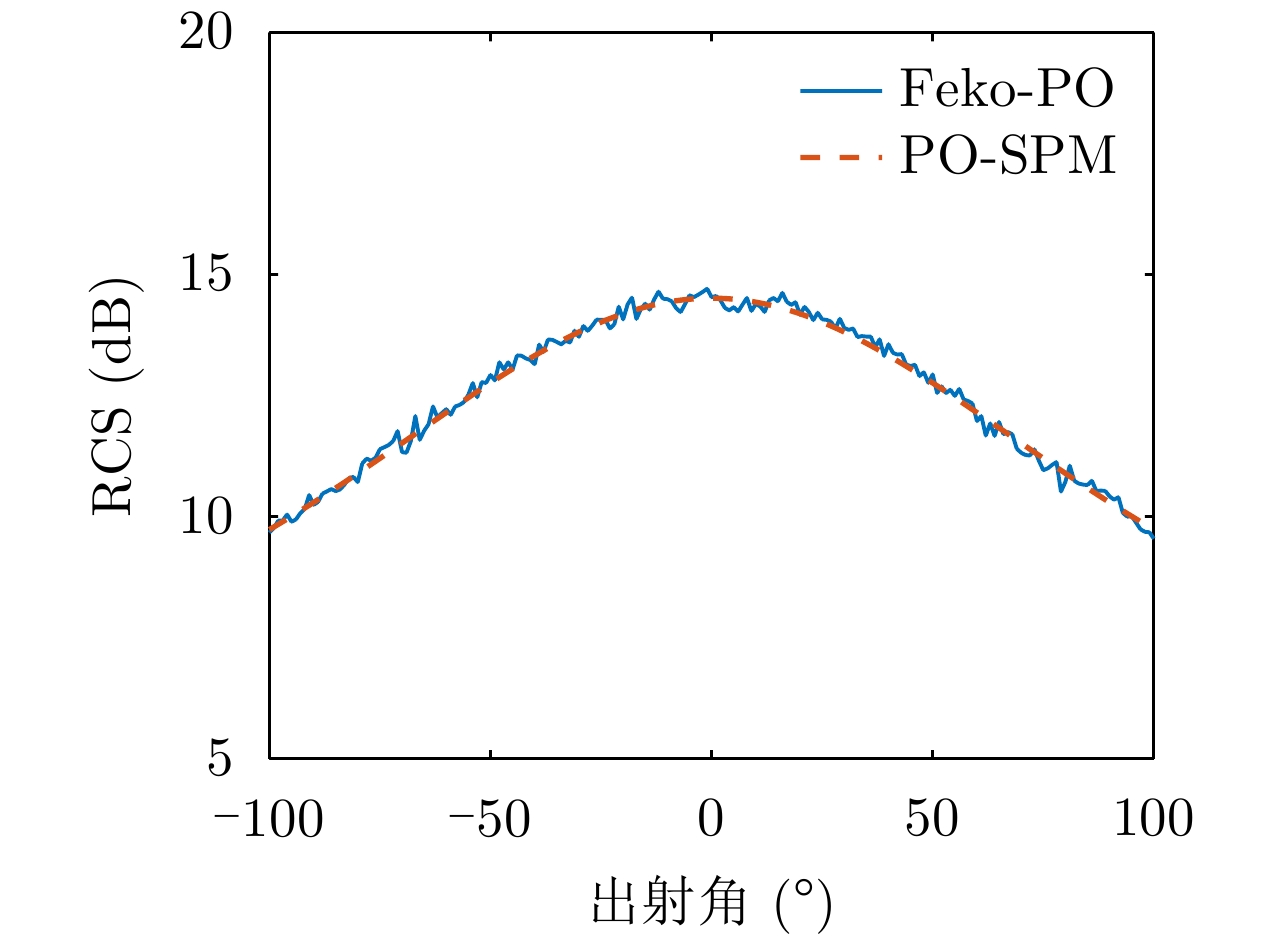
参数 数值 参数 数值 频率(GHz) 10 角度间隔(°) 1 入射角(°) 0 观测距离 远场 出射角(°) –100~100 半径(m) 3, 2, 2 表 3 球散射仿真参数表
Table 3. Scattering simulation parameters of sphere
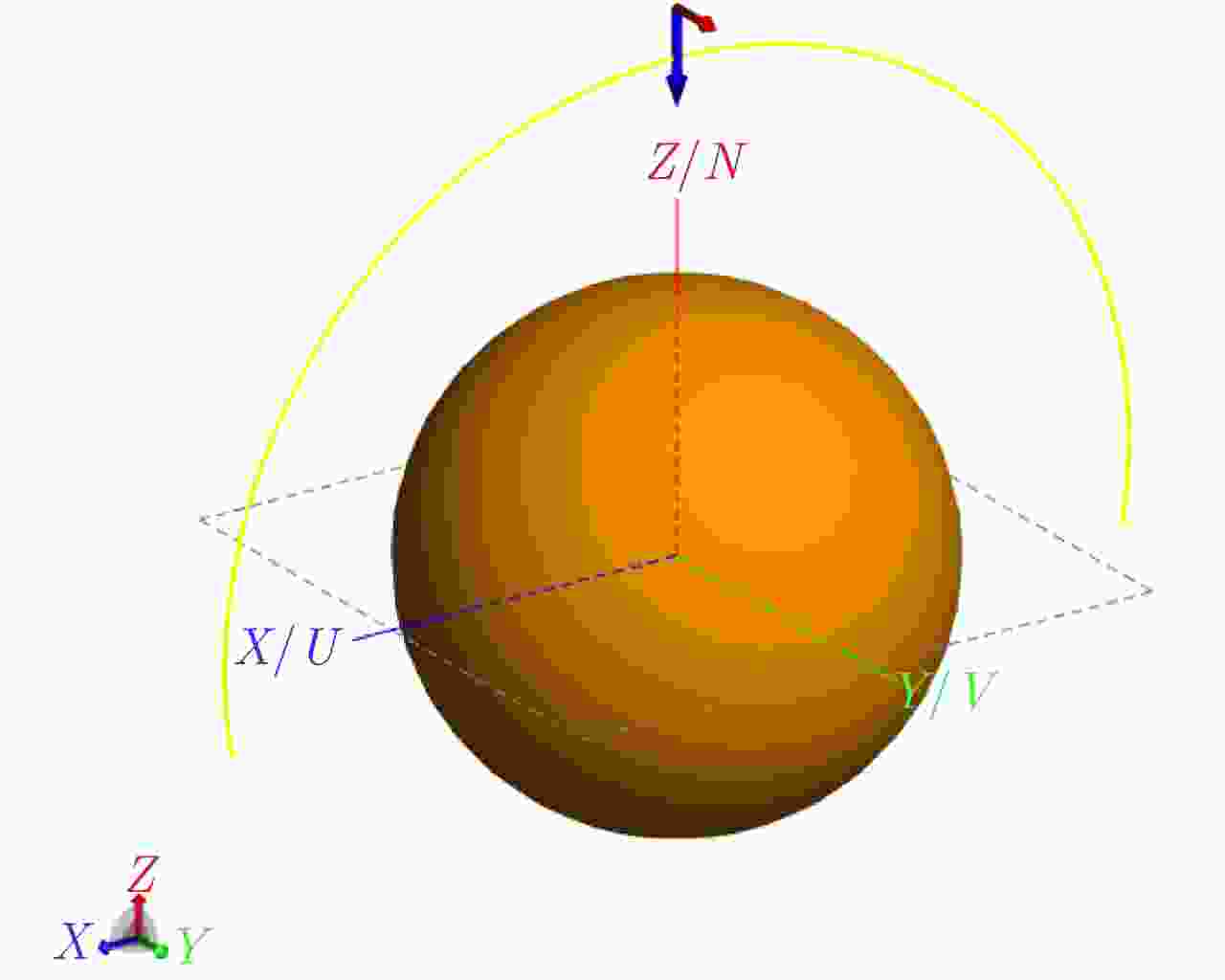
参数 数值 参数 数值 频率(GHz) 10 角度间隔(°) 1 入射角(°) 0 观测距离 远场 出射角(°) –100~100 半径(m) 3 表 4 组合曲面模型散射仿真参数表
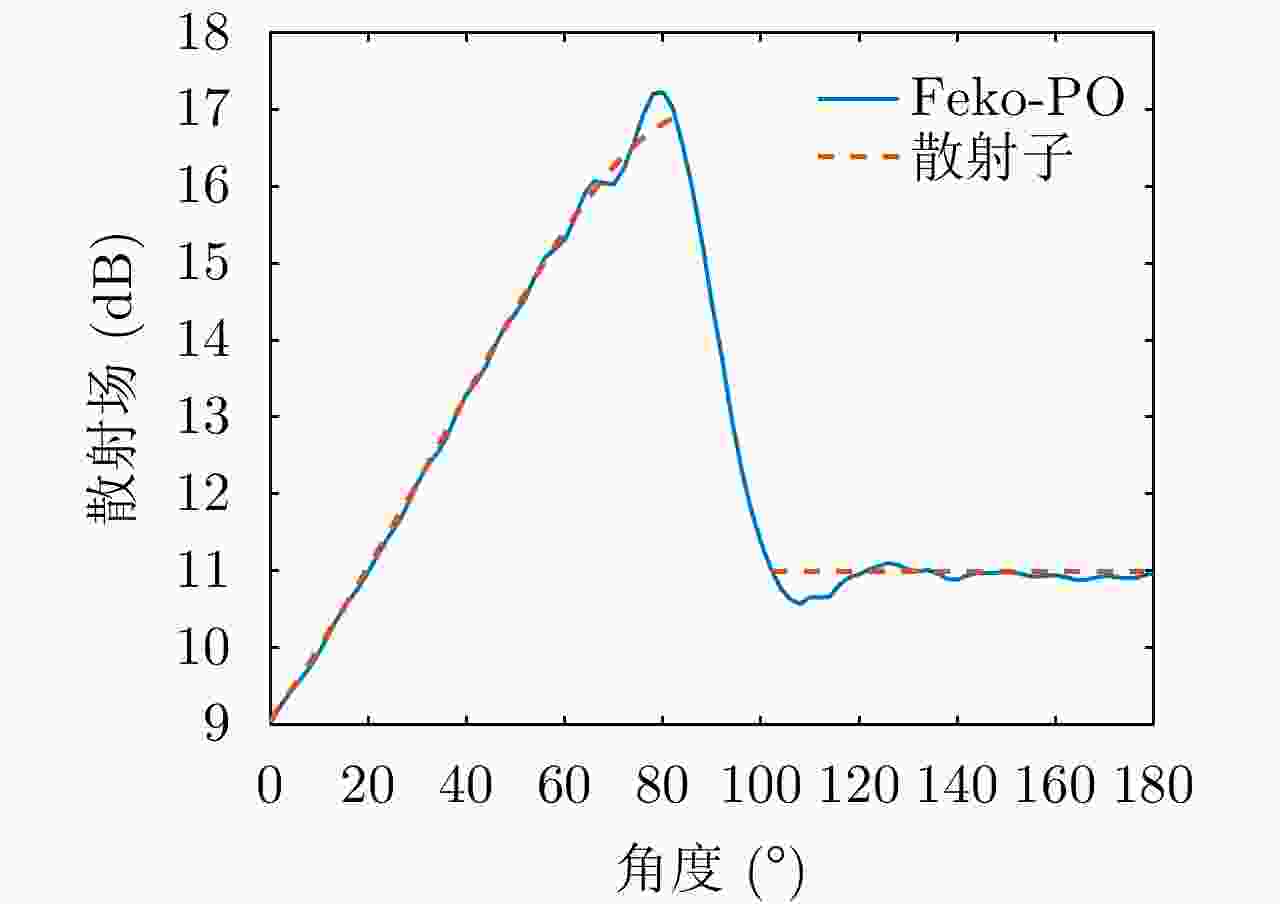
Table 4. Scattering simulation parameters of combined curve surface model
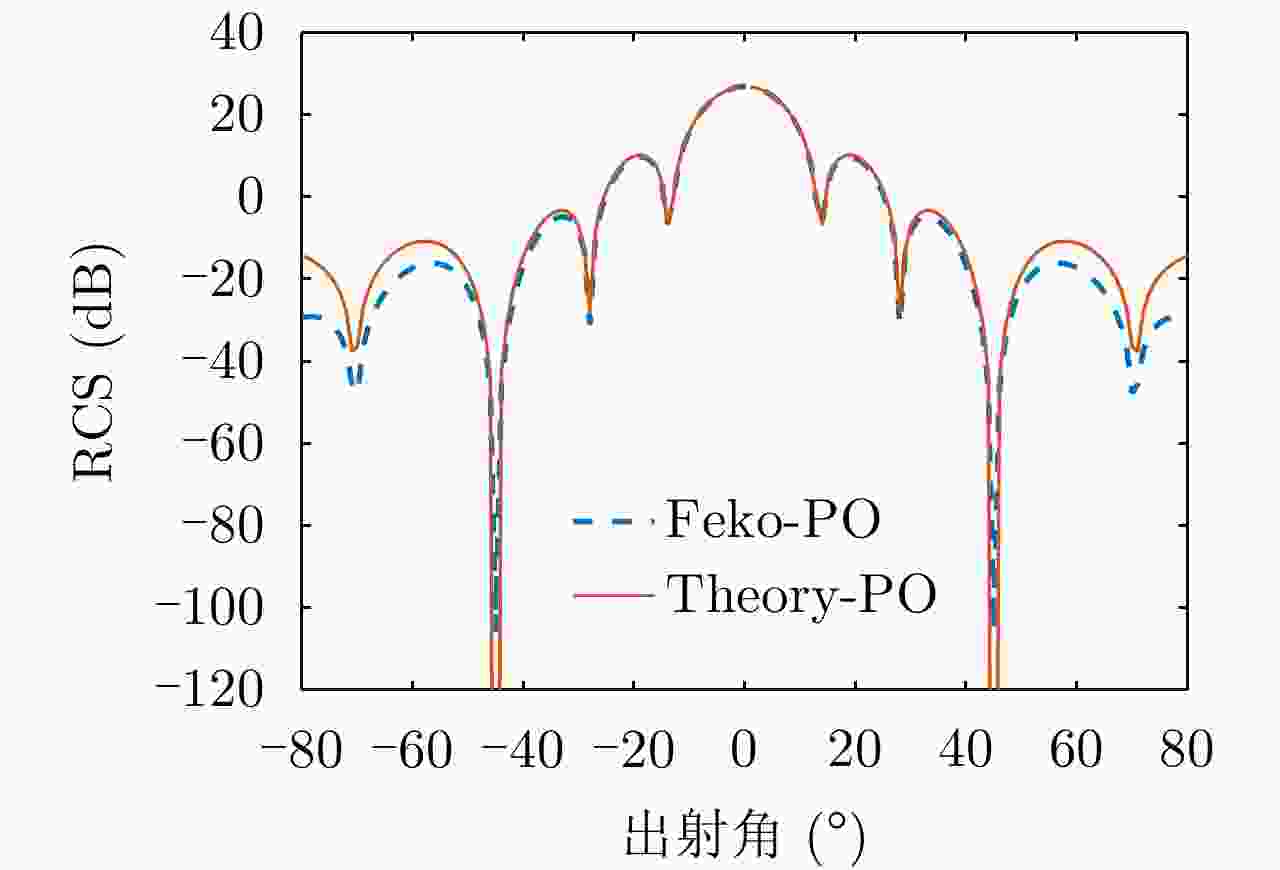
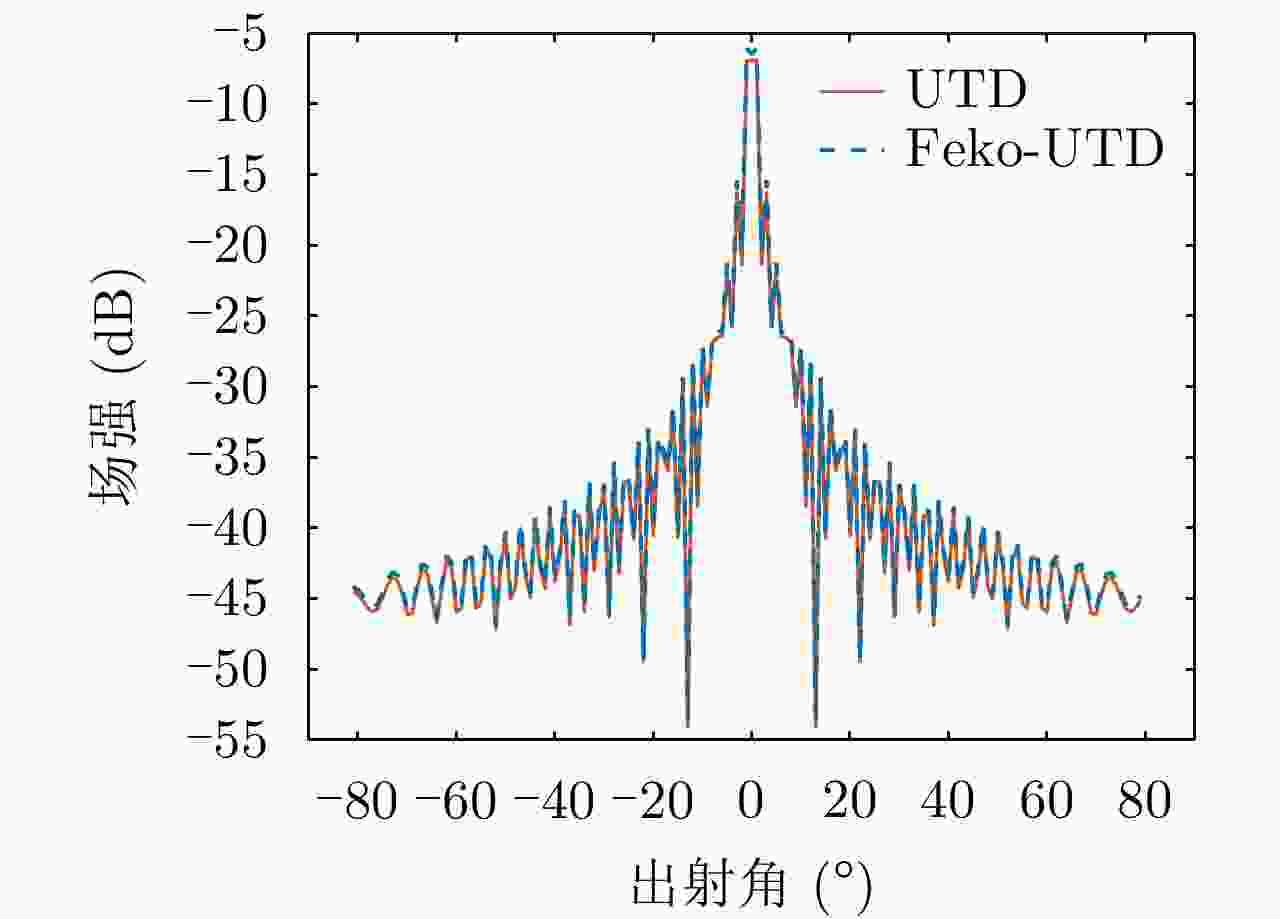
参数 数值 参数 数值 频率(GHz) 1 角度间隔(°) 2 入射角(°) 0 观测距离 远场 角度范围 0~180 表 5 平板散射仿真参数表
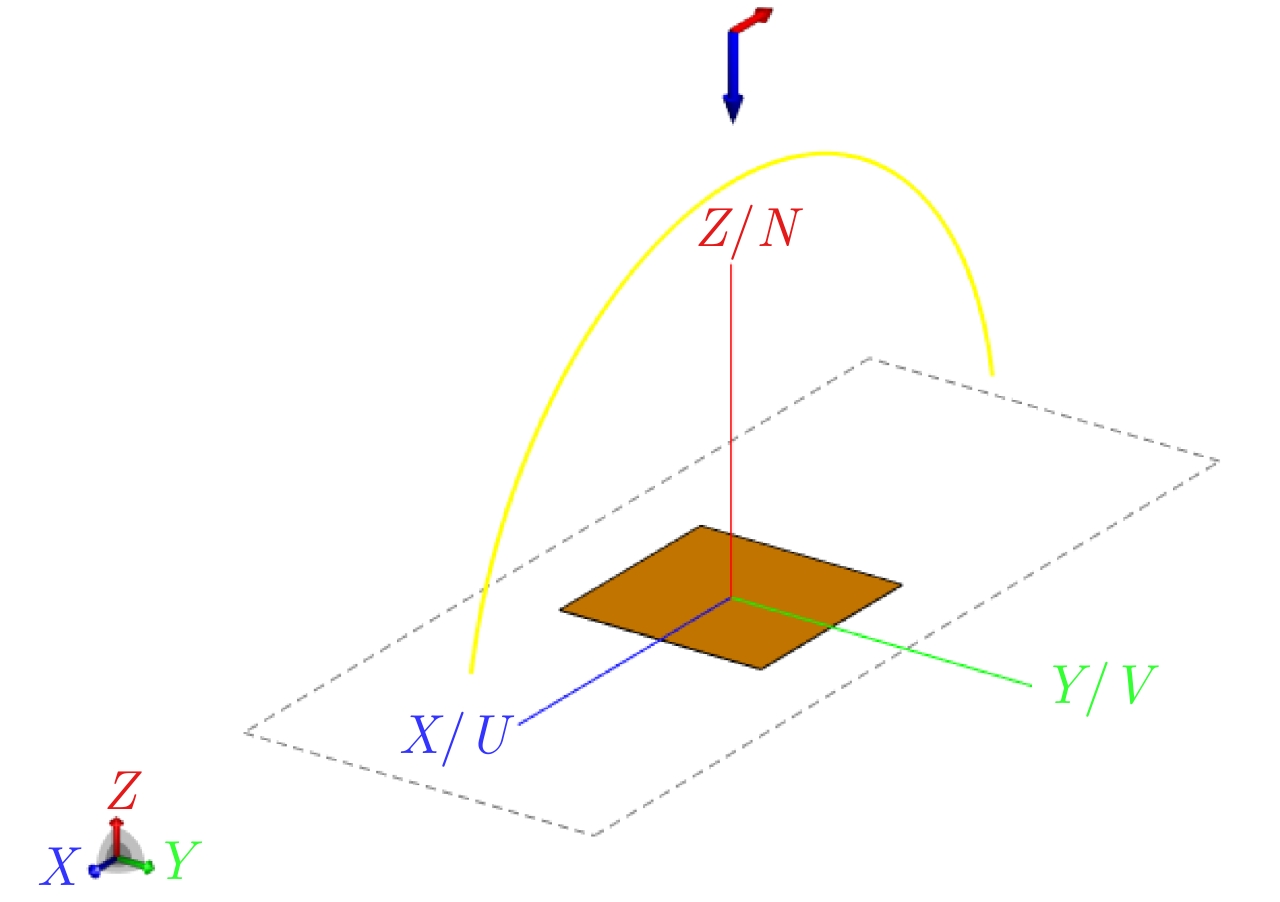
Table 5. Scattering simulation parameters of flat plane
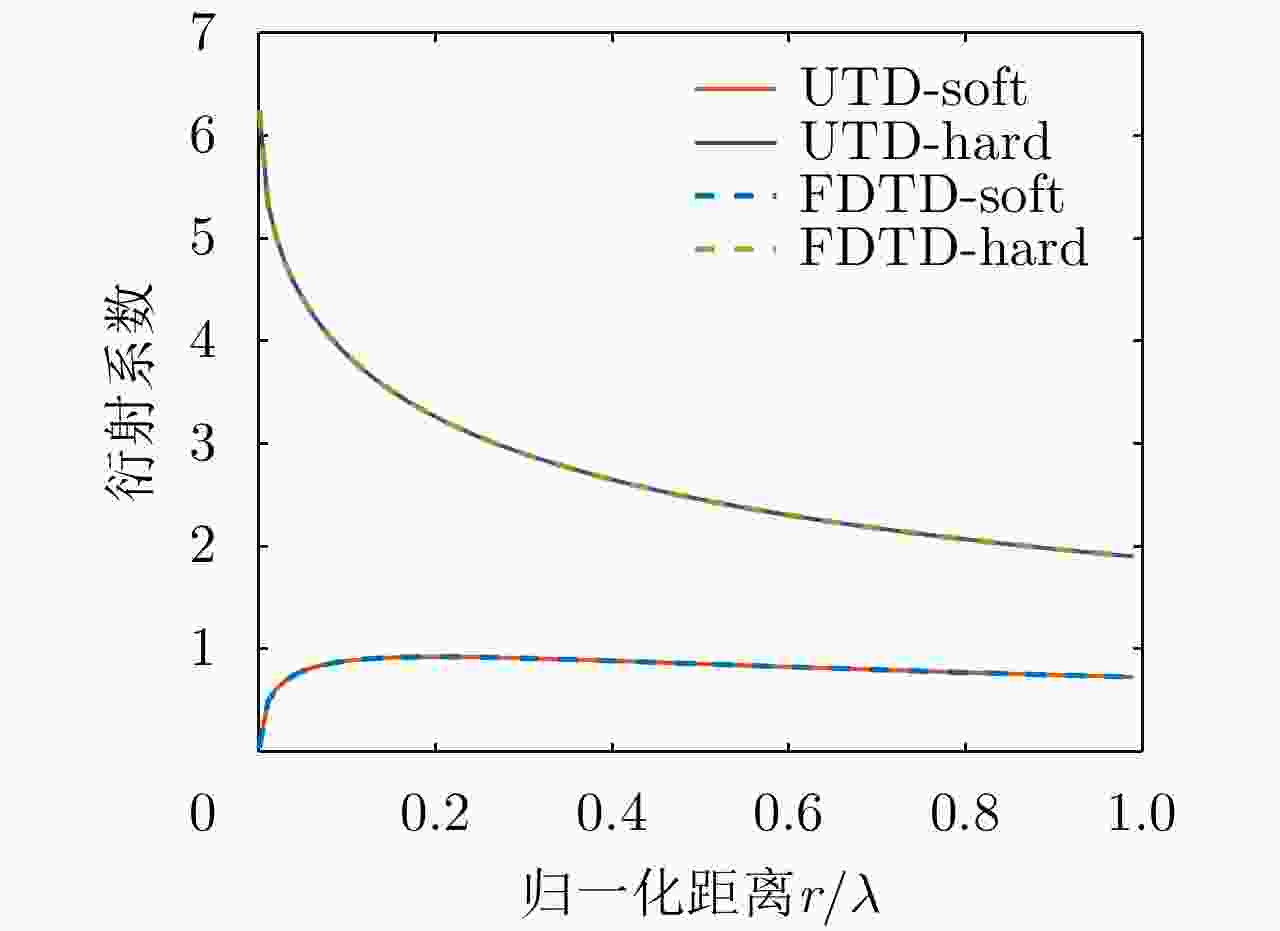
参数 数值 参数 数值 频率(GHz) 1 角度间隔(°) 1 入射角(°) 0 观测距离 300 出射角(°) –81~79 平板边长(m) 8 表 6 劈尖边散射仿真参数表
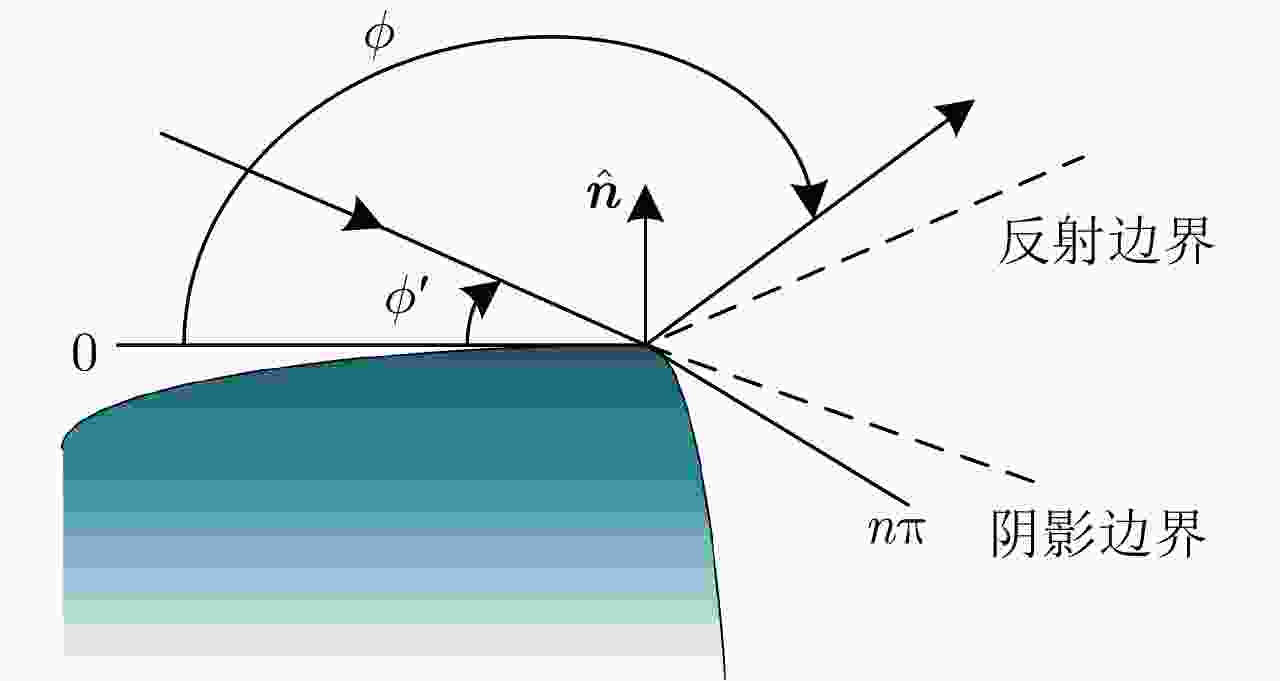
Table 6. Scattering simulation parameters of wedge
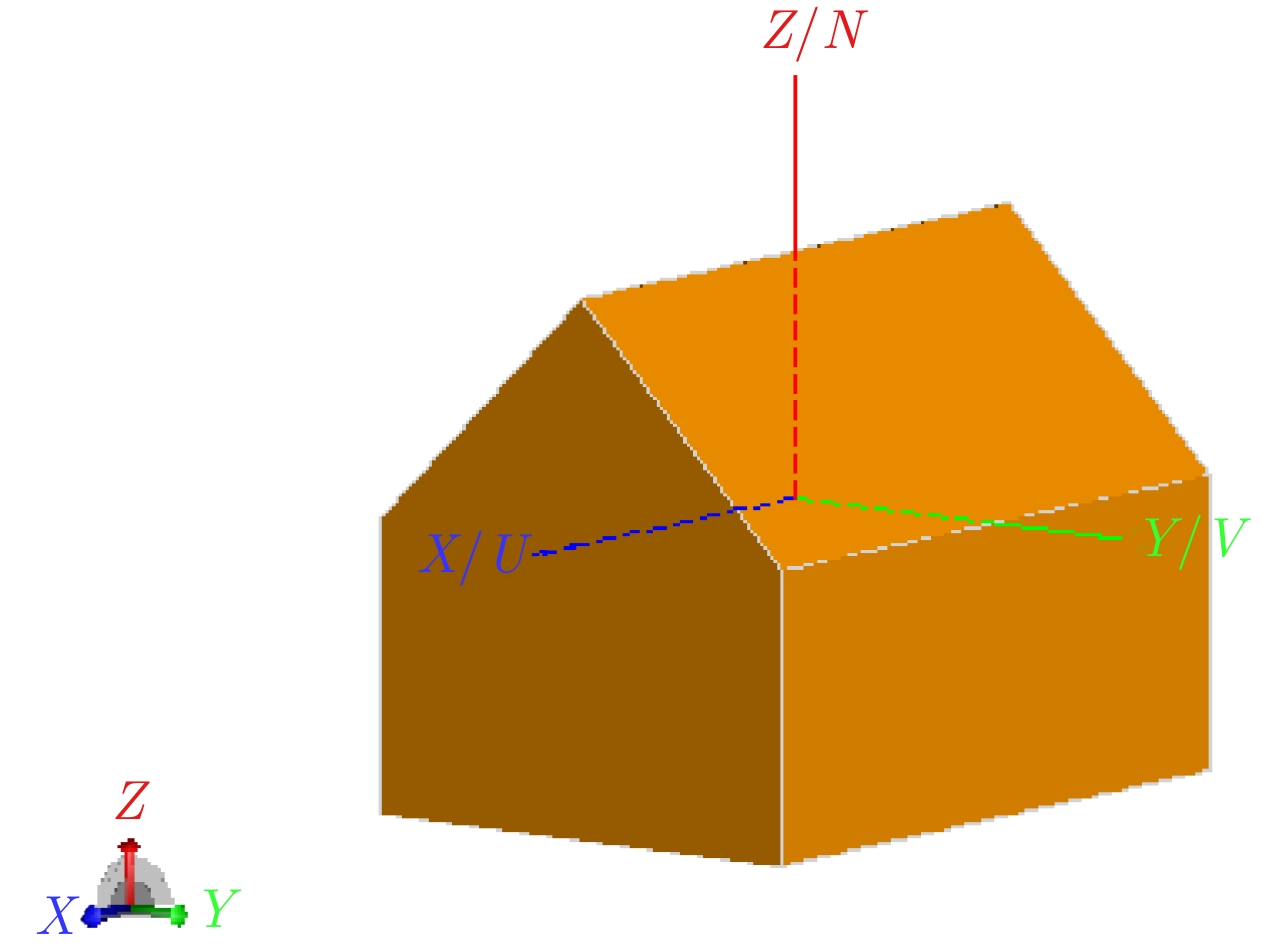
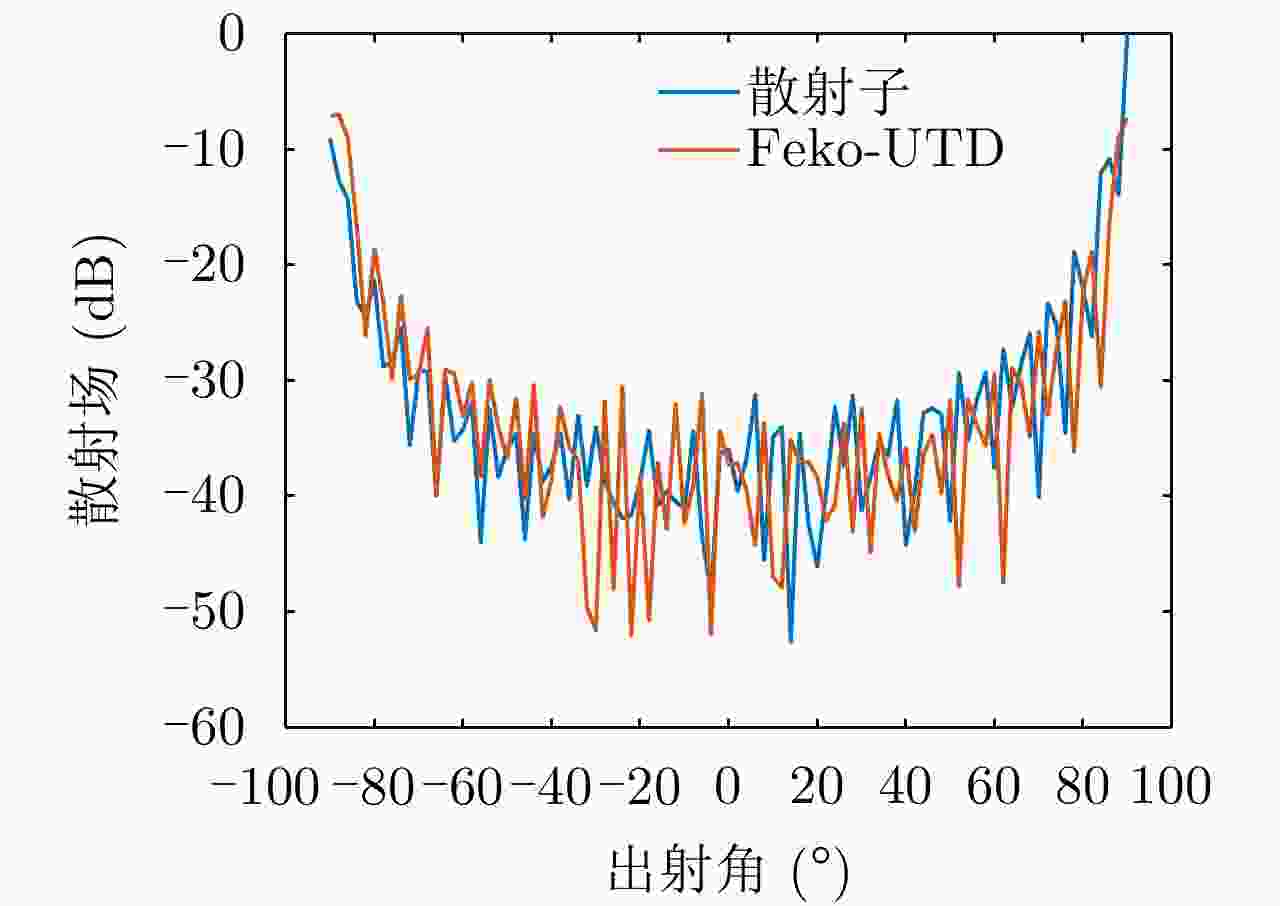
参数 数值 参数 数值 $ r/\lambda $ 0~1 $ n $ 0.6189 ${\phi }_{0}$ 45° $ {r}_{0} $ 212.15 m $\phi$ 90° $ r $ 50 m 表 7 房屋模型散射仿真参数表
Table 7. Scattering simulation parameters of house
参数 数值 参数 数值 频率(GHz) 1 角度间隔(°) 2 入射角(°) 1 观测距离 远场 角度范围(°) –90~90 -
[1] 丁赤飚, 仇晓兰, 徐丰, 等. 合成孔径雷达三维成像——从层析、阵列到微波视觉[J]. 雷达学报, 2019, 8(6): 693–709. doi: 10.12000/JR19090DING Chibiao, QIU Xiaolan, XU Feng, et al. Synthetic aperture radar three-dimensional imaging—from TomoSAR and array InSAR to microwave vision[J]. Journal of Radars, 2019, 8(6): 693–709. doi: 10.12000/JR19090 [2] COIFMAN R, ROKHLIN V, and WANDZURA S. The fast multipole method for electromagnetic scattering calculations[C]. IEEE Antennas and Propagation Society International Symposium, Ann Arbor, USA, 1993: 48–51. [3] HARRINGTON R F. Field Computation by Moment Method[M]. New York: MacMillan, 1968. [4] ZHAO Zihao and YE Hongxia. Sparse matrix canonical grid method for three-dimension rough surface[C]. 2018 International Conference on Microwave and Millimeter Wave Technology, Chengdu, China, 2018: 1–3. [5] FU W N, ZHAO Yanpu, HO S L, et al. An electromagnetic field and electric circuit coupled method for solid conductors in 3-D finite-element method[J]. IEEE Transactions on Magnetics, 2016, 52(3): 7401704. doi: 10.1109/TMAG.2015.2487362 [6] XU Feng and JIN Yaqiu. Bidirectional analytic ray tracing for fast computation of composite scattering from electric-large target over a randomly rough surface[J]. IEEE Transactions on Antennas and Propagation, 2009, 57(5): 1495–1505. doi: 10.1109/TAP.2009.2016691 [7] LOANE J and LEE S W. A geometrical optics approximation for refraction at a planar interface between arbitrarily lossy media[J]. Journal of Electromagnetic Waves and Applications, 1987, 1(4): 349–376. doi: 10.1163/156939387X00180 [8] ROEDDER J M. CADDSCAT version 2.3: A high-frequency physical optics code modified for trimmed IGES B-spline surfaces[J]. IEEE Antennas and Propagation Magazine, 1999, 41(3): 69–80. doi: 10.1109/74.775250 [9] UFIMTSEV P Y. Method of edge waves in the physical theory of diffraction[R]. FTD-HC-23-259-71, 1962. [10] KNOTT E. The relationship between Mitzner’s ILDC and Michaeli’s equivalent currents[J]. IEEE Transactions on Antennas and Propagation, 1985, 33(1): 112–114. doi: 10.1109/TAP.1985.1143482 [11] KELLER J B. Geometrical theory of diffraction[J]. Journal of the Optical Society of America, 1962, 52(2): 116–130. doi: 10.1364/josa.52.000116 [12] KOUYOUMJIAN R G and PATHAK P H. A uniform geometrical theory of diffraction for an edge in a perfectly conducting surface[J]. Proceedings of the IEEE, 1974, 62(11): 1448–1461. doi: 10.1109/PROC.1974.9651 [13] ALBANI M, CAPOLINO F, CARLUCCIO G, et al. UTD vertex diffraction coefficient for the scattering by perfectly conducting faceted structures[J]. IEEE Transactions on Antennas and Propagation, 2009, 57(12): 3911–3925. doi: 10.1109/TAP.2009.2027455 [14] ALBANI M, CARLUCCIO G, and PATHAK P H. A uniform geometrical theory of diffraction for vertices formed by truncated curved wedges[J]. IEEE Transactions on Antennas and Propagation, 2015, 63(7): 3136–3143. doi: 10.1109/TAP.2015.2427877 [15] JACKSON J A, RIGLING B D, and MOSES R L. Canonical scattering feature models for 3D and bistatic SAR[J]. IEEE Transactions on Aerospace and Electronic Systems, 2010, 46(2): 525–541. doi: 10.1109/TAES.2010.5461639 [16] POTTER L C and MOSES R L. Attributed scattering centers for SAR ATR[J]. IEEE Transactions on Image Processing, 1997, 6(1): 79–91. doi: 10.1109/83.552098 [17] GERRY M J, POTTER L C, GUPTA I J, et al. A parametric model for synthetic aperture radar measurements[J]. IEEE Transactions on Antennas and Propagation, 1999, 47(7): 1179–1188. doi: 10.1109/8.785750 [18] LI Jian, WU Renbiao, BI Zhaoqiang, et al. Robust semiparametric method for feature extraction and SAR image formation of targets consisting of trihedrals and dihedrals[C]. Proceedings of SPIE 3721, Algorithms for Synthetic Aperture Radar Imagery VI, Orlando, USA, 1999: 92–103. [19] AI Fazhi, ZHOU Jianxiong, HU Lei, et al. The parametric model of non-uniformly distributed scattering centers[C]. The IET International Conference on Radar Systems (Radar 2012), Glasgow, UK, 2012: 1–5. [20] 周剑雄. 光学区雷达目标三维散射中心重构理论与技术[D]. [博士论文], 国防科学技术大学, 2006.ZHOU Jianxiong. Theory and technology on reconstructing 3D scattering centers of radar targets in optical region[D]. [Ph. D. dissertation], National University of Defense Technology, 2006. [21] ZHOU Jianxiong, SHI Zhiguang, and FU Qiang. Three-dimensional scattering center extraction based on wide aperture data at a single elevation[J]. IEEE Transactions on Geoscience and Remote Sensing, 2015, 53(3): 1638–1655. doi: 10.1109/TGRS.2014.2346509 [22] HE Yang, HE Siyuan, ZHANG Yunhua, et al. A forward approach to establish parametric scattering center models for known complex radar targets applied to SAR ATR[J]. IEEE Transactions on Antennas and Propagation, 2014, 62(12): 6192–6205. doi: 10.1109/TAP.2014.2360700 [23] RICHARDS J A. Target model generation from multiple synthetic aperture radar images[D]. [Ph. D. dissertation], Massachusetts Institute of Technology, 1996. [24] RIGLING B D. Signal processing strategies for bistatic synthetic aperture radar[D]. [Ph. D. dissertation], The Ohio State University, 2003. [25] JACKSON J A and MOSES R L. An algorithm for 3D target scatterer feature estimation from sparse SAR apertures[C]. Proceedings of SPIE 7337, Algorithms for Synthetic Aperture Radar Imagery XVI, Orlando, USA, 2009: 1–12. [26] JACKSON J A. Three-dimensional feature models for synthetic aperture radar and experiments in feature extraction[D]. [Ph. D. dissertation], The Ohio State University, 2009. [27] 文贡坚, 朱国强, 殷红成, 等. 基于三维电磁散射参数化模型的SAR目标识别方法[J]. 雷达学报, 2017, 6(2): 115–135. doi: 10.12000/JR17034WEN Gongjian, ZHU Guoqiang, YIN Hongcheng, et al. SAR ATR based on 3D parametric electromagnetic scattering model[J]. Journal of Radars, 2017, 6(2): 115–135. doi: 10.12000/JR17034 [28] XING Xiaoyu, YAN Hua, YIN Hongcheng, et al. A bistatic attributed scattering center model for SAR ATR[J]. IEEE Transactions on Antennas and Propagation, 2021, 69(11): 7855–7866. doi: 10.1109/TAP.2021.3083817 [29] 文贡坚, 马聪慧, 丁柏圆, 等. 基于部件级三维参数化电磁模型的SAR目标物理可解释识别方法[J]. 雷达学报, 2020, 9(4): 608–621. doi: 10.12000/JR20099WEN Gongjian, MA Conghui, DING Baiyuan, et al. SAR target physics interpretable recognition method based on three dimensional parametric electromagnetic part model[J]. Journal of Radars, 2020, 9(4): 608–621. doi: 10.12000/JR20099 [30] PHAEBUA K, PHONGCHAROENPANICH C, and LERTWIRIYAPRAPA T. On an accuracy of the modified UTD solution for a convex impedance cylinder surface[C]. 2012 9th International Conference on Electrical Engineering/Electronics, Computer, Telecommunications and Information Technology, Phetchaburi, Thailand, 2012: 1–4. [31] 汪茂光. 几何绕射理论[M]. 2版. 西安: 西安电子科技大学出版社, 1994.WANG Maoguang. Geometrical Theory of Diffraction[M]. 2nd ed. Xi’an: Xidian University Press, 1994. [32] KLINE M. An asymptotic solution of Maxwell’s equations[J]. Communications on Pure and Applied Mathematics, 1951, 4(2/3): 225–262. doi: 10.1002/cpa.3160040203 [33] GORDON W. Far-field approximations to the Kirchoff-Helmholtz representations of scattered fields[J]. IEEE Transactions on Antennas and Propagation, 1975, 23(4): 590–592. doi: 10.1109/TAP.1975.1141105 [34] LUDWIG A. Computation of radiation patterns involving numerical double integration[J]. IEEE Transactions on Antennas and Propagation, 1968, 16(6): 767–769. doi: 10.1109/TAP.1968.1139296 [35] VICO-BONDIA F, FERRANDO-BATALLER M, and VALERO-NOGUEIRA A. A new fast physical optics for smooth surfaces by means of a numerical theory of diffraction[J]. IEEE Transactions on Antennas and Propagation, 2010, 58(3): 773–789. doi: 10.1109/TAP.2009.2039308 [36] ZHANG Jun, YU Wenming, ZHOU Xiaoyang, et al. Efficient evaluation of the physical-optics integrals for conducting surfaces using the uniform stationary phase method[J]. IEEE Transactions on Antennas and Propagation, 2012, 60(5): 2398–2408. doi: 10.1109/TAP.2012.2189737 [37] MOSCHOVITIS C G, KARAKATSELOS K T, PAPKELIS E G, et al. Scattering of electromagnetic waves from a rectangular plate using an enhanced stationary phase method approximation[J]. IEEE Transactions on Antennas and Propagation, 2010, 58(1): 233–238. doi: 10.1109/TAP.2009.2024015 [38] RUCK G T, BARRICK D E, STUART W D, et al. Radar Cross Section Handbook[M]. New York: Plenum Press, 1970. [39] CRISPIN J W JR and SIEGEL K M. Methods of Radar Cross-section Analysis[M]. New York: Academic Press, 1968. [40] BOWMAN J J, SENIOR T B A, and USLENGHI P L E. Electromagnetic and Acoustic Scattering by Simple Shapes[M]. New York: Hemisphere Publishing Corp. , 1987. [41] TROTT K D. Stationary phase derivation for RCS of an ellipsoid[J]. IEEE Antennas and Wireless Propagation Letters, 2007, 6: 240–243. doi: 10.1109/LAWP.2007.891521 [42] YUAN Haobo, WANG Nan, and LIANG Changhong. Combining the higher order method of moments with geometric modeling by NURBS surfaces[J]. IEEE Transactions on Antennas and Propagation, 2009, 57(11): 3558–3563. doi: 10.1109/TAP.2009.2023095 [43] HUANG Kai, HE Zhili, and LIANG Changhong. Efficient analysis of antenna around electrically large NURBS platform with accelerating MOM-PO method[J]. IEEE Antennas and Wireless Propagation Letters, 2010, 9: 134–137. doi: 10.1109/LAWP.2010.2044861 [44] GIOVAMPAOLA C D, CARLUCCIO G, PUGGELLI F, et al. Efficient algorithm for the evaluation of the physical optics scattering by NURBS surfaces with relatively general boundary condition[J]. IEEE Transactions on Antennas and Propagation, 2013, 61(8): 4194–4203. doi: 10.1109/TAP.2013.2261447 [45] TABOADA J M and OBELLEIRO F. Including multibounce effects in the moment-method physical-optics (MMPO) method[J]. Microwave and Optical Technology Letters, 2002, 32(6): 435–439. doi: 10.1002/mop.10202 [46] CONDE O M, PEREZ J, and CATEDRA M P. Stationary phase method application for the analysis of radiation of complex 3-D conducting structures[J]. IEEE Transactions on Antennas and Propagation, 2001, 49(5): 724–731. doi: 10.1109/8.929626 [47] ZHANG Yong and LIN Hai. MLFMA-PO hybrid technique for efficient analysis of electrically large structures[J]. IEEE Antennas and Wireless Propagation Letters, 2014, 13: 1676–1679. doi: 10.1109/LAWP.2014.2351422 [48] KELLER J. Diffraction of a convex cylinder[J]. IRE Transactions on Antennas and Propagation, 1956, 4(3): 312–321. doi: 10.1109/TAP.1956.1144427 [49] LEVY B R and KELLER J B. Diffraction by a smooth object[J]. Communications on Pure and Applied Mathematics, 1959, 12(1): 159–209. doi: 10.1002/cpa.3160120108 [50] PATHAK P, BURNSIDE W, and MARHEFKA R. A uniform GTD analysis of the diffraction of electromagnetic waves by a smooth convex surface[J]. IEEE Transactions on Antennas and Propagation, 1980, 28(5): 631–642. doi: 10.1109/TAP.1980.1142396 [51] ROUSSEAU P R. Time domain version of the uniform geometrical theory of diffraction[D]. [Ph. D. dissertation], The Ohio State University, 1995. [52] ROUSSEAU P R, PATHAK P H, and CHOU H T. A time domain formulation of the uniform geometrical theory of diffraction for scattering from a smooth convex surface[J]. IEEE Transactions on Antennas and Propagation, 2007, 55(6): 1522–1534. doi: 10.1109/TAP.2007.897204 [53] PATHAK P H. Techniques for High-frequency Problems[M]. LO Y T and LEE S W. Antenna Handbook: Theory, Applications, and Design. Boston: Springer, 1988: 195–311. [54] CHOU H T, PATHAK P H, and ROUSSEAU P R. TD-UTD solutions for the transient radiation and surface fields of pulsed antennas placed on PEC smooth convex surfaces[J]. IEEE Transactions on Antennas and Propagation, 2011, 59(5): 1626–1637. doi: 10.1109/TAP.2011.2122235 [55] KIM H T and WANG Nan. UTD solution for electromagnetic scattering by a circular cylinder with thin lossy coatings[J]. IEEE Transactions on Antennas and Propagation, 1989, 37(11): 1463–1472. doi: 10.1109/8.43566 [56] HUSSAR P E. A uniform GTD treatment of surface diffraction by impedance and coated cylinders[J]. IEEE Transactions on Antennas and Propagation, 1998, 46(7): 998–1008. doi: 10.1109/8.704801 [57] TOKGOZ C and MARHEFKA R J. A UTD based asymptotic solution for the surface magnetic field on a source excited circular cylinder with an impedance boundary condition[J]. IEEE Transactions on Antennas and Propagation, 2006, 54(6): 1750–1757. doi: 10.1109/TAP.2006.875490 [58] PAULI W. On asymptotic series for functions in the theory of diffraction of light[J]. Physical Review Journals Archive, 1938, 54(11): 924–931. doi: 10.1103/PhysRev.54.924 [59] BURNSIDE W and BURGENER K. High frequency scattering by a thin lossless dielectric slab[J]. IEEE Transactions on Antennas and Propagation, 1983, 31(1): 104–110. doi: 10.1109/TAP.1983.1143019 [60] HUTCHINS D L and KOUYOUMJIAN R G. Asymptomatic series describing the diffraction of a plane wave by a wedge[J]. ElectroScience Laboratory Department of Electrical Engineering, Ohio State University, Columbus, 1969. [61] PATHAK P H and KOUYOUMJIAN R G. The dyadic diffraction coefficient for a perfectly-conducting wedge[R]. DTIC Document, 1970. [62] AHLUWALIA D S, LEWIS R M, and BOERSMA J. Uniform asymptotic theory of diffraction by a plane screen[J]. SIAM Journal on Applied Mathematics, 1968, 16(4): 783–807. doi: 10.1137/0116065 [63] LEWIS R M and BOERSMA J. Uniform asymptotic theory of edge diffraction[J]. Journal of Mathematical Physics, 1969, 10(12): 2291–2305. doi: 10.1063/1.1664835 [64] AHLUWALIA D S. Uniform asymptotic theory of diffraction by the edge of a three-dimensional body[J]. SIAM Journal on Applied Mathematics, 1970, 18(2): 287–301. doi: 10.1137/0118024 [65] MEIXNER J. The behavior of electromagnetic fields at edges[J]. IEEE Transactions on Antennas and Propagation, 1972, 20(4): 442–446. doi: 10.1109/TAP.1972.1140243 [66] LUEBBERS R. Finite conductivity uniform GTD versus knife edge diffraction in prediction of propagation path loss[J]. IEEE Transactions on Antennas and Propagation, 1984, 32(1): 70–76. doi: 10.1109/TAP.1984.1143189 [67] CAKIR G, SEVGI L, and UFIMTSEV P Y. FDTD modeling of electromagnetic wave scattering from a wedge with perfectly reflecting boundaries: Comparisons against analytical models and calibration[J]. IEEE Transactions on Antennas and Propagation, 2012, 60(7): 3336–3342. doi: 10.1109/TAP.2012.2196948 [68] ALBANI M, CAPOLINO F, MACI S, et al. Diffraction at a thick screen including corrugations on the top face[J]. IEEE Transactions on Antennas and Propagation, 1997, 45(2): 277–283. doi: 10.1109/8.560346 [69] CAPOLINO F, ALBANI I M, MACI S, et al. Double diffraction at a pair of coplanar skew edges[J]. IEEE Transactions on Antennas and Propagation, 1997, 45(8): 1219–1226. doi: 10.1109/8.611240 [70] ALBANI M, PIAZZESI P, CAPOLINO F, et al. Shielding effect of a thick screen with corrugations[J]. IEEE Transactions on Electromagnetic Compatibility, 1998, 40(3): 235–239. doi: 10.1109/15.709421 [71] ALBANI M. A uniform double diffraction coefficient for a pair of wedges in arbitrary configuration[J]. IEEE Transactions on Antennas and Propagation, 2005, 53(2): 702–710. doi: 10.1109/TAP.2004.841289 [72] KRAUS L and LEVINE L M. Diffraction by an elliptic cone[J]. Communications on Pure and Applied Mathematics, 1961, 14(1): 49–68. doi: 10.1002/cpa.3160140104 [73] SATTERWHITE R. Diffraction by a quarter plane, the exact solution, and some numerical results[J]. IEEE Transactions on Antennas and Propagation, 1974, 22(3): 500–503. doi: 10.1109/TAP.1974.1140803 [74] SAHALOS J and THIELE G. The eigenfunction solution for scattered fields and surface currents of a vertex[J]. IEEE Transactions on Antennas and Propagation, 1983, 31(1): 206–211. doi: 10.1109/TAP.1983.1142987 [75] HANSEN T B. Diffraction by a plane angular sector, a new derivation[J]. IEEE Transactions on Antennas and Propagation, 1990, 38(11): 1892–1894. doi: 10.1109/8.102757 [76] BLUME S. Spherical-multipole analysis of electromagnetic and acoustical scattering by a semi-infinite elliptic cone[J]. IEEE Antennas and Propagation Magazine, 1996, 38(2): 33–44. doi: 10.1109/74.500230 [77] BLUME S and KREBS V. Numerical evaluation of dyadic diffraction coefficients and bistatic radar cross sections for a perfectly conducting semi-infinite elliptic cone[J]. IEEE Transactions on Antennas and Propagation, 1998, 46(3): 414–424. doi: 10.1109/8.662661 [78] KLINKENBUSCH L. Electromagnetic scattering by semi-infinite circular and elliptic cones[J]. Radio Science, 2007, 42(6): RS6S10. doi: 10.1029/2007RS003649 [79] RADLOW J. Diffraction by a quarter-plane[J]. Archive for Rational Mechanics and Analysis, 1961, 8(1): 139–158. doi: 10.1007/BF00277435 [80] RADLOW J. Note on the defraction at a corner[J]. Archive for Rational Mechanics and Analysis, 1965, 19(1): 62–70. doi: 10.1007/BF00252278 [81] ALBERTSEN N C. Diffraction by a quarterplane of the field from a halfwave dipole[J]. IEE Proceedings-Microwaves, Antennas and Propagation, 1997, 144(3): 191–196. doi: 10.1049/ip-map:19971151 [82] ALBANI M. On Radlow’s quarter-plane diffraction solution[J]. Radio Science, 2007, 42(6): RS6S11. doi: 10.1029/2006RS003528 [83] SIKTA F, BURNSIDE W, CHU T T, et al. First-order equivalent current and corner diffraction scattering from flat plate structures[J]. IEEE Transactions on Antennas and Propagation, 1983, 31(4): 584–589. doi: 10.1109/TAP.1983.1143116 [84] HILL K C. A UTD solution to the EM-scattering by the vertex of a perfectly conducting plane angular sector[D]. [Ph. D. dissertation], The Ohio State University, 1990. [85] HILL K C and PATHAK P H. A UTD solution for the EM diffraction by a corner in a plane angular sector[C]. The Antennas and Propagation Society Symposium 1991 Digest, London, Canada, 1991: 2–5. [86] HANSEN T B. Corner diffraction coefficients for the quarter plane[J]. IEEE Transactions on Antennas and Propagation, 1991, 39(7): 976–984. doi: 10.1109/8.86918 [87] MACI S, TIBERIO R, and TOCCAFONDI A. Diffraction at a plane angular sector[J]. Journal of Electromagnetic Waves and Applications, 1994, 8(9/10): 1247–1276. doi: 10.1163/156939394X01028 [88] CAPOLINO F and MACI S. Uniform high-frequency description of singly, doubly, and vertex diffracted rays for a plane angular sector[J]. Journal of Electromagnetic Waves and Applications, 1996, 10(9): 1175–1197. doi: 10.1163/156939396X00658 [89] MACI S, ALBANI M, and CAPOLINO F. ITD formulation for the currents on a plane angular sector[J]. IEEE Transactions on Antennas and Propagation, 1998, 46(9): 1318–1327. doi: 10.1109/8.719975 [90] MICHAELI A. Comments on "First-order equivalent current and corner diffraction scattering from flat plate structures"[J]. IEEE Transactions on Antennas and Propagation, 1984, 32(9): 1011–1012. doi: 10.1109/TAP.1984.1143436 [91] JONES D S. A uniform asymptotic expansion for a certain double integral[J]. Proceedings of the Royal Society of Edinburgh Section A:Mathematics, 1971, 69(3): 205–226. doi: 10.1017/S0080454100008694 [92] CLEMMOW P C and SENIOR T B A. A note on a generalized Fresnel integral[J]. Mathematical Proceedings of the Cambridge Philosophical Society, 1953, 49(3): 570–572. doi: 10.1017/S0305004100028723 [93] CAPOLINO F and MACI S. Simplified closed-form expressions for computing the generalized fresnel integral and their application to vertex diffraction[J]. Microwave and Optical Technology Letters, 1995, 9(1): 32–37. doi: 10.1002/mop.4650090113 [94] MACI S, TIBERIO R, and TOCCAFONDI A. Incremental diffraction coefficients for source and observation at finite distances from an edge[J]. IEEE Transactions on Antennas and Propagation, 1996, 44(5): 593. doi: 10.1109/8.496244 [95] SMYSHLYAEV V P. The high-frequency diffraction of electromagnetic waves by cones of arbitrary cross sections[J]. SIAM Journal on Applied Mathematics, 1993, 53(3): 670–688. doi: 10.1137/0153034 [96] BABICH V M, SMYSHLYAEV V P, DEMENT’EV D B, et al. Numerical calculation of the diffraction coefficients for an arbitrary shaped perfectly conducting cone[J]. IEEE Transactions on Antennas and Propagation, 1996, 44(5): 740. doi: 10.1109/8.496260 [97] ALBANI M, CARLUCCIO G, and PATHAK P H. Uniform ray description for the PO scattering by vertices in curved surface with curvilinear edges and relatively general boundary conditions[J]. IEEE Transactions on Antennas and Propagation, 2011, 59(5): 1587–1596. doi: 10.1109/TAP.2011.2123062 [98] SI Zhangzhang and ZHU Songchun. Learning AND-OR templates for object recognition and detection[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2013, 35(9): 2189–2205. doi: 10.1109/TPAMI.2013.35 -



 作者中心
作者中心 专家审稿
专家审稿 责编办公
责编办公 编辑办公
编辑办公
 下载:
下载: