Fast Tensor-based Three-dimensional Sparse Bayesian Learning Space-Time Adaptive Processing Method
-
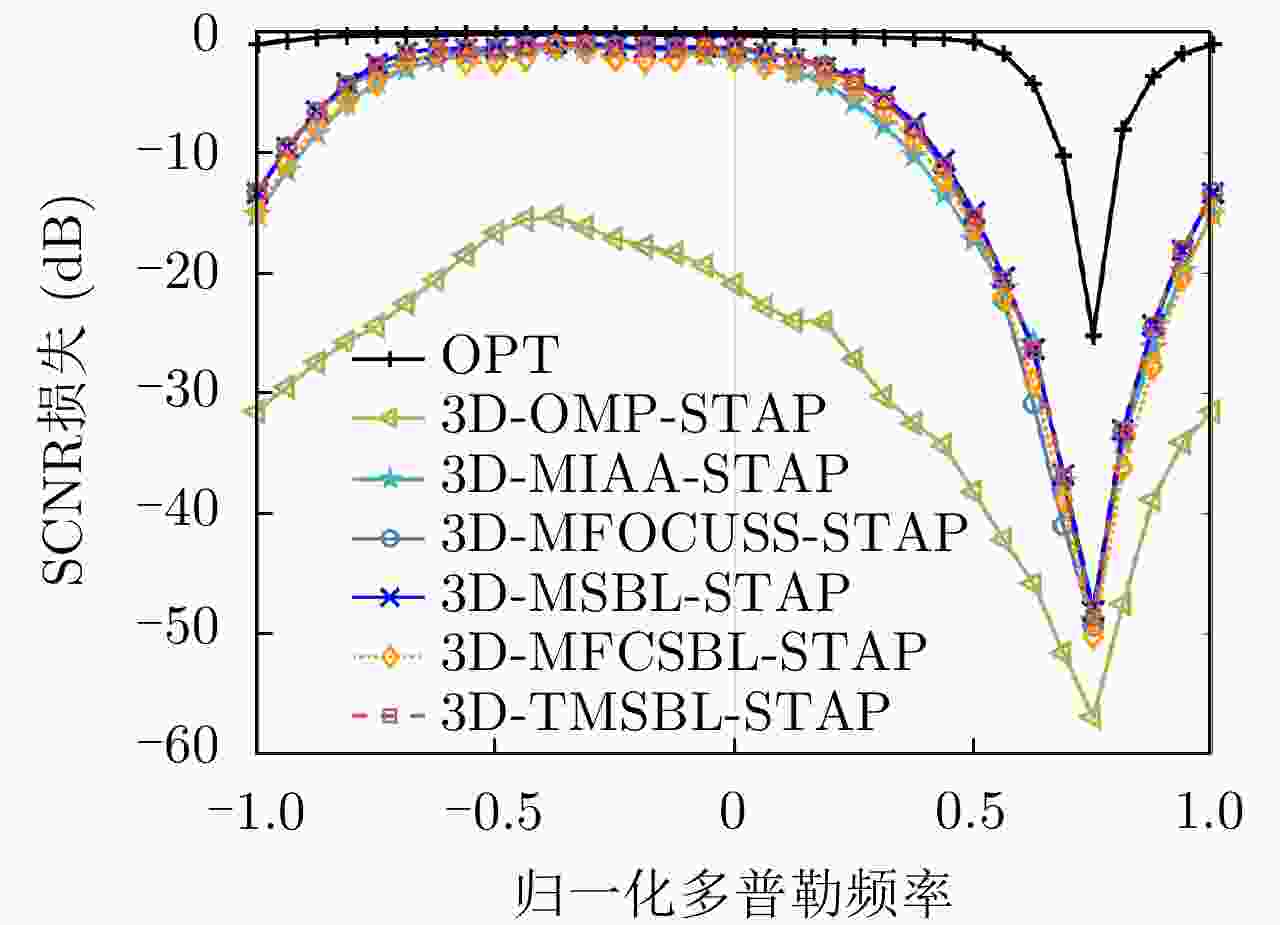
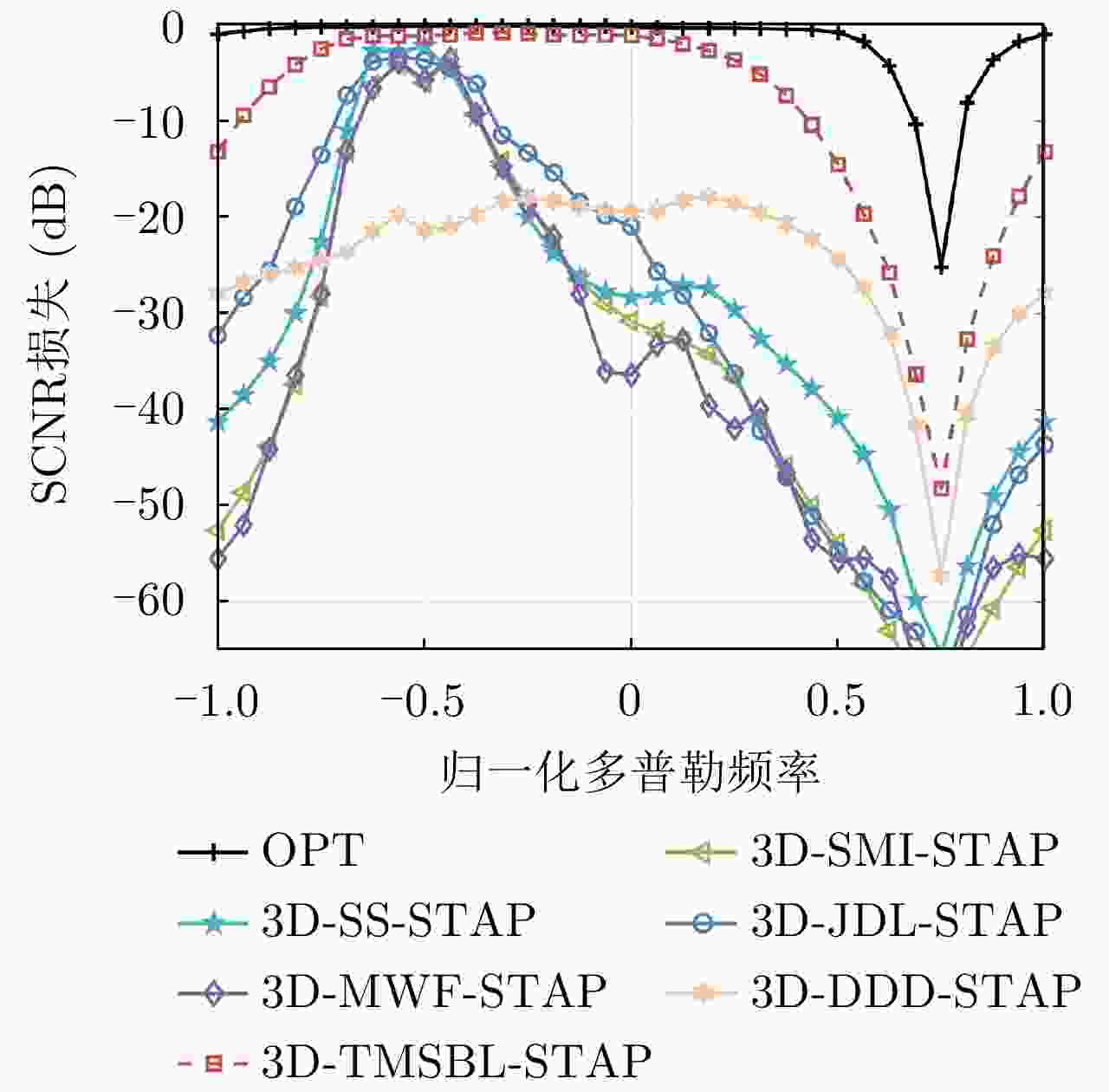
摘要: 当机载雷达处于非正侧视工作模式时,非平稳杂波会对运动目标检测造成严重干扰。传统三维空时自适应处理(3D-STAP)方法通过构造俯仰-方位-多普勒三维自适应滤波器,可有效抑制非平稳杂波,然而巨大的系统自由度导致其在非均匀杂波环境下训练样本严重不足。虽然稀疏恢复(SR)技术可有效改善样本需求,但庞大的运算开销又使得该技术难以应用于实际。针对上述问题,该文结合机载雷达回3阶张量结构提出一种新的快速三维稀疏贝叶斯学习STAP方法,通过采用运算开销更低的张量处理将大规模矩阵求解拆分为多个小规模矩阵计算,从而大幅降低运算复杂度。详尽的数值实验验证了所提张量基SR-STAP方法可在维持SR-STAP小样本处理性能不变的基础上,将运行时间直接降低数个量级,因此是一种更适用于实际工程的SR-STAP处理方式。Abstract: When airborne radar is applied to the non-side-looking mode, moving target detection performance considerably degrades because of the nonstationary clutter. Conventional three-dimensional (3D) Space-Time Adaptive Processing (STAP) can effectively eliminate the nonstationary clutter via adaptively constructing an elevation-azimuth-Doppler 3D filter. However, large system degrees of freedom lead to a shortage of training samples in a heterogeneous environment. Although introducing the Sparse Recovery (SR) technology substantially reduces the sample requirement, the practical application of this technology is limited by computational complexities. To solve the above problems, this paper proposes a fast 3D sparse Bayesian learning STAP, based on the third-order tensor structure of echo data. In the proposed method, large-scale matrix calculation is decomposed into small-scale matrix calculation using a low-complexity tensor-based operation, thus considerably reducing the computational load. Exhaustive numerical experiments verify that the proposed method directly reduces the computational load by several orders of magnitude compared with that of the existing SR-STAP algorithms, while maintaining the SR-STAP performance. Therefore, the tensor-based method is a superior processing method than the vector-based method in engineering.
-
表 1 TMSBL算法
Table 1. TMSBL algorithm
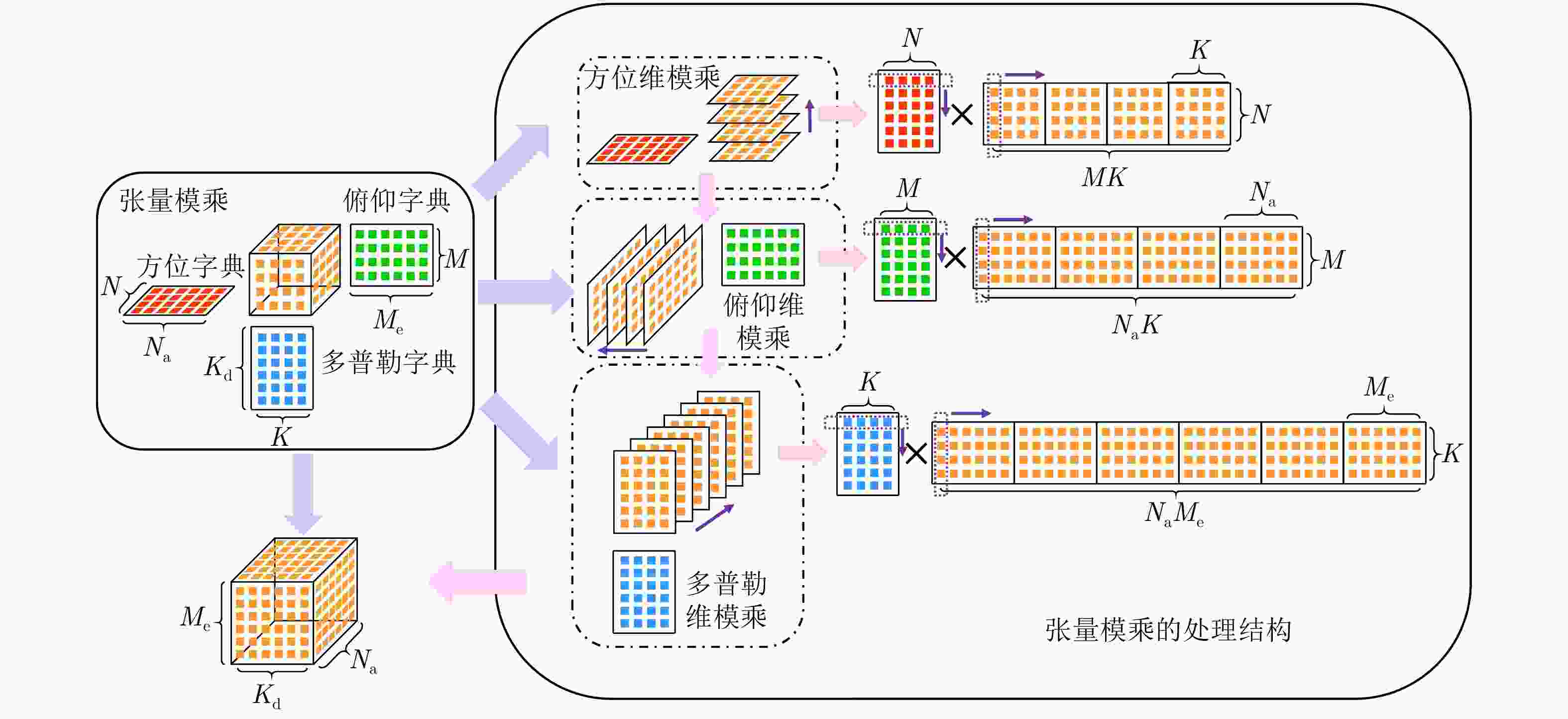
输入:方位字典${{\boldsymbol{S}}_{\rm{a}}}$,俯仰字典${{\boldsymbol{S}}_{\rm{e}}}$,多普勒字典${{\boldsymbol{S}}_{\rm{d}}}$,训练样本集合${\boldsymbol{X}}$。 输出:稀疏系数${\boldsymbol{\varXi}}$ 初始化:过完备字典${\boldsymbol{S}} = {{\boldsymbol{S}}_{\rm{e}}} \otimes {{\boldsymbol{S}}_{\rm{a}}} \otimes {{\boldsymbol{S}}_{\rm{d}}}$,稀疏控制系数
${{\boldsymbol{\gamma}} _0} = {{\boldsymbol{e}}_{ {N_{\rm{a} } }{M_{\rm{e} } }{K_{\rm{d} } } } }$,均值${Y_0} = 1$,噪声方差$\sigma _0^2$,最大迭代
次数${i_{\max} }$,收敛阈值$\mu $。1:对于 $i = 1:{i_{\max} }$执行 2: 对于$j = 1:{N_{\rm{a}}}{M_{\rm{e}}}{K_{\rm{d}}}$执行 3: 计算方位索引${ {\rm{loc} }_{\rm{a}}}$,俯仰索引${{\rm{loc}}_{\rm{e}}}$和多普勒索引${{\rm{loc}}_{\rm{d}}}$ 4: ${\mathcal{T}_{:,:,:,j} } = $
${\mathcal{F}_{N,M,K} }\left\{ { {\mathcal{V}_{NK} }\left\{ { {\gamma _j}{\boldsymbol{S} }_{:,{ {\rm{loc} }_{\rm{d} } } }^{\rm{d} }{ {\left( { {\boldsymbol{S} }_{:,{ {\rm{loc} }_{\rm{a} } } }^{\rm{a} } } \right)}^{\rm{T} } } } \right\}{ {\left( { {\boldsymbol{S} }_{:,{ {\rm{loc} }_{\rm{e} } } }^{\rm{e} } } \right)}^{\rm{T} } } } \right\}$5: 结束循环 6: ${\boldsymbol{C} } = {\mathcal{M}_{NMK,NMK} }\left\{ {\mathcal{T}{ \times _2}{\boldsymbol{S} }_{\rm{d} }^{\rm{H} }{ \times _3}{\boldsymbol{S} }_{\rm{a} }^{\rm{H} }{ \times _4}{\boldsymbol{S} }_{\rm{e} }^{\rm{H} } } \right\} + {\sigma ^2}{\boldsymbol{I}}$ 7: ${\boldsymbol{Y}} = {\mathcal{M}_{ {N_{\rm{a}}}{M_{\rm{e}}}{K_{\rm{d}}},NMK} } $
$\cdot\left\{ {\mathcal{D} \odot \left( { {\mathcal{C}^{ - 1} }{ \times _1}{\boldsymbol{S} }_{\rm{d} }^{\rm{H} }{ \times _2}{\boldsymbol{S} }_{\rm{a} }^{\rm{H} }{ \times _3}{\boldsymbol{S} }_{\rm{e} }^{\rm{H} } } \right)} \right\}{\boldsymbol{X} }$8: 对于$j = 1:{N_{\rm{a}}}{M_{\rm{e}}}{K_{\rm{d}}}$执行 9: ${\varSigma _{j,j} } = {\gamma _j} - { {\boldsymbol{Q} }_{j,:} }{ {\boldsymbol{T} }_{:,j} }$ 10: ${\gamma _{j + 1} } = \dfrac{1}{L}\left\| { { {\boldsymbol{Y} }_{j,:} } } \right\|_2^2 + {\varSigma _{j,j} }$ 11: ${D_j} = \dfrac{ { {\varSigma _{j,j} } } }{ { {\gamma _j} } }$ 12: 结束循环
13: ${\sigma ^2} = \dfrac{1}{ {NMKL} }\left\| {{\boldsymbol{X}} - {\boldsymbol{SY}}} \right\|_{\rm{F} }^2$
$+ \dfrac{ {\sigma _{i - 1}^2} }{ {NMK} }\mathop \sum \limits_{j = 1}^{ {N_{\rm{a} } }{M_{\rm{e} } }{K_{\rm{d} } } } \left( {1 - {D_j} } \right) $14: 如果 $\left\| {{\boldsymbol{Y}} - {{\boldsymbol{Y}}_{i - 1} } } \right\|_{\rm{F} }^2/\left\| {\boldsymbol{Y}} \right\|_{\rm{F} }^2 \le \mu$ 跳出循环 15:结束循环 表 2 计算复杂度
Table 2. Computational complexity
方法 复乘法次数 计算复杂度 OMP $\left( {NMK{N_{\rm a}}{M_{\rm e}}{K_{\rm d}} + r_{\rm s}^3 + NMKr_{\rm s}^2 + 2NMK{r_{\rm s}}} \right)L{K_{\rm OMP}}$ $O\left( {NMK{N_{\rm a}}{M_{\rm e}}{K_{\rm d}}L{K_{\rm OMP}}} \right)$ MIAA $\left( {2{N_{\rm a}}{M_{\rm e}}{K_{\rm d}}{{\left( {NMK} \right)}^2} + {{\left( {NMK} \right)}^3} + \left( {L + 1} \right){N_{\rm a}}{M_{\rm e}}{K_{\rm d}}NMK + L{N_{\rm a}}{M_{\rm e}}{K_{\rm d}}} \right){K_{\rm MIAA}}$ $O\left( {{N_{\rm a}}{M_{\rm e}}{K_{\rm d}}{{\left( {NMK} \right)}^2}{K_{\rm MIAA}}} \right)$ MFOCUSS $\left( {NMK{N_{\rm a}}{M_{\rm e}}{K_{\rm d}}L + {{\left( {NMK} \right)}^3} + 2{{\left( {NMK} \right)}^2}{N_{\rm a}}{M_{\rm e}}{K_{\rm d}} + NMK{{\left( {{N_{\rm a}}{M_{\rm e}}{K_{\rm d}}} \right)}^2}} \right){K_{\rm MFOC}}$ $O\left( {NMK{{\left( {{N_{\rm a}}{M_{\rm e}}{K_{\rm d}}} \right)}^2}{K_{\rm MFOC}}} \right)$ MSBL $ \begin{gathered} \left( {{{\left( {{N_{\rm a}}{M_{\rm e}}{K_{\rm d}}} \right)}^3} + 4NMK{{\left( {{N_{\rm a}}{M_{\rm e}}{K_{\rm d}}} \right)}^2} + \left( {3{{\left( {NMK} \right)}^2} + {L^2} + 2NMKL} \right){N_{\rm a}}{M_{\rm e}}{K_{\rm d}}} \right. \hfill \\ \left. { + 4{{\left( {NMK} \right)}^3}/3 + {{\left( {NMK} \right)}^2} + NMKL} \right){K_{\rm MSBL}} \hfill \\ \end{gathered} $ $O\left( {{{\left( {{N_{\rm a}}{M_{\rm e}}{K_{\rm d}}} \right)}^3}{K_{\rm MSBL}}} \right)$ MFCSBL $\left( { {N_{\rm a} }{M_{\rm e} }{K_{\rm d} }\left( {5{ {\left( {NMK} \right)}^2} + 2L{{NMK} } + 4{{NMK} } + 3} \right) + { {\left( {NMK} \right)}^3} + L{{NMK} } + L} \right){K_{ {\rm{MFCSBL} } } }$ $O\left( { {N_{\rm a} }{M_{\rm e} }{K_{\rm d} }{ {\left( {NMK} \right)}^2}{K_{\rm MFCSBL} } } \right)$ TMSBL $ \begin{gathered} \left( {{N_{\rm a}}{M_{\rm e}}{K_{\rm d}}(3NMK + NM + N + {L^2} + 2NMKL + NM{K^2} + NK{M^2})} \right. + 2{(NMK)^3}/3 \hfill \\ \left. { + {{(NMK)}^2}(1 + {K_{\rm d}} + {M_{\rm e}}) + NMK({N_{\rm a}}{M_{\rm e}}KN + NM{N_{\rm a}}{K_{\rm d}} + L)} \right){K_{\rm TMSBL}} \hfill \\ \end{gathered} $ $O\left( {{N_{\rm a}}{M_{\rm e}}{K_{\rm d}}NM{K^2}{K_{\rm TMSBL}}} \right)$ 表 3 雷达系统参数
Table 3. Radar system parameters
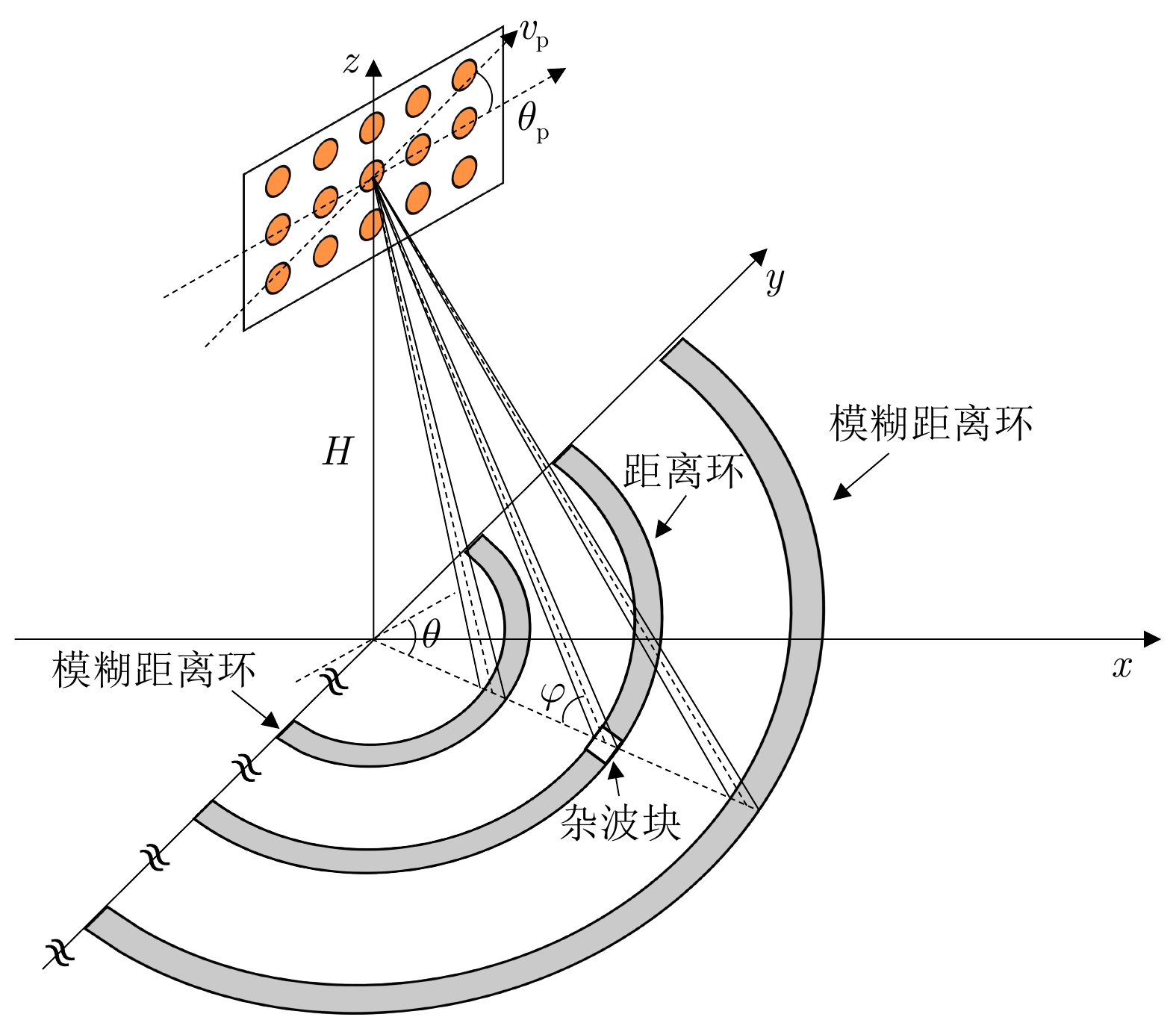
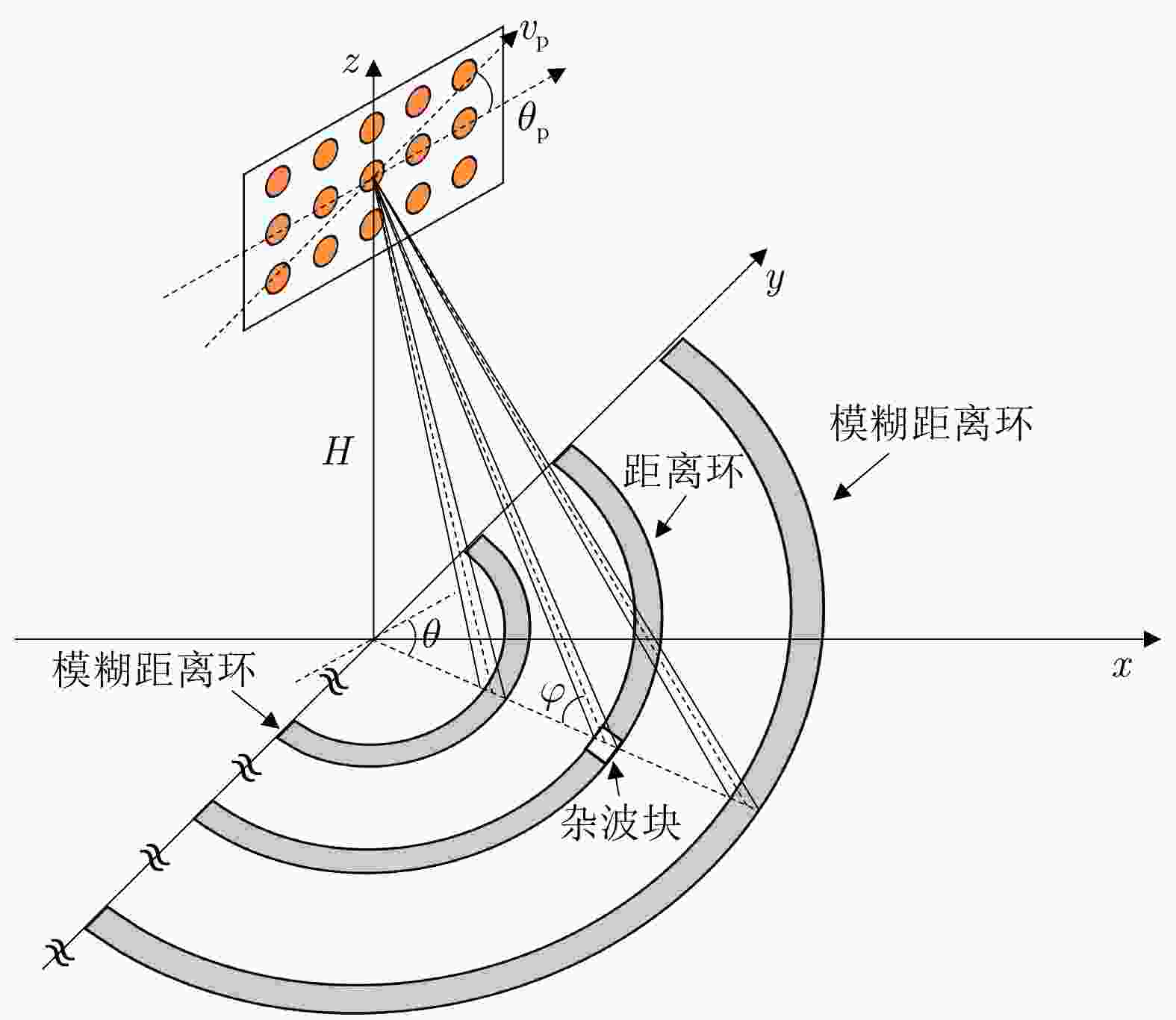
参数 符号 数值 载机速度 ${v_{\rm{p}}}$ 150 m/s 载机高度 $H$ 8000 m 行/列阵元数 $M/N$ 6/8 脉冲数 $K$ 8 雷达波长 $\lambda $ 0.1 m 脉冲重复频率 ${f_{\rm{r}}}$ 8100 Hz 阵元间距 $d$ 0.05 m 主波束指向 $\theta /\varphi $ –90°/0° 杂噪比 – 60 dB -
[1] REED I S, MALLETT J D, and BRENNAN L E. Rapid convergence rate in adaptive arrays[J]. IEEE Transactions on Aerospace and Electronic Systems, 1974, AES-10(6): 853–863. doi: 10.1109/TAES.1974.307893 [2] 谢文冲, 段克清, 王永良. 机载雷达空时自适应处理技术研究综述[J]. 雷达学报, 2017, 6(6): 575–586. doi: 10.12000/JR17073XIE Wenchong, DUAN Keqing, and WANG Yongliang. Space time adaptive processing technique for airborne radar: An overview of its development and prospects[J]. Journal of Radars, 2017, 6(6): 575–586. doi: 10.12000/JR17073 [3] MENG Xiangdong, WANG Tong, WU Jianxin, et al. Short-range clutter suppression for airborne radar by utilizing prefiltering in elevation[J]. IEEE Geoscience and Remote Sensing Letters, 2009, 6(2): 268–272. doi: 10.1109/LGRS.2008.2012126 [4] DUAN Keqing, XU Hong, YUAN Huadong, et al. Reduced-DOF three-dimensional STAP via subarray synthesis for nonsidelooking planar array airborne radar[J]. IEEE Transactions on Aerospace and Electronic Systems, 2020, 56(4): 3311–3325. doi: 10.1109/TAES.2019.2958174 [5] SUN Ke, MENG Huadong, WANG Yongliang, et al. Direct data domain STAP using sparse representation of clutter spectrum[J]. Signal Processing, 2011, 91(9): 2222–2236. doi: 10.1016/j.sigpro.2011.04.006 [6] YANG Zhaocheng, LI Xiang, WANG Hongqiang, et al. On clutter sparsity analysis in space-time adaptive processing airborne radar[J]. IEEE Geoscience and Remote Sensing Letters, 2013, 10(5): 1214–1218. doi: 10.1109/LGRS.2012.2236639 [7] DUAN Keqing, XU Hong, YUAN Huadong, et al. Three-dimensional sparse recovery space-time adaptive processing for airborne radar[J]. The Journal of Engineering, 2019, 2019(19): 5478–5482. doi: 10.1049/joe.2019.0343 [8] GUO Yiduo, LIAO Guisheng, and FENG Weike. Sparse representation based algorithm for airborne radar in beam-space post-Doppler reduced-dimension space-time adaptive processing[J]. IEEE Access, 2017, 5: 5896–5903. doi: 10.1109/ACCESS.2017.2689325 [9] HAN Sudan, FAN Chongyi, and HUANG Xiaotao. A novel STAP based on spectrum-aided reduced-dimension clutter sparse recovery[J]. IEEE Geoscience and Remote Sensing Letters, 2017, 14(2): 213–217. doi: 10.1109/LGRS.2016.2635104 [10] WANG Zetao, XIE Wenchong, DUAN Keqing, et al. Clutter suppression algorithm based on fast converging sparse Bayesian learning for airborne radar[J]. Signal Processing, 2017, 130: 159–168. doi: 10.1016/j.sigpro.2016.06.023 [11] QIU Wei, ZHOU Jianxiong, ZHAO Hongzhong, et al. Three-dimensional sparse turntable microwave imaging based on compressive sensing[J]. IEEE Geoscience and Remote Sensing Letters, 2015, 12(4): 826–830. doi: 10.1109/LGRS.2014.2363238 [12] SIDIROPOULOS N D, DE LATHAUWER L, FU Xiao, et al. Tensor decomposition for signal processing and machine learning[J]. IEEE Transactions on Signal Processing, 2017, 65(13): 3551–3582. doi: 10.1109/TSP.2017.2690524 [13] ZHAO Rongqiang, WANG Qiang, FU Jun, et al. Exploiting block-sparsity for hyperspectral Kronecker compressive sensing: A tensor-based Bayesian method[J]. IEEE Transactions on Image Processing, 2020, 29: 1654–1668. doi: 10.1109/TIP.2019.2944722 [14] 姜磊, 王彤. 机载雷达自适应对角加载参数估计方法[J]. 电子与信息学报, 2016, 38(7): 1752–1757. doi: 10.11999/JEIT151003JIANG Lei and WANG Tong. An adaptive estimation method of diagonal loading parameter for airborne radar[J]. Journal of Electronics &Information Technology, 2016, 38(7): 1752–1757. doi: 10.11999/JEIT151003 [15] MA Zeqiang, LIU Yimin, MENG Huadong, et al. Jointly sparse recovery of multiple snapshots in STAP[C]. 2013 IEEE Radar Conference, Ottawa, Canada, 2013: 1–4. doi: 10.1109/RADAR.2013.6586083 [16] DUAN Keqing, WANG Zetao, XIE Wenchong, et al. Sparsity-based STAP algorithm with multiple measurement vectors via sparse Bayesian learning strategy for airborne radar[J]. IET Signal Processing, 2017, 11(5): 544–553. doi: 10.1049/iet-spr.2016.0183 [17] TROPP J A and GILBERT A C. Signal recovery from random measurements via orthogonal matching pursuit[J]. IEEE Transactions on Information Theory, 2007, 53(12): 4655–4666. doi: 10.1109/TIT.2007.909108 [18] YANG Zhaocheng, LI Xiang, WANG Hongqiang, et al. Adaptive clutter suppression based on iterative adaptive approach for airborne radar[J]. Signal Processing, 2013, 93(12): 3567–3577. doi: 10.1016/j.sigpro.2013.03.033 [19] YANG Shuyuan, LI Bin, WANG Min, et al. Compressive direction-of-arrival estimation via regularized multiple measurement FOCUSS algorithm[C]. 2014 International Joint Conference on Neural Networks, New York, USA, 2014: 2800–2803. doi: 10.1109/IJCNN.2014.6889967. [20] BADER B W and KOLDA T G. Matlab tensor toolbox version 2.6[EB/OL]. http://www.sandia.gov/tgkolda/TensorToolbox. 2015. [21] GUERCI J R. Space-Time Adaptive Processing for Radar[M]. Boston: Artech House, 2014: 52–73. [22] HALE T B, TEMPLE M A, RAQUET J F, et al. Localized three-dimensional adaptive spatial-temporal processing for airborne radar[C]. 2002 International Radar Conference, Edinburgh, UK, 2002: 191–195. doi: 10.1049/cp:20020275. [23] 洪玺, 王文杰, 殷勤业. 基于多级维纳滤波器的空时自适应信号处理及其在无线通信系统中的应用[J]. 信号处理, 2017, 33(3): 430–436. doi: 10.16798/j.issn.1003-0530.2017.03.026HONG Xi, WANG Wenjie, and YIN Qinye. Multistage wiener filter based space and time adaptive signal processing and its application in wireless communication system[J]. Journal of Signal Processing, 2017, 33(3): 430–436. doi: 10.16798/j.issn.1003-0530.2017.03.026 [24] 王璐, 吴仁彪. 直接数据域空时自适应单脉冲方法[J]. 系统工程与电子技术, 2016, 38(12): 2738–2744. doi: 10.3969/j.issn.1001-506X.2016.12.09WANG Lu and WU Renbiao. Direct data domain space-time adaptive monopulse method[J]. Systems Engineering and Electronics, 2016, 38(12): 2738–2744. doi: 10.3969/j.issn.1001-506X.2016.12.09 -



 作者中心
作者中心 专家审稿
专家审稿 责编办公
责编办公 编辑办公
编辑办公
 下载:
下载: