若干层析SAR成像方法在解叠掩性能上的对比分析

任烨仙; 徐丰

doi:10.12000/JR21139

若干层析SAR成像方法在解叠掩性能上的对比分析

DOI: 10.12000/JR21139

任烨仙,
徐丰^,

复旦大学电磁波信息科学教育部重点实验室上海 200433

基金项目: 国家自然科学基金(61991422)

详细信息

作者简介:
任烨仙(1994–)，男，江苏无锡人，博士生，复旦大学信息科学与工程学院，研究方向为层析SAR影像三维成像、极化SAR影像处理

徐　丰(1982–)，男，浙江东阳人，复旦大学博士学位，教授，研究方向为SAR图像解译、电磁散射建模、智能信息技术

通讯作者:
徐丰 fengxu@fudan.edu.cn

责任主编：张冰尘 Corresponding Editor: ZHANG Bingchen
中图分类号: TN957.52
计量
- 文章访问数:
- HTML全文浏览量:
- PDF下载量:
- 被引次数: 0
出版历程
- 收稿日期: 2021-09-26
- 修回日期: 2022-01-09
- 网络出版日期: 2022-01-28
- 刊出日期: 2022-02-28

Comparative Experiments on Separation Performance of Overlapping Scatterers with Several Tomography Imaging Methods

REN Yexian,
XU Feng^,

Key Laboratory for Information Science of Electromagnetic Waves, MoE, Fudan University, Shanghai 200433, China

Funds: The National Natural Science Foundation of China (61991422)

More Information

Corresponding author: XU Feng, fengxu@fudan.edu.cn

摘要

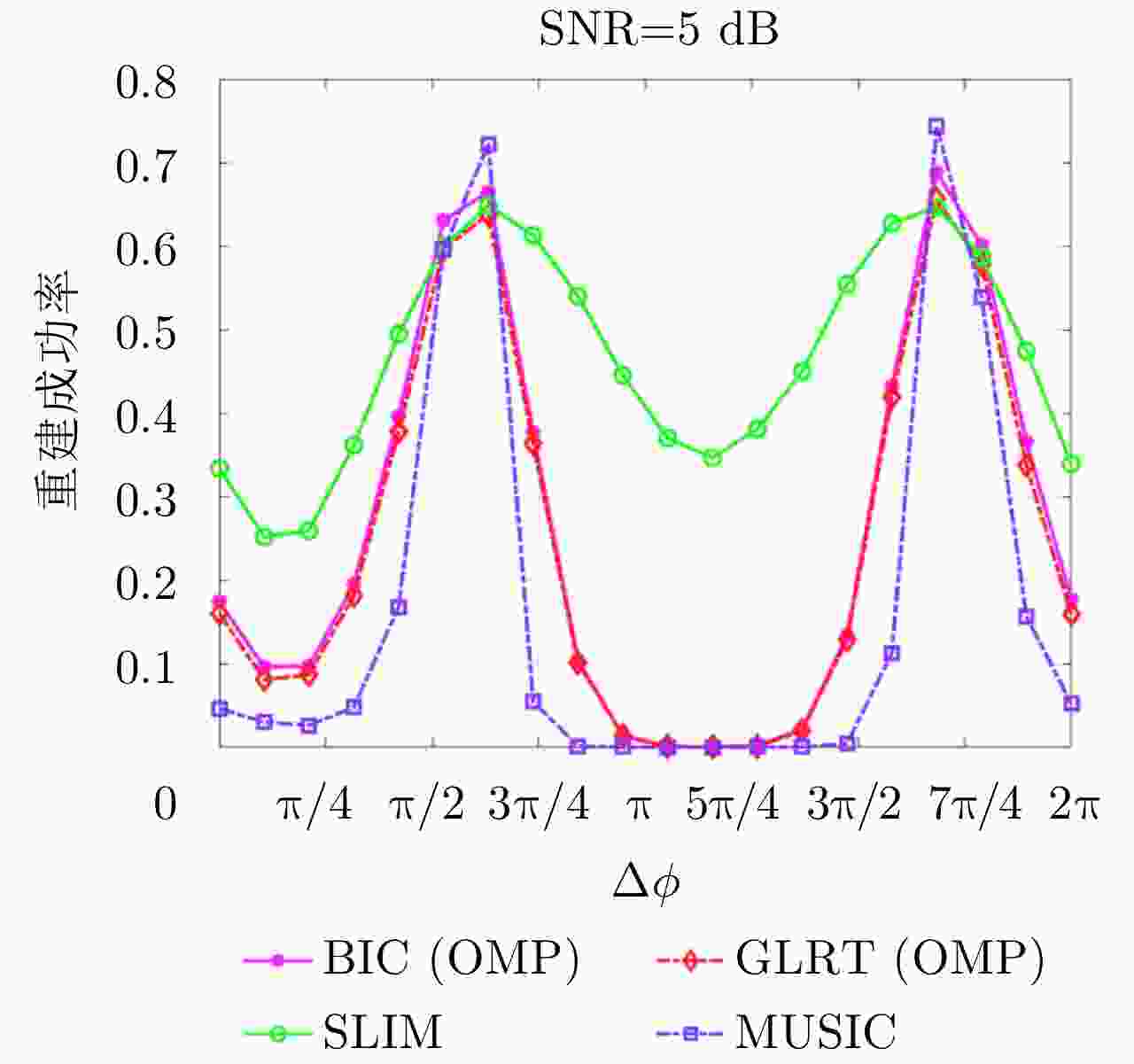
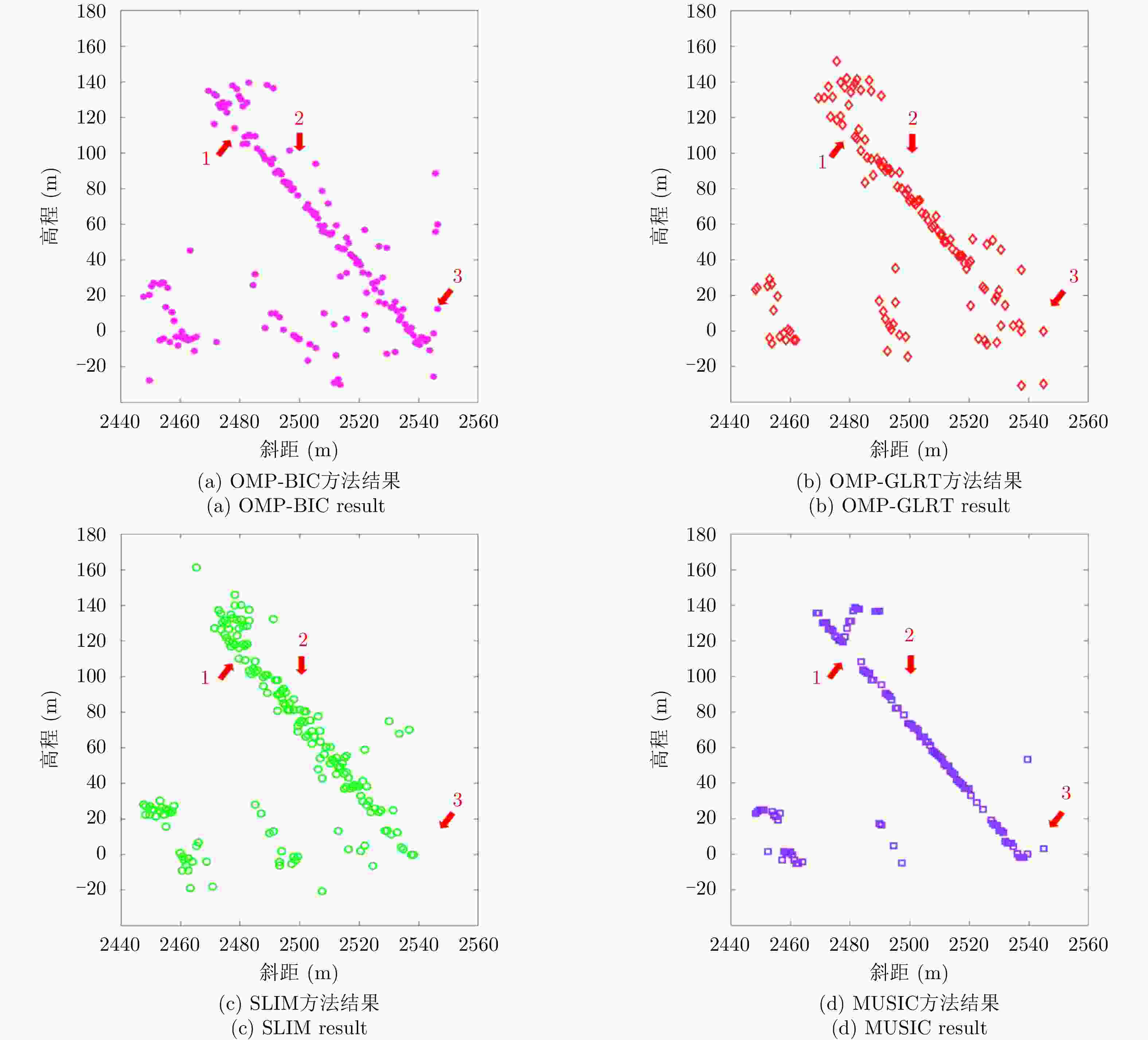
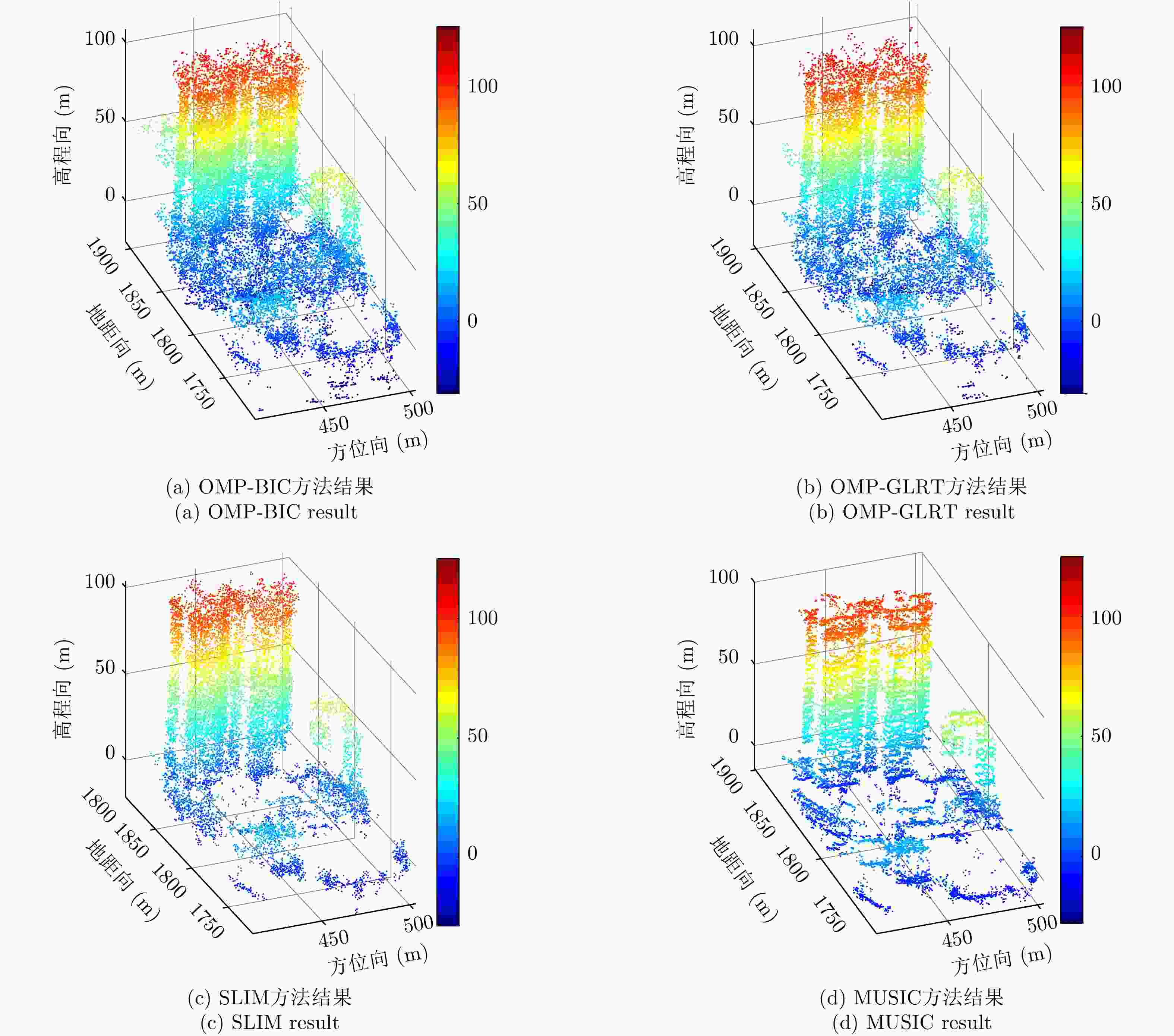
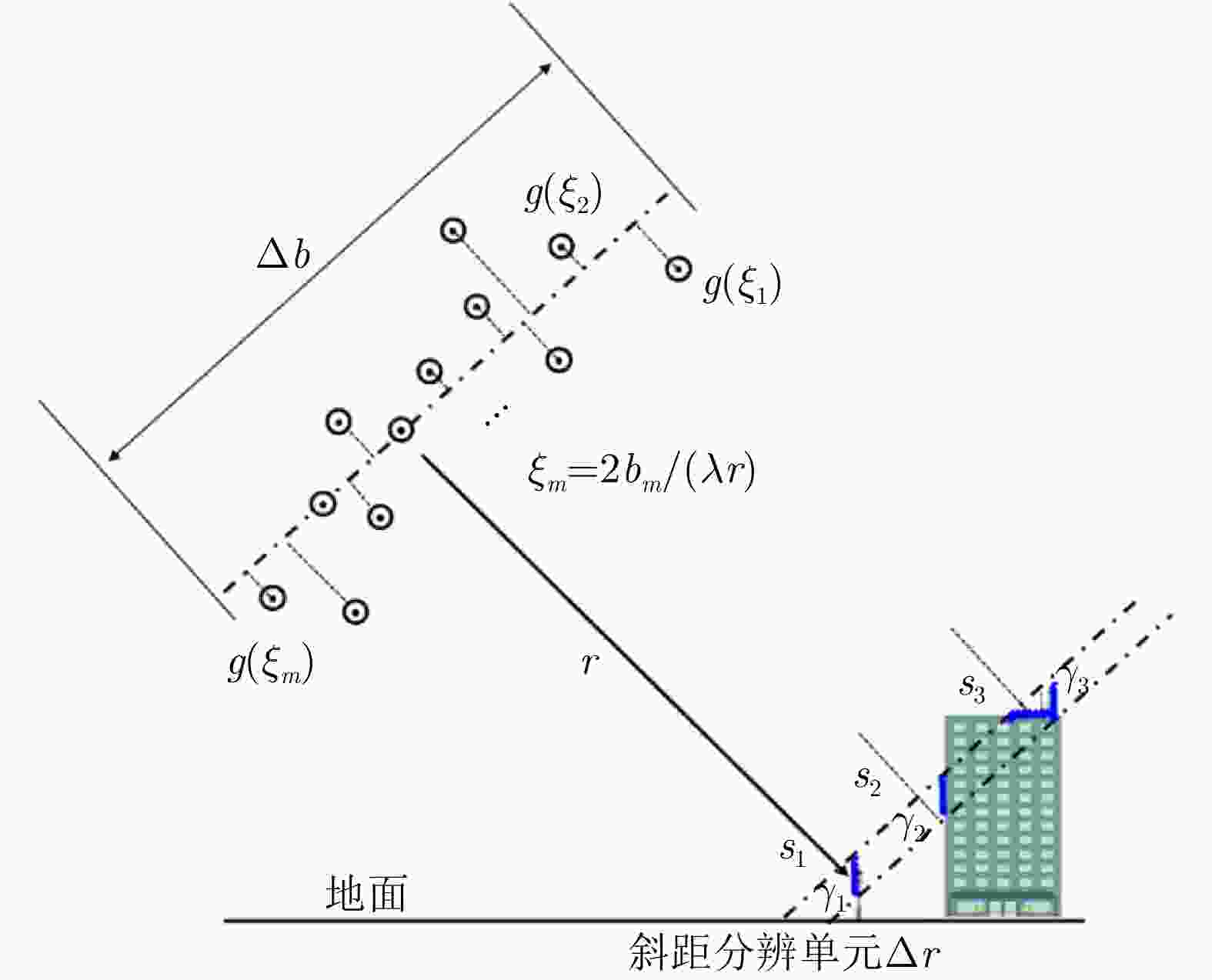
摘要: 层析技术因具有解译城区SAR影像上复杂叠掩场景的能力而备受关注。层析成像包含两个部分：估计散射体在高程向的分布和确定散射体在混叠像元内的真实数目。该文以中科院空天院峨眉数据的机载阵列干涉系统参数为基础，选取了若干代表性的方法，包括OMP, SLIM和MUSIC等层析谱估计方法以及BIC和GLRT等模型定阶方法，进行了模拟叠掩目标的层析反演实验，使用了克拉默-拉奥界和重建成功率来评估实验结果。实验表明：在机载阵列数很有限的条件下，(1)使用2阶统计量反演的高程估计量的方差比单个观测矢量反演结果的方差更小；(2)叠掩散射体间的幅度比、相位差和散射间距会影响层析算法解叠掩的成功率；(3)叠掩散射体间的相位差会使层析算法的高程估计发生偏差。
- 阵列干涉SAR /
- SAR层析成像 /
- 解叠掩 /
- 克拉默-拉奥界 /
- 重建成功率
Abstract: The tomographic technique has attracted much attention because of its ability to separate overlapping scatterers in urban Synthetic Aperture Radar (SAR) images. The general method of SAR Tomography (TomSAR) imaging combines the following two aspects: estimating the distribution of the scatterers in the elevation direction and determining the number of strong scatterers in an overlapped pixel. This study applied several sophisticated spectrum estimations (e.g., Orthogonal Matching Pursuit, Sparse Learning via Iterative Minimization and Multiple Signal Classification) and model order selection approaches (e.g., Bayesian information criterion and generalized likelihood ratio test) with highly technical potential to recover the simulated overlapping scatterers. This simulation experiment is based on the parameters of the AIRCAS X-band TomoSAR data from Emei, Sichuan, China. The Cramér-Rao Lower Bound (CRLB) and recovery probability are used to evaluate the performances of different methods for the separation of overlapped scatterers. The experimental results revealed the following: (1) the standard deviation of estimation using second-order statistics is smaller than that of a single observation vector, especially when the number of acquisitions is very limited; (2) the amplitude ratio, phase difference, and elevation spacing between overlapping scatterers will have a significant impact on the different kinds of algorithms; and (3) the phase difference between overlapping scatterers will make the phase center estimation of greedy algorithm or spectrum estimation algorithm biased.
- Array interferometric SAR /
- TomoSAR imaging /
- Separation of overlapped scatterers /
- Cramér-Rao Lower Bound (CRLB) /
- Recovery probability

HTML全文

1. 引言

合成孔径雷达(Synthetic Aperture Radar, SAR)可以实现全天时、全天候的高分辨率成像^[1]，星载SAR系统为全球地理遥感、地形测绘、形变监测等应用提供了丰富的高分辨数据。分布式星载SAR系统是一种特殊模式的合成孔径雷达系统，雷达发射机和接收机位于不同平台，这种收发分置的特点带来了很多优势，比如灵活的基线配置，多样的接收模式，可以提供更精细的地物分类信息等，具有单基情况无可比拟的优势。但是收发分置的特点也带来了很多新的挑战，尤其是时间同步、相位同步和波束同步等三大同步问题^[2,3]。由于收发雷达不共频率源，导致了时间同步和相位同步问题^[4]，时间同步问题是指，发射雷达和接收雷达使用不同的晶振产生脉冲信号，导致了触发脉冲不一致，进而导致信号发射时刻与接收窗起始时刻不一致，使距离向的录取回波减少，时间同步误差会在回波中引入相位误差，并且晶振偏差会随时间累积，对回波数据产生较大影响，严重降低雷达图像质量^[5,6]。为达到时间同步的要求，Tandem-X SAR系统采用频率一致性指标为10^–8量级的晶振，并采用跳跃PRI的方法，确保600 s内，时间同步误差小于5 μs^[7]。相位同步问题是指，由于晶振频率的差异，导致了发射信号调制频率和接收信号解调频率不一致，造成解调回波中存在沿方位时间变化的相位误差，该误差在成像后传递到图像域，导致方位向位置偏移、主瓣展宽、积分旁瓣比恶化等问题，并且相位误差最终会传递到干涉相位，造成干涉测高精度损失。TanDEM-X SAR系统采用脉冲交替对传的同步方案解决相位同步的问题。波束同步问题是指，由于收发天线的控制精度不同，使得收发天线无法在同一时刻完全覆盖地面同一区域，导致双基合成天线方向图的增益降低，同时接收天线无法获得全部的目标散射信号，造成有效观测幅宽损失。为保证系统系能，TanDEM-X SAR系统的波束指向精度控制在0.01°，最差情况下导致的天线增益损失小于0.1 dB。

为了消除相位同步带来的影响，可以建立专门的同步链路，文献[8]提出了卫星间连续波对传的同步方法，文献[9]和文献[10]进一步提出了脉冲交替对传的方法，文献[11]提出一种基于信号交换的调频连续波合成孔径雷达相位同步方法。无论采用哪种同步链路方式，目的都是获得相位误差信息，最后在进行数据处理时提取并补偿相位误差，这也是解决分布式卫星SAR相位同步的优选方法^[12]。文献[13]建立了一种时间同步误差模型，分析了时间同步误差对成像和干涉测高性能的影响，但是没有分析时间同步和相位同步的联系。时间同步和相位同步来自同一误差源，都是由于收发平台采用了独立的晶振系统来校准系统时钟^[14]，所以两者之间存在一定的关系。波束同步的研究主要集中在波束同步控制方法，以及波束同步误差对雷达成像性能的影响，文献[15]分析了几种可行的飞行控制策略，同时分析了波束同步对收发平台和姿态控制精度的要求，文献[16]分析了系统波束控制精度需要满足的要求。但是，在不同的卫星姿态控制精度和波束指向精度情况下，波束同步误差对分布式星载SAR系统的综合影响还需要进一步分析。

本文结构安排如下。第2节介绍了时间同步误差模型和波束同步误差模型。第3节基于误差模型分析了时间同步和相位同步导致的相位误差之间的关系，并分析晶振稳定度需要满足的条件。第4节分析了波束同步误差对合成天线方向图、双基图像信噪比、多普勒去相干以及波束覆盖偏差的具体影响。第5节，进行仿真验证，为分布式SAR系统设计提供参考。

2. 误差模型

2.1 时间同步误差模型

收发雷达之间的时间同步误差模型可以表示为常数项、线性项和随机项3部分^[13]，随机项由频率源的短期稳定性决定，由于随机的特点，该项影响结果不具备积累性，一般只有在频率源稳定度较低或者所需相干积累时间较长时有较大影响^[17–20]，因此该模型可以表达为：

$\varepsilon \left( t \right) = \Delta t + \beta t$

(1)

其中， $\Delta t$ 为常数项，表示初始状态主辅星间雷达累积的定时信号之差； $\beta t$ 为线性项，由主辅星晶振频率偏差导致， $\beta$ 可以表示为：

$\beta \!=\! \frac{{\Delta {\rm{PR}}{{\rm{I}}_1} \!-\! \Delta {\rm{PR}}{{\rm{I}}_2}}}{{{\rm{PRI}}}} \!=\! \frac{{\Delta {f_1}}}{{{f_1}}} \!-\! \frac{{\Delta {f_2}}}{{{f_2}}} \approx \frac{{\Delta {f_1} \!-\! \Delta {f_2}}}{{{f_0}}}$

(2)

其中，f₀表示标称频率， $\Delta {f_1}$ 和 $\Delta {f_2}$ 分别表示发射雷达和接收雷达的频率偏移。当存在同步误差时，在以发射信号为参考的时间坐标系中，不同脉冲的回波在接收雷达采样窗中的位置会发生偏移^[21]。

2.2 波束同步误差模型

卫星姿态误差会影响卫星和地面目标的波束传播距离，同时影响回波多普勒频率，如图1所示，X轴从星下点指向卫星方向，Y轴指向方位向方向，Z轴指向距离向方向，卫星姿态误差可以分解为偏航角、俯仰角和横滚角，其中R_s表示斜距，R₀表示最近斜距，P₀表示姿态导引后期望的波束中心地面落点，P表示波束中心实际落点， ${\theta _{\rm{y}}}$ 表示偏航角， ${\theta _{\rm{p}}}$ 表示俯仰角， ${\theta _{\rm{r}}}$ 表示横滚角。可见，偏航角和俯仰角分别导致波束中心线绕X轴和Z轴旋转，进而偏离零多普勒面，均会导致斜视角。横滚角导致波束中心线绕Y轴旋转，所以横滚角引起波束在距离向移动，在距离向产生波束指向误差。

图 1 卫星姿态对系统的影响

Figure 1. Impacts of yaw angle, pitch angle and roll angle

下载: 全尺寸图片幻灯片

根据几何关系可以得到，偏航角和俯仰角引起的斜视角分别为：

${\theta _{{\rm{sy}}}} = \arctan \left( {\tan {\theta _{\rm{y}}} \cdot \sin {\theta _{\rm{l}}}} \right)$

(3)

${\theta _{{\rm{sp}}}} = \arctan \left( {\tan {\theta _{\rm{p}}} \cdot \cos {\theta _{\rm{l}}}} \right)$

(4)

其中， ${\theta _{\rm{l}}}$ 为下视角。横滚角引起的距离向波束指向误差为：

${\theta _{{\rm{sr}}}} = {\theta _{\rm{r}}}$

(5)

3. 时间同步误差分析

主星发射的线性调频脉冲信号可以表示为：

$s\left( {\tau ,t} \right) = {\mathop{\rm rect}\nolimits} \left( {\frac{\tau }{{{T_{\rm{p}}}}}} \right)\exp \left( {{\rm j}{{π}} k{\tau ^2}} \right)\exp \left( {{\rm j}{{π}} {f_0}\tau } \right)$

(6)

其中， ${\mathop{\rm rect}\nolimits} \left[ \cdot \right]$ 为矩形窗函数， $\tau$ 为距离向快时间，t为方位向慢时间，T_p为脉冲宽度，f₀为发射信号载频，k为调频率。将时间同步误差模型代入发射信号，经辅星雷达接收解调后含有时间同步误差的回波信号为：

$\begin{aligned} {s_{\rm{D}}}\left( {\tau ,t} \right) = & {\mathop{\rm rect}\nolimits} \left( {\frac{{\tau - {R_t}/c - \varepsilon \left( t \right)}}{{{T_{\rm{p}}}}}} \right) \cdot {\rm{rect}}\left( {t - {t_{\rm{c}}}} \right)\\ & \cdot \exp \left( {{\rm j}{{π}} k{{\left( {\tau - {R_t}/c - \varepsilon \left( t \right)} \right)}^2}} \right)\\ & \cdot \exp \left( { - {\rm j}2{{π}} {R_t}/\lambda } \right)\exp \left( { - {\rm j}2{{π}} {f_0}\varepsilon \left( t \right)} \right) \end{aligned}$

(7)

其中，c为光速， $\lambda$ 为波长，t_c为波束中心偏离时间，R_t为雷达和卫星之间的波束传播距离，

$R\left( t \right) \!=\! \sqrt {{R_1}^{\!\!2} \!\!+\!\! V_1^2{{\left( {t \!-\! {t_{01}}} \right)}^2}} \!\!+\!\! \sqrt {{R_2}^{\!\! 2} \!+\! V_2^2{{\left( {t - {t_{02}}} \right)}^2}}$

(8)

其中，R₁和R₂分别表示收发最近斜距，t₀₁和t₀₂分别表示波束中心穿越时刻，V₁和V₂分别表示收发卫星的速度。为简化分析，下文中，假设两星同时穿越波束中心时刻且以该时刻为方位时间零点，即t₀₁=t₀₂=0。

以主星发射信号，辅星接收信号为例，采用距离多普勒聚焦算法，推导时间同步误差对SAR成像的影响，假设主星雷达晶振为标准频率源，辅星雷达晶振含有误差项，即时间同步误差全部表现在辅星获得的图像上。

3.1 固定时间误差分析

辅星雷达只存在固定时间误差的情况下，即

$\varepsilon \left( t \right) = \Delta t$

(9)

成像处理之后的辅星图像将存在时间同步误差项，具体可以表示为：

$\begin{aligned} \sigma \left( {\tau ,t} \right) = & {\rm{sinc}}\left( {B\left( {\tau - \left( {{R_1} + {R_2}} \right)/c - \Delta t} \right)} \right) \\ & \cdot {\rm{sinc}}\left( {{B_{\rm{d}}} \cdot t} \right) \cdot \exp \left( { - {\rm j}2{{π}} \frac{{{R_1} + {R_2}}}{\lambda }} \right)\\ & \cdot \exp \left( {{\rm j}2{{π}} {f_{{\rm{ac}}}}t} \right) \cdot \exp \left( { - {\rm j}2{{π}} {f_0}\Delta t} \right) \end{aligned}$

(10)

其中，B_d是多普勒带宽，f_ac是多普勒中心频率。由式(10)可以得到，固定时间同步误差在辅星图像中引入距离向主瓣偏移和固定相位误差，固定相位误差在经过干涉处理之后会产生常量干涉相位误差。主瓣偏移量和干涉相位误差分别为：

$\!\!\!\!\!\! \Delta r = \frac{{\Delta t \cdot c}}{2}$

(11)

${\varphi _{\rm{e}}} = - 2{{π}} {f_0}\Delta t$

(12)

常量相位误差会影响绝对测高精度。

3.2 时间同步与相位同步关系

辅星雷达只存在线性时间误差的情况下，即

$\varepsilon \left( t \right) = \beta t$

(13)

对式(7)中带有线性时间误差的相位项进一步推导可以得到

$\begin{aligned} {\varphi _{{\rm{linear}}}} & = {\rm{ - }}2{{π}} \beta {f_0}t = {\rm{ - }}2{{π}} \frac{{\Delta {f_1} - \Delta {f_2}}}{{{f_0}}}{f_0}t \\ &{\rm{ = - }}2{{π}} \left( {\Delta {f_1} - \Delta {f_2}} \right)t \end{aligned}$

(14)

由于晶振频率存在偏移，t时刻主星的晶振频率为 ${f_1} = {f_0} + \Delta {f_1}$ ，辅星的晶振频率为 ${f_2} = {f_0} + \Delta {f_2}$ ，根据文献[9]中对脉冲对传相位同步方案的分析，辅星需要补偿的相位偏差为：

$\begin{aligned} {\varphi _c}(t) = & 2{{π}} (\Delta {f_2} - \Delta {f_1})t + {{π}} (\Delta {f_2} - \Delta {f_1})({\tau _{12}} + {\tau _{{\rm{sys}}}}) \\ & - {{π}} {f_{\rm{d}}}{\tau _{{\rm{sys}}}} + \frac{1}{2}({n_{\varphi 2}}(t + {\tau _{{\rm{sys}}}}) + {n_{\varphi 2}}(t + \tau ) \\ & - {n_{\varphi 1}}(t) - {n_{\varphi 1}}(t + \tau + {\tau _{{\rm{sys}}}})) \\ &+ \frac{1}{2}({\varphi _{{\rm{SNR1}}}}(t) - {\varphi _{{\rm{SNR2}}}}(t)) \\ &+ \Delta {\varphi _{{\rm{sys}}}}(t) + \Delta {\varphi _{{\rm{ant}}}}(t) \end{aligned}$

(15)

其中，f_d是多普勒频率， ${\tau _{{\rm{sys}}}}$ 是同步脉冲的发射延迟， ${n_{\varphi 1}}$ 和 ${n_{\varphi 2}}$ 分别代表晶振的相位噪声， ${\varphi _{{\rm{SNR1}}}}$ 和 ${\varphi _{{\rm{SNR2}}}}$ 分别代表主星和辅星的接收机噪声， $\Delta {\varphi _{{\rm{sys}}}}\left( t \right)$ 代表通道链路的相位噪声， $\Delta {\varphi _{{\rm{ant}}}}\left( t \right)$ 代表天线方向图引入的相位噪声。

式(15)的第1项 $2{{π}} \left( {\Delta {f_2} - \Delta {f_1}} \right)$ ，等于式(7)中的线性偏差 ${\varphi _{{\rm{linear}}}}$ ，即随方位时间线性变化的相位误差部分可以通过相位同步方案补偿，补偿后的回波信号经过距离徙动校正后在方位频域的表达形式为：

$\begin{aligned} {S_{{\rm{R {{\scriptsize{-}}} com}}}}\left( {\tau ,{f_{\rm{a}}}} \right) = & {\rm{sinc}}\left( {B\left( {\tau - \frac{{{R_1} + {R_2}}}{c} + \beta \frac{{{f_{\rm{a}}}}}{{{K_{\rm{a}}}}}} \right)} \right) \\ & \cdot{W_{\rm{a}}}\left( {{f_{\rm{a}}} - {f_{{\rm{ac}}}}} \right) \\ & \cdot \exp \left( { - {\rm j}2{{π}} \left( {{R_1} + {R_2}} \right)/\lambda } \right) \\ & \cdot \exp \left( {{\rm j}{{π}} \frac{{f_{\rm{a}}^2}}{{{K_{\rm{a}}}}}} \right) \end{aligned}$

(16)

其中，K_a为方位向调频率。式(16)中 $\beta \left( {{{{f_{\rm{a}}}} \mathord{\left/ {\vphantom {{{f_{\rm{a}}}} {{K_{\rm{a}}}}}} \right. } {{K_{\rm{a}}}}}} \right)$ 项会造成距离徙动校正误差，使方位信号弥散在若干距离单元上，导致主瓣展宽。如果要求距离徙动校正误差造成的主瓣展宽小于2%，那么要求未被校正的徙动量小于半个分辨率单元^[22]，即

$\max \left( {\frac{\beta }{{{K_{\rm{a}}}}} \cdot {f_{\rm{a}}}} \right) < 0.5 \cdot \frac{{0.886}}{B}$

(17)

根据时频关系可以得到

$\frac{\beta }{{{K_{\rm{a}}}}} \cdot {K_{\rm{a}}} \cdot {T_{{\rm{sar}}}} < 0.5 \cdot \frac{{0.886}}{B}{\rm{ }} \Rightarrow {\rm{ }}\beta < \frac{{0.443}}{{B \cdot {T_{{\rm{sar}}}}}}$

(18)

其中T_sar为合成孔径时间。

满足式(18)的情况下，经方位压缩后的SAR信号为：

$\begin{aligned} \!\!\!\, \sigma \left( {\tau ,t} \right) \!=\! & {\rm{sinc}}\left( {B\left( {\tau - \frac{{{R_1} + {R_2}}}{c}} \right)} \right) \!\cdot {\rm{sinc}}\left( {{B_{\rm{d}}} \cdot t} \right)\\ & \cdot \exp\!\! \left( { - {\rm j}2{{π}} \frac{{{R_1} + {R_2}}}{\lambda }} \right)\!\ \cdot \exp \left( {{\rm j}2{{π}} {f_{{\rm{ac}}}}t} \right) \end{aligned}$

(19)

此时主要导致主瓣展宽，严重情况可能导致散焦。

4. 波束同步误差分析

理想情况下，SAR系统处于匀速运动状态，但是在实际工作情况下，卫星的运动受到控制系统精度的影响，会产生姿态误差，所以必须保证分布式系统的姿态控制精度^[23]。波束同步误差可以分为两个方面，一方面是卫星姿态引起的误差，另一方面是波束指向误差。波束同步误差会导致天线照射范围不一致，导致信噪比损失，多普勒带宽偏移，方位向天线增益降低等问题^[24]。同时，由于照射区域的偏差，还会导致距离向重叠幅宽减小。

4.1 对方位向影响

本节首先引入文献[7]中介绍的基于椭圆轨道的双星一发双收工作模式下的姿态导引方式，在此基础上，分析波束同步误差对多普勒去相干、天线增益以及双基图像信噪比损失的影响。

双星有两种姿态导引方式^[7]，一种是只针对主星进行零多普勒姿态导引，此时，场景内的回波多普勒中心频率不为0。另一种是主辅双星均进行零多普勒姿态导引，此时辅星与主星照射的共同区域等效为正侧视，即场景内多普勒中心频率为0。图2和图3给出了在主辅星顺轨基线从0到3 km情况下，不同姿态导引方式下方位向合成天线方向图的情况，其它仿真参数如表1所示。

图 2 仅辅星进行多普勒导引

Figure 2. The first attitude steering strategy

下载: 全尺寸图片幻灯片

图 3 主星辅星分别进行多普勒导引

Figure 3. The second attitude steering strategy

下载: 全尺寸图片幻灯片

图2中，由于仅主星进行零多普勒姿态导引，导致合成后的方位天线方向图指向等效于斜视，即场景回波的多普勒中心频率不为0，产生方位多普勒去相干，导致相干系数发生变化，如图4所示。

图 4 顺轨基线对相干系数的影响

Figure 4. Contributions to correlation coefficient versus along-track baseline

下载: 全尺寸图片幻灯片

考虑到顺轨基线和波束同步误差的综合影响，相干系数的计算方法可以表示为：

${\gamma _{{\rm{dc}}}} = 1 - \left| {\frac{{\Delta {f_{{\rm{Dop1}}}} + \Delta {f_{{\rm{Dop2}}}}}}{{{B_{\rm{d}}}}}} \right|$

(20)

$\Delta {f_{{\rm{Dop1}}}}$ 表示由顺轨基线导致的多普勒频率偏移，计算公式为^[7]：

$\Delta {f_{{\rm{Dop1}}}} \approx \frac{{v \cdot {d_{{\rm{along}}}}}}{{\lambda \cdot r}}$

(21)

其中，d_along为基线长度，r为平均斜距。

$\Delta {f_{{\rm{Dop2}}}}$ 表示由波束指向误差和卫星姿态误差导致的多普勒频率偏移，

$\Delta {f_{{\rm{Dop2}}}} = \frac{{2v \cdot \sin \left( {{\theta _{{\rm{sq}}}} + \Delta {\theta _{\rm{a}}}} \right)}}{\lambda } - \frac{{2v \cdot \sin \left( {{\theta _{{\rm{sq}}}}} \right)}}{\lambda }$

(22)

$\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\! \Delta {\theta _{\rm{a}}} = {\theta _{{\rm{err}}}} + {\theta _{{\rm{sy}}}} + {\theta _{{\rm{sp}}}}$

(23)

其中， ${\theta _{{\rm{sq}}}}$ 表示斜视角， $\Delta {\theta _{\rm{a}}}$ 表示方位向波束同步误差，包括方位向波束指向误差以及偏航角和俯仰角对斜视角的影响部分。

图3中，由于对主辅双星均进行零多普勒姿态导引，合成后的方位天线方向图等效于正侧视，此时对多普勒去相干影响很小。考虑到主辅双星之间顺轨基线的影响，合成后的天线方向图幅度会有一定的下降，从仿真中可以看出，在顺轨基线小于3 km的情况下，导致的幅度衰减小于0.05 dB，可以忽略。在不同顺轨基线情况下，主辅星同时进行零多普勒导引的合成天线方向图对频谱加权的计算公式为^[7]：

$\begin{aligned} {W_{{\rm{bistat}}}}({f_{{\rm{Dop}}}};\Delta {f_{{\rm{Dop}}}}) \!=\! & {\rm sinc}\left( {\frac{l}{{2v}}\left( {{f_{{\rm{Dop}}}} \!-\! \Delta {f_{{\rm{Dop}}}}} \right)} \right) \\ & \cdot {\rm sinc}\left( {\frac{l}{{2v}}\left( {{f_{{\rm{Dop}}}} \!+\! \Delta {f_{{\rm{Dop}}}}} \right)} \right) \end{aligned}$

(24)

其中，l为天线长度，v为卫星速度， $\Delta {f_{{\rm{Dop}}}}$ 是由顺轨基线导致的多普勒频率偏移。

在此基础上，加入波束指向误差和卫星姿态误差的影响，顺轨基线和波束同步误差的综合加权公式可以表示为：

$\begin{aligned} &{W_{{\rm{bistat}}}}({f_{{\rm{Dop}}}};\Delta {f_{{\rm{Dop}}}}) \\ & \quad= {\rm sinc}\left( {\frac{l}{{2v}}\left( {{f_{{\rm{Dop}}}} - \Delta {f_{{\rm{Dop1}}}} - \Delta {f_{{\rm{Dop2}}}}} \right)} \right)\\ & \quad \quad \cdot {\rm sinc}\left( {\frac{l}{{2v}}\left( {{f_{{\rm{Dop}}}} + \Delta {f_{{\rm{Dop1}}}} + \Delta {f_{{\rm{Dop2}}}}} \right)} \right) \end{aligned}$

(25)

由于波束同步误差，导致成像后辅星图像信噪比降低，信噪比损失量为^[25]：

$\begin{aligned} {\rm{SN}}{{\rm{R}}_{{\rm{loss}}}} {\rm{ = }}\frac{{\displaystyle\int_{ - {\theta _{{\rm{bw1}}}}/2}^{{\theta _{{\rm{bw1}}}}/2} {\left( {{\rm{sin}}{{\rm{c}}^2}\left( {l \cdot \sin \varphi /\lambda } \right) \cdot {\rm{sin}}{{\rm{c}}^2}\left( {l \cdot \sin \left( {\varphi \!-\! \Delta {\theta _{\rm{a}}}} \right)/\lambda } \right)} \right)} {\rm d}\varphi }}{{\displaystyle\int_{ \!-\! {\theta _{{\rm{bw1}}}}/2}^{{\theta _{{\rm{bw1}}}}/2} {\left( {{\rm{sin}}{{\rm{c}}^2}\left( {l \cdot \sin \varphi /\lambda } \right) \cdot {\rm{sin}}{{\rm{c}}^2}\left( {l \cdot \sin \varphi /\lambda } \right)} \right)} {\rm d}\varphi }} \end{aligned}$

(26)

其中， $\varphi$ 为方位向离轴角， ${\theta _{{\rm{bw1}}}}$ 为方位向波束宽度。

4.2 对距离向影响

针对距离向，波束控制误差主要影响主、辅星的重叠幅宽，当主、辅星距离向同时存在相反方向的指向偏差时，距离向的重叠区域(图5和图6中黄色区域)会大幅减小，影响后续的干涉处理。根据几何模型，可以推导出覆盖区域偏差的计算公式：

图 5 无误差的波束覆盖情况

Figure 5. No beam pointing error case

下载: 全尺寸图片幻灯片

图 6 有误差的波束覆盖情况

Figure 6. Beam pointing error exists case

下载: 全尺寸图片幻灯片

$\begin{aligned} \Delta W = & \left( {H + {\rm{Re}}} \right)\cos \left( {{\theta _{\rm{l}}} + {\theta _{{\rm{bw2}}}}/2 - \Delta {\theta _{\rm{r}}}} \right) - \sqrt {{{\left( {H + {\rm{Re}}} \right)}^2}{{\cos }^2}\left( {{\theta _{\rm{l}}} + {\theta _{{\rm{bw2}}}}/2 - \Delta {\theta _{\rm{r}}}} \right) - 2 \cdot H \cdot {\rm{Re}}} \\ & - \left( {H + {\rm{Re}}} \right)\cos \left( {{\theta _{\rm{l}}} + {\theta _{{\rm{bw2}}}}/2 + \Delta {\theta _{\rm{r}}}} \right) + \sqrt {{{\left( {H + {\rm{Re}}} \right)}^2}{{\cos }^2}\left( {{\theta _{\rm{l}}} + {\theta _{{\rm{bw2}}}}/2 + \Delta {\theta _{\rm{r}}}} \right) - 2 \cdot H \cdot {\rm{Re}}} \end{aligned}$

(27)

其中，H为卫星高度，Re为地球半径， ${\theta _{\rm{l}}}$ 为下视角， ${\theta _{{\rm{bw2}}}}$ 为俯仰向波束宽度， $\Delta {\theta _{\rm{r}}}$ 为距离向波束同步误差。

5. 仿真结果

仿真参数如表1所示。

表 1 仿真参数表

Table 1. Simulation parameters

参数	数值
载频(GHz)	1.30
卫星高度(km)	700
方位向天线长度(m)	6
脉冲宽度(μs)	80
距离向带宽(MHz)	100
PRF(Hz)	1600
卫星有效速度(m/s)	7500
距离向波束指向精度(°)	0.06
方位向波束指向精度(°)	0.05
姿态控制精度(°)	0.02
顺轨基线(km)	3

下载: 导出CSV

| 显示表格

5.1 时间同步误差

仿真中加入参数为 $\Delta t = 100 \ {\rm{ ns}}$ 的固定时间误差，点目标分析结果如图7所示，通过计算可以得到理论上的距离向位置偏移为 $\Delta r = \Delta t \cdot c/2{\rm{ = 15 \ m}}$ ，仿真得到的对应偏差为15 m，如图7(b)所示。

图 7 固定时间误差影响仿真

Figure 7. Constant time error simulations

下载: 全尺寸图片幻灯片

时间同步误差会引起主瓣展宽，如式(18)所示，仿真参数下，当 $\beta < 1.2 \times {10^{ - 9}}$ 时，引起的展宽可以忽略。当 $\beta = 5 \times {10^{ - 8}}$ 时，距离向和方位向剖面图如图8所示，由仿真结果可以看到明显的主瓣展宽。

图 8 回波域相位补偿后的结果

Figure 8. Time error simulations after compensation in echo domain

下载: 全尺寸图片幻灯片

5.2 波束同步误差

本节的仿真给出了当顺轨基线为3 km时，波束指向误差和卫星姿态误差对系统性能的影响。图9和图10分别比较了方位向波束指向精度在0.01°到0.05°情况下，对合成天线方向图及相干系数的影响，仿真结果表明，与无误差情况对比，0.05°波束指向误差造成方位天线增益下降小于0.05 dB，造成相干系数减小0.02。

图 9 波束指向引起的合成天线方向图增益损失

Figure 9. Gain loss versus beam pointing accuracy

下载: 全尺寸图片幻灯片

图 10 波束指向引起的相干系数变化

Figure 10. Coherent coefficient versus beam pointing accuracy

下载: 全尺寸图片幻灯片

图11和图12分别给出了卫星姿态控制精度在0.005°到0.020°的情况下，对方位向合成天线方向图及相干系数的影响，仿真结果表明，与无误差情况对比，0.020°的姿态控制误差造成方位天线增益下降小于0.02 dB，造成相干系数减小0.01。

图 11 卫星姿态引起的合成天线方向图增益损失

Figure 11. Gain loss versus satellite attitude accuracy

下载: 全尺寸图片幻灯片

图 12 卫星姿态引起的合成天线方向图增益损失

Figure 12. Coherent coefficient versus satellite attitude accuracy

下载: 全尺寸图片幻灯片

不同波束指向和卫星姿态误差情况下，对合成天线方向图及相干系数的综合影响结果如图13和图14所示。波束指向精度为0.05°，卫星姿态控制精度0.02°的情况下，和无误差情况对比，造成方位天线增益下降小于0.1 dB，造成相干系数减小0.03。

图 13 波束指向和卫星姿态对天线增益的综合影响

Figure 13. Overall influence on antenna gain versus beam pointing accuracy and attitude accuracy

下载: 全尺寸图片幻灯片

图 14 波束指向和卫星姿态对相干系数的综合影响

Figure 14. Overall influence on coherent coefficient versus beam pointing accuracy and attitude accuracy

下载: 全尺寸图片幻灯片

不同波束指向和卫星姿态误差情况下，辅星图像信噪比损失情况如表2所示，0.05°的波束指向误差和0.02°的姿态误差导致的辅星图像信噪比损失小于0.1 dB。

表 2 波束同步误差造成的辅星图像信噪比损失(dB)

Table 2. Influence of beam synchronization error on SNR (dB)

波束指向精度(°)	姿态控制精度(°)
波束指向精度(°)	0.01	0.02
0.01	0.021	0.025
0.02	0.028	0.032
0.03	0.036	0.039
0.04	0.046	0.048
0.05	0.055	0.057

下载: 导出CSV

| 显示表格

0°～0.06°的波束指向误差对距离向重叠幅宽的影响如图15所示。横滚角会在距离向产生波束控制误差，对距离向覆盖偏差产生影响，0.02°的姿态控制误差对重叠幅宽的影响如图16所示。横滚角从0°步进至0.02°，距离向波束指向精度从0°步进至0.06°情况下，两者对距离向重叠幅宽的综合影响如图17所示。上述结果表明，0.02°的姿态控制误差对距离向重叠幅宽的影响为368 m, 0.06°的波束指向误差对距离向重叠幅宽的影响为1100 m，由于波束指向和姿态控制导致的误差均为随机误差，所以综合影响采用几何平均数的形式，两者综合之后对距离向重叠幅宽的影响为1164 m。考虑到轨道控制精度的影响，在重轨工作模式下，两次测量中卫星的位置会在一定范围内偏移，在卫星姿态误差和波束指向误差基础上，系统设计中应综合考虑卫星位置偏移的影响。

图 15 波束指向对重叠幅宽的影响

Figure 15. Overlapping swath error versus beam pointing accuracy

下载: 全尺寸图片幻灯片

图 16 横滚角对重叠幅宽的影响

Figure 16. Overlapping swath error versus roll angle

下载: 全尺寸图片幻灯片

图 17 横滚角和波束指向对重叠幅宽的影响

Figure 17. Overlapping swath error versus roll angle and beam pointing error

下载: 全尺寸图片幻灯片

由上述分析可知，在仿真精度情况下，波束同步精度对多普勒去相干、天线增益以及双基图像信噪比损失的影响较小，但对距离向重叠幅宽影响较大，因此需要在波位设计中保留一定的幅宽余量，或者根据幅宽需求，对波束同步精度提出要求。不同卫星姿态控制精度和波束指向精度对重叠幅宽的综合影响总结在表3可供系统设计参考。针对不同的卫星系统，可以根据系统参数结合式(27)求得对波束同步误差的限制。

表 3 波束同步误差对重叠幅宽的影响(m)

Table 3. Influence of beam synchronization error to overlapping area (m)

波束指向精度(°)	姿态控制精度(°)
波束指向精度(°)	0.01	0.02
0.01	260	411
0.02	411	520
0.03	582	663
0.04	759	823
0.05	938	991
0.06	1119	1164

下载: 导出CSV

| 显示表格

6. 结论

本文分析了分布式SAR系统中时间同步误差和波束同步误差的影响，根据固定项和线性项的时间同步误差模型，推导时间同步和相位同步的关系，并分析线性项需要满足的条件。波束同步部分，本文分析了波束指向误差和卫星姿态误差对方位向合成天线方向图、多普勒去相干以及双基图像信噪比损失情况的影响，并根据几何关系推导距离向重叠幅宽的损失量。根据仿真参数，给出实验结果，以便在系统设计中充分考虑同步问题的影响，提出指标要求，为系统设计提供指导。

图 1 层析成像几何示意图

Figure 1. Imaging geometry of tomographic SAR

下载: 全尺寸图片幻灯片

图 2 峨眉数据的克拉默-拉奥界

Figure 2. The Cramér-Rao Lower Bound (CRLB) of the Emei data

下载: 全尺寸图片幻灯片

图 3 由OMP算法估计散射体位置分布及其对应的高斯混合分布拟合曲线

Figure 3. The probability density function of scattering position estimated by OMP and its corresponding Gaussian mixture distribution fitting curve

下载: 全尺寸图片幻灯片

图 4 不同算法的高程估计精度(M=11, SNR=5 dB, ρ_s=23.7805 m)

Figure 4. Elevation estimation accuracy of different algorithm (M=11, SNR=5 dB, ρ_s=23.7805 m)

下载: 全尺寸图片幻灯片

图 5 OMP-BIC, OMP-GLRT, SLIM, MUSIC的重建成功率与叠掩散射体的幅度比 ${a_1}/{a_2}$ 的函数关系

Figure 5. Recovery probability as a function of amplitude ratio ${a_1}/{a_2}$ obtained by using the OMP-BIC, OMP-GLRT, SLIM and MUSIC

下载: 全尺寸图片幻灯片

图 6 OMP-BIC, OMP-GLRT, SLIM, MUSIC的重建成功率与叠掩散射体的相位差 $\Delta \phi$ 的函数关系

Figure 6. Recovery probability as a function of phase difference $\Delta \phi$ obtained by using the OMP-BIC, OMP-GLRT, SLIM and MUSIC

下载: 全尺寸图片幻灯片

图 7 OMP-BIC, OMP-GLRT, SLIM, MUSIC的重建成功率与叠掩散射体的规范化高程间距 $\Delta s/{\rho _s}$ 的函数关系

Figure 7. Recovery probability as a function of elevation distance $\Delta s/{\rho _s}$ obtained by using the OMP-BIC, OMP-GLRT, SLIM and MUSIC

下载: 全尺寸图片幻灯片

图 8 叠掩散射体间的相位差对MUSIC算法谱估计结果造成的扰动效应(图 8是图 7中 $1.2{\rho _s}$ 附近发生重建成功率异常下降的解释)

Figure 8. The disturbance of height estimation caused by phase difference $\Delta \phi$ between overlapped scatterers (Fig. 8 is an explanation of the abnormal decrease in the recovery rate in Fig. 7)

下载: 全尺寸图片幻灯片

图 9 MUSIC算法的高程估计精度(当限定 ${a_1}/{a_2} = 0.5$ 时，能量小的散射体位置估计出现明显偏差)

Figure 9. Elevation estimation accuracy of MUSIC algorithm (When the amplitude ratio is fixed at 0.5, the position estimation of the scatterer with small energy is obviously deviated)

下载: 全尺寸图片幻灯片

图 10 峨眉数据的场景(红色的箭头标记了切面上的三处叠掩)

Figure 10. The scene of Emei data (The walls of tall buildings and the roofs of low buildings are overlapped)

下载: 全尺寸图片幻灯片

图 11 与图 10中红虚线对应的距离-高程切面图(未经过地理编码)

Figure 11. Range-Elevation section corresponding to the red dotted line in Fig. 10 (without geocoding)

下载: 全尺寸图片幻灯片

图 12 层析成像结果(经过地理编码)

Figure 12. Tomography results (after geocoding)

下载: 全尺寸图片幻灯片

表 1 峨眉数据的参数

Table 1. Parameters of Emei data

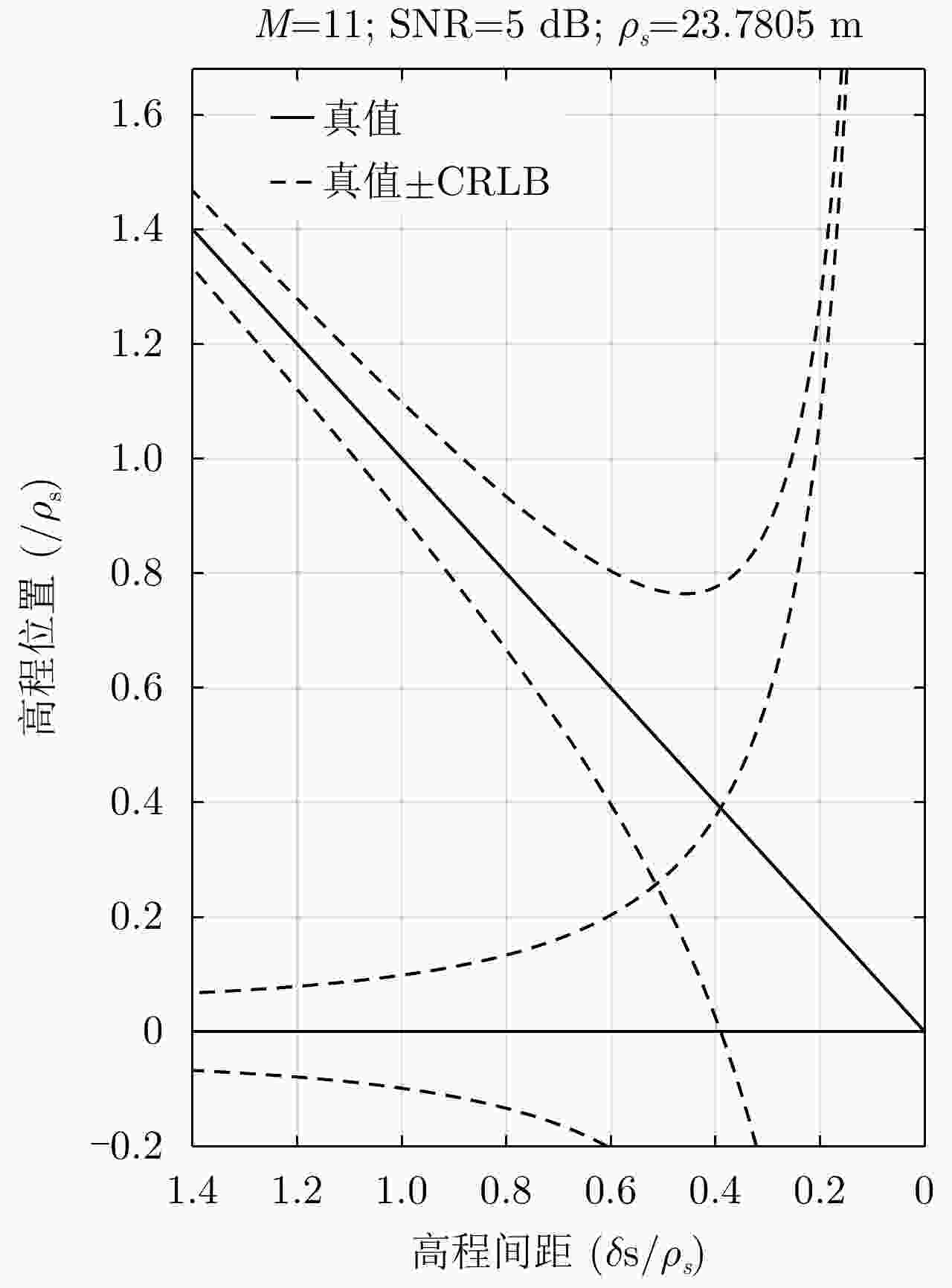
参数数值

波长 $\lambda$ 0.031 m
斜距 r 1629 m
入射角 $\theta$ ${47}^{\circ }$
基线 b 0.2 $\times$ 11 m
瑞利分辨率 ${\rho _s}$ 23.78 m

下载: 导出CSV

参考文献(31)

[1]	KNAELL K K and CARDILLO G P. Radar tomography for the generation of three-dimensional images[J]. IEE Proceedings-Radar, Sonar and Navigation, 1995, 142(2): 54–60. doi: 10.1049/ip-rsn:19951791
[2]	廖明生, 魏恋欢, 汪紫芸, 等. 压缩感知在城区高分辨率SAR层析成像中的应用[J]. 雷达学报, 2015, 4(2): 123–129. doi: 10.12000/JR15031 LIAO Mingsheng, WEI Lianhuan, WANG Ziyun, et al. Compressive sensing in high-resolution 3D SAR tomography of urban scenarios[J]. Journal of Radars, 2015, 4(2): 123–129. doi: 10.12000/JR15031
[3]	REIGBER A and MOREIRA A. First demonstration of airborne SAR tomography using multibaseline L-band data[J]. IEEE Transactions on Geoscience and Remote Sensing, 2000, 38(5): 2142–2152. doi: 10.1109/36.868873
[4]	FORNARO G, SERAFINO F, and SOLDOVIERI F. Three-dimensional focusing with multipass SAR data[J]. IEEE Transactions on Geoscience and Remote Sensing, 2003, 41(3): 507–517. doi: 10.1109/TGRS.2003.809934
[5]	BUDILLON A, EVANGELISTA A, and SCHIRINZI G. SAR tomography from sparse samples[C]. 2009 IEEE International Geoscience and Remote Sensing Symposium, Cape Town, South Africa, 2009: 865–868. doi: 10.1109/IGARSS.2009.5417514.
[6]	ZHU Xiaoxiang and BAMLER R. Super-resolution power and robustness of compressive sensing for spectral estimation with application to spaceborne tomographic SAR[J]. IEEE Transactions on Geoscience and Remote Sensing, 2012, 50(1): 247–258. doi: 10.1109/TGRS.2011.2160183
[7]	VRIEZE S I. Model selection and psychological theory: A discussion of the differences between the Akaike information criterion (AIC) and the Bayesian information criterion (BIC)[J]. Psychological Methods, 2012, 17(2): 228–243. doi: 10.1037/a0027127
[8]	BUDILLON A and SCHIRINZI G. GLRT based on support estimation for multiple scatterers detection in SAR tomography[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2016, 9(3): 1086–1094. doi: 10.1109/JSTARS.2015.2494376
[9]	ZHU Xiaoxiang, GE Nan, and SHAHZAD M. Joint sparsity in SAR tomography for urban mapping[J]. IEEE Journal of Selected Topics in Signal Processing, 2015, 9(8): 1498–1509. doi: 10.1109/JSTSP.2015.2469646
[10]	FERRO-FAMIL L, HUANG Yue, and TEBALDINI S. Polarimetric characterization of 3-D scenes using high-resolution and Full-Rank Polarimetric tomographic SAR focusing[C]. 2016 IEEE International Geoscience and Remote Sensing Symposium, Beijing, China, 2016: 5694–5697. doi: 10.1109/IGARSS.2016.7730487.
[11]	TEBALDINI S, ROCCA F, D’ALESSANDRO M M, et al. Phase calibration of airborne tomographic SAR data via phase center double localization[J]. IEEE Transactions on Geoscience and Remote Sensing, 2016, 54(3): 1775–1792. doi: 10.1109/TGRS.2015.2488358
[12]	NANNINI M, SCHEIBER R, HORN R, et al. First 3-D reconstructions of targets hidden beneath foliage by means of polarimetric SAR tomography[J]. IEEE Geoscience and Remote Sensing Letters, 2012, 9(1): 60–64. doi: 10.1109/LGRS.2011.2160329
[13]	柳祥乐. 多基线层析成像合成孔径雷达研究[D]. [博士论文], 中国科学院研究生院(电子学研究所), 2007. LIU Xiangle. Study on multibaseline tomography synthetic aperture radar[D]. [Ph. D. dissertation], Chinese Acedamy of Sciences, 2007.
[14]	王金峰. SAR层析三维成像技术研究[D]. [博士论文], 电子科技大学, 2010. WANG Jinfeng. Study of three-dimentional synthetic aperture radar tomography imaging technology[D]. [Ph. D. dissertation], University of Electronic Science and Technology of China, 2010.
[15]	WANG Xiao, XU Feng, and JIN Yaqiu. Numerical simulation of tomographic-SAR imaging and object reconstruction using compressive sensing with L_1/2-norm regularization[J]. Chinese Science Bulletin, 2014, 59(33): 4600–4607. doi: 10.1007/s11434-014-0554-5
[16]	刘康. 基于高分辨率SAR影像提取建筑物高度的研究[D]. [博士论文], 武汉大学, 2012. LIU Kang. Advanced methods for building height extraction from high resolution SAR images[D]. [Ph. D. dissertation], Wuhan University, 2012.
[17]	SUN Xilong, YU Anxi, DONG Zhen, et al. Three-dimensional SAR focusing via compressive sensing: The case study of angel stadium[J]. IEEE Geoscience and Remote Sensing Letters, 2012, 9(4): 759–763. doi: 10.1109/LGRS.2011.2181321
[18]	李震, 张平, 乔海伟, 等. 层析SAR地表参数信息提取研究进展[J]. 雷达学报, 2021, 10(1): 116–130. doi: 10.12000/JR20095 LI Zhen, ZHANG Ping, QIAO Haiwei, et al. Advances in information extraction of surface parameters using tomographic SAR[J]. Journal of Radars, 2021, 10(1): 116–130. doi: 10.12000/JR20095
[19]	仇晓兰, 焦泽坤, 彭凌霄, 等. SARMV3D-1.0: SAR微波视觉三维成像数据集[J]. 雷达学报, 2021, 10(4): 485–498. doi: 10.12000/JR21112 QIU Xiaolan, JIAO Zekun, PENG Lingxiao, et al. SARMV3D-1.0: Synthetic aperture radar microwave vision 3D imaging dataset[J]. Journal of Radars, 2021, 10(4): 485–498. doi: 10.12000/JR21112
[20]	JIAO Zekun, DING Chibiao, QIU Xiaolan, et al. Urban 3D imaging using airborne TomoSAR: Contextual information-based approach in the statistical way[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2020, 170: 127–141. doi: 10.1016/j.isprsjprs.2020.10.013
[21]	ZHANG Fubo, LIANG Xingdong, CHENG Ruichang, et al. Building corner reflection in MIMO SAR tomography and compressive sensing-based corner reflection suppression[J]. IEEE Geoscience and Remote Sensing Letters, 2020, 17(3): 446–450. doi: 10.1109/LGRS.2019.2926301
[22]	李杭, 梁兴东, 张福博, 等. 基于高斯混合聚类的阵列干涉SAR三维成像[J]. 雷达学报, 2017, 6(6): 630–639. doi: 10.12000/JR17020 LI Hang, LIANG Xingdong, ZHANG Fubo, et al. 3D imaging for array InSAR based on Gaussian mixture model clustering[J]. Journal of Radars, 2017, 6(6): 630–639. doi: 10.12000/JR17020
[23]	KAY S M, 罗鹏飞, 张文明, 刘忠, 等译. 统计信号处理基础: 估计与检测理论[M]. 北京: 电子工业出版社, 2011: 451–453. KAY S M, LUO Pengfei, ZHANG Wenming, LIU Zhong, et al. translation. Fundamentals of Statistical Signal Processing Volume I: Estimation Theory[M]. Beijing: Publishing House of Electronics Industry, 2011: 451–453.
[24]	BAMLER R, EINEDER M, ADAM N, et al. Interferometric potential of high resolution spaceborne SAR[J]. Photogrammetrie - Fernerkundung - Geoinformation, 2009, 5: 407–419. doi: 10.1127/1432-8364/2009/0029
[25]	CHEN S, BILLINGS S A, and LUO W. Orthogonal least squares methods and their application to non-linear system identification[J]. International Journal of Control, 1989, 50(5): 1873–1896. doi: 10.1080/00207178908953472
[26]	DONOHO D L. Compressed sensing[J]. IEEE Transactions on Information Theory, 2006, 52(4): 1289–1306. doi: 10.1109/TIT.2006.871582
[27]	MA Peifeng, LIN Hui, LAN Hengxing, et al. On the performance of reweighted L₁ minimization for tomographic SAR imaging[J]. IEEE Geoscience and Remote Sensing Letters, 2015, 12(4): 895–899. doi: 10.1109/LGRS.2014.2365613
[28]	TAN Xing, ROBERTS W, LI Jian, et al. Sparse learning via iterative minimization with application to MIMO radar imaging[J]. IEEE Transactions on Signal Processing, 2011, 59(3): 1088–1101. doi: 10.1109/TSP.2010.2096218
[29]	SCHMIDT R. Multiple emitter location and signal parameter estimation[J]. IEEE Transactions on Antennas and Propagation, 1986, 34(3): 276–280. doi: 10.1109/TAP.1986.1143830
[30]	MOON T K. The expectation-maximization algorithm[J]. IEEE Signal Processing Magazine, 1996, 13(6): 47–60. doi: 10.1109/79.543975
[31]	KRIEGER G, ROMMEL T, and MOREIRA A. MIMO-SAR tomography[C]. The 11th European Conference on Synthetic Aperture Radar, Berlin, Germany, 2016.

施引文献

资源附件(0)

访问统计

图(12) / 表(1)

计量

文章访问数:
HTML全文浏览量:
PDF下载量:
被引次数: 0

1. 引言
2. 误差模型
2.1 时间同步误差模型
2.2 波束同步误差模型
3. 时间同步误差分析
3.1 固定时间误差分析
3.2 时间同步与相位同步关系
4. 波束同步误差分析
4.1 对方位向影响
4.2 对距离向影响
5. 仿真结果
5.1 时间同步误差
5.2 波束同步误差
6. 结论

1. 引言
2. 误差模型
2.1 时间同步误差模型
2.2 波束同步误差模型
3. 时间同步误差分析
3.1 固定时间误差分析
3.2 时间同步与相位同步关系
4. 波束同步误差分析
4.1 对方位向影响
4.2 对距离向影响
5. 仿真结果
5.1 时间同步误差
5.2 波束同步误差
6. 结论

参考文献(31)

施引文献

资源附件(0)

访问统计

若干层析SAR成像方法在解叠掩性能上的对比分析

DOI: 10.12000/JR21139

通讯作者:
徐丰 fengxu@fudan.edu.cn

计量

Comparative Experiments on Separation Performance of Overlapping Scatterers with Several Tomography Imaging Methods

Corresponding author: XU Feng, fengxu@fudan.edu.cn

1. 引言

2. 误差模型

2.1 时间同步误差模型

2.2 波束同步误差模型

3. 时间同步误差分析

3.1 固定时间误差分析

3.2 时间同步与相位同步关系

4. 波束同步误差分析

4.1 对方位向影响

4.2 对距离向影响

5. 仿真结果

5.1 时间同步误差

5.2 波束同步误差

6. 结论

计量

目录

1. 引言

2. 误差模型

2.1 时间同步误差模型

2.2 波束同步误差模型

3. 时间同步误差分析

3.1 固定时间误差分析

3.2 时间同步与相位同步关系

4. 波束同步误差分析

4.1 对方位向影响

4.2 对距离向影响

5. 仿真结果

5.1 时间同步误差

5.2 波束同步误差

6. 结论

期刊介绍

联系我们

参数	数值
波长 $\lambda$	0.031 m
斜距 r	1629 m
入射角 $\theta$	${47}^{\circ }$
基线 b	0.2 $\times$ 11 m
瑞利分辨率 ${\rho _s}$	23.78 m

若干层析SAR成像方法在解叠掩性能上的对比分析

DOI: 10.12000/JR21139

通讯作者: 徐丰 fengxu@fudan.edu.cn

计量

出版历程

Comparative Experiments on Separation Performance of Overlapping Scatterers with Several Tomography Imaging Methods

Corresponding author: XU Feng, fengxu@fudan.edu.cn

1. 引言

2. 误差模型

2.1 时间同步误差模型

2.2 波束同步误差模型

3. 时间同步误差分析

3.1 固定时间误差分析

3.2 时间同步与相位同步关系

4. 波束同步误差分析

4.1 对方位向影响

4.2 对距离向影响

5. 仿真结果

5.1 时间同步误差

5.2 波束同步误差

6. 结论

计量

出版历程

目录

1. 引言

2. 误差模型

2.1 时间同步误差模型

2.2 波束同步误差模型

3. 时间同步误差分析

3.1 固定时间误差分析

3.2 时间同步与相位同步关系

4. 波束同步误差分析

4.1 对方位向影响

4.2 对距离向影响

5. 仿真结果

5.1 时间同步误差

5.2 波束同步误差

6. 结论

期刊介绍

联系我们

通讯作者:
徐丰 fengxu@fudan.edu.cn