作者中心
专家审稿
责编办公
编辑办公
High-resolution High-dimensional Imaging of Urban Building Based on GaoFen-3 SAR Data（in English）
-
摘要: 传统合成孔径雷达(SAR)只能获取方位-距离二维图像，无法准确反映目标的三维散射结构信息。层析合成孔径雷达(TomoSAR)是一种多基线干涉测量模式，它将合成孔径原理扩展至高程向，除了可对目标进行二维成像之外，还可以准确恢复目标的高度向散射信息，真正实现三维成像。差分层析合成孔径雷达(D-TomoSAR)将合成孔径原理延伸至高程和时间方向，不仅可以获得目标的三维散射结构，还可以高精度获取观测目标的形变速率，实现对目标形变的有效监测。高分三号是我国首颗1 m分辨率C频段多极化SAR卫星。它具有高分辨率、大成像幅宽、多成像模式等特点，对我国高分对地观测技术的发展具有重要意义。目前高分三号数据主要应用于目标识别等图像处理领域，没有充分利用SAR图像的相位信息。而且，由于设计之初未考虑后续高维成像应用，现有高分三号获取的SAR图像存在有一定的空间、时间去相干问题，对应用于后续干涉系列处理产生了一定影响。为解决上述问题，该文基于7景高分三号SAR复图像，开展了对北京雁栖湖周围建筑的三维、四维层析成像研究，在获取了建筑物三维散射结构信息的同时，实现了对建筑物形变的毫米级高精度监测。该初步实验结果证明了高分三号SAR数据的应用潜力，为后续进一步扩展高分三号SAR卫星在城市感知与监测中的应用提供了技术支撑。
-
关键词:
- 三维成像 /
- 四维成像 /
- 层析合成孔径雷达 /
- 差分层析合成孔径雷达 /
- 高分三号
Abstract: Conventional Synthetic Aperture Radar (SAR) can only obtain two-dimensional (2-D) azimuth-range images without accurately reflecting the three-Dimensional (3-D) scattering structure information of the targets. However, SAR Tomography (TomoSAR) is a multi-baseline interferometric measurement mode that extends the synthetic aperture principle into the elevation direction, making it possible to recover the true height of the target, thereby achieving 3-D imaging. Moreover, Differential SAR Tomography (D-TomoSAR) extends the synthetic aperture principle into the elevation and time directions simultaneously. Thus, it can obtain the target 3-D scattering structure along with the deformation speed of the observed target. GaoFen-3 (GF-3) is the first C-band multi-polarization 1 m resolution SAR satellite of China. It has several advantages, such as high-resolution, large swath width, and multiple imaging modes, which are crucial to the development of a high-resolution earth observation technology for China. Presently, GF-3 data are mainly used in the image processing field, such as target identification. However, the phase information of the SAR images is not yet fully utilized. Moreover, because of the high-dimensional imaging ability that was overlooked at the beginning of designing the system, existing SAR images acquired by GF-3 have spatial and temporal de-coherence problems. Thus, it is difficult to use the images in further interference series processing. To solve the above problems, this study achieved 3-D and four-Dimensional (4-D) imaging of buildings around Yanqi Lake, in Beijing, based on the data of seven SAR complex images. We obtained the 3-D scattering structure information of buildings and achieved millimeter-level high-precision monitoring of building deformation. The preliminary experimental results demonstrate the application potential of GF-3 SAR data and provide a technical support for the subsequent further application of the GF-3 SAR satellite in urban sensing and monitoring. -
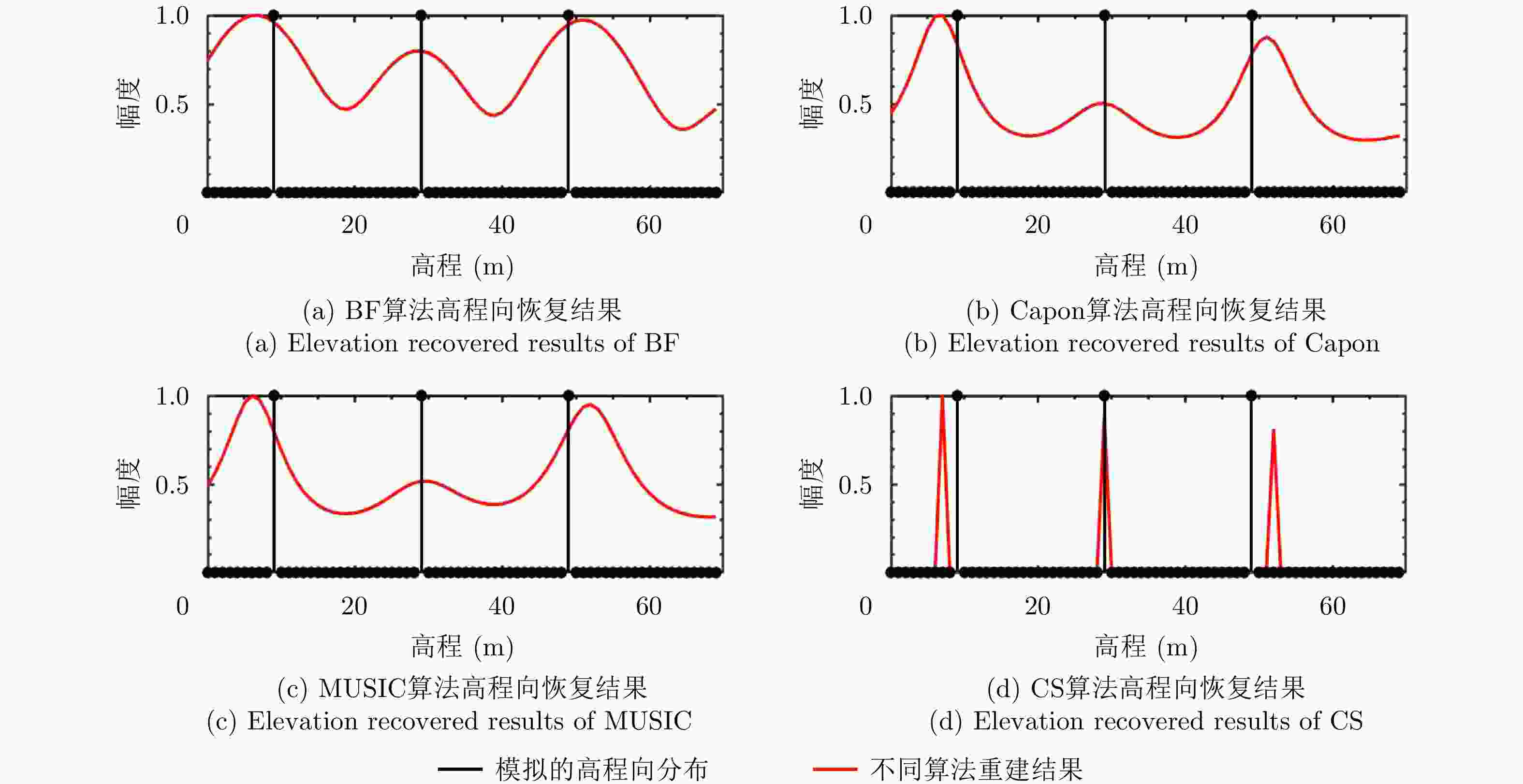
图 3 高程向两个散射点的TomoSAR成像结果(左图：两个散射点之间的距离为11 m；右图：两个散射点之间的距离为50 m)
Figure 3. TomoSAR reconstructed reflectivity profiles of two scattering points along the elevation direction (left image: the distance between two scattering points is 11 m; right image: the distance between two scattering points is 50 m)
图 4 高程向3个散射点的TomoSAR成像结果(3个散射点之间的间隔为20 m)
Figure 4. TomoSAR reconstructed reflectivity profiles of three scattering points along the elevation direction (the distance between three scattering points is 20 m)
图 5 D-TomoSAR仿真结果(两个散射体高程位置为–10 m, 10 m；散射体形变速率分别为4毫米/年、–7毫米/年)
Figure 5. D-TomoSAR simulation results (elevation position of two scatters are –10 m and 10 m; deformation velocity of two scatters are 4 mm/year and –7 mm/year, respectively)
图 7 生态农业公司高程图及形变速率图
Figure 7. Elevation and deformation velocity maps of ecological agricultural company
图 9 北京雁栖湖国际会展中心
Figure 9. Beijing Yanqi lake international convention and exhibition center
图 10 北京雁栖湖国际会展中心高程图及形变速率图
Figure 10. Elevation and deformation velocity maps of Beijing Yanqi lake international convention and exhibition center
图 11 北京雁栖湖国际会展中心三维点云图
Figure 11. 3-D point cloud of Beijing Yanqi lake international convention and exhibition center
图 13 顶秀美泉小镇区域的高程图及形变速率图
Figure 13. Elevation and deformation velocity maps of Dingxiumeiquan town
图 3 TomoSAR reconstructed reflectivity profiles of two scattering points along the elevation direction (left image: the distance between two scatterers is 11 m; right image: the distance between two scatters is 50 m)
图 4 TomoSAR reconstructed reflectivity profiles of three scattering points along the elevation direction (the distance between three scatterers is 20 m)
图 5 D-TomoSAR simulation results (elevation position of two scatterers are –10 m and 10 m; deformation velocity of two scatterers are 4 mm/year and –7 mm/year, respectively)
图 10 Elevation and deformation velocity maps of Beijing Yanqi Lake International Convention and Exhibition Center
图 11 3-D point cloud of Beijing Yanqi Lake International Convention and Exhibition Center
表 1 高分三号数据集参数
Table 1. Parameters of GF-3 dataset
参数名称 数值 参数名称 数值 空间基线跨度 1417.4 m 数据景数 7景 时间基线跨度 464 d 方位向分辨率 0.3626 m 斜距 1052747 m 距离向分辨率 0.765692 m 波长 0.056 m 高程向理论分辨率 20.6174 m 入射角 47.2330015° 形变理论分辨率 21.8毫米/年 
下载: 导出CSV
表 2 高分三号数据集时空基线参数
Table 2. Spatial-temporal baseline parameters of GF-3 dataset
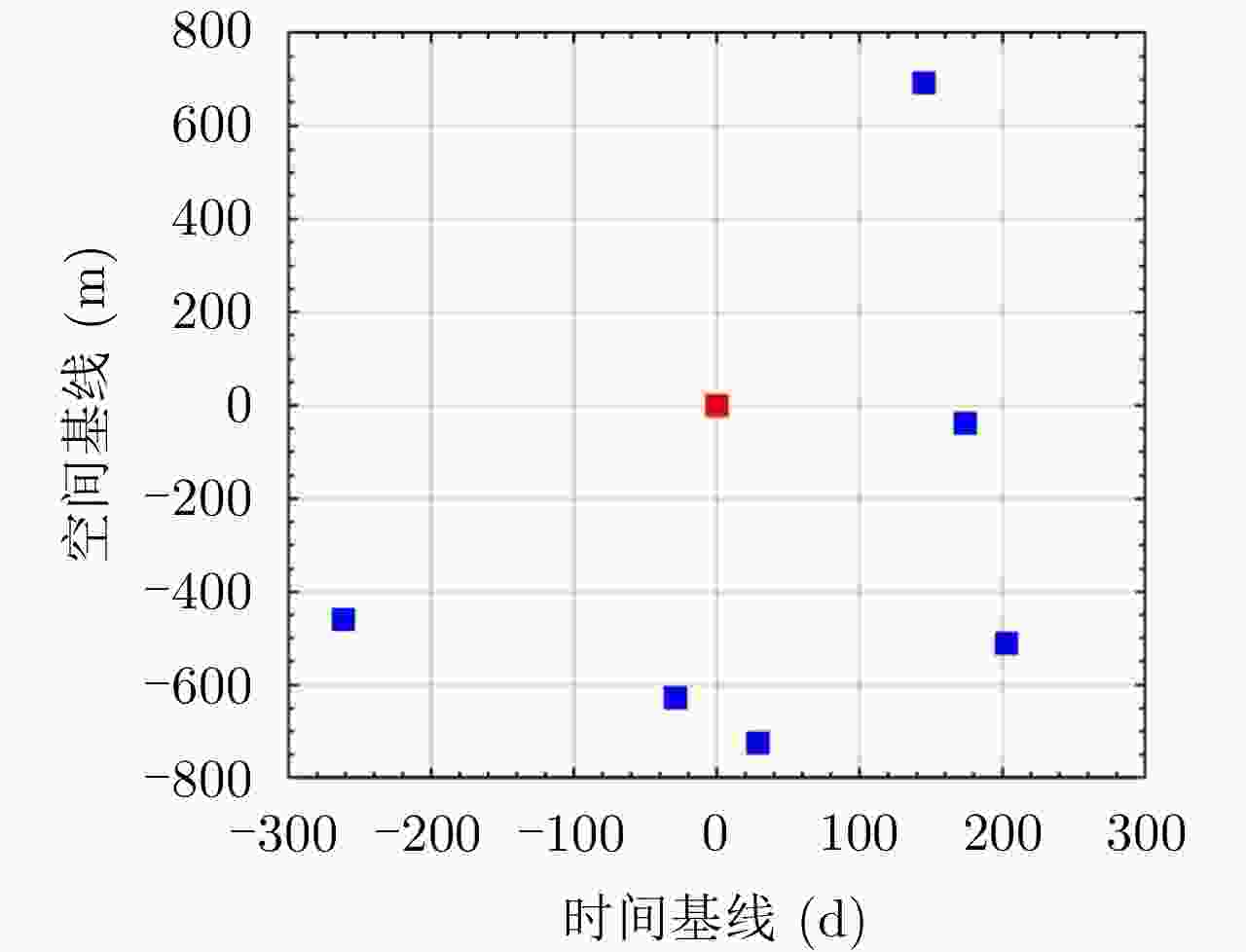
编号 获取时间 空间基线(m) 时间基线(d) 1 2018.06.13 –459.108 –261 2 2019.01.31 –628.551 –29 3 2019.03.01 0 0 4 2019.03.30 –724.517 29 5 2019.07.24 692.863 145 6 2019.08.22 –38.211 174 7 2019.09.20 –510.491 203
下载: 导出CSV
表 1 Parameters of the GF-3 dataset
Parameter Value Parameter Value Spatial baseline span 1417.4 m Number of scenes 7 Temporal baseline span 464 d Azimuth resolution 0.3626 m Slant range 1052747 m Range resolution 0.765692 m Wavelength 0.056 m Elevation resolution 20.6174 m Incident angle 47.2330015° Information resolution 21.8 mm/year
下载: 导出CSV
表 2 Spatio-temporal baseline parameters of the GF-3dataset
Number Time of acquisition Spatial baseline (m) Temporal baseline (d) 1 2018.06.13 –459.108 –261 2 2019.01.31 –628.551 –29 3 2019.03.01 0 0 4 2019.03.30 –724.517 29 5 2019.07.24 692.863 145 6 2019.08.22 –38.211 174 7 2019.09.20 –510.491 203
下载: 导出CSV
-
[1] CURLANDER J C and MCDONOUGH R N. Synthetic Aperture Radar: Systems and Signal Processing[M]. New York: Wiley, 1991. [2] BUDILLON A, JOHNSY A C, and SCHIRINZI G. Contextual information based SAR tomography of urban areas[C]. 2019 Joint Urban Remote Sensing Event (JURSE), Vannes, Italy, 2019: 1–4. doi: 10.1109/JURSE.2019.8809076. [3] REIGBER A, MOREIRA A, and PAPATHANASSIOU K P. First demonstration of airborne SAR tomography using multibaseline L-band data[C]. IEEE 1999 International Geoscience and Remote Sensing Symposium, Hamburg, Germany, 1999: 44–46. doi: 10.1109/IGARSS.1999.773395. [4] REIGBER A and MOREIRA A. First demonstration of airborne SAR tomography using multibaseline L-band data[J]. IEEE Transactions on Geoscience and Remote Sensing, 2000, 38(5): 2142–2152. doi: 10.1109/36.868873 [5] FORNARO G and SERAFINO F. Imaging of single and double scatterers in urban areas via SAR tomography[J]. IEEE Transactions on Geoscience and Remote Sensing, 2006, 44(12): 3497–3505. doi: 10.1109/TGRS.2006.881748 [6] REALE D, FORNARO G, PAUCIULLO A, et al. Tomographic imaging and monitoring of buildings with very high resolution SAR data[J]. IEEE Geoscience and Remote Sensing Letters, 2011, 8(4): 661–665. doi: 10.1109/LGRS.2010.2098845 [7] SHAHZAD M and ZHU Xiaoxiang. Reconstruction of building façades using spaceborne multiview TomoSAR point clouds[C]. 2013 IEEE International Geoscience and Remote Sensing Symposium - IGARSS, Melbourne, Australia, 2013: 624–627. doi: 10.1109/IGARSS.2013.6721234. [8] WANG Xiao, XU Feng, and JIN Yaqiu. The iterative reweighted alternating direction method of multipliers for separating structural layovers in SAR tomography[J]. IEEE Geoscience and Remote Sensing Letters, 2017, 14(11): 1883–1887. doi: 10.1109/LGRS.2017.2694825 [9] WANG Yuanyuan and ZHU Xiaoxiang. Robust nonlinear blind SAR tomography in urban areas[C]. 12th European Conference on Synthetic Aperture Radar, Aachen, Germany, 2018: 1–6. [10] 秦斐, 梁兴东, 张福博, 等. 基于机器学习的阵列层析SAR建筑物目标提取方法[J]. 信号处理, 2019, 35(2): 176–186. doi: 10.16798/j.issn.1003-0530.2019.02.003QIN Fei, LIANG Xingdong, ZHANG Fubo, et al. Building target extraction methods in array SAR tomography based on machine learning[J]. Journal of Signal Processing, 2019, 35(2): 176–186. doi: 10.16798/j.issn.1003-0530.2019.02.003 [11] LOMBARDINI F. Differential tomography: A new framework for SAR interferometry[C]. IGARSS 2003. 2003 IEEE International Geoscience and Remote Sensing Symposium, Toulouse, French, 2003: 1206–1208. doi: 10.1109/IGARSS.2003.1294059. [12] FORNARO G, PAUCIULLO A, and SERAFINO F. Multipass SAR processing for urbanized areas imaging and deformation monitoring at small and large scales[C]. 2007 Urban Remote Sensing Joint Event, Paris, 2007: 1–7. doi: 10.1109/URS.2007.371879. [13] FORNARO G, REALE D, and SERAFINO F. 4D SAR focusing: A tool for improved imaging and monitoring of urban areas[C]. IGARSS 2008 - 2008 IEEE International Geoscience and Remote Sensing Symposium, Boston, USA, 2008: V-475–V-478. doi: 10.1109/IGARSS.2008.4780132. [14] ZHU Xiaoxiang, ADAM N, and BAMLER R. Space-borne high resolution tomographic interferometry[C]. 2009 IEEE International Geoscience and Remote Sensing Symposium, Cape Town, South Africa, 2009: IV-869–IV-872. doi: 10.1109/IGARSS.2009.5417515. [15] FORNARO G, SERAFINO F, and REALE D. 4-D SAR imaging: The case study of Rome[J]. IEEE Geoscience and Remote Sensing Letters, 2010, 7(2): 236–240. doi: 10.1109/LGRS.2009.2032133 [16] ZHU Xiaoxiang and BAMLER R. Let’s do the time warp: Multicomponent nonlinear motion estimation in differential SAR tomography[J]. IEEE Geoscience and Remote Sensing Letters, 2011, 8(4): 735–739. doi: 10.1109/LGRS.2010.2103298 [17] SIDDIQUE M A, HAJNSEK I, AERSOSPACE G, et al. Investigating the combined use of differential SAR tomography and PSI for spatio-temporal inversion[C]. 2015 Joint Urban Remote Sensing Event (JURSE), Lausanne, Swiss, 2015: 1–4. doi: 10.1109/JURSE.2015.7120504. [18] WANG Zhigui and LIU Mei. Seasonal deformation and accelerated motion of infrastructure monitoring using a generalized differential SAR tomography[J]. IEEE Geoscience and Remote Sensing Letters, 2020, 17(4): 626–630. doi: 10.1109/LGRS.2019.2917324 [19] CANDÈS E J. Compressive sampling[C]. The International Congress of Mathematicians, Madrid, Spain, 2006: 1433–1452. [20] DONOHO D L. Compressed sensing[J]. IEEE Transactions on Information Theory, 2006, 52(4): 1289–1306. doi: 10.1109/TIT.2006.871582 [21] CANDÈS E J, ROMBERG J K, and TAO T. Stable signal recovery from incomplete and inaccurate measurements[J]. Communications on Pure and Applied Mathematics, 2006, 59(8): 1207–1223. doi: 10.1002/cpa.20124 [22] ZHU Xiaoxiang and BAMLER R. Tomographic SAR inversion by L1-Norm regularization—The compressive sensing approach[J]. IEEE Transactions on Geoscience and Remote Sensing, 2010, 48(10): 3839–3846. doi: 10.1109/TGRS.2010.2048117 [23] ZHU Xiaoxiang and BAMLER R. Super-resolution of sparse reconstruction for tomographic SAR imaging-demonstration with real data[C]. EUSAR 2012; 9th European Conference on Synthetic Aperture Radar, Nuremberg, USA, 2012: 215–218. [24] WEISS M, FORNARO G, and REALE D. Multi scatterer detection within tomographic SAR using a compressive sensing approach[C]. 2015 3rd International Workshop on Compressed Sensing Theory and its Applications to Radar, Sonar and Remote Sensing (CoSeRa), Pisa, 2015: 11–15. doi: 10.1109/CoSeRa.2015.7330254. [25] LI Xinwu, PENG Xing, and LIANG Lei. Sparse reconstruction-based SAR tomography and it’s application[C]. 2017 IEEE International Conference on Imaging Systems and Techniques (IST), Beijing, China, 2017: 1–5. doi: 10.1109/IST.2017.8261514. [26] ZHU Xiaoxiang and BAMLER R. Super-resolution for 4-D SAR tomography via compressive sensing[C]. 8th European Conference on Synthetic Aperture Radar, Aachen, Germany, 2010: 1–4. [27] ZHU Xiaoxiang and BAMLER R. Compressive sensing for high resolution differential SAR tomography - the SL1MMER algorithm[C]. 2010 IEEE International Geoscience and Remote Sensing Symposium, Honolulu, USA, 2010: 17–20. doi: 10.1109/IGARSS.2010.5654021. [28] LENG Ying, LI Fei, SHAO Yunfeng, et al. Elevation and deformation estimation based on TomoSAR[C]. EUSAR 2014; 10th European Conference on Synthetic Aperture Radar, Berlin, Germany, 2014: 1–4. [29] 姚天宇. 长征四号丙运载火箭成功发射高分三号卫星[J]. 中国航天, 2016(8): 8.YAO Tianyu. The Long March 4C carrier rocket successfully launched the GaoFen-3 satellite[J]. Aerospace China, 2016(8): 8. [30] 张庆君. 高分三号卫星总体设计与关键技术[J]. 测绘学报, 2017, 46(3): 269–277. doi: 10.11947/j.AGCS.2017.20170049ZHANG Qingjun. System design and key technologies of the GF-3 satellite[J]. Acta Geodaetica et Cartographica Sinica, 2017, 46(3): 269–277. doi: 10.11947/j.AGCS.2017.20170049 [31] 李胜阳, 许志辉, 陈子琪, 等. 高分3号卫星影像在黄河洪水监测中的应用[J]. 水利信息化, 2017(5): 22–26, 72.LI Shengyang, XU Zhihui, CHEN Ziqi, et al. Application of GF-3 satellite remote sensing image on Yellow River flood monitoring[J]. Water Resources Informatization, 2017(5): 22–26, 72. [32] 马建威, 孙亚勇, 陈德清, 等. 高分三号卫星在洪涝和滑坡灾害应急监测中的应用[J]. 航天器工程, 2017, 26(6): 161–166. doi: 10.3969/j.issn.1673-8748.2017.06.026MA Jianwei, SUN Yayong, CHEN Deqing, et al. Applications of GF-3 satellite in flood and landslide disasters emergency monitoring[J]. Spacecraft Engineering, 2017, 26(6): 161–166. doi: 10.3969/j.issn.1673-8748.2017.06.026 [33] 余博, 李如仁, 陈振炜, 等. 基于高分三号数据的干涉测量研究[J]. 测绘工程, 2019, 28(4): 19–23, 28.YU Bo, LI Ruren, CHEN Zhenwei, et al. Experimental research on interferometry based on GF-3 SAR data[J]. Engineering of Surveying and Mapping, 2019, 28(4): 19–23, 28. [34] 黄震, 赵双明, 常青. 国产高分三号卫星干涉测量试验[J]. 测绘地理信息, 2021, 46(4): 7–11. doi: 10.14188/j.2095-6045.2019083HUANG Zhen, ZHAO Shuangming, and CHANG Qing. Interferometric test using domestic GF-3 satellite[J]. Journal of Geomatics, 2021, 46(4): 7–11. doi: 10.14188/j.2095-6045.2019083 [35] FORNARO G, SERAFINO F, and SOLDOVIERI F. Three-dimensional focusing with multipass SAR data[J]. IEEE Transactions on Geoscience and Remote Sensing, 2003, 41(3): 507–517. doi: 10.1109/TGRS.2003.809934 [36] ZHU X. High-resolution spaceborne radar tomography[D]. Technische Universität München, 2008. [37] FORNARO G, REALE D, and SERAFINO F. Four-dimensional SAR imaging for height estimation and monitoring of single and double scatterers[J]. IEEE Transactions on Geoscience and Remote Sensing, 2009, 47(1): 224–237. doi: 10.1109/TGRS.2008.2000837 [38] PATI Y C, REZAIIFAR R, and KRISHNAPRASAD P S. Orthogonal matching pursuit: Recursive function approximation with applications to wavelet decomposition[C]. 27th Asilomar Conference on Signals, Systems and Computers, Pacific Grove, USA, 1993: 40–44. doi: 10.1109/ACSSC.1993.342465. [39] BI Hui and BI Guoan. Performance analysis of iterative soft thresholding algorithm for L1 regularization based sparse SAR imaging[C]. 2019 IEEE Radar Conference (RadarConf), Boston, USA, 2019: 1–6. doi: 10.1109/RADAR.2019.8835551. [40] 毕辉. 基于稀疏信号处理的SAR/TomoSAR成像方法研究[D]. [博士论文], 中国科学院大学, 2017: 33–41.BI Hui. Research on the imaging method of SAR/TomoSAR based on sparse signal processing[D]. [Ph. D. dissertation], University of Chinese Academy of Sciences, 2007: 33–41. [41] STOICA P and MOSES R. Spectral Analysis of Signals[M]. Upper Sadle River, New Jersey: Pearson Prentice Hall, 2005. [42] CAPON J. High-resolution frequency-wavenumber spectrum analysis[J]. Proceedings of the IEEE, 1969, 57(8): 1408–1418. doi: 10.1109/PROC.1969.7278 [43] SCHMIDT R. Multiple emitter location and signal parameter estimation[J]. IEEE Transactions on Antennas and Propagation, 1986, 34(3): 276–280. doi: 10.1109/TAP.1986.1143830 [44] STOICA P and NEHORAI A. MUSIC, maximum likelihood, and Cramer-Rao bound: Further results and comparisons[J]. IEEE Transactions on Acoustics,Speech,and Signal Processing, 1990, 38(12): 2140–2150. doi: 10.1109/29.61541 -
计量
- 文章访问数: 3861
- HTML全文浏览量: 1310
- PDF下载量: 418
- 被引次数: 0
