作者中心
专家审稿
责编办公
编辑办公
HRRP Target Recognition Method for Full Polarimetric Radars by Combining Cameron Decomposition and Fusing RKELM
-
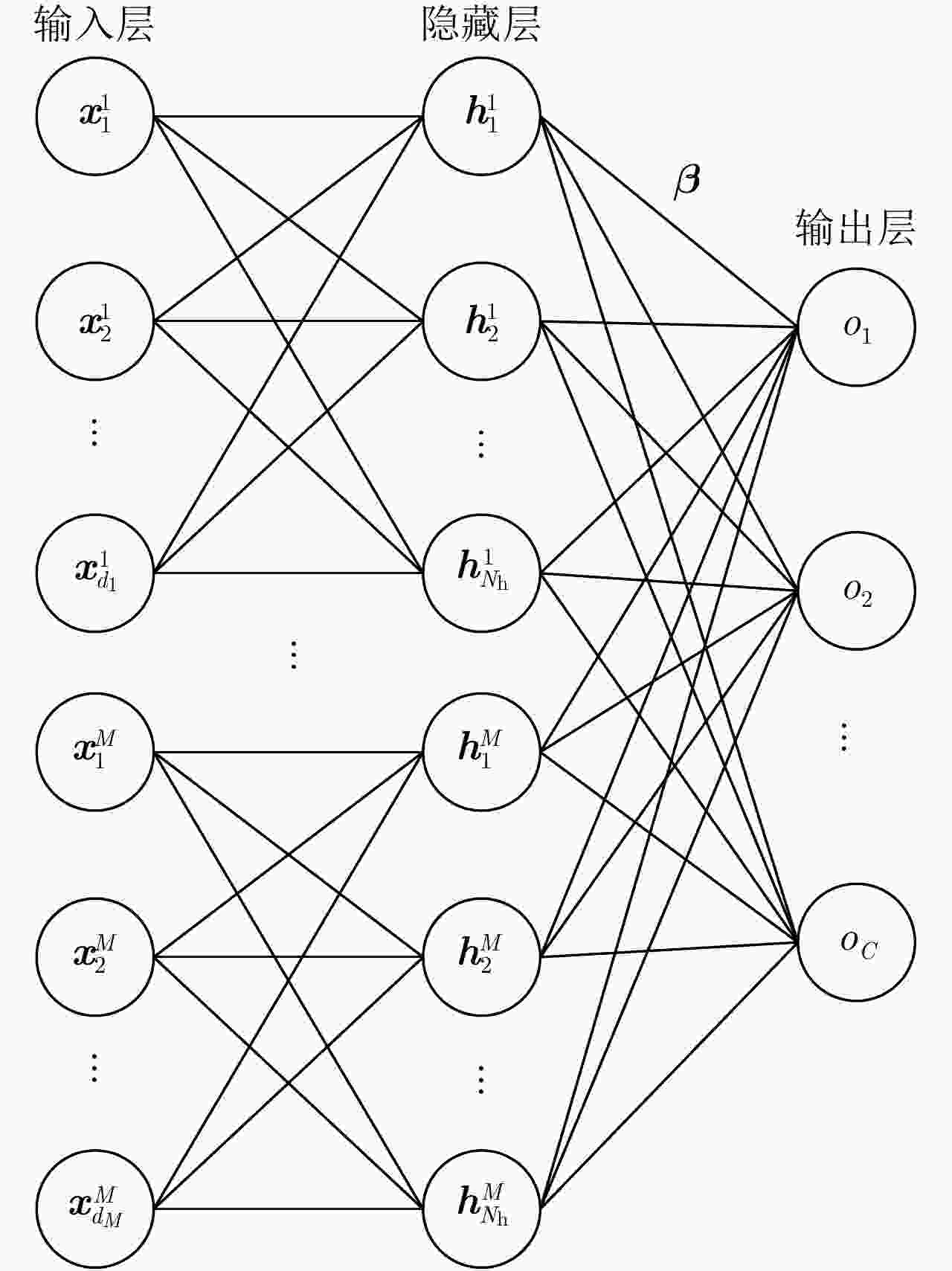
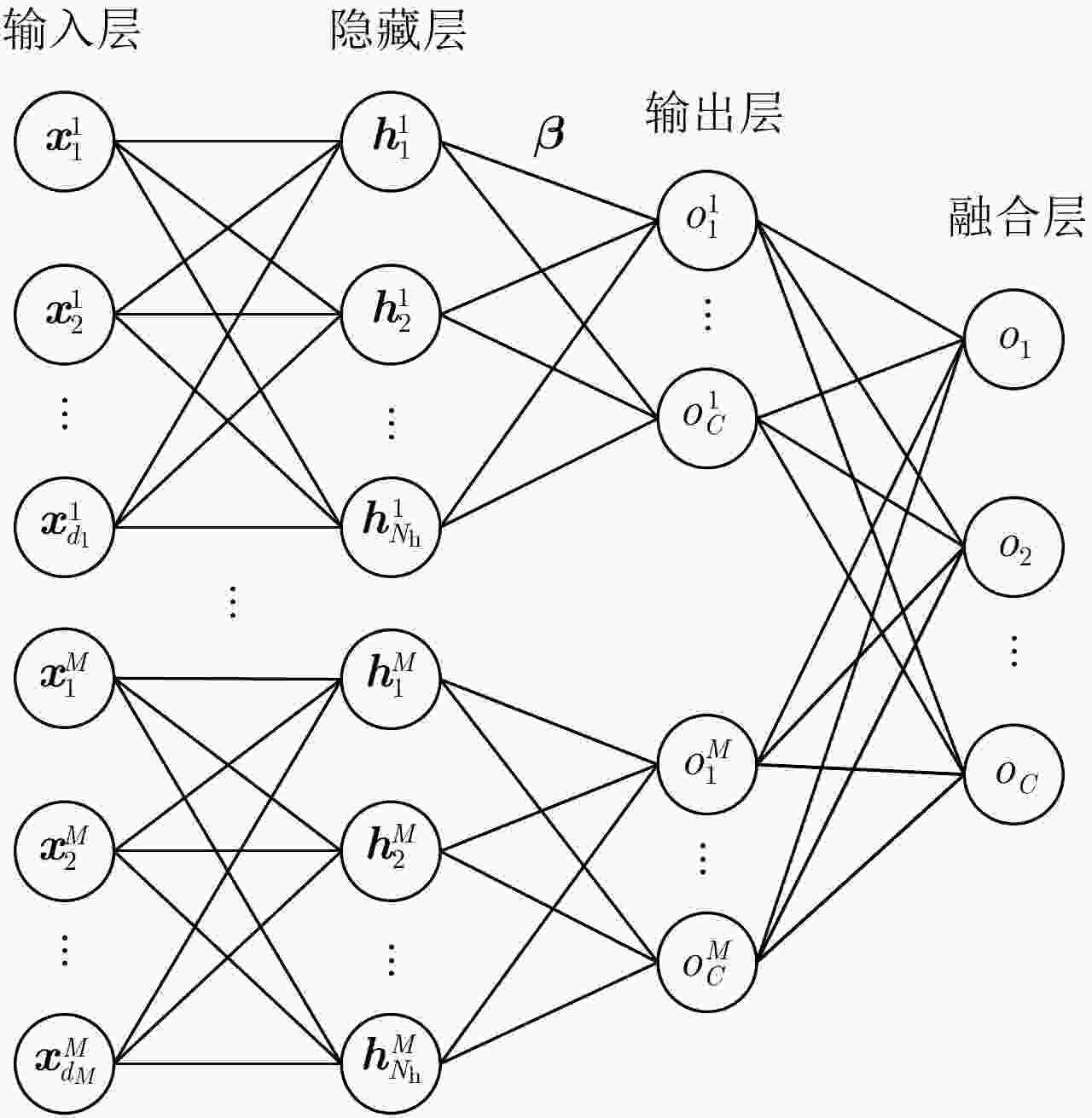
摘要: 该文针对传统全极化高分辨一维距离像(HRRP)雷达目标识别问题，提出了结合Cameron分解和融合简化核极限学习机(RKELM)的目标识别方法，旨在提高全极化HRRP目标识别性能。在特征提取阶段，所提方法利用Cameron分解定义了目标在各个标准散射体上的投影分量。通过分析，将目标在三面角、二面角和1/4波长器件这3个散射基上沿距离维的投影分量作为目标特征，实现对目标散射特性更加精细化的描述。在分类阶段，考虑到RKELM算法识别性能的不稳定性，提出了一种基于原型聚类预处理的RKELM方法，并在此基础上设计了特征级融合RKELM网络和决策级融合RKELM网络，以对投影特征进行融合分类。实验部分利用10类民用车辆的全极化HRRP数据将所提识别方法和现有方法进行了对比，结果表明：(1)所采用的Cameron分解投影特征表现出了较高的可分性和噪声稳健性；(2)当训练样本数较多时，特征级融合RKELM算法的泛化性能较好；当训练样本数较少时，决策级融合RKELM的泛化性能较好。Abstract: A recognition method combining Cameron decomposition and fusing Reduced Kernel Extreme Learning Machine (RKELM) is proposed for the Full Polarimetric (FP) High Resolution Range Profile (HRRP)-based radar target recognition task. In the feature extraction phase, Cameron decomposition is exploited to define the projection component of the target on the standard scatterers. Through analysis, the projection components on three scattering bases, i.e., trihedral, dihedral, and 1/4 wave device, are selected as target features, which achieve more detailed descriptions of the target characteristics. In the classification phase, considering the instability of the recognition performance of the RKELM algorithm, the RKELM based on prototype clustering preprocessing is first proposed. Then, to improve the recognition performance, we proposed the feature level fusing RKELM and the decision level fusing RKELM to fuse the three projection components of the targets. The experiments compared the performance of the proposed recognition method and the state-of-the-art methods using the FP HRRP data from 10 civilian vehicles. The results demonstrate that the projection features by Cameron decomposition exhibit higher separability and better noise robustness, and that the feature level fusing RKELM has better generalization performance with a large number of training samples, but the decision level fusing RKELM was better with a small number of training samples.
-
图 1 对称散射体所对应的
$z$ 值的单位圆盘表示Figure 1. Unit disc representation of
$z$ values and the corresponding symmetric scatterers
图 2 基于原型聚类预处理的特征级融合RKELM网络结构
Figure 2. Feature level fusing RKELM network based on prototype clustering preprocessing
图 3 基于原型聚类预处理的决策级融合RKELM网络结构
Figure 3. Decision level fusing RKELM network based on prototype clustering preprocessing
图 5 10类民用车辆的Cameron投影特征RGB图
Figure 5. RGB images of the Cameron projection features from 10 civilian vehicles
表 1 z值与对应的对称散射体
Table 1. z values and the corresponding symmetric scatterers
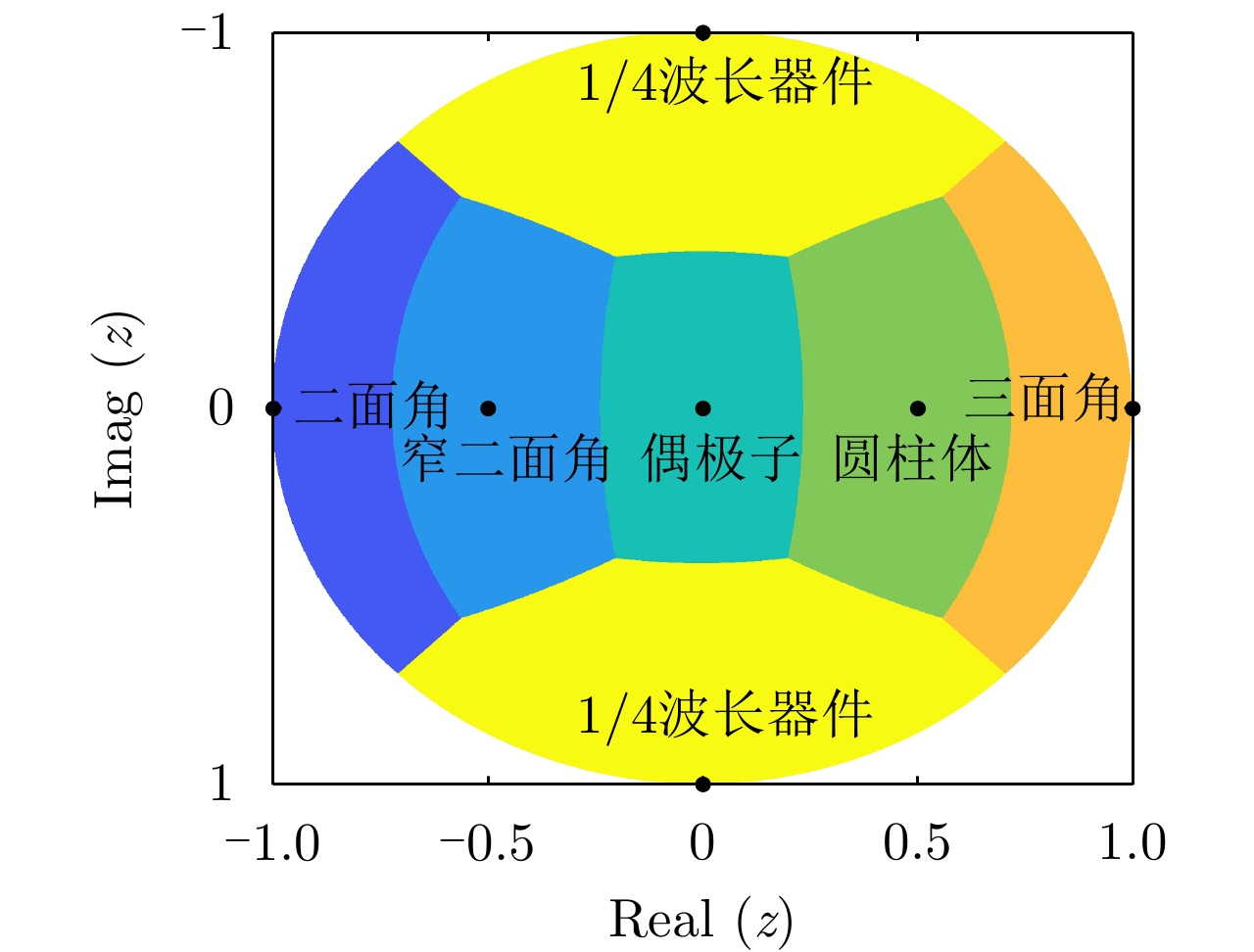
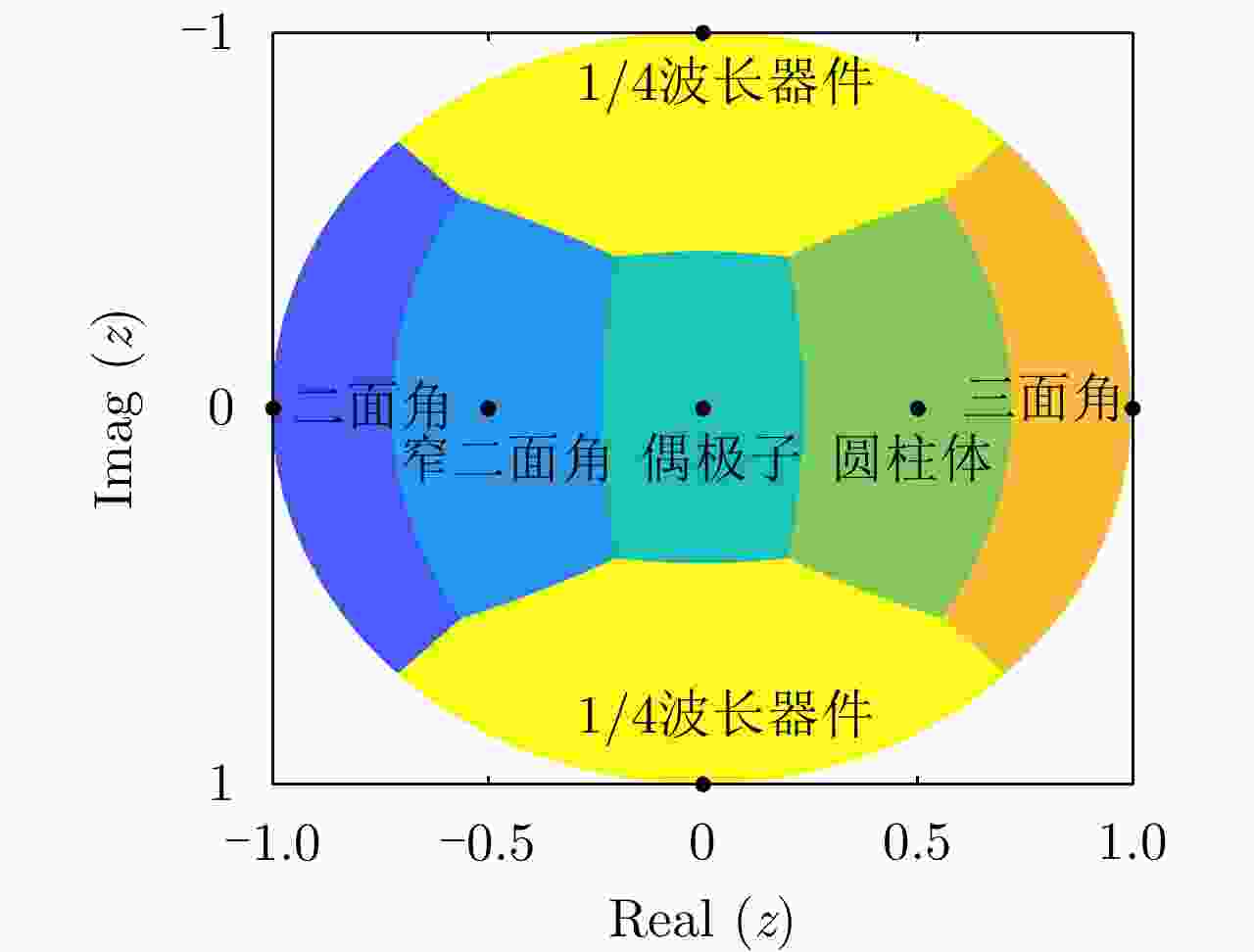
对称散射体类型 z 对称散射体类型 z 三面角 1.0 圆柱体 0.5 二面角 –1.0 窄二面角 –0.5 偶极子 0 1/4波长器件 $\pm \rm i$ 
下载: 导出CSV
表 2 任意散射体与标准对称散射体之间的相似性计算方式
Table 2. Calculation of similarity between arbitrary scatterers and standard symmetric scatterers
散射体 ${z_0}$ $\varphi \left( {z,{z_0}} \right)$ 散射体 ${z_0}$ $\varphi \left( {z,{z_0}} \right)$ 三面角 1.0 $\sqrt {\dfrac{1}{2} + \dfrac{{{z_{\rm{r}}}}}{{1 + {{\left| z \right|}^2}}}} $ 圆柱体 0.5 $\sqrt {\dfrac{1}{5} + \dfrac{{3 + 4{z_{\rm{r}}}}}{{5\left( {1 + {{\left| z \right|}^2}} \right)}}} $ 二面角 –1.0 $\sqrt {\dfrac{1}{2} - \dfrac{{{z_{\rm{r}}}}}{{1 + {{\left| z \right|}^2}}}} $ 窄二面角 –0.5 $\sqrt {\dfrac{1}{5} + \dfrac{{3 - 4{z_{\rm{r}}}}}{{5\left( {1 + {{\left| z \right|}^2}} \right)}}} $ 偶极子 0 $\sqrt {\dfrac{1}{{1 + {{\left| z \right|}^2}}}} $ 1/4波长器件 $\pm \rm i$ $\sqrt {\dfrac{1}{2} + \dfrac{{\left| {{z_{\rm{i}}}} \right|}}{{\left( {1 + {{\left| z \right|}^2}} \right)}}} $
下载: 导出CSV
表 3 标准散射体的Cameron分解参数和相似性参数
Table 3. Cameron decomposition parameters of the standard scatterers and their similairity parameters
散射体类型 最小对称分量能量 最大对称分量能量 与标准散射体之间的相似性 三面角 二面角 偶极子 圆柱体 窄二面角 1/4波长器件 三面角 0 1.0 1.000 0 0.707 0.949 0.316 0.707 二面角 0 1.0 0 1.000 0.707 0.316 0.949 0.707 偶极子 0 1.0 0.707 0.707 1.000 0.894 0.894 0.707 圆柱体 0 1.0 0.949 0.316 0.894 1.000 0.600 0.707 窄二面角 0 1.0 0.316 0.949 0.894 0.600 1.000 0.707 1/4波长器件 0 1.0 0.707 0.707 0.707 0.707 0.707 1.000 左螺旋 0.5 0.5 0 1.000 0.707 0.316 0.949 0.707 右螺旋 0.5 0.5 0 1.000 0.707 0.316 0.949 0.707
下载: 导出CSV
表 4 特征改进的ReliefF可分性值
Table 4. Seperability measure of features by the modified ReliefF
特征 可分性 Cameron分解 2.766 全极化幅度 2.594 Cloude分解 1.780 Krogager分解 2.600 HH 2.084 VV 2.455 HV 1.978
下载: 导出CSV
表 5 所提方法和对比方法在不同隐层节点数下的识别性能(%)
Table 5. Recognition performance of the proposed methods and comparative methods with different number of hidden layer nodes (%)
隐层节点数 Cameron+特征级RKELM 幅度+特征级RKELM Cameron+特征级RKELM(随机) Cloude+特征级RKELM Krogager+特征级RKELM Cameron+决策级RKELM 幅度+决策级RKELM 50 77.3 73.4 75.7 66.7 73.5 66.7 64.5 100 87.3 84.6 86.3 76.3 84.4 79.9 77.7 150 91.4 89.8 90.1 81.0 89.3 85.6 84.2 200 93.6 92.6 93.1 83.9 92.0 88.9 88.0 250 94.9 94.2 94.5 85.9 93.5 91.1 90.2 300 95.7 95.1 95.4 87.3 94.5 92.6 91.7 350 96.3 95.7 96.1 88.5 95.2 93.6 92.9 400 96.7 96.1 96.5 89.3 95.7 94.3 93.7 450 97.0 96.5 96.8 90.0 96.1 94.9 94.3 500 97.2 96.7 97.1 90.6 96.3 95.3 94.8 隐层节点数 Cameron+决策级RKELM(随机) Cloude+决策级RKELM Krogager+决策级RKELM HH+聚类-RKELM VV+聚类-RKELM HV+聚类-RKELM 50 66.0 59.2 65.3 51.3 52.2 43.0 100 79.0 68.8 77.9 62.0 65.1 52.2 150 84.7 74.3 84.1 69.2 72.7 56.3 200 88.4 77.8 87.0 74.4 77.8 58.8 250 90.7 80.4 89.6 78.1 81.2 60.5 300 92.2 82.2 91.0 80.8 83.8 61.8 350 93.3 83.7 92.2 82.9 85.8 62.9 400 94.0 84.8 92.6 84.5 87.3 63.8 450 94.7 85.8 93.7 85.8 88.6 64.5 500 95.0 86.6 94.2 86.9 89.6 65.1
下载: 导出CSV
-
[1] DU Lan, LIU Hongwei, WANG Penghui, et al. Noise robust radar HRRP target recognition based on multitask factor analysis with small training data size[J]. IEEE Transactions on Signal Processing, 2012, 60(7): 3546–3559. doi: 10.1109/TSP.2012.2191965 [2] WANG Jingjing, LIU Zheng, XIE Rong, et al. Radar HRRP target recognition based on dynamic learning with limited training data[J]. Remote Sensing, 2021, 13(4): 750. doi: 10.3390/RS13040750 [3] NOVAK L M, HALVERSEN S D, OWIRKA G, et al. Effects of polarization and resolution on SAR ATR[J]. IEEE Transactions on Aerospace and Electronic Systems, 1997, 33(1): 102–116. doi: 10.1109/7.570713 [4] GIUSTI E, MARTORELLA M, and CAPRIA A. Polarimetrically-persistent-scatterer-based automatic target recognition[J]. IEEE Transactions on Geoscience and Remote Sensing, 2011, 49(11): 4588–4599. doi: 10.1109/TGRS.2011.2164804 [5] 张玉玺, 王晓丹, 姚旭, 等. 基于H/A/α分解的全极化HRRP目标识别方法[J]. 系统工程与电子技术, 2013, 35(12): 2501–2506. doi: 10.3969/j.issn.1001-506X.2013.12.10ZHANG Yuxi, WANG Xiaodan, YAO Xu, et al. Target recognition of fully polarimetric HRRP based on H/A/α decomposition[J]. Systems Engineering and Electronics, 2013, 35(12): 2501–2506. doi: 10.3969/j.issn.1001-506X.2013.12.10 [6] 张玉玺, 王晓丹, 姚旭, 等. 一种融合多极化特征的雷达目标识别方法[J]. 计算机科学, 2012, 39(9): 208–210, 234. doi: 10.3969/j.issn.1002-137X.2012.09.047ZHANG Yuxi, WANG Xiaodan, YAO Xu, et al. Approach of radar target recognition based on multiple polarization features fusion[J]. Computer Science, 2012, 39(9): 208–210, 234. doi: 10.3969/j.issn.1002-137X.2012.09.047 [7] 王福友, 罗钉, 刘宏伟. 基于极化不变量特征的雷达目标识别技术[J]. 雷达科学与技术, 2013, 11(2): 165–172. doi: 10.3969/j.issn.1672-2337.2013.02.011WANG Fuyou, LUO Ding, and LIU Hongwei. Radar target classification based on some invariant properties of the polarization[J]. Radar Science and Technology, 2013, 11(2): 165–172. doi: 10.3969/j.issn.1672-2337.2013.02.011 [8] 吴佳妮, 陈永光, 代大海, 等. 基于快速密度搜索聚类算法的极化HRRP分类方法[J]. 电子与信息学报, 2016, 38(10): 2461–2467. doi: 10.11999/JEIT151457WU Jiani, CHEN Yongguang, DAI Dahai, et al. Target recognition for polarimetric HRRP based on fast density search clustering method[J]. Journal of Electronics &Information Technology, 2016, 38(10): 2461–2467. doi: 10.11999/JEIT151457 [9] LIU Shengqi, ZHAN Ronghui, WANG Wei, et al. Full-polarization HRRP recognition based on joint sparse representation[C]. 2015 IEEE Radar Conference, Johannesburg, South Africa, 2015: 333–338. doi: 10.1109/RadarConf.2015.7411903. [10] 刘盛启, 占荣辉, 翟庆林, 等. 基于联合稀疏性的多视全极化HRRP目标识别方法[J]. 电子与信息学报, 2016, 38(7): 1724–1730. doi: 10.11999/JEIT151019LIU Shengqi, ZHAN Ronghui, ZHAI Qinglin, et al. Multi-view polarization HRRP target recognition based on joint sparsity[J]. Journal of Electronics &Information Technology, 2016, 38(7): 1724–1730. doi: 10.11999/JEIT151019 [11] 翟庆林, 刘盛启, 胡杰民, 等. 全极化雷达的多任务压缩感知目标识别方法[J]. 国防科技大学学报, 2017, 39(3): 144–150. doi: 10.11887/j.cn.201703022ZHAI Qinglin, LIU Shengqi, HU Jiemin, et al. Full-polarization radar target recognition of multitask compressive sensing[J]. Journal of National University of Defense Technology, 2017, 39(3): 144–150. doi: 10.11887/j.cn.201703022 [12] 段佳, 邢孟道, 张磊, 等. 联合属性散射中心的极化目标重构新方法[J]. 西安电子科技大学学报: 自然科学版, 2014, 41(6): 18–24. doi: 10.3969/j.issn.1001-2400.2014.06.004DUAN Jia, XING Mengdao, ZHANG Lei, et al. Novel polarimetric target signal reconstruction method jointed with attributed scattering centers[J]. Journal of Xidian University, 2014, 41(6): 18–24. doi: 10.3969/j.issn.1001-2400.2014.06.004 [13] DUAN Jia, ZHANG Lei, XING Mengdao, et al. Polarimetric target decomposition based on attributed scattering center model for synthetic aperture radar targets[J]. IEEE Geoscience and Remote Sensing Letters, 2014, 11(12): 2095–2099. doi: 10.1109/LGRS.2014.2320053 [14] CAMERON W L, YOUSSEF N N, and LEUNG L K. Simulated polarimetric signatures of primitive geometrical shapes[J]. IEEE Transactions on Geoscience and Remote Sensing, 1996, 34(3): 793–803. doi: 10.1109/36.499784 [15] DENG Wanyu, ONG Y S, and ZHENG Qinghua. A fast reduced kernel extreme learning machine[J]. Neural Networks, 2016, 76: 29–38. doi: 10.1016/j.neunet.2015.10.006 [16] ARTHUR D and VASSILVITSKII S. K-means++: The advantages of careful seeding[C]. The Eighteenth Annual ACM-SIAM Symposium on Discrete Algorithms, New Orleans, USA, 2007: 1027–1035. [17] DUNGAN K E, AUSTIN C, NEHRBASS J, et al. Civilian vehicle radar data domes[C]. SPIE 7699, Algorithms for Synthetic Aperture Radar Imagery XVII, Orlando, USA, 2010: 76990P. doi: 10.1117/12.850151. [18] KROGAGER E. New decomposition of the radar target scattering matrix[J]. Electronics Letters, 1990, 26(18): 1525–1527. doi: 10.1049/el:19900979 [19] ROBNIK-ŠIKONJA M and KONONENKO I. Theoretical and empirical analysis of ReliefF and RReliefF[J]. Machine Learning, 2003, 53(1): 23–69. doi: 10.1023/A:1025667309714 -
计量
- 文章访问数: 1659
- HTML全文浏览量: 708
- PDF下载量: 156
- 被引次数: 0
