涡旋微波量子雷达

张超; 王元赫; 姜学峰

doi:10.12000/JR21095

涡旋微波量子雷达

DOI: 10.12000/JR21095

清华大学航天航空学院航空宇航电子系统实验室北京 100084

基金项目: 国家自然科学基金重点项目(61731011)，广东省科技厅重点项目(2019B010157001)，部委科技基础加强研究项目(JCJQ-ZD-164-12)

详细信息

作者简介:
张　超(1978–)，男，陕西城固人，清华大学航天航空学院教授、博士生导师。2005年获清华大学工学博士学位，2006年获日本国家信息学研究所(NII)信息学博士学位。IET会士(IET Fellow)、IEEE高级会员、IEICE高级会员。主要研究方向为涡旋电磁波轨道角动量传输与探测、涡旋微波量子、航空宇航电子系统

王元赫(1997–)，男，江苏涟水人，清华大学航天航空学院在读博士研究生。2019年获得西安电子科技大学通信工程专业学士学位。研究方向为电磁波轨道角动量传输与探测

姜学峰(1995–)，男，天津静海人，清华大学航天航空学院在读博士研究生。2017年获得清华大学电子信息科学与技术学士学位。研究方向为电磁波轨道角动量传输与探测，涡旋微波量子

通讯作者:
张超 zhangchao@tsinghua.edu.cn

责任主编：李龙 Corresponding Editor: LI Long
^①这里指涡旋微波量子具有的内禀OAM (Intrinsic OAM，不随空间坐标系的选择发生相应的变化)^[12]。相比之下，统计态涡旋波束利用的是微波量子的外部OAM (Extrinsic OAM)。
^②这里不是RCS的标准定义，但与RCS标准定义所反映目标散射性能一致。RCS标准定义见文献[26]。另外，考虑到本文对比参照对象为经典雷达系统，因此没有采用文献[27]中量子RCS的定义，仍采用经典RCS定义。^③文献[28]中直接给出了3种具有吸波能力的隐身材料在10 GHz下的相对复介电常数，其他频率下的相对复介电常数需要借助德拜弛豫方程求解，具体方法和参数可参考文献[28]。同时还需考虑到自由电子对复介电常数的贡献，故本文假设三者的K₀分别为0.01, 0.02和0.04，具体准确数据需要实验测量得到。^④为了便于表示，图2中给出的数值是与隐身材料1的平面波(模态0)等效后向RCS计算值进行归一化后形成的归一化等效后向RCS。
中图分类号: TN95
计量
- 文章访问数: 4148
- HTML全文浏览量: 2571
- PDF下载量: 516
- 被引次数: 0
出版历程
- 收稿日期: 2021-07-01
- 修回日期: 2021-09-06
- 网络出版日期: 2021-10-25
- 刊出日期: 2021-10-28

Quantum Radar with Vortex Microwave Photons

Labs of Avionics, School of Aerospace Engineering, Tsinghua University, Beijing 100084, China

Funds: The National Natural Science Foundation of China (61731011), The Science and Technology Key Project of Guangdong Province (2019B010157001), National Defense Science and Technology Basic Research (JCJQ-ZD-164-12)

More Information

Corresponding author: ZHANG Chao, zhangchao@tsinghua.edu.cn

摘要

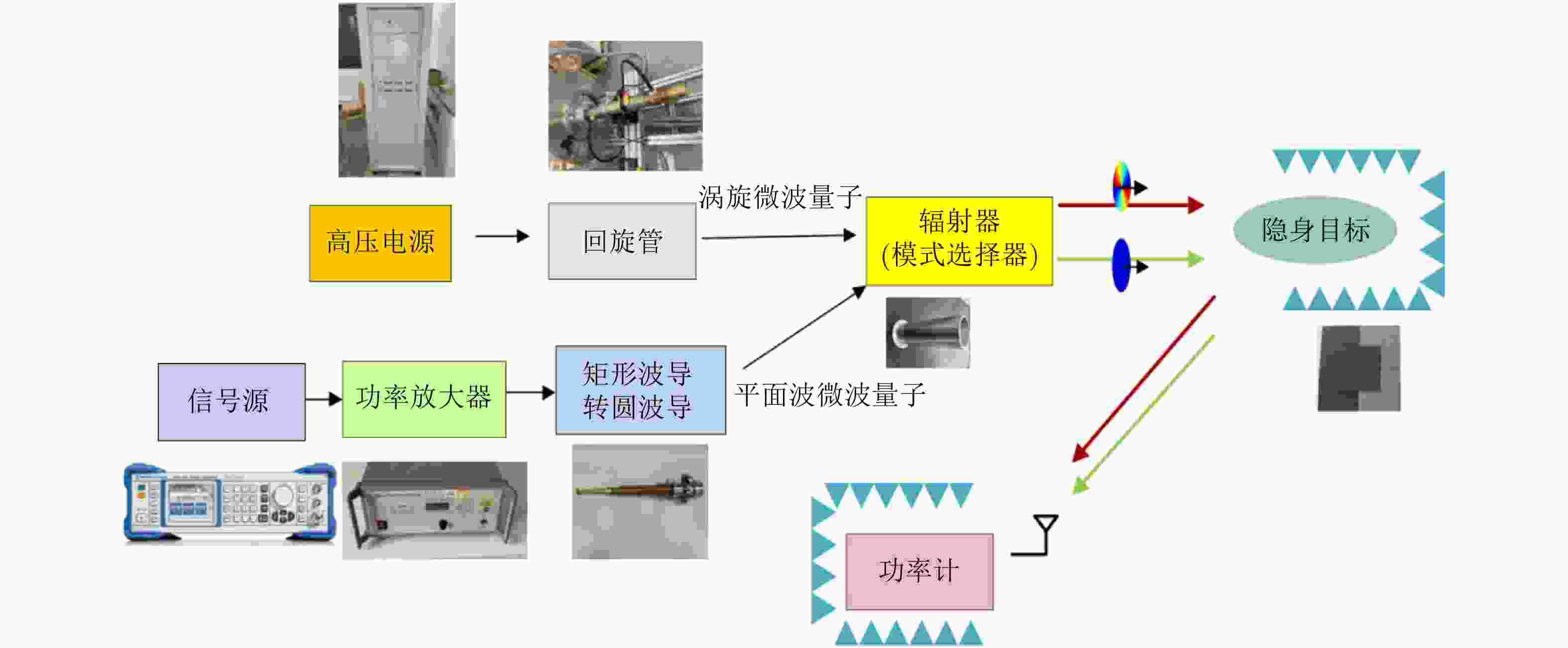
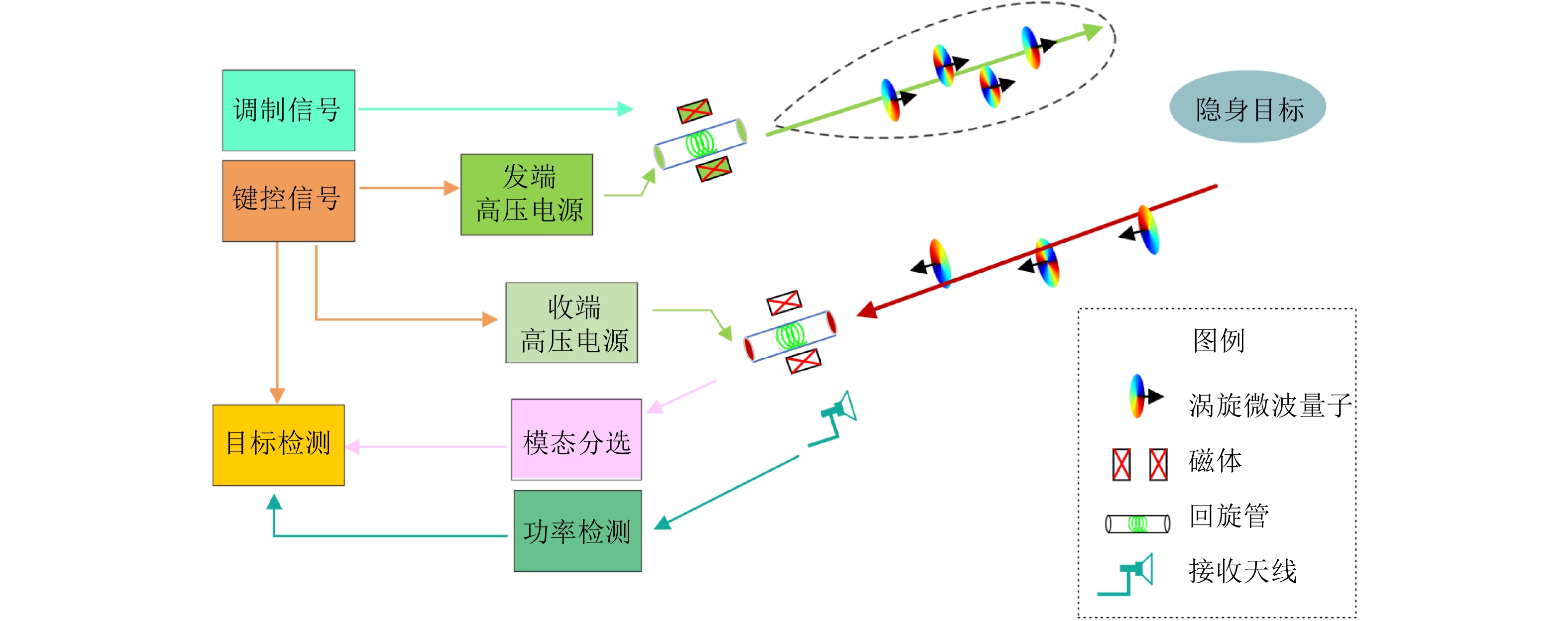
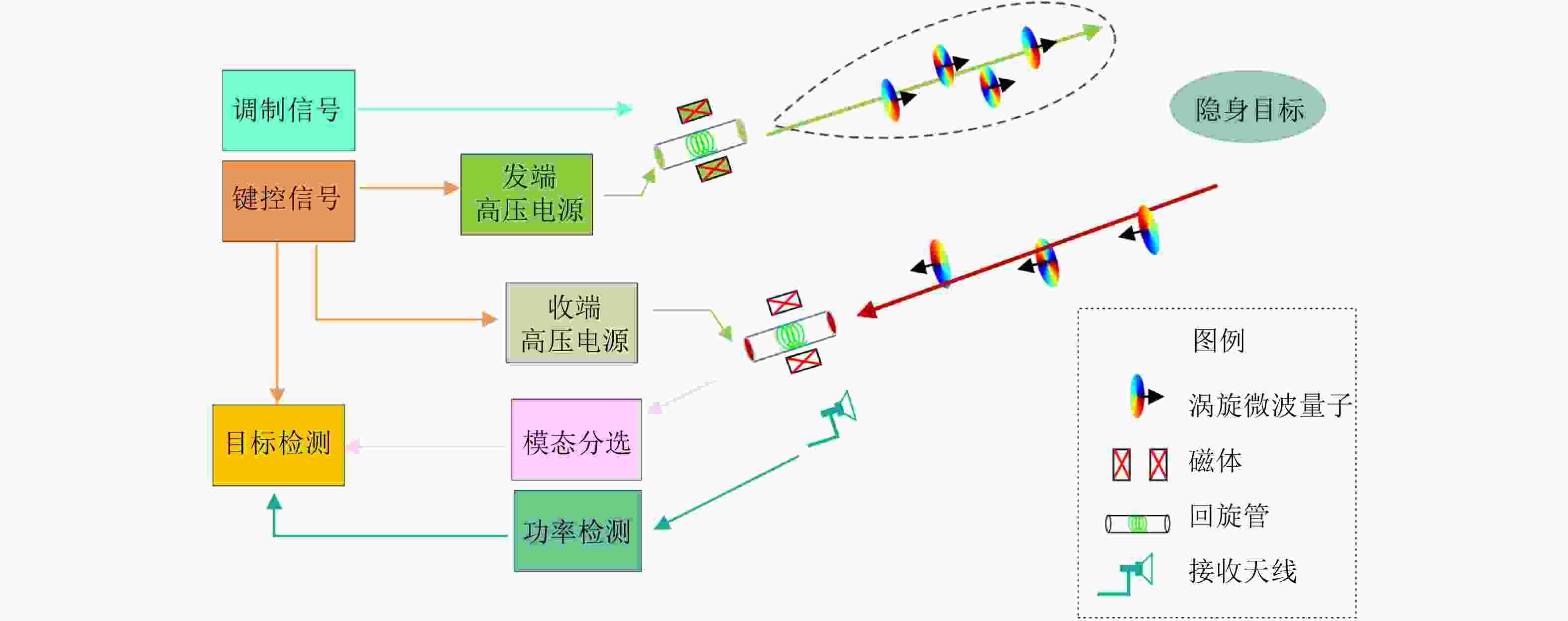
摘要: 电磁波轨道角动量(OAM)量子态指构成电磁波的每个电磁波量子均具有OAM，是涡旋电磁波的重要形态之一。在微波波段，这种电磁波量子称为“涡旋微波量子”。涡旋微波量子与传统平面波微波量子具有不同的物理特性，针对传统吸波材料具有强反射系数，造成雷达散射截面积(RCS)增加，并提升目标回波的接收信号功率和检测概率，是对抗基于吸波材料的隐身目标之利器。该文提出了基于OAM量子态的涡旋微波量子雷达，给出了基本物理架构和数学模型，借助量子电动力学(QED)从理论上分析了涡旋微波量子的高回波功率特性，并通过实验验证了理论分析的正确性。在收发端均采用相同极化方式下，与传统平面波雷达相比实验中回波功率提高约9 dB。同时，配合典型雷达工作参数进行了仿真，明确了涡旋微波量子雷达在接收功率和检测概率等性能指标上的提升，进一步展现了涡旋微波量子针对吸波材料的反隐身能力。
- 目标探测 /
- 轨道角动量 /
- 涡旋微波量子 /
- OAM量子态 /
- 反隐身雷达
Abstract: Quantum Orbital Angular Momentum (OAM) indicates that each Electro-Magnetic (EM) photon of an EM wave carries OAM. In the microwave band, such an EM wave photon is called a vortex microwave photon. Physical properties distinguish between EM waves with vortex and plane wave photons. When illuminating a traditional stealthy target composed of absorbing materials, a vortex microwave photon can achieve higher echo power, thereby improving the Radar Cross Section (RCS), the corresponding receiving signal power, and detection probability. Hence, the vortex microwave photon shows promise in antistealth technology. In this paper, a vortex microwave quantum radar based on the OAM quantum state is proposed. Its basic physical architecture and corresponding mathematical model are given, and the high echo power characteristics of the vortex microwave photon are analyzed using Quantum Electro-Dynamics (QED). The correctness of the theoretical calculation was experimentally verified with an approximate 9 dB improvement in echo power. Moreover, the simulations are performed to clarify the improvement in radar performance, including the receiving power and detection probability, illustrating the capability of the vortex microwave photon when applied to antistealth radar.
- Target detection /
- Orbital Angular Momentum (OAM) /
- Vortex microwave photon /
- Quantum OAM /
- Antistealth radar

HTML全文

图 1 涡旋微波量子雷达系统架构示意图

Figure 1. Vortex microwave quantum radar system

下载: 全尺寸图片幻灯片

图 2 RCS与入射电磁波OAM模态关系

Figure 2. Normalized RCS with regards to the OAM mode of incident wave considering different kinds of stealthy materials

下载: 全尺寸图片幻灯片

图 3 实验系统架构

Figure 3. Structure of vortex microwave photon experiment

下载: 全尺寸图片幻灯片

图 4 实际实验场景

Figure 4. The actual experimental scenarios

下载: 全尺寸图片幻灯片

图 5 涡旋微波量子雷达和平面波雷达探测隐身目标的接收信号功率

Figure 5. Normalized received signal power with different waves from the stealthy target

下载: 全尺寸图片幻灯片

图 6 涡旋微波量子雷达和平面波雷达接收机工作曲线

Figure 6. Receiver operating curve comparison

下载: 全尺寸图片幻灯片

表 1 3种不同电磁波雷达系统的特点对比

Table 1. Comparison of characteristics of three radar systems

电磁波	功能应用	局限与技术难点
平面波(球面波)	传统天线(天线阵)发射和接收，设计复杂电场强度信号进行探测与成像	仅利用电场强度(极化表示电场强度方向)，信号域资源有限，尚未开发利用电磁波其他物理量
OAM统计态波束 (涡旋波束)	利用波束螺旋相位面与空间对应关系进行探测与成像；利用螺旋相位面的空间相位梯度反结构隐身	直接产生高阶模态困难，有争议认为该形式OAM雷达是阵列合成波束雷达特例；合成大模态OAM波束计算复杂度高
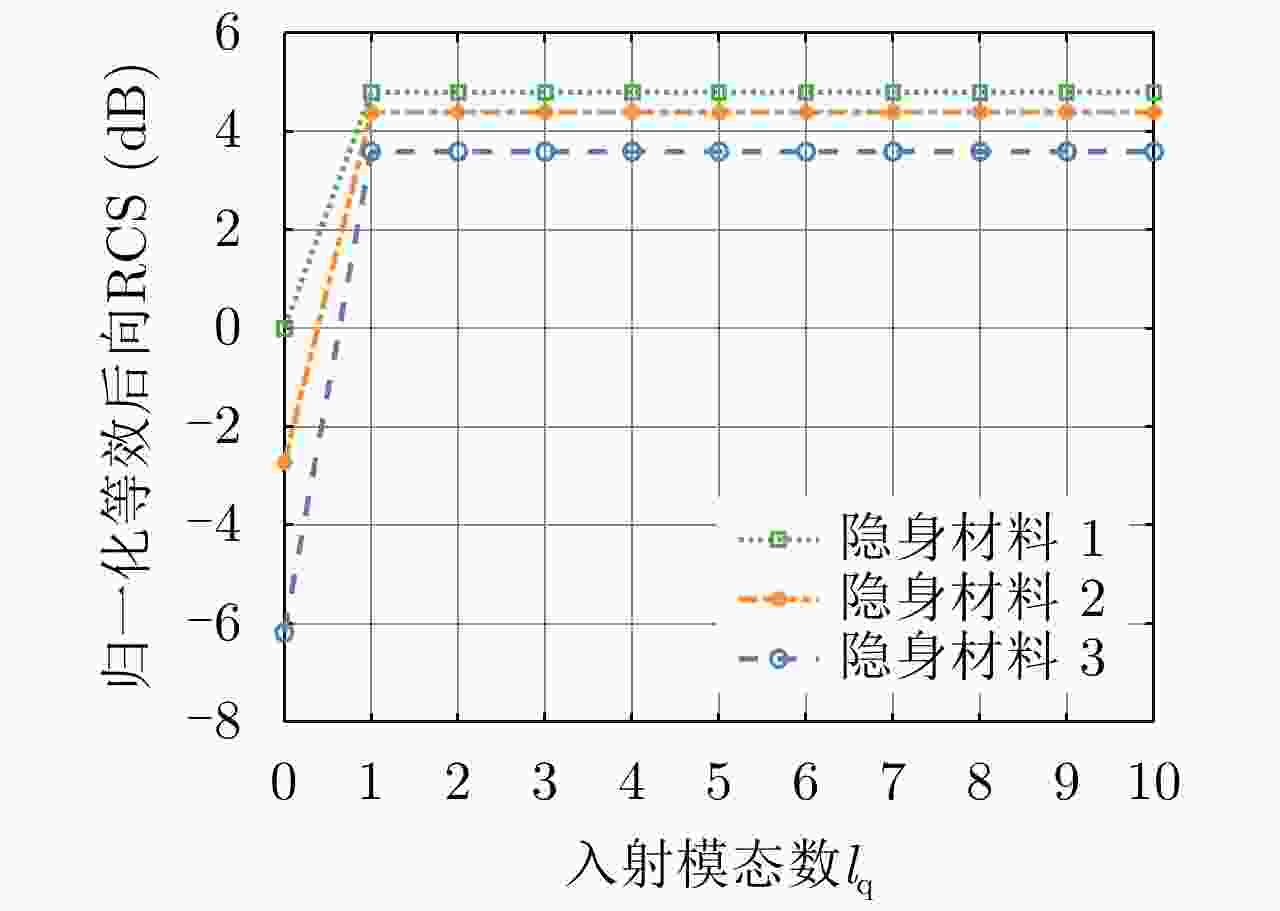
涡旋微波量子	利用涡旋微波量子针对吸波材料实现反隐身； OAM和电场强度的联合探测与成像	目前产生和接收装置复杂，缺少具体应用系统设计

下载: 导出CSV

表 2 实验中不同距离下平面波和涡旋微波量子的归一化回波功率

Table 2. Normalized echo power with regards to distance between the antenna and target considering the plane wave and vortex microwave photon in experiment

距离 (cm)	平面波 (dB) (V-V)	涡旋微波量子 (dB) (V-V)	平面波 (dB) (H-H)	涡旋微波量子 (dB) (H-H)
60	0	8.78	0	8.70
100	–9.01	–0.04	–8.84	0.17
140	–13.96	–8.11	–14.82	–7.83

下载: 导出CSV

参考文献(28)

[1]	ZIKIDIS K, SKONDRAS A, and TOKAS C. Low observable principles, stealth aircraft and anti-stealth technologies[J]. Journal of Computations & Modelling, 2014, 4(1): 129–165.
[2]	GALARREGUI J C I, PEREDA A T, DE FALCÓN J L M, et al. Broadband radar cross-section reduction using AMC technology[J]. IEEE Transactions on Antennas and Propagation, 2013, 61(12): 6136–6143. doi: 10.1109/TAP.2013.2282915
[3]	马井军, 赵明波, 张开锋, 等. 飞机隐身技术及其雷达对抗措施[J]. 国防科技, 2009, 30(3): 38–44,64. MA Jingjun, ZHAO Mingbo, ZHANG Kaifeng, et al. Aircraft stealth technology and its radar countermeasures[J]. National Defense Science &Technology, 2009, 30(3): 38–44,64.
[4]	ZHANG Chao, CHEN Dong, and JIANG Xuefeng. RCS diversity of electromagnetic wave carrying orbital angular momentum[J]. Scientific Reports, 2017, 7(1): 15412. doi: 10.1038/s41598-017-15250-7
[5]	ZHANG Chao, JIANG Jin, and ZHAO Yufei. Euclidean space with orbital angular momentum[C]. 2019 IEEE International Conference on Communications Workshops (ICC Workshops), Shanghai, China, 2019: 1–6. doi: 10.1109/ICCW.2019.8756875.
[6]	张超, 王元赫. 涡旋电磁波轨道角动量传输的量子电动力学分析[J]. 中国科学: 信息科学, 2021, in press. doi: 10.1360/SSI-2021-0066 ZHANG Chao and WANG Yuanhe. Quantum electro-dynamics analysis of vortex electro-magnetic wave transmission with orbital angular momentum[J]. Scientia Sinica Informationis, 2021, in press. doi: 10.1360/SSI-2021-0066
[7]	郭桂蓉, 胡卫东, 杜小勇. 基于电磁涡旋的雷达目标成像[J]. 国防科技大学学报, 2013, 35(6): 71–76. doi: 10.3969/j.issn.1001-2486.2013.06.013 GUO Guirong, HU Weidong, and DU Xiaoyong. Electromagnetic vortex based radar target imaging[J]. Journal of National University of Defense Technology, 2013, 35(6): 71–76. doi: 10.3969/j.issn.1001-2486.2013.06.013
[8]	LIU Kang, CHENG Yongqiang, YANG Zhaocheng, et al. Orbital-angular-momentum-based electromagnetic vortex imaging[J]. IEEE Antennas and Wireless Propagation Letters, 2014, 14: 711–714. doi: 10.1109/LAWP.2014.2376970
[9]	ZHANG Chao, JIANG Xuefeng, and CHEN Dong. Signal-to-noise ratio improvement by vortex wave detection with a rotational antenna[J]. IEEE Transactions on Antennas and Propagation, 2021, 69(2): 1020–1029. doi: 10.1109/TAP.2020.3016173
[10]	EDFORS O and JOHANSSON A J. Is orbital angular momentum (OAM) based radio communication an unexploited area?[J]. IEEE Transactions on Antennas and Propagation, 2012, 60(2): 1126–1131. doi: 10.1109/TAP.2011.2173142
[11]	TANG Bo, GUO Kunyi, WANG Jianping, et al. Resolution performance of the orbital-angular-momentum-based imaging radar[J]. IEEE Antennas and Wireless Propagation Letters, 2017, 16: 2975–2978. doi: 10.1109/LAWP.2017.2756094
[12]	HARRIS J, GRILLO V, MAFAKHERI E, et al. Structured quantum waves[J]. Nature Physics, 2015, 11(8): 629–634. doi: 10.1038/nphys3404
[13]	张超, 徐鹏飞. 电磁波量子态轨道角动量雷达探测和方法[P]. 中国发明专利, ZL201910953845.5, 2019. ZHANG Chao and XU Pengfei. Electromagnetic wave quantum state orbital angular momentum radar detection system and method[P]. CN, ZL201910953845.5, 2019.
[14]	徐鹏飞. 电磁波轨道角动量量子态研究[D]. [硕士论文], 清华大学, 2020. XU Pengfei. Research on orbital angular momentum quantum state[D]. [Master dissertation], Tsinghua University, 2020.
[15]	ZHANG Chao, XU Pengfei, and JIANG Xuefeng. Vortex electron generated by microwave photon with orbital angular momentum in a magnetic field[J]. AIP Advances, 2020, 10(10): 105230. doi: 10.1063/5.0019899
[16]	ZHANG Chao, XU Pengfei, and JIANG Xuefeng. Detecting superposed orbital angular momentum states in the magnetic field by the crystal diffraction[J]. The European Physical Journal Plus, 2021, 136(1): 60. doi: 10.1140/epjp/s13360-020-01043-x
[17]	JACKSON J D. Classical Electrodynamics[M]. New York: Wiley, 1999: 295–351.
[18]	HANC J, TULEJA S, and HANCOVA M. Symmetries and conservation laws: Consequences of Noether’s theorem[J]. American Journal of Physics, 2004, 72(4): 428–435. doi: 10.1119/1.1591764
[19]	MOLINA-TERRIZA G, TORRES J P, and TORNER L. Twisted photons[J]. Nature Physics, 2007, 3(5): 305–310. doi: 10.1038/nphys607
[20]	KATOH M, FUJIMOTO M, MIRIAN N S, et al. Helical phase structure of radiation from an electron in circular motion[J]. Scientific Reports, 2017, 7(1): 6130. doi: 10.1038/s41598-017-06442-2
[21]	YAO Yu, LIANG Xianling, ZHU Maohua, et al. Analysis and experiments on reflection and refraction of orbital angular momentum waves[J]. IEEE Transactions on Antennas and Propagation, 2019, 67(4): 2085–2094. doi: 10.1109/TAP.2019.2896760
[22]	徐克尊. 高等原子分子物理学[M]. 3版. 合肥: 中国科学技术大学出版社, 2012: 1–181. XU Kezun. Advanced Atomic Molecular Physics[M]. 3rd ed. Hefei: University of Science and Technology of China Press, 2012: 1–181.
[23]	FEYNMAN R P. Quantum Electrodynamics[M]. Jackson: Westview Press, 1998.
[24]	YUZCELIK C K. Radar absorbing material design[R]. NAVAL POSTGRADUATE SCHOOL MONTEREY CA, 2003: 1–18.
[25]	路宏敏, 赵永久, 朱满座. 电磁场与电磁波基础[M]. 北京: 科学出版社, 2006. doi: https://calhoun.nps.edu/handle/10945/6246. LU Hongmin, ZHAO Yongjiu, and ZHU Manzuo. Fundamentals of Electromagnetic Fields and Electromagnetic Waves[M]. Beijing: Science Press, 2006. doi: https://calhoun.nps.edu/handle/10945/6246.
[26]	SKOLNIK M I. Radar Handbook[M]. New York: McGraw-Hill, 2008: 190–248.
[27]	MACRO Lanzagorta. Quantum Radar[M], Morgan and Claypool Publisher, 2012.
[28]	张凯伦. 石墨烯复合材料介电性能及应用研究[D]. [硕士论文], 北京化工大学, 2018: 390–576. ZHANG Kailun. Study on dielectric property and applications of graphene composites[D]. [Master dissertation], Beijing University of Chemical Technology, 2018: 390–576.