-
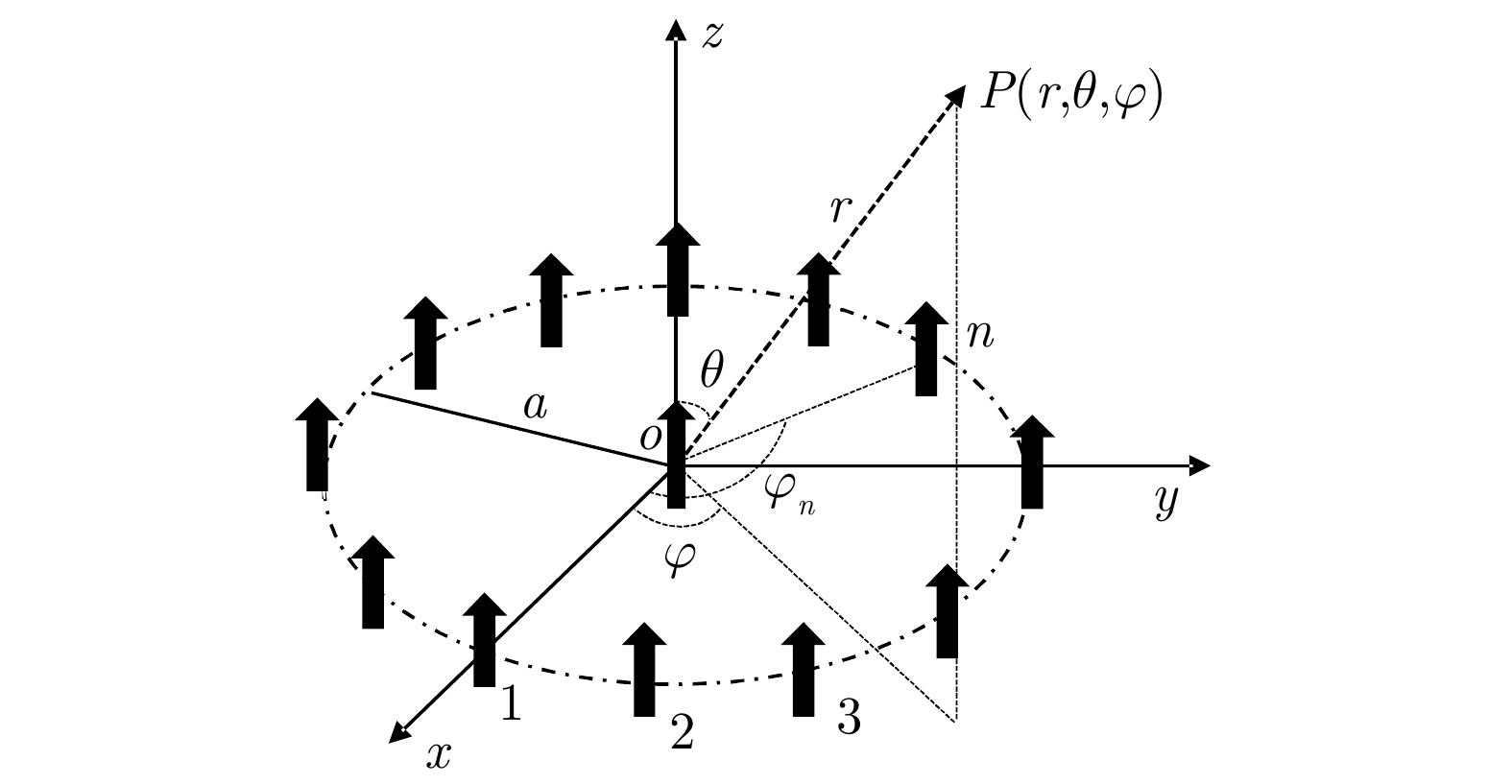
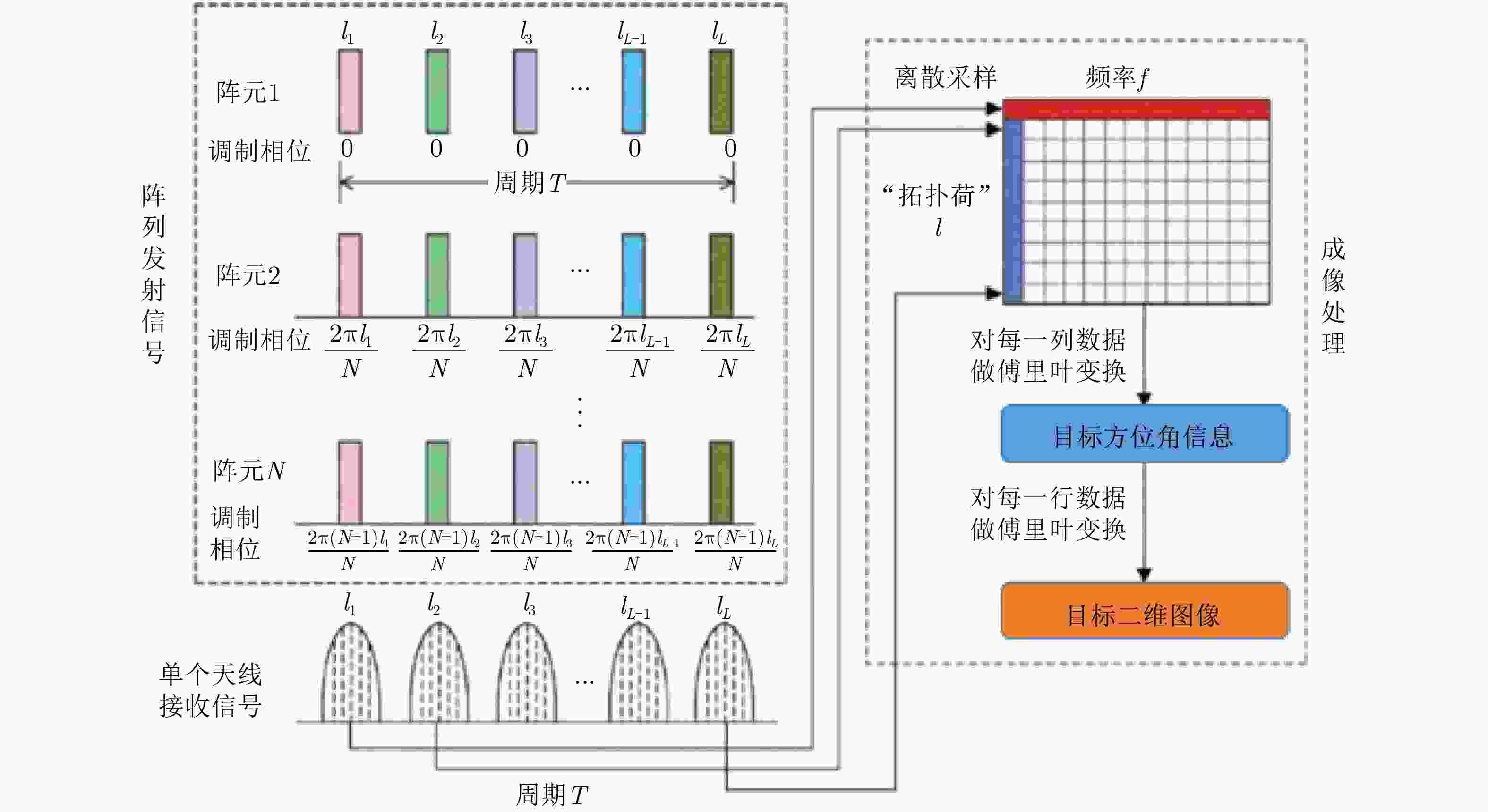
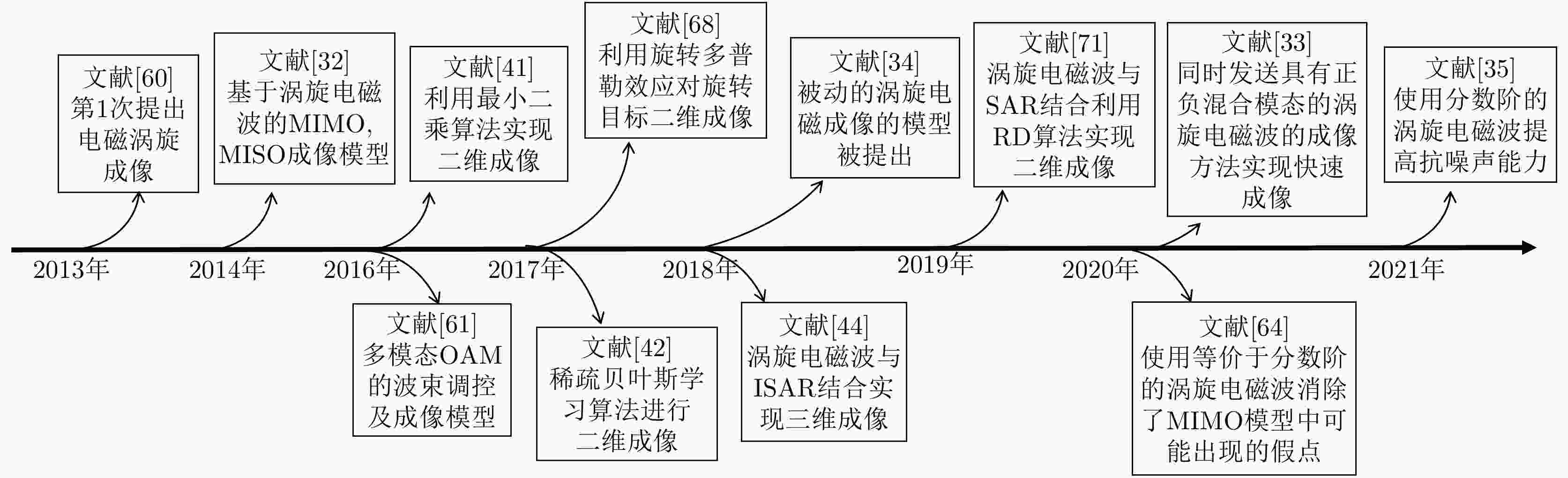
摘要: 涡旋电磁波,因携带有轨道角动量(OAM),从而具有螺旋状的波前结构。相比于平面波,涡旋电磁波在进行雷达成像时,回波信号中将包含有目标的方位向信息,所以这种电磁波在雷达探测和成像领域中展现出了巨大的应用潜力,有望成为新体制雷达的发展方向。该文主要介绍近年来涡旋雷达成像技术的研究进展,首先介绍了涡旋电磁波的特征和使用均匀圆形阵列进行雷达成像的原理,然后按照涡旋雷达成像模型、涡旋雷达凝视成像算法和涡旋雷达运动成像3种研究方向综述了涡旋雷达成像技术的发展历程和研究现状。最后,对涡旋电磁波在雷达成像中的发展前景进行了展望,并指出未来涡旋雷达成像发展的一些关键的科学问题和趋势。Abstract: Vortex electromagnetic wave carries the Orbital Angular Momentum (OAM), and thus has a spiral wavefront structure, which contains the azimuthal information of the target in the echo signal when performing radar imaging compared with planar waves. Hence, this kind of electromagnetic wave shows great potential for various applications in the field of radar detection and imaging, and it is expected to become the development direction of new-system radars. This paper describes in detail the research progress in vortex radar imaging technology in recent years. First, the characteristics of the vortex electromagnetic wave and the principles of imaging using a uniform circular array are introduced. Then the paper reviews the developmental history and research status of vortex radar imaging technology, according to three research directions: vortex radar imaging model, vortex radar gaze imaging algorithm, and vortex radar motion imaging. Finally, the prospects for the development of vortex radar imaging have been presented, along with the key scientific issues and trends for the future developments of vortex radar imaging.
-
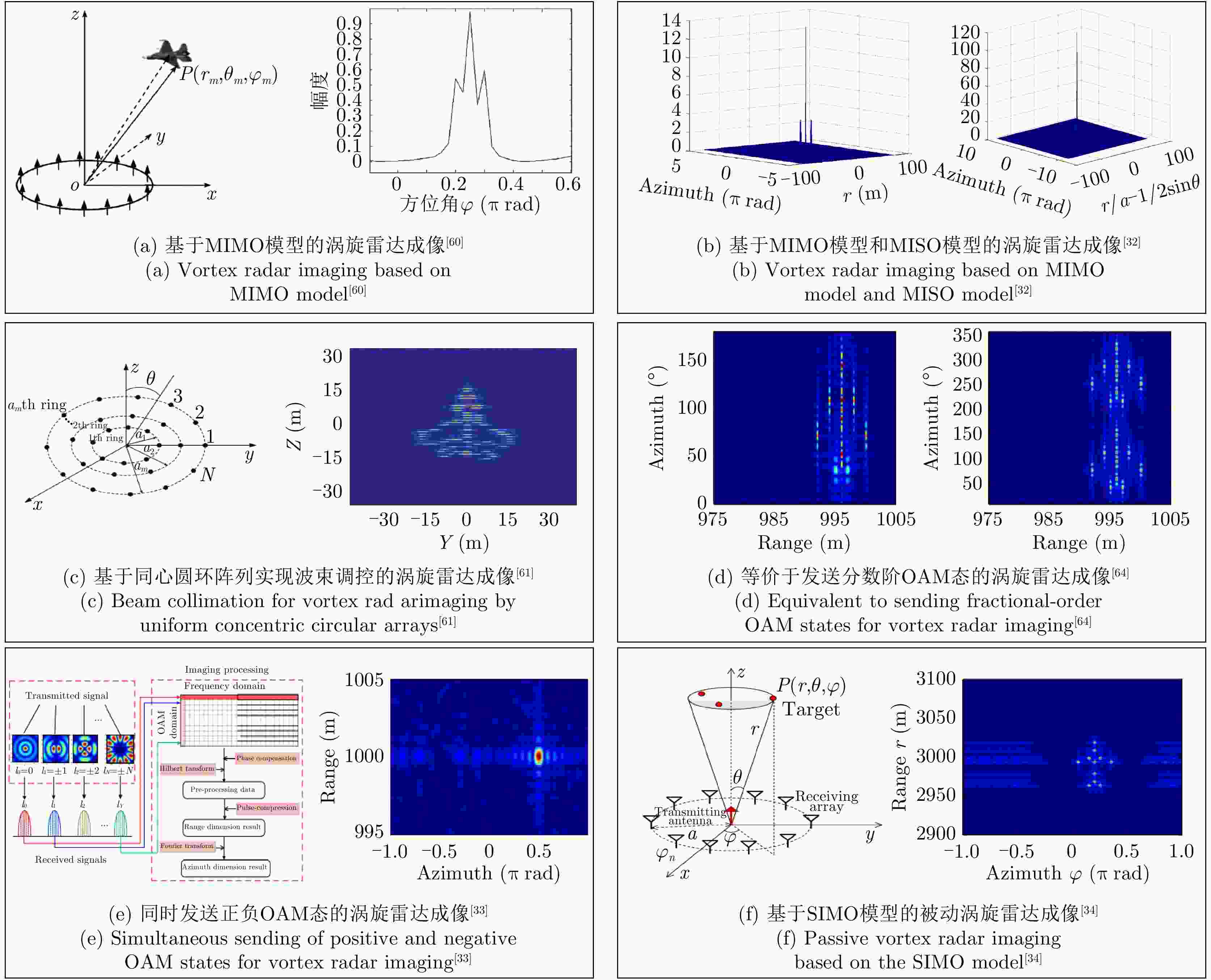
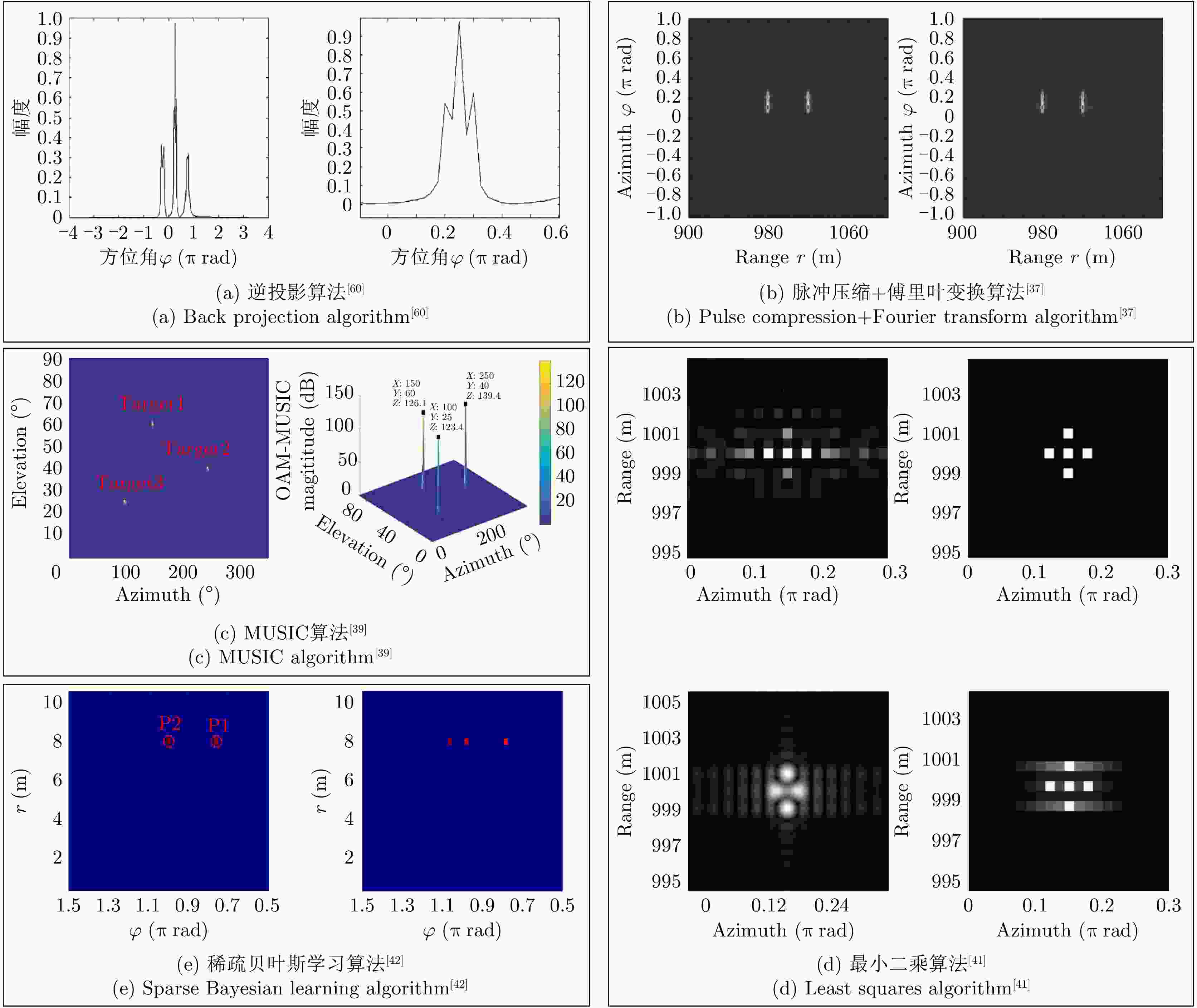
表 1 已报道的涡旋雷达成像模型的性能
Table 1. Performance of reported vortex radar imaging models
文献 成像模型 时间(年) 电磁波的发送形式 电磁波的接收形式 达到最大分辨率需要
发送电磁波的次数方位向分辨
率$ {\rho }_{\varphi } $ (rad)文献[60] MIMO 2013 UCA发送整数阶的OAM态为
α的涡旋电磁波UCA使用α整数阶OAM接收 N ${\rm{\pi } }/N$ 文献[64] 2020 UCA发送整数阶的OAM态为
α的涡旋电磁波UCA使用β整数阶OAM接收 N 文献[32] MISO 2014 UCA发送整数阶的OAM态为
α的涡旋电磁波单个天线接收 N $2{\rm{\pi } }/N$ 文献[33] 2020 UCA发送整数阶的OAM态为
±α的涡旋电磁波单个天线接收 $ (N+1)/2 $ 文献[35] 2021 UCA发送间隔为Δα分数阶的
涡旋电磁波单个天线接收 $ N/\Delta \alpha $ 文献[34] SIMO 2018 单个天线发送平面波 UCA使用α整数阶OAM接收 1 $2{\rm{\pi } }/N$ -
[1] AUSHERMAN D A, KOZMA A, WALKER J L, et al. Developments in radar imaging[J]. IEEE Transactions on Aerospace and Electronic Systems, 1984, AES-20(4): 363–400. doi: 10.1109/TAES.1984.4502060 [2] 江涛, 李敏慧, 刘瑾. 高分辨率SAR综合电子设备技术研究[J]. 现代雷达, 2017, 39(11): 7–10. doi: 10.16592/j.cnki.1004-7859.2017.11.002JIANG Tao, LI Minhui, and LIU Jin. A study on synthetic electronic instrument of high resolution SAR[J]. Modern Radar, 2017, 39(11): 7–10. doi: 10.16592/j.cnki.1004-7859.2017.11.002 [3] 朱晓秀, 胡文华, 郭宝锋. 基于压缩感知理论的稀疏孔径ISAR成像[J]. 现代雷达, 2018, 40(10): 18–22. doi: 10.16592/j.cnki.1004-7859.2018.10.005ZHU Xiaoxiu, HU Wenhua, and GUO Baofeng. ISAR imaging by exploiting sparse apertures based on compressive sensing[J]. Modern Radar, 2018, 40(10): 18–22. doi: 10.16592/j.cnki.1004-7859.2018.10.005 [4] MOHAMMADI S M, DALDORFF L K S, BERGMAN J E S, et al. Orbital angular momentum in radio—A system study[J]. IEEE Transactions on Antennas and Propagation, 2010, 58(2): 565–572. doi: 10.1109/TAP.2009.2037701 [5] WILLNER A E, HUANG H, YAN Y, et al. Optical communications using orbital angular momentum beams[J]. Advances in Optics and Photonics, 2015, 7(1): 66–106. doi: 10.1364/AOP.7.000066 [6] ALLEN L, BEIJERSBERGEN M W, SPREEUW R, et al. Orbital angular momentum of light and the transformation of Laguerre-Gaussian Laser modes[J]. Physical Review A, 1992, 45(11): 8185–8189. doi: 10.1103/PhysRevA.45.8185 [7] GUO Zhongyi, QU Shiliang, and LIU Shutian. Generating optical vortex with computer-generated hologram fabricated inside glass by femtosecond laser pulses[J]. Optics Communications, 2007, 273(1): 286–289. doi: 10.1016/j.optcom.2006.12.023 [8] CHENG Mingjian, GUO Lixin, LI Jiangting, et al. Propagation properties of an optical vortex carried by a Bessel-Gaussian beam in anisotropic turbulence[J]. Journal of the Optical Society of America A, 2016, 33(8): 1442–1450. doi: 10.1364/JOSAA.33.001442 [9] VAZIRI A, WEIHS G, and ZEILINGER A. Superpositions of the orbital angular momentum for applications in quantum experiments[J]. Journal of Optics B: Quantum and Semiclassical Optics, 2002, 4(2): S47–S51. doi: 10.1088/1464-4266/4/2/367 [10] 郭忠义, 龚超凡, 刘洪郡, 等. OAM光通信技术研究进展[J]. 光电工程, 2020, 47(3): 190593. doi: 10.12086/oee.2020.190593GUO Zhongyi, GONG Chaofan, LIU Hongjun, et al. Research advances of orbital angular momentum based optical communication technology[J]. Opto-Electronic Engineering, 2020, 47(3): 190593. doi: 10.12086/oee.2020.190593 [11] DEDO M I, WANG Zikun, GUO Kai, et al. OAM mode recognition based on joint scheme of combining the Gerchberg-Saxton (GS) algorithm and convolutional neural network (CNN)[J]. Optics Communications, 2020, 456: 124696. doi: 10.1016/j.optcom.2019.124696 [12] 郭忠义, 潘珍珍, 龚超凡, 等. OAM光通信路由器件研究[J]. 通信学报, 2020, 41(11): 185–197. doi: 10.11959/j.issn.1000-436x.2020184GUO Zhongyi, PAN Zhenzhen, GONG Chaofan, et al. Research on router device of OAM optical communication[J]. Journal on Communications, 2020, 41(11): 185–197. doi: 10.11959/j.issn.1000-436x.2020184 [13] 郭忠义, 刘洪郡, 李晶晶, 等. 声涡旋信息应用研究进展[J]. 物理学报, 2020, 69(24): 244301. doi: 10.7498/aps.69.20200826GUO Zhongyi, LIU Hongjun, LI Jingjing, et al. Research progress of applications of acoustic-vortex information[J]. Acta Physica Sinica, 2020, 69(24): 244301. doi: 10.7498/aps.69.20200826 [14] GONG Chaofan, LI Jingjing, GUO Kai, et al. Measuring orbital angular momentum of acoustic vortices based on Fraunhofer’s diffraction[J]. Chinese Physics B, 2020, 29(10): 104301. doi: 10.1088/1674-1056/ab9c11 [15] GUO Zhongyi, LIU Hongjun, ZHOU Hong, et al. High-order acoustic vortex field generation based on a metasurface[J]. Physical Review E, 2019, 100(5): 053315. doi: 10.1103/PhysRevE.100.053315 [16] TRINDER J R. Parabolic reflector[P]. WO2005069443A1, 2005. [17] THIDÉ B, THEN H, SJÖHOLM J, et al. Utilization of photon orbital angular momentum in the low-frequency radio domain[J]. Physical Review Letters, 2007, 99(8): 087701. doi: 10.1103/PhysRevLett.99.087701 [18] YANG Yang, LIU Gao, SHEN Fei, et al. Generating and detecting broad-band underwater multiple OAMs based on water-immersed array[J]. IEEE Access, 2020, 8: 149586–149594. doi: 10.1109/ACCESS.2020.3016389 [19] YANG Yang, GONG Yubin, GUO Kai, et al. Broad-band multiple OAMs’ generation with eight-arm archimedean spiral antenna (ASA)[J]. IEEE Access, 2020, 8: 53232–53239. doi: 10.1109/ACCESS.2020.2980751 [20] GUO Kai, ZHENG Qun, YIN Zhiping, et al. Generation of mode-reconfigurable and frequency-adjustable OAM beams using dynamic reflective metasurface[J]. IEEE Access, 2020, 8: 75523–75529. doi: 10.1109/ACCESS.2020.2988914 [21] YANG Yang, GUO Kai, SHEN Fei, et al. Generating multiple OAM based on a nested dual-arm spiral antenna[J]. IEEE Access, 2019, 7: 138541–138547. doi: 10.1109/ACCESS.2019.2942601 [22] SHEN Fei, MU Jiangnan, GUO Kai, et al. Generating circularly polarized vortex electromagnetic waves by the conical conformal patch antenna[J]. IEEE Transactions on Antennas and Propagation, 2019, 67(9): 5763–5771. doi: 10.1109/TAP.2019.2922545 [23] WANG Lulu, CHEN Huiyong, GUO Kai, et al. An inner- and outer-fed dual-arm archimedean spiral antenna for generating multiple orbital angular momentum modes[J]. Electronics, 2019, 8(2): 251. doi: 10.3390/electronics8020251 [24] SHEN Fei, YIN Chaoyi, GUO Kai, et al. Low-cost dual-band multipolarization aperture-shared antenna with single-layer substrate[J]. IEEE Antennas and Wireless Propagation Letters, 2019, 18(7): 1337–1341. doi: 10.1109/LAWP.2019.2916321 [25] 郭忠义, 汪彦哲, 郑群, 等. 涡旋电磁波天线技术研究进展[J]. 雷达学报, 2019, 8(5): 631–655. doi: 10.12000/JR19091GUO Zhongyi, WANG Yanzhe, ZHENG Qun, et al. Advances of research on antenna technology of vortex electromagnetic waves[J]. Journal of Radars, 2019, 8(5): 631–655. doi: 10.12000/JR19091 [26] TURNBULL G A, ROBERTSON D A, SMITH G M, et al. The generation of free-space Laguerre-Gaussian modes at millimetre-wave frequencies by use of a spiral phaseplate[J]. Optics Communications, 1996, 127(4/6): 183–188. [27] LIU Kang, LIU Hongyan, QIN Yuliang, et al. Generation of OAM beams using phased array in the microwave band[J]. IEEE Transactions on Antennas and Propagation, 2016, 64(9): 3850–3857. doi: 10.1109/TAP.2016.2589960 [28] CHEN Rui, ZHOU Hong, LONG Wenxuan, et al. Spectral and energy efficiency of line-of-sight OAM-MIMO communication systems[J]. China Communications, 2020, 17(9): 119–127. doi: 10.23919/JCC.2020.09.010 [29] LEI Yi, YANG Yang, WANG Yanzhe, et al. Throughput performance of wireless multiple-input multiple-output systems using OAM antennas[J]. IEEE Wireless Communications Letters, 2021, 10(2): 261–265. doi: 10.1109/LWC.2020.3027006 [30] ZHOU Zhenglong, CHENG Yongqiang, LIU Kang, et al. Rotational Doppler resolution of spinning target detection based on OAM beams[J]. IEEE Sensors Letters, 2019, 3(3): 5500404. doi: 10.1109/LSENS.2019.2900227 [31] ZHENG Jiayu, ZHENG Shilie, SHAO Zhenlei, et al. Analysis of rotational Doppler effect based on radio waves carrying orbital angular momentum[J]. Journal of Applied Physics, 2018, 124(16): 164907. doi: 10.1063/1.5050448 [32] LIU Kang, CHENG Yongqiang, YANG Zhaocheng, et al. Orbital-angular-momentum-based electromagnetic vortex imaging[J]. IEEE Antennas and Wireless Propagation Letters, 2014, 14: 711–714. doi: 10.1109/LAWP.2014.2376970 [33] LIU Hongyan, LIU Kang, CHENG Yongqiang, et al. Microwave vortex imaging based on dual coupled OAM beams[J]. IEEE Sensors Journal, 2020, 20(2): 806–815. doi: 10.1109/JSEN.2019.2943698 [34] LIU Kang, CHENG Yongqiang, LI Xiang, et al. Passive OAM-based radar imaging with Single-In-Multiple-Out mode[J]. IEEE Microwave and Wireless Components Letters, 2018, 28(9): 840–842. doi: 10.1109/LMWC.2018.2852146 [35] LIU Hongyan, WANG Yu, WANG Jianqiu, et al. Electromagnetic vortex enhanced imaging using fractional OAM beams[J]. IEEE Antennas and Wireless Propagation Letters, 2021, 20(6): 948–952. doi: 10.1109/LAWP.2021.3067914 [36] CHEN Yiling, ZHENG Shilie, JIN Xiaofeng, et al. Single-frequency computational imaging using OAM-carrying electromagnetic wave[J]. Journal of Applied Physics, 2017, 121(18): 184506. doi: 10.1063/1.4983358 [37] LIU Kang, CHENG Yongqiang, LI Xiang, et al. Study on the theory and method of vortex-electromagnetic-wave-based radar imaging[J]. IET Microwaves, Antennas & Propagation, 2016, 10(9): 961–968. doi: 10.1049/iet-map.2015.0842 [38] LIU Kang, CHENG Yongqiang, GAO Yue, et al. Super-resolution radar imaging based on experimental OAM beams[J]. Applied Physics Letters, 2017, 110(16): 164102. doi: 10.1063/1.4981253 [39] ZENG Yanzhi, WANG Yang, CHEN Zhihui, et al. Two-dimensional OAM radar imaging using uniform circular antenna arrays[C]. 2020 14th European Conference on Antennas and Propagation (EuCAP), Copenhagen, Denmark, 2020: 1–4. doi: 10.23919/EuCAP48036.2020.9135917. [40] 孙丽华, 闫晓鹏, 刘强, 等. 基于PM算法的涡旋电磁波引信超分辨测向方法[J]. 北京航空航天大学学报, in press, 2021. doi: 10.13700/j.bh.1001-5965.2021.0020.SUN Lihua, YAN Xiaopeng, LIU Qiang, et al. PM based super_resolution method of azimuth detection for electromagnetic vortex wave fuze[J]. Journal of Beijing University of Aeronautics and Astronautics, in press, 2021. doi: 10.13700/j.bh.1001-5965.2021.0020. [41] YUAN Tiezhu, LIU Hongyan, CHENG Yongqiang, et al. Orbital-angular-momentum-based electromagnetic vortex imaging by least-squares method[C]. 2016 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Beijing, China, 2016: 6645–6648. doi: 10.1109/IGARSS.2016.7730735. [42] LIU Kang, LI Xiang, GAO Yue, et al. High-resolution electromagnetic vortex imaging based on sparse Bayesian learning[J]. IEEE Sensors Journal, 2017, 17(21): 6918–6927. doi: 10.1109/JSEN.2017.2754554 [43] ZHAO Hao and WANG Kaizhi. Orbital-angular-momentum-based radar imaging by dice regularized orthogonal matching pursuit[C]. 2020 IEEE 5th International Conference on Signal and Image Processing (ICSIP), Nanjing, China, 2020: 446–450. doi: 10.1109/ICSIP49896.2020.9339258. [44] JIANG Yanwen, LIU Kang, WANG Hongqiang, et al. Orbital-angular-momentum-based ISAR imaging at terahertz frequencies[J]. IEEE Sensors Journal, 2018, 18(22): 9230–9235. doi: 10.1109/JSEN.2018.2869047 [45] WANG Jianqiu, LIU Kang, CHENG Yongqiang, et al. Three-dimensional target imaging based on vortex stripmap SAR[J]. IEEE Sensors Journal, 2019, 19(4): 1338–1345. doi: 10.1109/JSEN.2018.2879814 [46] WANG Lin, TAO Lujing, LI Zhongyu, et al. Three dimensional electromagnetic vortex radar imaging based on the modified RD algorithm[C]. 2020 IEEE Radar Conference (RadarConf20), Florence, Italy, 2020: 1–5. doi: 10.1109/RadarConf2043947.2020.9266329. [47] GHALEH S R, AHMADI-KANDJANI S, KHERADMAND R, et al. Improved edge detection in computational ghost imaging by introducing orbital angular momentum[J]. Applied Optics, 2018, 57(32): 9609–9614. doi: 10.1364/AO.57.009609 [48] COCHENOUR B, RODGERS L, LAUX A, et al. The detection of objects in a turbid underwater medium using orbital angular momentum (OAM)[C]. Proceedings of SPIE 10186 Ocean Sensing and Monitoring IX, Anaheim, USA, 2017: 1018603. doi: 10.1117/12.2264626. [49] PAVONE S C, SORBELLO G and DONATO L D. On the orbital angular momentum incident fields in linearized microwave imaging[J]. Sensors, 2020, 20(7): 1905. doi: 10.3390/s20071905 [50] JACKSON J D. Classical Electrodynamics[M]. 3th ed. New York: Wiley, 1998. [51] 刘康, 黎湘, 王宏强, 等. 涡旋电磁波及其在雷达中应用研究进展[J]. 电子学报, 2018, 46(9): 2283–2290. doi: 10.3969/j.issn.0372-2112.2018.09.034LIU Kang, LI Xiang, WANG Hongqiang, et al. The advances of vortex electromagnetic wave in radar applications[J]. Acta Electronica Sinica, 2018, 46(9): 2283–2290. doi: 10.3969/j.issn.0372-2112.2018.09.034 [52] ZHANG Zongtang, XIAO Shaoqiu, LI Yan, et al. A circularly polarized multimode patch antenna for the generation of multiple orbital angular momentum modes[J]. IEEE Antennas and Wireless Propagation Letters, 2016, 16: 521–524. doi: 10.1109/LAWP.2016.2586975 [53] ZHENG Shilie, HUI Xiaonan, JIN Xiaofeng, et al. Transmission characteristics of a twisted radio wave based on circular traveling-wave antenna[J]. IEEE Transactions on Antennas and Propagation, 2015, 63(4): 1530–1536. doi: 10.1109/TAP.2015.2393885 [54] HAN Jiaqi, LI Long, YI Hao, et al. 1-bit digital orbital angular momentum vortex beam generator based on a coding reflective metasurface[J]. Optical Materials Express, 2018, 8(11): 3470–3478. doi: 10.1364/OME.8.003470 [55] HAN Jiaqi, LI Long, YI Hao, et al. Versatile orbital angular momentum vortex beam generator based on reconfigurable reflective metasurface[J]. Japanese Journal of Applied Physics, 2018, 57(12): 120303. doi: 10.7567/JJAP.57.120303 [56] ZHANG Lei, LIU Shuo, LI Lianlin, et al. Spin-controlled multiple pencil beams and vortex beams with different polarizations generated by pancharatnam-berry coding metasurfaces[J]. ACS Applied Materials & Interfaces, 2017, 9(41): 36447–36455. doi: 10.1021/acsami.7b12468 [57] WU Ruiyuan, ZHANG Lei, BAO Lei, et al. Digital metasurface with phase code and reflection-transmission amplitude code for flexible full-space electromagnetic manipulations[J]. Advanced Optical Materials, 2019, 7(8): 1801429. doi: 10.1002/adom.201801429 [58] YIN Zhiping, ZHENG Qun, GUO Kai, et al. Tunable beam steering, focusing and generating of orbital angular momentum vortex beams using high-order patch array[J]. Applied Sciences, 2019, 9(15): 2949. doi: 10.3390/app9152949 [59] 刘康. 电磁涡旋成像理论与方法研究[D]. [博士论文], 国防科技大学, 2017: 28–29.LIU Kang. Study on the theory and method of electromagnetic vortex imaging[D]. [Ph. D. dissertation], National University of Defense Technology, 2017: 28–29. [60] 郭桂蓉, 胡卫东, 杜小勇. 基于电磁涡旋的雷达目标成像[J]. 国防科技大学学报, 2013, 35(6): 71–76. doi: 10.3969/j.issn.1001-2486.2013.06.013GUO Guirong, HU Weidong, and DU Xiaoyong. Electromagnetic vortex based radar target imaging[J]. Journal of National University of Defense Technology, 2013, 35(6): 71–76. doi: 10.3969/j.issn.1001-2486.2013.06.013 [61] YUAN Tiezhu, WANG Hongqiang, QIN Yuliang, et al. Electromagnetic vortex imaging using uniform concentric circular arrays[J]. IEEE Antennas and Wireless Propagation Letters, 2015, 15: 1024–1027. doi: 10.1109/LAWP.2015.2490169 [62] QIN Yuliang, LIU Kang, CHENG Yongqiang, et al. Sidelobe suppression and beam collimation in the generation of vortex electromagnetic waves for radar imaging[J]. IEEE Antennas and Wireless Propagation Letters, 2016, 16: 1289–1292. doi: 10.1109/LAWP.2016.2633008 [63] YUAN Tiezhu, CHENG Yongqiang, WANG Hongqiang, et al. Beam steering for electromagnetic vortex imaging using uniform circular arrays[J]. IEEE Antennas and Wireless Propagation Letters, 2016, 16: 704–707. doi: 10.1109/LAWP.2016.2600404 [64] GUO Shaoqing, HE Zi, FAN Zhenhong, et al. CUCA based equivalent fractional order OAM mode for electromagnetic vortex imaging[J]. IEEE Access, 2020, 8: 91070–91075. doi: 10.1109/ACCESS.2020.2995149 [65] OPENNHEIM A V, WILLSKY A S, and NAWAB S H. Signal and System[M]. 2nd ed. Prentice-Hall, 1997. [66] POTTER L C, CHIANG D M, CARRIERE R, et al. A GTD-based parametric model for radar scattering[J]. IEEE Transactions on Antennas and Propagation, 1995, 43(10): 1058–1067. doi: 10.1109/8.467641 [67] LAVERY M P J, SPEIRITS F C, BARNETT S M, et al. Detection of a spinning object using light’s orbital angular momentum[J]. Science, 2013, 341(6145): 537–540. doi: 10.1126/science.1239936 [68] LIU Kang, LI Xiang, GAO Yue, et al. Microwave imaging of spinning object using orbital angular momentum[J]. Journal of Applied Physics, 2017, 122(12): 124903. doi: 10.1063/1.4991655 [69] BU Xiangxi, ZHANG Zhuo, CHEN Longyong, et al. Implementation of vortex electromagnetic waves high-resolution synthetic aperture radar imaging[J]. IEEE Antennas and Wireless Propagation Letters, 2018, 17(5): 764–767. doi: 10.1109/LAWP.2018.2814980 [70] 杜永兴, 仝宗俊, 秦岭, 等. 基于改进BP算法的电磁涡旋成像方法[J]. 雷达科学与技术, 2020, 18(5): 539–545. doi: 10.3969/j.issn.1672-2337.2020.05.012DU Yongxing, TONG Zongjun, QIN Ling, et al. Electromagnetic vortex imaging method based on improved BP algorithm[J]. Radar Science and Technology, 2020, 18(5): 539–545. doi: 10.3969/j.issn.1672-2337.2020.05.012 [71] WANG Jianqiu, LIU Kang, CHENG Yongqiang, et al. Vortex SAR imaging method based on OAM beams design[J]. IEEE Sensors Journal, 2019, 19(24): 11873–11879. doi: 10.1109/JSEN.2019.2937976 [72] SHEN Yizhu, YANG Jiawei, MENG Hongfu, et al. Generating millimeter-wave Bessel beam with orbital angular momentum using reflective-type metasurface inherently integrated with source[J]. Applied Physics Letters, 2018, 112(14): 141901. doi: 10.1063/1.5023327 [73] 张倬钒. 平面螺旋轨道角动量电磁波及其应用研究[D]. [硕士论文], 浙江大学, 2017: 14–15.ZHANG Zhuofan. Plane spiral orbital angular momentum waves and its applications[D]. [Master dissertation], Zhejiang University, 2017: 14–15. [74] CHEN Menglin, JIANG Lijun, and SHA W E I. Orbital angular momentum generation and detection by geometric-phase based metasurfaces[J]. Applied Sciences, 2018, 8(3): 362. doi: 10.3390/app8030362 [75] CHEN Menglin, JIANG Lijun, and SHA W E I. Ultrathin complementary metasurface for orbital angular momentum generation at microwave frequencies[J]. IEEE Transactions on Antennas and Propagation, 2017, 65(1): 396–400. doi: 10.1109/TAP.2016.2626722 -



 作者中心
作者中心 专家审稿
专家审稿 责编办公
责编办公 编辑办公
编辑办公
 下载:
下载: