中段弹道目标分离过程动态散射特性分析

赵锋; 徐志明; 吴其华; 艾小锋

doi:10.12000/JR21047

中段弹道目标分离过程动态散射特性分析

doi: 10.12000/JR21047

国防科技大学电子科学学院电子信息系统复杂电磁环境效应国家重点实验室长沙 410073

基金项目: 国家自然科学基金(62071475, 61890541, 61890542, 62001481)

详细信息

作者简介:
赵　锋(1978–)，男，江苏南京人，教授。主要研究方向为电子信息系统仿真建模评估

徐志明(1995–)，男，山东潍坊人，在读博士研究生。主要研究方向为双基地雷达目标特性与特征提取、目标识别

吴其华(1990–)，男，江苏盐城人，讲师。主要研究方向为雷达成像与电子信息系统仿真建模评估

艾小锋(1983–)，男，四川安岳人，副研究员。主要研究方向为双基地雷达成像、特征提取

通讯作者:
赵锋 zhfbee@tom.com

徐志明 zhimingxu@nudt.edu.cn

责任主编：冯存前 Corresponding Editor: FENG Cunqian
中图分类号: TN955
计量
- 文章访问数: 1337
- HTML全文浏览量: 293
- PDF下载量: 192
- 被引次数: 0
出版历程
- 收稿日期: 2021-04-12
- 修回日期: 2021-06-01
- 网络出版日期: 2021-06-18
- 刊出日期: 2021-06-28

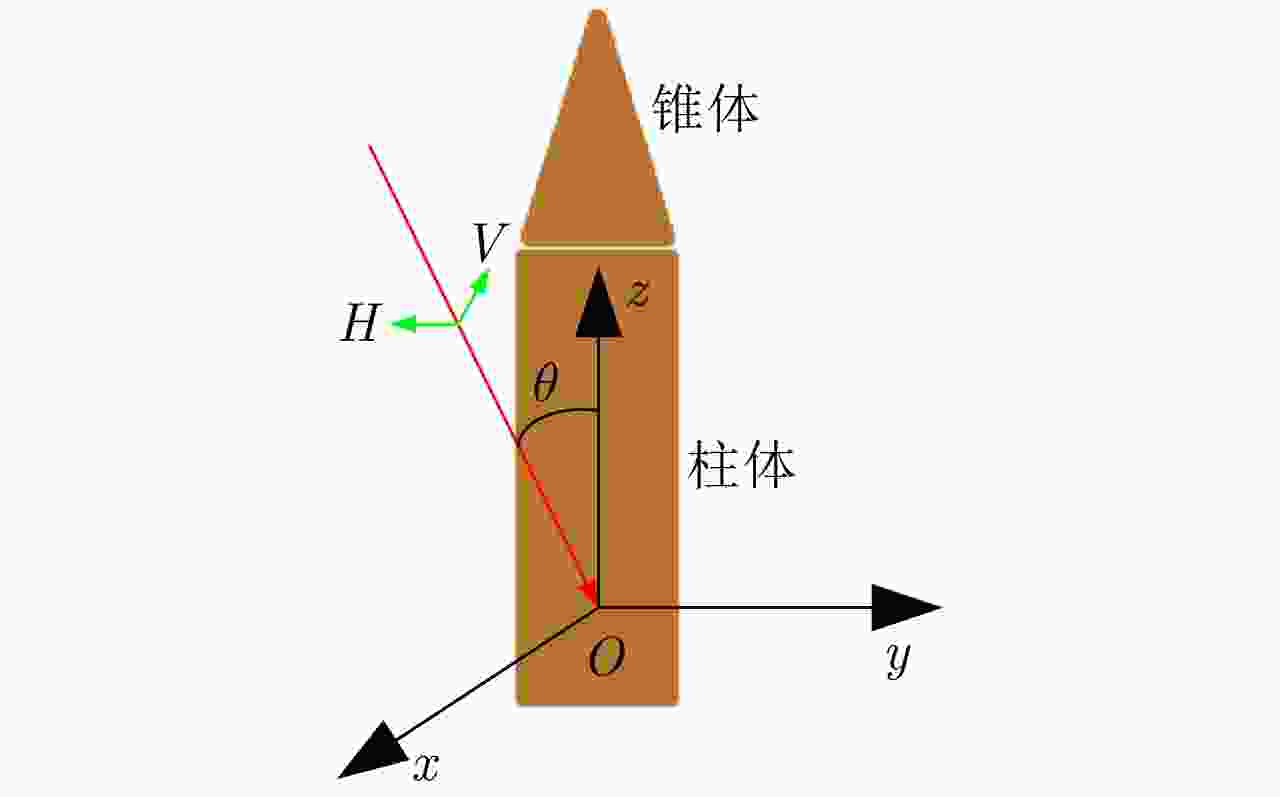
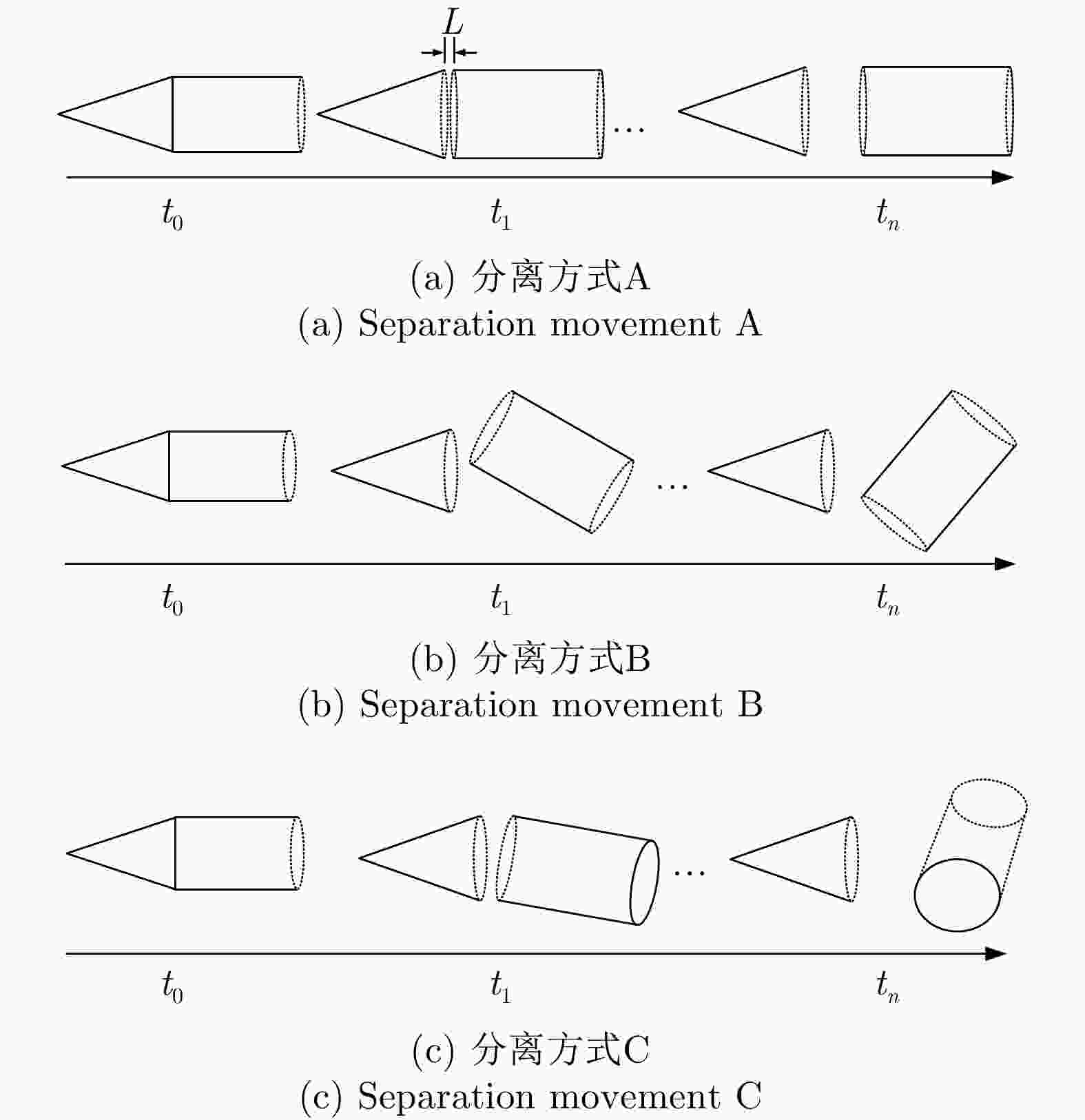
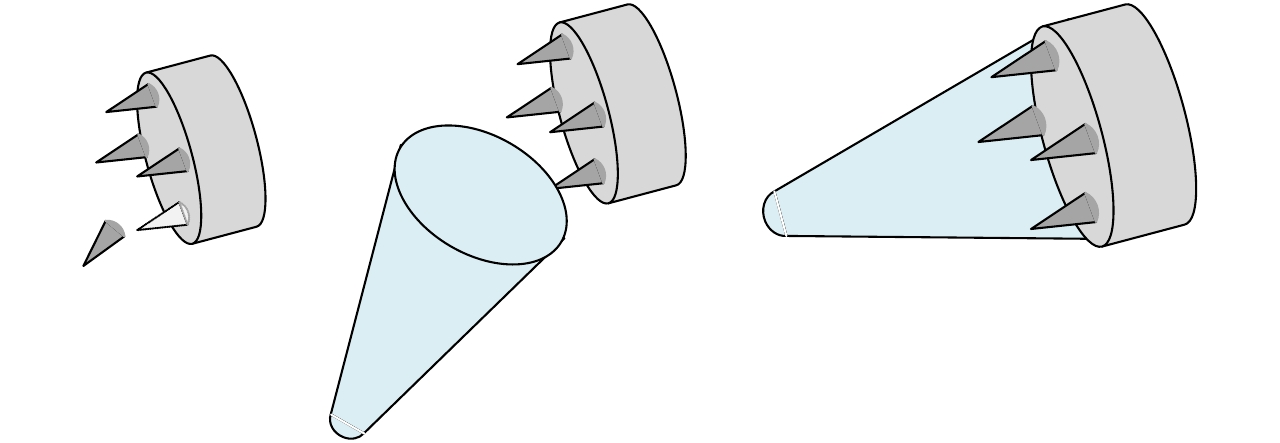
Dynamic Scattering Analysis of Midcourse Ballistic Targets with Separation Movements

The State Key Laboratory of Complex Electromagnetic Environment Effects on Electronics and Information System, College of Electronic Science, National University of Defense Technology, Changsha 410073, China

Funds: The National Natural Science Foundation of China (62071475, 61890541, 61890542, 62001481)

More Information

Corresponding author: ZHAO Feng, zhfbee@tom.com; XU Zhiming, zhimingxu@nudt.edu.cn

摘要

摘要: 中段弹道目标会发生释放弹头、抛洒诱饵等多种形式的目标分离事件。在目标分离的前期，多目标之间距离较近，存在电磁耦合现象，诱发目标雷达散射截面积、极化等维度的电磁特征变化。准确地捕获这些变化就能辅助雷达进行资源调度，提高预警雷达对弹道目标的跟踪和识别能力。该文对中段弹道目标3种分离方式的动态散射特性进行了深入分析，在此基础上提出了可以判断目标分离事件发生的特征量，促进弹道目标行为辨识的发展。
- 弹道目标 /
- 目标分离 /
- 多目标 /
- 特征提取
Abstract: In the midcourse trajectory of ballistic targets, warhead releasing and decoy throwing are two of the several types of target separation events. In the early stages, multiple targets are close to each other, and coupling scattering usually leads to variations in the radar cross section and polarization. If these variation features are investigated clearly, the tracking and recognition ability of an early warning radar will improve for ballistic targets. In this study, dynamic scattering of ballistic targets with three types of separation movements is analyzed; and several separation features that promote the action recognition development of midcourse ballistic targets are proposed.
- Ballistic targets /
- Target separation /
- Multiple targets /
- Feature extraction

HTML全文

图 1 中段弹道目标动态分离过程示意图

Figure 1. Diagram of dynamic separation movement for mid-course ballistic targets

下载: 全尺寸图片幻灯片

图 2 中段弹道目标结构示意图

Figure 2. Structure of mid-course ballistic targets

下载: 全尺寸图片幻灯片

图 3 锥柱组合体目标3种分离方式示意图(纸面代表图2中的xOz平面)

Figure 3. Three types of separation movements for cone-cylinder-shaped ballistic targets (xOz plane in Fig. 2 coincides with the paper)

下载: 全尺寸图片幻灯片

图 4 锥柱组合体分离方式A动态RCS分布

Figure 4. Dynamic RCS distribution of cone-cylinder-shaped targets with separation movement A

下载: 全尺寸图片幻灯片

图 5 锥柱组合体分离方式B动态RCS分布

Figure 5. Dynamic RCS distribution of cone-cylinder-shaped targets with separation movement B

下载: 全尺寸图片幻灯片

图 6 锥柱组合体分离方式C动态RCS分布

Figure 6. Dynamic RCS distribution of cone-cylinder-shaped targets with separation movement C

下载: 全尺寸图片幻灯片

图 7 锥柱组合体RCS均值随着目标分离的变化

Figure 7. Mean variation of RCS for cone-cylinder-shaped targets with separation movements

下载: 全尺寸图片幻灯片

图 8 锥柱组合体极化比(S_HH/S_VH)随着目标分离的变化

Figure 8. Polarization ratio variation of cone-cylinder-shaped targets with separation movements

下载: 全尺寸图片幻灯片

图 9 锥柱组合体特征角随着目标分离的变化

Figure 9. Characterization angle variation of cone-cylinder-shaped targets with separation movements

下载: 全尺寸图片幻灯片

图 10 锥柱组合体对称角随着目标分离的变化

Figure 10. Symmetry angle variation of cone-cylinder-shaped targets with separation movement

下载: 全尺寸图片幻灯片

图 11 锥柱组合体RCS随着目标分离的变化(θ=15°)

Figure 11. RCS variation of cone-cylinder-shaped targets with separation movements (θ=15°)

下载: 全尺寸图片幻灯片

图 12 锥柱组合体极化比随着目标分离的变化(θ=15°)

Figure 12. Polarization ratio variation of cone-cylinder-shaped targets with separation movements (θ=15°)

下载: 全尺寸图片幻灯片

图 13 锥柱组合体特征角随着目标分离的变化(θ=15°)

Figure 13. Characterization angle variation of cone-cylinder-shaped targets with separation movements (θ=15°)

下载: 全尺寸图片幻灯片

图 14 锥柱组合体对称角随着目标分离的变化(θ=15°)

Figure 14. Symmetry angle variation of cone-cylinder-shaped targets with separation movements (θ=15°)

下载: 全尺寸图片幻灯片

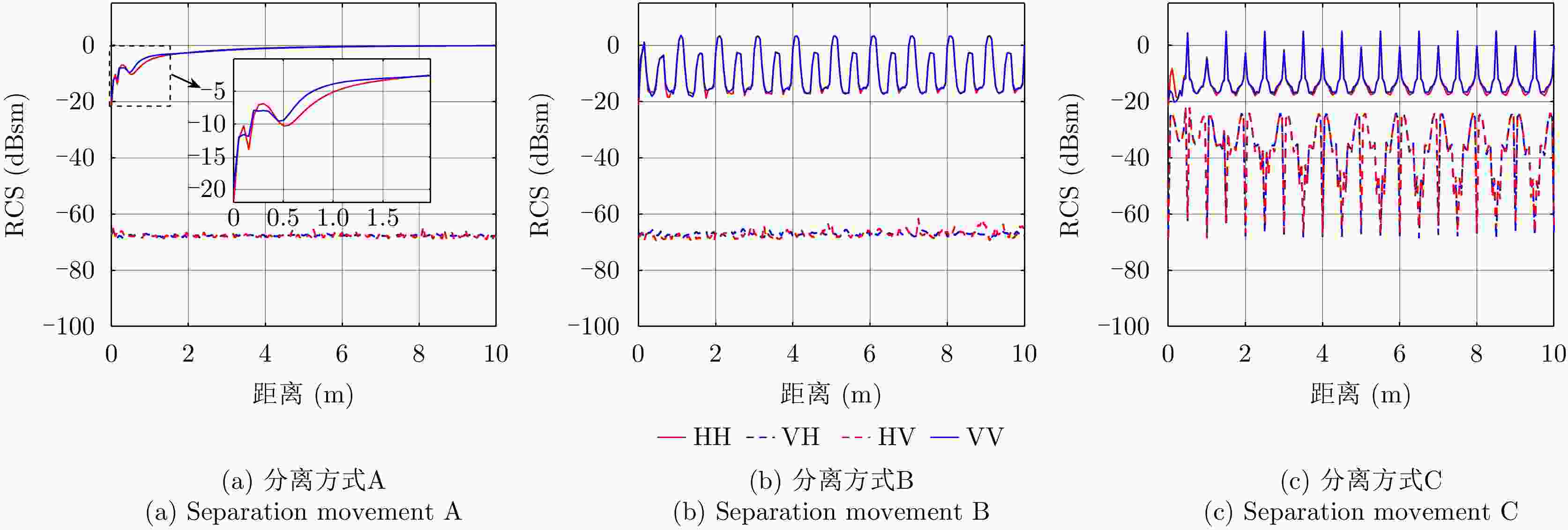
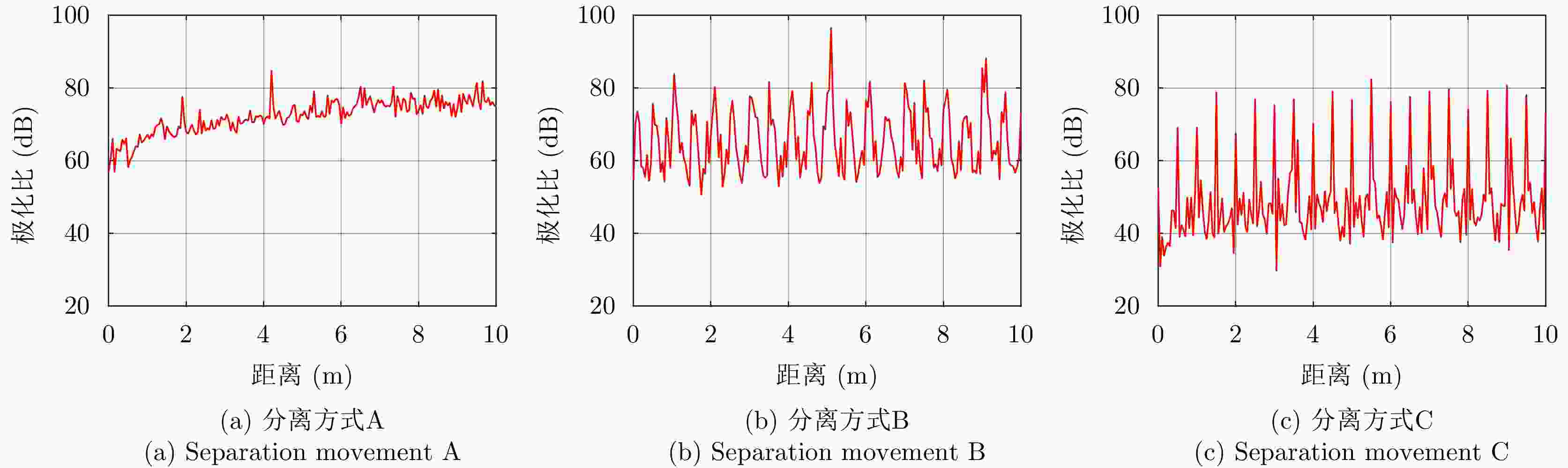
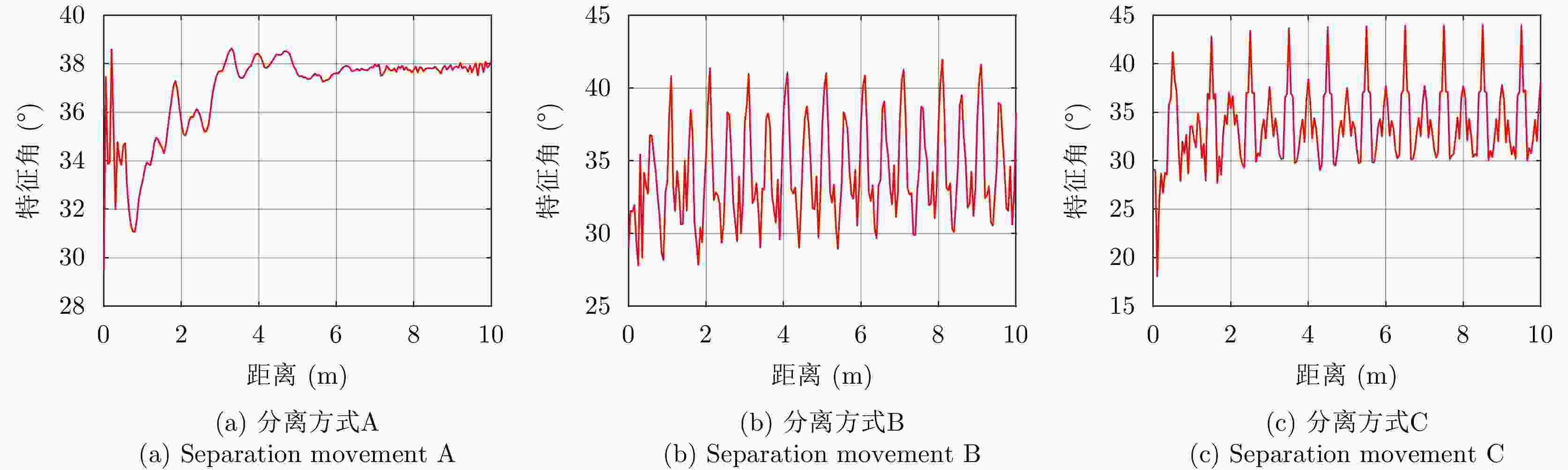
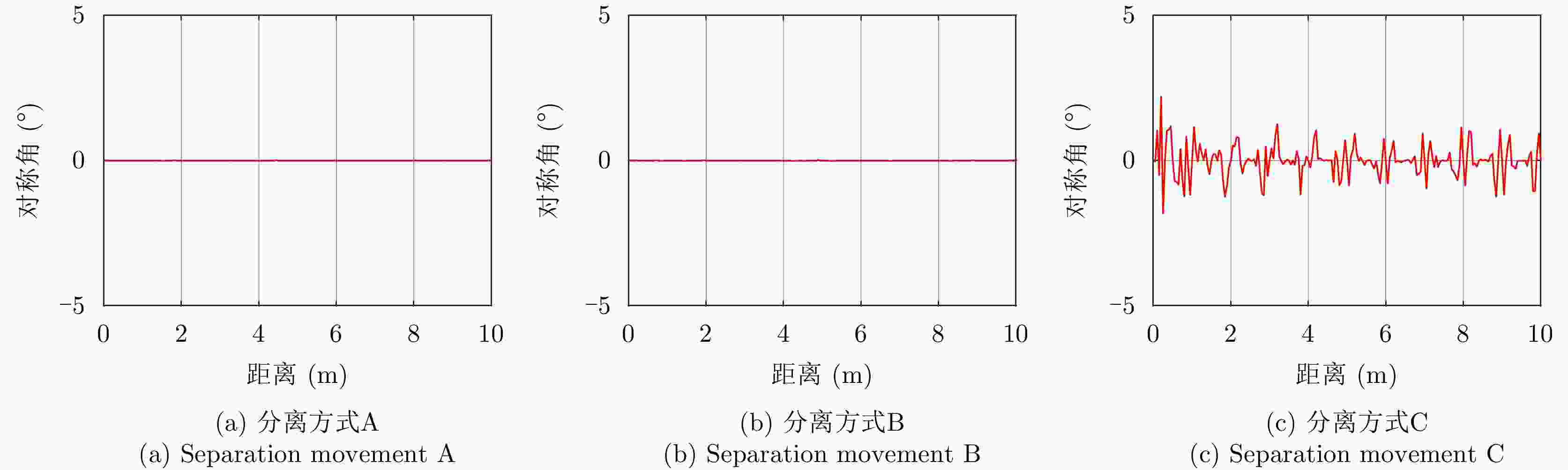
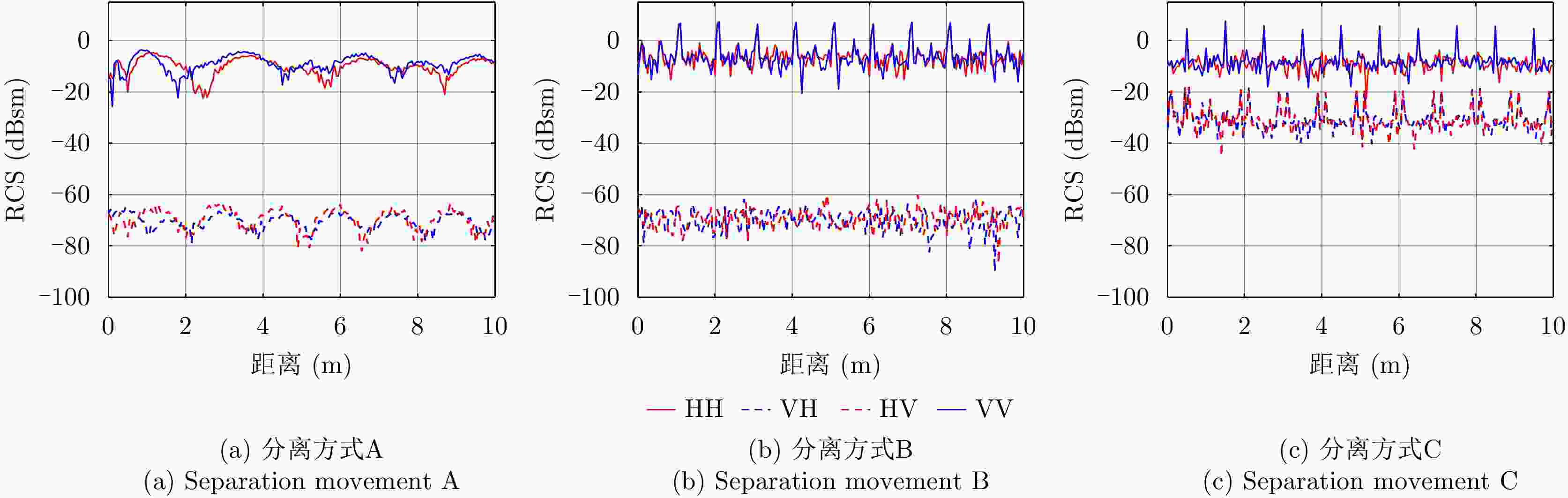
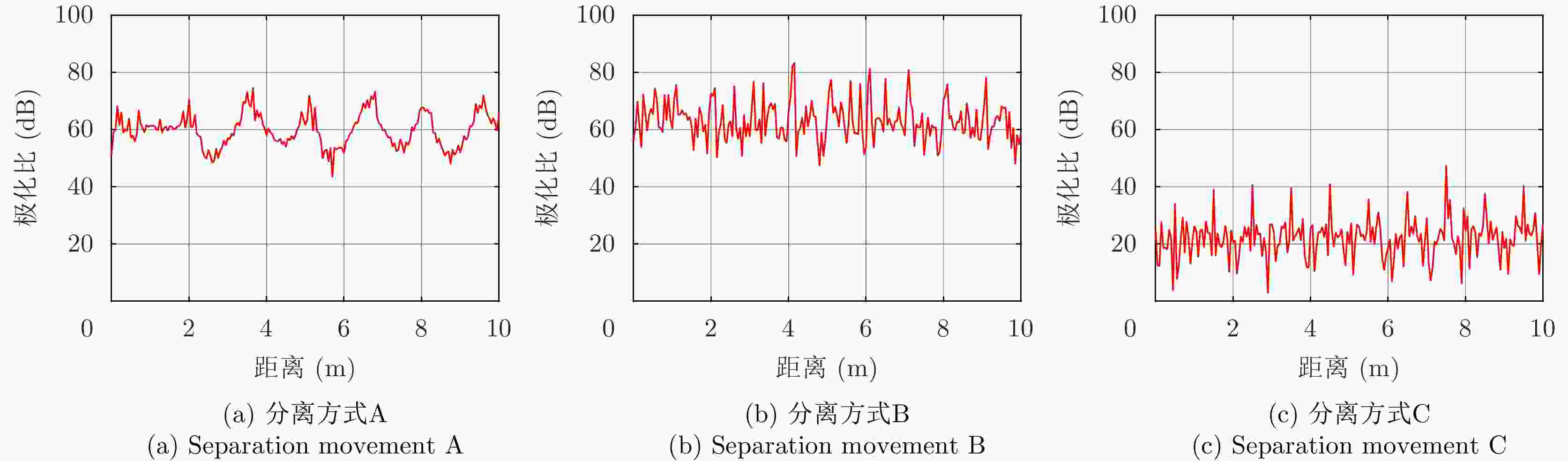
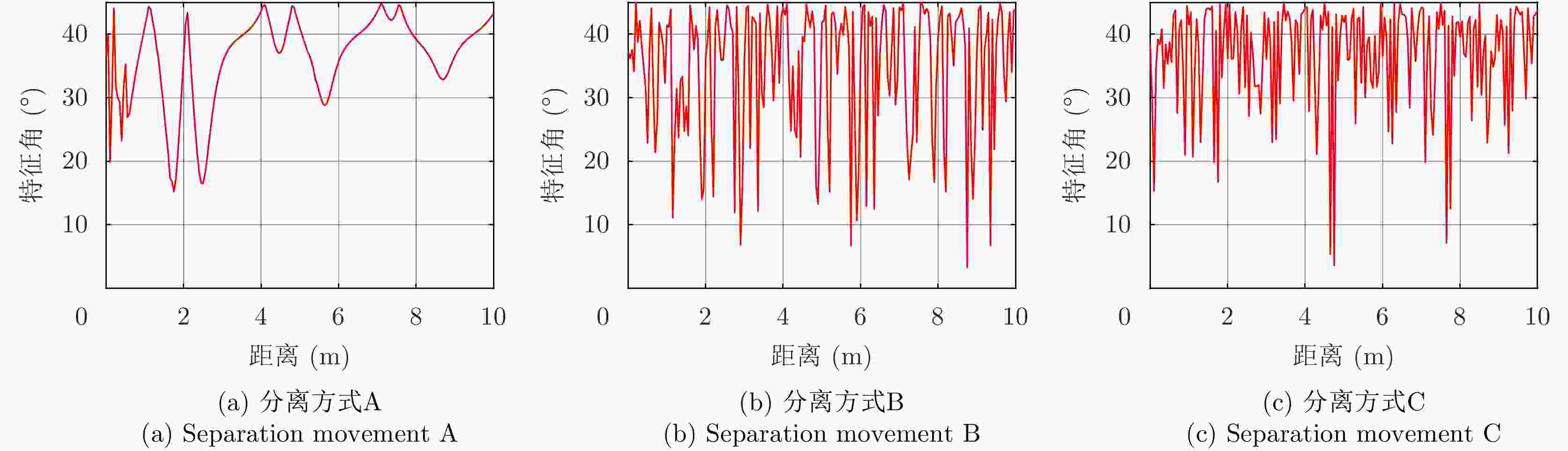
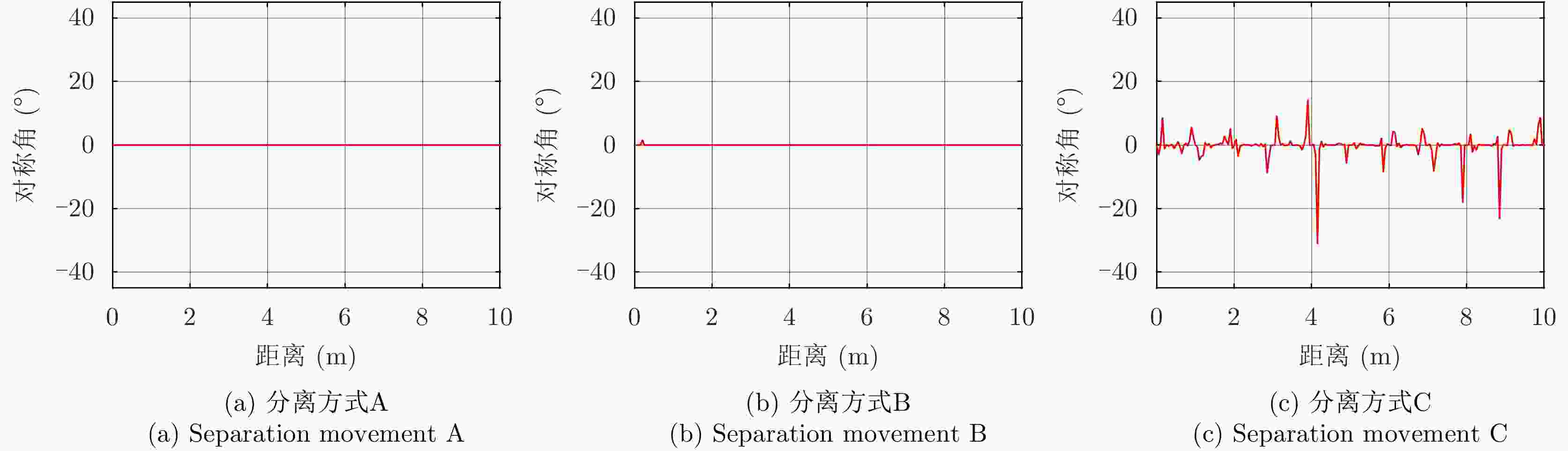
表 1 空间目标分离事件特征的定量化表征

Table 1. Separation accident features characterization for space targets

特征值	RCS			极化比			特征角			对称角
特征值	A	B	C	A	B	C	A	B	C	A	B	C
均值	–10.12	–6.25	–9.01	59.81	63.12	21.93	36.42	34.68	36.98	0	0	–0.18
极差	15.63	25.88	27.08	33.24	30.54	44.10	29.69	41.71	41.37	0	1.55	45.25
标准差	3.26	4.78	4.14	5.86	6.21	6.67	6.77	10.33	8.09	0	0.11	3.82
变异系数	–0.32	–0.76	–0.46	0.10	0.10	0.30	0.19	0.30	0.22	–2.77	14.51	–21.75
平滑度	0.91	0.96	0.94	0.97	0.97	0.98	0.98	0.99	0.98	0	0.011	0.94
偏度系数	–0.63	1.09	1.69	0.36	0.69	0.33	–1.29	–1.07	–1.56	–6.17	14.06	–3.85
峰度系数	2.97	4.55	8.27	3.03	3.04	4.64	4.21	3.11	5.58	48.68	198.81	32.27

下载: 导出CSV

表 2 不同分离方式之间的隔离度

Table 2. Isolation measurement between separation movements characterization features

组合	A, B	A, C	B, C
RCS隔离度	0.3346	0.2882	0.1437
极化比隔离度	0.0566	0.5917	0.6445
特征角隔离度	0.1977	0.1553	0.0708
对称角隔离度	0.2347	0.9362	0.9893

下载: 导出CSV

参考文献(18)

[1]	AI Xiaofeng, XU Zhiming, WU Qihua, et al. Parametric representation and application of micro-doppler characteristics for cone-shaped space targets[J]. IEEE Sensors Journal, 2019, 19(24): 11839–11849. doi: 10.1109/JSEN.2019.2937995
[2]	PERSICO A R, CLEMENTE C, GAGLIONE D, et al. On model, algorithms, and experiment for micro-Doppler-based recognition of ballistic targets[J]. IEEE Transactions on Aerospace and Electronic Systems, 2017, 53(3): 1088–1108. doi: 10.1109/TAES.2017.2665258
[3]	靳俊峰, 曾怡, 廖圣龙. 弹道导弹群目标跟踪分裂算法研究[J]. 雷达科学与技术, 2020, 18(3): 321–326. doi: 10.3969/j.issn.1672-2337.2020.03.014 JIN Junfeng, ZENG Yi, and LIAO Shenglong. Group target splitting algorithm for ballistic missile target tracking[J]. Radar Science and Technology, 2020, 18(3): 321–326. doi: 10.3969/j.issn.1672-2337.2020.03.014
[4]	修建娟, 韩蕾蕾, 董凯, 等. 空间密集群目标关联与跟踪算法研究[J]. 火力与指挥控制, 2020, 45(8): 51–56. doi: 10.3969/j.issn.1002-0640.2020.08.008 XIU Jianjuan, HAN Leilei, DONG Kai, et al. Study on correlation and tracking algorithm of space dense group targets[J]. Fire Control &Command Control, 2020, 45(8): 51–56. doi: 10.3969/j.issn.1002-0640.2020.08.008
[5]	CHEN Jian, XU Shiyou, and CHEN Zengping. Convolutional neural network for classifying space target of the same shape by using RCS time series[J]. IET Radar, Sonar & Navigation, 2018, 12(11): 1268–1275. doi: 10.1049/iet-rsn.2018.5237
[6]	XU Zhiming, AI Xiaofeng, WU Qihua, et al. Micro-Doppler characteristics of streamlined ballistic target[J]. Electronics Letters, 2019, 55(3): 149–151. doi: 10.1049/el.2018.7251
[7]	向前, 王晓丹, 李睿, 等. 基于DCNN的弹道中段目标HRRP图像识别[J]. 系统工程与电子技术, 2020, 42(11): 2426–2433. doi: 10.3969/j.issn.1001-506X.2020.11.03 XIANG Qian, WANG Xiaodan, LI Rui, et al. HRRP image recognition of midcourse ballistic targets based on DCNN[J]. Systems Engineering and Electronics, 2020, 42(11): 2426–2433. doi: 10.3969/j.issn.1001-506X.2020.11.03
[8]	WANG Tao, WANG Xuesong, CHANG Yuliang, et al. Estimation of precession parameters and generation of ISAR images of ballistic missile targets[J]. IEEE Transactions on Aerospace and Electronic Systems, 2010, 46(4): 1983–1995. doi: 10.1109/TAES.2010.5595608
[9]	张胜峰, 马超, 朱新国, 等. 弹道目标宽带极化特征提取分析[J]. 现代雷达, 2020, 42(1): 45–50. doi: 10.16592/j.cnki.1004-7859.2020.01.010 ZHANG Shengfeng, MA Chao, ZHU Xinguo, et al. Wideband polarization feature extraction of ballistic targets[J]. Modern Radar, 2020, 42(1): 45–50. doi: 10.16592/j.cnki.1004-7859.2020.01.010
[10]	ZHAO Mengmeng, ZHANG Qun, LUO Ying, et al. Micromotion feature extraction and distinguishing of space group targets[J]. IEEE Geoscience and Remote Sensing Letters, 2017, 14(2): 174–178. doi: 10.1109/LGRS.2016.2633426
[11]	赵盟盟, 张群, 陈怡君, 等. 一种用于空间群目标分辨的滑动窗轨迹跟踪算法[J]. 宇航学报, 2015, 36(10): 1187–1194. doi: 10.3873/j.issn.1000-1328.2015.10.013 ZHAO Mengmeng, ZHANG Qun, CHEN Yijun, et al. A sliding window tracking algorithm for distinguishing space group targets[J]. Journal of Astronautics, 2015, 36(10): 1187–1194. doi: 10.3873/j.issn.1000-1328.2015.10.013
[12]	邵长宇, 杜兰, 李飞, 等. 基于多目标跟踪的空间锥体目标微多普勒频率提取方法[J]. 电子与信息学报, 2012, 34(12): 2972–2977. doi: 10.3724/SP.J.1146.2012.00656 SHAO Changyu, DU Lan, LI Fei, et al. Micro-doppler extraction from space cone target based on multiple target tracking[J]. Journal of Electronics &Information Technology, 2012, 34(12): 2972–2977. doi: 10.3724/SP.J.1146.2012.00656
[13]	陈帅, 冯存前, 张蓉. 基于离散正弦调频变换的中段多微动目标分离[J]. 北京航空航天大学学报, 2020, 46(2): 371–378. doi: 10.13700/j.bh.1001-5965.2019.0128 CHEN Shuai, FENG Cunqian, and ZHANG Rong. Separation of midcourse multiple micro-motion targets based on DSFMT[J]. Journal of Beijing University of Aeronautics and Astronautics, 2020, 46(2): 371–378. doi: 10.13700/j.bh.1001-5965.2019.0128
[14]	陈帅, 冯存前, 李晓华. 基于时频图像背景差分的中段多弹道目标分离[J]. 弹箭与制导学报, 2019, 39(6): 66–70. doi: 10.15892/j.cnki.djzdxb.2019.06.015 CHEN Shuai, FENG Cunqian, and LI Xiaohua. Separation of multiple ballistic targetsin midcourse based on background difference of time-frequency images[J]. Journal of Projectiles,Rockets,Missiles and Guidance, 2019, 39(6): 66–70. doi: 10.15892/j.cnki.djzdxb.2019.06.015
[15]	陈帅, 冯存前, 许旭光. 基于Viterbi算法和ROMP的多弹道目标分离与特征提取[J]. 火力与指挥控制, 2020, 45(3): 22–27. doi: 10.3969/j.issn.1002-0640.2020.03.004 CHEN Shuai, FENG Cunqian, and XU Xuguang. Multi-ballistic target separation and feature extraction based on viterbi and ROMP algorithm[J]. Fire Control &Command Control, 2020, 45(3): 22–27. doi: 10.3969/j.issn.1002-0640.2020.03.004
[16]	贺思三, 赵会宁, 张永顺. 基于时频域联合滤波的中段群目标信号分离[J]. 雷达学报, 2015, 4(5): 545–551. doi: 10.12000/JR15008 HE Sisan, ZHAO Huining, and ZHANG Yongshun. Signal separation for target group in midcourse based on time-frequency filtering[J]. Journal of Radars, 2015, 4(5): 545–551. doi: 10.12000/JR15008
[17]	涂世杰, 陈航. 反导系统对弹道群目标分离识别仿真[J]. 计算机仿真, 2017, 34(4): 61–65. doi: 10.3969/j.issn.1006-9348.2017.04.013 TU Shijie and CHEN Hang. Simulation of ballistic target group separation and identification in anti-missile system[J]. Computer Simulation, 2017, 34(4): 61–65. doi: 10.3969/j.issn.1006-9348.2017.04.013
[18]	张俊, 胡生亮, 杨庆, 等. 浮空式角反射体RCS统计特征及识别模型研究[J]. 系统工程与电子技术, 2019, 41(4): 780–786. doi: 10.3969/j.issn.1001-506X.2019.04.12 ZHANG Jun, HU Shengliang, YANG Qing, et al. RCS statistical features and recognition model of air-floating corner reflector[J]. Systems Engineering and Electronics, 2019, 41(4): 780–786. doi: 10.3969/j.issn.1001-506X.2019.04.12