基于深度神经网络的可编程超表面智能波束形成

李商洋; 符士磊; 徐丰

doi:10.12000/JR21039

基于深度神经网络的可编程超表面智能波束形成

doi: 10.12000/JR21039

复旦大学电磁波信息科学教育部重点实验室上海 200433

基金项目: 国家重点研发计划(2017YFA0700203)

详细信息

作者简介:
李商洋(1993–)，男，安徽人，复旦大学电磁波信息科学教育部重点实验室博士研究生，研究方向为天线理论和设计、可编程超表面、深度学习在电磁领域的应用

符士磊(1995–)，男，江苏人，复旦大学电磁波信息科学教育部重点实验室博士研究生，研究方向为SAR图像解译、深度学习

徐　丰(1982–)，男，浙江人，复旦大学信息科学与工程学院教授，电磁波信息科学教育部重点实验室副主任，研究方向为电磁散射建模、SAR图像解译

通讯作者:
徐丰 fengxu@fudan.edu.cn

责任主编：张安学 Corresponding Editor: ZHANG Anxue
中图分类号: TN95
计量
- 文章访问数: 2214
- HTML全文浏览量: 806
- PDF下载量: 368
- 被引次数: 0
出版历程
- 收稿日期: 2021-03-26
- 修回日期: 2021-04-26
- 网络出版日期: 2021-04-28

DNN-based Intelligent Beamforming on a Programmable Metasurface

Key Laboratory for Information Science of Electromagnetic Waves, MoE, Fudan University, Shanghai 200433, China

Funds: The National Key Research and Development Program of China (2017YFA0700203)

More Information

Corresponding author: XU Feng, fengxu@fudan.edu.cn

摘要

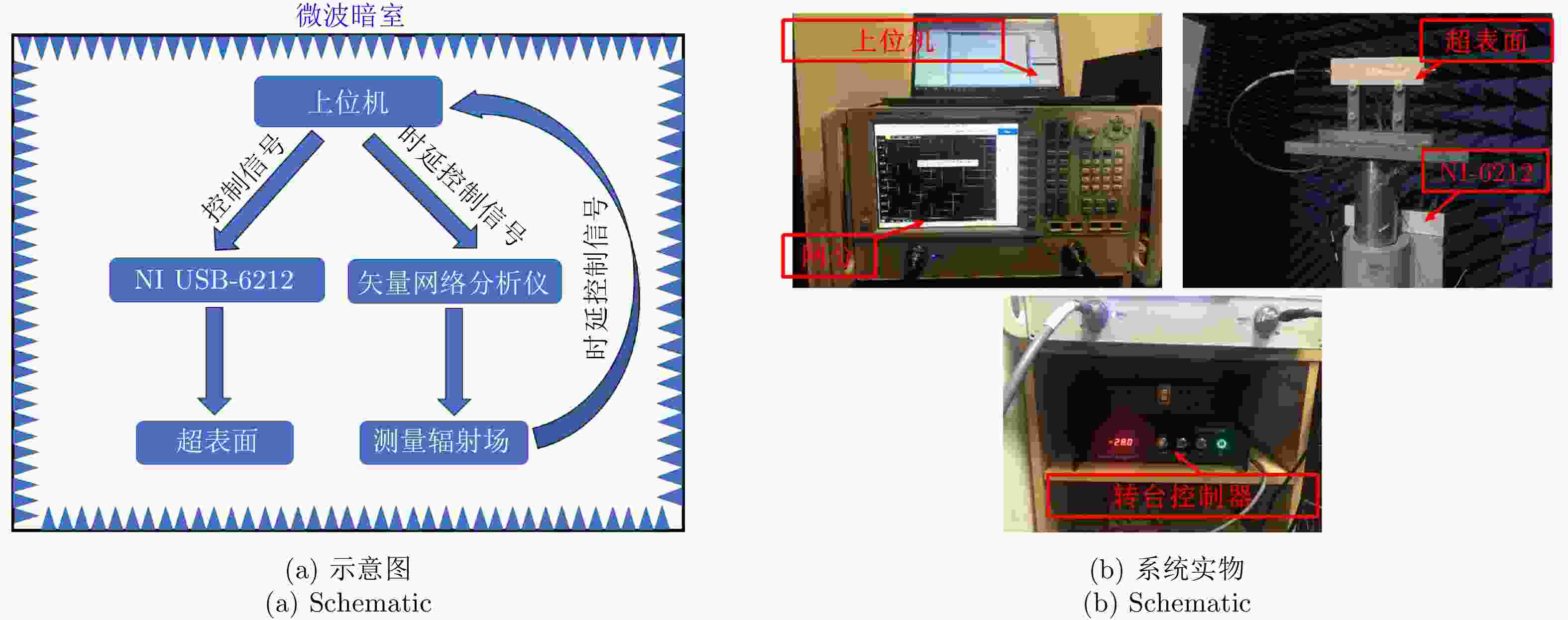
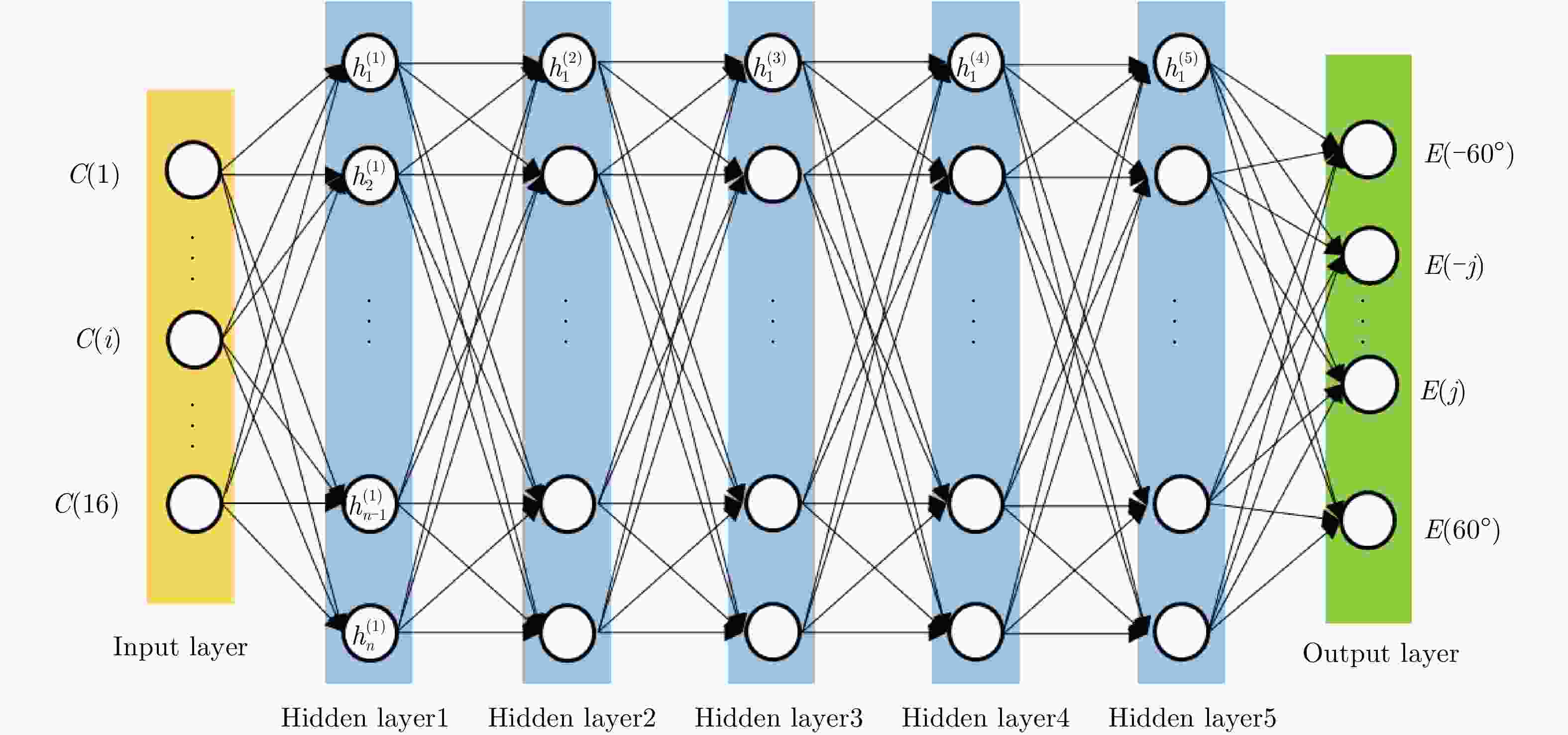
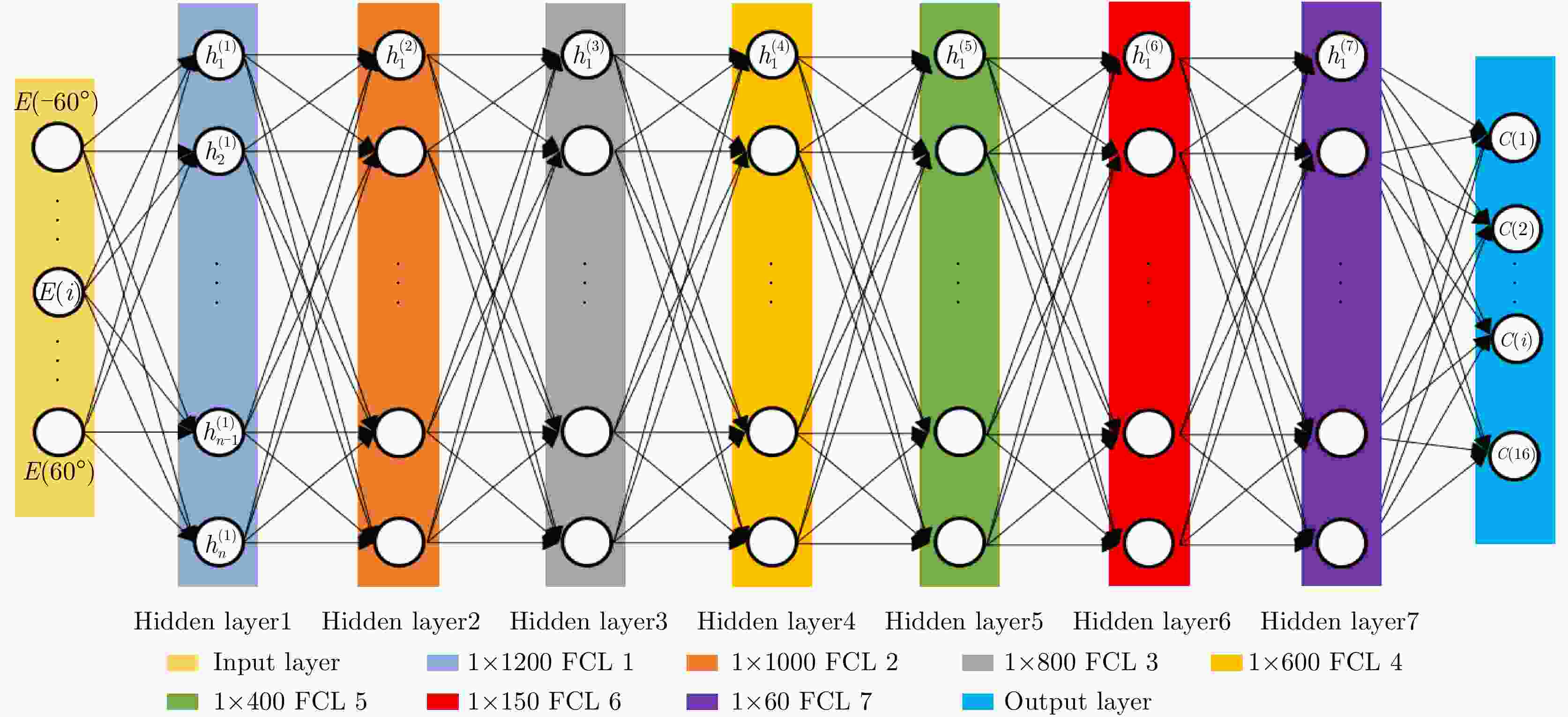
摘要: 通过在超表面单元上加载二极管等有源器件，可编程超表面可实现对电磁波的实时灵活调控。通常利用全波仿真软件计算可编程超表面的辐射场，但该方法需要消耗大量的时间，因而降低了设计效率。为了实现准确高效求解给定编码序列计算辐射场，该文首先设计了辐射场自动测试系统，利用该测试系统实测了少量的编码和辐射场数据，其后提出了一个正向深度神经网络，基于实测的数据训练该神经网络，最终实现了给定编码准确高效预测辐射场。对于给定辐射场求解编码的逆问题，该文提出了一个逆向深度神经网络。基于正向网络生成的数据训练所提出的逆向网络，最终实现了给定辐射场实时准确求解编码。该文所提出的方法为雷达波束形成提供了一种新可选方案，在雷达智能波束形成、微波成像等领域有一定的应用价值。
- 可编程超表面 /
- 离散偶极子近似 /
- 深度学习 /
- 全连接网络 /
- 辐射场预测
Abstract: The Programmable Metasurface (PM) can flexibly manipulate electromagnetic waves in real time using loading active devices on the meta-element. Calculating the radiation fields of the PM with complex structures using full-wave simulation software is time-consuming, which results in design efficiency. To accurately and efficiently solve the mapping relationship from coding schemes to radiation fields, an Auto-Measuring System (AMS) of radiation patterns is designed. A few Code-to-Pattern (C-P) data are measured via the AMS. Then, a forward Deep Neural Network (DNN) is proposed, the DNN is trained by the measured data, and an accurate and efficient prediction of C-P is realized. More C-P data are generated based on the proposed forward neural network, and the data are used to train another proposed inverse DNN and realize the accurate prediction of codes when given patterns in real time. This method provides a new alternative scheme for radar beamforming and has application values in intelligent radar beamforming and microwave imaging.
- Programmable metasurface /
- Deep neural network /
- Full connected network /
- Code-to-pattern /
- Pattern-to-code

HTML全文

图 1 基于文献[4]提出的可编程超表面

Figure 1. The proposed metasurface based on Ref. [4]

下载: 全尺寸图片幻灯片

图 2 不同状态下单元散射参数

Figure 2. Scattering parameters of the element

下载: 全尺寸图片幻灯片

图 3 不同编码下超表面方向图

Figure 3. Radiation patterns under different codes

下载: 全尺寸图片幻灯片

图 4 自动测试系统

Figure 4. Auto-measuring system

下载: 全尺寸图片幻灯片

图 5 仿真结果、实测结果、自动测试结果对比

Figure 5. Comparison results of simulated results, measured results and auto-measuring results

下载: 全尺寸图片幻灯片

图 6 全连接网络结构

Figure 6. Structure of the fully connected network

下载: 全尺寸图片幻灯片

图 7 训练和验证均方根误差

Figure 7. RMSE of training and validation

下载: 全尺寸图片幻灯片

图 8 归一化方向图神经网络预测值和真值对比结果

Figure 8. Comparison results of normalized pattern of prediction results and true value

下载: 全尺寸图片幻灯片

图 9 逆向映射网络结构

Figure 9. Structure of the reverse mapping network

下载: 全尺寸图片幻灯片

图 10 训练和验证均方根误差

Figure 10. RMSE of the training and validation results

下载: 全尺寸图片幻灯片

图 11 合成值和真值对比

Figure 11. Comparison results of prediction results and true value

下载: 全尺寸图片幻灯片

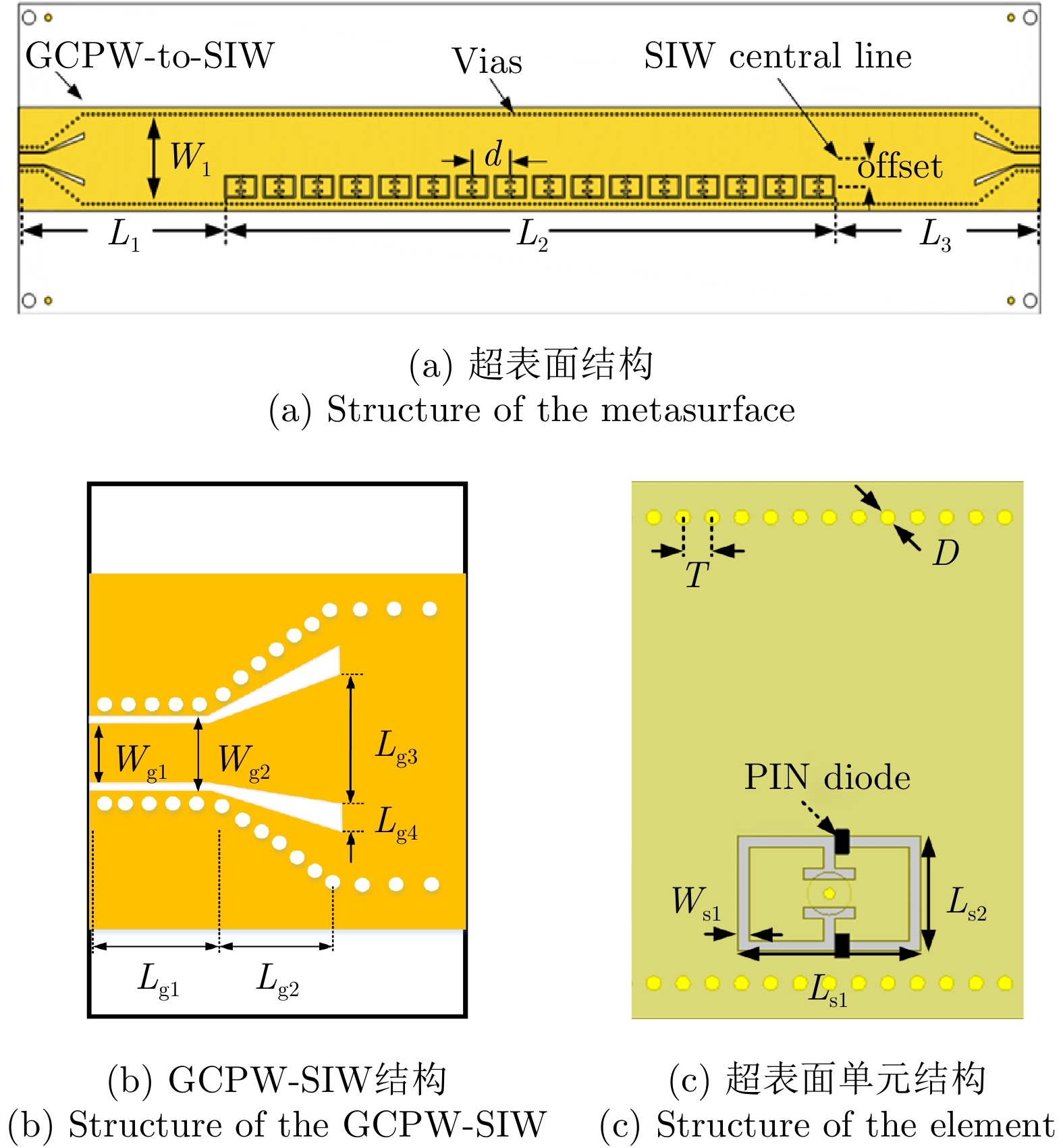
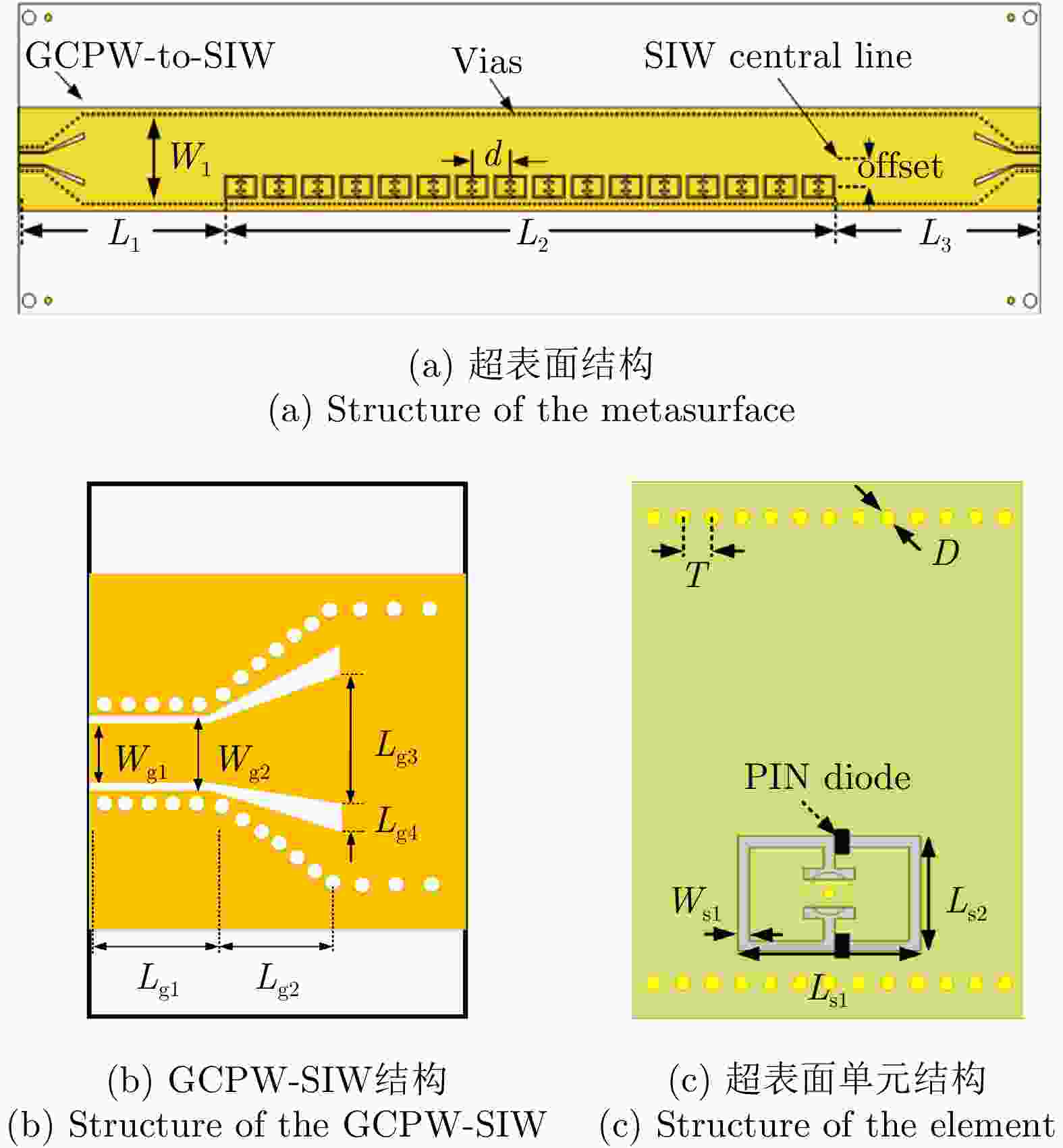
表 1 超表面相关参数(mm)

Table 1. Parameters of the metasurface (mm)

L₁	L₂	L₃	W₁	offset	d	W_feed	L_g1	L_g2	L_g3
32.1	95	32.1	13	4	6	1.65	3.7	6.3	6

L_g4	W_g1	W_g2	L_s1	L_s2	W_s1	T	D	h₁	h₂
0.8	1.65	2.05	5	3.2	0.3	0.8	0.4	1.524	0.508

下载: 导出CSV

表 2 单波束编码

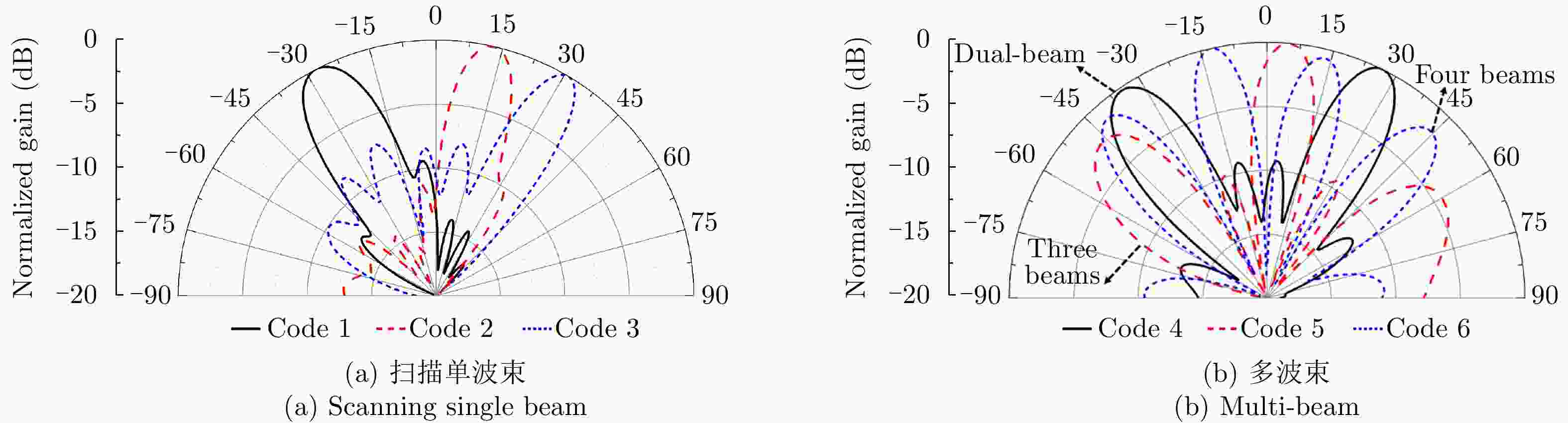
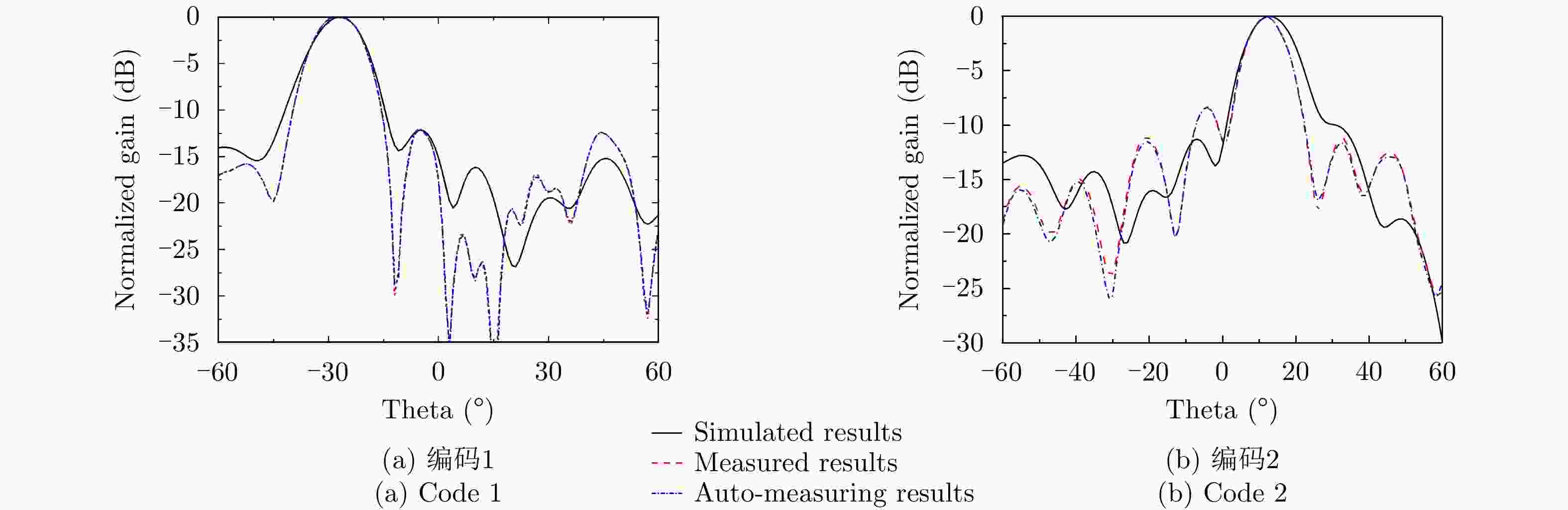
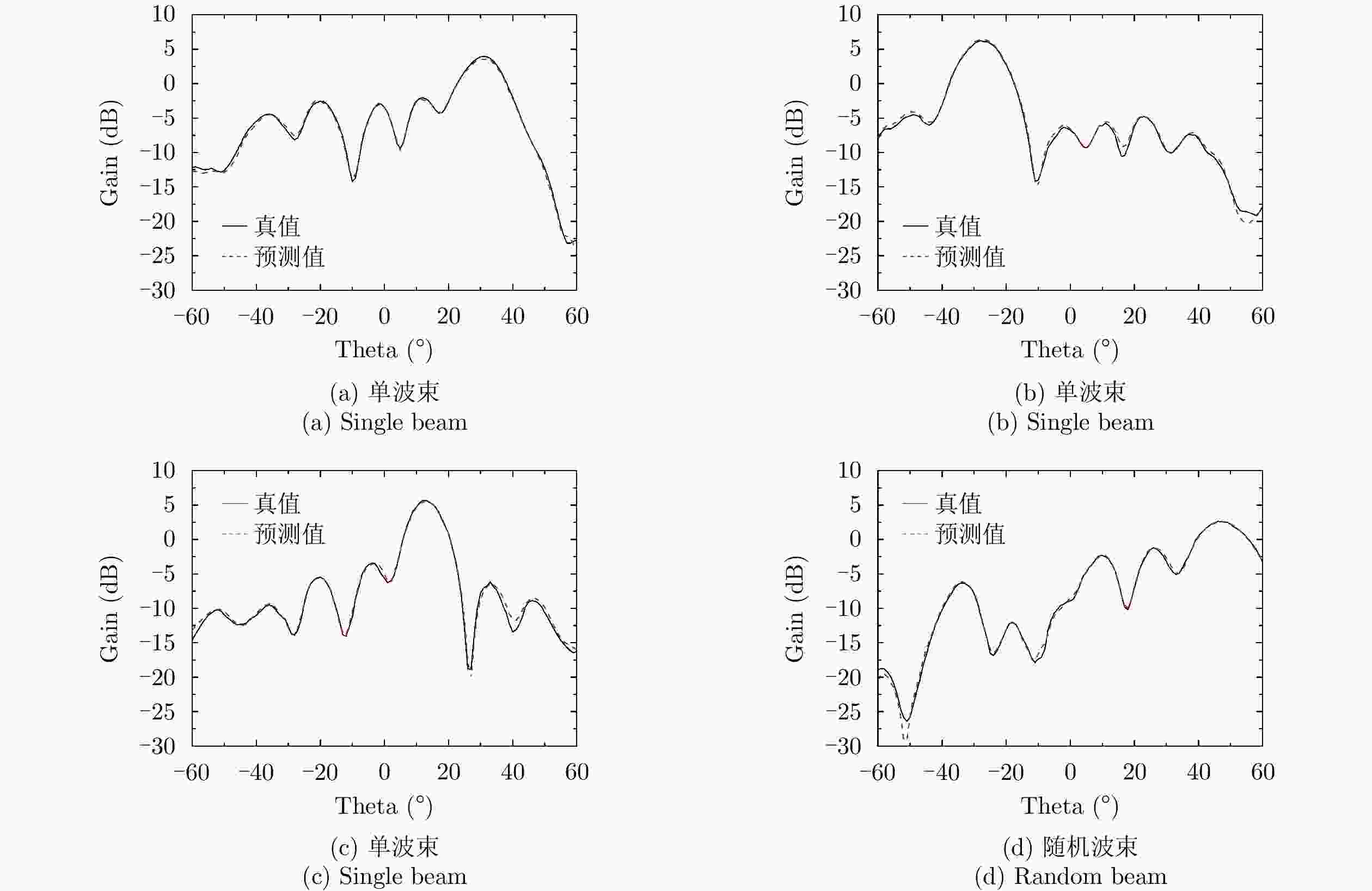
Table 2. Codes for single beams

编码号	编码序列	主瓣指向	波束宽度
Code 1	0101010101010101	–28°	13.5°
Code 2	1001001001001001	13°	10.0°
Code 3	1001100110011001	31°	8.5°

下载: 导出CSV

表 3 多波束编码

Table 3. Codes for multi-beam

编码号	编码序列	波束个数
Code 4	0001000100010001	2
Code 5	0000100001000010	3
Code 6	0000010000010000	4

下载: 导出CSV

表 4 计算编码准确率

Table 4. Accuracy for calculated codes

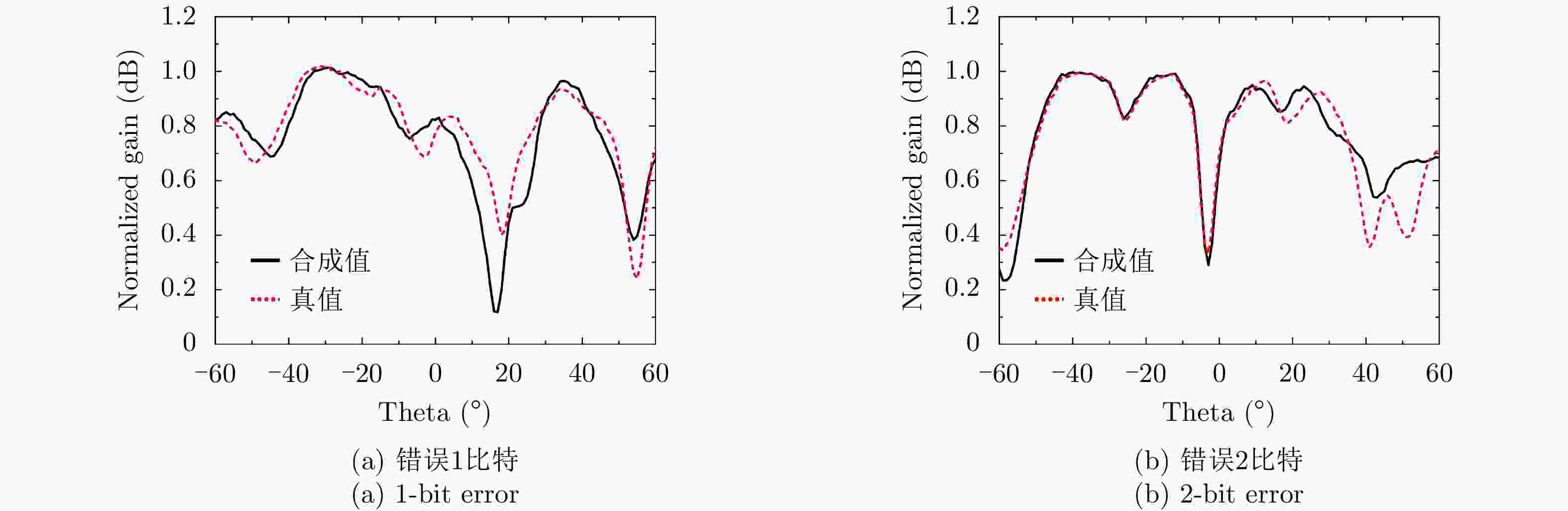
${ {\rm{{A}{c}{c}}}{u} }_{ {\rm{{m}{e}{a}{n}}} }$	${ {\rm{{A}{c}{c}}}{u} }_{0-{\rm{{b}{i}{t}}} }$	${ {\rm {{A}{c}{c}}}{u} }_{1-{\rm{{b}{i}{t}}} }$	${ {\rm {{A}{c}{c}}}{u} }_{2-{\rm {{b}{i}{t}}} }$	${ {\rm {{A}{c}{c}}}{u} }_{3+{\rm{{b}{i}{t}}} }$
99.09%	90.25%	6.56%	2.12%	1.07%

下载: 导出CSV

参考文献(9)

[1]	VESELAGO V G and LEBEDEV P N. The electrodynamics of substances with simultaneously negative values of ε and μ[J]. Soviet Physics Uspekhi, 1968, 10(4): 509–514. doi: 10.1070/PU1968v010n04ABEH003699
[2]	PENDRY J B, HOLDEN A J, STEWART W J, et al. Extremely low frequency plasmons in metallic mesostructures[J]. Physical Review Letters, 1996, 76(25): 4773–4776. doi: 10.1103/PhysRevLett.76.4773
[3]	CUI Tiejun, QI Meiqing, WAN Xiang, et al. Coding metamaterials, digital metamaterials and programmable metamaterials[J]. Light: Science & Applications, 2014, 3(10): e218.
[4]	LI Shangyang, XU Feng, WAN Xiang, et al. Programmable metasurface based on substrate-integrated waveguide for compact dynamic-pattern antenna[J]. IEEE Transactions on Antennas and Propagation, 2021, 69(5): 2958–2962. doi: 10.1109/TAP.2020.3023581
[5]	https://www.ni.com/zh-cn/support/model.usb-6212.html.
[6]	SAINATH T N, MOHAMED A R, KINGSBURY B, et al. Deep convolutional neural networks for LVCSR[C]. IEEE International Conference on Acoustics, Speech and Signal Processing, Vancouver, Canada, 2013: 8614–8618.
[7]	TOMPSON J, JAIN A, LECUN Y, et al. Joint training of a convolutional network and a graphical model for human pose estimation[C]. The 27th International Conference on Neural Information Processing Systems, Montreal, Canada, 2014: 1799–1807.
[8]	PULIDO-MANCERA L M, ZVOLENSKY T, IMANI M F, et al. Discrete dipole approximation applied to highly directive slotted waveguide antennas[J]. IEEE Antennas and Wireless Propagation Letters, 2016, 15: 1823–1826. doi: 10.1109/LAWP.2016.2538202
[9]	SHAN Tao, PAN Xiaotian, LI Maokun, et al. Coding programmable metasurfaces based on deep learning techniques[J]. IEEE Journal on Emerging and Selected Topics in Circuits and Systems, 2020, 10(1): 114–125. doi: 10.1109/JETCAS.2020.2972764