基于智能算法的超材料快速优化设计方法研究进展

贾宇翔,  王甲富,  陈维,  随赛,  朱瑞超,  邱天硕,  李勇峰,  韩亚娟,  屈绍波

downloadPDF
文章导航 > 雷达学报  > 2021 >  10(2): 220-239
贾宇翔, 王甲富, 陈维, 等. 基于智能算法的超材料快速优化设计方法研究进展[J]. 雷达学报, 2021, 10(2): 220–239. doi: 10.12000/JR21027
引用本文: 贾宇翔, 王甲富, 陈维, 等. 基于智能算法的超材料快速优化设计方法研究进展[J]. 雷达学报, 2021, 10(2): 220–239. doi: 10.12000/JR21027
shu
JIA Yuxiang, WANG Jiafu, CHEN Wei, et al. Research progress on rapid optimization design methods of metamaterials based on intelligent algorithms[J]. Journal of Radars, 2021, 10(2): 220–239. doi: 10.12000/JR21027
Citation: JIA Yuxiang, WANG Jiafu, CHEN Wei, et al. Research progress on rapid optimization design methods of metamaterials based on intelligent algorithms[J]. Journal of Radars, 2021, 10(2): 220–239. doi: 10.12000/JR21027
shu

基于智能算法的超材料快速优化设计方法研究进展

doi: 10.12000/JR21027
  • 1.

    空军工程大学基础部 西安 710051

  • 2.

    93704部队 北京 101100

基金项目: 国家自然科学基金(61971435, 61971341, 61801509, 61901508)，科技部国家重点研发计划(2017YFA0700201)
详细信息
    作者简介:

    贾宇翔(1993–)，男，河北衡水人，2016年在空军工程大学获电子科学与技术专业硕士学位，现在空军工程大学基础部攻读博士学位，主要研究方向为基于人工表面等离激元的电磁散射调控。E-mail: jiayuxiang93@163.com

    王甲富(1981–)，男，山东聊城人，教授，博士生导师，博士学位论文获2012年“全国优秀博士学位论文”提名，荣立个人三等功三次。主要研究方向为超材料设计及其在微波器件中的应用，目前已发表学术论文390余篇。E-mail: wangjifu1981@126.com

    陈　维(1982–)，男，陕西三原人，2009年在空军工程大学导弹学院军事装备学获硕士学位，现为93704部队任雷达工程师，主要研究方向为制导雷达指控仓。E-mail: chenwei918113@126.com

    随　赛(1993–)，男，安徽亳州人，博士，讲师，2019年毕业于空军工程大学，现任职于空军工程大学，主要研究方向为隐身新材料与新技术，目前已发表学术论文35篇。E-mail: suisai_mail@foxmail.com

    朱瑞超(1996–)，男，山东济南人，2020年在空军工程大学获电子科学与技术专业硕士学位，现在空军工程大学基础部攻读博士学位。主要研究方向为基于智能算法的超表面设计。E-mail: zhuruichao1996@163.com

    邱天硕(1992–)，男，吉林长春人，博士，讲师。2019年于空军工程大学获得博士学位，现任空军工程大学基础部讲师。主要研究方向为智能材料与设计、有源超材料等。E-mail: qiutianshuo1992@163.com

    李勇峰(1986–)，男，甘肃平凉人，2010年在空军工程大学获物理电子学硕士学位，2015年在空军工程大学获物理电子学博士学位。现为空军工程大学基础部讲师，主要研究方向为电磁超构表面、天线、隐身材料与隐身技术、雷达目标特性仿真评估等，目前已发表学术论文40余篇。E-mail: liyf217130@126.com

    韩亚娟 (1989–)，女，陕西礼泉人，博士，讲师。2020年获西安电子科技大学博士学位，现担任空军工程大学基础部讲师，主要研究方向为超表面、人工表面等离激元及其在天线设计中的应用。目前已发表学术论文30余篇。E-mail: mshyj_mail@126.com

    屈绍波(1965–)，男，安徽亳州人，教授，博士生导师，全国模范教师，全军学科拔尖人才，空军级专家，享受政府特殊津贴，荣立个人二等功一次。主要研究方向为材料物理、超材料，目前已发表学术论文490余篇。承担各类课题60余项，国家自然科学基金项目20余项。E-mail: qushaobo@mail.xjtu.edu.cn

    通讯作者:

    王甲富 wangjifu1981@126.com

  • 责任主编：李龙 Corresponding Editor: LI Long

  • 中图分类号: TB34

Research Progress on Rapid Optimization Design Methods of Metamaterials Based on Intelligent Algorithms

  • 1.

    Department of Basic Sciences, Air Force Engineering University, Xi’an 710051, China

  • 2.

    Unit 93704 of PLA, Beijing 101100, China

Funds: The National Natural Science Foundation of China (61971435, 61971341, 61801509, 61901508), The National Key Research and Development Program of China (2017YFA0700201)
More Information

    摘要
  • 摘要: 目前，超材料研究不断向工程化应用推进，在物理机理与效应、设计理论与方法、加工制备与测试等方面取得了突飞猛进的发展。但是，传统的超材料设计主要依赖人工设计和优化，面对大规模的工程化应用设计时，无法实现数量庞大的超材料结构单元的快速整体设计。近几年，涵盖传统启发式算法和神经网络算法的智能算法在超材料设计中所占的比重逐步上升，基于智能算法设计超材料能够打破传统设计方法在不同基材体系、不同频段以及不同性能指标下设计的局限性，展现出快速设计和架构创新的独特优势。该文综述了包括遗传算法、Hopfield网络算法和深度学习在内的几种典型智能算法在超材料设计中的应用，包括正向设计方法和逆向设计方法。基于智能算法能够实现不同性能指标的频率选择表面、多机理复合吸波超材料、平板聚焦超表面以及异常反射超表面的快速设计，为推动超材料技术的工程化应用提供必要设计手段支撑。

     

    Abstract: At present, research on metamaterials is continuously advancing to engineering applications, and great progress is being achieved in the areas of physical mechanisms and effects, design theory and methods, and fabrication and measurement. However, traditional metamaterials design mainly relies on artificial design and optimization. In the face of large-scale engineering applications, it is impossible to realize the rapid overall design of a large number of metamaterial structural units. In recent years, the proportion of intelligent algorithms covering traditional heuristic algorithms and neural network algorithms in metamaterials design has increased gradually. Metamaterials design based on intelligent algorithms can surpass the limitation of traditional methods in different substrate systems, frequency variation, and different performance indicators, offering the unique advantages of rapid design and architectural innovation. This paper summarizes the application of several typical intelligent algorithms, including the genetic algorithm, Hopfield network algorithm, and deep learning algorithm in metamaterials design, which include forward designs and an inverse design. The use of intelligent algorithms can achieve the rapid design of frequency selective surfaces under different performance indexes, multi-mechanisms composite absorber metamaterials, flat focusing, and abnormal reflection metasurfaces, providing the necessary support for design methods while promoting the engineering applications of metamaterials.

     

    • HTML全文

  • 图  1  神经网络应用方法

    Figure  1.  Application methods of neural network

    下载: 全尺寸图片 幻灯片

    图  2  拓扑构型FSS[23]

    Figure  2.  Topological FSS[23]

    下载: 全尺寸图片 幻灯片

    图  3  优化后的带通型FSS[23]

    Figure  3.  The optimized bandpass FSS[23]

    下载: 全尺寸图片 幻灯片

    图  4  宽带吸波复合材料拓扑构型[23]

    Figure  4.  Schematic illustration of wideband absorber topology configuration[23]

    下载: 全尺寸图片 幻灯片

    图  5  吸收率随极化方式和入射角变化[23]

    Figure  5.  Variation of absorptivity with polarization mode and incident angle[23]

    下载: 全尺寸图片 幻灯片

    图  6  基于拓扑优化设计的超表面吸波体

    Figure  6.  Metaurface absorber based on topology optimization design

    下载: 全尺寸图片 幻灯片

    图  7  对称性破缺超表面吸波体结构示意图[29]

    Figure  7.  Structure illustration of the symmetry broken metasurface absorber[29]

    下载: 全尺寸图片 幻灯片

    图  8  金属板与超表面的对比[29]

    Figure  8.  Comparisons between metal plate and metasurfaces[29]

    下载: 全尺寸图片 幻灯片

    图  9  低RCS编码超表面[30]

    Figure  9.  Low RCS coded metasurface[30]

    下载: 全尺寸图片 幻灯片

    图  10  RCS远场图[30]

    Figure  10.  RCS far-fields[30]

    下载: 全尺寸图片 幻灯片

    图  11  拓扑结构单元[23]

    Figure  11.  Topology unit[23]

    下载: 全尺寸图片 幻灯片

    图  12  编码超表面[23]

    Figure  12.  Coded metasurface[23]

    下载: 全尺寸图片 幻灯片

    图  13  超表面样品[23]

    Figure  13.  Metasurface sample[23]

    下载: 全尺寸图片 幻灯片

    图  14  基于遗传算法的优化流程示意图[37]

    Figure  14.  Optimization flow illustration based on genetic algorithm[37]

    下载: 全尺寸图片 幻灯片

    图  15  曲线与金属线形[37]

    Figure  15.  Curve and metal line shape[37]

    下载: 全尺寸图片 幻灯片

    图  16  吸波体的电磁响应[37]

    Figure  16.  Electromagnetic response of the absorber[37]

    下载: 全尺寸图片 幻灯片

    图  17  Hopfield网络[41]

    Figure  17.  Hopfield network[41]

    下载: 全尺寸图片 幻灯片

    图  18  Hopfield网络的联想记忆功能[41]

    Figure  18.  Associative memory function of Hopfield network[41]

    下载: 全尺寸图片 幻灯片

    图  19  异常反射超表面[41]

    Figure  19.  Abnormal reflection metasurface[41]

    下载: 全尺寸图片 幻灯片

    图  20  基于深度学习-遗传算法复合优化流程图[48]

    Figure  20.  Flow chart of composite optimization based on deep learning and genetic algorithm[48]

    下载: 全尺寸图片 幻灯片

    图  21  Inception V3网络结构[46]

    Figure  21.  Network structure of Inception V3[46]

    下载: 全尺寸图片 幻灯片

    图  22  超表面电磁性能[46]

    Figure  22.  Electromagnetic performances of metasureface[46]

    下载: 全尺寸图片 幻灯片

    表  1  不同智能算法在超材料优化设计中优缺点对比

    Table  1.   Comparison of advantages and disadvantages of different intelligent algorithms in metamaterial optimization designs

    算法类型优点缺点
    启发式算法[9—12]全局搜索能力强，高度自定义，兼容性高计算速度慢，易陷入局部最优解
    机器学习[13—16,21—23]学习能力强，适应性好，领域优势明显训练成本高，硬件要求高，模型设计复杂
    下载: 导出CSV
    • 参考文献(50)
  • [1] PENDRY J B. A chiral route to negative refraction[J]. Science, 2004, 306(5700): 1353–1355. doi: 10.1126/science.1104467
    [2] PENDRY J B, HOLDEN A J, STEWART W J, et al. Extremely low frequency plasmons in metallic mesostructures[J]. Physical Review Letters, 1996, 76(25): 4773–4776. doi: 10.1103/PhysRevLett.76.4773
    [3] PENDRY J B, HOLDEN A J, ROBBINS D J, et al. Magnetism from conductors and enhanced nonlinear phenomena[J]. IEEE Transactions on Microwave Theory and Techniques, 1999, 47(11): 2075–2084. doi: 10.1109/22.798002
    [4] SMITH D R, PADILLA W J, VIER D C, et al. Composite medium with simultaneously negative permeability and permittivity[J]. Physical Review Letters, 2000, 84(18): 4184–4187. doi: 10.1103/PhysRevLett.84.4184
    [5] CUI Tiejun, LIU Shuo, and LI Lianlin. Information entropy of coding metasurface[J]. Light: Science & Applications, 2016, 5(11): e16172.
    [6] XIE Boyang, TANG Kun, CHENG Hua, et al. Coding acoustic metasurfaces[J]. Advanced Materials, 2017, 29(6): 1603507. doi: 10.1002/adma.201603507
    [7] 史峰, 王辉, 郁磊, 等. MATLAB智能算法30个案例分析[M]. 北京: 北京航空航天大学出版社, 2011.

    SHI Feng, WANG Hui, YU Lei, et al. Analysis of 30 Cases of MATLAB Intelligent Algorithm[M]. Beijing: Beijing University of Aeronautics and Astronautics Press, 2011.
    [8] 武飞周, 薛源. 智能算法综述[J]. 工程地质计算机应用, 2005, (2): 9–15.

    WU Feizhou and XUE Yuan. Review of intelligent algorithms[J]. Engineering Geology Computer Application, 2005, (2): 9–15.
    [9] 胡涵, 李振宇. 多目标进化算法性能评价指标综述[J]. 软件导刊, 2019, 18(9): 1–4. doi: 10.11907/rjdk.191024

    HU Han and LI Zhenyu. A survey of performance indicators for multi-objective evolutionary algorithms[J]. Software Guide, 2019, 18(9): 1–4. doi: 10.11907/rjdk.191024
    [10] 梅志伟. 多目标进化算法综述[J]. 软件导刊, 2017, 16(6): 204–207. doi: 10.11907/rjdk.171169

    MEI Zhiwei. Overview of multi objective evolutionary algorithm[J]. Software Guide, 2017, 16(6): 204–207. doi: 10.11907/rjdk.171169
    [11] CAI Haoyuan, SUN Yi, WANG Xiaoping, et al. Design of an ultra-broadband near-perfect bilayer grating metamaterial absorber based on genetic algorithm[J]. Optics Express, 2020, 28(10): 15347–15359. doi: 10.1364/OE.393423
    [12] HUANG Yixing, FAN Qunfu, CHEN Jin, et al. Optimization of flexible multilayered metastructure fabricated by dielectric-magnetic nano lossy composites with broadband microwave absorption[J]. Composites Science and Technology, 2020, 191: 108066. doi: 10.1016/j.compscitech.2020.108066
    [13] QIU Tianshuo, SHI Xin, WANG Jiafu, et al. Deep learning: A rapid and efficient route to automatic metasurface design[J]. Advanced Science, 2019, 6(12): 1900128. doi: 10.1002/advs.201900128
    [14] TITTL A, LEITIS A, LIU Mingkai, et al. Imaging-based molecular barcoding with pixelated dielectric metasurfaces[J]. Science, 2018, 360(6393): 1105–1109. doi: 10.1126/science.aas9768
    [15] MA Wei, CHENG Feng, and LIU Yongmin. Deep-learning enabled on-demand design of chiral metamaterials[J]. ACS Nano, 2018, 12(6): 6326–6334. doi: 10.1021/acsnano.8b03569
    [16] LIU Che, YU Wenming, MA Qian, et al. Intelligent coding metasurface holograms by physics-assisted unsupervised generative adversarial network[J]. Photonics Research, 2021, 9(4): B159–B167. doi: 10.1364/PRJ.416287
    [17] PEURIFOY J, SHEN Yichen, YANG Yi, et al. Nanophotonic inverse design using artificial neural network[C]. Frontiers in Optics 2017, Washington, USA, 2017: FTh4A.4. doi: 10.1364/FIO.2017.FTh4A.4.
    [18] VAI M M, WU Shuichi, LI Bin, et al. Reverse modeling of microwave circuits with bidirectional neural network models[J]. IEEE Transactions on Microwave Theory and Techniques, 1998, 46(10): 1492–1494. doi: 10.1109/22.721152
    [19] KABIR H, WANG Ying, YU Ming, et al. Neural network inverse modeling and applications to microwave filter design[J]. IEEE Transactions on Microwave Theory and Techniques, 2008, 56(4): 867–879. doi: 10.1109/TMTT.2008.919078
    [20] SELLERI S, MANETTI S, and PELOSI G. Neural network applications in microwave device design[J]. International Journal of RF and Microwave Computer-Aided Engineering, 2002, 12(1): 90–97. doi: 10.1002/mmce.7001
    [21] LIU Dianjing, TAN Yixuan, KHORAM E, et al. Training deep neural networks for the inverse design of nanophotonic structures[J]. ACS Photonics, 2018, 5(4): 1365–1369. doi: 10.1021/acsphotonics.7b01377
    [22] PEURIFOY J, SHEN Yichen, JING Li, et al. Nanophotonic particle simulation and inverse design using artificial neural networks[J]. Science Advances, 2018, 4(6): eaar4206. doi: 10.1126/sciadv.aar4206
    [23] 随赛. 新型人工电磁表面拓扑优化设计与应用研究[D]. [博士论文], 空军工程大学, 2019.

    SUI Sai. Research on topology optimization design and application of new artificial electromagnetic surface[D]. [Ph. D. dissertation], Air Force Engineering University, 2019.
    [24] LANDY N I, SAJUYIGBE S, MOCK J J, et al. Perfect metamaterial absorber[J]. Physical Review Letters, 2008, 100(20): 207402. doi: 10.1103/PhysRevLett.100.207402
    [25] 鲍迪, 沈晓鹏, 崔铁军. 太赫兹人工电磁媒质研究进展[J]. 物理学报, 2015, 64(22): 228701. doi: 10.7498/aps.64.228701

    BAO Di, SHEN Xiaopeng, and CUI Tiejun. Progress of terahertz metamaterials[J]. Acta Physica Sinica, 2015, 64(22): 228701. doi: 10.7498/aps.64.228701
    [26] SHEN Yang, ZHANG Jieqiu, PANG Yongqiang, et al. Transparent broadband metamaterial absorber enhanced by water-substrate incorporation[J]. Optics Express, 2018, 26(12): 15665–15674. doi: 10.1364/OE.26.015665
    [27] PANG Yongqiang, SHEN Yang, LI Yongfeng, et al. Water-based metamaterial absorbers for optical transparency and broadband microwave absorption[J]. Journal of Applied Physics, 2018, 123(15): 155106. doi: 10.1063/1.5023778
    [28] PANG Yongqiang, LI Yongfeng, WANG Jiafu, et al. Electromagnetic reflection reduction of carbon composite materials mediated by collaborative mechanisms[J]. Carbon, 2019, 147: 112–119. doi: 10.1016/j.carbon.2019.03.004
    [29] SUI Sai, MA Hua, WANG Jiafu, et al. Absorptive coding metasurface for further radar cross section reduction[J]. Journal of Physics D: Applied Physics, 2018, 51(6): 065603. doi: 10.1088/1361-6463/aaa3be
    [30] SUI Sai, MA Hua, WANG Jiafu, et al. Synthetic design for a microwave absorber and antireflection to achieve wideband scattering reduction[J]. Journal of Physics D: Applied Physics, 2019, 52(3): 035103. doi: 10.1088/1361-6463/aaeb12
    [31] CUI Yanxia, FUNG K H, XU Jun, et al. Ultrabroadband light absorption by a sawtooth anisotropic metamaterial slab[J]. Nano Letters, 2012, 12(3): 1443–1447. doi: 10.1021/nl204118h
    [32] FU Jiahui, WU Qun, ZHANG Shaoqing, et al. Design of multi-layers absorbers for low frequency applications[C]. 2010 Asia-Pacific International Symposium on Electromagnetic Compatibility, Beijing, China, 2010. doi: 10.1109/APEMC.2010.5475478.
    [33] SHEN Yang, ZHANG Jieqiu, WANG Jiafu, et al. Multistage dispersion engineering in a three-dimensional plasmonic structure for outstanding broadband absorption[J]. Optical Materials Express, 2019, 9(3): 1539–1550. doi: 10.1364/OME.9.001539
    [34] WU C, NEUNER III B, SHVETS G, et al. Large-area wide-angle spectrally selective plasmonic absorber[J]. Physical Review B, 2011, 84(7): 075102. doi: 10.1103/PhysRevB.84.075102
    [35] CHENG Yongzhi, GONG Rongzhou, NIE Yan, et al. A wideband metamaterial absorber based on a magnetic resonator loaded with lumped resistors[J]. Chinese Physics B, 2012, 21(12): 127801. doi: 10.1088/1674-1056/21/12/127801
    [36] SHEN Yang, ZHANG Jieqiu, WANG Wenjie, et al. Overcoming the pixel-density limit in plasmonic absorbing structure for broadband absorption enhancement[J]. IEEE Antennas and Wireless Propagation Letters, 2019, 18(4): 674–678. doi: 10.1109/LAWP.2019.2900846
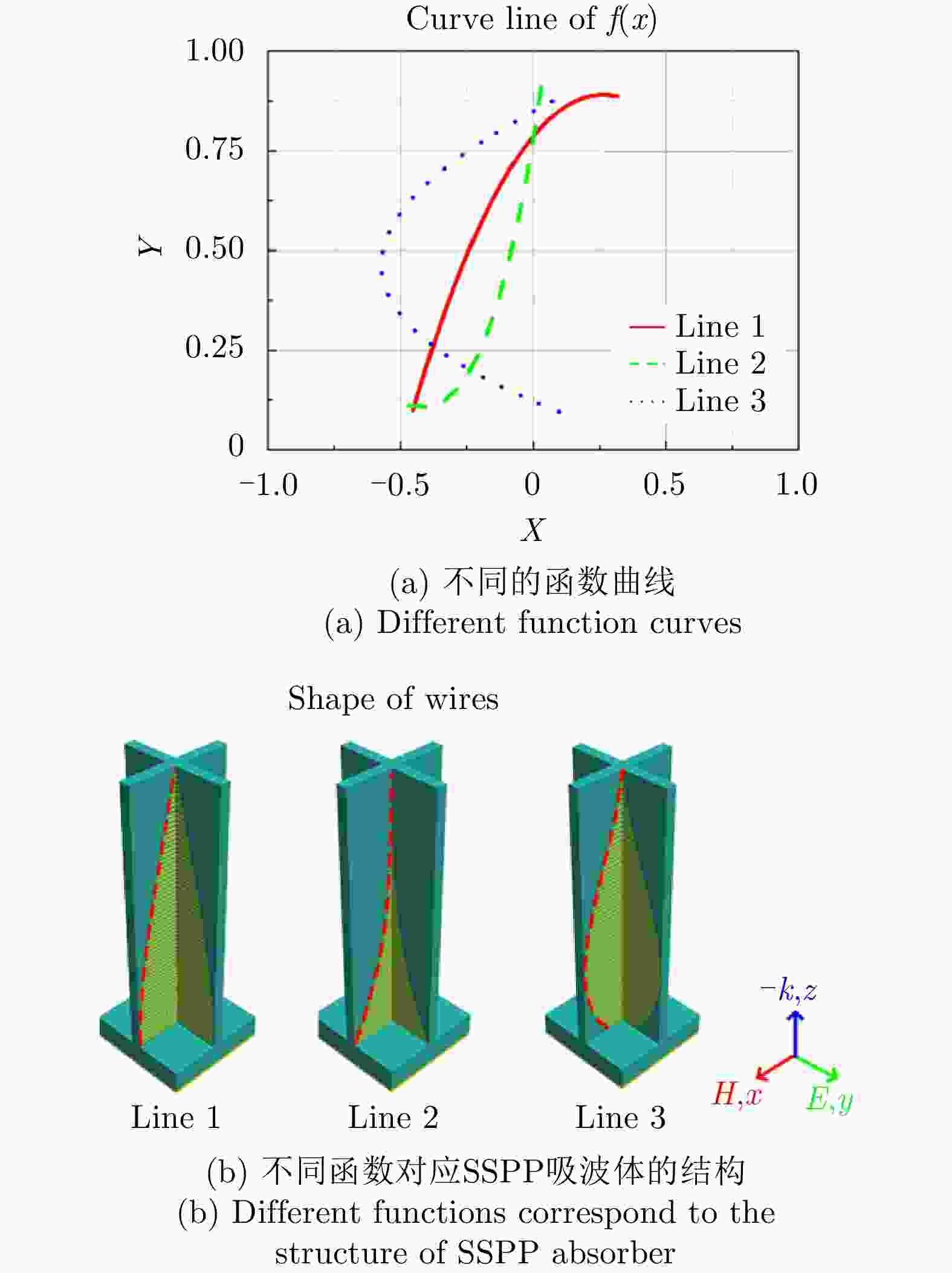
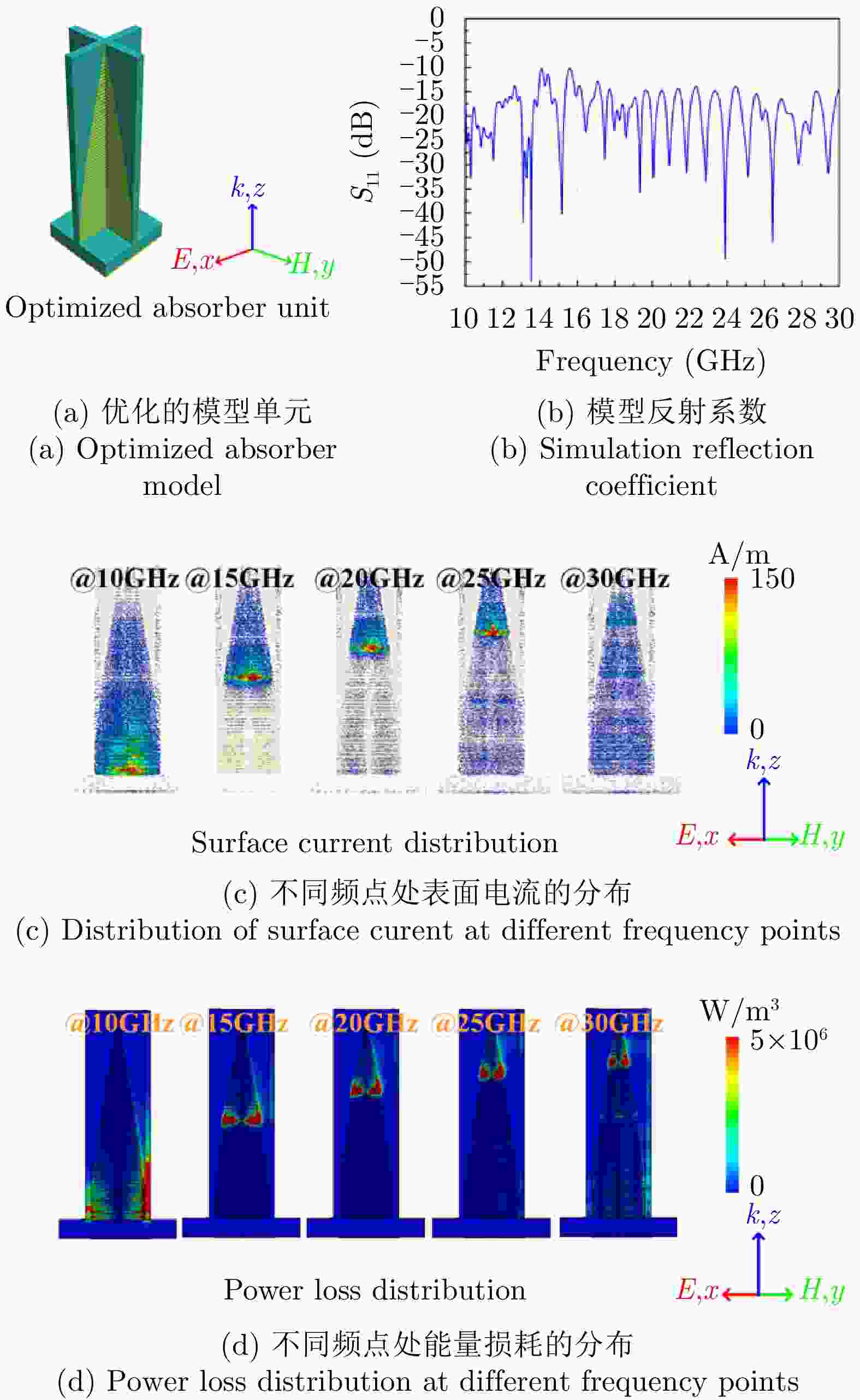
    [37] ZHU Ruichao, WANG Jiafu, SUI Sai, et al. Wideband absorbing plasmonic structures via profile optimization based on genetic algorithm[J]. Frontiers in Physics, 2020, 8: 231. doi: 10.3389/fphy.2020.00231
    [38] NONG Jifu. Global exponential stability of delayed Hopfield neural networks[C]. 2012 International Conference on Computer Science and Information Processing, Xi’an, China, 2012. doi: 10.1109/CSIP.2012.6308827.
    [39] AN Jinliang, GAO Jia, LEI Jinhui, et al. An improved algorithm for TSP problem solving with Hopfield neural networks[J]. Advanced Materials Research, 2010, 143/144: 538–542. doi: 10.4028/www.scientific.net/AMR.143-144.538
    [40] AIYER S V B, NIRANJAN M, and FALLSIDE F. A theoretical investigation into the performance of the Hopfield model[J]. IEEE Transactions on Neural Networks, 1990, 1(2): 204–215. doi: 10.1109/72.80232
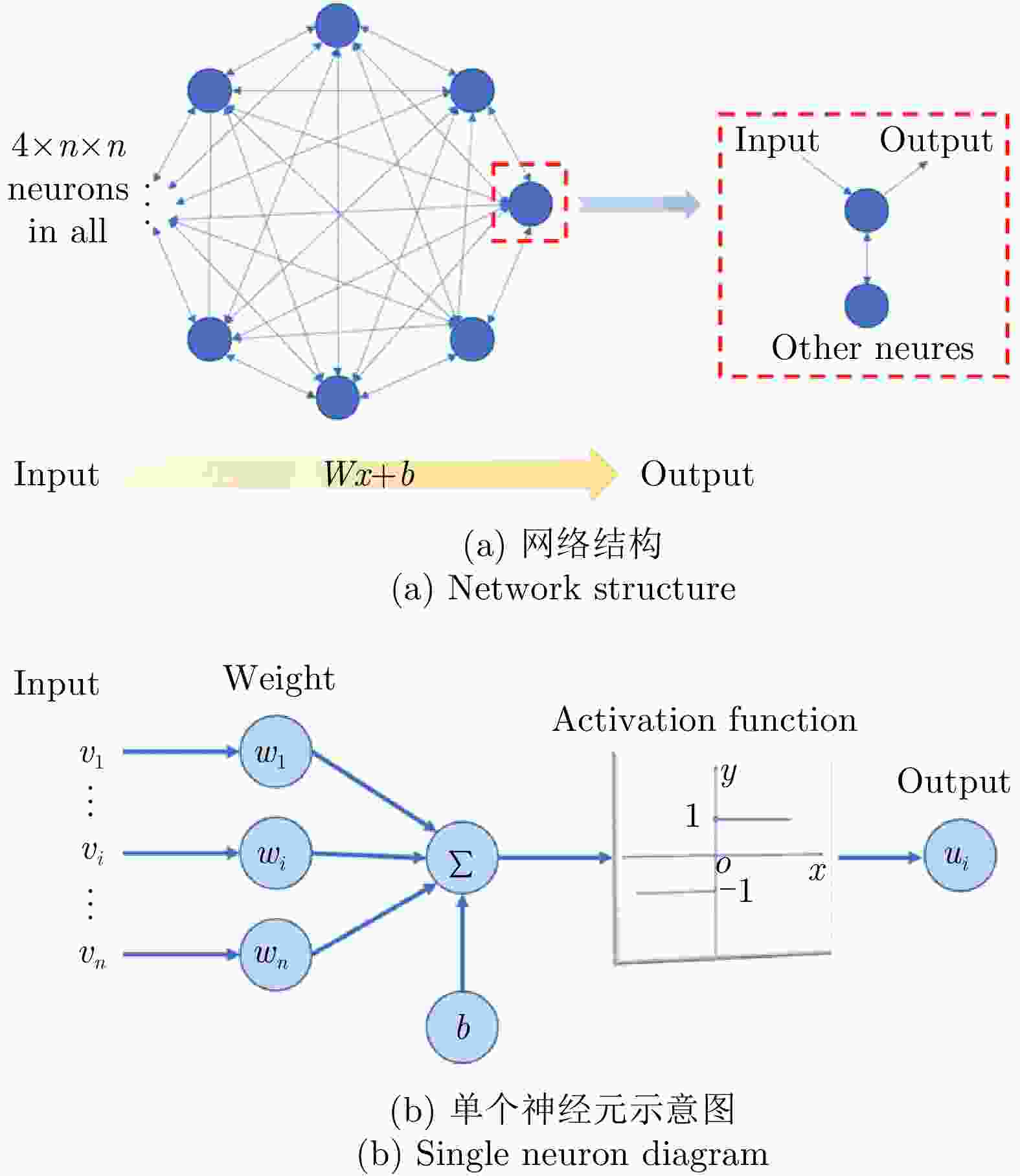
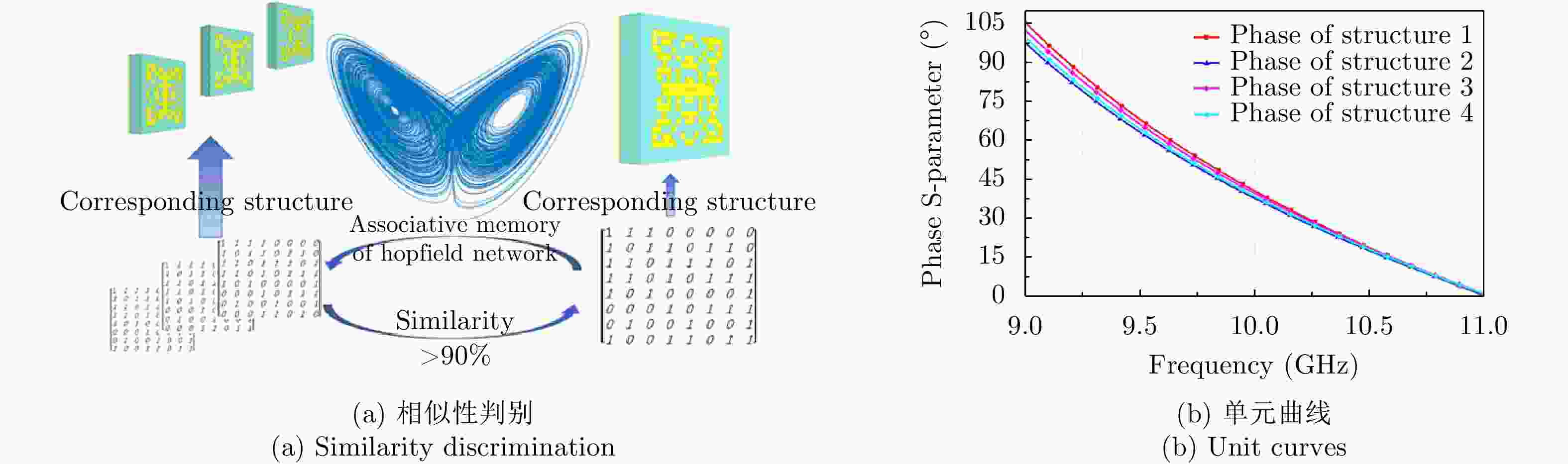
    [41] ZHU Ruichao, QIU Tianshuo, WANG Jiafu, et al. Metasurface design by a hopfield network: Finding a customized phase response in a broadband[J]. Journal of Physics D: Applied Physics, 2020, 53(41): 415001. doi: 10.1088/1361-6463/ab9785
    [42] VAN DEN DRIESSCHE P and ZOU Xingfu. Global attractivity in delayed hopfield neural network models[J]. SIAM Journal on Applied Mathematics, 1998, 58(6): 1878–1890. doi: 10.1137/S0036139997321219
    [43] RECH P C. Chaos and hyperchaos in a Hopfield neural network[J]. Neurocomputing, 2011, 74(17): 3361–3364. doi: 10.1016/j.neucom.2011.05.016
    [44] SELL D, YANG Jianji, DOSHAY S, et al. Large-angle, multifunctional metagratings based on freeform multimode geometries[J]. Nano Letters, 2017, 17(6): 3752–3757. doi: 10.1021/acs.nanolett.7b01082
    [45] FOROUZMAND A and MOSALLAEI H. Composite multilayer shared-aperture nanostructures: A functional multispectral control[J]. ACS Photonics, 2018, 5(4): 1427–1439. doi: 10.1021/acsphotonics.7b01441
    [46] TIPRAQSA P, CRASWELL E T, NOBLE A D, et al. Resource integration for multiple benefits: Multifunctionality of integrated farming systems in Northeast Thailand[J]. Agricultural Systems, 2007, 94(3): 694–703. doi: 10.1016/j.agsy.2007.02.009
    [47] LING Yonghong, HUANG Lirong, HONG Wei, et al. Polarization-switchable and wavelength-controllable multi-functional metasurface for focusing and surface-plasmon-polariton wave excitation[J]. Optics Express, 2017, 25(24): 29812–29821. doi: 10.1364/OE.25.029812
    [48] MAGUID E, YULEVICH I, YANNAI M, et al. Multifunctional interleaved geometric-phase dielectric metasurfaces[J]. Light: Science & Applications, 2017, 6(8): e17027.
    [49] HUANG Cheng, ZHANG Changlei, YANG Jianing, et al. Reconfigurable metasurface for multifunctional control of electromagnetic waves[J]. Advanced Optical Materials, 2017, 5(22): 1700485. doi: 10.1002/adom.201700485
    [50] ZHU Ruichao, QIU Tianshuo, WANG Jiafu, et al. Multiplexing the aperture of a metasurface: Inverse design via deep-learning-forward genetic algorithm[J]. Journal of Physics D: Applied Physics, 2020, 53(45): 455002. doi: 10.1088/1361-6463/aba64f
    • 相关文章
    • 施引文献
  • 资源附件(0)
  • 加载中
WeChat 点击查看大图
图(22) / 表(1)
计量
  • 文章访问数:  2432
  • HTML全文浏览量:  1546
  • PDF下载量:  412
  • 被引次数: 0
出版历程
  • 收稿日期:  2021-03-11
  • 修回日期:  2021-04-20
  • 网络出版日期:  2021-04-28

目录

    /

    返回文章
    返回

    京ICP备20021838号-8   本系统由 北京仁和汇智信息技术有限公司 开发    百度统计