考虑运动补偿的机载SAR定位误差传递模型及航迹标定方法

高铭; 仇晓兰; 孟大地; 黄丽佳; 丁赤飚

doi:10.12000/JR21018

考虑运动补偿的机载SAR定位误差传递模型及航迹标定方法

DOI: 10.12000/JR21018

高铭^{1, 2, 3,},
仇晓兰^{1, 2, ,},
孟大地^{1, 2,},
黄丽佳^{1, 2,},
丁赤飚^{1, 2, 3,}

1.
中国科学院空间信息处理与应用系统技术重点实验室北京 100190
2.
中国科学院空天信息创新研究院北京 100190
3.
中国科学院大学北京 100049

基金项目: 国家自然科学基金(62022082, 61991424)

详细信息

作者简介:
高　铭(1997–)，女，山西忻州人，中国科学院空天信息创新研究院在读博士，研究方向为机载SAR信号处理。

仇晓兰(1982–)，女，江苏苏州人，中国科学院空天信息创新研究院研究员，博士生导师，IEEE高级会员、IEEE地球科学与遥感快报副主编、雷达学报青年编委。主要研究方向为SAR成像处理、SAR图像理解。

孟大地(1979–)，男，陕西西安人，博士，中国科学院空天信息创新研究院研究员，硕士生导师，研究方向为合成孔径雷达信号处理。

黄丽佳(1984–)，女，山东莱州人，博士，中国科学院空天信息创新研究院研究员，硕士生导师，研究方向为合成孔径雷达信号处理与图像分析。

丁赤飚(1969–)，男，山西原平人，研究员，博士生导师，先后主持多项国家重点项目和国家级遥感卫星地面系统工程建设等项目，曾获国家科技进步奖一等奖、二等奖，国家发明奖二等奖等奖励。研究方向为合成孔径雷达、遥感信息处理和应用系统等。

通讯作者:
仇晓兰 xlqiu@mail.ie.ac.cn

责任主编：胡程 Corresponding Editor: HU Cheng
中图分类号: TN957.52
计量
- 文章访问数: 2023
- HTML全文浏览量: 635
- PDF下载量: 212
- 被引次数: 0
出版历程
- 收稿日期: 2021-03-02
- 修回日期: 2021-05-08
- 网络出版日期: 2021-08-28

Geolocation Error Transfer Model and Trajectory Calibration Method for Airborne SAR Considering Motion Compensation Residual Error

GAO Ming^{1, 2, 3
,},
QIU Xiaolan^{1, 2
, ,},
MENG Dadi^{1, 2
,},
HUANG Lijia^{1, 2
,},
DING Chibiao^{1, 2, 3
,}

1.
Key Laboratory of Technology in Geospatial Information Processing and Application System, Chinese Academy of Sciences, Beijing 100190, China
2.
Aerospace Information Research Institute, Chinese Academy of Sciences, Beijing 100190, China
3.
University of Chinese Academy of Sciences, Beijing 100049, China

Funds: The National Natural Science Foundation of China (62022082, 61991424)

More Information

Corresponding author: QIU Xiaolan, xlqiu@mail.ie.ac.cn

摘要

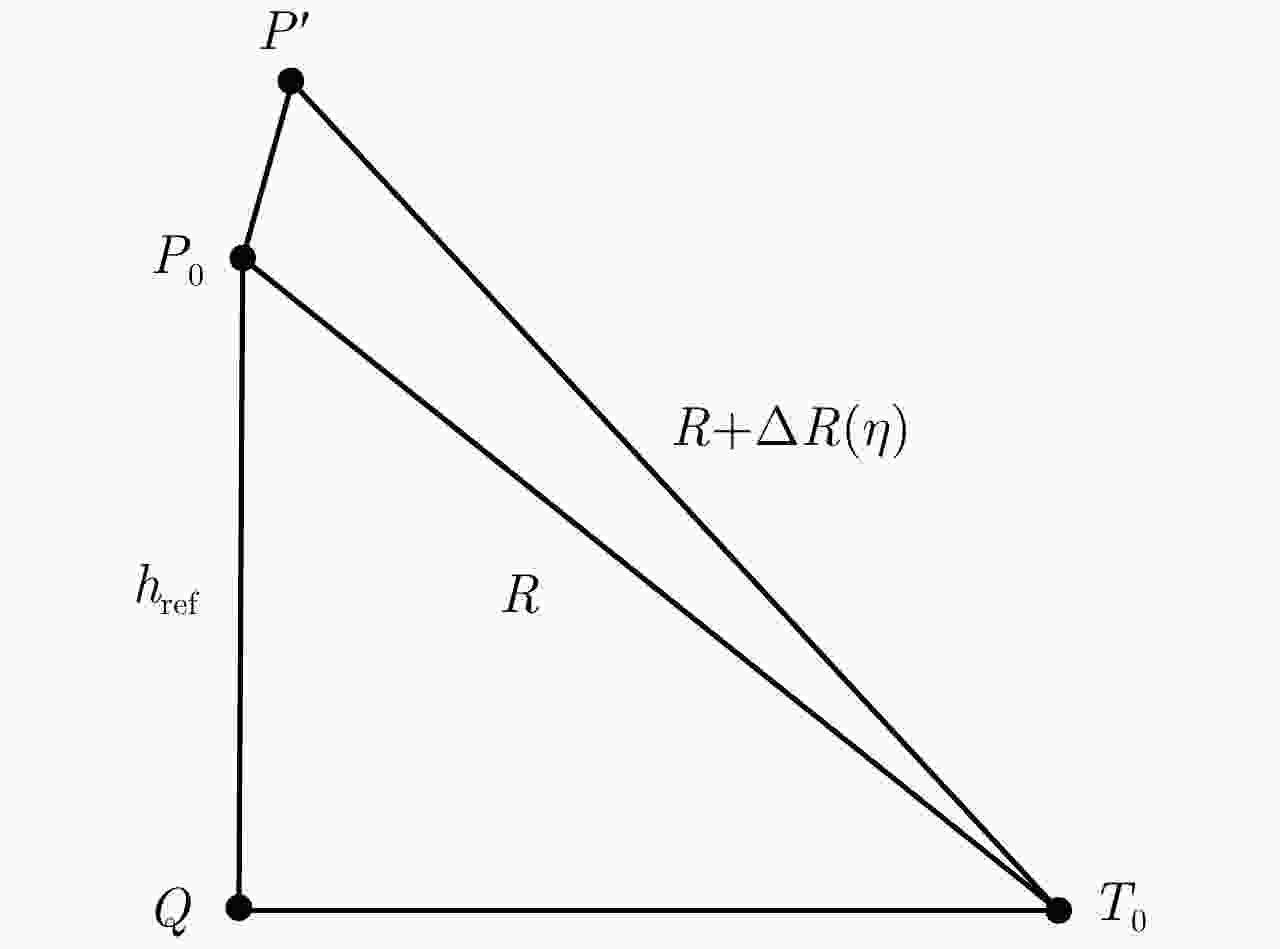
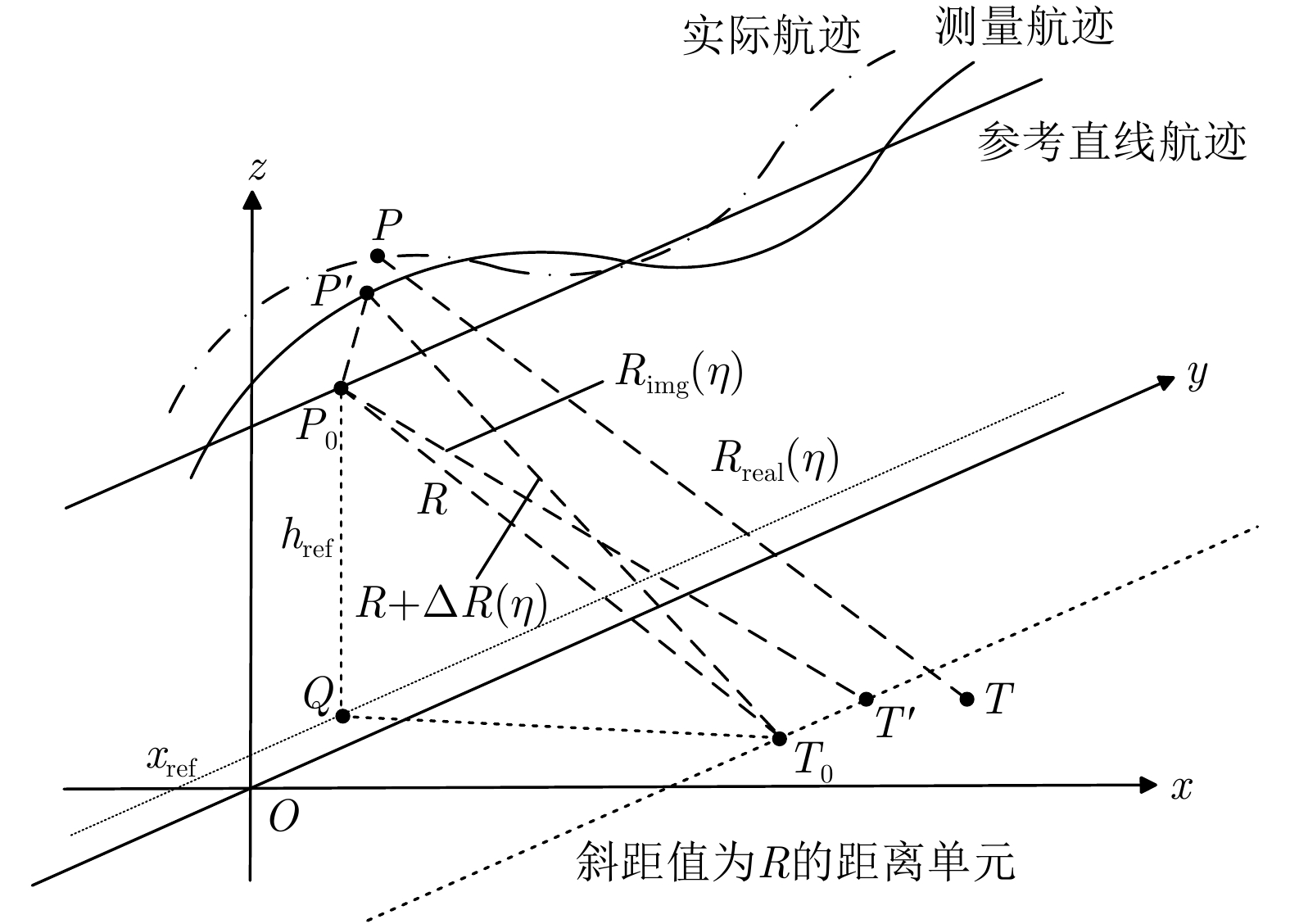
摘要: 机载合成孔径雷达(SAR)定位误差不仅受载机位置/速度测量误差、系统时间误差等的影响，还与运动补偿残余误差有关。然而现有机载SAR定位模型很少考虑运动补偿误差的影响。该文针对实际中普遍存在的含运动误差和载机航迹测量误差的情况，结合运动补偿和频域成像算法，推导了机载SAR图像定位误差传递模型，阐明了运动补偿残余误差影响下航迹测量误差对定位偏差的影响方式，并基于该模型给出了载机航迹测量误差的标定方法。仿真实验验证了该定位误差传递模型的正确性，相比于不考虑运动补偿残余误差的定位模型，得到了更高精度的航迹测量误差标定结果，证明了该方法的优越性。
- 机载合成孔径雷达 /
- 定位误差传递模型 /
- 航迹测量误差标定 /
- 运动补偿 /
- 频域成像算法
Abstract: Airborne Synthetic Aperture Radar (SAR) location error is affected by the position/speed measurement error of the aircraft, system time error, etc., and also related to the residual error of motion compensation. However, the existing airborne SAR location model rarely considers the effect of residual motion error. Considering that motion and trajectory measurement errors are common in practice, this paper derives a location error transfer model of an airborne SAR image based on the motion compensation and frequency-domain imaging algorithms. The proposed model clarifies the influence of trajectory measurement error on location deviation when residual motion error exists and provides a method of error calibration measurement. The simulation experiments validate the correctness of the proposed location error transfer model. The present method obtains a more accurate error calibration measurement result than the location error model that does not consider the residual motion error, proving the superiority of the proposed model.
- Airborne synthetic aperture radar /
- Geolocation error transfer model /
- Trajectory measurement error calibration /
- Motion compensation /
- Frequency-domain imaging algorithm

HTML全文

图 1 机载SAR几何关系

Figure 1. Airborne SAR geometry

下载: 全尺寸图片幻灯片

图 2 跨航迹平面内的SAR几何关系

Figure 2. SAR geometric relationship in the cross-track plane

下载: 全尺寸图片幻灯片

图 3 成像结果图

Figure 3. Diagram of imaging results

下载: 全尺寸图片幻灯片

图 4 航迹设置示意图

Figure 4. Schematic diagram of trajectory setting

下载: 全尺寸图片幻灯片

图 5 仿真场景示意图

Figure 5. Schematic diagram of simulation scene

下载: 全尺寸图片幻灯片

图 6 航迹标定示意图

Figure 6. Schematic diagram of calibration trajectory

下载: 全尺寸图片幻灯片

图 7 x方向航迹偏差对比图

Figure 7. Contrastive diagram of trajectory deviation in x direction

下载: 全尺寸图片幻灯片

图 8 z方向航迹偏差对比图

Figure 8. Contrastive diagram of trajectory deviation in z direction

下载: 全尺寸图片幻灯片

图 9 使用标定航迹的成像结果

Figure 9. Imaging results using the calibration trajectory

下载: 全尺寸图片幻灯片

图 10 仿真场景示意图

Figure 10. Schematic diagram of simulation scene

下载: 全尺寸图片幻灯片

图 11 整条航迹标定结果图

Figure 11. Calibration result of the whole trajectory

下载: 全尺寸图片幻灯片

图 12 标定结果对比图

Figure 12. Contrastive diagram of calibration results

下载: 全尺寸图片幻灯片

图 13 x方向整条航迹偏差对比图

Figure 13. Contrastive diagram of deviation of the whole trajectory in x direction

下载: 全尺寸图片幻灯片

图 14 z方向整条航迹偏差对比图

Figure 14. Contrastive diagram of deviation of the whole trajectory in z direction

下载: 全尺寸图片幻灯片

图 15 航迹标定示意图

Figure 15. Schematic diagram of calibration trajectory

下载: 全尺寸图片幻灯片

图 16 x方向航迹偏差对比图

Figure 16. Contrastive diagram of trajectory deviation in x direction

下载: 全尺寸图片幻灯片

图 17 z方向航迹偏差对比图

Figure 17. Contrastive diagram of trajectory deviation in z direction

下载: 全尺寸图片幻灯片

图 18 使用标定航迹的成像结果

Figure 18. Imaging results using the calibration trajectory

下载: 全尺寸图片幻灯片

表 1 定位误差仿真参数

Table 1. Simulation parameters of location error

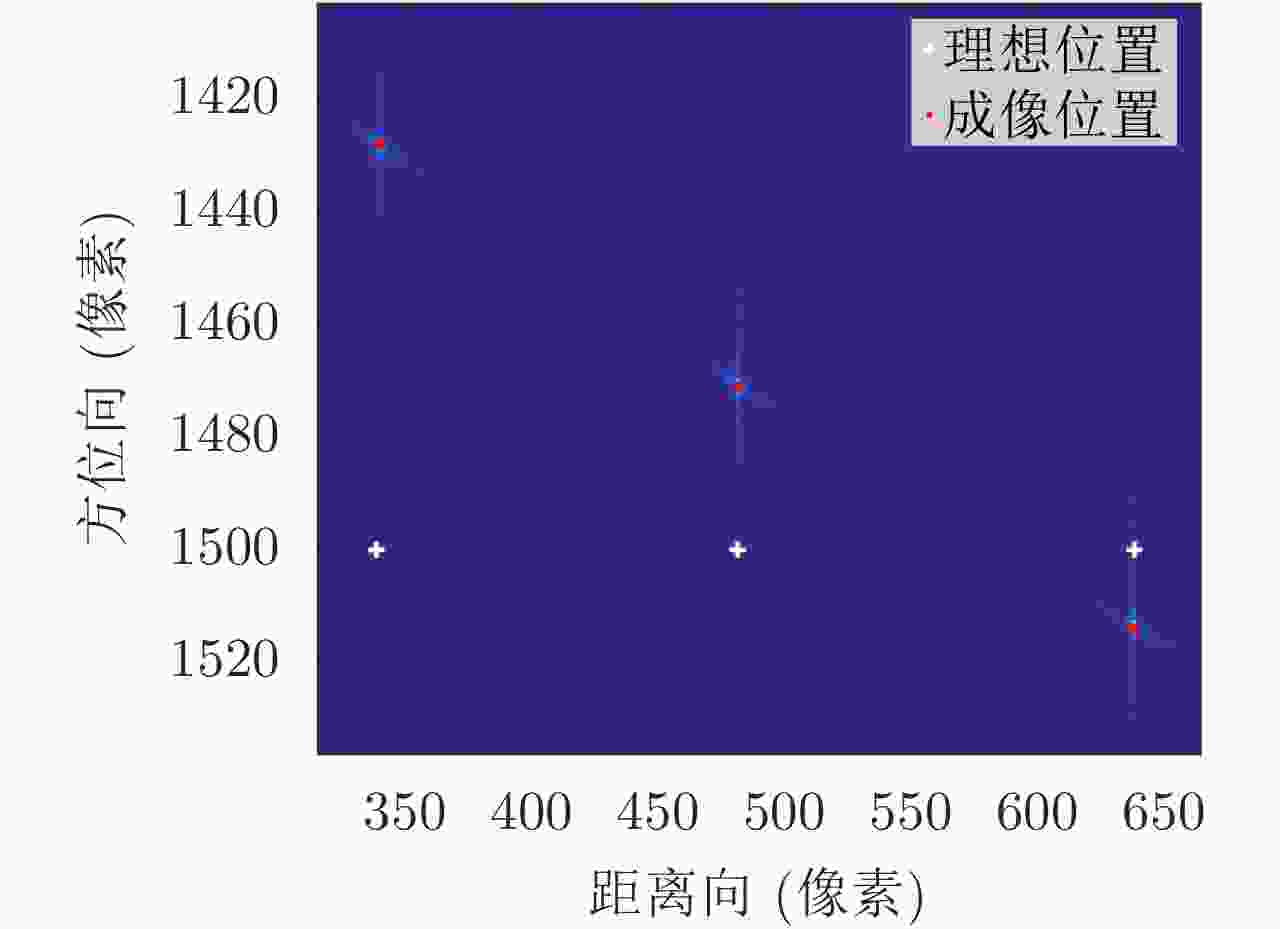
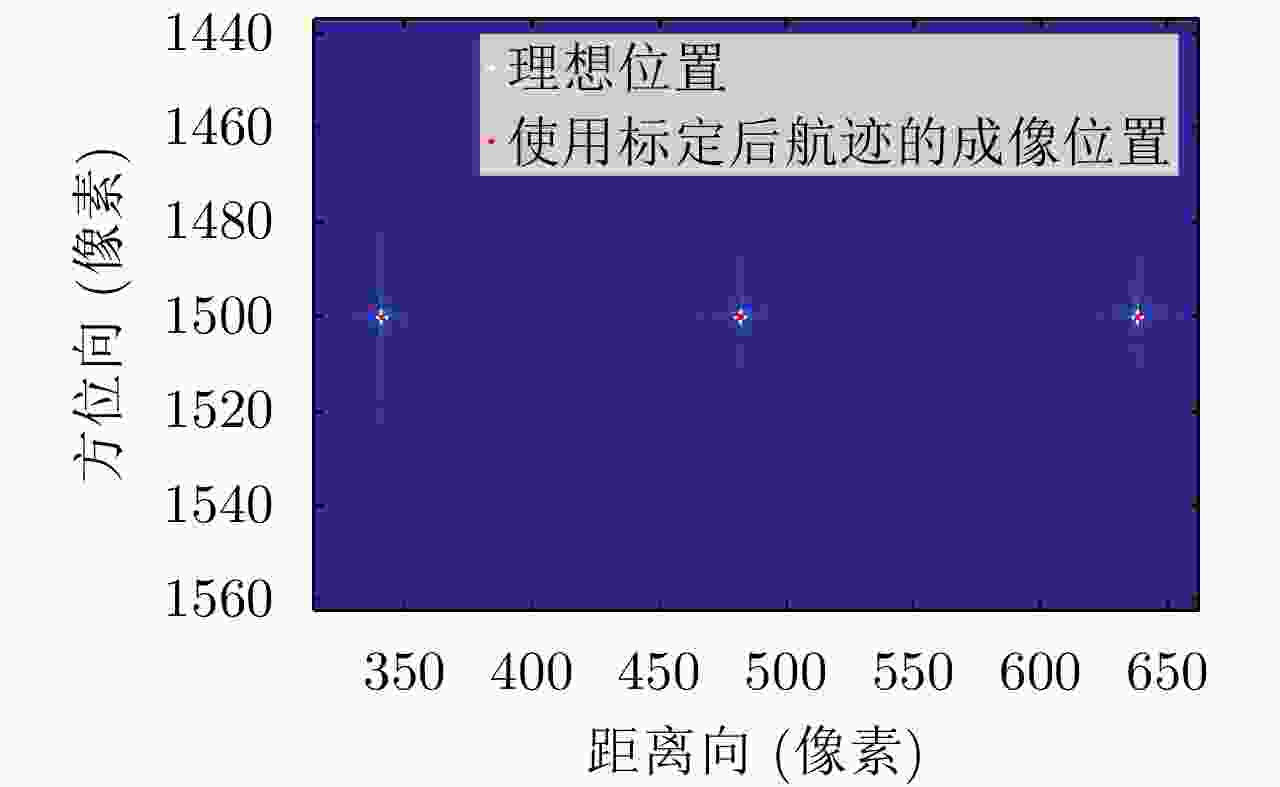
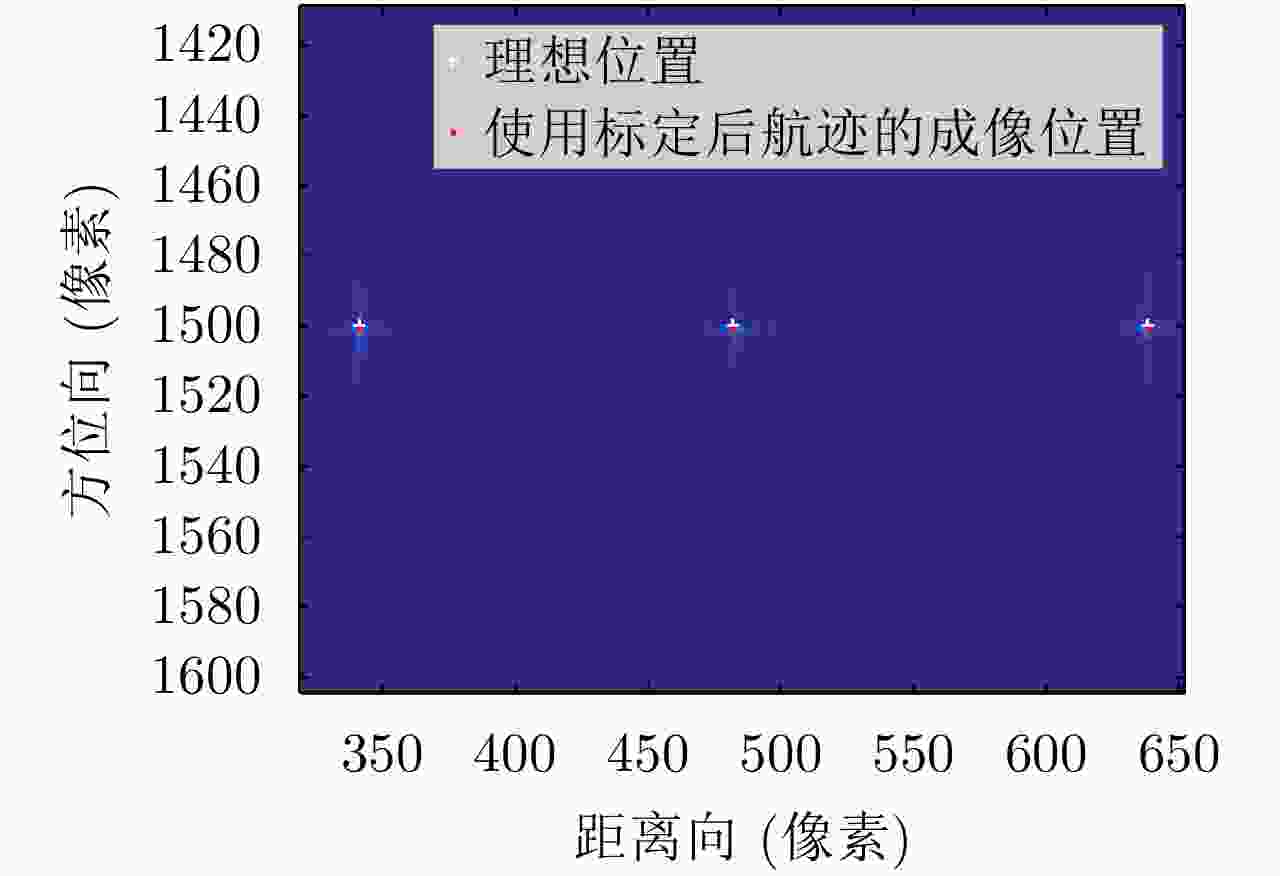
参数	数值
载波频率(${\rm{GHz}}$)	$30$
信号带宽(${\rm{MHz}}$)	${\rm{2}}00$
脉冲持续时间(μs)	$1$
脉冲重复频率(${\rm{Hz}}$)	$1000$
方位向天线尺寸(${\rm{m}}$)	${\rm{2}}$
平台速度(${\rm{m}}{\rm{/}}{\rm{s}}$)	$70$
斜视角(°)	$0$
目标点1坐标(${\rm{m}}$)	$(330,0,0)$
目标点2坐标(${\rm{m}}$)	$(400,0,0)$
目标点3坐标(${\rm{m}}$)	$(470,0,0)$

下载: 导出CSV

表 2 ${\boldsymbol{y}} $方向定位误差

Table 2. Location error in y direction

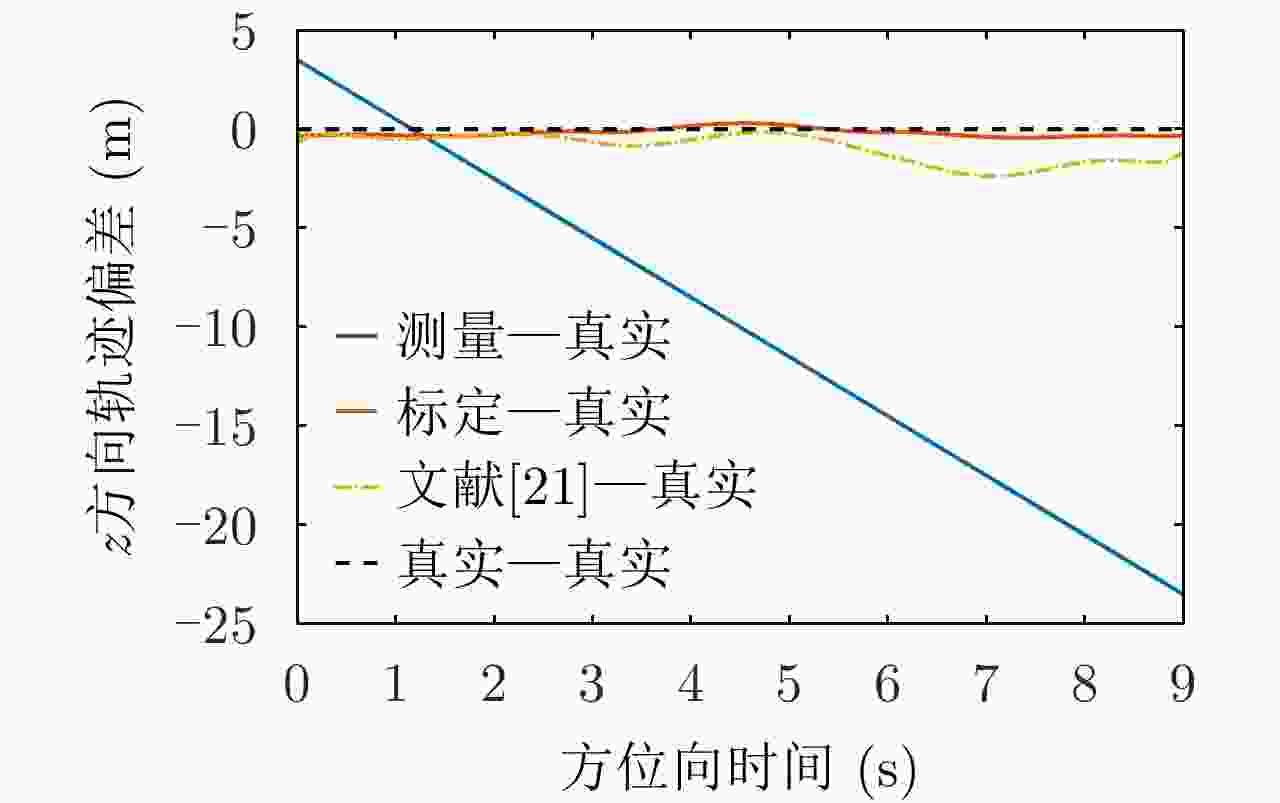
目标点	实际定位误差	公式算得误差	两误差的偏差
目标点1 (m)	–4.5500	–4.5254	–0.0246
目标点2 (m)	–1.6100	–1.6270	0.0170
目标点3 (m)	1.3300	1.3030	0.0270

下载: 导出CSV

表 3 ${\boldsymbol{x}} $方向定位误差

Table 3. Location error in x direction

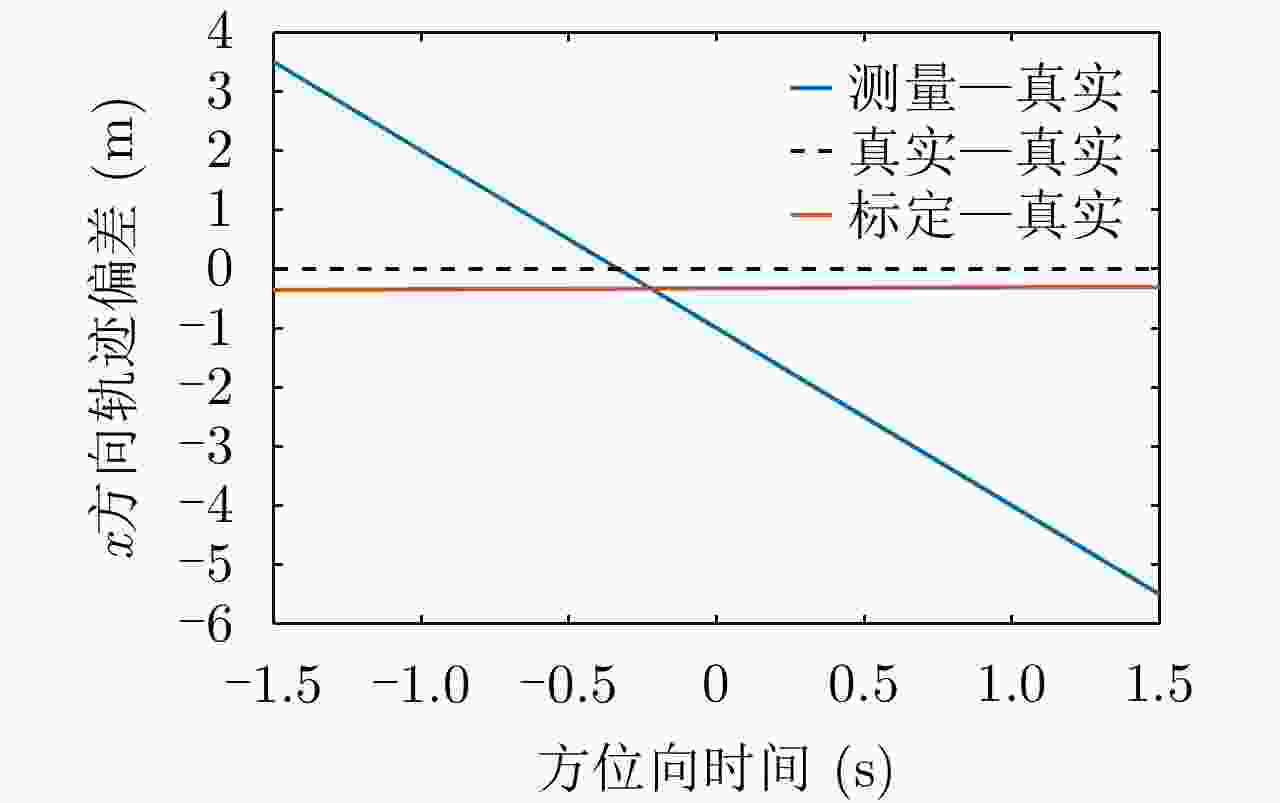
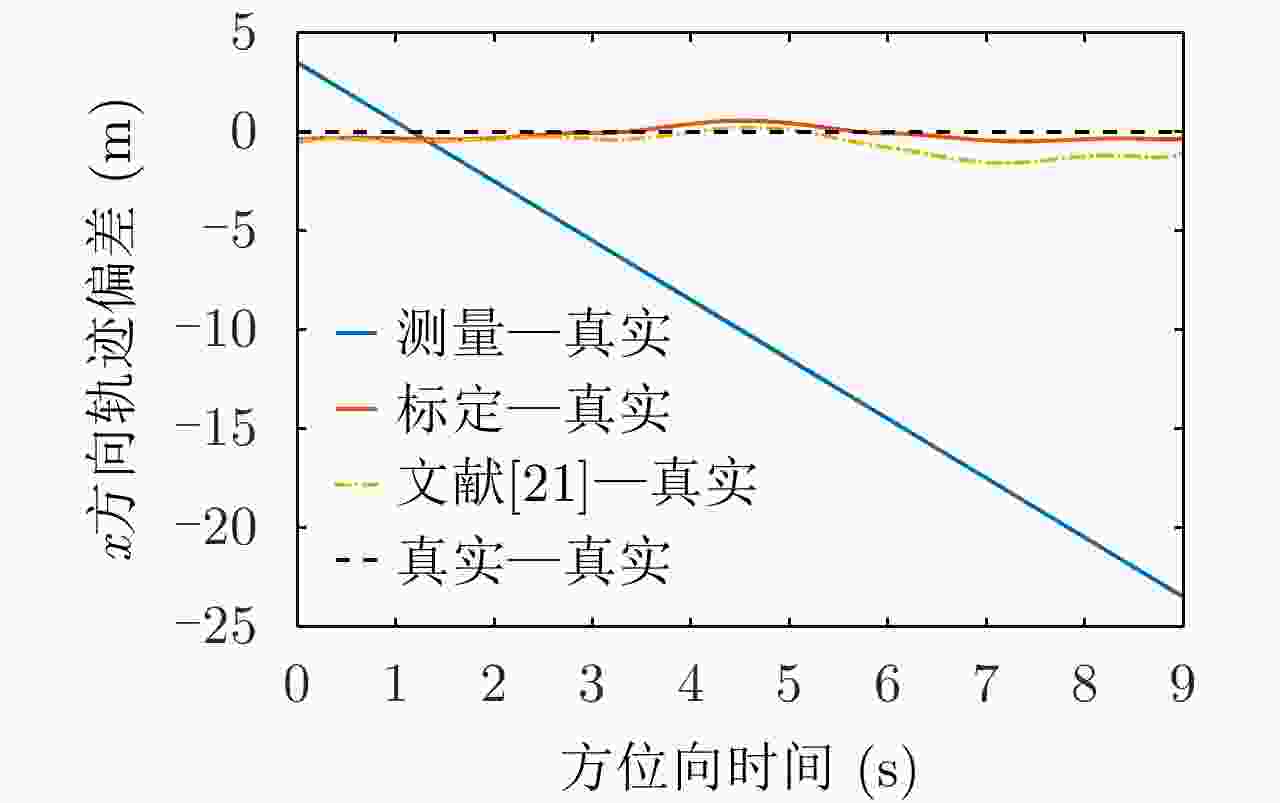
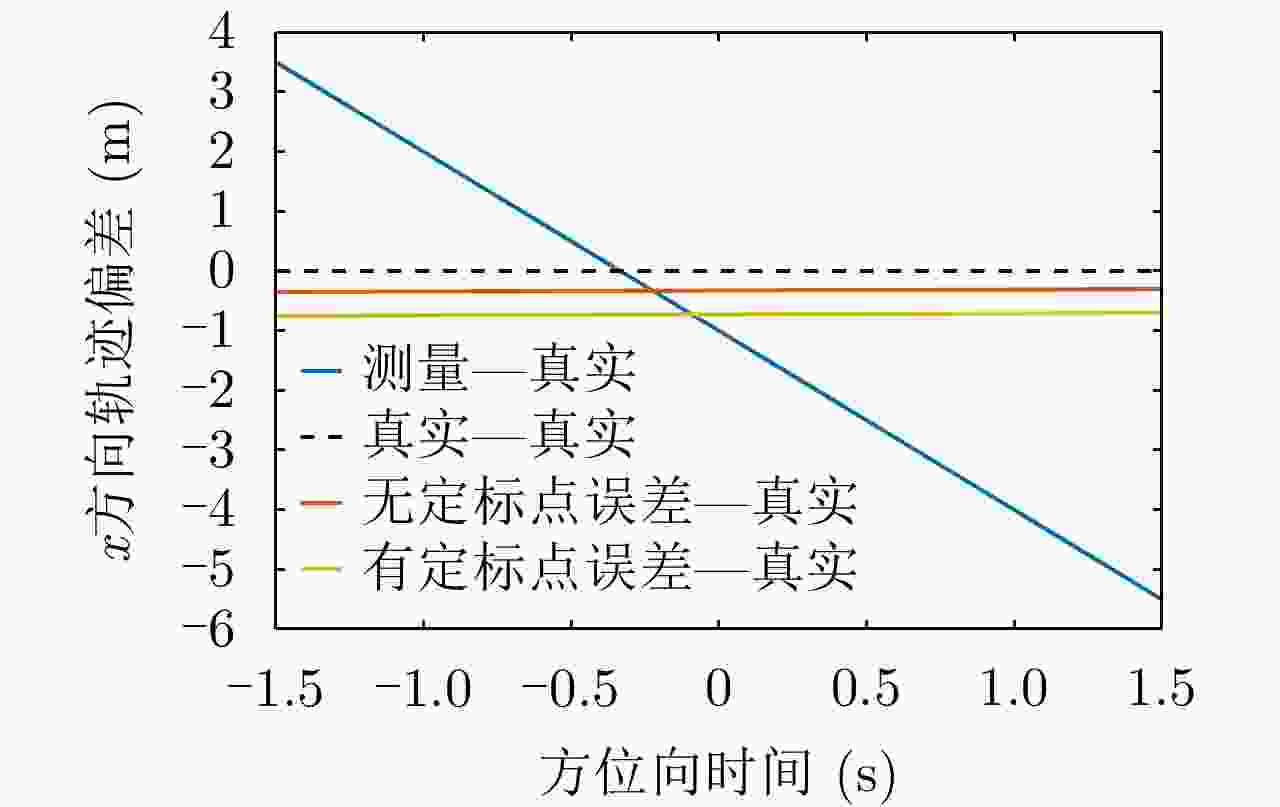
目标点	实际定位误差	公式算得误差	两误差的偏差
目标点1 (m)	3.4980	3.4192	0.0788
目标点2 (m)	1.2034	1.0431	0.1603
目标点3 (m)	–0.4437	–0.6014	0.1577

下载: 导出CSV

表 4 测量误差标定结果

Table 4. Calibration results of measurement error

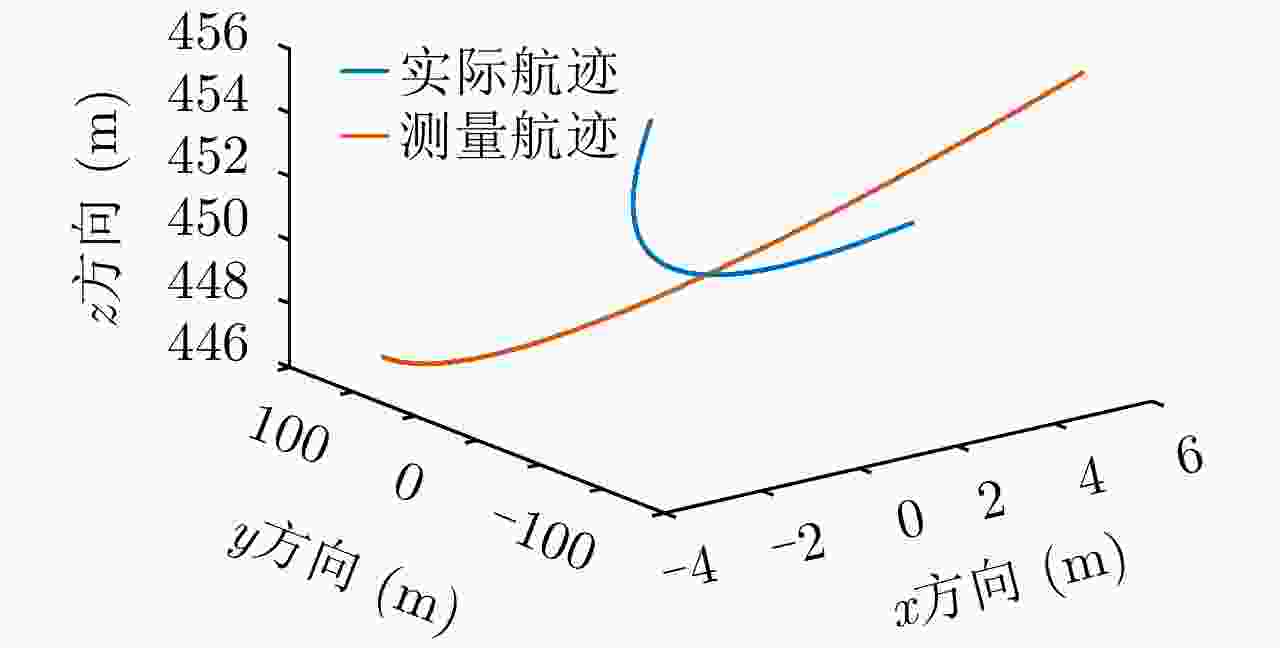
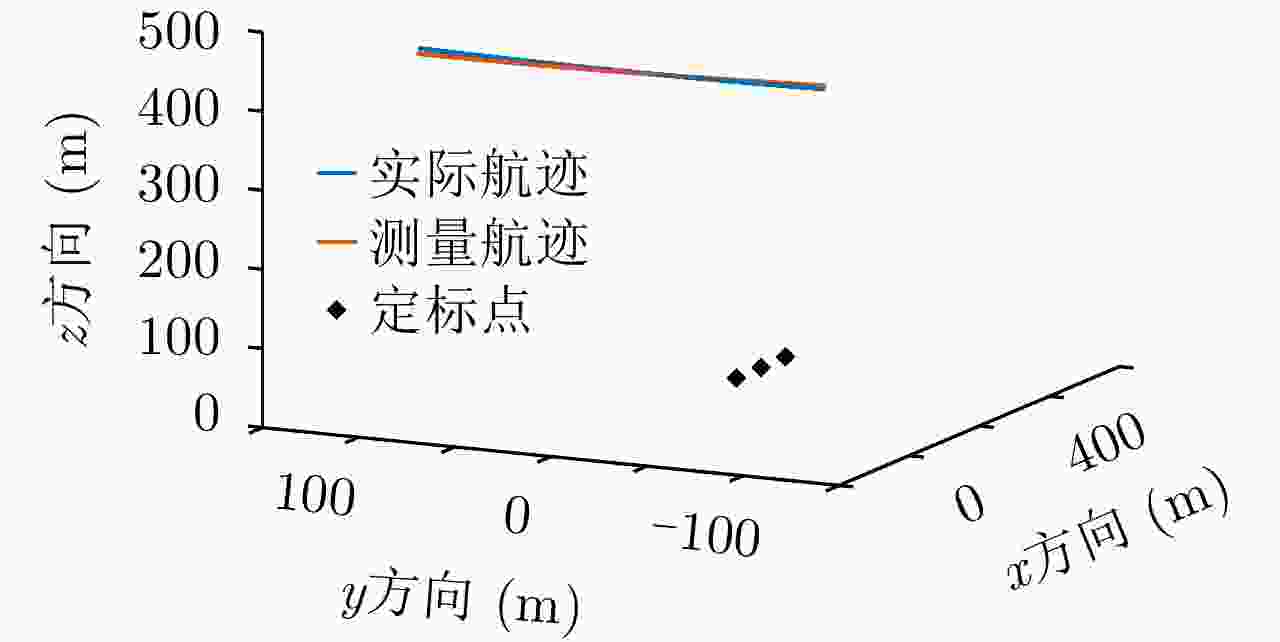
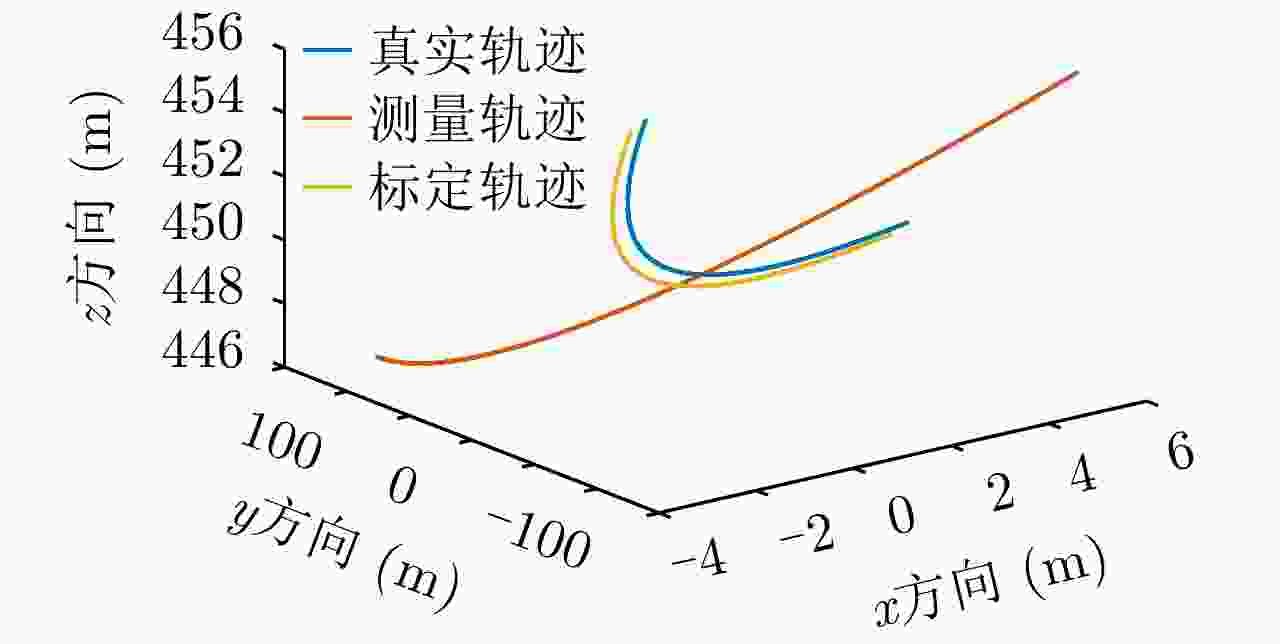
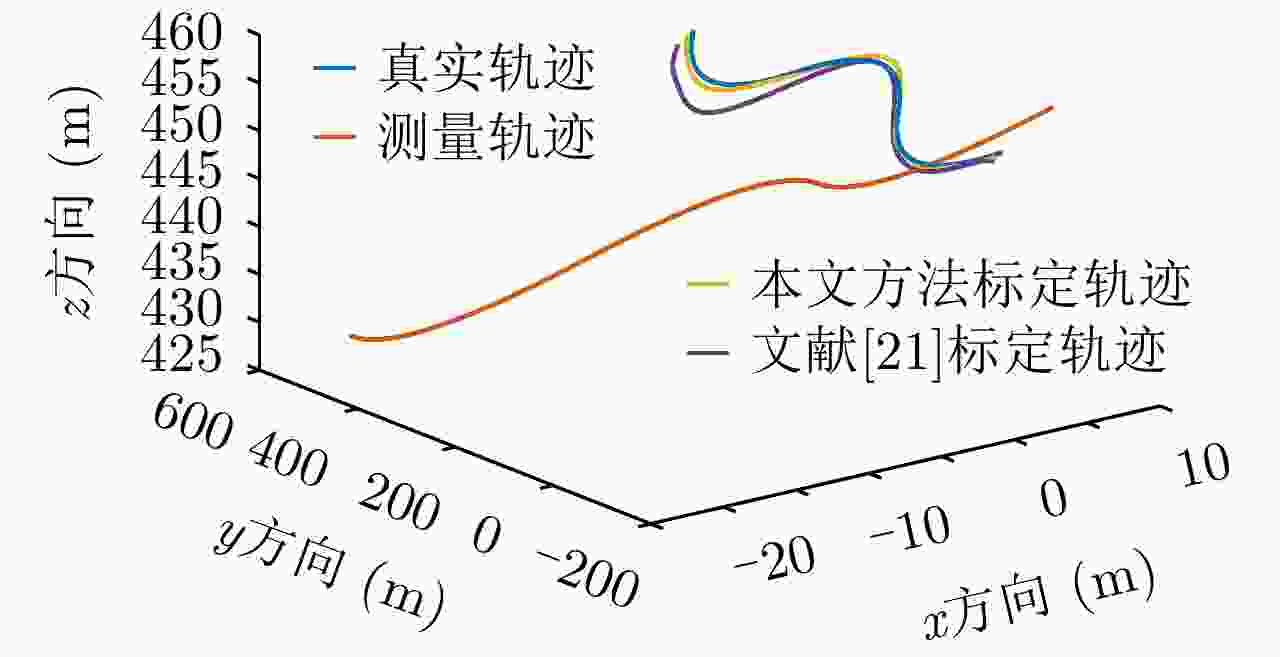
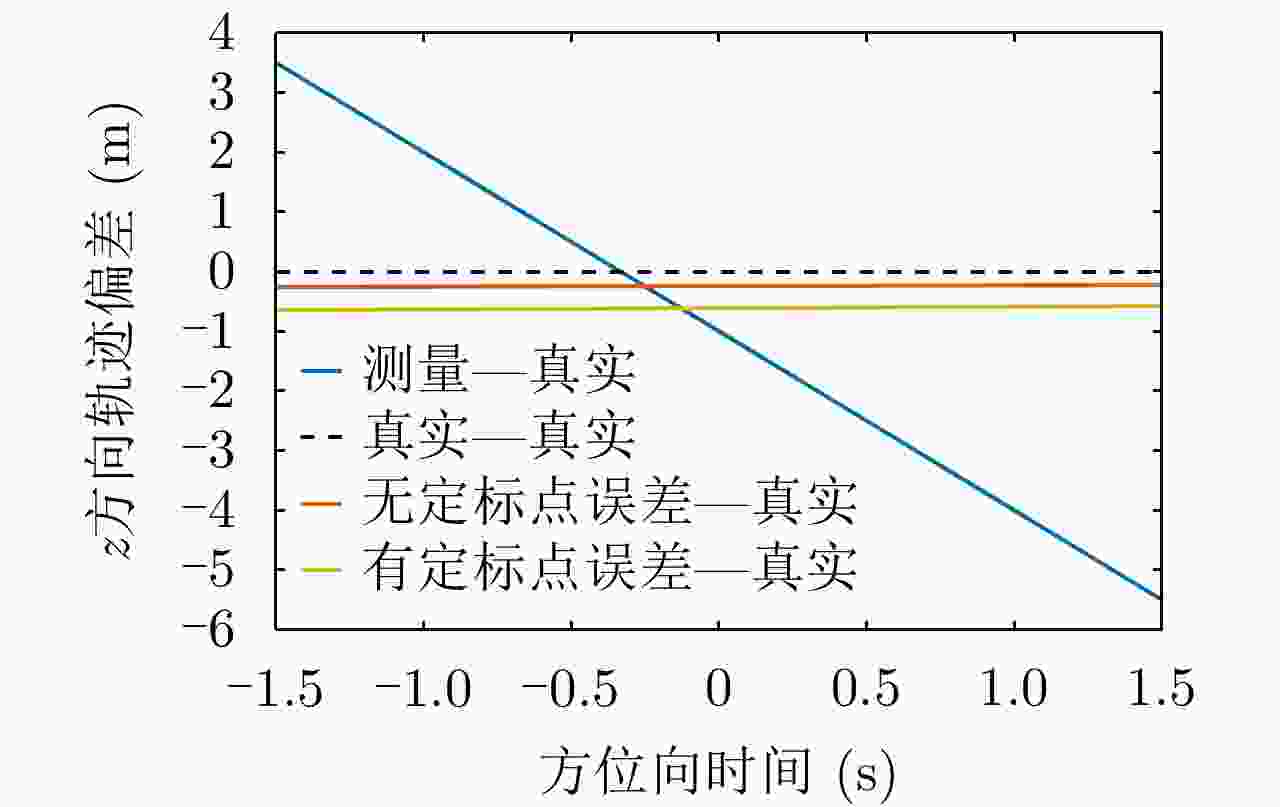
方向	测量航迹	真实航迹	标定出的测量误差	标定航迹
x方向	${\eta ^2} - 3\eta - 1$	${\eta ^2}$	$ - 3.0161\eta - 0.6755$	${\eta ^2} + 0.0161\eta - 0.3245$
z方向	${\eta ^2} - 3\eta + 449$	${\eta ^2} + 450$	$ - 3.0113\eta - 0.7585$	${\eta ^2} + 0.0113\eta $$ + 449.7585$

下载: 导出CSV

表 5 测量误差标定结果

Table 5. Calibration results of measurement error

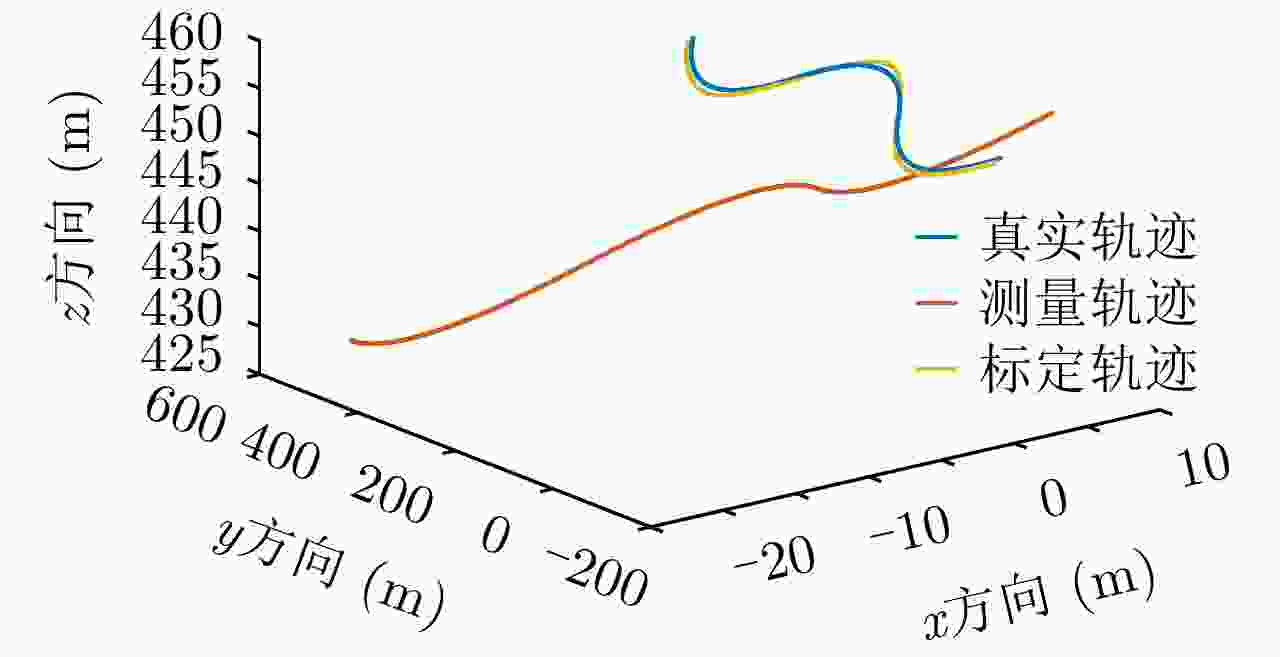
方向	测量航迹	真实航迹	标定出的测量误差	标定航迹
x方向	${\eta ^2} - 3\eta - 1$	${\eta ^2}$	$ - 3.0161\eta - 0.{\rm{2751}}$	${\eta ^2} + 0.0161\eta - 0.{\rm{7249}}$
z方向	${\eta ^2} - 3\eta + 449$	${\eta ^2} + 450$	$ - 3.0{\rm{222}}\eta - 0.{\rm{3882}}$	${\eta ^2} + 0.0{\rm{222}}\eta $$ + 449.{\rm{3882}}$

下载: 导出CSV

参考文献(23)

[1]	郑波浪. 机载高分辨率合成孔径雷达运动补偿研究[D]. [硕士论文], 中国科学院电子学研究所, 2006. ZHENG Bolang. A research on motion compensation of high-resolution airborne SAR[D]. [Master dissertation], Institute of Electronics, Chinese Academy of Sciences, 2006.
[2]	CANTALLOUBE H M J and NAHUM C E. Airborne SAR-efficient signal processing for very high resolution[J]. Proceedings of the IEEE, 2013, 101(3): 784–797. doi: 10.1109/JPROC.2012.2232891
[3]	苗慧. 机载SAR定位精度的研究[D]. [博士论文], 中国科学院电子学研究所, 2007. MIAO Hui. Research on airborne SAR geolocation accuracy[D]. [Ph. D dissertation], Institute of Electronics, Chinese Academy of Sciences, 2007.
[4]	高祥武, 黄广民, 杨汝良. 机载SAR目标快速定位方法和定位精度分析[J]. 现代雷达, 2004, 26(9): 4–7. doi: 10.3969/j.issn.1004-7859.2004.09.002 GAO Xiangwu, HUANG Guangmin, and YANG Ruliang. Study on a fast target location method for airborne SAR and location precision analysis[J]. Modern Radar, 2004, 26(9): 4–7. doi: 10.3969/j.issn.1004-7859.2004.09.002
[5]	彭代强, 林幼权, 杜鹏飞. 机载SAR图像快速经纬度计算及精度分析[J]. 现代雷达, 2010, 32(3): 48–52, 79. doi: 10.3969/j.issn.1004-7859.2010.03.013 PENG Daiqiang, LIN Youquan, and DU Pengfei. A fast algorithm for latitude and longitude calculation of airborne SAR and its location precision analysis[J]. Modern Radar, 2010, 32(3): 48–52, 79. doi: 10.3969/j.issn.1004-7859.2010.03.013
[6]	LIU Junbin, QIU Xiaolan, HUANG Lijia, et al. Curved-path SAR geolocation error analysis based on BP algorithm[J]. IEEE Access, 2019, 7: 20337–20345. doi: 10.1109/ACCESS.2019.2897361
[7]	XING Mengdao, JIANG Xiuwei, WU Renbiao, et al. Motion compensation for UAV SAR based on raw radar data[J]. IEEE Transactions on Geoscience and Remote Sensing, 2009, 47(8): 2870–2883. doi: 10.1109/TGRS.2009.2015657
[8]	DE MACEDO K A C and SCHEIBER R. Precise topography- and aperture-dependent motion compensation for airborne SAR[J]. IEEE Geoscience and Remote Sensing Letters, 2005, 2(2): 172–176. doi: 10.1109/LGRS.2004.842465
[9]	MAO Yongfei, XIANG Maosheng, WEI Lideng, et al. Error analysis of SAR motion compensation[C]. 2012 IEEE International Conference on Imaging Systems and Techniques Proceedings, Manchester, UK, 2012: 377–380. doi: 10.1109/IST.2012.6295562.
[10]	李芳芳, 仇晓兰, 孟大地, 等. 机载双天线InSAR运动补偿误差的影响分析[J]. 电子与信息学报, 2013, 35(3): 559–567. doi: 10.3724/SP.J.1146.2012.00850 LI Fangfang, QIU Xiaolan, MENG Dadi, et al. Effects of motion compensation errors on performance of airborne dual-antenna InSAR[J]. Journal of Electronics &Information Technology, 2013, 35(3): 559–567. doi: 10.3724/SP.J.1146.2012.00850
[11]	PRATS P, REIGBER A, MALLORQUI J J, et al. Efficient detection and correction of residual motion errors in airborne SAR interferometry[C]. IGARSS 2004. 2004 IEEE International Geoscience and Remote Sensing Symposium, Anchorage, USA, 2004: 992–995. doi: 10.1109/IGARSS.2004.1368576.
[12]	REIGBER A, PRATS P, and MALLORQUI J J. Refined estimation of time-varying baseline errors in airborne SAR interferometry[J]. IEEE Geoscience and Remote Sensing Letters, 2006, 3(1): 145–149. doi: 10.1109/LGRS.2005.860482
[13]	刘云龙, 李焱磊, 周良将, 等. 一种机载SAR快速几何精校正算法[J]. 雷达学报, 2016, 5(4): 419–424. doi: 10.12000/JR16064 LIU Yunlong, LI Yanlei, ZHOU Liangjiang, et al. A fast precise geometric calibration method for airborne SAR[J]. Journal of Radars, 2016, 5(4): 419–424. doi: 10.12000/JR16064
[14]	REIGBER A, ALIVIZATOS E, POTSIS A, et al. Extended wavenumber-domain synthetic aperture radar focusing with integrated motion compensation[J]. IEE Proceedings-Radar, Sonar and Navigation, 2006, 153(3): 301–310. doi: 10.1049/ip-rsn:20045087
[15]	MOREIRA A, MITTERMAYER J, and SCHEIBER R. Extended chirp scaling algorithm for air- and spaceborne SAR data processing in stripmap and ScanSAR imaging modes[J]. IEEE Transactions on Geoscience and Remote Sensing, 1996, 34(5): 1123–1136. doi: 10.1109/36.536528
[16]	孟大地. 机载合成孔径雷达运动补偿算法研究[D]. [博士论文], 中国科学院电子学研究所, 2006. MENG Dadi. Research on motion compensation algorithm for airborne SAR[D]. [Ph. D dissertation], Institute of Electronics, Chinese Academy of Sciences, 2006.
[17]	YANG Mingdong, ZHU Daiyin, and SONG Wei. Comparison of two-step and one-step motion compensation algorithms for airborne synthetic aperture radar[J]. Electronics Letters, 2015, 51(14): 1108–1110. doi: 10.1049/el.2015.1350
[18]	FORNARO G, FRANCESCHETTI G, and PERNA S. On center-beam approximation in SAR motion compensation[J]. IEEE Geoscience and Remote Sensing Letters, 2006, 3(2): 276–280. doi: 10.1109/LGRS.2005.863391
[19]	曾乐天, 邢孟道, 陈士超. 基于窄波束和平地假设的运动补偿方向研究[J]. 电子与信息学报, 2014, 36(10): 2464–2468. doi: 10.3724/SP.J.1146.2013.01671 ZENG Letian, XING Mengdao, and CHEN Shichao. The research on the direction of motion compensation according to the narrow beam and flat earth hypothesis[J]. Journal of Electronics &Information Technology, 2014, 36(10): 2464–2468. doi: 10.3724/SP.J.1146.2013.01671
[20]	杨鸣冬, 俞翔, 朱岱寅. 基于距离子带的机载SAR高精度多级空变运动补偿[J]. 航空学报, 2018, 39(2): 321557. doi: 10.7527/S1000-6893.2017.21557 YANG Mingdong, YU Xiang, and ZHU Daiyin. High-precision space-variant motion compensation with multi-level processing for airborne SAR based on subswath[J]. Acta Aeronautica et Astronautica Sinica, 2018, 39(2): 321557. doi: 10.7527/S1000-6893.2017.21557
[21]	柳俊斌. 弱导航信息下的SAR自主定位与航迹修正技术研究[D]. [硕士论文], 中国科学院空天信息创新研究院, 2020. LIU Junbin. Research on SAR autonomous positioning and track correction technology under weak navigation information[D]. [Master dissertation], Aerospace Information Research Institute, Chinese Academy of Sciences, 2020.
[22]	孙立军, 刘鑫, 刘兴春. 关于差分GPS精度的分析[C]. 第十届东北三省测绘学术与信息交流会论文集, 漠河, 2009. SUN Lijun, LIU Xin, and LIU Xingchun. Analysis on the accuracy of differential GPS-DGPS[C]. The 10th Academic and Information Exchange Meeting of Surveying and Mapping in Northeast China, Mohe, China, 2009.
[23]	BAMLER R and EINEDER M. Accuracy of differential shift estimation by correlation and split-bandwidth interferometry for wideband and delta-k SAR systems[J]. IEEE Geoscience and Remote Sensing Letters, 2005, 2(2): 151–155. doi: 10.1109/LGRS.2004.843203