作者中心
专家审稿
责编办公
编辑办公
Research on the Method of Composing Very Low Frequency Signals Based on the Staggered Array
-
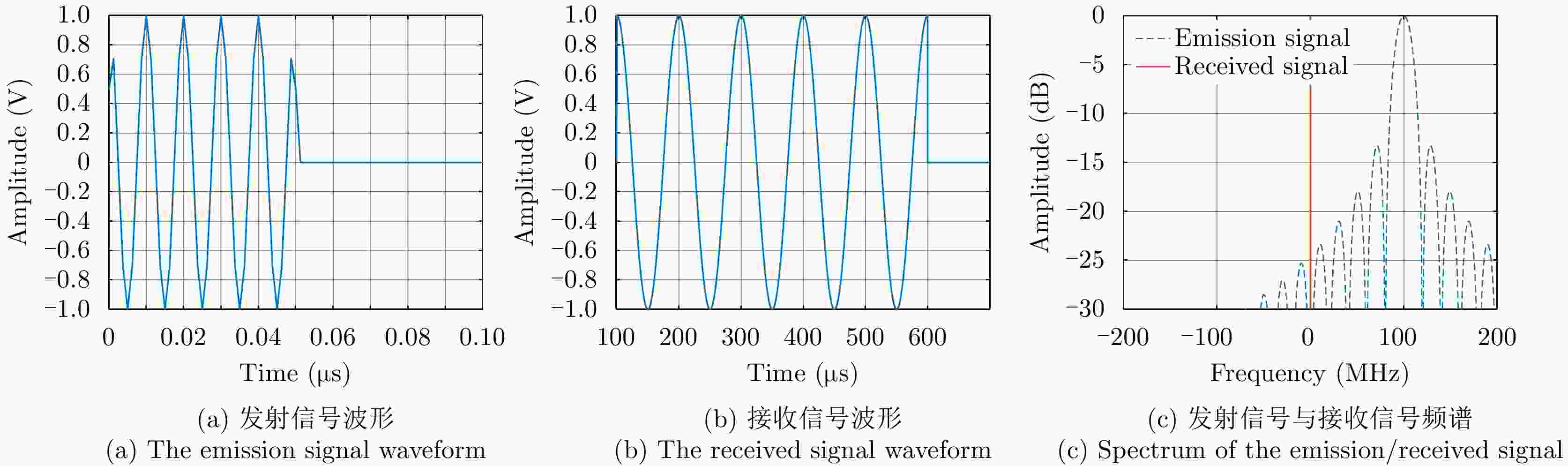
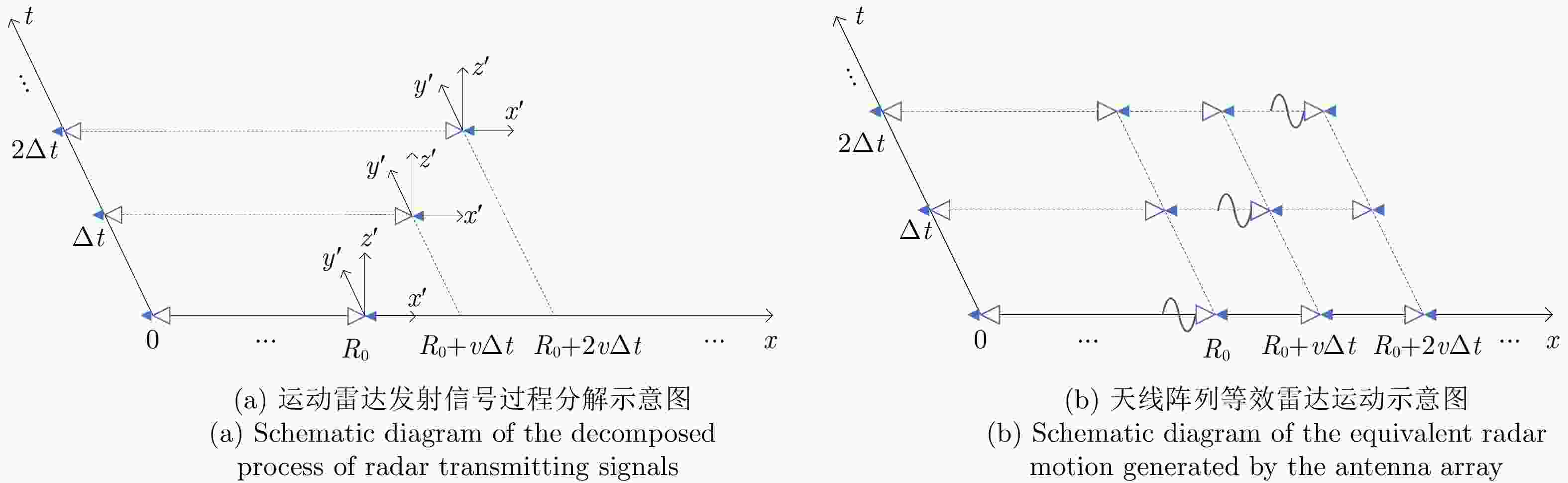
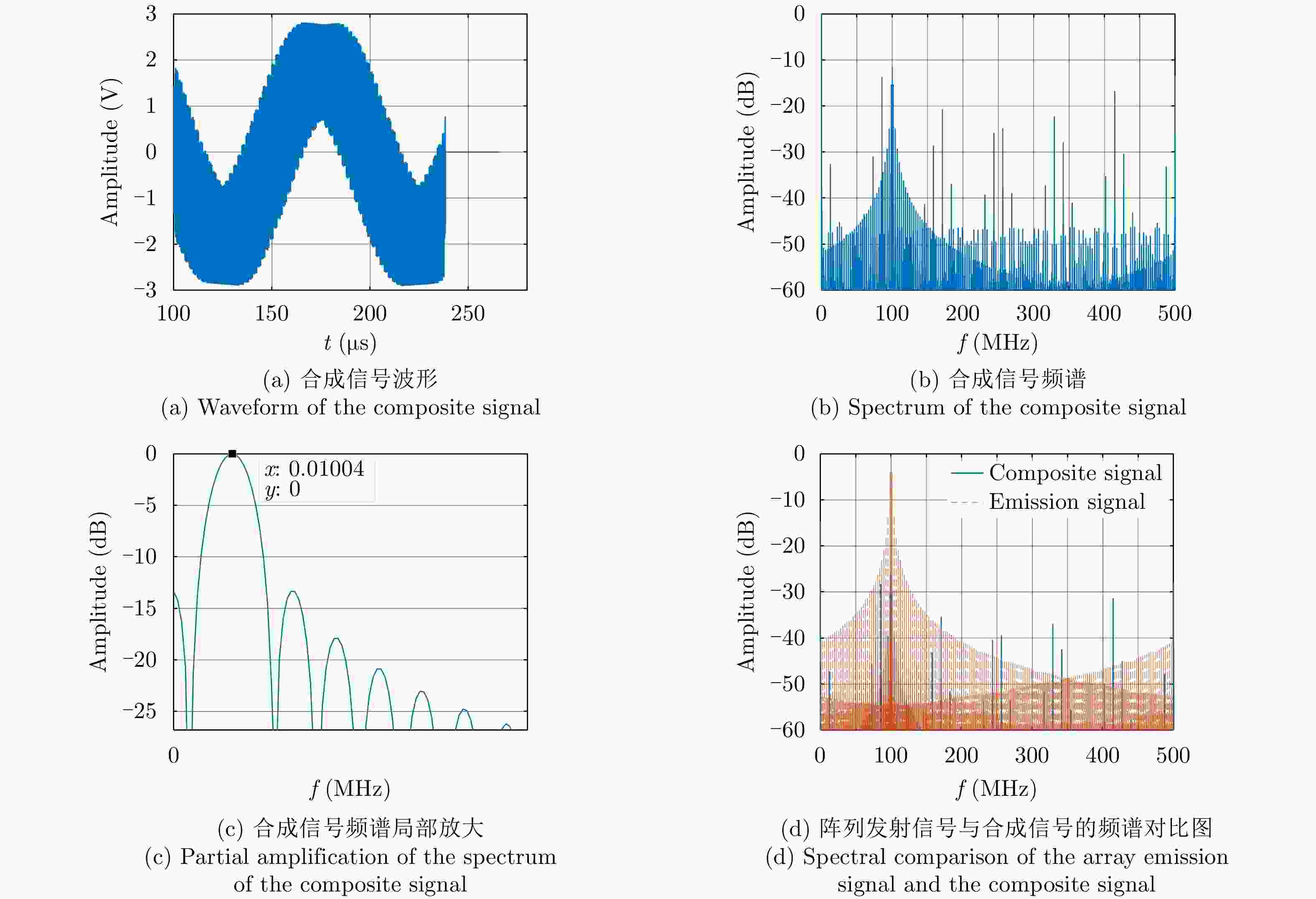
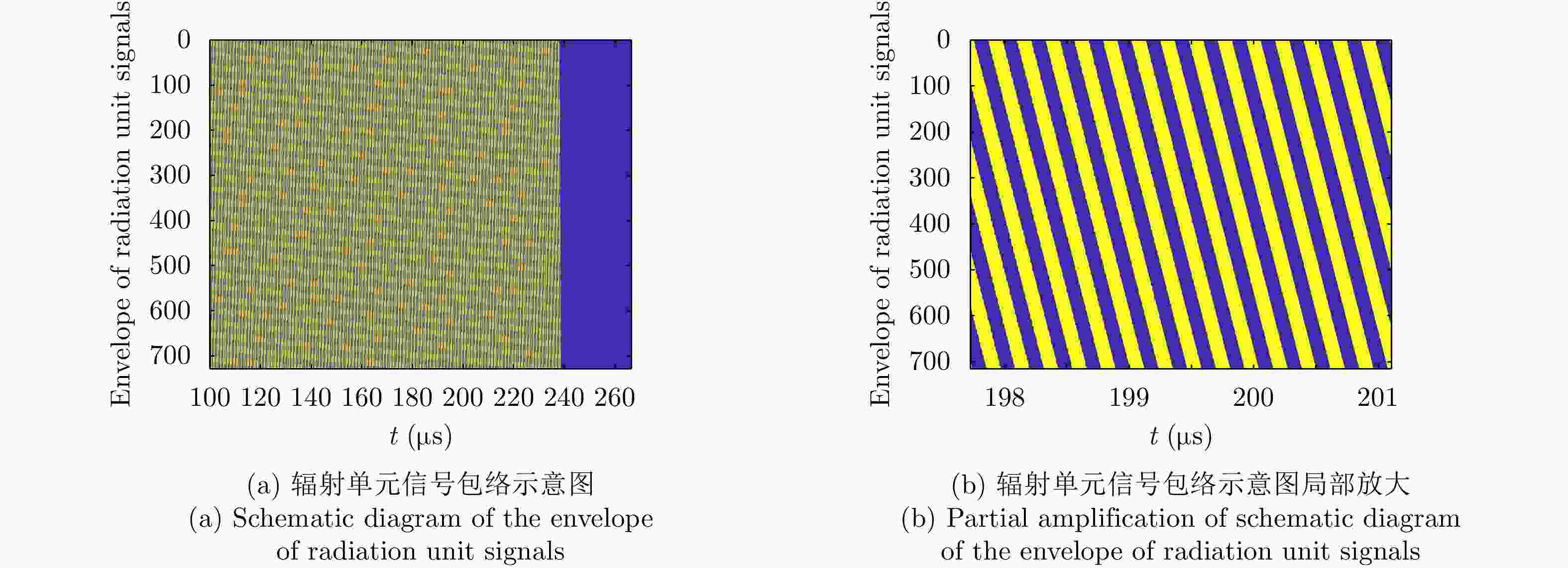
摘要: 10 kHz量级甚低频电磁波信号具有较强的地物穿透能力，可用于地质勘探。由于其天线尺寸在10 km量级，其应用场合受到限制，研究基于适当尺寸高频雷达天线的甚低频电磁波信号产生方法具有重要意义。该文提出基于高频阵列天线产生甚低频信号的概念，利用阵列天线合成产生近光速远离运动雷达多普勒信号，实现信号频率的大幅降低。给出了发射波形、交错阵列设计和阵列参数选择方法。将周期脉冲串信号作为辐射单元信号，增大合成信号脉宽。利用阵列产生的脉宽展宽量填补脉冲信号的休止期，在目标区合成时间连续的甚低频信号。采用峰值旁瓣比(PSLR)、积分旁瓣比(ISLR)、阵列发射信号与合成信号的频谱对比评价合成低频信号的性能和发射信号的能量利用率。该文仿真了百米量级阵列100 MHz辐射单元信号在目标区合成10 kHz甚低频信号的情况：9行阵列构成交错阵列、辐射单元信号脉宽设置为0.115 μs时，合成信号频谱的峰值旁瓣比和积分旁瓣比分别为–13.34 dB和–9.44 dB, 10 kHz低频信号在合成信号中的能量占比为89.79%。该文分析了辐射单元间距误差、辐射单元信号时间、相位与幅度误差以及目标偏离预定位置的影响。仿真结果表明了该文方法的有效性。Abstract: The Very Low Frequency (VLF) signal of 10 kHz has strong penetrability of ground objects. Because of the antenna size, its application is limited. Therefore, it is important to study the VLF signal generation method based on appropriately sized high frequency radar antennas. The concept of generating VLF signal with high frequency array antenna is proposed in this paper. The waveform of the emission signal, staggered array structure design, and array parameter selection methods are presented and discussed. The pulse width of the composite signal is increased by using periodic pulse signals as radiation element signals. The resting period of the pulse signals is filled with the pulse width expansion generated by the array and the VLF signal with continuous time is composed in the target area. The performance of the composite VLF signal and the energy utilization of the emission signal are evaluated using Peak SideLobe Ratio (PSLR), Integrated SideLobe Ratio (ISLR) and through the spectrum comparison between the emission signal and the composite signal. With the 10 kHz VLF signal composed by 100 MHz radiant element signals, the hundred meter array is simulated. When the staggered array is constituted by nine arrays and the pulse width of the radiation element is set to 0.115 μs, PSLR and ISLR of the composite signal spectrum are –13.34 dB and –9.44 dB respectively, and the energy proportion of 10 kHz low-frequency signal in the composite signal is 89.79%. The effects of radiation element spacing error, time error, phase error and amplitude error of the radiation element signal and the target’s deviation are analyzed. It is found that the proposed method is an effective one and the simulation results have illustrated the effectiveness.
-
图 2 多普勒效应中的发射/接收信号波形与频谱
Figure 2. The emission/received signal waveform and spectrum of Doppler effect
图 3 运动雷达发射信号过程分解和天线阵列等效雷达运动示意图
Figure 3. Schematic diagram of the decomposed process of radar transmitting signals and the equivalent radar motion generated by the antenna array
图 6 辐射单元信号周期为
${{{T_0}} / 2}$ 时合成信号的波形、频谱与频谱对比图Figure 6. Waveform, spectrum and spectral contrast diagram of the composite signal when the radiation unit signal period being
${{{T_0}} / 2}$ 
图 7 辐射单元信号周期为
${{{T_0}} / 6}$ 时合成信号的波形、频谱与频谱对比图Figure 7. Waveform, spectrum and spectral contrast diagram of the composite signal when the radiation unit signal period being
${{{T_0}} / 6}$ 
图 8 辐射单元信号周期为
${{{T_0}} / 6}$ 时9行阵列构成的交错阵列在目标区合成信号的波形、频谱与频谱对比图Figure 8. Waveform, spectrum and spectral contrast diagram of the composite signal generated by the 9-row staggered array when the radiation unit signal period being
${{{T_0}} / 6}$ 
图 10 辐射单元间距误差分布、目标区合成信号的波形与频谱图
Figure 10. The distribution of spacing error, waveform and spectrum of the composite signal in target area
图 11 辐射单元信号时间误差分布、目标区合成信号的波形与频谱图
Figure 11. The distribution of radiation unit signal time error, waveform and spectrum of the composite signal in target area
图 12 辐射单元信号相位误差分布、目标区合成信号的波形与频谱图
Figure 12. The distribution of radiation unit signal phase error, waveform and spectrum of the composite signal in target area
图 13 辐射单元信号幅度误差分布、目标区合成信号的波形与频谱图
Figure 13. The distribution of radiation unit signal amplitude error, waveform and spectrum of the composite signal in target area
图 14 目标在xoy平面内45°扫描角方向距离阵列近端20 km时目标区合成信号的波形与频谱
Figure 14. Waveform and spectrum of the composite signal in the target area when the target is 20 km away from the near end of the array at 45° scanning angle in xoy plane
图 15 目标在xoy平面内45°扫描角方向距离阵列近端40 km时目标区合成信号的波形与频谱
Figure 15. Waveform and spectrum of the composite signal in the target area when the target is 40 km away from the near end of the array at 45° scanning angle in xoy plane
图 16 目标沿
$z$ 轴偏离1 km时目标区合成信号的波形与频谱Figure 16. Waveform and spectrum of the composite signal in the target area when the target deviates 1 km along the z-axis
图 17 受综合误差影响时目标区合成信号的波形与频谱
Figure 17. Waveform and spectrum of the composite signal in the target area influenced by synthetical error
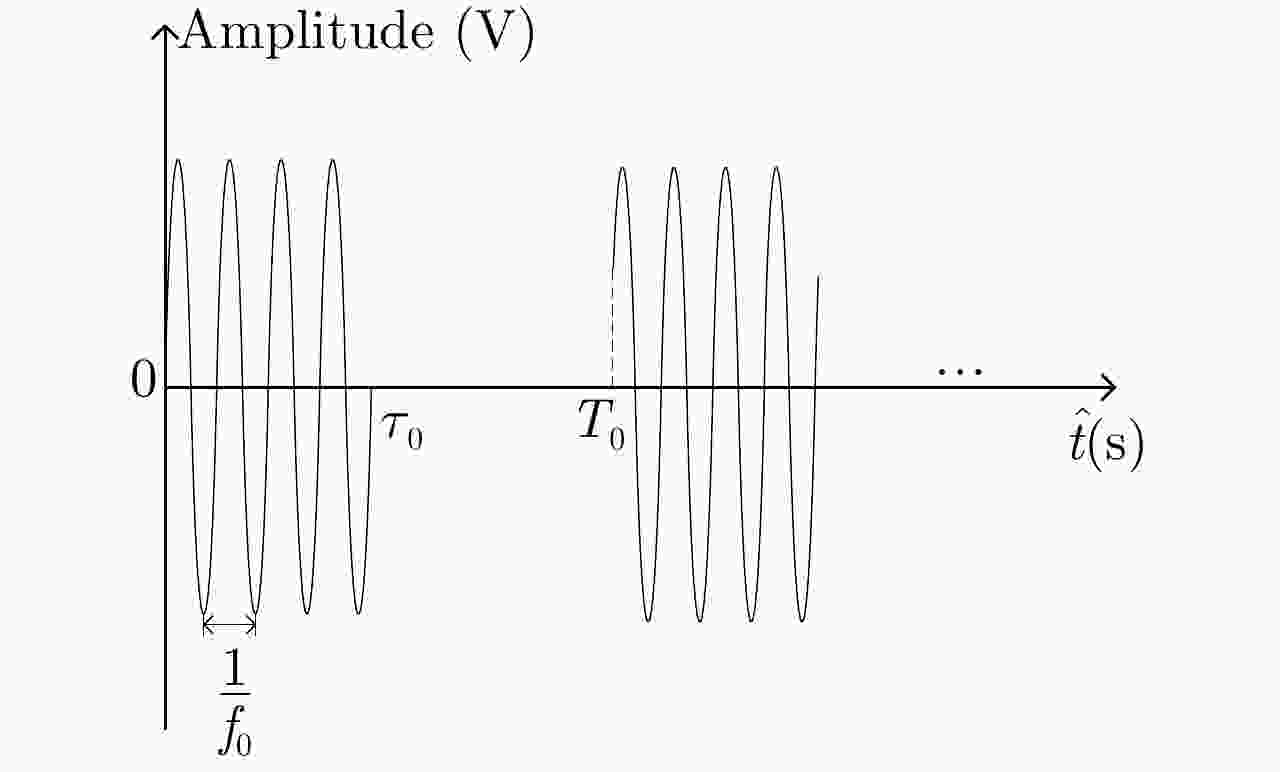
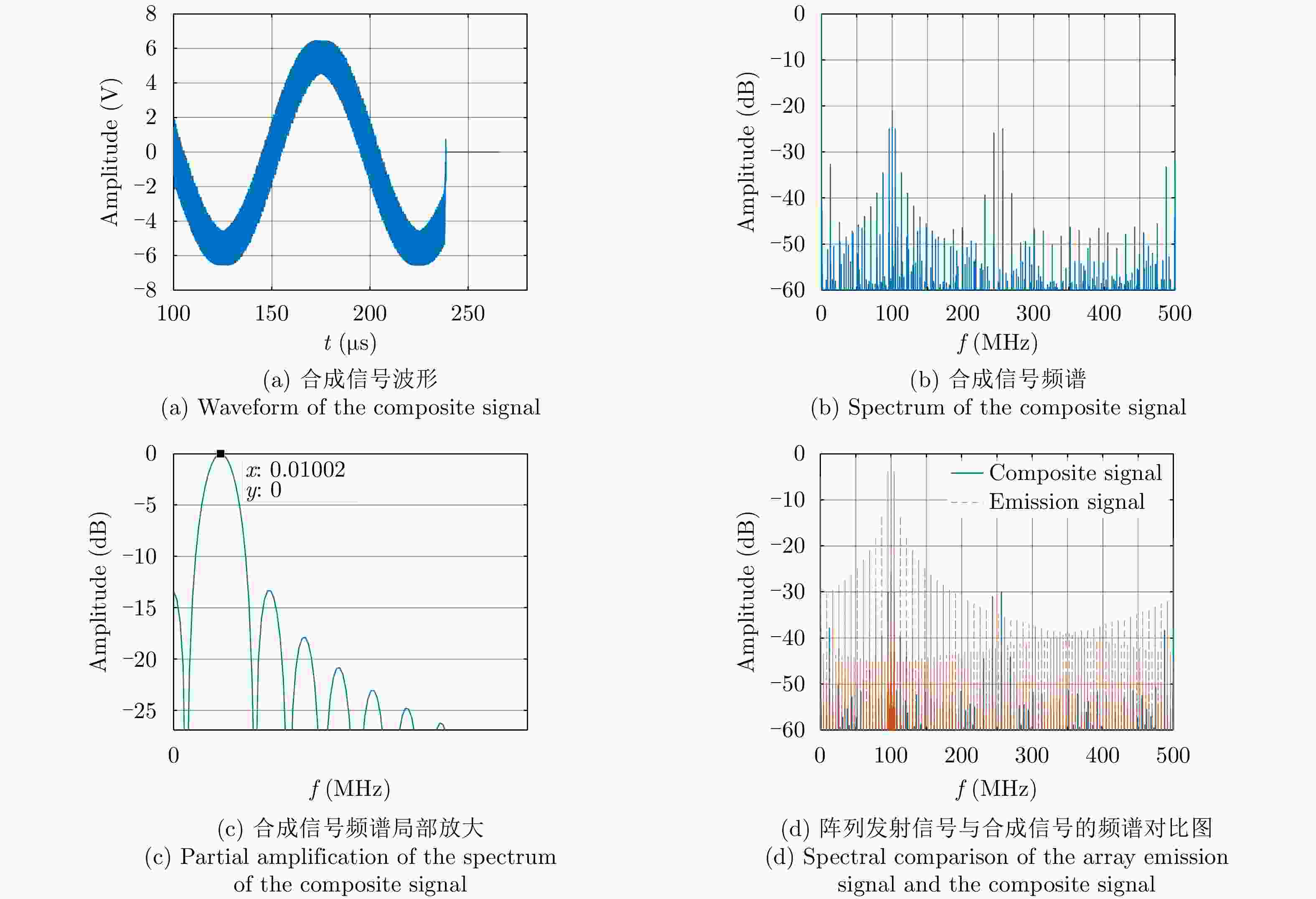
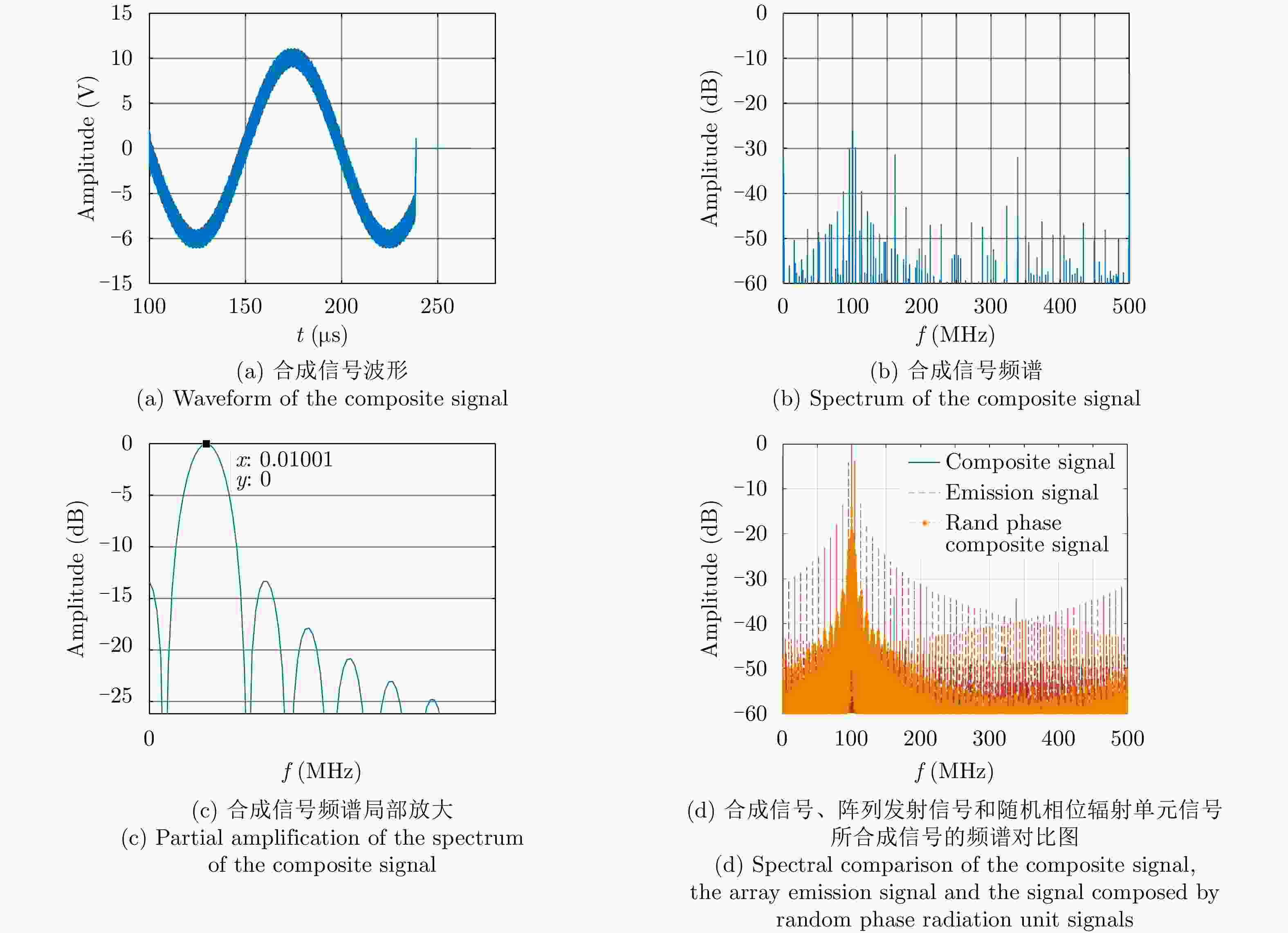
表 1 辐射单元信号周期取
${{{{{T_0}}}} / {{2}}}$ 和${{{{{T_0}}}} / {{6}}}$ 时的仿真参数与结果Table 1. Simulation parameters and results when the radiation unit signal period being
${{{{{T_0}}}} / {{2}}}$ and${{{{{T_0}} / 6}}}$ respectively参数 辐射单元信号周期取${{{T_0}} / 2}$ 辐射单元信号周期取${{{T_0}} / 6}$ 最大辐射单元信号周期${T_0}$(μs) 1.38 1.38 辐射单元信号周期数(个) 200 600 辐射单元信号脉宽(μs) 0.345 0.115 辐射单元信号脉宽展宽(μs) 0.345 0.115 辐射单元信号周期(μs) 0.69 0.23 辐射单元信号休止期(μs) 0.345 0.115 合成信号脉宽(μs) 138.36 138.59 峰值旁瓣比(dB) –11.45 –13.34 积分旁瓣比(dB) –4.33 –8.77 低频信号能量占比(%) 73.05 88.29 频谱对比图中的10 kHz分量(dB) –14.610 –5.081 发射信号能量利用率(%) 18.60 55.71 
下载: 导出CSV
表 2 不同误差影响下合成信号频谱参数(dB)
Table 2. Spectrum parameters of the composite signal influenced by different errors (dB)
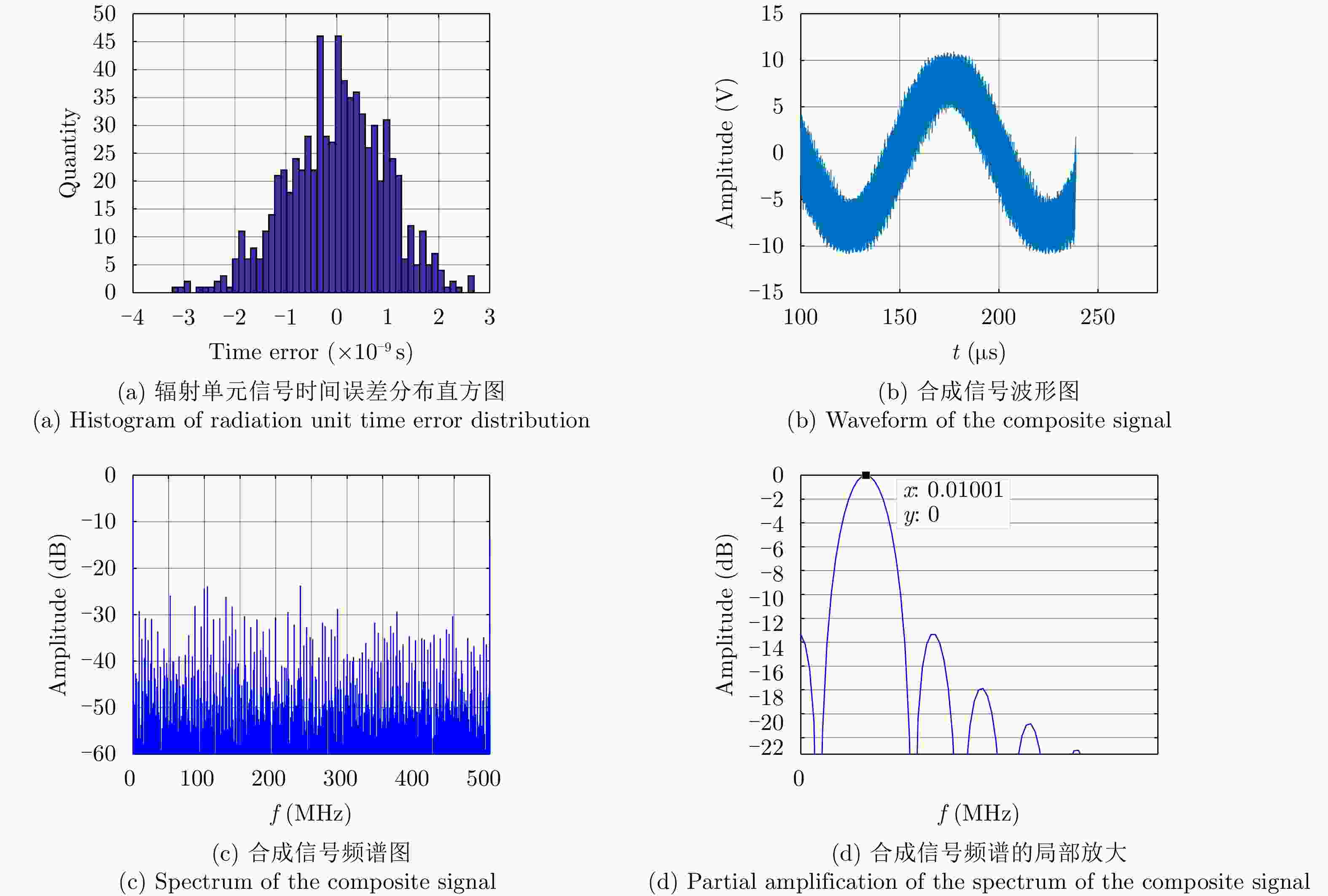
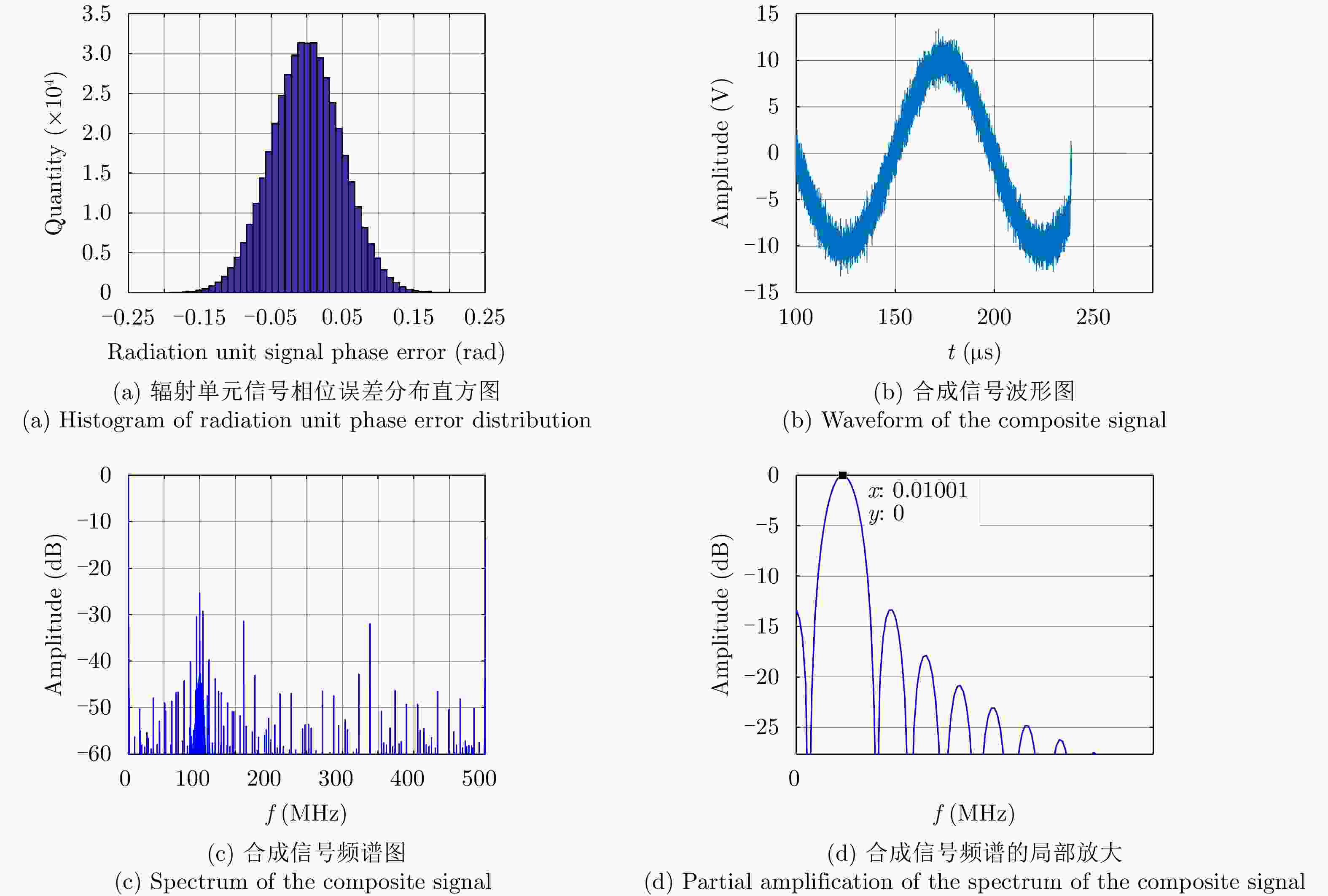
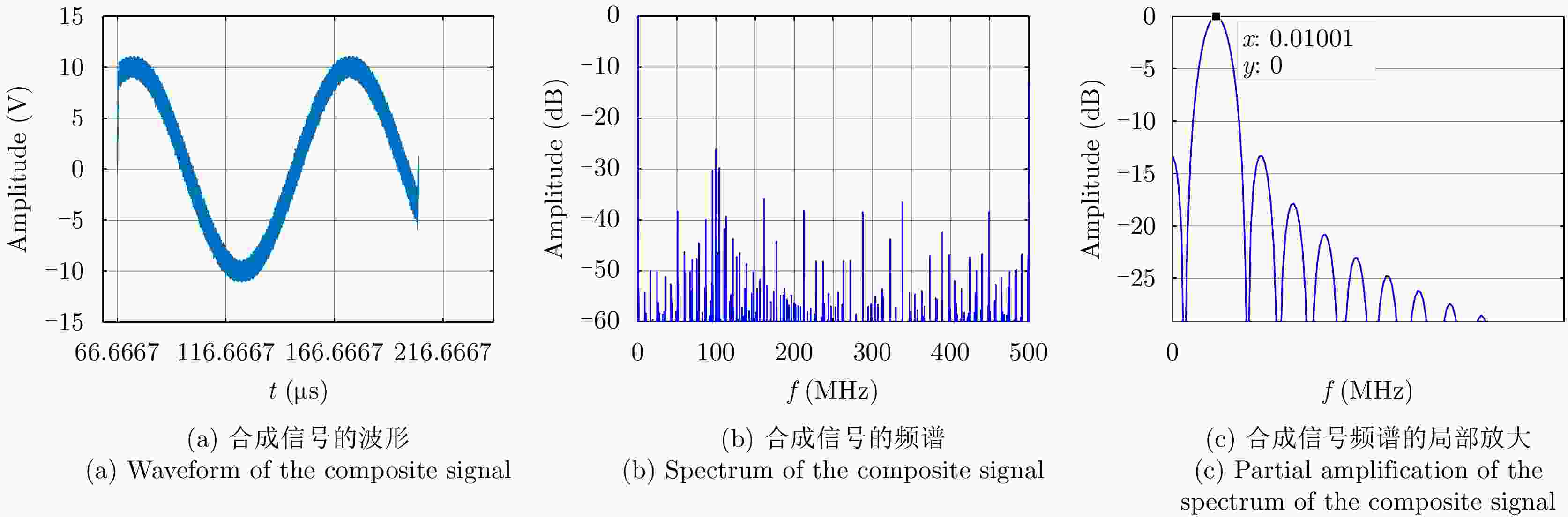
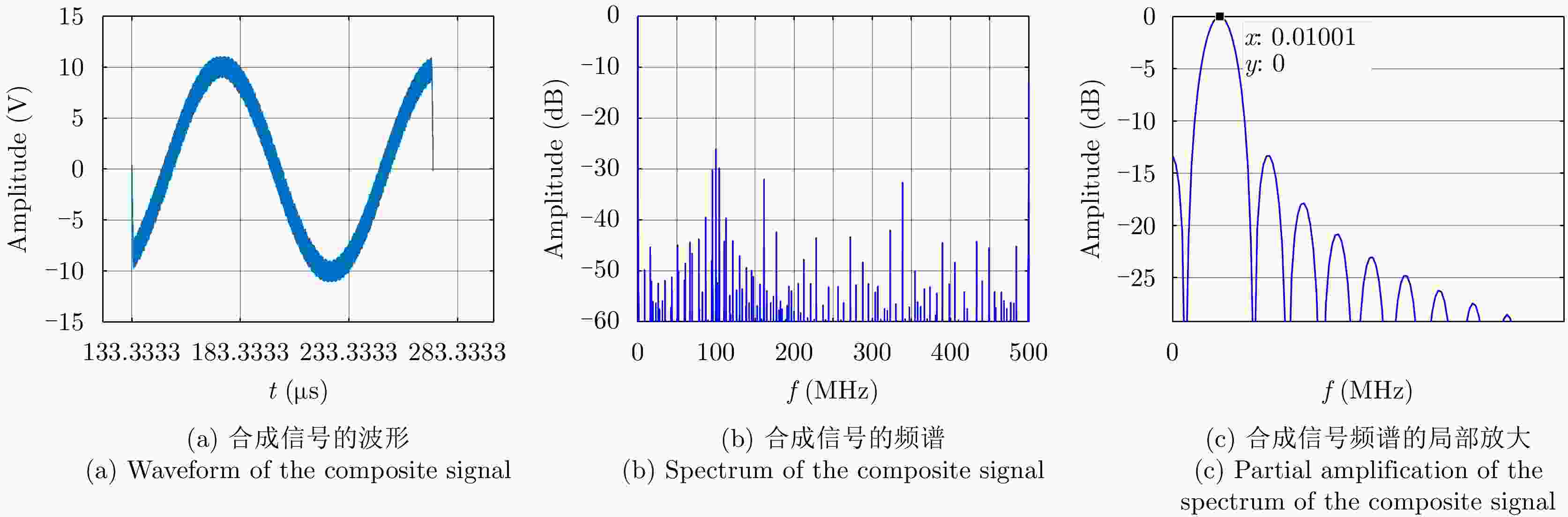
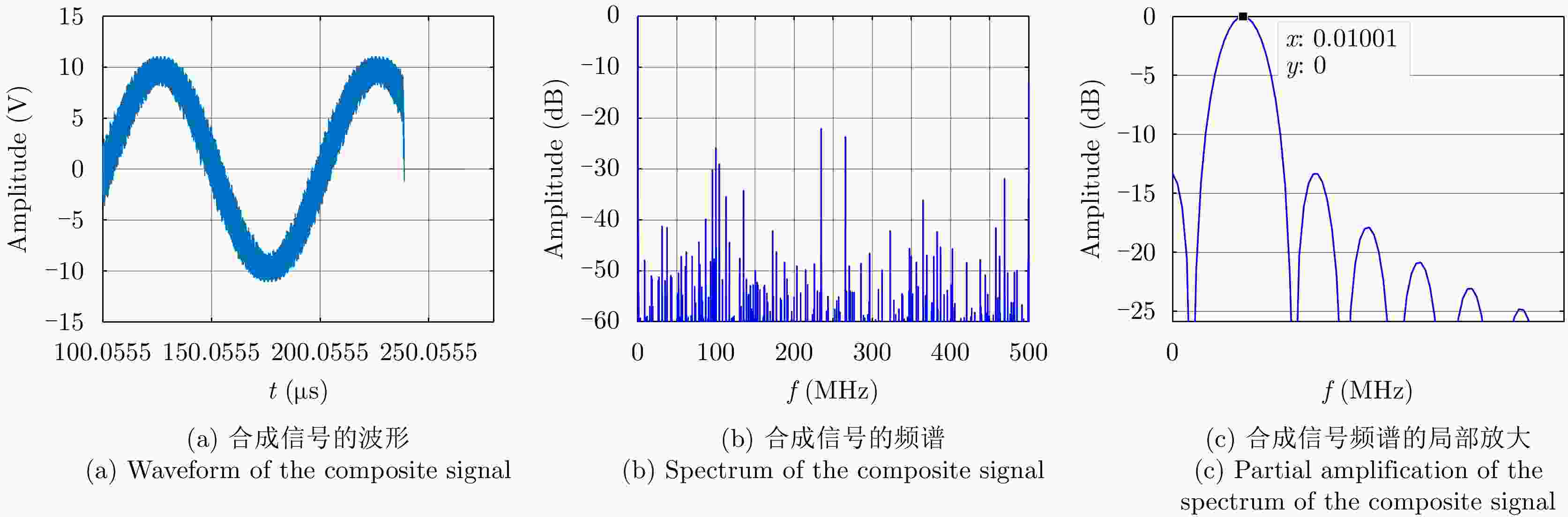
误差 峰值旁瓣比 积分旁瓣比 辐射单元间距误差 –13.31 –8.95 辐射单元信号时间误差 –13.34 –7.64 辐射单元信号相位误差 –13.34 –9.07 辐射单元信号幅度误差 –13.34 –9.33 目标在xoy平面内距离阵列近端20 km –13.34 –9.44 目标在xoy平面内距离阵列近端40 km –13.34 –9.44 目标在z轴偏离1 km –13.34 –8.97 综合误差 –13.28 –6.63
下载: 导出CSV
-
[1] 汪谋. 地质雷达探测效果影响因素研究[J]. 雷达科学与技术, 2007, 5(2): 86–90.WANG Mou. Research on influencing factors of GPR’s detection effectiveness[J]. Radar Science and Technology, 2007, 5(2): 86–90. [2] 卓贤军, 陆建勋, 赵国泽, 等. 极低频探地(WEM)工程[J]. 中国工程科学, 2011, 13(9): 42–50.ZHUO Xianjun, LU Jianxun, ZHAO Guoze, et al. The extremely low frequency engineering project using WEM for underground exploration[J]. Strategic Study of CAE, 2011, 13(9): 42–50. [3] 卓贤军, 陆建勋. “极低频探地工程”在资源探测和地震预测中的应用与展望[J]. 舰船科学技术, 2010, 32(6): 3–7, 30.ZHUO Xianjun and LU Jianxun. Application and prospect of WEM to resource exploration and earthquake predication[J]. Ship Science and Technology, 2010, 32(6): 3–7, 30. [4] 施伟, 周强, 刘斌. 基于旋转永磁体的超低频机械天线电磁特性分析[J]. 物理学报, 2019, 68(18): 188401.SHI Wei, ZHOU Qiang, and LIU Bin. Performance analysis of spinning magnet as mechanical antenna[J]. Acta Physica Sinica, 2019, 68(18): 188401. [5] 周强, 姚富强, 施伟, 等. 机械式低频天线机理及其关键技术研究[J]. 中国科学: 技术科学, 2020, 50(1): 69–84. doi: 10.1360/SST-2019-0118ZHOU Qiang, YAO Fuqiang, SHI Wei, et al. Research on mechanism and key technology of mechanical antenna for a low-frequency transmission[J]. Scientia Sinica Technologica, 2020, 50(1): 69–84. doi: 10.1360/SST-2019-0118 [6] 崔岸婧, 李道京, 周凯, 等. 阵列结构下的低频信号合成方法研究[J]. 物理学报, 2020, 69(19): 194101. doi: 10.7498/aps.69.20200501CUI Anjing, LI Daojing, ZHOU Kai, et al. Research on the method of composing low frequency signals based on array structures[J]. Acta Physica Sinica, 2020, 69(19): 194101. doi: 10.7498/aps.69.20200501 [7] 王劲东, 薛洪波, 张艺腾, 等. 高精度航空地磁矢量测量技术[C]. 2018年中国地球科学联合学术年会论文集(二十八)——专题56: 煤炭资源与矿山地球物理、专题58: 地球物理探测方法与仪器新技术, 北京, 2018: 28, 44.WANG Jindong, XUE Hongbo, ZHANG Yiteng, et al. High precision airborne geomagnetic vector measurement technique[C]. Annual Meeting of Chinese Geoscience Union, Beijing, China, 2018: 28, 44. [8] HALLIDAY D, RESNICK R, and WALKER J. Fundamentals of Physics[M]. Weinheim: Wiley, 2014: 1135–1137. [9] 别业广. 电磁波的多普勒效应[J]. 物理与工程, 2003, 13(4): 62, 32.BIE Yeguang. The Doppler effect of electromagnetic waves[J]. Physics and Engineering, 2003, 13(4): 62, 32. [10] 高炳坤, 王凤林. 相对论多普勒效应的简易推导[J]. 大学物理, 2003, 22(8): 15–16.GAO Bingkun and WANG Fenglin. A concise deduction of relativistic Doppler effect[J]. College Physics, 2003, 22(8): 15–16. [11] 严欣达, 程先卿. 由相位不变性讨论光波的多普勒效应[J]. 大学物理, 1987, (11): 25.YAN Xinda and CHENG Xianqing. The Doppler effect of light wave is discussed from phase invariance[J]. College Physics, 1987, (11): 25. [12] 王景雪, 汤正新, 陈庆东, 等. 基于同时的相对性对钟慢尺缩效应的再认识[J]. 大学物理, 2009, 28(10): 24–27.WANG Jingxue, TANG Zhengxin, CHEN Qingdong, et al. Recognition on time dilation and length contraction effect based on relativity of simultaneity[J]. College Physics, 2009, 28(10): 24–27. [13] 张三慧. 时间膨胀与多普勒效应[J]. 大学物理, 1990, (9): 31–32.ZHANG Sanhui. Time dilation and Doppler effect[J]. College Physics, 1990, (9): 31–32. [14] 王建, 郑一农, 何子远. 阵列天线理论与工程应用[M]. 北京: 电子工业出版社, 2015: 8.WANG Jian, ZHENG Yinong, and HE Ziyuan. Antenna Array Theory and Engineering Applications[M]. Beijing: Publishing House of Electronics Industry, 2015: 8. [15] 丁鹭飞, 耿富录, 陈建春. 雷达原理[M]. 5版. 北京: 电子工业出版社, 2014: 253–254.DING Lufei, GENG Fulu, and CHEN Jianchun. Radar Principles[M]. 5th ed. Beijing: Publishing House of Electronics Industry, 2014: 253–254. [16] 吴翊, 朱炬波, 易东云, 等. 关于多普勒频率转换成距离变化率公式的讨论[J]. 中国空间科学技术, 1997, (6): 45–49.WU Yi, ZHU Jubo, YI Dongyun, et al. Discuss on formula of Doppler frequency to velocity[J]. Chinese Space Science and Technology, 1997, (6): 45–49. [17] 魏钟铨. 合成孔径雷达卫星[M]. 北京: 科学出版社, 2001: 204–206.WEI Zhongquan. Synthetic Aperture Radar Satellite[M]. Beijing: Science Press, 2001: 204–206. [18] 保铮, 邢孟道, 王彤. 雷达成像技术[M]. 北京: 电子工业出版社, 2005: 125–132.BAO Zheng, XING Mengdao, and WANG Tong. Radar Imaging Technology[M]. Beijing: Publishing House of Electronics Industry, 2005: 125–132. -
计量
- 文章访问数: 1640
- HTML全文浏览量: 660
- PDF下载量: 121
- 被引次数: 0
