Multi-temporal InSAR for Urban Deformation Monitoring: Progress and Challenges (in English)
DOI: 10.12000/JR20037 cstr: 32380.14.JR20037
-
Abstract:
Multi-temporal Interferometric Synthetic Aperture Radar (MT-InSAR) is one of the most powerful Earth observation techniques, especially useful for measuring highly detailed ground deformation over large ground areas. Much research has been carried out to apply MT-InSAR to monitor ground and infrastructure deformation in urban areas related to land reclamation, underground construction and groundwater extraction. This paper reviews the progress in the research and identifies challenges in applying the technology, including the inconsistency in coherent point identification when different approaches are used, the reliability issue in parameter estimation, difficulty in accurate geolocation of measured points, the one-dimensional line-of-sight nature of InSAR measurements, the inability of making complete measurements over an area due to geometric distortions, especially the shadowing effects, the challenges in processing large SAR datasets, the decrease of the number of coherent points with the increase of the length of SAR time series, and the difficulty in quality control of MT-InSAR results.
-
Key words:
- Urban deformation /
- Monitoring /
- Multi-temporal InSAR
-
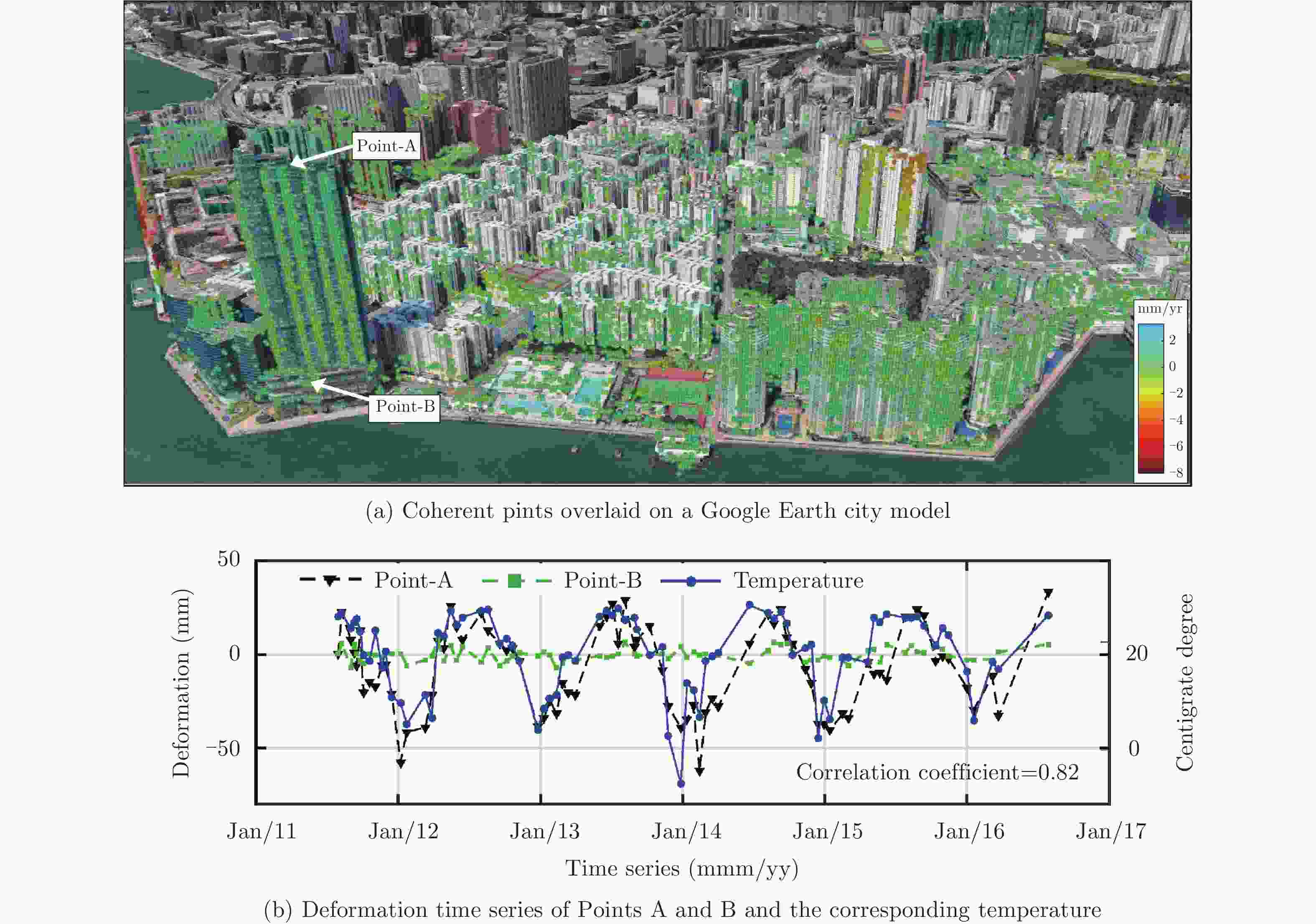
Figure 7. An example of deformation rates of the buildings[78]
Table 1. A sample of MT-InSAR approaches and their characteristics
MT-InSAR Method (references) Baseline configuration Observation
phaseTarget selection Solver Model
parametersPS-InSAR / Ferretti et al.
(2000, 2001)Single Master wrapped ADI Periodogram Δh, Δv SBAS / Berardino et al. (2002) Multi-Master unwrapped Coherence Least squares $ h $, $ v $ IPTA / Werner et al. (2003) Single/Multiple Master wrapped ADI Periodogram Δh, Δv Adaptive modelvan / Leijen (2007) Single Master wrapped ADI Integer least squares Δh, $ \rm AM $ StaMPS / Hooper (2004, 2008) Single/Multiple Master wrapped Phase stability 3-D phase unwrapping – STUN / Kampes (2005) Single Master wrapped ADI Integer least squares Δh, Δv CPT / Blanco-Sanchez et al. 2008 Single/Multiple Master wrapped Signal to clutter ratio Conjugate gradient method Δh, Δv PSP / Costantini et al.
(2008 & 2012)Single/Multiple Master wrapped ADI Minimum cost flow Δh, Δv TCP-InSAR / Zhang et al. (2011) Multi-Master wrapped Offset deviation Least squares with ambiguity detection Δh, Δv SqueeSAR / Ferretti et al. (2011) Single Master wrapped Homogeneity test Periodogram Δh, Δv QPS-InSAR / Perissin and
Wang (2012)Target-dependent interferogram subset wrapped Quasi-PS Periodogram Δh, Δv EMCF-SBAS / Pepe et al. (2015) Multi-Master wrapped Coherence Minimum cost flow Δh, Δv CSI / Dong et al. (2018) Multi-Master wrapped ADI & Homogeneity test 3-D phase unwrapping – *AM- Adaptive model; ADI-Amplitude Dispersion Index -
[1] PERISSIN D and WANG Teng. Time-series InSAR applications over urban areas in China[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2011, 4(1): 92–100. doi: 10.1109/JSTARS.2010.2046883 [2] NG AHM, WANG Hua, and DAI Yiwei, et al. InSAR reveals land deformation at Guangzhou and Foshan, China between 2011 and 2017 with COSMO-SkyMed data[J]. Remote Sensing, 2018, 10(6): 813. doi: 10.3390/rs10060813 [3] DING XL, LIU Guoxiang, and LI ZW, et al. Ground subsidence monitoring in Hong Kong with satellite SAR interferometry[J]. Photogrammetric Engineering & Remote Sensing, 2004, 70(10): 1151–1156. doi: 10.14358/PERS.70.10.1151 [4] JIANG Liming and LIN Hui. Integrated analysis of SAR interferometric and geological data for investigating long-term reclamation settlement of Chek Lap Kok Airport, Hong Kong[J]. Engineering Geology, 2010, 110(3/4): 77–92. doi: 10.1016/j.enggeo.2009.11.005 [5] BELL J W, AMELUNG F, and FERRETTI A, et al. Permanent scatterer InSAR reveals seasonal and long-term aquifer-system response to groundwater pumping and artificial recharge[J]. Water Resources Research, 2008, 44(2): W02407. doi: 10.1029/2007WR006152 [6] CHANG Ling. Monitoring civil infrastructure using satellite radar interferometry[D]. [Ph.D. dissertation], Delft University of Technology, 2015. [7] LIN Hui, MA Peifeng, and WANG Weixi. Urban infrastructure health monitoring with spaceborne multi-temporal synthetic aperture radar interferometry[J]. Acta Geodaetica et Cartographica Sinica, 2017, 46(10): 1421–1433. doi: 10.11947/j.AGCS.2017.20170339 [8] GABRIEL A K, GOLDSTEIN R M, and ZEBKER H A. Mapping small elevation changes over large areas: Differential radar interferometry[J]. Journal of Geophysical Research: Solid Earth, 1989, 94(B7): 9183–9191. doi: 10.1029/JB094iB07p09183 [9] BAMLER R and HARTL P. Synthetic aperture radar interferometry[J]. Inverse Problems, 1998, 14(4): R1–R54. doi: 10.1088/0266-5611/14/4/001 [10] MASSONNET D and FEIGL K L. Radar interferometry and its application to changes in the Earth’s surface[J]. Reviews of Geophysics, 1998, 36(4): 441–500. doi: 10.1029/97RG03139 [11] ROSEN P A, HENSLEY S, JOUGHIN I R, et al. Synthetic aperture radar interferometry[J]. Proceedings of the IEEE, 2000, 88(3): 333–382. doi: 10.1109/5.838084 [12] FERRETTI A, PRATI C, and ROCCA F. Nonlinear subsidence rate estimation using permanent scatterers in differential SAR interferometry[J]. IEEE Transactions on Geoscience and Remote Sensing, 2000, 38(5): 2202–2212. doi: 10.1109/36.868878 [13] FERRETTI A, PRATI C, and ROCCA F. Permanent scatterers in SAR interferometry[J]. IEEE Transactions on Geoscience and Remote Sensing, 2001, 39(1): 8–20. doi: 10.1109/36.898661 [14] COLESANTI C, FERRETTI A, PRATI C, et al. Monitoring landslides and tectonic motions with the Permanent Scatterers Technique[J]. Engineering Geology, 2003, 68(1/2): 3–14. doi: 10.1016/S0013-7952(02)00195-3 [15] YUE Huanyin, HANSSEN R, VAN LEIJEN F, et al. Land subsidence monitoring in city area by time series interferometric SAR data[C]. 2005 IEEE International Geoscience and Remote Sensing Symposium, Seoul, South Korea, 2005: 4590–4592. [16] HOOPER A J. Persistent scatter radar interferometry for crustal deformation studies and modeling of volcanic deformation[D]. [Ph.D. dissertation], Stanford University, 2006. [17] COLESANTI C and WASOWSKI J. Investigating landslides with space-borne Synthetic Aperture Radar (SAR) interferometry[J]. Engineering Geology, 2006, 88(3/4): 173–199. doi: 10.1016/j.enggeo.2006.09.013 [18] BIGGS J, WRIGHT T, LU Zhong, et al. Multi-interferogram method for measuring interseismic deformation: Denali Fault, Alaska[J]. Geophysical Journal International, 2007, 170(3): 1165–1179. doi: 10.1111/j.1365-246X.2007.03415 [19] STRAMONDO S, BOZZANO F, MARRA F, et al. Subsidence induced by urbanisation in the city of Rome detected by advanced InSAR technique and geotechnical investigations[J]. Remote Sensing of Environment, 2008, 112(6): 3160–3172. doi: 10.1016/j.rse.2008.03.008 [20] LIU Guoxiang, JIA Hongguo, ZHANG Rui, et al. Exploration of subsidence estimation by persistent scatterer InSAR on time series of high resolution TerraSAR-X images[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2011, 4(1): 159–170. doi: 10.1109/JSTARS.2010.2067446 [21] ZHANG Lei, DING Xiaoli, and LU Zhong. Ground settlement monitoring based on temporarily coherent points between two SAR acquisitions[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2011, 66(1): 146–152. doi: 10.1016/j.isprsjprs.2010.10.004 [22] ZHU Xiaoxiang and BAMLER R. Very high resolution spaceborne SAR tomography in urban environment[J]. IEEE Transactions on Geoscience and Remote Sensing, 2010, 48(12): 4296–4308. doi: 10.1109/TGRS.2010.2050487 [23] ZHU Xiaoxiang, MONTAZERI S, GISINGER C, et al. Geodetic SAR tomography[J]. IEEE Transactions on Geoscience and Remote Sensing, 2016, 54(1): 18–35. doi: 10.1109/TGRS.2015.2448686 [24] LIAO Mingsheng and LIN Hui. Synthetic Aperture Radar Interferometry——Principle and Signal Processing[M]. Beijing: Surveying and Mapping Press, 2003. [25] WANG Chao, ZHANG Hong, and LIU Zhi. Spaceborne Synthetic Aperture Radar Interferometry[M]. Beijing: Science Press, 2002. [26] BERARDINO P, FORNARO G, LANARI R, et al. A new algorithm for surface deformation monitoring based on small baseline differential SAR interferograms[J]. IEEE Transactions on Geoscience and Remote Sensing, 2002, 40(11): 2375–2383. doi: 10.1109/TGRS.2002.803792 [27] WERNER C, WEGMULLER U, STROZZI T, et al. Interferometric point target analysis for deformation mapping[C]. 2003 IEEE International Geoscience and Remote Sensing Symposium, Toulouse, France, 2003: 4362–4364. doi: 10.1109/IGARSS.2003.1295516. [28] KAMPES B M. Radar interferometry[D]. [Ph.D. dissertation], Delft University of Technology, 2006. [29] HOOPER A, ZEBKER H, SEGALL P, et al. A new method for measuring deformation on volcanoes and other natural terrains using InSAR persistent scatterers[J]. Geophysical Research Letters, 2004, 31(23): L23611. doi: 10.1029/2004GL021737 [30] FERRETTI A, FUMAGALLI A, NOVALI F, et al. A new algorithm for processing interferometric data-stacks: SqueeSAR[J]. IEEE Transactions on Geoscience and Remote Sensing, 2011, 49(9): 3460–3470. doi: 10.1109/TGRS.2011.2124465 [31] BLANCO-SÁNCHEZ P, MALLORQUÍ J J, DUQUE S, et al. The coherent pixels technique (CPT): An advanced DInSAR technique for nonlinear deformation monitoring[M]. CAMACHO A G, DÍAZ J I, and FERNÁNDEZ F. Earth Sciences and Mathematics. Basel: Birkhäuser Basel, 2008: 1167–1193. doi: 10.1007/978-3-7643-8907-9_10. [32] COSTANTINI M, FALCO S, MALVAROSA F, et al. Persistent scatterer pair interferometry: Approach and application to COSMO-SkyMed SAR data[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2014, 7(7): 2869–2879. doi: 10.1109/JSTARS.2014.2343915 [33] ZHANG Lei, LU Zhong, DING Xiaoli, et al. Mapping ground surface deformation using temporarily coherent point SAR interferometry: Application to Los Angeles Basin[J]. Remote Sensing of Environment, 2012, 117: 429–439. doi: 10.1016/j.rse.2011.10.020 [34] DONG Jie, ZHANG Lu, TANG Minggao, et al. Mapping landslide surface displacements with time series SAR interferometry by combining persistent and distributed scatterers: A case study of Jiaju landslide in Danba, China[J]. Remote Sensing of Environment, 2018, 205: 180–198. doi: 10.1016/j.rse.2017.11.022 [35] PEPE A, YANG Yang, MANZO M, et al. Improved EMCF-SBAS processing chain based on advanced techniques for the noise-filtering and selection of small baseline multi-look DInSAR interferograms[J]. IEEE Transactions on Geoscience and Remote Sensing, 2015, 53(8): 4394–4417. doi: 10.1109/TGRS.2015.2396875 [36] VAN LEIJEN F J and HANSSEN R F. Persistent scatterer density improvement using adaptive deformation models[C]. 2007 IEEE International Geoscience and Remote Sensing Symposium, Barcelona, Spain, 2007: 2102–2105. doi: 10.1109/IGARSS.2007.4423248. [37] CHANG Ling and HANSSEN R F. A probabilistic approach for InSAR time-series postprocessing[J]. IEEE Transactions on Geoscience and Remote Sensing, 2015, 54(1): 421–430. doi: 10.1109/TGRS.2015.2459037 [38] LI Tao, LIU Guoxiang, LIN Hui, et al. A hierarchical multi-temporal InSAR method for increasing the spatial density of deformation measurements[J]. Remote Sensing, 2014, 6(4): 3349–3368. doi: 10.3390/rs6043349 [39] GE Daqing. Research on the key techniques of SAR interferometry for regional land subsidence monitoring[D]. [Ph.D. dissertation], China University of Geosciences (Beijing), 2013. [40] JIANG Mi, DING Xiaoli, TIAN Xin, et al. A hybrid method for optimization of the adaptive Goldstein filter[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2014, 98: 29–43. doi: 10.1016/j.isprsjprs.2014.09.012 [41] FATTAHI H and AMELUNG F. InSAR uncertainty due to orbital errors[J]. Geophysical Journal International, 2014, 199(1): 549–560. doi: 10.1093/gji/ggu276 [42] MANCON S, GUARNIERI A M, TEBALDINI S, et al. Orbital error estimation through multi-squint analysis[C]. The 10th European Conference on Synthetic Aperture Radar, Berlin, Germany, 2014: 1–4. [43] ZHANG Lei, DING Xiaoli, LU Zhong, et al. A novel multitemporal InSAR model for joint estimation of deformation rates and orbital errors[J]. IEEE Transactions on Geoscience and Remote Sensing, 2014, 52(6): 3529–3540. doi: 10.1109/TGRS.2013.2273374 [44] YU Chen, LI Zhenhong, PENNA N T, et al. Generic atmospheric correction model for Interferometric Synthetic Aperture Radar observations[J]. Journal of Geophysical Research, 2018, 123(10): 9202–9222. doi: 10.1029/2017JB015305 [45] LI Zhiwei, CAO Yunmeng, WEI Jianchao, et al. Time-series InSAR ground deformation monitoring: Atmospheric delay modeling and estimating[J]. Earth-Science Reviews, 2019, 192: 258–284. doi: 10.1016/j.earscirev.2019.03.008 [46] GOMBA G, PARIZZI A, DE ZAN F, et al. Toward operational compensation of ionospheric effects in SAR interferograms: The split-spectrum method[J]. IEEE Transactions on Geoscience and Remote Sensing, 2015, 54(3): 1446–1461. doi: 10.1109/TGRS.2015.2481079 [47] ZHANG Bochen, DING Xiaoli, ZHU Wu, et al. Mitigating ionospheric artifacts in coseismic interferogram based on offset field derived from ALOS-PALSAR data[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2016, 9(7): 3050–3059. doi: 10.1109/JSTARS.2016.2533441 [48] ZHANG Bochen, WANG Chisheng, DING Xiaoli, et al. Correction of ionospheric artifacts in SAR data: Application to fault slip inversion of 2009 southern sumatra earthquake[J]. IEEE Geoscience and Remote Sensing Letters, 2018, 15(9): 1327–1331. doi: 10.1109/LGRS.2018.2844686 [49] SAMSONOV S, VAN DER KOOIJ M, and TIAMPO K. A simultaneous inversion for deformation rates and topographic errors of DInSAR data utilizing linear least square inversion technique[J]. Computers & Geosciences, 2011, 37(8): 1083–1091. doi: 10.1016/j.cageo.2011.01.007 [50] FATTAHI H and AMELUNG F. DEM error correction in InSAR time series[J]. IEEE Transactions on Geoscience and Remote Sensing, 2013, 51(7): 4249–4259. doi: 10.1109/TGRS.2012.2227761 [51] LIANG Hongyu, ZHANG Lei, LU Zhong, et al. Nonparametric estimation of DEM error in multitemporal InSAR[J]. IEEE Transactions on Geoscience and Remote Sensing, 2019, 67(12): 10004–10014. doi: 10.1109/TGRS.2019.2930802 [52] ZHANG Yonghong, WU Hong’an, KANG Yonghui, et al. Ground subsidence in the Beijing-Tianjin-Hebei region from 1992 to 2014 revealed by multiple sar stacks[J]. Remote Sensing, 2016, 8(8): 675. doi: 10.3390/rs8080675 [53] NG H M A, GE Linlin, LI Xiaojing, et al. Monitoring ground deformation in Beijing, China with persistent scatterer SAR interferometry[J]. Journal of Geodesy, 2012, 86(6): 375–392. doi: 10.1007/s00190-011-0525-4 [54] LYU Mingyuan, KE Yinghai, GUO Lin, et al. Change in regional land subsidence in Beijing after south-to-north water diversion project observed using satellite radar interferometry[J]. GIScience & Remote Sensing, 2020, 57(1): 140–156. doi: 10.1080/15481603.2019.1676973 [55] OSMANOĞLU B, DIXON T H, WDOWINSKI S, et al. Mexico City subsidence observed with persistent scatterer InSAR[J]. International Journal of Applied Earth Observation and Geoinformation, 2011, 13(1): 1–12. doi: 10.1016/j.jag.2010.05.009 [56] CIGNA F, TAPETE D, GARDUÑO-MONROY V H, et al. Wide-area InSAR survey of surface deformation in urban areas and geothermal fields in the eastern Trans-Mexican Volcanic Belt, Mexico[J]. Remote Sensing, 2019, 11(20): 2341. doi: 10.3390/rs11202341 [57] CASTELLAZZI P, MARTEL R, RIVERA A, et al. Groundwater depletion in Central Mexico: Use of GRACE and InSAR to support water resources management[J]. Water Resources Research, 2016, 52(8): 5985–6003. doi: 10.1002/2015WR018211 [58] SUN Qishi, JIANG Liming, JIANG Mi, et al. Monitoring coastal reclamation subsidence in Hong Kong with distributed scatterer interferometry[J]. Remote Sensing, 2018, 10(11): 1738. doi: 10.3390/rs10111738 [59] PEPE A, BONANO M, ZHAO Qing, et al. The use of C-/X-band time-gapped SAR data and geotechnical models for the study of Shanghai’s ocean-reclaimed lands through the SBAS-DInSAR technique[J]. Remote Sensing, 2016, 8(11): 911. doi: 10.3390/rs8110911 [60] ZHAO Qing, MA Guanyu, WANG Qiang, et al. Generation of long-term InSAR ground displacement time-series through a novel multi-sensor data merging technique: The case study of the Shanghai coastal area[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2019, 154: 10–27. doi: 10.1016/j.isprsjprs.2019.05.005 [61] XU Bing, FENG Guangcai, LI Zhiwei, et al. Coastal subsidence monitoring associated with land reclamation using the point target based SBAS-InSAR method: A case study of Shenzhen, China[J]. Remote Sensing, 2016, 8(8): 652. doi: 10.3390/rs8080652 [62] LIU Peng, CHEN Xiaofei, LI Zhenhong, et al. Resolving surface displacements in Shenzhen of China from time series InSAR[J]. Remote Sensing, 2018, 10(7): 1162. doi: 10.3390/rs10071162 [63] HU Bo, CHEN Junyu, and ZHANG Xingfu. Monitoring the land subsidence area in a coastal urban area with InSAR and GNSS[J]. Sensors, 2019, 19(14): 3181. doi: 10.3390/s19143181 [64] SHI Guoqiang, LIN Hui, BÜRGMANN R, et al. Early soil consolidation from magnetic extensometers and full resolution SAR interferometry over highly decorrelated reclaimed lands[J]. Remote Sensing of Environment, 2019, 231: 111231. doi: 10.1016/j.rse.2019.111231 [65] COSTANTINI M, FERRETTI A, MINATI F, et al. Analysis of surface deformations over the whole Italian territory by interferometric processing of ERS, Envisat and COSMO-SkyMed radar data[J]. Remote Sensing of Environment, 2017, 202: 250–275. doi: 10.1016/j.rse.2017.07.017 [66] FERRETTI A, COLOMBO D, FUMAGALLI A, et al. InSAR data for monitoring land subsidence: Time to think big[J]. Proceedings of the International Association of Hydrological Sciences, 2015, 372: 331–334. doi: 10.5194/piahs-372-331-2015 [67] NOVELLINO A, CIGNA F, BRAHMI M, et al. Assessing the feasibility of a national InSAR ground deformation map of Great Britain with Sentinel-1[J]. Geosciences, 2017, 7(2): 19. doi: 10.3390/geosciences7020019 [68] CHANG Ling, DOLLEVOET R P B J, and HANSSEN R F. Nationwide railway monitoring using satellite SAR interferometry[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2016, 10(2): 596–604. doi: 10.1109/JSTARS.2016.2584783 [69] GE Daqing, ZHANG Ling, LI Man, et al. Beijing subway tunnelings and high-speed railway subsidence monitoring with PSInSAR and TerraSAR-X data[C]. 2016 IEEE International Geoscience and Remote Sensing Symposium, Beijing, China, 2016: 6883–6886. doi: 10.1109/IGARSS.2016.7730796. [70] CHEN Wenfeng, GONG Huili, CHEN Beibei, et al. Spatiotemporal evolution of land subsidence around a subway using InSAR time-series and the entropy method[J]. GIScience & Remote Sensing, 2017, 54(1): 78–94. doi: 10.1080/15481603.2016.1257297 [71] WANG Huiqiang, FENG Guangcai, XU Bing, et al. Deriving spatio-temporal development of ground subsidence due to subway construction and operation in delta regions with PS-InSAR Data: A case study in Guangzhou, China[J]. Remote Sensing, 2017, 9(10): 1004. doi: 10.3390/rs9101004 [72] MILILLO P, GIARDINA G, DEJONG M J, et al. Multi-temporal InSAR structural damage assessment: The London crossrail case study[J]. Remote Sensing, 2018, 10(2): 287. doi: 10.3390/rs10020287 [73] COLOMBO D and TRE. Measuring deformation from space. InSAR as an operational tool for mining sector[C]. SASGI, 2013. [74] SHARMA J, EPPLER J, and BUSLER J. Urban infrastructure monitoring with a spatially adaptive multi-looking InSAR technique[C]. Fringe 2015, Frascati, Italy, 2015. [75] ZHU Mao, WAN Xiaoli, FEI Bigang, et al. Detection of building and infrastructure instabilities by automatic spatiotemporal analysis of satellite SAR interferometry measurements[J]. Remote Sensing, 2018, 10(11): 1816. doi: 10.3390/rs10111816 [76] YANG Kui, YAN Li, HUANG Guoman, et al. Monitoring building deformation with InSAR: Experiments and validation[J]. Sensors, 2016, 16(12): 2182. doi: 10.3390/s16122182 [77] CROSETTO M, MONSERRAT O, CUEVAS-GONZÁLEZ M, et al. Measuring thermal expansion using X-band persistent scatterer interferometry[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2015, 100: 84–91. doi: 10.1016/j.isprsjprs.2014.05.006 [78] WU Songbo, ZHANG Lei, DING Xiaoli, et al. Pixel-wise MTInSAR estimator for integration of coherent point selection and unwrapped phase vector recovery[J]. IEEE Transactions on Geoscience and Remote Sensing, 2018, 57(5): 2659–2668. doi: 10.1109/TGRS.2018.2876115 [79] CHEN Fulong, LIN Hui, LI Zhen, et al. Interaction between permafrost and infrastructure along the Qinghai-Tibet railway detected via jointly analysis of C- and L-band small baseline SAR interferometry[J]. Remote Sensing of Environment, 2012, 123: 532–540. doi: 10.1016/j.rse.2012.04.020 [80] QIN Xiaoqiong, ZHANG Lu, YANG Mengshi, et al. Mapping surface deformation and thermal dilation of arch bridges by structure-driven multi-temporal DInSAR analysis[J]. Remote Sensing of Environment, 2018, 216: 71–90. doi: 10.1016/j.rse.2018.06.032 [81] LIU Xianglei, WANG Peipei, LU Zhao, et al. Damage detection and analysis of urban bridges using terrestrial laser scanning (TLS), ground-based microwave interferometry, and permanent scatterer interferometry synthetic aperture radar (PS-InSAR)[J]. Remote Sensing, 2019, 11(5): 580. doi: 10.3390/rs11050580 [82] LU Zhong and DZURISIN D. InSAR Imaging of Aleutian Volcanoes[M]. Berlin, Heidelberg: Springer, 2014: 87–345. [83] PEPE A and LANARI R. On the extension of the minimum cost flow algorithm for phase unwrapping of multitemporal differential SAR interferograms[J]. IEEE Transactions on Geoscience and Remote Sensing, 2006, 44(9): 2374–2383. doi: 10.1109/TGRS.2006.873207 [84] JIANG Mi and GUARNIERI A M. Distributed scatterer interferometry with the refinement of spatiotemporal coherence[J]. IEEE Transactions on Geoscience and Remote Sensing, 2020: 1–11. doi: 10.1109/TGRS.2019.2960007 [85] ZHANG Yunjun, FATTAHI H, and AMELUNG F. Small baseline InSAR time series analysis: Unwrapping error correction and noise reduction[J]. Computers & Geosciences, 2019, 133: 104331. doi: 10.1016/j.cageo.2019.104331 [86] LAUKNES T R, ZEBKER H A, and LARSEN Y. InSAR deformation time series using an L1-norm small-baseline approach[J]. IEEE Transactions on Geoscience and Remote Sensing, 2010, 49(1): 536–546. doi: 10.1109/TGRS.2010.2051951 [87] COSTANTINI M. A novel phase unwrapping method based on network programming[J]. IEEE Transactions on Geoscience and Remote Sensing, 1998, 36(3): 813–821. doi: 10.1109/36.673674 [88] HOOPER A and ZEBKER H A. Phase unwrapping in three dimensions with application to InSAR time series[J]. Journal of the Optical Society of America A, 2007, 24(9): 2737–2747. doi: 10.1364/JOSAA.24.002737 [89] FORNARO G, PAUCIULLO A, and REALE D. A null-space method for the phase unwrapping of multitemporal SAR interferometric stacks[J]. IEEE Transactions on Geoscience and Remote Sensing, 2011, 49(6): 2323–2334. doi: 10.1109/TGRS.2010.2102767 [90] PEPE A, EUILLADES L D, MANUNTA M, et al. New advances of the extended minimum cost flow phase unwrapping algorithm for SBAS-DInSAR analysis at full spatial resolution[J]. IEEE Transactions on Geoscience and Remote Sensing, 2011, 49(10): 4062–4079. doi: 10.1109/TGRS.2011.2135371 [91] ZHANG Lei, JIA Hongguo, LU Zhong, et al. Minimizing height effects in MTInSAR for deformation detection over built areas[J]. IEEE Transactions on Geoscience and Remote Sensing, 2019, 57(11): 9167–9176. doi: 10.1109/TGRS.2019.2925115 [92] LUO Hui, LI Zhenhong, DONG Zhen, et al. A new baseline linear combination algorithm for generating urban digital elevation models with multitemporal InSAR observations[J]. IEEE Transactions on Geoscience and Remote Sensing, 2019, 58(2): 1120–1133. doi: 10.1109/TGRS.2019.2943919 [93] HUSSAIN E, HOOPER A, WRIGHT T J, et al. Interseismic strain accumulation across the central North Anatolian Fault from iteratively unwrapped InSAR measurements[J]. Journal of Geophysical Research: Solid Earth, 2016, 121(12): 9000–9019. doi: 10.1002/2016JB013108 [94] AGRAM P S and SIMONS M. A noise model for InSAR time series[J]. Journal of Geophysical Research: Solid Earth, 2015, 120(4): 2752–2771. doi: 10.1002/2014JB011271 [95] YANG Y, PEPE A, MANZO M, et al. A region-growing technique to improve multi-temporal DInSAR interferogram phase unwrapping performance[J]. Remote Sensing Letters, 2013, 4(10): 988–997. doi: 10.1080/2150704X.2013.826835 [96] MONTAZERI S, RODRÍGUEZ GONZÁLEZ F, and ZHU Xiaoxiang. Geocoding error correction for InSAR point clouds[J]. Remote Sensing, 2018, 10(10): 1523. doi: 10.3390/rs10101523 [97] DHEENATHAYALAN P, SMALL D, SCHUBERT A, et al. High-precision positioning of radar scatterers[J]. Journal of Geodesy, 2016, 90(5): 403–422. doi: 10.1007/s00190-015-0883-4 [98] DHEENATHAYALAN P, SMALL D, and HANSSEN R F. 3-D positioning and target association for medium-resolution SAR sensors[J]. IEEE Transactions on Geoscience and Remote Sensing, 2018, 56(11): 6841–6853. doi: 10.1109/TGRS.2018.2844108 [99] YANG Mengshi, LÓPEZ-DEKKER P, DHEENATHAYALAN P, et al. On the value of corner reflectors and surface models in InSAR precise point positioning[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2019, 158: 113–122. doi: 10.1016/j.isprsjprs.2019.10.006 [100] FATTAHI H and AMELUNG F. InSAR bias and uncertainty due to the systematic and stochastic tropospheric delay[J]. Journal of Geophysical Research, 2015, 120(12): 8758–8773. doi: 10.1002/2015JB012419 [101] BÄHR H. Orbital Effects in Spaceborne Synthetic Aperture Radar Interferometry[M]. Karlsruhe: KIT Scientific Publishing, 2013. [102] DU Yanan, ZHANG Lei, FENG Guangcai, et al. On the accuracy of topographic residuals retrieved by MTInSAR[J]. IEEE Transactions on Geoscience and Remote Sensing, 2017, 55(2): 1053–1065. doi: 10.1109/TGRS.2016.2618942 [103] LIU Hongyu, ZHANG Lei, LI Bofeng, et al. Impacts of systematic errors on topographic parameter estimation in multitemporal InSAR: A quantitative description[J]. IEEE Geoscience and Remote Sensing Letters, 2020. doi: 10.1109/LGRS.2020.2971758 [104] DAI Keren, LIU Guoxiang, LI Zhenhong, et al. Extracting vertical displacement rates in Shanghai (China) with multi-platform SAR images[J]. Remote Sensing, 2015, 7(8): 9542–9562. doi: 10.3390/rs70809542 [105] CHANG L and HANSSEN R F. Detection of permafrost sensitivity of the Qinghai-Tibet railway using satellite radar interferometry[J]. International Journal of Remote Sensing, 2015, 36(3): 691–700. doi: 10.1080/01431161.2014.999886 [106] HU J, LI Z W, DING X L, et al. Resolving three-dimensional surface displacements from InSAR measurements: A review[J]. Earth-Science Reviews, 2014, 133: 1–17. doi: 10.1016/j.earscirev.2014.02.005 [107] CHANG Ling and HANSSEN R F. Near real-time, semi-recursive, deformation monitoring of infrastructure using satellite radar interferometry[C]. 2012 IEEE International Geoscience and Remote Sensing Symposium, Munich, Germany, 2012: 1876–1879. doi: 10.1109/IGARSS.2012.6351141. [108] RABUS B T and GHUMAN P. Automated generation of near realtime, optimum accuracy movement products with Sentinel-1A IW data[C]. The FRINGE 15 Meeting in Frascati, Italy, 2015. [109] ANSARI H, DE ZAN F, and BAMLER R. Sequential estimator: Toward efficient InSAR time series analysis[J]. IEEE Transactions on Geoscience and Remote Sensing, 2017, 55(10): 5637–5652. doi: 10.1109/TGRS.2017.2711037 [110] MARINKOVIC P S, VAN LEIJEN F, and KETELAAR G, et al. Recursive data processing and data volume minimization for PS-InSAR[C]. 2005 IEEE International Geoscience and Remote Sensing Symposium, Seoul, South Korea, 2005: 2697–2700. [111] RUYT D R, EUILLADES P, and EUILLADES L, et al. Updating a DInSAR time series using a modified SBAS algorithm with an Incremental SVD: Preliminary results[C]. FRINGE 17 Meeting, Helsinki, Finland, 2017. [112] WU Songbo, DING Xiaoli, and ZHANG Bochen. Continuous monitoring the ground deformation by a step-by-step estimator in MTInSAR[C]. 2019 IEEE International Geoscience and Remote Sensing Symposium, Yokohama, Japan, 2019: 1994–1997. doi: 10.1109/IGARSS.2019.8898400. [113] PERISSIN D and WANG Teng. Repeat-pass SAR interferometry with partially coherent targets[J]. IEEE Transactions on Geoscience and Remote Sensing, 2012, 50(1): 271–280. doi: 10.1109/TGRS.2011.2160644 [114] MARINKOVIC P, KETELAAR G, VAN LEIJEN F, et al. InSAR quality control: Analysis of five years of corner reflector time series[C]. Fringe 2007 Workshop, Frascati, Italy, 2007: 30. [115] FERRETTI A, SAVIO G, BARZAGHI R, et al. Submillimeter accuracy of InSAR time series: Experimental validation[J]. IEEE Transactions on Geoscience and Remote Sensing, 2007, 45(5): 1142–1153. doi: 10.1109/TGRS.2007.894440 [116] ZHANG Lei, DING Xiaoli, and LU Zhong. Ground deformation mapping by fusion of multi-temporal interferometric synthetic aperture radar images: A review[J]. International Journal of Image and Data Fusion, 2015, 6(4): 289–313. doi: 10.1080/19479832.2015.1068874 -



 作者中心
作者中心 专家审稿
专家审稿 责编办公
责编办公 编辑办公
编辑办公
 下载:
下载: